Effects of Aluminum/Carbon and Morphology on Optical Characteristics and Radiative Forcing of Alumina Clusters Emitted by Solid Rockets in the Stratosphere
Abstract
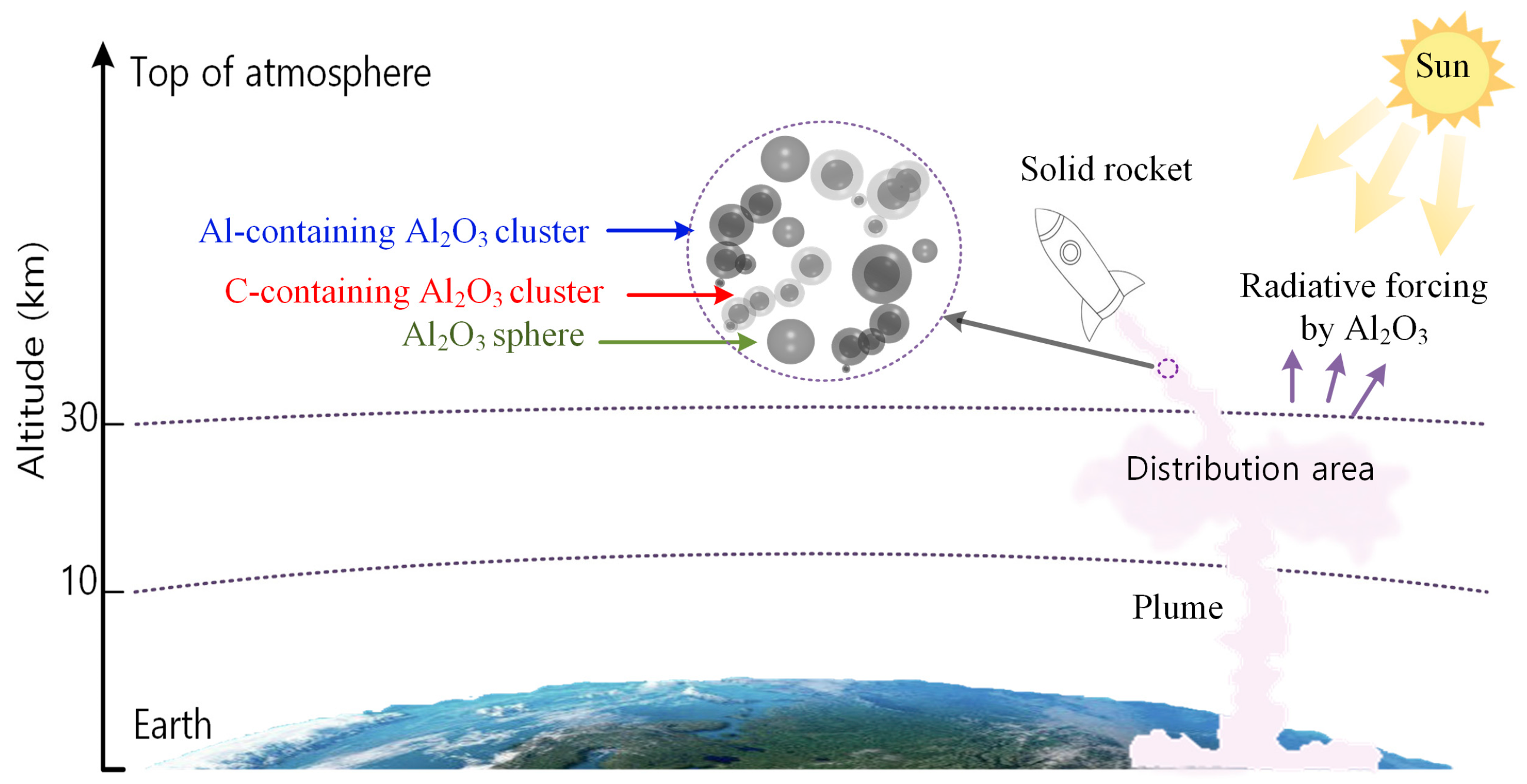
1. Introduction
2. Materials and Methods
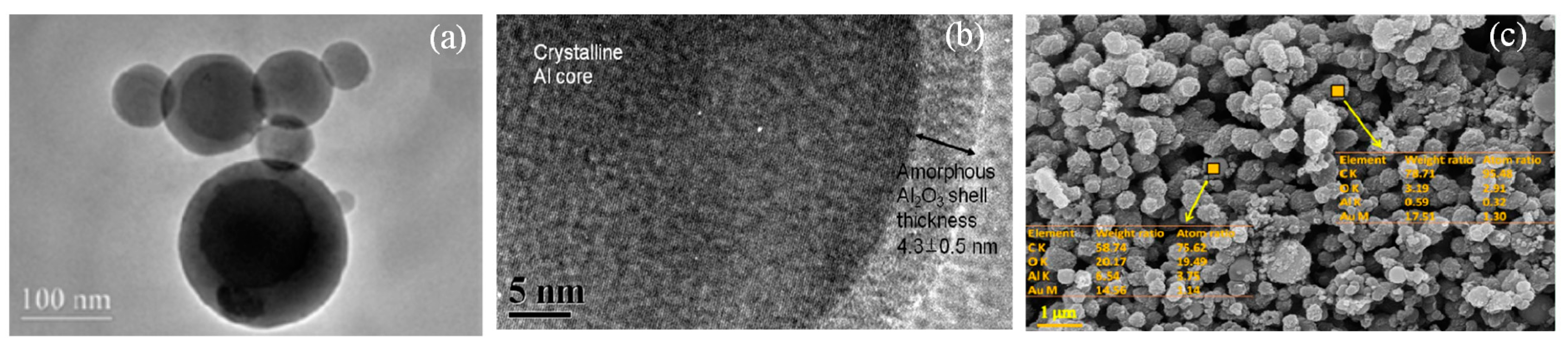
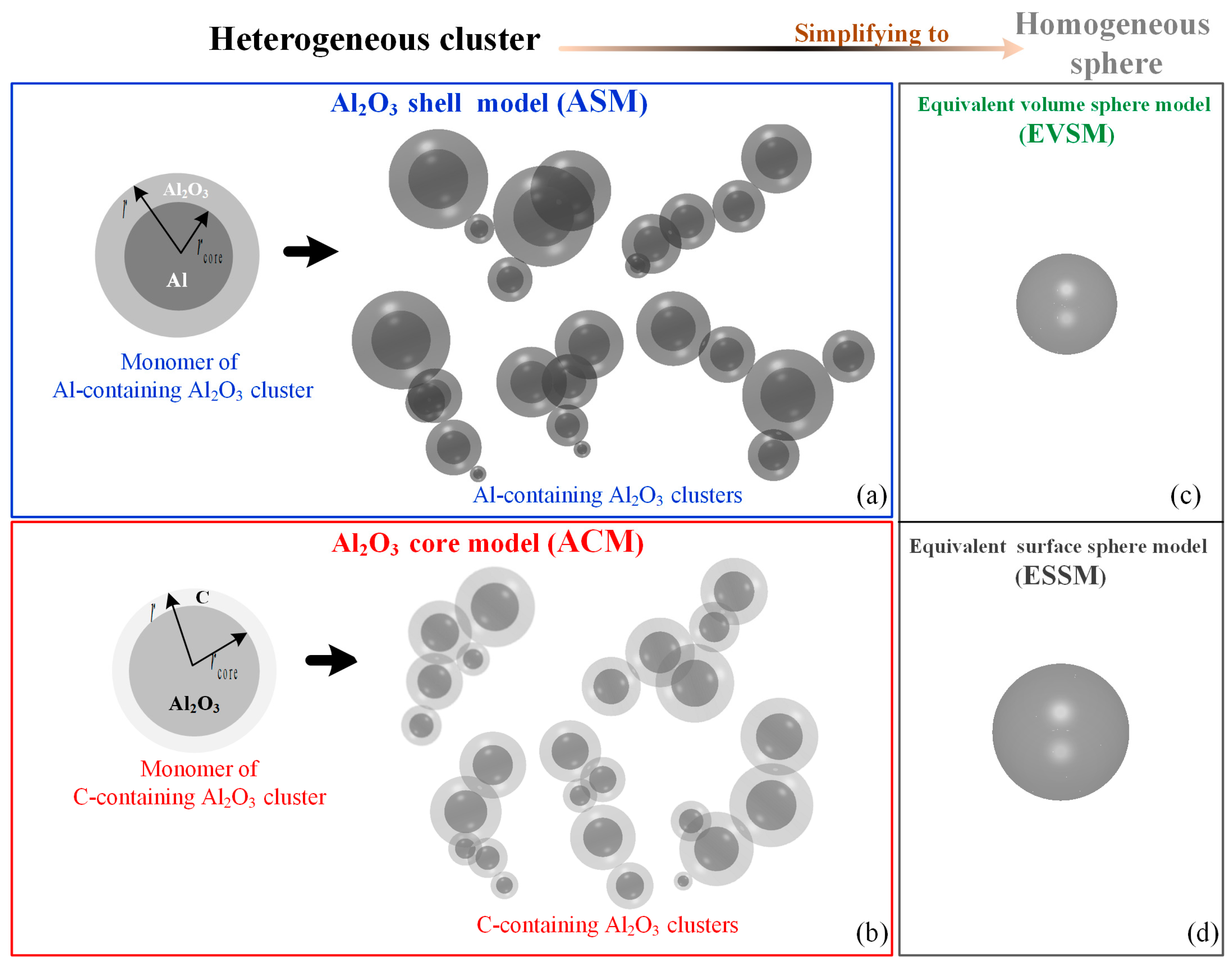
2.1. Models of Al-Containing and C-Containing Al2O3 Clusters
2.1.1. Monomers of Al-Containing and C-Containing Al2O3 Cluster
2.1.2. Al-Containing and C-Containing Al2O3 Cluster Models
2.1.3. Methods of Simplifying Cluster to Sphere
2.2. STMM
2.3. Mass Burden and Accumulation Area of Al2O3 Particles in the Stratosphere
2.3.1. Mass Burden
2.3.2. Accumulation Aera
2.4. Radiative Forcing
2.4.1. The Method for Radiative Forcing by Impurity-Containing Al2O3 Clusters
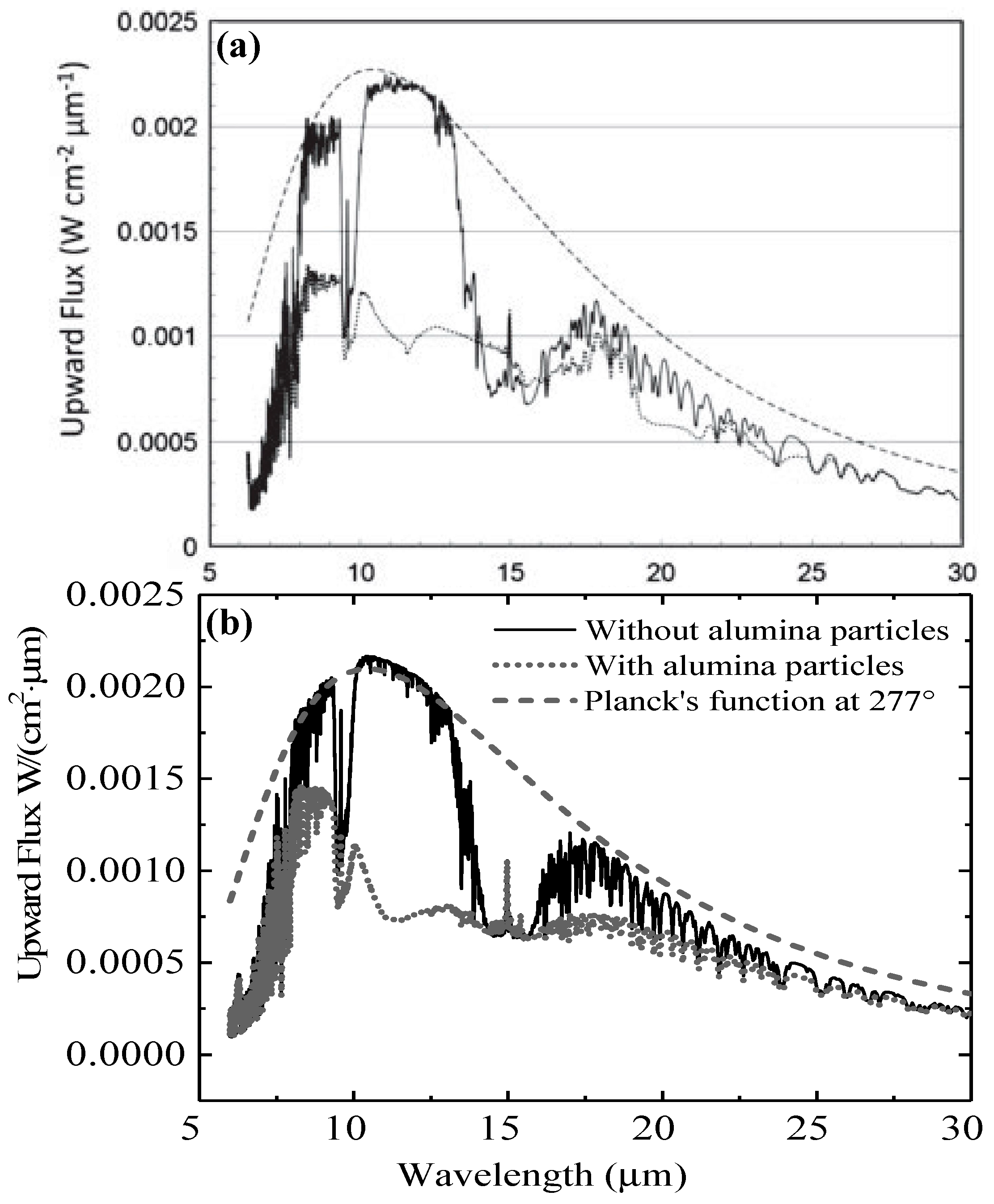
2.4.2. Validation of the Method
3. Results and Discussion
3.1. Optical Characteristics
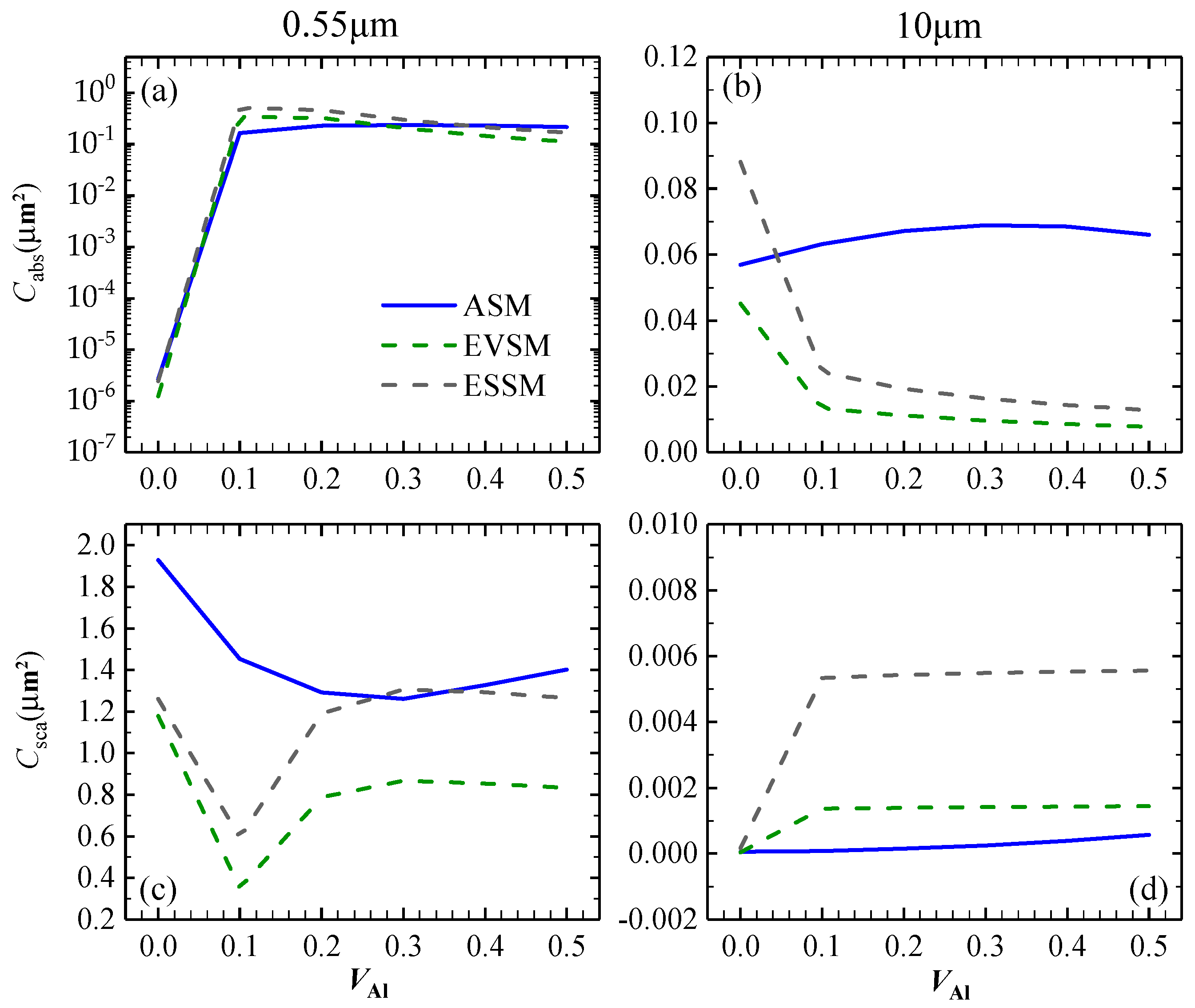
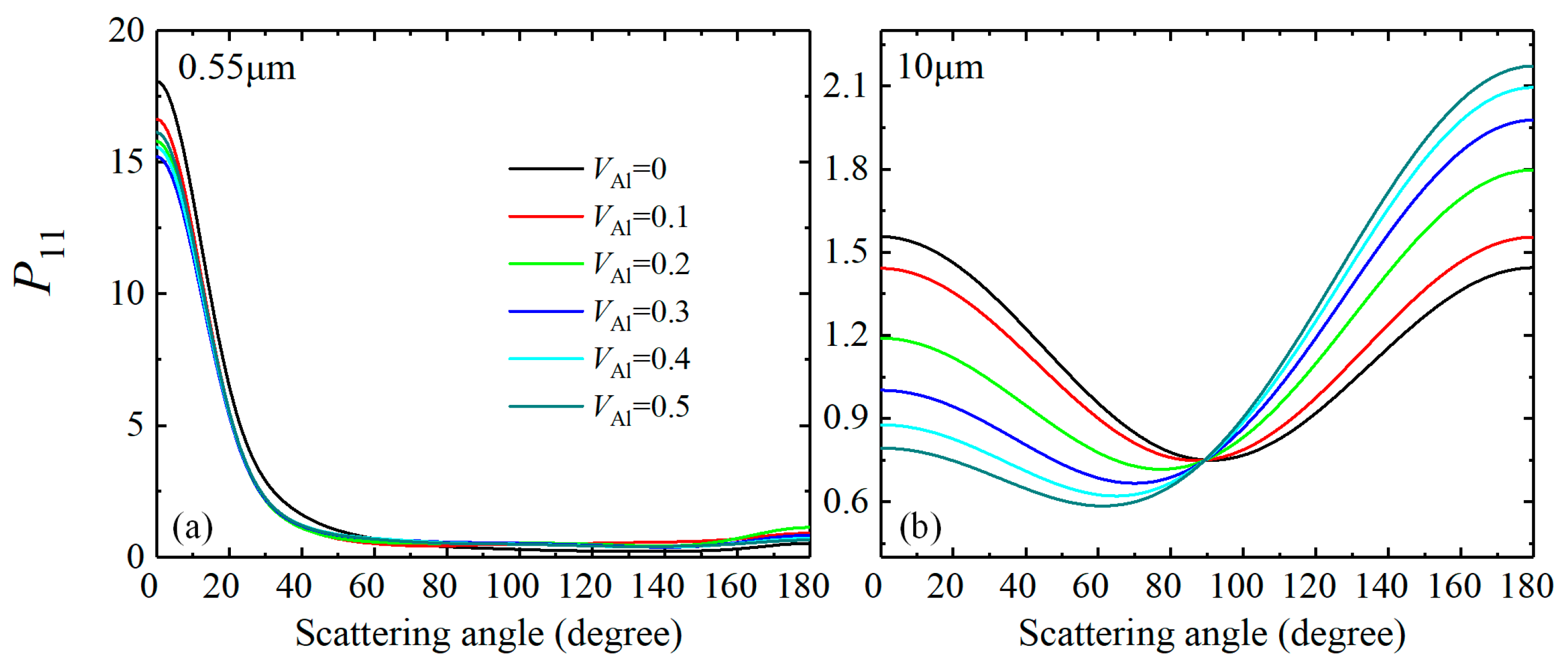
3.1.1. Optical Characteristics of Al-containing Al2O3 Clusters
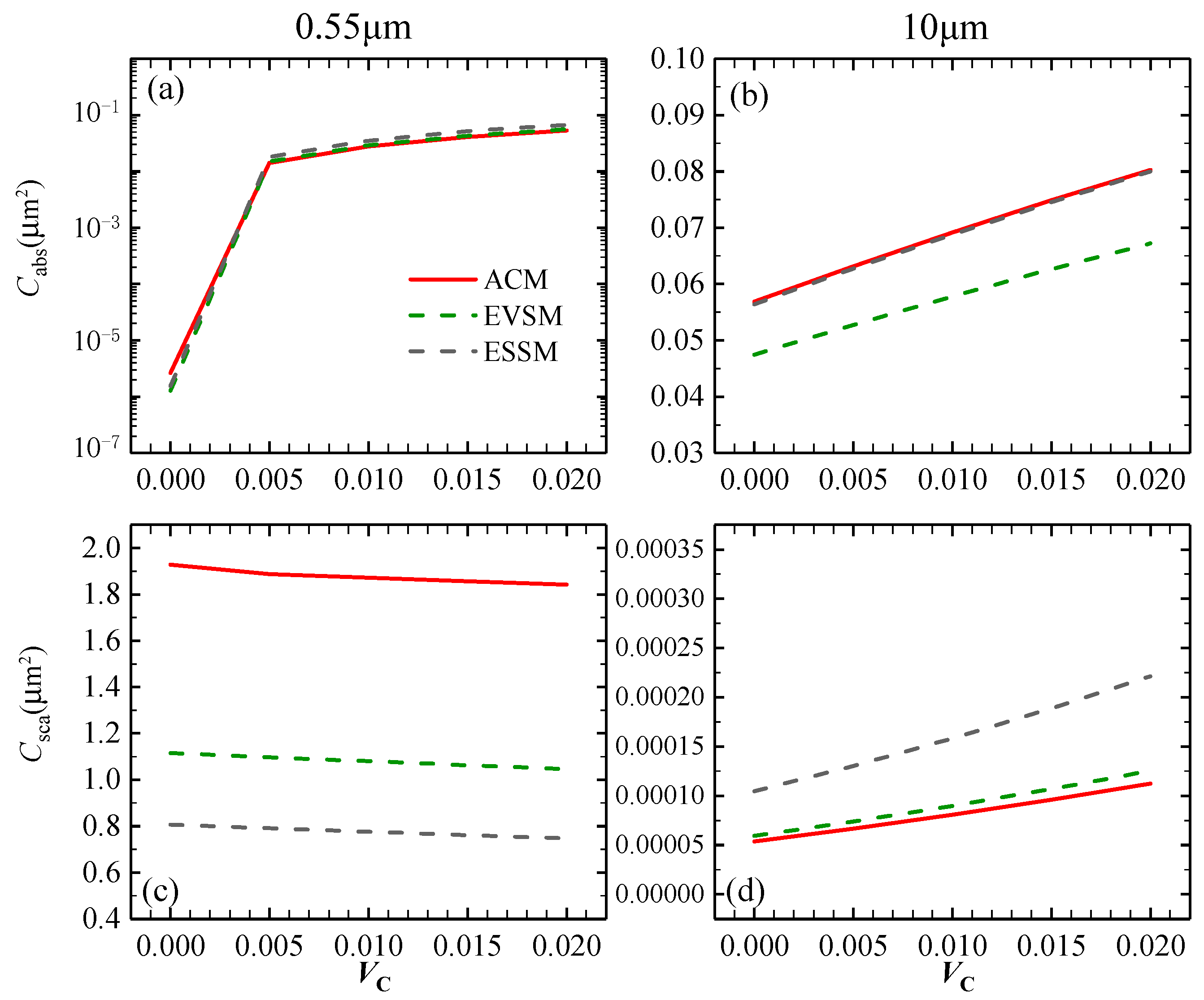
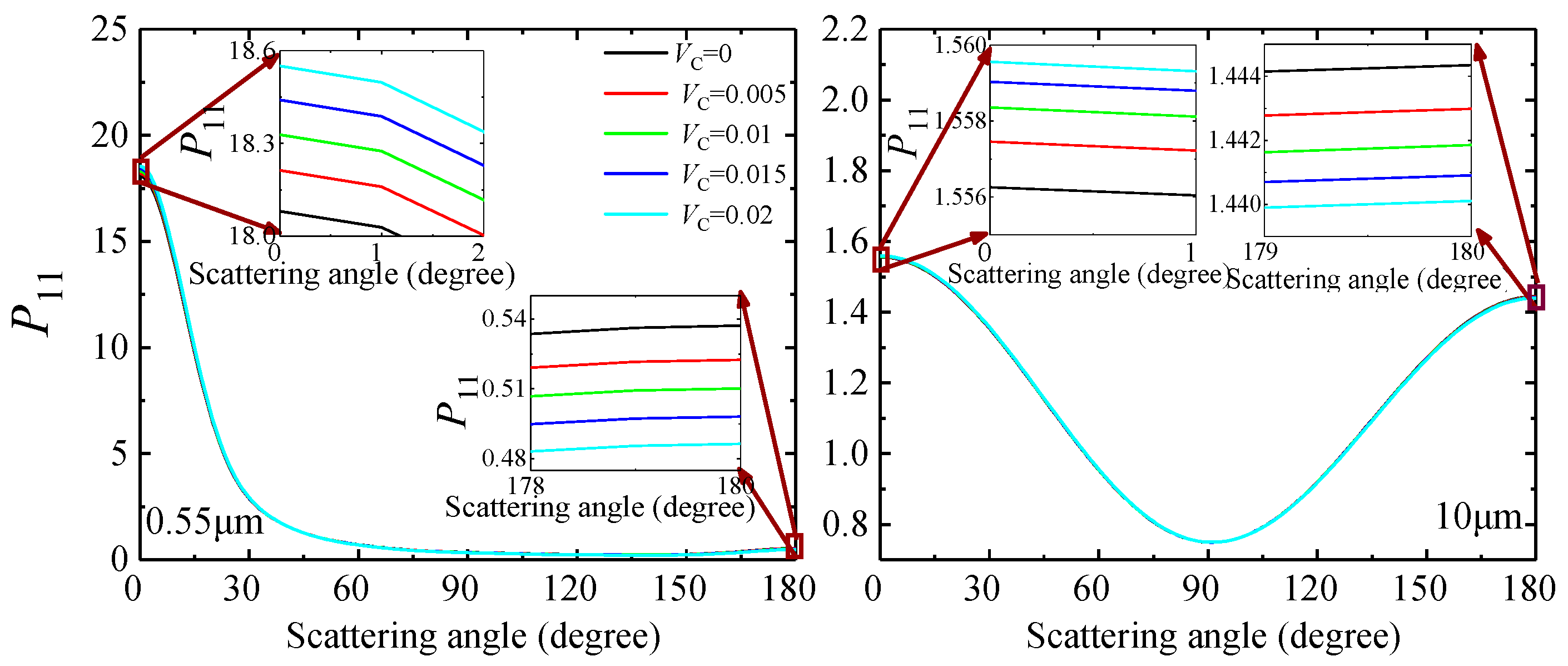
3.1.2. Optical Characteristics of C-Containing Al2O3 Clusters
3.2. Radiative Forcing
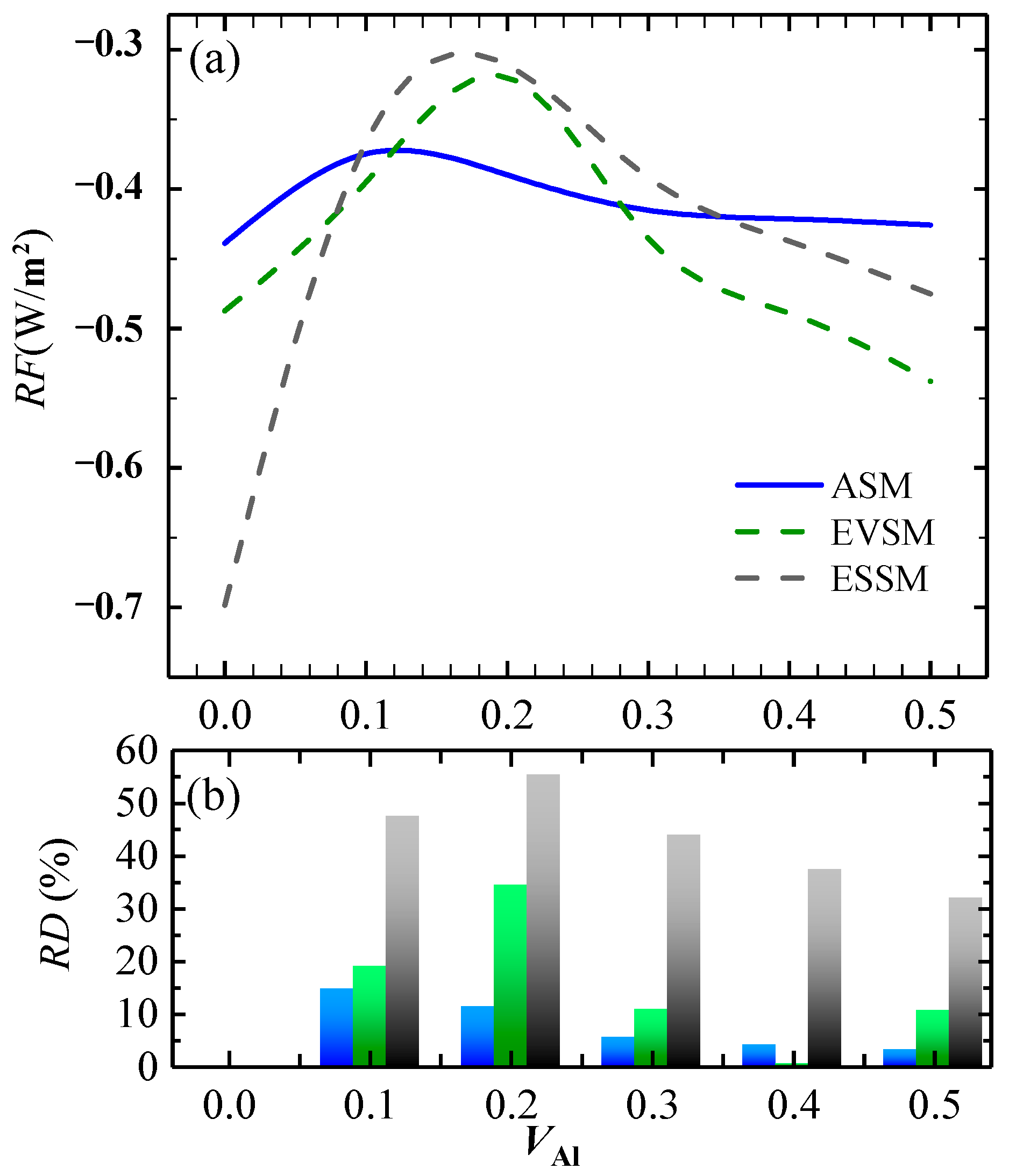
3.2.1. Radiative Forcing of Al-Containing Al2O3 Clusters
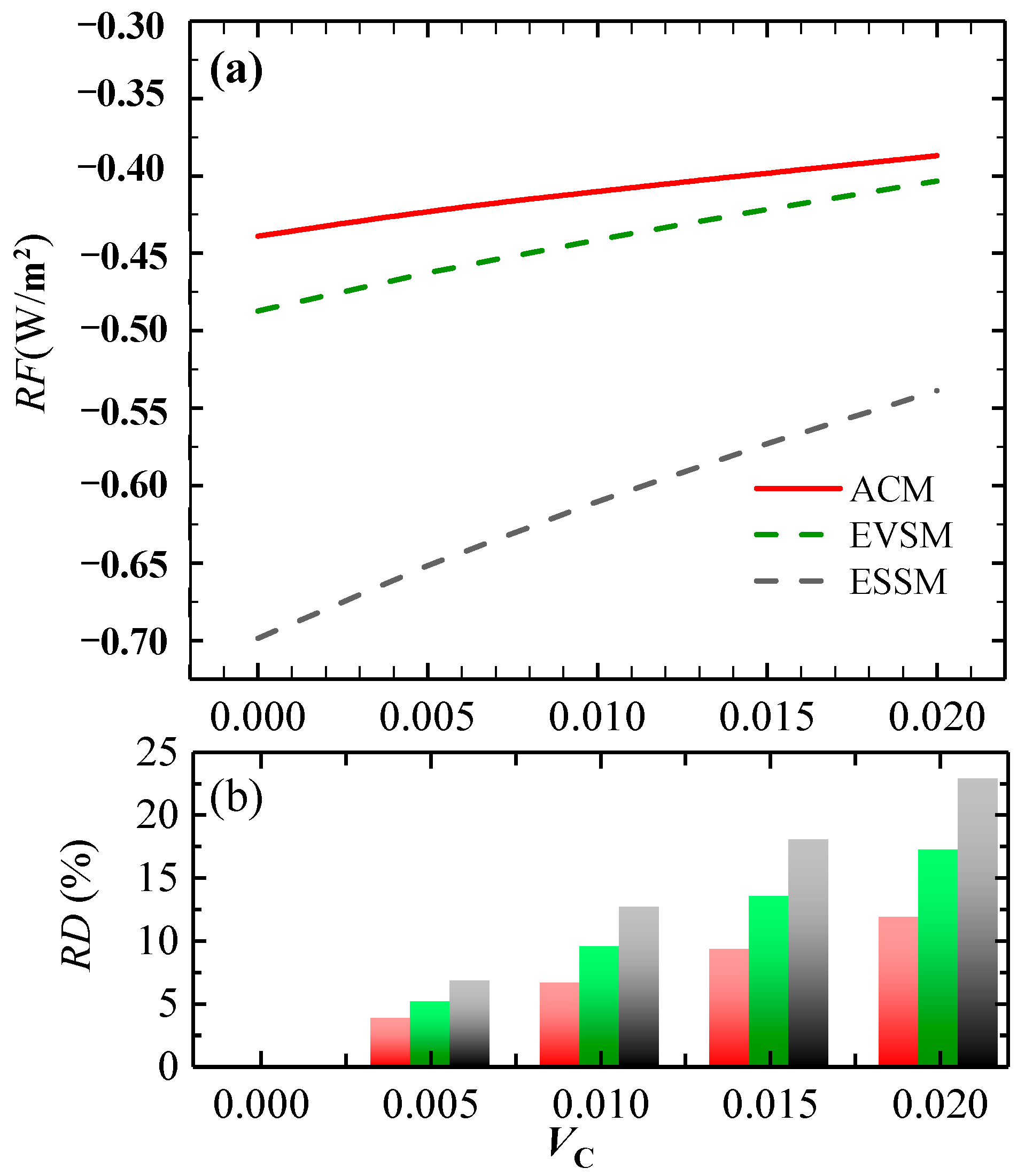
3.2.2. Radiative Forcing of C-Containing Al2O3 Clusters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gisler, M.; Sornette, D. Exuberant Innovations: The Apollo Program. Society 2008, 46, 55–68. [Google Scholar] [CrossRef]
- Hammel, H.B.; Gardner, J.P. The James Webb Space Telescope. In Proceedings of the AU XXVI General Assembly, Baltimore, MD, USA, 22–26 May 2006. [Google Scholar] [CrossRef]
- Shirley, D.L.; Mccleese, D.J. Mars Exploration Program Strategy: 1995-2020. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996. [Google Scholar] [CrossRef]
- Vago, J.; Witasse, O.; Svedhem, H.; Baglioni, P.; Haldemann, A.; Gianfiglio, G.; Blancquaert, T.; Mccoy, D.; Groot, R.D. ESA ExoMars program: The next step in exploring Mars. Solar Syst. Res. 2015, 49, 518–528. [Google Scholar] [CrossRef]
- Collaboration, G.; Prusti, T.; de Bruijne, J.H.J. The Gaia mission. Astron. Astrophys. 2016, A1, 1–36. [Google Scholar] [CrossRef]
- Denis, G.; Alary, D.; Pasco, X.; Toulza, S. From new space to big space:How commercial space dream is becoming a reality. Acta Astronaut. 2019, 166, 431–443. [Google Scholar] [CrossRef]
- Kremser, S.; Thomason, L.W.; Marc, H.V.; Hermann, M. Stratospheric aerosol-Observations, processes, and impact on climate. Rev. Geophys. 2016, 54, 278–335. [Google Scholar] [CrossRef]
- Miraux, L. Environmental limits to the space sector’s growth. Sci. Total Environ. 2022, 806, 150862. [Google Scholar] [CrossRef] [PubMed]
- Leckey, J.P.; Damadeo, R.; Hill, C.A. Stratospheric Aerosol and Gas Experiment (SAGE) from SAGE III on the ISS to a free flying SAGE IV cubesat. Remote Sens. 2021, 13, 4664. [Google Scholar] [CrossRef]
- Voudouri, K.A.; Michailidis, K.; Koukouli, M.-E.; Rémy, S.; Inness, A.; Taha, G.; Peletidou, G.; Siomos, N.; Balis, D.; Parrington, M. Investigating a Persistent Stratospheric Aerosol Layer Observed over Southern Europe during 2019. Remote Sens. 2023, 15, 5394. [Google Scholar] [CrossRef]
- Kim, H.O.; Laredo, D.; Netzer, D.W. Measurement of submicrometer Al2O3 particles in plumes. Appl. Opt. 1993, 32, 6834–6840. [Google Scholar] [CrossRef]
- Waugh, D.W.; Hall, T.M. Age of Stratospheric Air: Theory, Observations, and Models. Rev. Geophys. 2002, 40, 1–26. [Google Scholar] [CrossRef]
- Danilin, M.Y.; Shia, R.L.; Ko, M.K.W.; Weisenstein, D.K.; Sze, N.D.; Lamb, J.J.; Smith, T.W.; Lohn, P.D.; Prather, M.J. Global stratospheric effects of the alumina emissions by solid-fueled rocket motors. J. Geophys. Res.-Atmos. 2001, 106, 12727–12738. [Google Scholar] [CrossRef]
- Kloss, C.; Sellitto, P.; Renard, J.B.; Baron, A.; Bègue, N.; Legras, B.; Berthet, G.; Briaud, E.; Carboni, E.; Duchamp, C. Aerosol characterization of the stratospheric plume from the volcanic eruption at Hunga Tonga 15 January 2022. Geophys. Res. Lett. 2022, 49, e2022GL099394. [Google Scholar] [CrossRef]
- Sun, Q.; Lu, T.; Li, D.; Xu, J. The Impact of the Hunga Tonga–Hunga Ha’apai Volcanic Eruption on the Stratospheric Environment. Atmosphere 2024, 15, 483. [Google Scholar] [CrossRef]
- Vernier, J.P.; Fairlie, T.D.; Deshler, T.; Natarajan, M.; Knepp, T.; Foster, K.; Wienhold, F.G.; Bedka, K.M.; Thomason, L.; Trepte, C. In situ and space-based observations of the Kelud volcanic plume: The persistence of ash in the lower stratosphere. J. Geophys. Res.-Atmos. 2016, 121, 11, 104–111, 118. [Google Scholar] [CrossRef]
- Renard, J.-B.; Berthet, G.; Levasseur-Regourd, A.-C.; Beresnev, S.; Miffre, A.; Rairoux, P.; Vignelles, D.; Jégou, F. Origins and spatial distribution of non-pure sulfate particles (Nsps) in the stratosphere detected by the balloon-borne light optical aerosols counter (loac). Atmosphere 2020, 11, 1031. [Google Scholar] [CrossRef]
- Antuña-Marrero, J.-C.; Mann, G.W.; Barnes, J.; Calle, A.; Dhomse, S.S.; Cachorro, V.E.; Deshler, T.; Li, Z.; Sharma, N.; Elterman, L. The Recovery and Re-Calibration of a 13-Month Aerosol Extinction Profiles Dataset from Searchlight Observations from New Mexico, after the 1963 Agung Eruption. Atmosphere 2024, 15, 635. [Google Scholar] [CrossRef]
- Lysien, K.; Lysien, K.; Stolarczyk, A.; Stolarczyk, A.; Jarosz, T.; Jarosz, T. Solid Propellant Formulations: A Review of Recent Progress and Utilized Components. Materials 2021, 14, 6657. [Google Scholar] [CrossRef] [PubMed]
- Pradon, C.V.; Eastham, S.D.; Chossière, G.; Sabnis, J.; Speth, R.L.; Barrett, S.R.; André Jooste, J. Global Three-Dimensional Emission Inventory for Launch Vehicles from 2009 to 2018. J. Spacecraft. Rocket. 2023, 60, 716–727. [Google Scholar] [CrossRef]
- Ross, M.N.; Sheaffer, P.M. Radiative forcing caused by rocket engine emissions. Earth’s Future 2014, 2, 177–196. [Google Scholar] [CrossRef]
- Weisenstein, D.K.; Keith, D.W.; Dykema, J.A. Solar geoengineering using solid aerosol in the stratosphere. Atmos. Chem. Phys. 2015, 15, 11835–11859. [Google Scholar] [CrossRef]
- Jeenu, R.; Pinumalla, K.; Deepak, D. Size Distribution of Particles in Combustion Products of Aluminized Composite Propellant. J. Propul. Power 2012, 26, 715–723. [Google Scholar] [CrossRef]
- Firmansyah, D.A.; Sullivan, K.; Lee, K.S.; Kim, Y.H.; Zahaf, R.; Zachariah, M.R.; Lee, D. Microstructural Behavior of the Alumina Shell and Aluminum Core Before and After Melting of Aluminum Nanoparticles. J. Phys. Chem. 2011, 116, 404–411. [Google Scholar] [CrossRef]
- Reed, R.A.; Calia, V.S. Review of aluminum oxide rocket exhaust particles. In Proceedings of the AIAA 28th Thermaophysics Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar] [CrossRef]
- Pluchino, A.B.; Masturzo, D.E. Emissivity of Al2O3 particles in a rocket plume. AIAA 1981, 19, 1234–1237. [Google Scholar] [CrossRef]
- Ao, W.; Liu, P.; Yang, W. Agglomerates, smoke oxide particles, and carbon inclusions in condensed combustion products of an aluminized GAP-based propellant. Acta Astronaut. 2016, 129, 147–153. [Google Scholar] [CrossRef]
- Simmons, F.S. Rocket Exhaust Plume Phenomenology; Aerospace Press: El Segundo, CA, USA, 2000. [Google Scholar]
- Raki Aleksandar, D. Algorithm for the determination of intrinsic optical constants of metal films: Application to aluminum. AO 1995, 34, 4755–4767. [Google Scholar] [CrossRef]
- Fuquan, L.; Chen, S.; Zeyong, H.; Han, Z.; Khan, A.; Hongyu, L.; Hongru, B.; Junyan, C.; Xinyang, G. Sensitivity and uncertainties assessment in radiative forcing due to aerosol optical properties in diverse locations in China. Sci. Total Environ. 2023, 860, 160477. [Google Scholar] [CrossRef]
- Pluchino, A.B.; Masturzo, D.E. Emissivity spectra of composite microscopic particles. AIAA 1981, 19, 531–533. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Lu, B.; Li, J.; Li, J.; Gao, P. Effects of phase transformation on the ultraviolet optical properties of alumina clusters in aircraft plumes. OE 2020, 28, 25606–25617. [Google Scholar] [CrossRef]
- Sundaram, D.; Yang, V.; Yetter, R.A. Metal-based nanoenergetic materials: Synthesis, properties, and applications. Prog. Energ. Combust. 2017, 61, 293–365. [Google Scholar] [CrossRef]
- Skorupski, K.; Mroczka, J.; Wriedt, T.; Riefler, N. A fast and accurate implementation of tunable algorithms used for generation of fractal-like aggregate models. Phys. A 2014, 404, 106–117. [Google Scholar] [CrossRef]
- Braga, F.L.; Ribeiro, M.S. Diffusion Limited Aggregation: Algorithm optimization revisited. Comput. Phys. Commun. 2011, 182, 1602–1605. [Google Scholar] [CrossRef]
- Li, J.; Bai, L.; Wu, Z.; Guo, L.; Gong, Y. Scattering Properties of Alumina Particle Clusters with Different Radius of Monomers in Aerocraft Plume. J. Quant. Spectrosc. Radiat. Transf. 2017, 202, 233–239. [Google Scholar] [CrossRef]
- Garnett, J. Colors in metal glasses and in metallic films. Phil. Trans. Roy. Soc. Lond. A 1904, 203, 385–420. [Google Scholar]
- Mishchenko, M.I. Comprehensive thematic T-matrix reference database: A 2017–2019 update. J. Quant. Spectrosc. Radiat. Transf. 2020, 242, 106692. [Google Scholar] [CrossRef]
- Liu, L.; Mishchenko, M.l. Scattering and Radiative Properties of Morphologically Complex Carbonaceous Aerosols: A Systematic Modeling Study. Remote Sens. 2018, 10, 1634. [Google Scholar] [CrossRef]
- Mackowski, D.W. A general superposition solution for electromagnetic scattering by multiple spherical domains of optically active media. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 264–270. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University: Cambridge, UK, 2002. [Google Scholar]
- Mackowski, D.W.; Mishchenko, M.I. A multiple sphere T-matrix Fortran code for use on parallel computer clusters. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2182–2192. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, T.; Zheng, L.; Chen, H. Models for the optical simulations of fractal aggregated soot particles thinly coated with non-absorbing aerosols. J. Quant. Spectrosc. Radiat. Transf. 2016, 182, 1–11. [Google Scholar] [CrossRef]
- Dong, J.; Zhao, J.M.; Liu, L.H. Morphological effects on the radiative properties of soot aerosols in different internally mixing states with sulfate. J. Quant. Spectrosc. Radiat. Transf. 2015, 165, 43–55. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; Yin, Y.; Zhu, B.; Feng, Q. Optical properties of black carbon aggregates with non-absorptive coating. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 443–452. [Google Scholar] [CrossRef]
- Lee Bray, E. 2018 Minerals Yearbook: Bauxite and Alumina; (United States Geological Survey, USGS), U.S.G.S., Ed.; National Minerals Information Center: Washington, DC, USA, 2018.
- Anderson, G.P.; Berk, A.; Acharya, P.K.; Matthew, M.W.; Hoke, M.L. MODTRAN4 version 2: Radiative transfer modeling. In Proceedings of the SPIE the International Society for Optical Engineering, Orlando, FL, USA, 16-20 April 2001; pp. 455–459. [Google Scholar] [CrossRef]
- Jin, Z.; Long, Z.; Wang, S.; Liu, Y. Performance of the Atmospheric Radiative Transfer Simulator (ARTS) in the 600–1650 cm−1 Region. Remote Sens. 2023, 15, 4889. [Google Scholar] [CrossRef]
- Calì Quaglia, F.; Meloni, D.; Muscari, G.; Di Iorio, T.; Ciardini, V.; Pace, G.; Becagli, S.; Di Bernardino, A.; Cacciani, M.; Hannigan, J.W. On the Radiative Impact of Biomass-Burning Aerosols in the Arctic: The August 2017 Case Study. Remote Sens. 2022, 14, 313. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover Publications: New York, UK, 1950. [Google Scholar]
- Begemann, B.; Dorschner, J.; Henning, T. Aluminum Oxide and the Opacity of Oxygen-rich Circumstellar Dust in the 12–17 Micron Range. Astrophys. J. 1997, 476, 199–208. [Google Scholar] [CrossRef]
- Markowicz, K.M.; Chilinski, M.T.; Lisok, J.; Zawadzka, O.; Stachlewska, I.S.; Janicka, L.; Rozwadowska, A.; Makuch, P.; Pakszys, P.; Zielinski, T. Study of aerosol optical properties during long-range transport of biomass burning from Canada to Central Europe in July 2013. J. Aerosol. Sci. 2016, 101, 156–173. [Google Scholar] [CrossRef]
- Danilin, M.Y.; Ko, M.K.W.; Weisenstein, D.K. Global implications of ozone loss in a space shuttle wake. J. Geophys. Res.-Atmos. 2001, 106, 3591–3601. [Google Scholar] [CrossRef]
- Frol’Kis, V.A.; Kokorin, A.M. The Influence of the Internal Structure of Particles on Optical Properties of Stratospheric Aerosol, Radiative Forcing, and Global Annual Average Temperature. Atmos. Ocean. Opt. 2019, 32, 306–315. [Google Scholar] [CrossRef]
| Wavelength (μm) | 0.55 | 10 | |
|---|---|---|---|
| Refractive | Al2O3 | 1.77 + 1.65 × 10−7i | 0.994 + 0.28i |
| Al | 1.015 + 6.63i | 25 + 85.96i | |
| C | 1.917 + 0.41i | 3.67 + 3.03i | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Bai, L.; Bai, J.; Guo, L. Effects of Aluminum/Carbon and Morphology on Optical Characteristics and Radiative Forcing of Alumina Clusters Emitted by Solid Rockets in the Stratosphere. Atmosphere 2024, 15, 812. https://doi.org/10.3390/atmos15070812
Xu Y, Bai L, Bai J, Guo L. Effects of Aluminum/Carbon and Morphology on Optical Characteristics and Radiative Forcing of Alumina Clusters Emitted by Solid Rockets in the Stratosphere. Atmosphere. 2024; 15(7):812. https://doi.org/10.3390/atmos15070812
Chicago/Turabian StyleXu, Yueyuan, Lu Bai, Jingyu Bai, and Lixin Guo. 2024. "Effects of Aluminum/Carbon and Morphology on Optical Characteristics and Radiative Forcing of Alumina Clusters Emitted by Solid Rockets in the Stratosphere" Atmosphere 15, no. 7: 812. https://doi.org/10.3390/atmos15070812
APA StyleXu, Y., Bai, L., Bai, J., & Guo, L. (2024). Effects of Aluminum/Carbon and Morphology on Optical Characteristics and Radiative Forcing of Alumina Clusters Emitted by Solid Rockets in the Stratosphere. Atmosphere, 15(7), 812. https://doi.org/10.3390/atmos15070812







