Computational Fluid Dynamics Simulation of High-Resolution Spatial Distribution of Sensible Heat Fluxes in Building-Congested Area
Abstract
1. Introduction
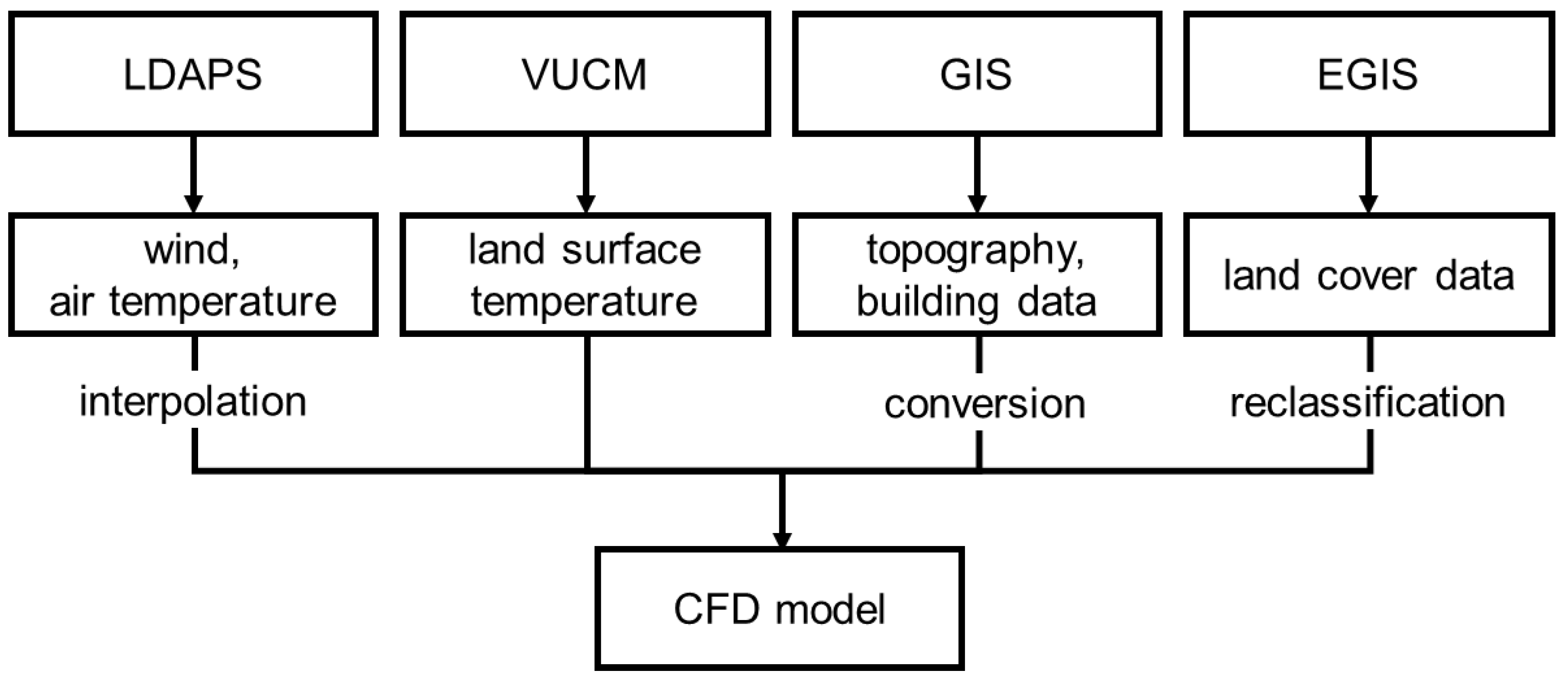
2. Methodology
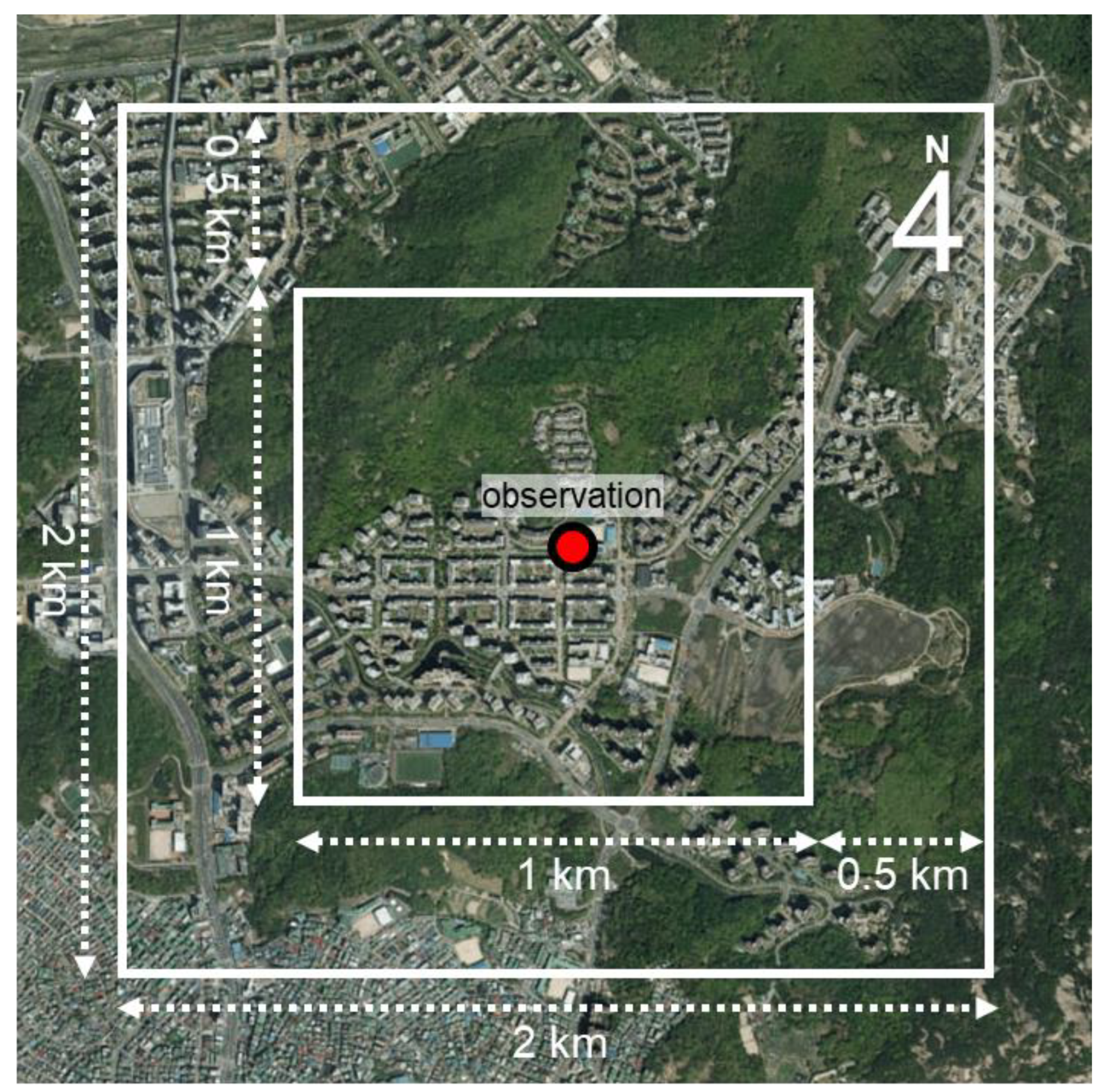
2.1. Target Area and Period
2.2. Measurement Data
2.3. Numerical Models
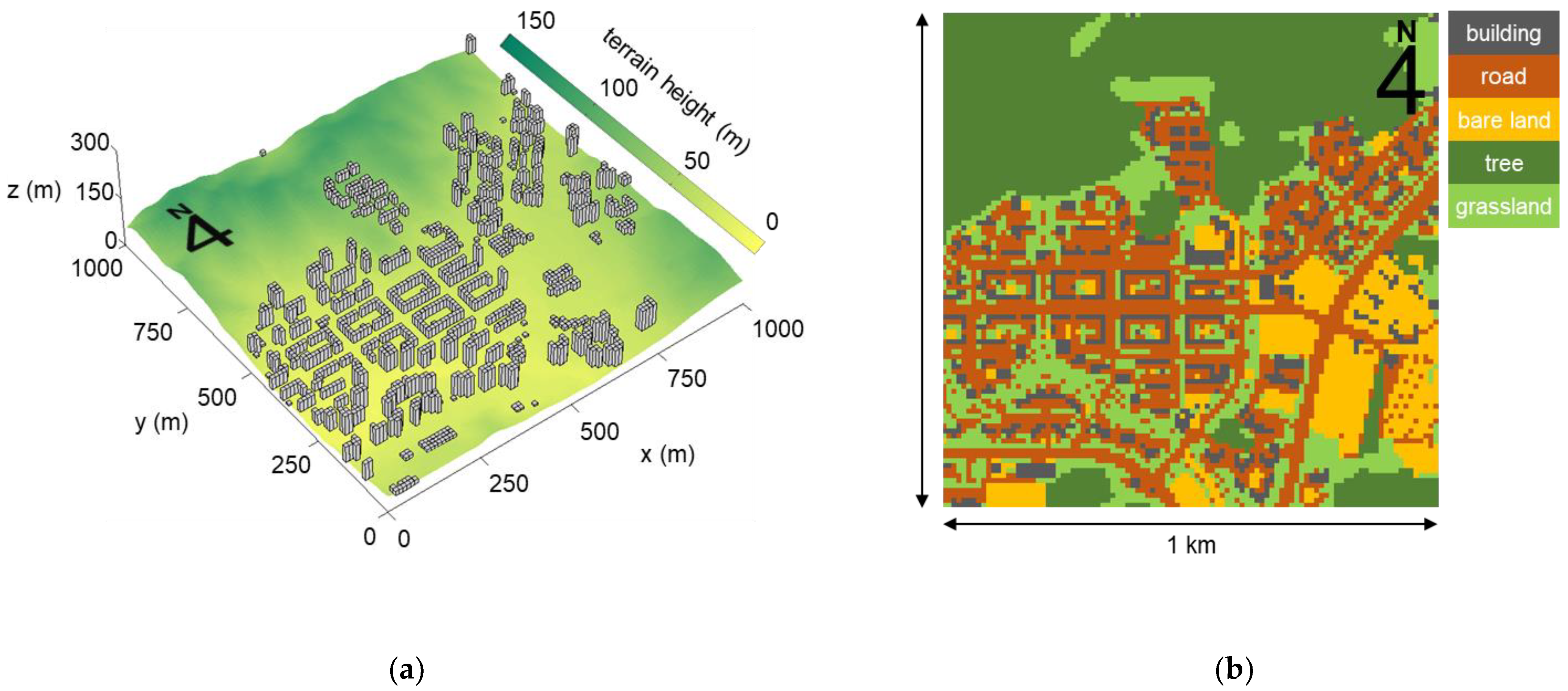
2.4. Numerical Setup
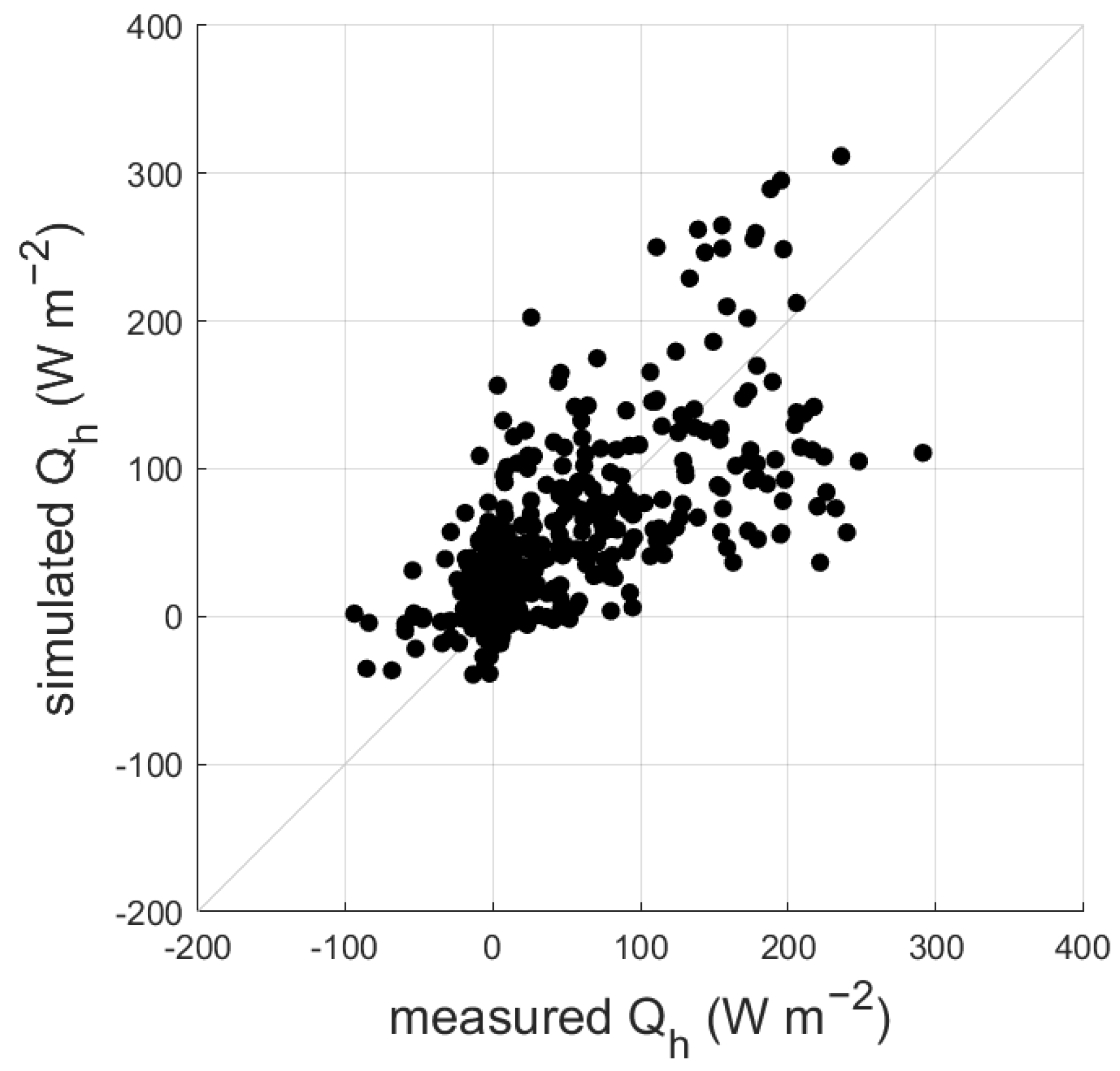
3. Model Validation
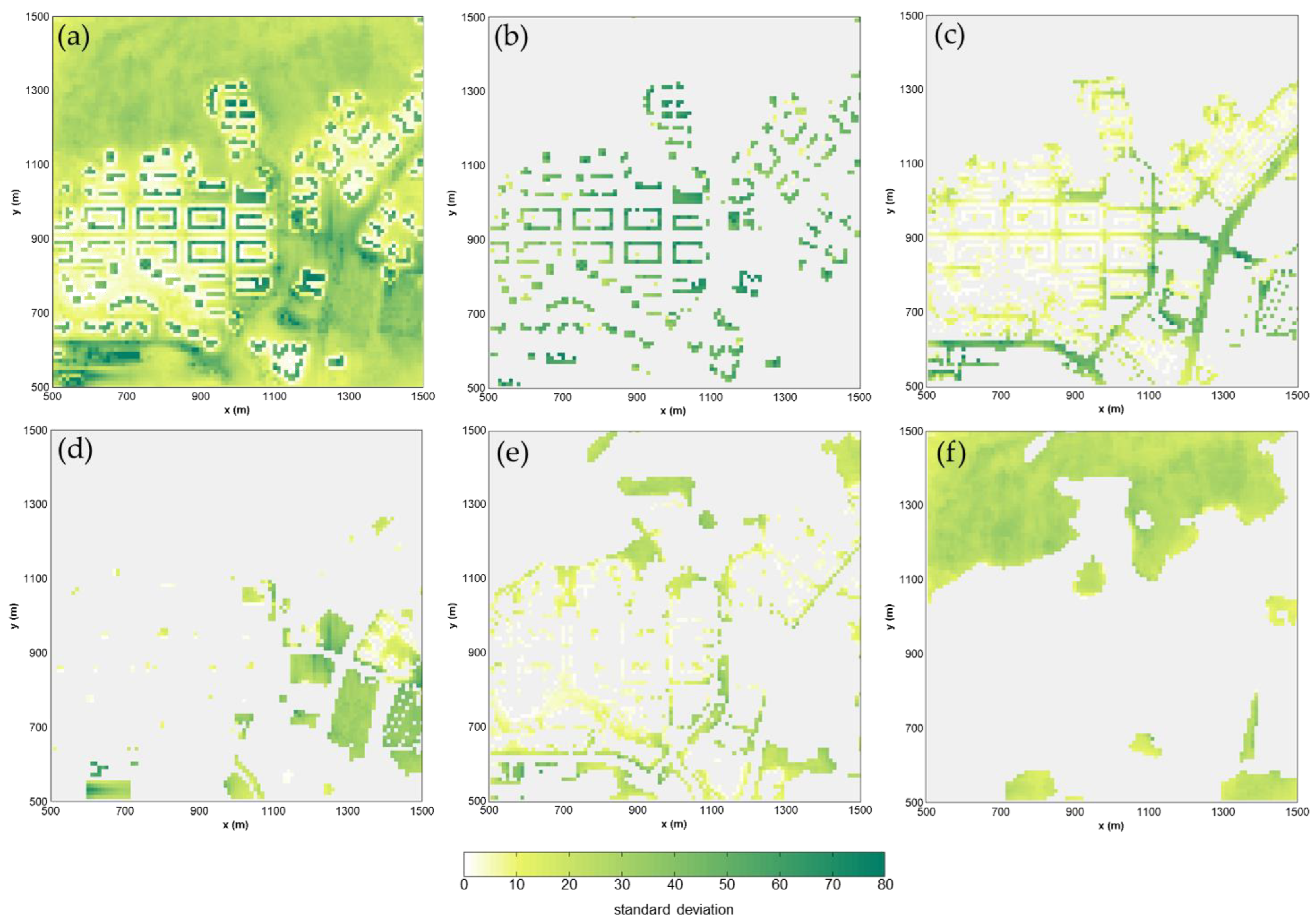
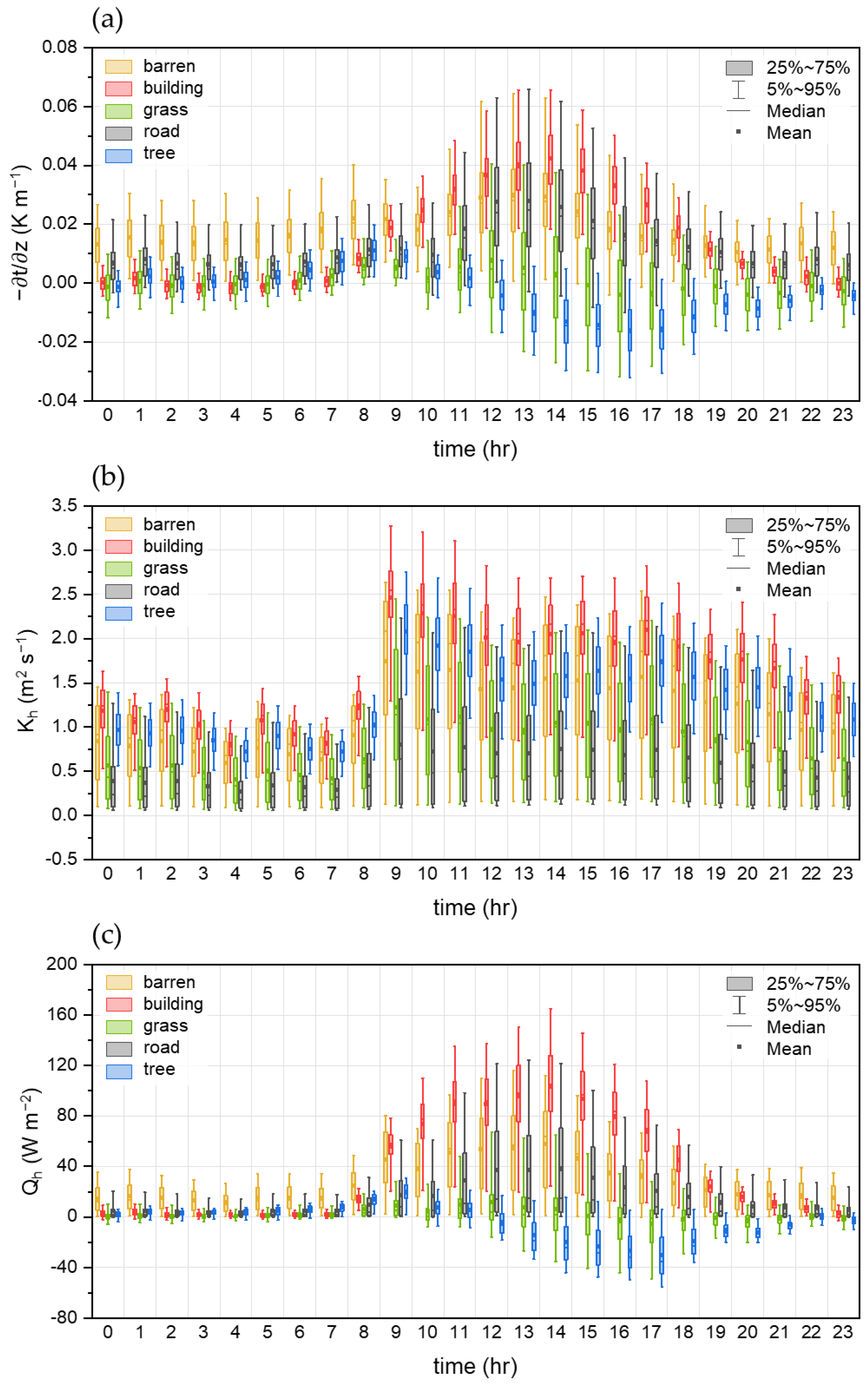
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nadeau, D.F.; Brutsaert, W.; Parlange, M.B.; Bou-Zeid, E.; Barrenetxea, G.; Couach, O.; Boldi, M.-O.; Selker, J.S.; Vetterli, M. Estimation of urban sensible heat flux using a dense wireless network of observations. Environ. Fluid Mech. 2009, 9, 635–653. [Google Scholar] [CrossRef]
- Hong, J.W.; Hong, J. Changes in the Seoul metropolitan area urban heat environment with residential redevelopment. J. Appl. Meteorol. Climatol. 2016, 55, 1091–1106. [Google Scholar] [CrossRef]
- Marelle, L.; Myhre, G.; Steensen, B.M.; Hodnebrog, Ø.; Alterskjær, K.; Sillmann, J. Urbanization in megacities increases the frequency of extreme precipitation events far more than their intensity. Environ. Res. Lett. 2020, 15, 124072. [Google Scholar] [CrossRef]
- Pham, J.V.; Baniassadi, A.; Brown, K.E.; Heusinger, J.; Sailor, D.J. Comparing photovoltaic and reflective shade surfaces in the urban environment: Effects on surface sensible heat flux and pedestrian thermal comfort. Urban Clim. 2019, 29, 100500. [Google Scholar] [CrossRef]
- Scherba, A.; Sailor, D.J.; Rosenstiel, T.N.; Wamser, C.C. Modeling impacts of roof reflectivity, integrated photovoltaic panels and green roof systems on sensible heat flux into the urban environment. Build. Environ. 2011, 46, 2542–2551. [Google Scholar] [CrossRef]
- Coutts, A.M.; Daly, E.; Beringer, J.; Tapper, N.J. Assessing practical measures to reduce urban heat: Green and cool roofs. Build. Environ. 2013, 70, 266–276. [Google Scholar] [CrossRef]
- Song, H.J.; Lim, B.; Joo, S. Evaluation of rainfall forecasts with heavy rain types in the high-resolution unified model over South Korea. Weather Forecast. 2019, 34, 1277–1293. [Google Scholar] [CrossRef]
- Tan, Z.; Lau, K.K.L.; Ng, E. Urban tree design approaches for mitigating daytime urban heat island effects in a high-density urban environment. Energy Build. 2016, 114, 265–274. [Google Scholar] [CrossRef]
- Xu, X.; Asawa, T. Systematic numerical study on the effect of thermal properties of building surface on its temperature and sensible heat flux. Build. Environ. 2020, 168, 106485. [Google Scholar] [CrossRef]
- Takahashi, K.; Yoshida, H.; Tanaka, Y.; Aotake, N.; Wang, F. Measurement of thermal environment in Kyoto city and its prediction by CFD simulation. Energy Build. 2004, 36, 771–779. [Google Scholar] [CrossRef]
- Xu, W.; Wooster, M.J.; Grimmond, C.S.B. Modelling of urban sensible heat flux at multiple spatial scales: A demonstration using airborne hyperspectral imagery of Shanghai and a temperature–emissivity separation approach. Remote Sens. Environ. 2008, 112, 3493–3510. [Google Scholar] [CrossRef]
- Salamanca, F.; Martilli, A. A new building energy model coupled with an urban canopy parameterization for urban climate simulations—Part II. Validation with one dimension off-line simulations. Theor. Appl. Climatol. 2010, 99, 345–356. [Google Scholar] [CrossRef]
- Barlow, J.F.; Halios, C.H.; Lane, S.E.; Wood, C.R. Observations of urban boundary layer structure during a strong urban heat island event. Environ. Fluid Mech. 2015, 15, 373–398. [Google Scholar] [CrossRef]
- Feigenwinter, C.; Vogt, R.; Parlow, E.; Lindberg, F.; Marconcini, M.; Del Frate, F.; Chrysoulakis, N. Spatial distribution of sensible and latent heat flux in the city of Basel (Switzerland). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2717–2723. [Google Scholar] [CrossRef]
- Machado, N.G.; Biudes, M.S.; Angelini, L.P.; Querino, C.A.S.; da Silva Angelini, P.C.B. Impact of Changes in surface cover on energy balance in a tropical city by remote sensing: A study case in Brazil. Remote Sens. Appl. 2020, 20, 100373. [Google Scholar] [CrossRef]
- Kato, S.; Yamaguchi, Y. Analysis of urban heat-island effect using ASTER and ETM+ Data: Separation of anthropogenic heat discharge and natural heat radiation from sensible heat flux. Remote Sens. Environ. 2005, 99, 44–54. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, X.; Peng, Z. Large-eddy simulation of mesoscale circulations forced by inhomogeneous urban heat island. Bound.-Layer Meteor. 2014, 151, 179–194. [Google Scholar] [CrossRef]
- Antoniou, N.; Montazeri, H.; Neophytou, M.; Blocken, B. CFD simulation of urban microclimate: Validation using high-resolution field measurements. Sci. Total Environ. 2019, 695, 133743. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Kwok, K.C.; Liu, H.; Jiang, Y.; Dong, K.; Wang, B. A CFD study of wind assessment in urban topology with complex wind flow. Sustain. Cities Soc. 2021, 71, 103006. [Google Scholar] [CrossRef]
- Brozovsky, J.; Simonsen, A.; Gaitani, N. Validation of a CFD model for the evaluation of urban microclimate at high latitudes: A case study in Trondheim, Norway. Build. Environ. 2021, 205, 108175. [Google Scholar] [CrossRef]
- Brozovsky, J.; Radivojevic, J.; Simonsen, A. Assessing the impact of urban microclimate on building energy demand by coupling CFD and building performance simulation. J. Build. Eng. 2022, 55, 104681. [Google Scholar] [CrossRef]
- Moradpour, M.; Hosseini, V. An investigation into the effects of green space on air quality of an urban area using CFD modeling. Urban Clim. 2020, 34, 100686. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.Y.; Kim, J.J.; Kim, M.J. Thermal effects on dispersion of secondary inorganic aerosols in an urban street canyon. Urban Clim. 2023, 47, 101375. [Google Scholar] [CrossRef]
- Maggiotto, G.; Buccolieri, R.; Santo, M.A.; Leo, L.S.; Di Sabatino, S. Validation of temperature-perturbation and CFD-based modelling for the prediction of the thermal urban environment: The Lecce (IT) case study. Environ. Model. Softw. 2014, 60, 69–83. [Google Scholar] [CrossRef]
- Huang, H.; Ooka, R.; Kato, S. Urban thermal environment measurements and numerical simulation for an actual complex urban area covering a large district heating and cooling system in summer. Atmos. Environ. 2005, 39, 6362–6375. [Google Scholar] [CrossRef]
- Ashie, Y.; Kono, T. Urban-scale CFD analysis in support of a climate-sensitive design for the Tokyo Bay area. Int. J. Climatol. 2011, 31, 174–188. [Google Scholar] [CrossRef]
- Allegrini, J.; Dorer, V.; Carmeliet, J. Coupled CFD, radiation and building energy model for studying heat fluxes in an urban environment with generic building configurations. Sustain. Cities Soc. 2015, 19, 385–394. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, S.U. A vegetated urban canopy model for meteorological and environmental modelling. Bound.-Layer Meteor. 2008, 126, 73–102. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Longman: London, England, 1995; p. 257. [Google Scholar]
- Kim, J.J.; Baik, J.J. Effects of street-bottom and building-roof heating on flow in three-dimensional street canyons. Adv. Atmos. Sci. 2010, 27, 513–527. [Google Scholar] [CrossRef]
- Park, S.J.; Kim, J.J.; Kim, M.J.; Park, R.J.; Cheong, H.B. Characteristics of flow and reactive pollutant dispersion in urban street canyons. Atmos. Environ. 2015, 108, 20–31. [Google Scholar] [CrossRef]
- Park, S.J.; Choi, W.; Kim, J.J.; Kim, M.J.; Park, R.J.; Han, K.S.; Kang, G. Effects of building–roof cooling on the flow and dispersion of reactive pollutants in an idealized urban street canyon. Build. Environ. 2016, 109, 175–189. [Google Scholar] [CrossRef]
- Kang, G.; Kim, J.J.; Kim, D.J.; Choi, W.; Park, S.J. Development of a computational fluid dynamics model with tree drag parameterizations: Application to pedestrian wind comfort in an urban area. Build. Environ. 2017, 124, 209–218. [Google Scholar] [CrossRef]
- Kang, G.; Kim, J.J. Effects of Vertical Forests on Air Quality in Step-up Street Canyons. Sustain. Cities Soc. 2023, 94, 104537. [Google Scholar] [CrossRef]
- Hayati, A.N.; Stoll, R.; Kim, J.J.; Harman, T.; Nelson, M.A.; Brown, M.J.; Pardyjak, E.R. Comprehensive evaluation of fast-response, Reynolds-averaged Navier–Stokes, and large-eddy simulation methods against high-spatial-resolution wind-tunnel data in step-down street canyons. Bound.-Layer Meteor. 2017, 164, 217–247. [Google Scholar] [CrossRef]
- Hayati, A.N.; Stoll, R.; Pardyjak, E.R.; Harman, T.; Kim, J.J. Comparative metrics for computational approaches in non-uniform street-canyon flows. Build. Environ. 2019, 158, 16–27. [Google Scholar] [CrossRef]
- Baik, J.J.; Park, S.B.; Kim, J.J. Urban flow and dispersion simulation using a CFD model coupled to a mesoscale model. J. Appl. Meteorol. Climatol. 2009, 48, 1667–1681. [Google Scholar] [CrossRef]
- Kang, G.; Kim, J.J.; Choi, W. Computational fluid dynamics simulation of tree effects on pedestrian wind comfort in an urban area. Sustain. Cities Soc. 2020, 56, 102086. [Google Scholar] [CrossRef]
- Park, I.; Kim, H.S.; Lee, J.; Kim, J.H.; Song, C.H.; Kim, H.K. Temperature prediction using the missing data refinement model based on a long short-term memory neural network. Atmosphere 2019, 10, 718. [Google Scholar] [CrossRef]
- Song, J.; Wang, Z.H.; Wang, C. The regional impact of urban heat mitigation strategies on planetary boundary layer dynamics over a semiarid city. J. Geophys. Res. Atmos. 2018, 123, 6410–6422. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational design of the basic dynamical process of the UCLA general circulation model. Methods Comput. Phys. 1977, 17, 173–265. [Google Scholar]
- Charney, J.G.; Philips, N.A. Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flow. J. Meteorol. 1953, 10, 71–99. [Google Scholar] [CrossRef]
- Bürger, C.M.; Kolditz, O.; Fowler, H.J.; Blenkinsop, S. Future climate scenarios and rainfall–runoff modelling in the Upper Gallego catchment (Spain). Environ. Pollut. 2007, 148, 842–854. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Jia, Y.; Zhang, Q.; Gong, D.; Cui, N. National-scale assessment of pan evaporation models across different climatic zones of China. J. Hydrol. 2018, 564, 314–328. [Google Scholar] [CrossRef]
- Wang, Y.; Chan, A.; Lau, G.N.C.; Li, Q.; Yang, Y.; Yim, S.H.L. Effects of urbanization and global climate change on regional climate in the Pearl River Delta and thermal comfort implications. Int. J. Climatol. 2019, 39, 2984–2997. [Google Scholar] [CrossRef]
- Rios, G.; Ramamurthy, P. A novel model to estimate sensible heat fluxes in urban areas using satellite-derived data. Remote Sens. Environ. 2022, 270, 112880. [Google Scholar] [CrossRef]
- Lian-Tong, Z.; Ren-Guang, W.; Rong-Hui, H. Variability of surface sensible heat flux over Northwest China. Atmos. Ocean. Sci. Lett. 2010, 3, 75–80. [Google Scholar] [CrossRef]
- Zieliński, M.; Fortuniak, K.; Pawlak, W.; Siedlecki, M. Long-term turbulent sensible-heat-flux measurements with a large-aperture scintillometer in the Centre of Łódź, Central Poland. Bound.-Layer Meteor. 2018, 167, 469–492. [Google Scholar] [CrossRef]




| RMSE [W m−2] | ] | IOA | R | |
|---|---|---|---|---|
| all day | 42.68 | 26.95 | 0.84 | 0.73 |
| day | 58.61 | 42.35 | 0.77 | 0.60 |
| night | 21.22 | 13.78 | 0.41 | 0.15 |
| sunny day | 47.00 | 29.81 | 0.85 | 0.73 |
| cloudy day | 35.76 | 23.05 | 0.81 | 0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.-E.; Lee, S.-H.; Hong, J.-K.; Kim, J.-J. Computational Fluid Dynamics Simulation of High-Resolution Spatial Distribution of Sensible Heat Fluxes in Building-Congested Area. Atmosphere 2024, 15, 681. https://doi.org/10.3390/atmos15060681
Kang J-E, Lee S-H, Hong J-K, Kim J-J. Computational Fluid Dynamics Simulation of High-Resolution Spatial Distribution of Sensible Heat Fluxes in Building-Congested Area. Atmosphere. 2024; 15(6):681. https://doi.org/10.3390/atmos15060681
Chicago/Turabian StyleKang, Jung-Eun, Sang-Hyun Lee, Jin-Kyu Hong, and Jae-Jin Kim. 2024. "Computational Fluid Dynamics Simulation of High-Resolution Spatial Distribution of Sensible Heat Fluxes in Building-Congested Area" Atmosphere 15, no. 6: 681. https://doi.org/10.3390/atmos15060681
APA StyleKang, J.-E., Lee, S.-H., Hong, J.-K., & Kim, J.-J. (2024). Computational Fluid Dynamics Simulation of High-Resolution Spatial Distribution of Sensible Heat Fluxes in Building-Congested Area. Atmosphere, 15(6), 681. https://doi.org/10.3390/atmos15060681








