Abstract
The seasonal variability of Southern Hemisphere (SH) synoptic-scale weather systems is analysed for the 20-year timespan 1997 to 2016. The relationships between the SH jet streams and storm tracks based on lower tropospheric circulation anomalies filtered into the high-pass (periods < 4 days) and band-pass (periods between 4 and 8 days) bands are examined based on 6-hourly reanalysis data. Leading Empirical Orthogonal Functions (EOFs) and storm tracks based on all (growing and decaying) disturbances are determined. As well, the structure and standard deviations of streamfunction fluctuations are determined separately in three growth rate and three decay rate bins focusing on explosive growth and decay. In all cases, and in each season, the band-pass storm tracks are more zonally symmetric than the high-pass standard deviations and this is also reflected by the EOFs. Leading EOFs in both bands are monopole wavetrains of highs and lows located in the storm tracks with some band-pass disturbances having dipole structures consistent with blocking and northwest cloud bands. EOFs based on the bin with slow-growing fluctuations are structurally similar to the standard EOFs based on all disturbances. EOFs for moderately and explosively growing disturbances are increasingly displaced equatorward with a larger growth rate.
1. Introduction
Synoptic-scale weather systems generated by baroclinic instability and propagating eastward in the mid-latitude jet streams are major determinants of extratropical weather and climate in both hemispheres. These Rossby wavetrains of cyclones and anticyclones that tilt westward with height contribute to the fluxes of heat, momentum, and moisture between latitudes. Predicting and understanding the development and behaviour of extratropical storms has been an area of intense research interest for more than a hundred years going back at least to the work of the Bergen school and the frontal model of the Northern Hemisphere (NH) storm formation [1,2].
1.1. Storm Tracks Determined by Regions of Maximum Variance of Weather Fluctuations
Over the last seventy years, there have been major advances in the quality of atmospheric circulation datasets and in analysis products produced by an increasing number of forecast centres. This has greatly increased our knowledge of the behaviour of weather systems through diagnostic studies, as well as posed important theoretical questions on the causes of their genesis and evolutions. In the NH, the works of Blackmon [3], and Blackmon, et al. [4] made definitive determinations of the extratropical storm tracks defined as the regions of maximum variance of sub-weekly geopotential height fluctuations or related fields.
In the Southern Hemisphere (SH), the subject of this paper, the early works on extratropical storm formation, based on manually prepared charts, were encapsulated and reviewed in the articles by van Loon [5] and Taljaard [6]. The annual average 500 hPa SH storm track was determined by Trenberth [7], and the associated January and July storm tracks by Trenberth [8]. He used Australian Bureau of Meteorology (BoM) analyses. Subsequently, Trenberth [9] determined the locations and structures of SH storm tracks based on European Centre for Medium Range Weather Forecasting (ECMWF) analyses. He examined geopotential height and meridional wind fluctuations with periods between 2 and 8 days. The storm track was again defined as the extratropical band around the regions of maximum variance or standard deviation (STD) of the geopotential height or meridional wind, as in Blackmon, et al. [4]. Trenberth [9] focused on the geographical locations of the storm tracks at 300 hPa but also analysed the vertical cross sections of zonally averaged STDs of important flow field variables, as well as heat and momentum fluxes. He found that meridional heat fluxes peak in the lower troposphere while the standard deviations of meridional winds peak near 300 hPa where they are slightly more than twice as strong as at 850 hPa.
Berbery and Vera [10] determined the geographical structure of the austral winter (JJA) SH storm track at 300 hPa for filtered (2.5–6 day periods) and unfiltered meridional wind and vorticity fluctuations based on ECMWF analyses. Rao, et al. [11] examined the seasonal variability of the 300 hPa SH storm track based on unfiltered meridional wind anomalies taken from National Center for Environmental Prediction (NCEP)/National Center for Atmospheric Research (NCAR) reanalysis products (hereafter, NNR data). These two studies also examined the wavetrain structures of the storm track disturbances and their downstream development based on lagged key-point analyses. Chang [12] used both ECMWF and NNR data for the period June 1980 to January 1993 to calculate the 300 hPa DJF and JJA storm tracks for both hemispheres based on unfiltered meridional wind fluctuations. He computed spatial correlations of 300 hPa meridional winds between the ECMWF and NNR data which were found to be very high (>0.92) in both hemispheres. He also determined the wave packet characteristics of the upper tropospheric fluctuations based on key-point analysis.
Nakamura and Shimpo [13] made a detailed analysis of the seasonal variations of the SH jet streams and storm tracks for a 16-year period between 1979 and 1995 based on NNR data. They focused on the role of zonal asymmetries in the jet streams and their role in determining the locations and structures of the SH storm tracks. They determined the storm tracks by the 250 hPa eddy amplitude of the geopotential height, scaled by sin(45° S)/sin(latitude), which approximates the streamfunction, and the 850 hPa poleward heat flux. The geopotential height fluctuations were high-pass-filtered to retain fluctuations with periods less than 8 days.
1.2. Storm Tracks Determined by Tracking Methods
Storm centre tracking methods have been extensively used to examine the trajectories of individual extratropical lows and highs, and, through compositing, the average SH storm tracks were determined [14,15,16,17,18,19,20,21]. Sinclair [18] made some important findings about issues that can arise with the Lagrangian storm tracking method. He noted that this method can result in large counts of cyclones near land masses associated with heat lows and lee troughs. Moreover, by focusing on travelling weather systems, he was able [18] (Figure 14) to obtain cyclone track densities for the four SH seasons that were in much better agreement with the results from eddy statistics of circulation fluctuations.
More detailed reviews of Lagrangian tracking methods are presented by Barnes, et al. [22], Zhan and Chen [23], and Messmer and Simmonds [24], who also analyse compound precipitation and wind extreme events induced by cyclones.
Hoskins and Hodges [19] make a direct comparison of SH storm tracks for the four seasons based on both the 2–6-day band-pass-filtered Eulerian variance and Lagrangian tracking of extratropical cyclones and anticyclones. They used 45 years of 6-hourly ECMWF ERA-40 from 1958 to 2002 for their studies with a focus on vorticity fields and meridional velocity fields at 250 and 850 hPa, upper tropospheric potential temperature and mean sea level pressure. As in the study of Sinclair [18], their analysis considered mobile disturbances which lasted longer than 2 days and moved more than 10° or 1000 km. Hoskins and Hodges [19] found that there was close agreement between their storm tracks based on Eulerian variance and Lagrangian tracking in each season, although the subtropical storm track is already present in the Lagrangian results for 250 hPa vorticity in MAM.
1.3. Theories and Modelling of Storm Tracks
Along with advances in our knowledge and understanding of storm tracks from improved datasets and diagnostic methods have come more realistic theoretical models of cyclogenesis and the maturation of storms. The theory of baroclinic instability for extratropical cyclogenesis by Charney [25], Eady [26], and Phillips [27] was the pioneering breakthrough that provided a mathematical formalism for understanding the basic mechanism for storm formation. Storms have since been depicted as the low-pressure centres in generally eastward propagating baroclinic Rossby waves [28,29]. The early seminal works examined the instability of simple zonally symmetric basic states on f-planes or beta-planes. Next followed models of storm formation in jets with meridional as well as vertical shear, and then the inclusion of spherical geometry, the use of primitive equations, and studies of the nonlinear evolution of initial instability modes with reviews in Refs. [30,31,32,33].
The atmospheric large-scale flow and the storm tracks, however, contain significant zonal asymmetries. Frederiksen [30,34,35] developed a theoretical model of localised cyclogenesis in confluent–diffluent zonally asymmetric basic states. It provided explanations for the regions of preferential cyclogenesis and for the structures of heat and momentum fluxes. Preferential cyclogenesis was shown to occur slightly downstream and poleward of the regions of maximum vertical shear of the zonal flow basic state. This was followed by the determination of some of the leading cyclogenesis modes for the January and July observed climatological basic states for the NH in quasigeostrophic [36] and primitive equation [37] instability models, and for the SH in quasigeostrophic [38] and primitive equation [39] models.
1.4. Comparison of Observational and Theoretical Determinations of Storm Tracks
Extratropical cyclones go through a growth cycle of initial exponential growth followed by occlusion and nonlinear saturation or vacillation cycles, with downstream development, as found for both idealised NH initial zonally symmetric basic states [40,41] and for observed SH initial basic states [31]. Nevertheless, the instability theory of three-dimensional basic states is very successful in explaining the mechanisms of localised cyclogenesis and the regional structures of the storm tracks in both hemispheres. Trenberth [7], for example, notes that the observed location of the storm in his Figures 17b and 18a fits quite well with the results in Frederiksen [35,42] with the regions of preferential development slightly downstream of the long wave troughs. Trenberth [9] compared his data-derived storm tracks with the quasigeostrophic results of Frederiksen [38] who used a SH climatological basic state with zonal asymmetries. The theoretical finding that the model storm tracks are in the eastern part of the hemisphere and slightly downstream and poleward of the jet stream maxima agrees with Trenberth’s observational results in his Figures 4 to 7. Frederiksen and Frederiksen [39] also compare their storm tracks based on leading primitive equation instability modes with the diagnostic results of Trenberth [9]. They note the general agreement between the theory and observations but with the instability maxima of the dominant fast-growing modes slightly downstream of the observations. This may be partly explained by the fact that many modes contribute to the observations.
Berbery and Vera [10], Rao, et al. [11], and Nakamura and Shimpo [13] also note the broad agreement between storm tracks derived from the three-dimensional instability theory, as in Frederiksen and Frederiksen [39], and their diagnostic findings based on reanalysis data. In particular, Nakamura and Shimpo conjecture that “a realistic reproduction by Frederiksen and Frederiksen [39] of some of the fundamental features of the SH storm tracks, as revealed in this study, may be attributable to the inclusion of zonal asymmetries”.
1.5. Data-Driven Determination of Growing and Decaying Weather Systems
Recently, Osbrough and Frederiksen [43] examined the changes in the SH July storm track over the last 70 years. Their study, based on NNR data, focused on the 850 hPa streamfunction fluctuations in two frequency bands of high-pass (period days) and band-pass (period days) data. They analysed the storm tracks and their changes based on all fluctuations in each frequency band and, as well, determined growing and decaying weather systems that they separated into several growth rate bins. Osbrough and Frederiksen [43] also examined the structures of the Rossby wavetrains primarily through an EOF analysis based on all fluctuations and those in the bin representing the fastest growth rate ().
Fluctuations at 300 hPa were also analysed in the study by Osbrough and Frederiksen [43]. They found that the scale of the EOFs of the westward tilting synoptic-scale disturbances were similar to those at lower levels. However, the presentation by Osbrough and Frederiksen [43] focused on 850 hPa, since it was found that changes at this level were closely related to rainfall changes over Southern Australia. In particular, changes in the fastest growing storms were found to be related to the rainfall changes. It was noted that this is also consistent with observational studies of explosive storms with the rate of growth and rainfall strongly correlated [44,45,46,47,48,49]. Sinclair [17] also considered the development and regional characteristics of SH explosive storms based on the tracking of pressure and relative geostrophic vorticity minima. He noted that “relating cyclone intensity to pressure deepening can be misleading”. This is because of the frequent contribution of propagation to changes in pressure. Storms may move rapidly into a region of climatological low pressure. In contrast, the methodology in Ref. [43] separates growth and propagation effects.
1.6. Impact of Storms on Australian Rainfall
As reviewed by Osbrough and Frederiksen [43] and Frederiksen and Osbrough [50], the Australian Millennium Drought (AMD) was one of the most severe Australian droughts of the 20th century. Southeast Australia (SEA) was particularly affected by reductions in rainfall [51,52,53,54,55,56,57]. Trewin [58] notes that Melbourne rainfall was 20% lower than average between 1997 and 2006 and SEA rainfall 11% lower between 1997 and 2009 [59]. The rainfall changes were related to changes in the large-scale circulation and reductions in growth rates of extratropical storms affecting southern Australia [60]. Risbey, et al. [56] also found that, during the AMD, there were fewer intense frontal storms and cut-off lows over the southern Australian region associated with reduced jet strength and baroclinicity [60,61,62]. The drought, of course, broke with the La Niña of 2011 and the subsequent La Niña of 2014 with a return to a more average circulation for the 20-year period 1997 to 2016 analysed in our study. The link between the large-scale circulation, weather systems, rainfall, and droughts during the AMD is, in fact, a particular example of a general principle as reviewed by Straus, et al. [63].
1.7. Aims and Structure
This study extends the existing research on the seasonal variability of synoptic-scale disturbances and storm tracks in several ways. First, it examines the fluctuations in both high-pass and band-pass frequencies with more zonally symmetric storm tracks for periods days, while those for the periods days are weaker over the South Pacific Ocean. The band-pass disturbances also include Australian North-West Cloud Band (NWCB) disturbances and blocking dipoles. Second, the investigation documents the statistics of high-pass and band-pass storm track disturbances in three growth rate bins and three decay rate bins, as well as the standard analysis based on the combined fluctuations. This allows the determination of the regions of preferential growth of explosive extratropical cyclones at lower latitudes than more slowly growing disturbances.
The main aims of this article are to analyse the SH seasonal variations in:
- The large-scale flow, particularly the zonal winds;
- The ‘standard’ EOFs based on all 850 hPa meridional wind fluctuations in high-pass ( days) and band-pass ( days) bands;
- The ‘instability’ EOFs based on filtered 850 hPa meridional wind anomalies in three growth rate bins with , and ;
- The STDs of storm tracks based on all filtered 850 hPa streamfunction disturbances in high-pass and band-pass data;
- The STDs of storm tracks based on growing and decaying filtered 850 hPa streamfunction anomalies in six growth rate bins.
We focus on the 20-year timespan 1997 to 2016 that includes the Australian Millennium Drought and we use 6-hourly NNR data in our study. In a sequel paper, we will examine the decadal changes in STDs of storm tracks in the last 70 years and the relationships to Australian rainfall.
In detail, the structure of the article is as follows: In Section 2, the NNR reanalysis dataset used in the study is described. Section 3 presents the methodology that is used to filter the 6-hourly atmospheric flow fields into high-pass and band-pass fluctuations, to extract statistics on growing and decaying weather systems in six growth rate bins. As well, we discuss the calculation of ‘standard’ EOFs based on all growing and decaying filtered disturbances and ‘instability’ EOFs characterising the anomalies in different growth rate bins. The main results of this article are presented in Section 4, Section 5, Section 6, Section 7 and Section 8. The seasonal variability of the SH jet streams is examined in Section 4 for the 20-year timespan 1997 to 2016 that includes the AMD. Seasonal changes in some of the leading standard EOFs characterising Rossby wavetrains of 850 hPa storms and high-pressure systems, as well as blocking and Australian North-West Cloud Band (NWCB) disturbances, are analysed in Section 5. In Section 6, leading instability EOFs typical of growing weather systems are studied. The seasonal cycle of STDs of 850 hPa SH streamfunction fluctuations is described in Section 7, and, in Section 8, these STDs are separated into the contributions of growing and decaying disturbances in six growth rate bins. In Section 9, a discussion of the implications of the findings is presented, and, in Section 10, conclusions are drawn. Appendix A presents the method of calculating growth rates and Appendix B documents the method of calculating EOFs.
2. Datasets
The dataset used in our study of seasonal storm track characteristics in the Southern Hemisphere is the ‘Reanalysis 1’ dataset produced by the National Centers for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR) [64], herein referred to as NNR. It is also used in a follow-on investigation where the seasonal and decadal variability of synoptic-scale disturbances, relative to the current 1997 to 2016 baseline period, are analysed and related to circulation and Australian rainfall changes, going back to the mid-20th century. For that, we need a reanalysis dataset that spans seven decades and which has been found to have dynamical consistency with independent Australian rainfall changes, like the NNR (results and reviews are given in Refs. [43,50]).
The climate fields of interest are the six-hourly zonal and meridional winds, and temperature and humidity taken at the pressure level of 850 hPa with a grid resolution of 2.5° latitude by 2.5° longitude. We have chosen the 20-year period from 1997 to 2016 for our analysis, which includes the onset and breaking of the Australian Millennium Drought that effected regions of southeast Australia (SEA).
3. Method for Determining Growing and Decaying Weather Systems
Our study uses 6-hourly NNR data, converted to streamfunction, as well as wind data, that are spectrally analysed with, for example,
Here, the streamfunction is represented by spherical harmonics with , the zonal, and , the total wavenumber. The Legendre functions also depend on , the sine of the latitude (), and is the longitude. The spectral coefficients satisfy the complex conjugate property that ensures that the physical space fields are real. The chosen spectral resolution is, again, rhomboidal 31 and corresponds to a resolution of 375 km by 250 km in longitude by latitude at 30° S as described in Section 5 in Ref. [43]. The methodology for determining the separate growing and decaying components of the fluctuations is as developed by Osbrough and Frederiksen [43]. Briefly, the climatological annual cycle is removed from the spectrally analysed six-hourly NNR reanalysis data and the resulting streamfunction dataset is filtered into two bands for examination. The optimal number of frequency components to be passed through the filter is approximated by the filter length, , as defined in Ref. [43], Appendix 2. The first high-pass band consists of small, fast-moving propagating disturbances at less than 4 days, while the second band consists of longer disturbances with periods occurring between 4 and 8 days. The growth rates of disturbances in each band are calculated as described in Appendix A, and then dispensed into separate bins. A number of growth rate bins are chosen for this study consisting of half-day growing and decaying bins, up to and greater than 1 day. The associated EOFs and standard deviations (STDs) of the fluctuations in each bin, and for all fluctuations, are subsequently analysed. A more detailed description of our methods including equations can be found in Appendix A and Appendix B.
4. Seasonal Variability of Southern Hemisphere Circulation
Jet streams are a striking feature of the Earth’s atmospheric circulation. They are condensed bands of strong predominately westerly winds with maxima near the tropopause that circumnavigate the globe in both hemispheres. Regions of maximum jet stream wind speed and baroclinicity permit synoptic-scale disturbances to form and propagate downstream along storm tracks. This affects storm activity at lower levels of the atmosphere and, in turn, influences our weather in the midlatitudes. There are essentially two types of jet streams. Polar jets form at the latitudes of the polar-frontal region with strong temperature gradients between cold polar air and the warmer temperatures of the mid-latitudes. Subtropical jets lie at the latitudes of the descending branch of the Hadley circulation.
There is a strong connection between the structure of the jet streams and the development of extratropical storms as summarised in the Introduction. A simple approximate criterion for storm formation is given by Phillips’ (1954) [27] formula for baroclinic instability based on simple zonally symmetric flows. The Phillips criterion in spherical geometry is
where and are the specified upper and lower pressure level zonal winds and σ is the static stability measuring the potential temperature shear between these pressure levels and includes the effects of moisture. The physical constants for the earth’s radius and its angular rotation speed are expressed as m and rad s−1, respectively. The specific heat of air at constant pressure is given by JK−1kg−1 and the nondimensional constant is as defined in (Equation (2.2) of [42]). For instability to occur, the value of the Phillips criterion at a given latitude, , needs to be positive.
The 300 hPa and 700 hPa zonal winds for the period 1997 to 2016 are shown in Figure 1 for the standard seasons of DJF, MAM, JJA, and SON. Particularly notable are the strong subtropical 300 hPa jets extending from around 90° E to 240° E, in a latitude band between 30° S to 35° S, that cross Australia. This is the case particularly in JJA and SON with the winds somewhat weaker in MAM and largely absent in DJF. In the summer and transition seasons, the southern or polar jet at 300 hPa extends across, essentially, the whole hemisphere, with peaks between 45° S and 55° S, that are particularly strong over the South Atlantic and South Indian Oceans, and somewhat weaker areas over the South Pacific Ocean.
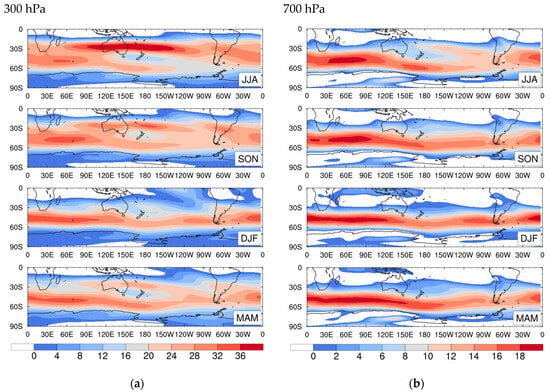
Figure 1.
Southern Hemisphere zonal wind averages between 1997 and 2016 at (a) u300 hPa and (b) u700 hPa levels for each season: (i) JJA (ii) SON (iii) DJF, and (iv) MAM.
At 700 hPa, the subtropical jet is weaker with the polar jet somewhat more zonally symmetric, particularly in DJF and MAM with relatively increased strength over the South Pacific Ocean compared with the 300 hPa flow.
The double jet structure of the 300 hPa flow in JJA, SON, and MAM in the Australia and New Zealand region is, of course, conducive to the formation of blocks in the Australian region, over the Tasman Sea and downstream of New Zealand. The seasonal variability of the polar jet is considerably less than for the subtropical jet with the polar jet being strong and deep in all seasons.
The zonal wind shear given by the 300 hPa minus 700 hPa zonal winds is a measure of the mid-tropospheric baroclinicity and related to the Phillips criterion for incipient storm formation. As noted by Frederiksen and Frederiksen [65], the changes in the static stability that also enters the Phillips criterion (Equation (2)) are less on decadal timescales than the zonal flows. Since the surface zonal flow is generally considerably weaker than the tropospheric zonal winds even at 700 hPa, the wind at this level can also be regarded as an approximate measure of lower tropospheric baroclinicity. Indeed, as found by Osbrough and Frederiksen [43] and Frederiksen and Osbrough [50], changes in the 700 hPa zonal wind are quite good predictors or descriptors of change in Australian rainfall in July [43] and in the southern wet (April to November) and cool (April to October) seasons [50]. Interestingly, Nakamura and Shimpo [13] note that their alternative definition of baroclinicity, based just on the lower tropospheric vertical zonal wind shear (their Figure 12), is in very good agreement with regions of storm formation. Further, their low-level baroclinicity, lower tropospheric zonal wind, and 850 hPa meridional heat flux are essentially geographical coincident. These results are also consistent with the findings of Osbrough and Frederiksen [43] discussed above.
The broad features of the jet streams in Figure 1 for the 20-year period 1997 to 2016 also apply to other long-time averages taken over the last 70 years. However, as has been discussed in Refs. [65] for July and in Ref. [50] for April to November, there has been a general reduction in the strength of the subtropical jet near 30° S, particularly in the upper troposphere, and an increase in the polar jet near 50° S since circa 1970. These changes also apply to the 20-year period 1997 to 2016 compared with 1949 to 1968, and also with 1975 to 1994, and have implications for storm formation and rainfall [43,50]. This will be discussed in more detail in a sequel paper.
5. Standard EOFs—All Fluctuations
Next, we examine the wavetrain structures of some of the dominant SH storm track disturbances by using the methodology for calculating EOFs described in Appendix B. We focus on EOFs since, as discussed in Ref. [43], they are more generally applicable for analysing the separate growing and decaying disturbances than Principal Oscillation Patterns (POPs). As well, the EOFs associated with travelling disturbances generally come in pairs of phase-shifted patterns which, between them, capture the essence of POPs and instability modes [43,66]. In our analyses, we discuss only one of these pairs, or, where there are more similar pairs, we choose one of the leading pairs. We will sometimes choose several of the leading EOFs that have qualitatively different wavetrains to illustrate a point. EOFs are ranked in descending order by the amount of variance explained.
In this section, we examine EOFs for the ‘standard’ case based on all—growing and decaying—disturbances within our high-pass () and band-pass () ranges. In Section 6, we then consider EOFs associated with separate growing and decaying fluctuations in several growth rate bins. These EOFs, based on the 6-hour evolved 850 hPa meridional wind anomaly fields, we refer to as ‘instability’ EOFs. We note that disturbances with longer periods also tend to be of a larger amplitude, as well as scale, and, thus, EOFs in the two bands will tend to most reflect anomalies with periods near 4 days (respectively, 8 days) for the high-pass (respectively, band-pass) filtered data.
As noted by Osbrough and Frederiksen [43], SH rainfall tends to be most related to lower tropospheric weather anomalies. For this reason, and for the sake of brevity, our study of synoptic-scale weather systems focuses on the 850 hPa level with EOFs based on meridional wind anomalies ( weighted). Our emphasis will be on the twenty-year period 1997 to 2016 which included the Australian Millennial Drought (AMD). However, we also briefly discuss how the results depend on other 20-year timespans during the last 70 years.
We analyse the EOFs in the central months of the seasons starting in austral winter (July), followed in sequence by spring (October), summer (January), and autumn (April). This order turns out to be convenient and reflects the important storminess and rainfall correlations over Southern Australia during winter as reviewed in Osbrough and Frederiksen [43]. We find that, overall, the leading EOFs in all months of a given season, for both filtered datasets, have broadly similar properties to those of the central month.
5.1. High-Pass-Filtered Weather Systems with Periods Tr < 4 Days
The 850 hPa streamfunction for the meridional wind EOF1 for July, shown in Figure 2a(i), is a monopole wavetrain whose amplitude reflects that of the 700 hPa winter zonal wind shown in Figure 1. This storm track mode characterises eastward propagation, with significant strength above the Southern Atlantic Ocean from South America, peaking above the Southern Ocean at the longitudes of South Africa, transiting across the boundary of the Indian and Southern Oceans and waning at the longitudes of Eastern Australia and New Zealand near 45° S. Indeed, as might be expected, the structure of EOF1 in Figure 2a(i) is very similar to EOF1 for 1949 to 1968 shown in Figure 2c of Ref. [43]. Osbrough and Frederiksen [43] also found EOFs with prominent wavetrains across the Southern Pacific Ocean and EOFs that were essentially hemispheric in nature. The same applies for the 20 years 1997 to 2016. In particular, the July EOF5 in Figure 2a(ii) is largely hemispheric but with peak amplitudes at the latitudes of the Australian continent. EOF7 in Figure 2a(iii) is also largely hemispheric but with more prominent features across the Southern Pacific Ocean and on the eastern side of South America like EOF5 in Figure 2d in Ref. [43]. Particularly in the Australian region, our current EOF7 is displaced somewhat to the south compared with EOF5 in Ref. [43]. This shift is consistent with the poleward shift of the SH jet streams and baroclinicity that have occurred during the last 70 years [43,50,65,67,68,69,70,71].
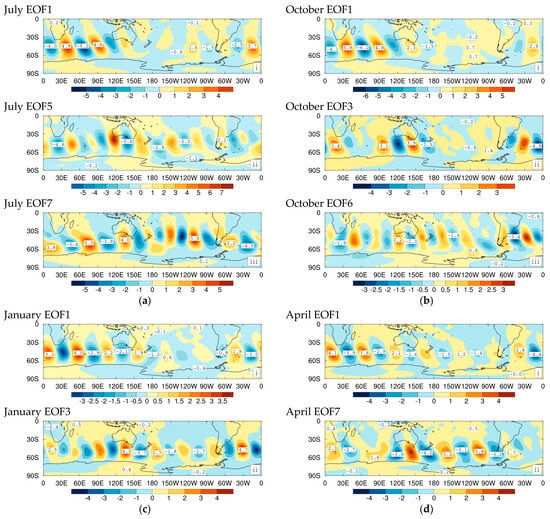
Figure 2.
Streamfunction at 850 hPa of Southern Hemisphere high-pass (period days) synoptic weather systems during 1997 to 2016 for leading ‘Standard’ EOFs with all filtered fluctuations for (a) July, (b) October, (c) January, and (d) April. Figure parts (i), (ii) and (iii) distinguish different EOFs in a given month.
Following on from winter, we examine EOFs for October, the central month of austral spring. The October EOF1 (Figure 2b(i)) depicts closely similar storm track characteristics to EOF1 for July, but with relatively smaller amplitudes over the Southern Atlantic. EOF3 for October (Figure 2b(ii)) has some broad similarities to EOF5 for July but with little wavetrain over the Pacific Ocean and a larger amplitude across the Southern Atlantic Ocean. EOF6 for October (Figure 2b(iii)), like EOF7 for July, has a hemispheric wide wavetrain.
In January, at the peak of summer, two characteristic EOF patterns emerge. The first, EOF1, (Figure 2c(i)), in keeping with the leading July and October modes, has storm track wavetrains traversing from South America across the Southern Oceans to the longitudes of Australia and New Zealand, with little strength over the Pacific Ocean. The EOF3 pattern (Figure 2c(ii)), is a hemispheric monopole wavetrain, also seen in July and October. An important point of difference between these patterns in different seasons is that the storm centres largely miss the Australian continent during January, with the storm tracks displaced poleward.
In April, the patterns for EOFs 1 and 7 (Figure 2d(i) and Figure 2d(ii), respectively) most resemble those for January. Again, the wavetrains occur further south, compared with winter and spring, making little impact on not only the Australian continent, but also on Southern Africa and to some extent on South America. In particular, EOF7 for April resembles EOF3 for January with a hemispheric wide wavetrain, but with enhanced amplitudes over the Southern Pacific Ocean and a diminished structure over the remainder of the hemisphere.
5.2. Band-Pass-Filtered Weather Systems with Periods 4 ≤ Tr < 8 Days
Next, we analyse the standard EOFs for band-pass-filtered disturbances. We start by considering monopole cyclone wavetrain modes with, now, the longer periods, and then examine dipole modes associated with blocking and with NWCBs.
5.2.1. Monopole Cyclone Wavetrain Modes
Figure 3 shows the 850 hPa streamfunctions of EOF1 for each of the central months of the seasons (July—Figure 3a(i); October—Figure 3b(i); January—Figure 3c; and April—Figure 3d). As expected, the lower frequency disturbances with () are also of larger-scale but have broad similarities with corresponding leading EOFs with shorter periods considered in Section 5.1. They are again monopole cyclone wavetrains with the largest amplitudes stretching from South America across the Southern Atlantic and Indian Oceans with an equatorward trajectory towards Australia and peaks just upstream. EOF1 for July in Figure 3a(i) is structurally very similar to the corresponding EOF1 for 1949 to 1968 shown in Figure 3a of Ref. [43]. EOF5 for July and EOF3 for October, in Figure 3a(ii) and Figure 3b(ii), respectively, have wavetrains stretching from the west coast of Australia across the Southern Pacific Ocean to South America and the South Atlantic Ocean. Interestingly, as shown in Section 7, the standard deviations of 850 hPa band-pass-filtered streamfunction anomalies are more zonally symmetric, with larger relative amplitudes across the Southern Pacific Ocean, than is the case for the high-pass-filtered fluctuations.
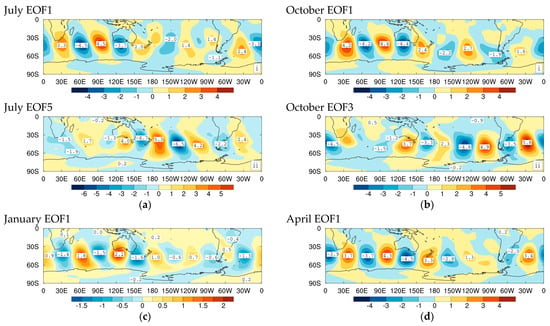
Figure 3.
Streamfunction at 850 hPa of Southern Hemisphere band-pass (period days) synoptic weather systems during 1997 to 2016 for leading ‘Standard’ EOFs with all filtered fluctuations for (a) July, (b) October, (c) January, and (d) April. Figure parts (i) and (ii) distinguish different EOFs in a given month.
5.2.2. Dipole Modes
Some of the subdominant EOFs with periods between 4 to 8 days also have dipole wavetrains that, with suitable signs, capture east coast low and blocking high structures in the region of the Tasman Sea and New Zealand. EOFs 12 and 14 for July (Figure 4a(i) and Figure 4a(ii), respectively) are such dipolar modes with EOF12 also having dipoles straddling the eastern South Pacific and Southern Ocean boundary. EOF12 for July also has a large amplitude anomaly over the Indian Ocean to the northwest of Western Australia in the genesis region of NWCBs. Somewhat similar dipole wavetrains are also captured by subdominant EOFs in Figure 4 in the other three central months of the seasons. This is shown in Figure 4b(i),(ii) for EOFs 8 and 10 for October, in Figure 4c for EOF15 for January, and in Figure 4d for EOF15 for April. Indeed, these dipoles occur in months throughout the year.
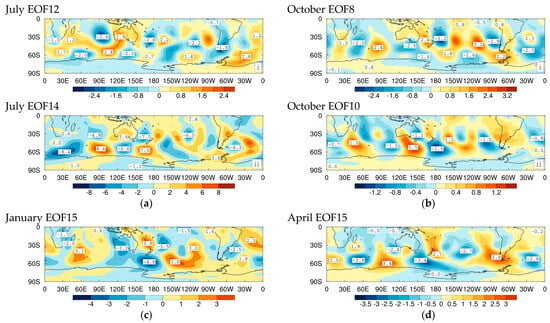
Figure 4.
As in Figure 3 for subdominant ‘Standard’ EOFs that show dipole atmospheric blocking during different months.
The EOFs in Figure 4 also have dipole wavetrains extending downstream of Australia and New Zealand with structures of the Pacific South America (PSA) pattern [39,72,73,74].
6. Instability EOFs—Separate Growing Fluctuations
In this section, we continue our investigation into the dominant modes of variability in 850 hPa high-pass- and band-pass-filtered NNR meridional wind data (-weighted). We separate the 6-hour evolved anomaly data into bins of growing and decaying disturbances, and then apply EOF analysis to the covariance matrices based on composites in each bin. We have experimented with different bin sizes and selected six bins with three for growing disturbances and another three for decaying fluctuations.
Table 1 lists the six bins that we use throughout this study. We focus on EOFs for growing modes because they are most related to rainfall variability. As well, disturbances contributing to bins with equal decay and growth rates have leading EOFs with somewhat similar structures. The three growth rate bins are denoted as bins of slow ()-, moderate ()-, and fast ()-growing disturbances.

Table 1.
Growth rate ranges of six growth rate bins and associated bin numbers.
As in Section 5, our interest is on seasonal variations of the EOFs with our analysis performed for the central month of each season, and we depict the streamfunction fields.
6.1. High-Pass-Filtered Weather Systems with Periods Tr < 4 Days
We first consider EOFs of growing disturbances with periods and follow up with an analysis of the band-pass-filtered data for which .
6.1.1. Slow-Growing Disturbances (0 ≤ ϖi < 0.5 Day−1)
Figure 5 shows the structures of EOF1 for 6-hour evolved disturbances for July, October, April, and January. The EOF1 for July (Figure 5a), based on slow-growing and high-pass-filtered disturbances, shows a familiar storm track wavetrain pattern at 45° S to 55° S that spans the southern hemisphere, reflecting similar characteristics of the standard leading July EOFs in Figure 2. The behaviour of the leading EOFs in the remaining central months (October—Figure 5b; January—Figure 5c; and April—Figure 5d) is broadly like the July case but with less amplitude over the South Pacific Ocean for October. Again, their patterns are broadly comparable to the respective standard leading EOFs in Figure 2.
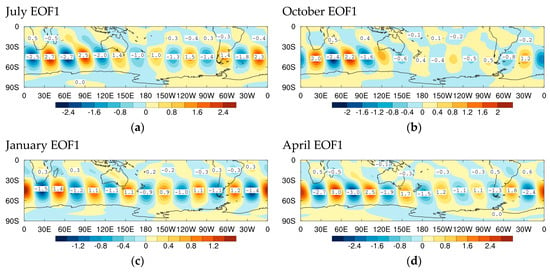
Figure 5.
Leading Southern Hemisphere 850 hPa streamfunction ‘Instability’ EOFs of high-pass-filtered weather systems for period days, for slowly growing disturbances, , during 1997 to 2016 for (a) July, (b) October, (c) January, and (d) April.
6.1.2. Moderately Growing Disturbances (0.5 ≤ ϖi < 1 Day−1)
Next, we consider leading EOFs based on evolved high-pass-filtered disturbances that are growing with moderate growth rates. Figure 6a shows EOF1 for July, which, compared with Figure 5a, for the slow-growing anomalies, tracks slightly more equatorward particularly over the Great Australian Bight. EOF1 results are again similar for October (Figure 6b), but with slightly weakened activity across the South Pacific Ocean. This also contrasts with January EOF2 (Figure 6c), which has a strong monopole wavetrain right across the southern hemisphere, and peak amplitudes south of and across southern Australia. Moving from summer into autumn, EOF1 for April (Figure 6d) has transitioned into a pattern more like that for July. We note the familiar hemispheric monopole wavetrain, somewhat weaker over the South Pacific Ocean, and more like the standard EOF1 for April in Figure 2d(i).
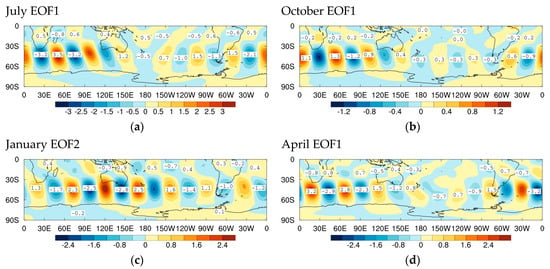
Figure 6.
Leading Southern Hemisphere 850 hPa streamfunction ‘Instability’ EOFs of high-pass-filtered weather systems for period days, for moderately growing disturbances, , during 1997 to 2016 for (a) July, (b) October, (c) January, and (d) April.
6.1.3. Fast-Growing Disturbances (ϖi ≥ 1 Day−1)
Lastly, the fast-growing high-pass-filtered instabilities are examined in this subsection. The changing nature of the structures and amplitudes of the fluctuations in the bin with are of particular interest since they are most related to changes in rainfall as detailed in Ref. [43]. Figure 7a shows the 850 hPa streamfunction of EOF2 for July which, expectedly is very similar to the corresponding EOF1 for 1949 to 1968 shown in Figure 2e in Ref. [43], but with a larger amplitude over the South Pacific Ocean in Figure 7a. Both depict a monopole wavetrain, from South America across to the NZ region, with an equatorward shift, particularly in the Australian and South American regions, compared with the standard EOFs of Section 5 and those based on slow- or moderate-growing disturbances above. For July, there are also EOFs, like the third mode, that have wavetrains more prominent in the eastern hemisphere with no identifying pattern across the Pacific Ocean. As well, the fifth EOF has a hemispheric monopole wavetrain like that of EOF3 for 1949 to 1968 shown in Figure 2f in Ref. [43] but of a slightly smaller scale.
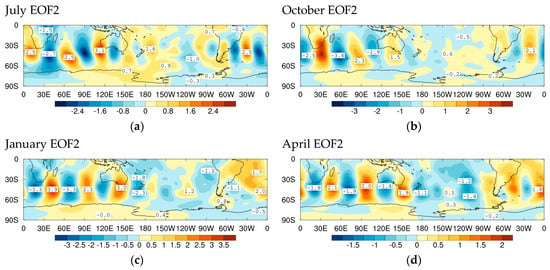
Figure 7.
Leading Southern Hemisphere 850 hPa streamfunction ‘Instability’ EOFs of high-pass-filtered weather systems for period days, for fastest growing disturbances, , during 1997 to 2016 for (a) July, (b) October, (c) January, and (d) April.
For October, EOF2 in Figure 7b is broadly like EOF2 for July in the eastern hemisphere but slightly weaker over the South Pacific Ocean. In fact, EOF3 for October is most like EOF2 for July. Again, the patterns for EOF2 in January (Figure 7c) and EOF2 in April (Figure 7d) follow closely that for July. In all seasons, the leading SH EOFs in the bin with fast-growing instabilities are displaced to lower latitudes, particularly in the Australian region and, to some extent, over the South Atlantic Ocean.
6.2. Band-Pass-Filtered Weather Systems with Periods 4 ≤ Tr < 8 Days
Lower frequency disturbances are considered in this subsection for the three growth rate bins corresponding to amplifying disturbances with periods . We examine, first, monopole cyclone wavetrain EOFs in the three separate bins, in Section 6.2.1, Section 6.2.2 and Section 6.2.3 and then consider dipole EOFs characteristic of blocking and NWCB instabilities in Section 6.2.4.
6.2.1. Slow-Growing Monopole Cyclone Wavetrains (0 ≤ ϖi < 0.5 Day−1)
July EOF1 in Figure 8a(i), for disturbances with growth rates , is structurally very similar to the standard EOF1 in Figure 3a. It also has a likeness to July EOF1 in Figure 5a based on high-pass-filtered data, and in the same growth rate bin, but is of a larger scale as expected. These three patterns all have the dominant wavetrains from South America across the South Atlantic and Indian Oceans to the Australian–NZ region with smaller amplitudes across the South Pacific Ocean. In contrast, July EOF3, for slow-growing instabilities in Figure 8a(ii), is largely a South Pacific disturbance like the standard EOF5 in Figure 3d(ii) based on all fluctuations. The patterns for EOFs 1 and 3 for October in Figure 8b(i) and Figure 8b(ii), respectively, closely match those for July and the standard October EOFs 1 and 3 in Figure 3c,d. Indeed, for each of the central months of the seasons, EOF1 has essentially the same wavetrain (see Figure 8c for January and Figure 8d for April) and also shadows the respective standard EOF1 in Figure 3.
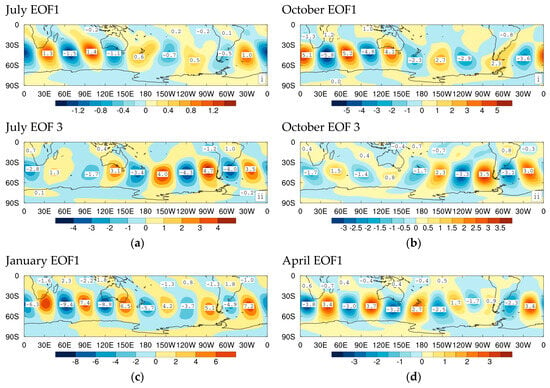
Figure 8.
Leading Southern Hemisphere 850 hPa streamfunction ‘Instability’ EOFs of band-pass-filtered weather systems for period days, for slowly growing disturbances, , during 1997 to 2016 for (a) July, (b) October, (c) January, and (d) April. Figure parts (i) and (ii) distinguish different EOFs in a given month.
6.2.2. Moderately Growing Monopole Cyclone Wavetrain Modes (0.5 ≤ ϖi < 1 Day−1)
The cyclone wavetrain EOFs based on instabilities in the middle growth rate bin, for which , can again be categorised into three broad groups of (1) wavetrains between South America and the Australian–New Zealand region, (2) South Pacific wavetrains, and (3) hemispheric wavetrains. Figure 9 shows examples of EOF1 for the central months of the seasons (July—Figure 9a(i); October—Figure 9b(i); January—Figure 9c; and April—Figure 9d), and, as well, EOF3 in July (Figure 9a(ii)) and EOF3 for October (Figure 9b(ii)). Some of the EOFs swap roles in different months, as seen for July and October. Irrespective of the type of pattern, the EOFs of moderately growing storm track disturbances are displaced equatorward to a latitude band centred on 30° S compared with corresponding standard EOFs in Figure 3, and with EOFs based on slow-growing instabilities in Figure 8, that lie further poleward. This, of course, agrees with the results for the high-pass-filtered instabilities as discussed in Section 6.1.
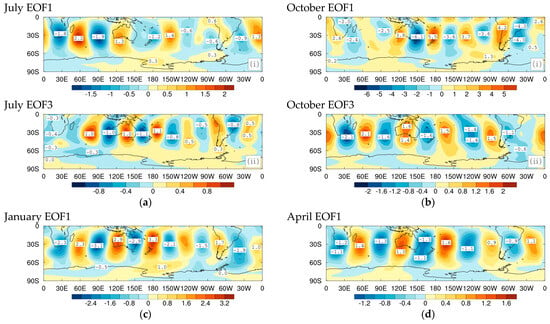
Figure 9.
Leading Southern Hemisphere 850 hPa streamfunction ‘Instability’ EOFs of band-pass-filtered weather systems for period days, for moderately growing disturbances, , during 1997 to 2016 for (a) July, (b) October, (c) January, and (d) April. Figure parts (i) and (ii) distinguish different EOFs in a given month.
6.2.3. Fast-Growing Monopole Cyclone Wavetrain Modes (ϖi ≥ 1 Day−1)
Instabilities in the fastest growth rate bin with again have EOFs characterising storm track modes of the three broad types described in Section 6.2.2. Figure 10 shows EOF1 for each of the four central months of the seasons. They are largely hemispheric modes. There are also EOF variants that represent the three types in each season. Importantly, the patterns of fast-growing instabilities are displaced even further equatorward than for the moderately growing modes of Section 6.2.2. The leading fast-growing instability modes are in a band centred on 25° S.
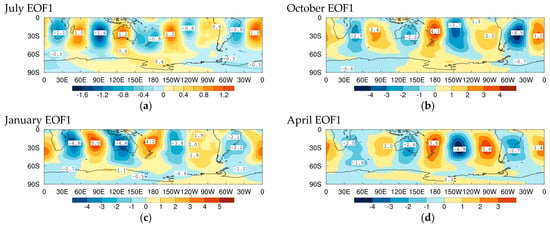
Figure 10.
Leading Southern Hemisphere 850 hPa streamfunction ‘Instability’ EOFs of band-pass-filtered weather systems for period days, for fastest growing disturbances, , during 1997 to 2016 for (a) July, (b) October, (c) January, and (d) April.
EOF1 for July 1997 to 2016 shown in Figure 10a is very like the corresponding EOF1 for July 1949 to 1968 in Figure 3e of Ref. [43] with both equatorward-displaced compared with leading EOFs for disturbances in slower growing bins. However, the current EOF1 is more hemispheric with also significant amplitudes over the South Pacific Ocean. Interestingly EOF4, and its phase-shifted pair, EOF3 for July, consist largely of wavetrains extending from over the Indian Ocean, across Australia, and to the area over the mid-South Pacific Ocean. The leading EOF1 for October in Figure 10b is, as noted, largely hemispheric and equatorward-displaced like EOF1 for July and EOF3 for October, and has a comparable structure to EOF3 and EOF4 for July. These results are consistent with the theme of leading July and October EOFs having much in common. Again, EOF1 for December (Figure 10c) and EOF1 for April (Figure 10d) are akin to those for the other 3 months with hemispheric wavetrains that are larger-scale and further equatorward-displaced than the more tightly formed structures of EOFs for slower-growing instabilities.
6.2.4. Dipole Modes
In each of the seasons, and, particularly, in the cooler months, there are also modes with dipoles in the north–south direction that, at suitable phases, are characteristic of blocking or NWCBs. Figure 11 shows the 850 hPa streamfunction of such EOFs, for four of the cool months based on disturbances in the growth rate bin with . Indeed, amongst the leading 20 or so EOFs, we mainly find dipole modes in this, our bin with the slowest growing disturbances (as well as among the standard EOF of Section 5). Interestingly, this is what would be expected based on the theory of Frederiksen [75] on blocking and localised cyclogenesis. Frederiksen found that, when the climatological confluent–diffluent basic state was quite unstable, cyclogenesis modes would be the fastest-growing with the onset-of-blocking modes having lower growth rates. As the basic state was made less unstable, growth rates, of course, dropped but the onset-of-blocking modes became relatively more prevalent.
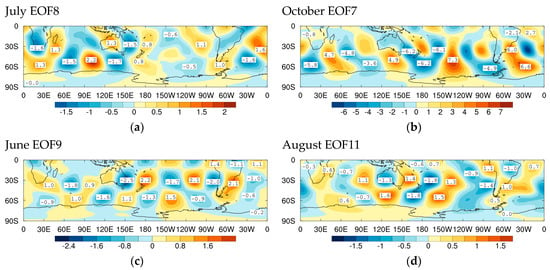
Figure 11.
As in Figure 9 for subdominant ‘Instability’ EOFs that show dipole atmospheric blocking during different months: (a) July, (b) October, (c) June and (d) August.
EOF8 for July in Figure 11a shows dipole structures, particularly in the Australian and New Zealand region. EOF7 for October in Figure 11b has a very distinct dipole to the east of New Zealand embedded in a wavetrain arching from Australia into the Pacific South American region where it resembles the Pacific South American (PSA) pattern (Figure 12 in Ref. [39], Figure 5e in Ref. [72], Figures 4b and 4c in Ref. [73], and Figure 6 in Ref. [74]). EOF9 for July has a similar PSA wavetrain. EOF9 for June in Figure 11c has the iconic structure of blocking near 150° E over the Southern Ocean and an associated east coast low on the east coast of Australia and over the Tasman Sea. The downstream dipole wavetrain can also represent blocks to the east of New Zealand for suitable signs of the anomaly. EOF11 for August in Figure 11d is particularly characteristic of an NWCB disturbance with a wavetrain extending downstream across the Southern Pacific Ocean [60,76,77].
7. Statistics of Weather Systems—All Fluctuations
The standard EOFs based on all Southern Hemisphere high-pass- and band-pass-filtered weather systems, considered in Section 5, show typical wavetrains in the storm tracks. Next, we make further analyses of the statistical properties of the storm tracks determined by the standard deviation (STD) of the 850 hPa streamfunction anomalies for 1997 to 2016. As noted by Osbrough and Frederiksen [43], STDs of meridional winds (in ms−1) are related to the streamfunction STDs (in km2s−1) by multiplying by circa 1.8 (respectively, 1.2) for high-pass (respectively, band-pass) fluctuations. In this section, we examine the seasonal variability of the STDs in the two frequency bands based on all growing and decaying fluctuations, and, in the following, Section 8 the STDs of separate growing and decaying instabilities are analysed. As found by Osbrough and Frederiksen [43], examining the two bands compared with just one band up to periods of 8 days has considerable advantages. It allows the separation of the leading purely monopole cyclone wavetrain modes from more complex structures like dipoles associated with blocking and NWCB disturbances. It also shows that the STD-associated fluctuations with periods are more zonally symmetric than those for .
7.1. Standard Deviations of Weather Systems with Periods Tr < 4 Days
The standard deviation of the 850 hPa streamfunction anomalies for each season is shown in Figure 12 for filtered high-pass disturbances. In each season, the characteristic storm tracks extend from southern South America across the southern South Atlantic and South Indian Oceans to the latitudes of Australia and New Zealand with centres between 45° S and 55° S and with smaller amplitudes across the South Pacific Ocean. The storm track has the largest peak strength in JJA, the weakest in DJF, and with the SON peak slightly larger than MAM. The storm tracks closely follow the structures of the 700 hPa zonal winds shown in Figure 1.
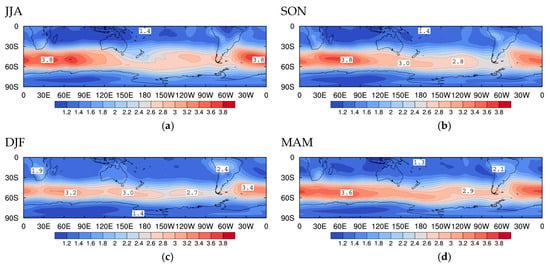
Figure 12.
Standard deviation of Southern Hemisphere 850 hPa streamfunction anomalies (km2s−1) (growing and decaying) for all seasons, using high-pass-filtered data (period ) for 1997 to 2016: (a) JJA, (b) SON, (c) DJF and (d) MAM.
These results conform with the data studies of Trenberth ([9], Figure 6 and Figure 7) and Nakamura and Shimpo ([13], Figure 1 and Figure 2), and the theoretical results of Frederiksen ([38], Figure 5, Figure 6 and Figure 7) and Frederiksen and Frederiksen ([39], Figure 4 and Figure 7). This is so, even though Trenberth [9] considered the January and July 2–8 day-filtered geopotential height and meridional wind anomalies at 300 hPa while [13] focused on the January and July filtered 250 hPa geopotential height anomalies with a cut-off of periods between 6 hours and 8 days. As noted by Osbrough and Frederiksen [43], mid-latitude STDs based on geopotential height, meridional wind, and streamfunction are expected to be similar and the July 300 hPa storm tracks in Ref. [43] are also very similar to our winter results.
7.2. Standard Deviations of Weather Systems with Periods 4 ≤ Tr < 8 Days
Figure 13 shows the corresponding storm tracks to those in Figure 12, but for band-pass-filtered data. In all seasons, Figure 13 depicts a broader and more zonally symmetric band than in Figure 12 for the high-pass results. The larger-scale and slower propagating disturbances have significant peaks over the central South Pacific Ocean, as well as over the South Atlantic and Indian Oceans stretching to the Southern Ocean south of Australia.
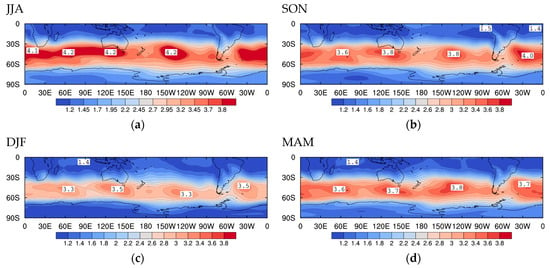
Figure 13.
Standard deviation of Southern Hemisphere 850 hPa streamfunction anomalies (km2s−1) (growing and decaying) for all seasons, using band-pass-filtered data (period days) for 1997 to 2016: (a) JJA, (b) SON, (c) DJF and (d) MAM.
These results differ from those of Trenberth [9] and Nakamura and Shimpo [13] over the central South Pacific since they effectively combine our two bands into one averaged band. Both sets of our storm tracks share common seasonal characteristics with strongest peaks during JJA and weakest in DJF.
8. Statistics of Growing and Decaying Weather Systems
Next, we present a more detailed analysis of the statistics of Southern Hemisphere synoptic-scale weather systems. We consider the STDs of 6-hourly evolved disturbances in each of the six growth rate bins in Table 1. The typical features characterised by some of the leading instability EOFs in the three bins of slow-, moderate-, and fast-growing disturbances have been presented in Section 6.
8.1. Standard Deviations of Weather Systems with Periods Tr < 4 Days
Figure 14 shows the standard deviation of the 6-hour evolved high-pass-filtered, (), 850 hPa Southern Hemisphere streamfunction anomalies for all seasons. Here, the STDs are depicted for each of the six growth rate bins in Table 1. In each panel in Figure 14, the STDs have a largely zonally symmetric band of peak values centred between 45° S to 55° S, like the results based on all fluctuations in Figure 12. As noted in Section 5 and Section 6, this is also the latitude region within which the amplitudes of both the standard and instability EOFs, based on high-pass-filtered data, have their largest values. We note that the peak STDs of disturbances in each growth rate () bin are larger than those for the bin with the same decay rate ( growth rate) because the disturbances have evolved for 6 h. Further, the STDs for the slowly decaying disturbances (panel (iii)) mirror the characteristics of those found in the slowly growing bin (panel (iv)), with maxima upstream of Australia, and smaller amplitudes over the Pacific Ocean. The same applies for STDs in the moderately decaying and growing bins, although, for these, there is more disparity in the magnitude of values.
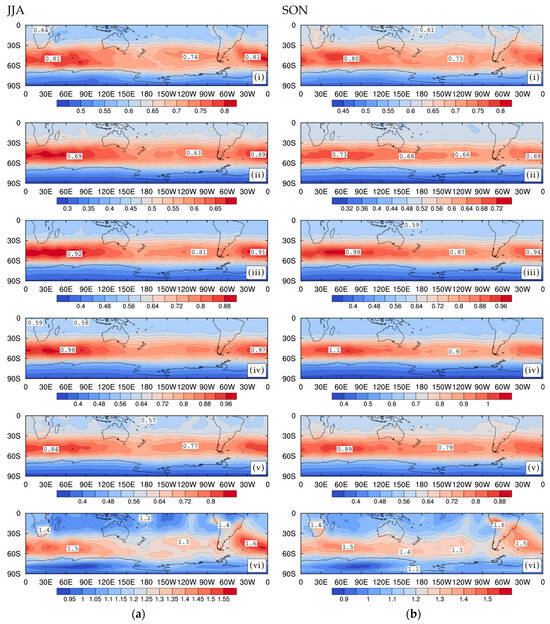
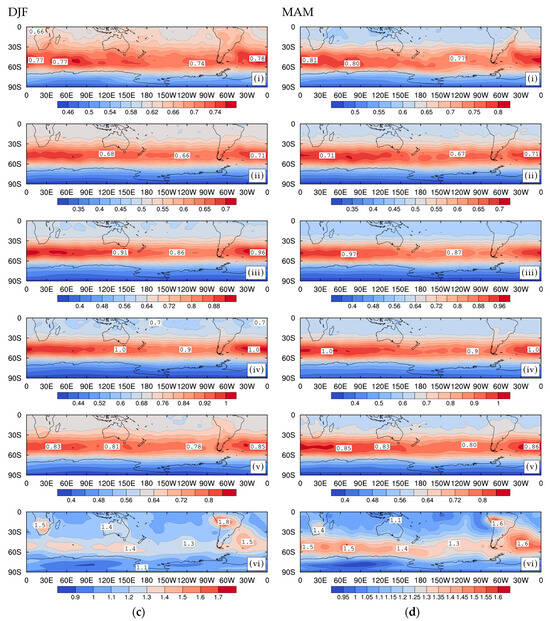
Figure 14.
Standard deviation of 850 hPa Southern Hemisphere streamfunction anomalies (km2s−1) with growth rates separated into bins (i) through (vi), as defined in Table 1, for high-pass-filtered data (period days) during 1997 to 2016 for all seasons: (a) winter, (b) spring, (c) summer, and (d) autumn.
Interestingly, as shown in the last panel (vi) of each figure part in Figure 14, the STDs for disturbances in the fast-growth-rate bin, (), also extend equatorward, particularly in DJF and MAM with maximum values over the continents comparable to those in the primary storm track between 45° S to 55° S. As well, the latitudinal extent between 30° S and 60° S of the storm track is wider than for slower growing or decaying weather systems. This is the case mainly over the South Atlantic Ocean. Particularly in JJA, the storm track across the South Pacific is also strong and has a broad latitudinal extent. The breadth of the intense zonal band shown in winter decreases as we move into spring, with a narrowing of the maximum contours around 50° S. Summer-time peaks occur further poleward in the main storm track, with less intense activity in this zonal band.
The winter-time STD analysis, based on growth rate bins for the 1997 to 2016 period and shown in Figure 14a, is comparable with that for July 1949 to 1968, depicted in Figure 5a of Ref. [43]. There, only four growth rate bins were used, but with the fast-growth and fast-decay bins the same as here. Panel (vi) of Figure 14a is broadly similar to panel (iv) in Figure 5a of Ref. [43] for July 1949 to 1968. However, in the current period, the peak directly over the Australian Bight is absent, but the STDs are larger and has a broader latitudinal impact over the South Pacific Ocean.
8.2. Standard Deviations of Weather Systems with Periods 4 ≤ Tr < 8 Days
Figure 15 shows the seasonal variability STDs of band-pass-filtered () Southern Hemisphere 850 hPa streamfunction anomalies for 1997 to 2016 based on 6-hour evolved NNR data. Again, the results have been stratified by the growth rate bins documented in Table 1. The disturbances with periods between 4 and 8 days are correspondingly slower-propagating and of a larger scale than the high-pass-filtered disturbances as discussed earlier. As we have noted previously, and as is also evident from the STDs of the growing and decaying disturbances considered in this section, there are advantages of filtering our data into our two separate time periods. These include capturing the changing structures and associated processes and, here, the changes in statistics for the different instability modes.
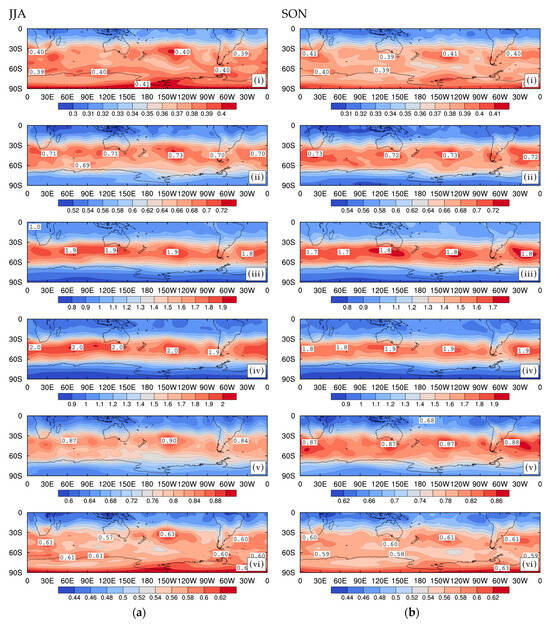
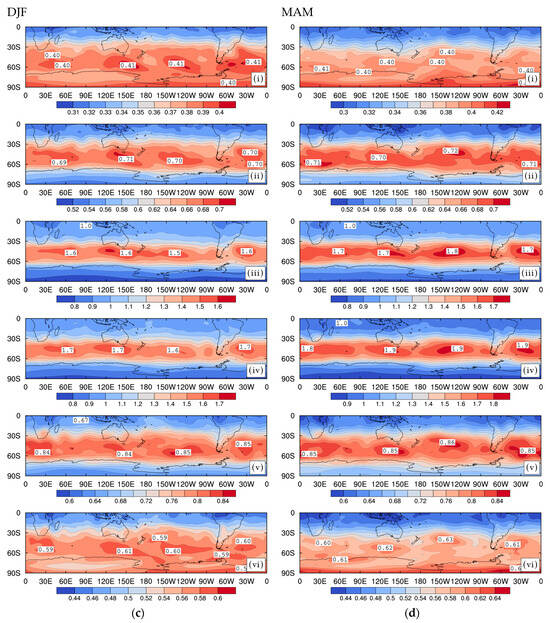
Figure 15.
As in Figure 14 but for band-pass-filtered data with period days.
From Figure 15, we, again, see that the largest STDs, of the 6-hour evolved weather systems, in a particular growth rate () bin are greater than the peak STDs for the corresponding bin with an equal decay rate ( growth rate). As might be expected, the more zonally symmetric structure of the STDs defining the storm tracks for the longer period disturbances with reflect those of Section 7.2 based on all growing and decaying fluctuations. For each season, the storm tracks of the growing and decaying disturbances have significant peaks over the central South Pacific Ocean, unlike the high-pass-filtered results in Section 7.1 and Section 8.1.
In all seasons, Figure 15 depicts a broader and more zonally symmetric band than in Figure 14 for the high-pass results. The larger-scale and slower-propagating disturbances have significant peaks over the central South Pacific Ocean, as well as over the South Atlantic and Indian Oceans stretching to the Southern Ocean south of Australia. Again, the largest differences in magnitude along the central storm tracks in Figure 15 are between the generally lower peak values in summer compared with winter. As is also the case for the high-pass-filtered disturbances, the band-pass results also show an approximate symmetry between those for a given growth rate bin and the corresponding bin with decaying disturbances. The magnitudes of the decaying disturbances are of course generally less because of the 6-hour development.
9. Discussion
We have analysed the seasonal variability of synoptic-scale weather systems for a 20-year timespan in recent years between 1997 and 2016 that includes the AMD. Our study has examined the structures of the SH jet streams and their relationships to the storm tracks based on 850 hPa streamfunction and meridional wind anomalies that have been filtered into a high-pass band where the period is days and a band-pass band with a period days. The NNR 6-hourly data has been used to establish and analyse the leading standard EOFs based on the meridional wind, and we have displayed them in the streamfunction space. As well, we have examined the structure of the standard deviations (STDs) of streamfunction fluctuations based on all (growing and decaying) disturbances in the two frequency bands.
We have also used the new data-driven methodology developed by Osbrough and Frederiksen [43], in which the NNR data are decomposed spectrally in space and time and the weather systems analysed in six growth rate bins for both filter bands. This has allowed us to study the statistical structures of the growing disturbances in three bins through leading instability EOFs. We have also determined the storm tracks based on STDs of 850 hPa streamfunction anomalies associated with both growing and decaying anomalies in the six bins.
The seasonal evolution of the SH subtropical and polar jet streams for our 20-year timespan 1997 to 2016 is, as expected, broadly similar to the seasonal march described by Nakamura and Shimpo [13] for 1979 to 1995 and Hoskins and Hodges [19] for 1958 to 2002. Nevertheless, the SH zonal winds have undergone significant changes in strength during the last 70 years as noted in Refs. [60,65] for July and in Ref. [50] more generally. The upper tropospheric and lower stratospheric subtropical jet has been reducing in strength and the polar jet increasing with significant shifts, particularly after the mid-1970s.
Throughout the seasonal cycle, the polar jet is strong and deep with significant westerly winds extending throughout the troposphere but with the largest wind speeds in the upper troposphere and lower stratosphere of the SH. The polar jets at 300 hPa and 700 hPa extend across the whole hemisphere with the largest values in a band between 45–55° S, particularly over the South Atlantic, and the South Indian Ocean, and waning over the South Pacific Ocean at the longitudes of Australia.
The subtropical jet at 300 hPa lies in a latitude band between 30–35° S and is strong between longitudes of 90–240° E, particularly in austral winter when it dominates the polar jet in the upper troposphere and lower stratosphere. The subtropical jet at 300 hPa is also prominent in austral spring when there is an increase in intensity of the polar jet. In austral autumn, the upper tropospheric subtropical jet is still evident but at a reduced strength, and it is greatly reduced or essentially absent in austral summer. The subtropical jet is shallow compared with the polar jet with much weaker winds at 700 hPa compared with 300 hPa even in austral winter.
The zonal asymmetries and seasonal variability of the large-scale SH circulation, particularly the zonal jets and baroclinicity, in turn, affect the structures and amplitudes of the mid-latitude weather systems. Generally speaking, the baroclinic Rossby waves and their storm tracks are most similar for the austral winter and autumn circulations and for the austral summer and spring seasons.
Throughout the year, the standard storm tracks and standard leading EOFs based on all growing and decaying 850 hPa high-pass-filtered weather systems have prominent peaks that coincide with the 700 hPa polar jet stream between 45° S and 55° S. This is also the case for the band-pass-filtered cyclone wavetrain modes except the storm tracks, and some leading standards EOFs also have significant amplitudes across the South Pacific Ocean. There are, however, seasonal variations in the structures of the standard EOFs, particularly in the Australian region where leading EOFs generally cross the continent in austral winter and autumn, while they mainly have centres and storm tracks displaced to slightly higher latitudes in summer and spring. Earlier diagnostic studies have tended to combine our high-pass- and band-pass-filtered results into a single band, and, hence, different behaviours between the larger-scale band-pass disturbances and the high-pass storms and high-pressure systems are not evident. In fact, the zonal asymmetry of our high-pass storm tracks is most reflected in earlier studies with broader filters.
Some of the standard EOFs for band-pass-filtered anomalies have dipole wavetrains, particularly in the cooler months, that generally extend from the Australian region to around 240° E. These modes have structures that, with suitable signs, are consistent with dipole blocking anomalies or NWCBs.
10. Conclusions
In this data-driven study, we have made a first and detailed analysis of the seasonal cycle of SH storm tracks associated with growing and decaying instabilities using the methodology of Osbrough and Frederiksen [43]. Results have been presented for disturbances in six growth rate bins, three for each of the growing and decaying weather systems. The STDs of 850 hPa streamfunction anomalies representing the instability storm tracks have, again, been examined for high-pass- and band-pass-filtered data. As well, the leading instability EOFs have been calculated and their structures examined for growing weather systems in the three bins corresponding to slow (), medium (), and fast () growth. As found in Ref. [43], the growing disturbances, notably, explosive storms, and their variability are strongly related to mid-winter rainfall variations over southern Australian and are especially of interest.
Instability EOFs for the slow-growth bin are structurally similar to the corresponding standard EOFs for both filtered bands, as might perhaps be expected. As the growth rate is increased by going to the instability EOFs for the moderate-growth bin, we find that the patterns of leading storm track modes are shifted slightly equatorward, particularly so for the larger-scale and longer-period EOFs that have peaks near 30° S. This equatorward displacement is even more evident for leading monopole storm track instability EOFs for the fast-growth bin, particularly in the Australian region.
Some instability EOFs for band-pass-filtered weather systems also have dipole wavetrains, broadly similar to some of the standard EOFs, with these anomalies again mainly located between 100° E to 240° E. These dipoles that resemble blocking and NWCB disturbances primarily occur for the bin of slow-growing anomalies.
Author Contributions
Conceptualisation, S.L.O. and J.S.F.; methodology, S.L.O. and J.S.F.; software, S.L.O.; validation, S.L.O. and J.S.F.; formal analysis, S.L.O. and J.S.F.; investigation, S.L.O. and J.S.F.; resources, S.L.O.; data curation, S.L.O.; writing—original draft preparation, S.L.O.; writing—review and editing, J.S.F.; visualisation, S.L.O.; supervision, J.S.F.; project administration, S.L.O.; funding acquisition, S.L.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Australian Government’s National Environmental Science Program’s Climate Systems Hub. Stacey L. Osbrough is an employee of the Commonwealth Scientific and Industrial Research Organisation. Jorgen S. Frederiksen is an honorary fellow at the Commonwealth Scientific and Industrial Research Organisation.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The atmospheric circulation data are available from the NOAA/ESRL website: https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html (accessed on 17 May 2024). The data displayed in our figures are available upon request.
Acknowledgments
We acknowledge the support of Australian Government’s National Environmental Science Program’s Climate Systems Hub. This work contributes to the Ph.D. thesis of Stacey Osbrough at Monash University (2023).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
Correction Statement
This article has been republished with a minor correction to resolve spelling and grammatical errors. This change does not affect the scientific content of the article.
Appendix A. Method for Determining Growing and Decaying Weather Systems
The mathematical method for separating the total field of fluctuating disturbances into growing and decaying components in different growth rate bins is described in Ref. [43]. As noted there, POPs and dynamical instability modes have a time dependence of the form , where is the complex angular frequency, with the real part being the frequency and the imaginary part the growth rate. Similarly, the time dependence of the spectral coefficient of the growing or decaying disturbance is presented in the form with
where is the angular frequency, is the growth rate, and
Here, is the spectral coefficient in Equation (1). Suppose is the time interval between observations; then, the ratio of the spectral coefficients at times and becomes
Thus, the growth rate between and is determined by the modulus as
with
Equation (A3) also yields the equation for frequency, :
Appendix B. Empirical Orthogonal Functions
Suppose we denote by the column vector of length of our field variables in physical space or in spectral space. Then, the Empirical Orthogonal functions (EOFs) are just the eigenvectors of the covariance matrix:
Here, + denotes the Hermitian conjugate if represents complex spectral components and transpose for physical fields. The eigenvalues η give a measure of the percent variance that a given EOF explains.
References
- Bjerknes, J.; Solberg, H. Life cycle of cyclones and the polar front theory of atmospheric circulation. Geofysiske Publikationer 1922, 3, 3–18. [Google Scholar]
- Bjerknes, J.; Solberg, H. Meteorological Conditions for the Formation of Rain. Geofysiske Publikationer 1921, 2, 3–61. [Google Scholar]
- Blackmon, M.L. A Climatological Spectral Study of 500 Mb Geopotential Height of Northern Hemisphere. J. Atmos. Sci. 1976, 33, 1607–1623. [Google Scholar] [CrossRef]
- Blackmon, M.L.; Wallace, J.M.; Lau, N.-C.; Mullen, S.L. An Observational Study of the Northern Hemisphere Wintertime Circulation. J. Atmos. Sci. 1977, 34, 1040–1053. [Google Scholar] [CrossRef]
- van Loon, H. A climatological study of the atmospheric circulation in the Southern Hemisphere during the IGY, Part I: 1 July 1957–31 March 1958. J. Appl. Meteorol. Climatol. 1965, 4, 479–491. [Google Scholar] [CrossRef]
- Taljaard, J.J. Development, distribution and movement of cyclones and anticyclones in the Southern Hemisphere during the IGY. J. Appl. Meteorol. Climatol. 1967, 6, 973–987. [Google Scholar] [CrossRef]
- Trenberth, K.E. Observed Southern Hemisphere Eddy Statistics at 500 mb: Frequency and Spatial Dependence. J. Atmos. Sci. 1981, 38, 2585–2605. [Google Scholar] [CrossRef][Green Version]
- Trenberth, K.E. Seasonality in Southern-Hemisphere Eddy Statistics at 500 Mb. J. Atmos. Sci. 1982, 39, 2507–2520. [Google Scholar] [CrossRef]
- Trenberth, K.E. Storm Tracks in the Southern-Hemisphere. J Atmos Sci 1991, 48, 2159–2178. [Google Scholar] [CrossRef]
- Berbery, E.H.; Vera, C.S. Characteristics of the Southern Hemisphere winter storm track with filtered and unfiltered data. J. Atmos. Sci. 1996, 53, 468–481. [Google Scholar] [CrossRef]
- Rao, V.B.; Do Carmo, A.; Franchito, S.H. Seasonal variations in the Southern Hemisphere storm tracks and associated wave propagation. J. Atmos. Sci. 2002, 59, 1029–1040. [Google Scholar] [CrossRef]
- Chang, E.K. Characteristics of wave packets in the upper troposphere. Part II: Seasonal and hemispheric variations. J. Atmos. Sci. 1999, 56, 1729–1747. [Google Scholar] [CrossRef]
- Nakamura, H.; Shimpo, A. Seasonal variations in the Southern Hemisphere storm tracks and jet streams as revealed in a reanalysis dataset. J. Clim. 2004, 17, 1828–1844. [Google Scholar] [CrossRef]
- Lim, E.-P.; Simmonds, I. Southern Hemisphere Winter Extratropical Cyclone Characteristics and Vertical Organization Observed with the ERA-40 Data in 1979–2001. J. Clim. 2007, 20, 2675–2690. [Google Scholar] [CrossRef]
- Quinting, J.F.; Catto, J.L.; Reeder, M.J. Synoptic climatology of hybrid cyclones in the Australian region. Q. J. R. Meteorol. Soc. 2019, 145, 288–302. [Google Scholar] [CrossRef]
- Simmonds, I.; Keay, K. Variability of Southern Hemisphere extratropical cyclone behavior, 1958–97. J. Clim. 2000, 13, 550–561. [Google Scholar] [CrossRef]
- Sinclair, M.R. A climatology of cyclogenesis for the Southern Hemisphere. Mon. Weather Rev. 1995, 123, 1601–1619. [Google Scholar] [CrossRef]
- Sinclair, M.R. An Objective Cyclone Climatology for the Southern Hemisphere. Mon. Weather Rev. 1994, 122, 2239–2256. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Hodges, K.I. A new perspective on Southern Hemisphere storm tracks. J. Clim. 2005, 18, 4108–4129. [Google Scholar] [CrossRef]
- Simmonds, I.; Murray, R.J. Southern extratropical cyclone behavior in ECMWF analyses during the FROST special observing periods. Weather Forecast. 1999, 14, 878–891. [Google Scholar] [CrossRef]
- Wang, X.L.L.; Swail, V.R.; Zwiers, F.W. Climatology and changes of extratropical cyclone activity: Comparison of ERA-40 with NCEP-NCAR reanalysis for 1958–2001. J. Clim. 2006, 19, 3145–3166. [Google Scholar] [CrossRef]
- Barnes, M.A.; King, M.; Reeder, M.; Jakob, C. The dynamics of slow-moving coherent cyclonic potential vorticity anomalies and their links to heavy rainfall over the eastern seaboard of Australia. Q. J. R. Meteorol. Soc. 2023, 149, 2233–2251. [Google Scholar] [CrossRef]
- Zhan, X.Y.; Chen, L. Climatology and Changes in Extratropical Cyclone Activity in the Southern Hemisphere during Austral Winters from 1948 to 2017. J. Appl. Meteorol. Climatol. 2023, 62, 971–983. [Google Scholar] [CrossRef]
- Messmer, M.; Simmonds, I. Global analysis of cyclone-induced compound precipitation and wind extreme events. Weather Clim. Extrem. 2021, 32, 100324. [Google Scholar] [CrossRef]
- Charney, J.G. The Dynamics of Long Waves in a Baroclinic Westerly Current. J. Meteorology. 1947, 4, 136–162. [Google Scholar] [CrossRef]
- Eady, E.T. Long Waves and Cyclone Waves. Tellus 1949, 1, 33–52. [Google Scholar] [CrossRef]
- Phillips, N.A. Energy Transformations and Meridional Circulations associated with simple Baroclinic Waves in a two-level, Quasi-geostrophic Model. Tellus 1954, 6, 273–286. [Google Scholar] [CrossRef]
- Rossby, C.-G. Planetary flow patterns in the atmosphere. Q. J. R. Meteorol. Soc. 1940, 66, 68–87. [Google Scholar] [CrossRef]
- Rossby, C.-G. On the propagation of frequencies and energy in certain types of oceanic and atmospheric waves. J. Atmos. Sci. 1945, 2, 187–204. [Google Scholar] [CrossRef]
- Frederiksen, J.S. The Effects of Long Planetary Waves on the Regions of Cyclogenesis: Linear Theory. J. Atmos. Sci. 1979, 36, 195–204. [Google Scholar] [CrossRef][Green Version]
- Frederiksen, J.S. Growth and Vacillation Cycles of Disturbances in Southern-Hemisphere Flows. J. Atmos. Sci. 1981, 38, 1360–1375. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; Webster, P.J. Alternative Theories of Atmospheric Teleconnections and Low-Frequency Fluctuations. Rev. Geophys. 1988, 26, 459–494. [Google Scholar] [CrossRef]
- Frederiksen, J.S. Instability Theory and Predictability of Atmospheric Disturbances. In Frontiers in Turbulence and Coherent Structures; World Scientific Lecture Notes in Complex Systems; Denier, J., Frederiksen, J.S., Eds.; World Scientific Publishing: Singapore, 2007; Volume 2007, pp. 29–57. [Google Scholar]
- Frederiksen, J.S. Instability of planetary waves and zonal flows in two-layer models on a sphere. Q. J. R. Meteorol. Soc. 1978, 104, 841–872. [Google Scholar] [CrossRef]
- Frederiksen, J.S. Zonal and Meridional Variations of Eddy Fluxes Induced by Long Planetary Waves. Q. J. R. Meteorol. Soc. 1980, 106, 63–84. [Google Scholar] [CrossRef]
- Frederiksen, J.S. Disturbances and Eddy Fluxes in Northern Hemisphere Flows: Instability of 3-Dimensional January and July Flows. J. Atmos. Sci. 1983, 40, 836–855. [Google Scholar] [CrossRef]
- Frederiksen, C.S.; Frederiksen, J.S. Northern Hemisphere Storm Tracks and Teleconnection Patterns in Primitive Equation and Quasi-Geostrophic Models. J. Atmos. Sci. 1992, 49, 1443–1458. [Google Scholar] [CrossRef]
- Frederiksen, J.S. The Geographical Locations of Southern Hemisphere Storm Tracks: Linear Theory. J. Atmos. Sci. 1985, 42, 710–723. [Google Scholar] [CrossRef][Green Version]
- Frederiksen, J.S.; Frederiksen, C.S. Southern Hemisphere Storm Tracks, Blocking, and Low-Frequency Anomalies in a Primitive Equation Model. J. Atmos. Sci. 1993, 50, 3148–3163. [Google Scholar] [CrossRef]
- Gall, R. A Comparison of Linear Baroclinic Instability Theory with Eddy Statistics of a General Circulation Model. J. Atmos. Sci. 1976, 33, 349–373. [Google Scholar] [CrossRef]
- Simmons, A.J.; Hoskins, B.J. The Life Cycles of Some Nonlinear Baroclinic Waves. J. Atmos. Sci. 1978, 35, 414–432. [Google Scholar] [CrossRef]
- Frederiksen, J.S. Baroclinic Instability of Zonal Flows and Planetary Waves in Multilevel Models on a Sphere. J. Atmos. Sci. 1979, 36, 2320–2335. [Google Scholar] [CrossRef]
- Osbrough, S.L.; Frederiksen, J.S. Interdecadal changes in Southern Hemisphere winter explosive storms and Southern Australian rainfall. Clim. Dyn. 2021, 56, 3103–3130. [Google Scholar] [CrossRef]
- Sanders, F.; Gyakum, J.R. Synoptic-Dynamic Climatology of the “Bomb”. Mon. Weather Rev. 1980, 108, 1589–1606. [Google Scholar] [CrossRef]
- Roebber, P.J. Statistical Analysis and Updated Climatology of Explosive Cyclones. Mon. Weather Rev. 1984, 112, 1577–1589. [Google Scholar] [CrossRef]
- Petty, G.W.; Miller, D.K. Satellite Microwave Observations of Precipitation Correlated with Intensification Rate in Extratropical Oceanic Cyclones. Mon. Weather Rev. 1995, 123, 1904–1911. [Google Scholar] [CrossRef][Green Version]
- McMurdie, L.A.; Katsaros, K.B. Satellite-Derived integrated water vapor and rain intensity patterns: Indicators for rapid cyclogenesis. Weather Forecast. 1996, 11, 230–245. [Google Scholar] [CrossRef][Green Version]
- Martin, J.E.; Otkin, J.A. The rapid growth and decay of an extratropical cyclone over the central Pacific Ocean. Weather Forecast. 2004, 19, 358–376. [Google Scholar] [CrossRef]
- Risbey, J.S.; Pook, M.J.; McIntosh, P.C. Spatial trends in synoptic rainfall in southern Australia. Geophys. Res. Lett. 2013, 40, 3781–3785. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; Osbrough, S.L. Tipping Points and Changes in Australian Climate and Extremes. Climate 2022, 10, 73. [Google Scholar] [CrossRef]
- Fawcett, R.J.B. Seasonal climate summary southern hemisphere (summer 2003/04): A warm summer in the east and wet conditions in the northwest. In Aust. Meteorol. Mag.; 2004; 53, pp. 305–317. Available online: http://www.bom.gov.au/jshess/docs/2004/fawcett_hres.pdf (accessed on 30 April 2024).
- Gallant, A.J.E.; Hennessy, K.J.; Risbey, J. Trends in rainfall indices for six Australian regions: 1910–2005. Aust. Meteorol. Mag. 2007, 56, 223–239. [Google Scholar]
- Watkins, A.; Trewin, B. Australian climate summary: 2006. In Bull. Aust. Meteorol. Oceanogr. Soc.; 2007; 20, pp. 10–17. Available online: http://www.bom.gov.au/climate/annual_sum/2006/AnClimSum06.pdf (accessed on 30 April 2024).
- Ummenhofer, C.C.; England, M.H.; McIntosh, P.C.; Meyers, G.A.; Pook, M.J.; Risbey, J.S.; Gupta, A.S.; Taschetto, A.S. What causes southeast Australia’s worst droughts? Geophys. Res. Lett. 2009, 36, L04706. [Google Scholar] [CrossRef]
- Gallant, A.J.E.; Reeder, M.J.; Risbey, J.S.; Hennessy, K.J. The characteristics of seasonal-scale droughts in Australia, 1911–2009. Int. J. Climatol. 2013, 33, 1658–1672. [Google Scholar] [CrossRef]
- Risbey, J.S.; McIntosh, P.C.; Pook, M.J. Synoptic components of rainfall variability and trends in southeast Australia. Int. J. Climatol. 2013, 33, 2459–2472. [Google Scholar] [CrossRef]
- Cai, W.; Purich, A.; Cowan, T.; van Rensch, P.; Weller, E. Did Climate Change–Induced Rainfall Trends Contribute to the Australian Millennium Drought? J. Clim. 2014, 27, 3145–3168. [Google Scholar] [CrossRef]
- Trewin, B. An Exceptionally Dry Decade in Parts of Southern and Eastern Australia October 1996–September 2006; Special Climate Statement 9; Australian Bureau of Meteorlogy: Melbourne, Australia, 2006; 9p. Available online: http://www.bom.gov.au/climate/current/statements/scs9a.pdf (accessed on 30 April 2024).
- Timbal, B.; Arblaster, J.; Braganza, K.; Fernandez, E.; Hendon, H.; Murphy, B.; Raupach, M.; Rakich, C.; Smith, I.; Whan, K.; et al. Understanding the Anthropogenic Nature of the Observed Rainfall Decline across South Eastern Australia; CAWCR technical report 26; Australian Bureau of Meteorology: Melbourne, Australia, 2010; 202p. Available online: https://www.cawcr.gov.au/technical-reports/CTR_026.pdf (accessed on 30 April 2024).
- Frederiksen, J.S.; Frederiksen, C.S. Twentieth Century Winter Changes in Southern Hemisphere Synoptic Weather Modes. Adv. Meteorol. 2011, 2011, 353829. [Google Scholar] [CrossRef]
- O’Kane, T.J.; Risbey, J.S.; Franzke, C.; Horenko, I.; Monselesan, D.P. Changes in the Metastability of the Midlatitude Southern Hemisphere Circulation and the Utility of Nonstationary Cluster Analysis and Split-Flow Blocking Indices as Diagnostic Tools. J. Atmos. Sci. 2013, 70, 824–842. [Google Scholar] [CrossRef]
- Franzke, C.L.E.; O’Kane, T.J.; Monselesan, D.P.; Risbey, J.S.; Horenko, I. Systematic attribution of observed Southern Hemisphere circulation trends to external forcing and internal variability. Nonlinear Process. Geophys. 2015, 22, 513–525. [Google Scholar] [CrossRef]
- Straus, D.M.; Molteni, F.; Corti, S. Atmospheric regimes: The link between weather and the large scale circulation. In Nonlinear Stochast Clim Dyn; Franzke, C.L.E., O’Kane, T., Eds.; Cambridge University Press: Cambridge, UK, 2017; pp. 105–135. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; Frederiksen, C.S. Interdecadal changes in southern hemisphere winter storm track modes. Tellus A Dyn. Meteorol. Oceanogr. 2007, 59, 599–617. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; Lin, H. Tropical–extratropical interactions of intraseasonal oscillations. J. Atmos. Sci. 2013, 70, 3180–3197. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; Frederiksen, C. Decadal Changes in Southern Hemisphere Winter Cyclogenesis; CSIRO Marine and Atmospheric research paper No. 002; CSIRO Publishing: Canberra, Australia, 2005; 29p, Available online: http://www.cmar.csiro.au/e-print/open/frederiksenjs_2005b.pdf (accessed on 30 April 2024).
- Hope, P.K.; Drosdowsky, W.; Nicholls, N. Shifts in the synoptic systems influencing southwest Western Australia. Clim. Dyn. 2006, 26, 751–764. [Google Scholar] [CrossRef]
- Hope, P.K.; Grose, M.R.; Timbal, B.; Dowdy, A.J.; Bhend, J.; Katzfey, J.J.; Bedin, T.; Wilson, L.; Whetton, P.H. Seasonal and regional signature of the projected southern Australian rainfall reduction. Aust. Meteorol. Oceanogr. J. 2015, 65, 54–71. [Google Scholar] [CrossRef]
- Frederiksen, C.S.; Frederiksen, J.S.; Sisson, J.M.; Osbrough, S.L. Trends and projections of Southern Hemisphere baroclinicity: The role of external forcing and impact on Australian rainfall. Clim. Dyn. 2017, 48, 3261–3282. [Google Scholar] [CrossRef]
- Archer, C.L.; Caldeira, K. Historical trends in the jet streams. Geophys. Res. Lett. 2008, 35, L08803. [Google Scholar] [CrossRef]
- Karoly, D.J. Southern-Hemisphere Circulation Features Associated with Elnino—Southern Oscillation Events. J. Clim. 1989, 2, 1239–1252. [Google Scholar] [CrossRef]
- Kidson, J.W. Interannual Variations in the Southern Hemisphere Circulation. J. Clim. 1988, 1, 1177–1198. [Google Scholar] [CrossRef]
- O’Kane, T.J.; Monselesan, D.P.; Risbey, J.S. A Multiscale Reexamination of the Pacific–South American Pattern. Mon. Weather Rev. 2017, 145, 379–402. [Google Scholar] [CrossRef]
- Frederiksen, J.S. A Unified 3-Dimensional Instability Theory of the Onset of Blocking and Cyclogenesis. J. Atmos. Sci. 1982, 39, 969–982. [Google Scholar] [CrossRef]
- Frederiksen, C.S.; Frederiksen, J.S. A theoretical model of Australian northwest cloudband disturbances and southern hemisphere storm tracks: The role of SST anomalies. J. Atmos. Sci. 1996, 53, 1410–1432. [Google Scholar] [CrossRef]
- Reid, K.J.; Simmonds, I.; Vincent, C.L.; King, A.D. The Australian Northwest Cloudband: Climatology, Mechanisms, and Association with Precipitation. J. Clim. 2019, 32, 6665–6684. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).