The Recovery and Re-Calibration of a 13-Month Aerosol Extinction Profiles Dataset from Searchlight Observations from New Mexico, after the 1963 Agung Eruption
Abstract
1. Introduction
1.1. A Brief Historical Context for the Searchlight Atmospheric Profiling Technique
1.2. The New Mexico Searchlight Observations and the SSiRC Focus on the Agung Aerosol Cloud
2. Searchlight Instrument and Observations Processing
2.1. The Searchlight Instrument
2.2. Searchlight Observations and Its Original Processing
- (1)
- The operational time that could be allowed was limited;
- (2)
- Operations were conducted only during moonless nights in order to keep noise background at a minimum;
- (3)
- Operations were canceled when meteorological conditions were unfavorable. This included high winds as well as cloudy skies. July and August seasonally are months when both dust storms and cloudy skies occur daily in New Mexico;
- (4)
- Equipment difficulties accounted for the absence of data in January 1964 and at other times;
- (5)
- Failure of site facilities, especially telephone lines, resulted in considerable loss of time. Synchronous rectification and amplification depended on the transmission of the synchronizing signal by telephone.
3. The Recovery of the Searchlight 550 nm Aerosol Extinction Profiles and Estimated Errors
4. The Re-Calibration Procedure: Constrains, Improvements, and Design
4.1. Constrains
4.2. Improvements
4.3. Design of the Re-Calibration
5. Retrieving the Normalized Detector Response
5.1. Retrieval Procedure of the Normalized Detector Response
5.2. Slant Transmission Algorithm
5.3. Variables Used for the Retrieval
5.4. Retrieved Normalized Detector Response
6. Parameters Used to Re-Calibrate
6.1. Daily Rayleigh Extinction Profiles from Radiosondes
6.2. Tropospheric and Stratospheric Aerosol Phase Functions
6.2.1. Tropospheric Aerosol Phase Function
6.2.2. Stratospheric Aerosol Phase Function
6.3. Rayleigh, Aerosol, and Ozone Slant Transmissions
6.4. Tropopause Altitudes
7. Re-Calibration, Adjustments, Errors Not Accounted for in the Original Dataset, and Estimated Errors
7.1. Preliminary Re-Calibrated Results
7.2. Subsequent Adjustments of the Updated Parameters
7.3. Errors Not Accounted for in the Original DatasetOK
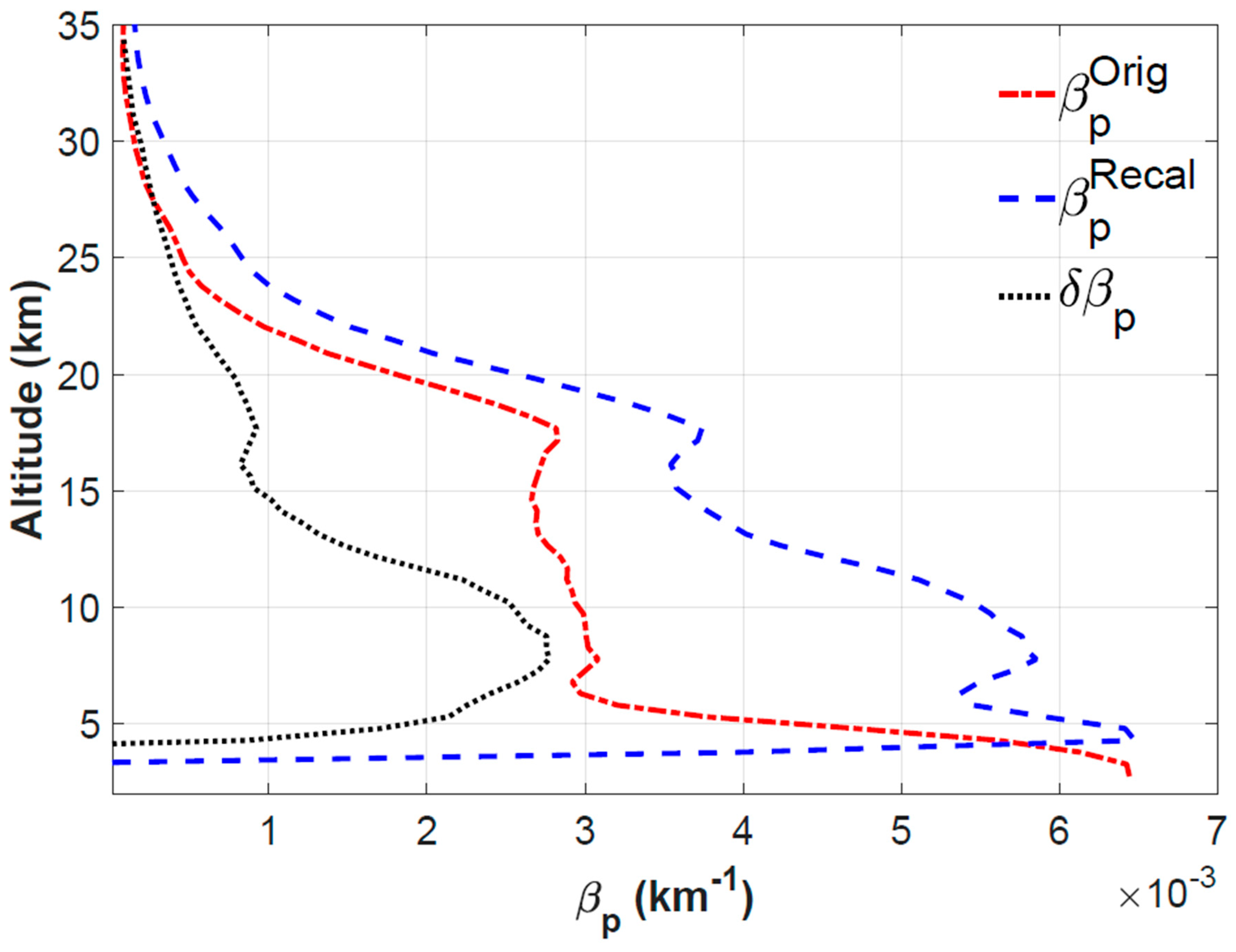
7.4. Estimated Errors
8. Results and Discussion
8.1. Rescued Profiles of
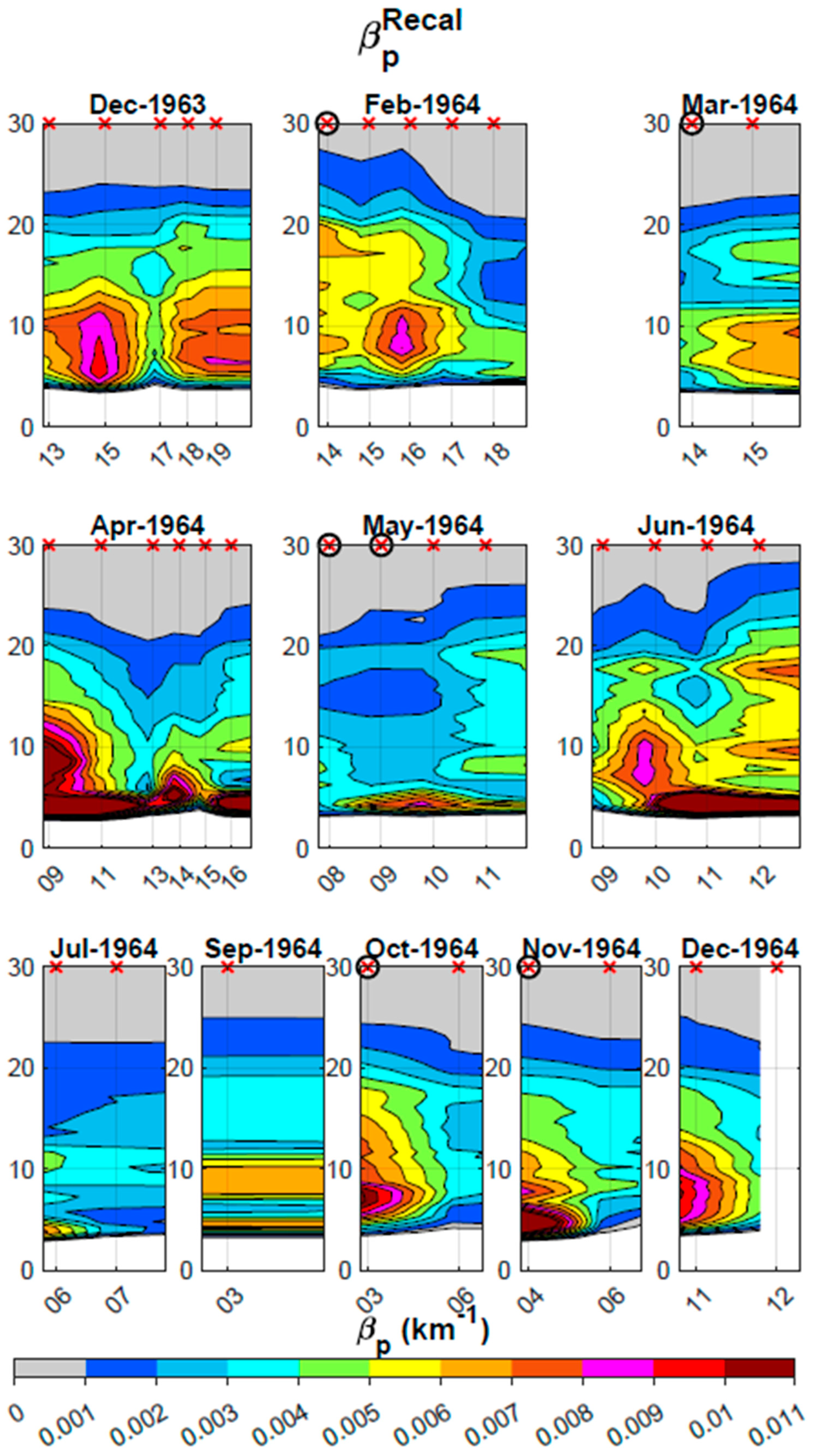
8.2. Re-Calibrated Profiles
8.3. Averaged Rescued and Re-Calibrated Aerosol Extinction Profiles
8.4. Daily Tropospheric AOD from the Rescued and Re-Calibrated Aerosol Extinction Profiles
8.5. Stratospheric AOD from the Rescued (Original) and Re-Calibrated Aerosol Extinction Profiles
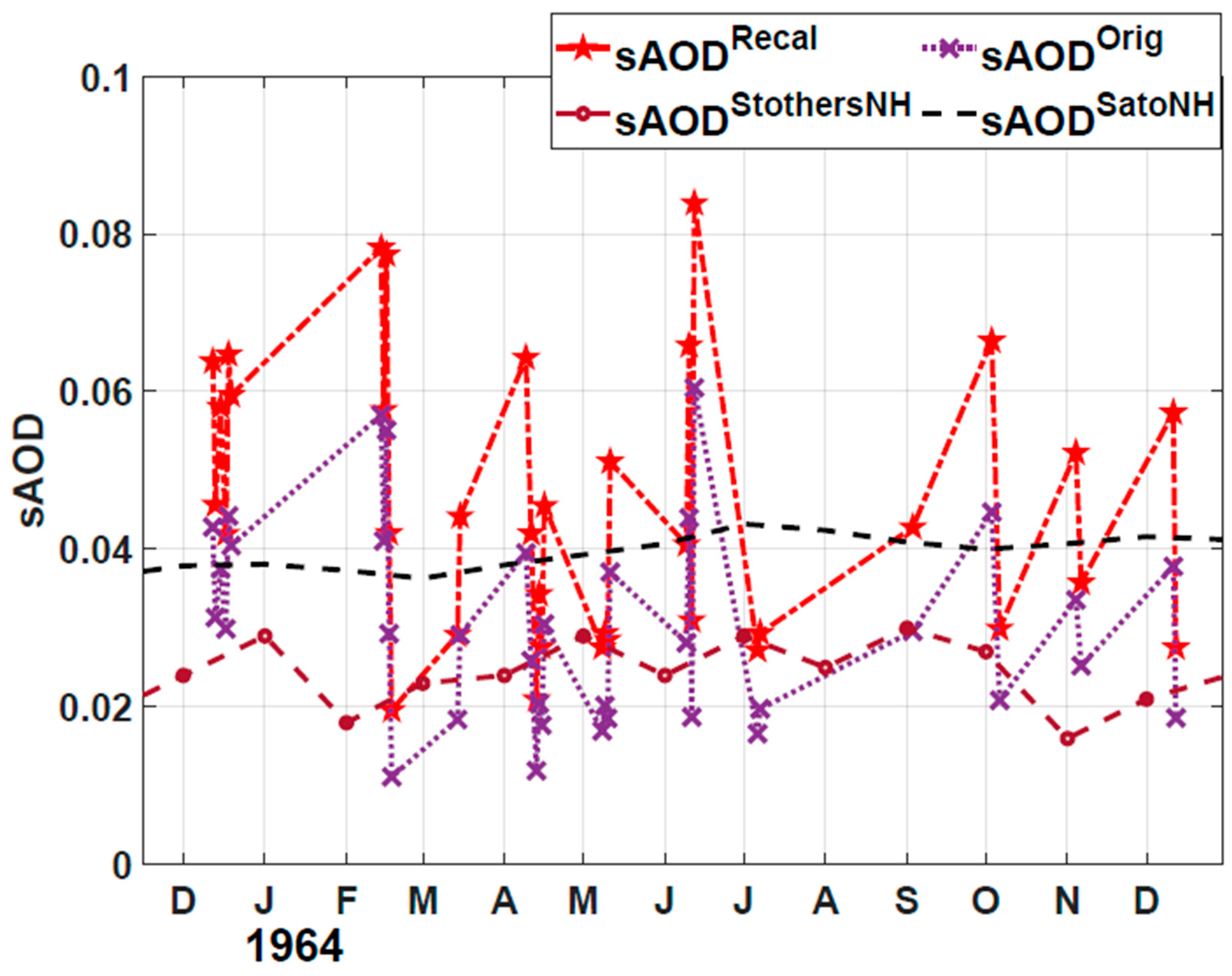
8.5.1. Daily Original and Re-Calibrated sAOD
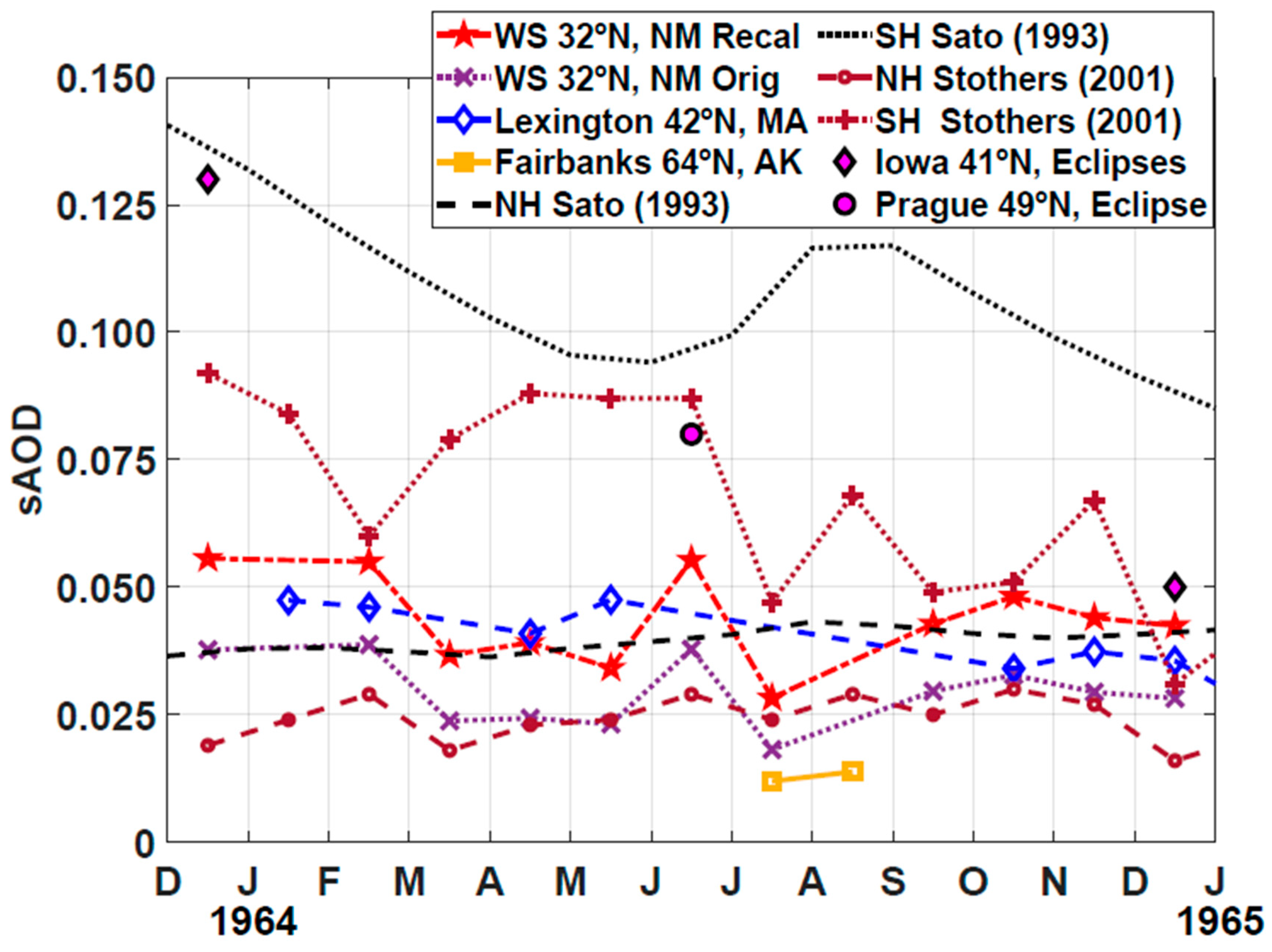
8.5.2. Monthly Mean sAOD
9. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Timmreck, C. Modeling the climatic effects of large explosive volcanic eruptions. WIREs Clim. Chang. 2012, 3, 545–564. [Google Scholar] [CrossRef]
- Robock, A. Volcanic eruptions and climate. Rev. Geophys. 2000, 38, 191–219. [Google Scholar] [CrossRef]
- Kremser, S.; Thomason, L.W.; von Hobe, M.; Hermann, M.; Deshler, T.; Timmreck, C.; Toohey, M.; Stenke, A.; Schwarz, J.P.; Weigelet, R.; et al. Stratospheric aerosol—Observations, processes, and impact on climate. Rev. Geophys. 2016, 54, 278–335. [Google Scholar] [CrossRef]
- Zanchettin, D.; Khodri, M.; Timmreck, C.; Toohey, M.; Schmidt, A.; Gerber, E.; Hegerl, G.; Robock, A.; Pausata, F.; Ball, W.T.; et al. The Model Intercomparison Project on the climatic response to volcanic forcing (VolMIP): Experimental design and forcing input data. Geosci. Model Dev. 2016, 9, 2701–2719. [Google Scholar] [CrossRef]
- Zanchettin, D.; Timmreck, C.; Khodri, M.; Schmidt, A.; Toohey, M.; Abe, M.; Bekki, S.; Cole, J.; Fang, S.-W.; Feng, W.; et al. Effects of forcing differences and initial conditions on inter-model agreement in the VolMIP volc-pinatubo-full experiment. Geosci. Model Dev. 2022, 15, 2265–2292. [Google Scholar] [CrossRef]
- Timmreck, C.; Mann, G.W.; Aquila, V.; Hommel, R.; Lee, L.A.; Schmidt, A.; Brühl, C.; Carn, S.; Chin, M.; Dhomse, S.S.; et al. The Interactive Stratospheric Aerosol Model Intercomparison Project (ISA-MIP): Motivation and experimental design. Geosci. Model Dev. 2018, 11, 2581–2608. [Google Scholar] [CrossRef]
- Dhomse, S.S.; Mann, G.W.; Antuña Marrero, J.C.; Shallcross, S.E.; Chipperfield, M.P.; Carslaw, K.S.; Marshall, L.; Abraham, N.L.; Johnson, C.E. Evaluating the simulated radiative forcings, aerosol properties, and stratospheric warmings from the 1963 Mt Agung, 1982 El Chichón, and 1991 Mt Pinatubo volcanic aerosol clouds. Atmos. Chem. Phys. 2020, 20, 13627–13654. [Google Scholar] [CrossRef]
- Niemeier, U.; Timmreck, C.; Krüger, K. Revisiting the Agung 1963 volcanic forcing—Impact of one or two eruptions. Atmos. Chem. Phys. 2019, 19, 10379–10390. [Google Scholar] [CrossRef]
- Luo, B. Stratospheric Aerosol Data for Use in CMIP6 Models Data Description. 2016. Available online: ftp://iacftp.ethz.ch/pub_read/luo/CMIP6/Readme_Data_Description.pdf (accessed on 12 January 2022).
- Sato, M.; Hansen, J.E.; McCornick, M.P.; Pollack, J.B. Stratospheric aerosol optical depths, 1850 to 1990. J. Geophys. Res. 1993, 98, 22987–22994. [Google Scholar] [CrossRef]
- McCormick, M.P.; Swissler, T.J. Stratospheric aerosol mass and latitudinal distribution of the El Chichón eruption cloud for October 1982. Geophys. Res. Lett. 1983, 10, 877–880. [Google Scholar] [CrossRef]
- Thomason, L.W.; Ernest, N.; Millán, L.; Rieger, L.; Bourassa, A.; Vernier, J.-P.; Manney, G.; Luo, B.; Arfeuille, F.; Peter, T. A global space-based stratospheric aerosol climatology: 1979–2016. Earth Syst. Sci. Data 2018, 10, 469–492. [Google Scholar] [CrossRef]
- Antuña-Marrero, J.-C.; Mann, G.W.; Keckhut, P.; Avdyushin, S.; Nardi, B.; Thomason, L.W. Shipborne lidar measurements showing the progression of the tropical reservoir of volcanic aerosol after the June 1991 Pinatubo eruption. Earth Syst. Sci. Data 2020, 12, 2843–2851. [Google Scholar] [CrossRef]
- Antuña-Marrero, J.-C.; Mann, G.W.; Barnes, J.; Rodríguez-Vega, A.; Shallcross, S.; Dhomse, S.S.; Fiocco, G.; Grams, G.W. Recovery of the first ever multi-year lidar dataset of the stratospheric aerosol layer, from Lexington, MA, and Fairbanks, AK, January 1964 to July 1965. Earth Syst. Sci. Data 2021, 13, 4407–4423. [Google Scholar] [CrossRef]
- Elterman, L.; Toolin, R.B.; Essex, J.D. Stratospheric Aerosol Measurements with Implications for Global Climate. Appl. Opt. 1973, 12, 330–337. [Google Scholar] [CrossRef] [PubMed]
- Synge, E.H. A method of investigating the higher atmosphere. Phil. Mag. 1930, 9, 1014–1020. [Google Scholar] [CrossRef]
- Tuve, M.A.; Johnson, E.A.; Wulf, O.R. A new experimental method for study of the upper atmosphere. Terr. Mag. 1935, 40, 452–454. [Google Scholar] [CrossRef]
- Hulburt, E.O. Observations of a searchlight beam to an altitude of 28 kilometers. J. Opt. Soc. Amer. 1937, 27, 377–382. [Google Scholar] [CrossRef]
- Johnson, E.A.; Meyer, R.C.; Hopkins, R.E.; Mock, W.H. The measurement of light scattered by the upper atmosphere from a searchlight beam. J. Opt. Soc. Amer. 1939, 29, 512–517. [Google Scholar] [CrossRef]
- Friedland, S.S.; Katzenstein, J.; Zatzick, M.R. Pulsed searchlighting the atmosphere. J. Geophys. Res. 1956, 61, 415–434. [Google Scholar] [CrossRef]
- Dodd, K.N. The Determination of Upper Atmosphere Densities by Scattering of Searchlight Beam; Technical Note No. M.S. 58; Royal Aircraft Establishment: Farnborough, UK, 1959. [Google Scholar]
- Rozenberg, G.V. (Ed.) Prozhetornyi Luch v Atmosfere (Searchlight Beams in the Atmosphere); lzd-vo AN SSSR: Moskow, Russia, 1960. [Google Scholar]
- Maiman, T. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Schawlow, A.L.; Townes, C.H. Infrared and Optical Masers. Phys. Rev. 1958, 112, 1940–1949. [Google Scholar] [CrossRef]
- Elterman, L. Aerosol measurements since 1973 for normal and volcanic stratospheres. Appl. Opt. 1976, 15, 1113–1114. [Google Scholar] [CrossRef]
- Grams, G.W.; Fiocco, G. Stratospheric aerosol layer during 1964 and 1965. J. Geophys. Res. 1967, 72, 3523–3542. [Google Scholar] [CrossRef]
- Grams, G.W. Optical Radar Studies of Stratospheric Aerosols. Ph.D. Thesis, Massachusetts Institute for Technology, Cambridge, MA, USA, 1966. Available online: https://dspace.mit.edu/handle/1721.1/13502 (accessed on 10 May 2024).
- Antuña Marrero, J.-C.; Mann, G.W.; Barnes, J.; Rodríguez-Vega, A.; Shallcross, S.; Dhomse, S.S.; Fiocco, G.; Grams, G.W. The first ever multi-year lidar dataset of the stratospheric aerosol layer, from Lexington, MA, and Fairbanks, AK, Jan 1964 to Jul 1965. In PANGAEA Open-Access Dataset Repository; PANGAEA: Bremen, Germany, 2020. [Google Scholar] [CrossRef]
- Elterman, L. The measurement of stratospheric density distribution with the searchlight technique. J. Geophys. Res. 1951, 56, 509–520. [Google Scholar] [CrossRef]
- Elterman, L. Seasonal trends of temperature, density, and pressure to 67.6 km obtained with the searchlight probing technique. J. Gephys. Res. 1954, 59, 351–358. [Google Scholar] [CrossRef]
- Elterman, L.; Campbell, A.B. Atmospheric Aerosol Observations with Searchlight Probing. J. Atmos. Sci. 1964, 21, 457–458. [Google Scholar] [CrossRef][Green Version]
- Elterman, L. An Atlas of Aerosol Attenuation and Extinction Profiles for the Troposphere and Stratosphere; Report AFCRL-66-828; AFCRL: Bedford, MA, USA, 1966; 128p, Available online: https://apps.dtic.mil/sti/pdfs/AD0649778.pdf (accessed on 3 May 2022).
- Elterman, L. Aerosol Measurements in the Troposphere and Stratosphere. Appl. Opt. 1966, 5, 1769–1776. [Google Scholar] [CrossRef]
- Hinds, B.D.; Kimberlin, R.F., III; Hoidale, G.B. Boundary Layer Dust Occurrence. I: Atmospheric Dust over the White Sands Missile Range, New Mexico, Area; ECOM-DR-75-2; Atmospheric Sciences Laboratory, US Army Electronics Command: White Sands Missile Range, NM, USA; 67p.
- Elterman, L. Rayleigh and Extinction Coefficients to 50 km for the Region 0.27 μ to 0.55 μ. Appl. Opt. 1964, 3, 1139–1147. [Google Scholar] [CrossRef]
- Elterman, L. Atmospheric Attenuation Model, 1964, in the Ultraviolet, Visible, and Infrared Regions for Altitudes to 50 km. AFCRL-64-740; 1964; 40p. Available online: https://apps.dtic.mil/sti/pdfs/AD0607859.pdf (accessed on 3 May 2022).
- Rohatgi, A. WebPlotDigitizer. 2022. Available online: https://automeris.io/WebPlotDigitizer (accessed on 17 September 2022).
- Antuña Marrero, J.-C.; Mann, G.W.; Barnes, J.; Calle, A.; Dhomse, S.S.; Cachorro Revilla, V.E.; Deshler, T.; Li, Z.; Sharma, N. Tropospheric and stratospheric aerosol extinction from searchlight measurements conducted at White Sands, New Mexico, US between December 1963 and December 1964. [dataset publication series] 2023. In PANGAEA Open-Access Dataset Repository; PANGAEA: Bremen, Germany, 2023. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- U.S. Standard Atmosphere—1976; U.S. Government Printing Office: Washington, DC, USA, 1976. Available online: https://www.ngdc.noaa.gov/stp/space-weather/online-publications/miscellaneous/us-standard-atmosphere-1976/us-standard-atmosphere_st76-1562_noaa.pdf (accessed on 5 October 2022).
- Reeger, E.; Siedentopf, H. Die Streufunktion des Atmospharischen Dunstes nach Scheinwerfer Messungen. Optik 1946, 1, 15–41. [Google Scholar]
- Gibson, F. Atmospheric Aerosol Scattering Background Observations, AFGL-TR-88-0146; Environmental Research Paper No.1006; Air Force Geophysics Lab: Hanscom Air Force Base, MA, USA, 1988; 34p, Available online: https://apps.dtic.mil/sti/tr/pdf/ADA206752.pdf (accessed on 23 May 2022).
- Wells, M.B. Monte Carlo Analysis of Searchlight Scattering Measurements; AFCRL-68-0311, AD0675153; Air Force Cambridge Research Laboratories, Office of Aerospace Research, United States Air Force: Bedford, MA, USA, 1968; 23p, Available online: https://apps.dtic.mil/sti/pdfs/AD0675153.pdf (accessed on 11 May 2022).
- Durre, I.; Yin, X.; Vose, R.; Applequist, S.; Arnfield, J. Integrated Global Rad iosonde Archive (IGRA), Version 2; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2016. [CrossRef]
- Durre, I.; Yin, X.; Vose, R.S.; Applequist, S.; Arnfield, J. Enhancing the Data Coverage in the Integrated Global Radiosonde Archive. J. Atmos. Ocean. Technol. 2018, 35, 1753–1770. [Google Scholar] [CrossRef]
- Fleming, E.L.; Chandra, S.; Barnett, J.J.; Corney, M. Zonal mean temperature, pressure, zonal wind, and geopotential height as functions of latitude, COSPAR International Reference Atmosphere: 1986, Part II: Middle Atmosphere Models. Adv. Space Res. 1990, 10, 11–59. [Google Scholar] [CrossRef]
- Hostetler, C.A.; Liu, Z.; Regan, J.; Vaughan, M.; Winker, D.; Osborn, M.; Hunt, W.H.; Powell, K.A.; Trepte, C. CALIOP Algorithm Theoretical Basis Document (ATBD): Calibration and Level 1 Data Products, Doc. PC-SCI-201; Langley Research Center: Hampton, VA, USA, 2006. Available online: https://www-calipso.larc.nasa.gov/resources/pdfs/PC-SCI-201v1.0.pdf (accessed on 19 December 2022).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalyses. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- AERONET. White Sands. 2022. Available online: https://aeronet.gsfc.nasa.gov/cgi-bin/data_display_aod_v3?site=White_Sands&nachal=2&level=3&place_code=10 (accessed on 5 January 2022).
- AERONET. AERONET Inversion Products (Version 3). 2022. Available online: https://aeronet.gsfc.nasa.gov/new_web/Documents/Inversion_products_for_V3.pdf (accessed on 5 January 2022).
- Friend, J.P. Properties of the stratospheric aerosol. Tellus 1966, 465, 465–473. [Google Scholar] [CrossRef]
- Cachorro, V.E.; Salcedo, L.L. New Improvements for Mie Scattering Calculations. J. Electromagn. Waves Appl. 1991, 5, 913–926. [Google Scholar] [CrossRef]
- Borden, T.R.; Hering, W.S. Ozonesonde Observations over North America; AFRCRL-64-30(IV); Air Force Cambridge Research Laboratories, Office of Aerospace Research, U.S. Air Force: Hanscom Field, MA, USA, 1964; 365p, Available online: https://catalog.hathitrust.org/Record/102197526 (accessed on 7 June 2022).
- Serdyuchenko, A.; Gorshelev, V.; Weber, M.; Chehade, W.; Burrows, J.P. High spectral resolution ozone absorption cross sections—Part 2: Temperature dependence. Atmos. Meas. Tech. 2014, 7, 625–636. [Google Scholar] [CrossRef]
- Añel, J.A.; Antuña, J.C.; de la Torre, L.; Castanheira, J.M.; Gimeno, L. Climatological features of global multiple tropopause events. J. Geophys. Res. 2008, 113, D00B08. [Google Scholar] [CrossRef]
- Randel, W.J.; Seidel, D.J.; Pan, L.L. Observational characteristics of double tropopauses. J. Geophys. Res. 2007, 112, D07309. [Google Scholar] [CrossRef]
- NWS. Surface Observations: Abridged from Federal Meteorological Handbook No. 1 for FAA, LAWR, and A-Type Stations; National Weather Service: Silver Spring, MD, USA, 1973; 318p. Available online: https://babel.hathitrust.org/cgi/pt?id=mdp.39015018277957&seq=7 (accessed on 26 July 2022).
- Meinel, A.B.; Meinel, M.P. Height of the glow stratum from the eruption of Agung on Bali. Nature 1964, 201, 657–658. [Google Scholar] [CrossRef]
- Meinel, M.P.; Meinel, A.B. Late Twilight Glow of the Ash Stratum from the Eruption of Agung Volcano. Science 1963, 142, 582–583. [Google Scholar] [CrossRef]
- Pittock, A.B. A thin stable layer of anomalous ozone and dust content. J. Atmos. Sci. 1966, 23, 538–542. [Google Scholar] [CrossRef][Green Version]
- Rozenberg, G.V.; Nikolaeva-Tereshkova, V.V. Stratospheric aerosol according to measurements from a spacecraft. In Izvestiya AN SSSR: Physics of the Atmosphere and Ocean; Izvestiya Akademii Nauk SSSR: Moscow, Russia, 1965; Volume 1, pp. 386–394. (In Russian) [Google Scholar]
- Sushkevich, T.A. To the 55th Anniversary of the Discovery of Stratospheric Aerosol Layers from Space: Volcanoes and Climate Problems (Dedicated to the 65th Anniversary of the M.V. Keldysh Institute of Applied Mathematics and Its Achievements in Manned Astronautics). 2018; 32p. Available online: http://library.keldysh.ru/preprint.asp?id=2018-125 (accessed on 4 July 2022). (In Russian).
- Rider, L.J.; Armendariz, M. Nocturnal Maximum Winds in the Planetary Boundary White Sands Missile Range. New Mex. J. Appl. Meteorol. 1971, 10, 1154–1161. [Google Scholar] [CrossRef][Green Version]
- Norton, C.L.; Hoidale, G.B. The Diurnal Variation of Mixing Height by Season over White Sands Missile Range. New Mex. Mon. Weather Rev. 1976, 104, 1317–1320. [Google Scholar] [CrossRef][Green Version]
- Dyer, A.J.; Hicks, B.B. Global spread of volcanic dust from the Bali eruption of 1963. Q. J. R. Meteorol. Soc. 1968, 94, 545–554. [Google Scholar] [CrossRef]
- Keen, R.A. Volcanic aerosols and lunar eclipses. Science 1983, 222, 1011–1013. [Google Scholar] [CrossRef]
- Stothers, R.B. Major optical depth perturbations to the stratosphere from volcanic eruptions: Stellar extinction period, 1961-1978. J. Geophys. Res. 2001, 106, 2993–3003. [Google Scholar] [CrossRef]
- Matsushima, S. Site selection for a small observatory in the Midwest. Publ. Astron. Soc. Pac. 1964, 76, 224–230. [Google Scholar] [CrossRef]
- Matsushima, S.; Zink, J.R. Three-Color Photometry of Mare Crisium during the Total Eclipse of 30 December 1963. Astron. J. 1964, 69, 481–484. [Google Scholar] [CrossRef]
- Matsushima, S.; Zink, J.R.; Hansen, J.E. Atmospheric Extinction by Dust Particles as Determined from Three-Color Photometry of the Lunar Eclipse of 19 December 1964*. Astron. J. 1966, 71, 103–110. [Google Scholar] [CrossRef]
- Bouska, J.; Mayer, P. Photoelectric observation of the lunar eclipse of 24–25 June 1964. Bull. Astron. Inst. Czechoslov. 1964, 16, 252–254. [Google Scholar]
- Matsushima, S. Atmospheric extinction: Czech lunar photometry of the 25 June 1964 eclipse. Publ. Astron. Soc. Pac. 1967, 79, 178–180. [Google Scholar] [CrossRef]
- Feely, H.W.; Katzman, D.; Seitz, H.; Davidson, B.; Friend, J.P. Final Report on Project Stardust; DASA 2166-1 Report, Chapters 1–6; Isotopes Inc.: Westwood, NJ, USA, 1967; Volume I, 223p, Available online: https://apps.dtic.mil/sti/pdfs/AD0850378.pdf (accessed on 3 June 2022).
- Fleming, E.L.; Chandra, S.; Schoeberl, M.R.; Barnett, J.J. Monthly mean global climatology of temperature, wind, geopotential height, and pressure for 0–120 km. In NASA Technical Reports Server; NASA TM-100697; NASA: Washington, DC, USA, 1988; 85p. Available online: https://ntrs.nasa.gov/api/citations/19880013119/downloads/19880013119.pdf (accessed on 5 June 2022).
- SPARC. The SPARC Intercomparison of Middle Atmosphere Climatologies. J. Clim. 2004, 17, 986–1003. [Google Scholar] [CrossRef]
- U.S. Standard Atmosphere 1962; U.S. Government Printing Office: Washington, DC, USA, 1962. Available online: https://ntrs.nasa.gov/api/citations/19630003300/downloads/19630003300.pdf (accessed on 5 October 2022).

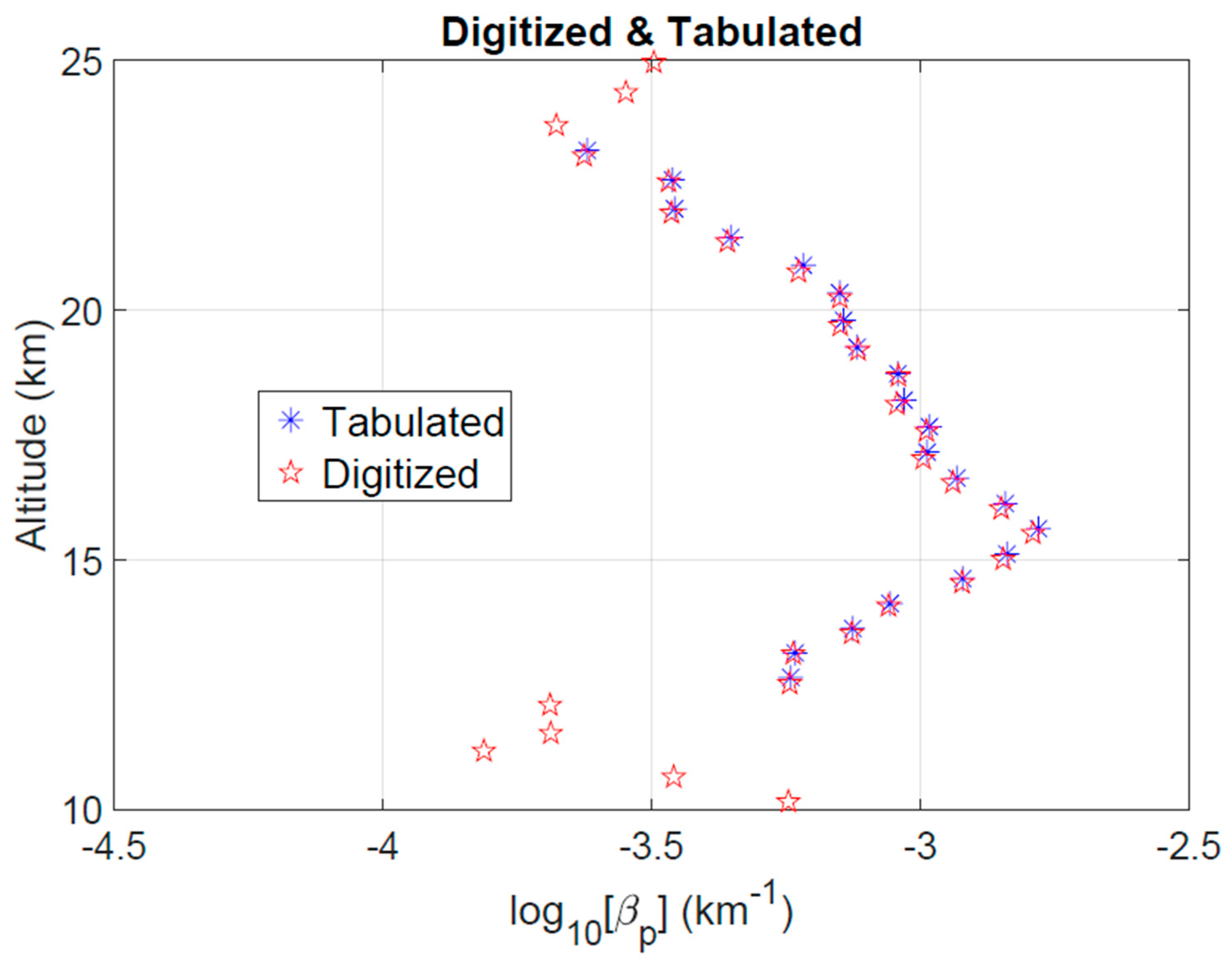
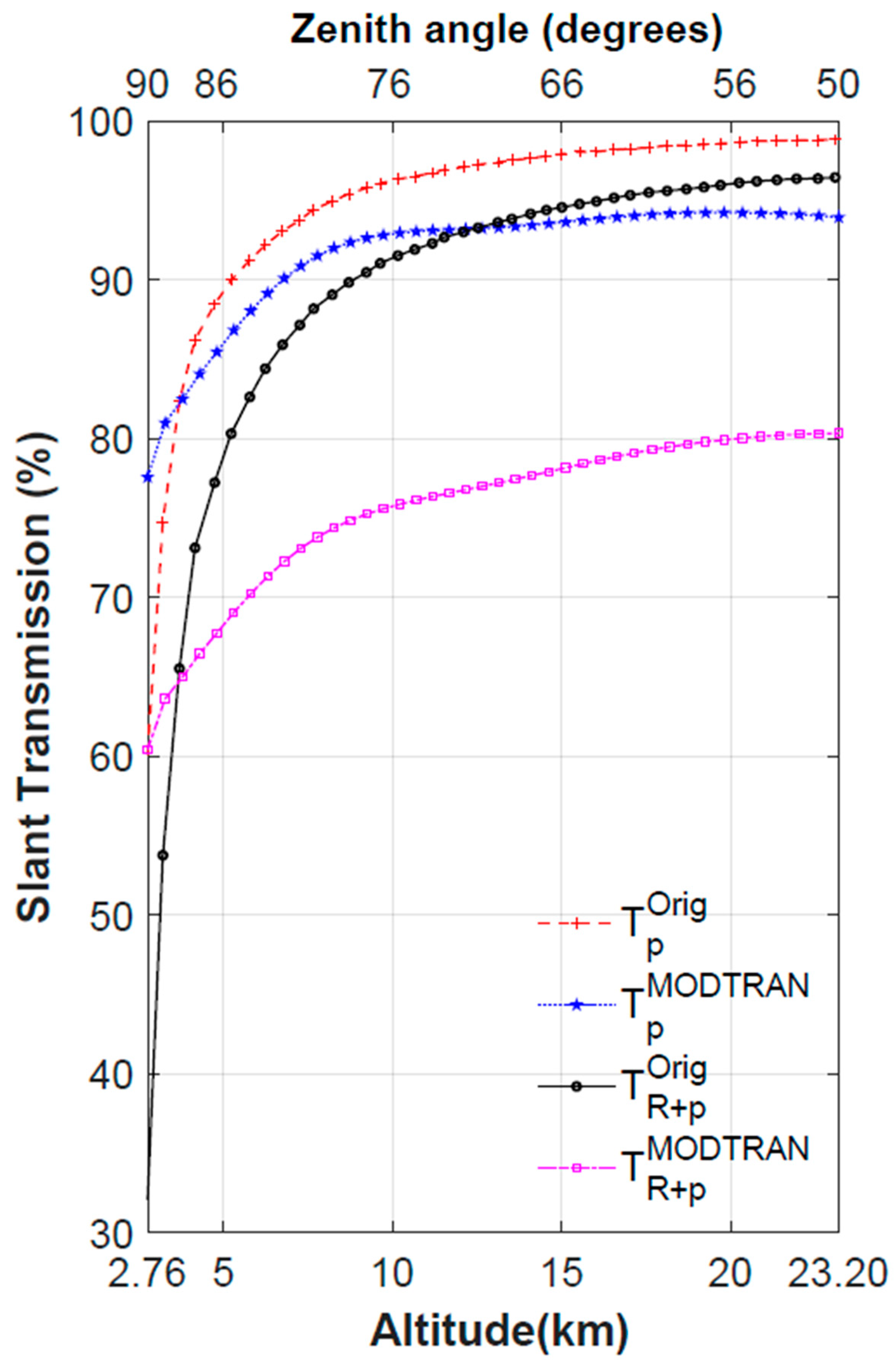

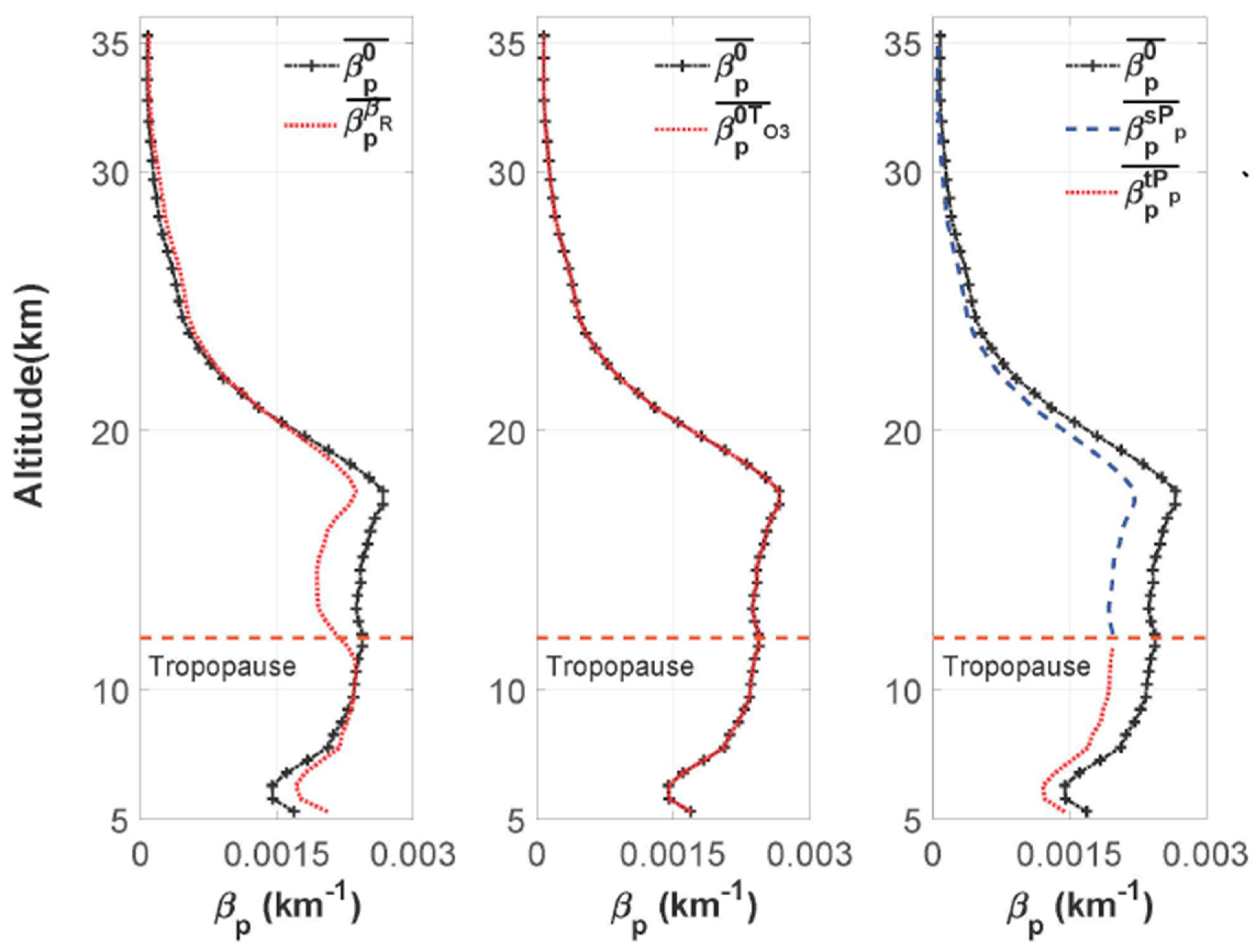
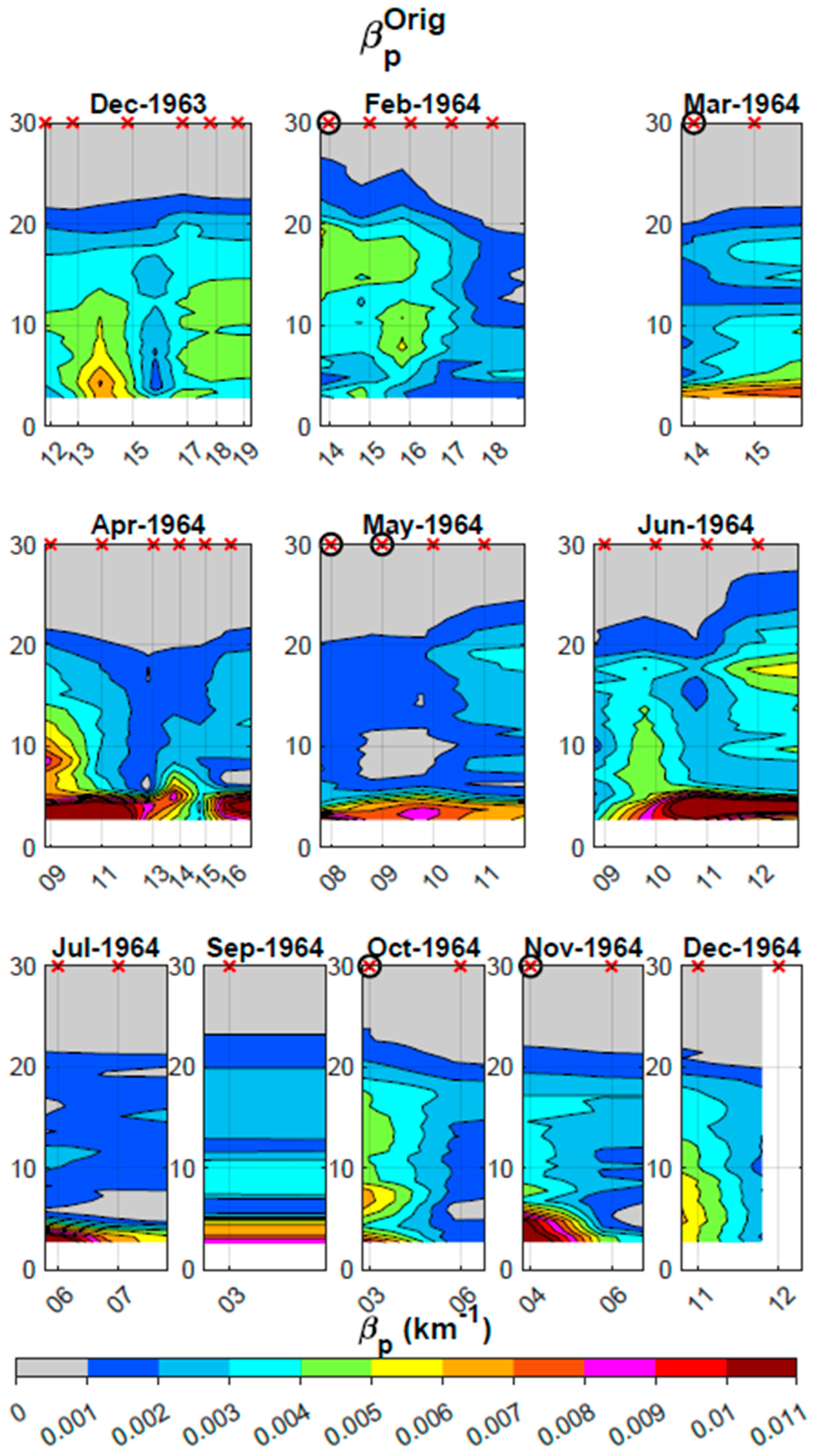

| Updated Parameters | 5–12 km | 12–35 km | ||
|---|---|---|---|---|
| (km−1) | % | (km−1) | % | |
| −3.5 × 10−4 | −12 | ------- | ||
| ------- | −2.2 × 10−4 | −20 | ||
| 1.0 × 10−4 | 3 | −1.2 × 10−4 | −9 | |
| ------- | 2.0 × 10−7 | 0 | ||
| Duration | Month | Year | Day | ToD (LST) | DD | Station |
|---|---|---|---|---|---|---|
| 55 min | 2 | 1964 | 12 | 1200–1800 | W | WSWS |
| 134 min | 2 | 1964 | 14 | 1200–1800 | SW | HWS |
| 210 min | 3 | 1964 | 13 | 1200–1800 | SW | HWS |
| 403 min | 5 | 1964 | 07 | 1200–1800 | W | WSWS |
| 568 min | 5 | 1964 | 07 | 1200–1800 | SW | HWS |
| 49 min | 10 | 1964 | 02 | 1200–1800 | C | HWS |
| 59 min | 11 | 1964 | 03 | 0600–1200 | NE | HWS |
| Month | Height (05:30) | Height (20:30) | Max. Height | Max. Time |
|---|---|---|---|---|
| December | 37 m | 8 m | 929 m | 14:30 MST |
| March | 68 m | 148 m | 2257 m | 14:30 MST |
| June | 18 m | 137 m | 3418 m | 15:30 MST |
| September | 40 m | 49 m | 1784 m | 13:30 MST |
| Variable | Mean | σ | rV | Max. | Min. |
|---|---|---|---|---|---|
| sAODOrig | 0.032 | 0.013 | 42% | 0.060 | 0.011 |
| sAODRecal | 0.046 | 0.017 | 37% | 0.084 | 0.020 |
| Variable | Mean | σ | Max. | Min. | N |
|---|---|---|---|---|---|
| sAODOrig | 0.029 | 0.007 | 0.038 | 0.018 | 11 |
| sAODRecal | 0.043 | 0.009 | 0.056 | 0.028 | 11 |
| sAODLex | 0.041 | 0.006 | 0.048 | 0.034 | 7 |
| sAODSatoNH | 0.040 | 0.002 | 0.043 | 0.036 | 13 |
| sAODSatoSH | 0.105 | 0.013 | 0.132 | 0.085 | 13 |
| sAODStothersNH | 0.025 | 0.006 | 0.039 | 0.015 | 13 |
| sAODStothersSH | 0.081 | 0.029 | 0.148 | 0.047 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antuña-Marrero, J.-C.; Mann, G.W.; Barnes, J.; Calle, A.; Dhomse, S.S.; Cachorro, V.E.; Deshler, T.; Li, Z.; Sharma, N.; Elterman, L. The Recovery and Re-Calibration of a 13-Month Aerosol Extinction Profiles Dataset from Searchlight Observations from New Mexico, after the 1963 Agung Eruption. Atmosphere 2024, 15, 635. https://doi.org/10.3390/atmos15060635
Antuña-Marrero J-C, Mann GW, Barnes J, Calle A, Dhomse SS, Cachorro VE, Deshler T, Li Z, Sharma N, Elterman L. The Recovery and Re-Calibration of a 13-Month Aerosol Extinction Profiles Dataset from Searchlight Observations from New Mexico, after the 1963 Agung Eruption. Atmosphere. 2024; 15(6):635. https://doi.org/10.3390/atmos15060635
Chicago/Turabian StyleAntuña-Marrero, Juan-Carlos, Graham W. Mann, John Barnes, Abel Calle, Sandip S. Dhomse, Victoria E. Cachorro, Terry Deshler, Zhengyao Li, Nimmi Sharma, and Louis Elterman. 2024. "The Recovery and Re-Calibration of a 13-Month Aerosol Extinction Profiles Dataset from Searchlight Observations from New Mexico, after the 1963 Agung Eruption" Atmosphere 15, no. 6: 635. https://doi.org/10.3390/atmos15060635
APA StyleAntuña-Marrero, J.-C., Mann, G. W., Barnes, J., Calle, A., Dhomse, S. S., Cachorro, V. E., Deshler, T., Li, Z., Sharma, N., & Elterman, L. (2024). The Recovery and Re-Calibration of a 13-Month Aerosol Extinction Profiles Dataset from Searchlight Observations from New Mexico, after the 1963 Agung Eruption. Atmosphere, 15(6), 635. https://doi.org/10.3390/atmos15060635






