Abstract
The NO/NO2/O3 reaction mechanism of the standard VDI 3783 Part 19 was coupled to the Lagrangian particle model LASAT and quasi-stationary, individual plumes were calculated for a point source under various conditions. First-order conversion rates between NO and NO2 were derived by fitting to these plumes and further simplified to sets of categorized conversion rates which depend on background NO2 concentration, atmospheric stability and time of the day. The rates were applied in the standard airport dispersion model system LASPORT and compared to measured NO2 concentrations at Los Angeles International Airport. The agreement between modelled and measured NO2 concentrations (weekly averages) and ratios NO2 over NOx at monitor stations dominated by airport emissions was in most cases better than a factor of 2 with a Pearson correlation coefficient of about 0.9 or above.
1. Introduction
In the emission from combustion processes, only a fraction of the emitted nitrogen oxide (NOx) is in the form of nitrogen dioxide (NO2). The usually larger part is in the form of nitrogen monoxide (NO). During subsequent atmospheric transport, chemical conversion processes then lead to an effective increase in the fraction of NO2 in NOx. Limit values on ambient air quality usually refer to NO2; therefore, atmospheric dispersion modelling requires an estimate of the effective conversion between NO and NO2 after emission. Dedicated meso-scale chemical transport models can account for complex reaction mechanisms of higher order. On the other hand, local dispersion models often have limited capabilities.
NO/NO2 chemistry is governed by reactions of higher order [1]. A standardized description of gas-phase reactions is provided in the German standard VDI 3783 Part 19 (2017) [2]. Its mechanism M1 covers the photolysis of NO2 and the oxidation of NO with O3, and mechanism M2 contains several additional reaction paths. These reactions can be accounted for in a model system (LASREA) which combines the Lagrangian particle model LASAT with a chemical QSSA solver. This allows the modelling of the mixing of ambient air into a pollutant plume together with the dynamics of the higher-order reactions at a high temporal (order of seconds) and spatial (order of metres) resolution.
LASREA was developed for the investigation of specific situations and it is computationally expensive. It was applied to derive simplified conversion rates of first order that can be easily applied in standard dispersion models. In a recent project [3], this concept was applied to derive effective conversion rates between NO and NO2 for application with the regulatory model AUSTAL [4], which implements the specifications of Annex 2 (dispersion calculation) of the German Technical Instructions on Air Quality Control (TA Luft) [5].
In the work presented here, the effective conversion rates were implemented into the airport dispersion model system LASPORT [6,7] and applied in a dispersion calculation for Los Angeles International Airport, for which measured concentrations of NO and NO2 were available. Further details are provided in [3]. Figure 1 shows a schematic diagram of the applied standards and model systems.
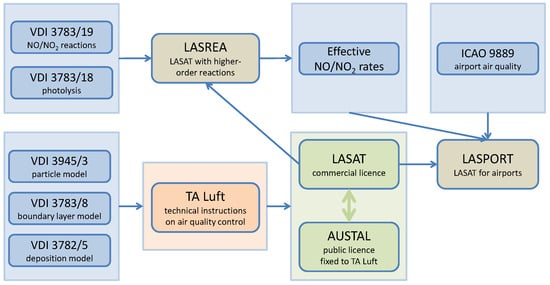
Figure 1.
Schematic diagram of the standards and models that were used to derive the effective conversion rates between NO and NO2, and their application in an airport dispersion model system.
2. Foundations
2.1. Reaction Mechanism
The reaction mechanism M1 of the standard VDI 3783 Part 19 reads
Reaction (2) is very fast so that the mechanism can be simplified to
The conserved quantities are and . If quantities of , and (and a practically infinite reservoir of O2) are inserted into a closed volume, the reactions take place and lead after a certain time to a quasi-stationary state with the steady-state concentration
where is the steady-state concentration of O3. The temporal behaviour of can be solved fully analytically [3]. The characteristic time to reach the steady-state is
Another presentation of the steady state concentration is
Figure 2 shows an example for the characteristic time and the ratio [NO2]/[NOx] as a function of the NOx concentration and initial O3 concentration.
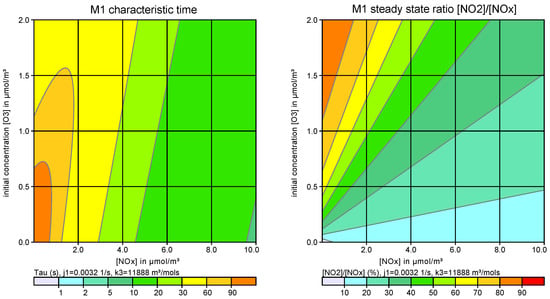
Figure 2.
Example for the characteristic time (left) and the steady state ratio [NO2]/[NOx] (right) as a function of the NOx concentration and initial O3 concentration.
2.2. Photolysis Frequency
Photolysis frequencies were taken from the standard VDI 3783 Part 18 [8]. Their parametrisation is based on the solar zenith angle, optical cloud depth, ozone column density and aerosol pollution. Different levels of cloudiness are accounted for by a cloud modification factor. Figure 3 shows as an example the photolysis frequency of Reaction (1) as a function of the solar zenith angle and cloud optical depth.
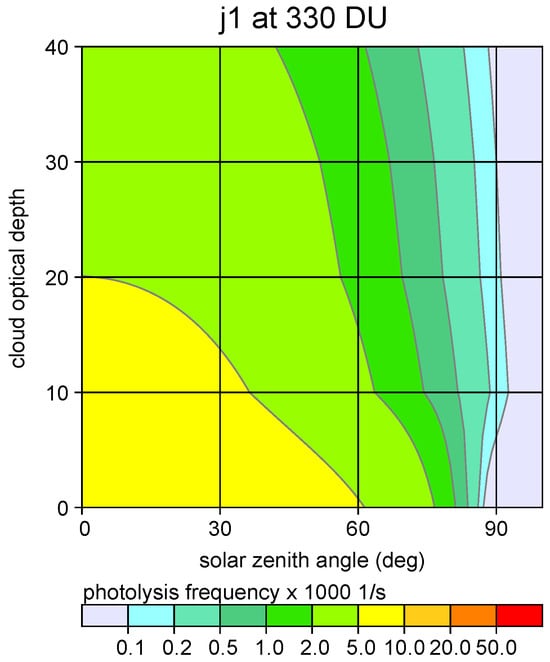
Figure 3.
Photolysis frequency of Reaction (1) as a function of zenith angle and cloud optical depth for a typical value of the ozon column density (330 DU), medium aerosol pollution and clear sky.
2.3. LASREA
The tool LASREA serves to handle higher-order chemical reactions in combination with the Lagrangian particle model LASAT. LASAT (Lagrangian Simulation of Aerosol Transport) [9] is a particle model according to the standard VDI 3945 Part 3 [10]. It is applied in various model systems [11] and served as the basis of the regulatory model AUSTAL [4].
Usually, a particle model only handles reactions of first order because in this case the change of quantity (e.g., mass) carried by a simulation particle per unit time is independent of the other particles, such that the simulations particles can be processed independent of each other. In contrast for reactions of higher order, it is necessary to determine first the concentrations of the species in a given volume in order to obtain the reaction rate, and this requires information of all particles in the volume. LASREA performs the following steps to simulate the dispersion in a time interval of length T:
- LASAT carries out the dispersion calculation for the time interval 0 to without conversions, writes out the particle tables (locations, species quantities and other parameters) and pauses.
- LASREA reads the particle tables, calculates on the LASAT grid the current concentrations (volume average over a grid cell) and adds the pre-defined background concentrations.
- LASREA calculates for each grid cell the chemical reactions for the time interval 0 to T using a QSSA method.
- LASREA subtracts the background concentrations, distributes in each grid cell the calculated species quantities over the particles of the grid cell and writes out the particle tables.
- LASAT reads in the particles tables and continues the dispersion calculation for the time interval to T.
As LASREA defines the plume as a difference to a homogeneous background, it is important that the background concentrations are in equilibrium according to the implemented reaction mechanism. Otherwise changes of background concentration within the plume volume would be assigned to the plume itself. A different approach is reported in [12]. The QSSA procedure is based on a formulation by Dabdub and Seinfeld (1995) [13]. In a series of verification tests, LASREA was applied to a closed, single grid cell and the calculated concentrations were in agreement with the ones from a direct QSSA integration of the chemical differential equations [3].
Figure 4 shows as an example the quasi-stationary concentration plumes near ground from a calculation with LASREA and the mechanism M1 (left side) and from a calculation with a first order conversion from NO to NO2 at a time constant of 600 s (right side). The emission height was 20 m and the emission rate 0.1 mol/s NOx (4.6 g/s) with an initial fraction of 10% NO2 in NOx. The LASREA plumes on the left side show the difference to the background, for which an ozone concentration of about 1 mol/m3 (50 g/m3) and a NO2 concentration of about 0.2 mol/m3 (10 g/m3) were assumed. The background concentration of NO was determined from the M1 equilibrium (about 0.2 mol/m3), the rate constants were 1/s and m3/mol s.
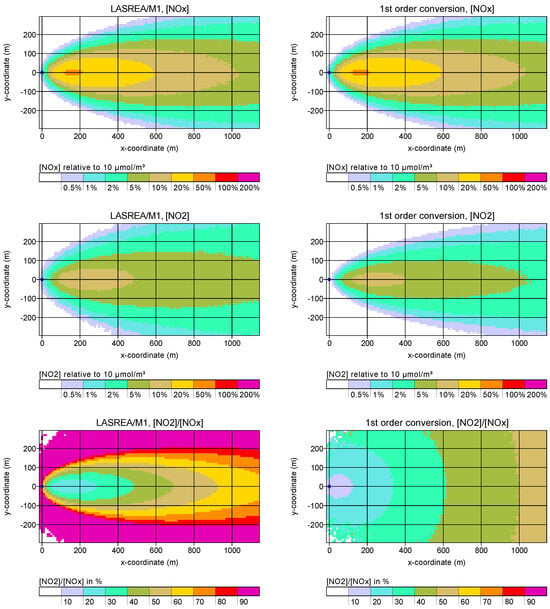
Figure 4.
Example calculation for a 20 m point source and an NOx emission of 0.1 mol/s with 10% primary NO2. Left: results of LASREA/M1. Right: results of a first order conversion of NO to NO2 with rate constant 1/600 s.
The concentration distribution of NOx is the same in both cases. The calculation with the first-order rate constant 1/600 s yields a somewhat smaller NO2 concentration. The most remarkable difference between the two calculations becomes apparent for the ratio NO2 over NOx concentration. In the first-order conversion, the ratio is simply a function of transport time. With M1, it strongly depends on the location inside the plume: At the edges of the plume it is high because of the small concentrations (relative to the background) together with the mixing of ozone-rich ambient air, while at the plume centre it is limited by the available ozone.
The comparison shows that the effective conversion time in this LASREA/M1 example is of the order of 10 min. This is much longer than the characteristic time of M1 (see Figure 2), because the limiting factor for NO2 production in the plume is the entrainment of ambient air. This explains why simplified or measurement-based approaches for effective first order conversions in pollutant plumes may apply conversion times considerably larger than the characteristic time of M1 itself.
3. Effective Conversion Rates
3.1. Plume Calculations
Test calculations showed that, for transport times of the order of 1 hour or below, the mechanism M1 of the standard VDI 3783 Part 19 is sufficiently accurate and that other reactions included in the standard (mechanism M2, e.g., conversion of NOx to HNO3, HCHO conversion and HO radicals) can be neglected on this time scale [3]. A variety of single-plume calculations were performed with LASREA/M1 and a boundary layer model according to the standard VDI 3783 Part 8 [14] for various emission heights, emission rates, ambient temperatures, background concentrations and solar zenith angles.
To categorize the ambient background, measured and extrapolated data of NO2 and O3 at various monitor stations in Germany [15] were used to assign for different levels of the NO2 concentration an average O3 concentration. Then, the M1 equilibrium was applied to derive the according NO and NOx concentration for day and night time. The resulting background categories are listed in Table 1.

Table 1.
Categories of ambient background concentrations applied for the derivation of effective conversion rates.
For daytime, the solar zenith angle was set to 0 deg (maximum photolysis rates), and for night time to 85 deg. The value smaller than 90 deg for night time allows a small photolysis and O3 production. Test calculations showed that these assumptions and the assumed cloudiness were not critical for the derivation of effective conversion rates.
3.2. Conversion Rates
The plumes calculated with LASREA/M1 were compared to LASAT plume calculations that applied a first-order conversion between the two substances A (NO) and B (NO2) with concentrations a and b:
The conversion rate from A to B is , the one from B to A is , the according conversion times are and . The characteristic time of this reaction mechanism is . The ansatz
yields
and there remain two conditions that can be used to fit the values of and to a plume calculated by LASREA/M1. The concentrations a and b were identified with the cross-integrated concentrations of NO and NO2 at the emission height. The ratio
with
was used for fitting. The value was set to the ratio of the according background concentrations . This corresponds to the assumption that, after sufficient transport time and dilution, the plume should adjust to the properties of the background. As second condition, the ratio f at a fixed transport time (tests yielded a suitable time of s) was set to the value derived from the LASREA/M1 calculation . These two conditions yield
If , then and .
3.3. Categorized Conversion Rates
Each LASREA/M1 plume was re-calculated with the first order conversion scheme and the fitted values of and . It was shown that it is possible to reproduce in this way the NO2 plumes from LASREA/M1 quite accurately, both in view of near-ground maximum values and in view of near-ground cross-integrated concentrations [3].
The values of and depend, among other things, on the source height and the NOx emission rate. For practical applications it is desirable to define the effective conversion rates independent of the source properties, otherwise plumes and their conversions must be handled separately for every source. Hence, different averages over the data sets were performed and tested to obtain categorized, averaged and effective conversion rates. One set was derived by extracting the values for a source height of 20 m and an emission rate of NOx (4.6 g/s) together with categorized values of the atmospheric stability and the NO2 background concentration. Table 2 lists the according conversion times and .

Table 2.
Categorized conversion times (: NO to NO2, : NO2 to NO) as a function of background NO2, atmospheric stability and time of the day.
These categorized conversion rates can be applied in a standard dispersion calculation for NO and NO2. For a calculation over a calendar year, the conversion rates are specified for example in a time series of hourly means as a function of atmospheric stability (stable, neutral, unstable) and time of the day (day, night) for a selected level of background NO2.
4. Airport Application
The effective conversion rates were implemented into the airport dispersion modelling system LASPORT, applied in a dispersion calculation for Los Angeles International Airport and compared to measurements.
4.1. LASPORT
LASPORT (LASAT for Airports) is a program system for the calculation of emissions and concentrations at and around an airport [6,7]. It is the standard model tool of the German Airport Association and has been applied in various national and international projects (see, e.g., [6,16,17]). It has been approved for use in ICAO/CAEP [18] and complies to ICAO document 9889 [19].
LASPORT applies the Lagrangian particle model LASAT as dispersion core. Aircraft can be modelled individually as moving emission sources with a time resolution down to 10 s. Other sources (e.g., APU, GPU, GSE, landside and airside motor traffic) can be modelled as point, line, area, or volume sources with time-dependent emissions. Typical results from LASPORT are the annual emission inventory of an airport, the near-ground concentration distributions according to EU regulations (e.g., annual means and maximum daily means) and the time series of concentrations (usually hourly means) at given monitor stations.
4.2. Los Angeles International Airport
For Los Angeles International Airport (LAX) and a period of 6 weeks in summer 2012, meteorological data, flight data and measurements of NO and NO2 at various monitor stations were available [20].
Figure 5 shows the locations of monitor stations at the airport, Table 3 provides a short description of their characterization in view of the presumably dominant emission contributors together with a description of their encoding in subsequent scatter plots. Note that, in the summer period of 2012, the prevailing wind direction was wind from west.
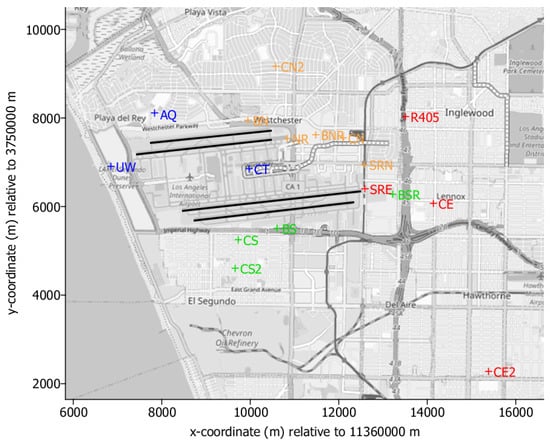
Figure 5.
Location of the monitor stations at and around Los Angeles International Airport in the measurement campaign 2012 (background map: OpenStreetMap Contributors).

Table 3.
List of monitor stations, their characterization in view of assumed dominant emission contributors and their symbol in the scatter plots.
Measured concentrations of NO and NO2 were available at all monitor stations in form of weekly averages over 6 subsequent weeks (18 July 2012 to 28 August 2012). They were compared to the calculated weekly concentrations of LASPORT (Version 2.4). The calculation applied measured meteorological data (hourly means) and a detailed flight journal of the airport. Every movement was modelled as a moving emission source with a time-resolution down to 10 s. The concentrations were stored as hourly mean concentrations and then averaged to provide successive weekly averages.
In the calculations, emissions from the main emission sources of the airport were accounted for: aircraft main engines (AC), auxiliary power units (APU), ground support equipment (GSE). The total NOx emission over the 42 days up to a height of 600 m above ground level was 333 Mg. 95% of this mass resulted from aircraft main engines and about 50% from main engine emissions near ground (taxiing, departure).
To allow for a better comparison with the measured data, estimated background concentrations of NO and NO2 were subtracted from the measured data. Background was estimated in a simplified and approximate way for each week as 90% of the measured concentration at the station with the lowest measured value. If the resulting background corrected concentration was negative, then the station was excluded from the analysis for the given week.
In the modelling, the categorized conversion rates for a background concentration of 30 g/m3 NO2 were applied. The values for stable stratification were replaced by the ones for neutral stratification because the dynamics of the aircraft engine exhaust is expected to circumvent the very low mixing process that was assumed in the underlying LASREA calculations for stable stratification. For each engine and load setting, the NOx emission rate was determined from the ICAO Engine Emission Databank. Based on estimates [21,22], the initial NO2 fraction was set to 5% for take-off and climb, 15% for approach and 40% for taxiing.
4.3. Results
Figure 6 shows as an example the calculated concentration distributions of NOx for the first two weeks and the according measured concentrations. A further analysis revealed that several monitor stations were influenced by local sources not accounted for in the dispersion calculation (in particular landside motor traffic and industrial sites). For a subset of stations, the airport was likely the main contributor (stations NR, BNR, CN, SRN, BS, CT, SRE, BSR) and a more detailed evaluation was performed for these stations. Stations UW and AQ were excluded because they were assumed to be dominated by background concentration due to the strong prevailing wind direction from West.
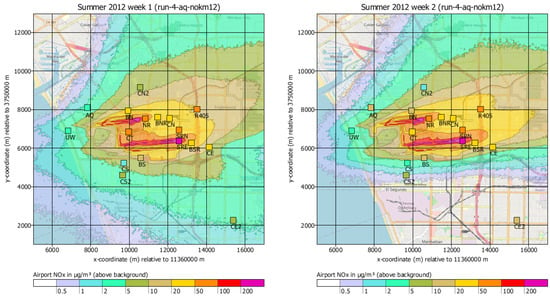
Figure 6.
Calculated (background) and measured (symbols) near-ground concentration distribution of NOx for the first two weeks (18 July 2012 to 24 July 2012, 25 July 2012 to 31 July 2012) of the measurement campaign (background map: OpenStreetMap Contributors). The spatial resolution in the calculation was 50 m and the concentrations were interpolated to isolines for the purpose of plotting.
Figure 7 shows a scatter plot of measured and modelled concentrations for this subset for each week and averaged over all 6 weeks. The overall agreement is mostly better than a factor of 2, the Pearson product-moment correlation coefficient is 0.98, the slope of a linear regression fit without offset is 0.61 (dominated by the underestimation of the high concentration at station SRE) and the root mean square error is 62.1 g/m3. Figure 8 shows the scatter plot of NO2 concentrations.
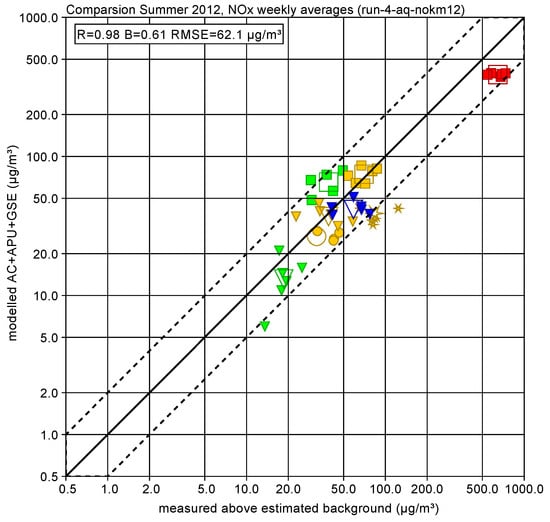
Figure 7.
Measured and modelled NOx concentration for each week (filled symbols) and averaged over all 6 weeks (open symbols) at the airport-dominated monitor stations: terminal (CT blue triangle), airport general (CN orange circle, SRN orange star, BNR orange triangle, BS green triangle), runways (NR orange square, SRE red square, BSR green square). The dotted lines indicate a factor of 2 difference.
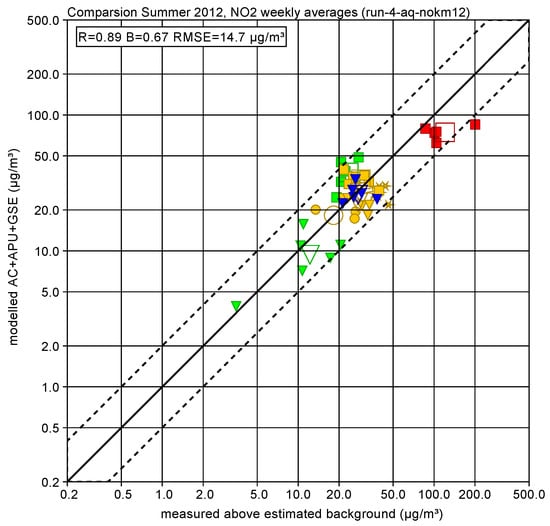
Figure 8.
Measured and modelled NO2 concentrations for each week (filled symbols) and averaged over all 6 weeks (open symbols) at the airport-dominated monitor stations: terminal (CT blue triangle), airport general (CN orange circle, SRN orange star, BNR orange triangle, BS green triangle), runways (NR orange square, SRE red square, BSR green square). The dotted lines indicate a factor of 2 difference.
Figure 9 shows the scatter plot of the ratio NO2 over NOx (without background adjustment). The overall agreement between modelled and measured concentrations and ratios gives a Pearson correlation coefficient of about 0.9 or above and an absolute difference smaller than a factor of 2 in almost all cases.
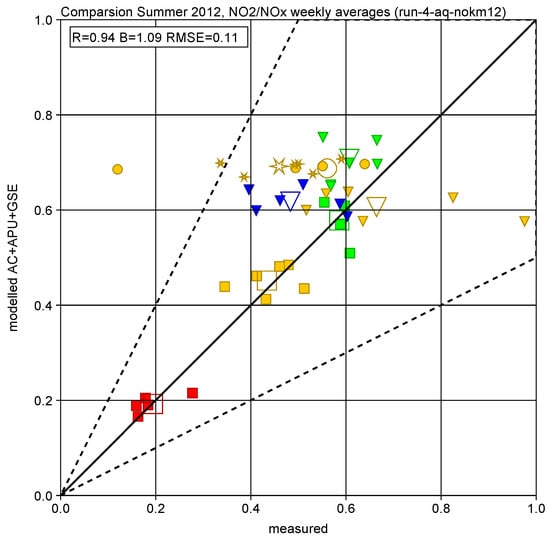
Figure 9.
Measured and modelled concentration ratio NO2 over NOx for each week (filled symbols) and averaged over all 6 weeks (open symbols) at the airport-dominated monitor stations: terminal (CT blue triangle), airport general (CN orange circle, SRN orange star, BNR orange triangle, BS green triangle), runways (NR orange square, SRE red square, BSR green square). The dotted lines indicate a factor of 2 difference.
Investigating the differences between the concentration ratios shown in Figure 9 in more detail, it can be observed that the agreement is very good for most of the runway-dominated stations (NR, SRE, BSR). As the transport times between these stations and the adjacent runway thresholds are rather short, this mainly implies that the assumed fraction of primary NO2 at take-off is adequate and that the applied conversion times are generally not too short. The ratios for the other stations (airport contributions in general) show a larger spread with some tendency of overestimation.
Finally, Figure 10 shows the near-ground concentration distributions of NO2 for the first two weeks.
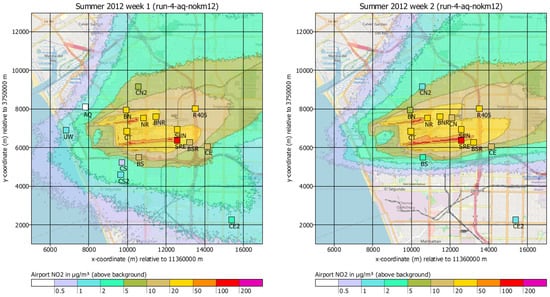
Figure 10.
Calculated (background) and measured (symbols) near-ground concentration distribution of NO2 for the first two weeks of the measurement campaign (background map: OpenStreetMap Contributors).
5. Discussion
When interpreting the results it must be considered that the modelled concentrations depend not only on the conversion rates but also on the dispersion model, the meteorological boundary layer model, the modelling of engine exhaust dynamics and the assumed emission rates. In addition, not all emission sources contributing to the measured concentrations were accounted for, and the measured data are subject to uncertainties. Nevertheless, the results for NOx give an indication of the overall quality of model performance for the simpler case of an (approximately) chemically inert substance. The results for NO2, which are driven by the effective conversion rates, were of a comparable quality.
The comparison focused on weekly averages because such averages were available from measurement at all the monitor stations. The total period of 6 weeks in summer 2012 was likely influenced to seasonal effects, hence it is not directly possible to deduce the model quality for a period of a complete calendar year. The definition of effective conversion rates as a function of atmospheric stability and time of the day (with and without daylight) is expected to be flexible enough to account for the main effects in other seasons of the year.
Ambient limit values of NO2 exist for the annual mean, e.g., 40 g/m3 in the European Union [23] and 53 ppbv (103 g/m3 at standard atmosphere) in the United States of America [24], and also for the hourly mean (200 g/m3 and 100 ppbv/195 g/m3, respectively). Therefore it is of interest to carry out comparisons also for the hourly mean concentrations, which is planned as subsequent work. In addition, the annual mean of NO2 will attract increasing interest in the European Union in view of the planned reduction of the annual limit value from 40 g/m3 to 20 g/m3 [25].
6. Conclusions
Based on the reaction mechanism M1 of the standard VDI 3783 Part 19 and its coupling to the Lagrangian particle model LASAT, effective conversion rates of first order between NO and NO2 were derived. The results showed that mixing of ambient air into the plume was usually the limiting factor for the effective oxidation of NO to NO2.
The rates were further simplified into sets of categorized rates, distinguished by NO2 background concentration, atmospheric stability and time of the day. A set of rates was applied to a complex emission system (Los Angeles International Airport) with the standard model system LASPORT. The modelled NO2 concentrations (weekly averages) and their ratios NO2 over NOx agreed with the measured ones by usually better than a factor of 2 with a Pearson correlation coefficient around 0.9 or above.
The results support the validity and practicability of the applied approach of deriving effective conversion rates. The categorized rates are simple enough such that they can be applied in almost any dispersion model on local air quality and they seem to be detailed enough to provide a useful estimate of NO2 concentrations.
Further validation work is required to demonstrate the performance for other seasons of the year, for annual averages, and for short-time averages such as hourly means.
Funding
This research was partly funded by the German Environment Agency (project FKZ 3719 51 203 0) and the US Volpe Center.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data obtained from the US Volpe Center for internal use.
Acknowledgments
The author gratefully acknowledges the US Volpe Center for the provision of datasets from the LAX AQSAS study and additional aircraft information.
Conflicts of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Aircraft |
| APU | Auxiliary power unit |
| AUSTAL | Ausbreitungsrechnung nach TA Luft |
| CAEP | Committee on aviation environmental protection in ICAO |
| EU | European Union |
| GPU | Ground power unit |
| GSE | Ground support equipment |
| ICAO | International civil aviation organisation |
| LASAT | Lagrangian simulation of aerosol transport |
| LASPORT | LASAT for airports |
| LASREA | LASAT and reactions |
| LAX | Los Angeles international airport |
| M1 | Reaction mechanism number 1 |
| M2 | Reaction mechanism number 2 |
| QSSA | Quasi stationary state approximation |
| TA Luft | Technische Anleitung zur Reinhaltung der Luft |
| VDI | Verein Deutscher Ingenieure |
References
- Seinfeld, J.; Pandis, S. Atmospheric Chemistry and Physics; Wiley & Sons: New York, NY, USA, 2016. [Google Scholar]
- VDI 3783 Part 19. Environmental Meteorology—Reaction Mechanism for the Determination of the Nitrogen Dioxide Concentration; Beuth: Berlin, Germany, 2017; Available online: https://www.vdi.de/en/home/vdi-standards/details/vdi-3783-blatt-19-environmental-meteorology-reaction-mechanism-for-the-determination-of-the-nitrogen-dioxide-concentration (accessed on 10 April 2024).
- Janicke, U. Effektive Umsetzungsraten Zwischen NO und NO2 für die Verwendung in Ausbreitungsmodellen [Effective Conversion Rates between NO and NO2 for the Application in Dispersion Models]; Reports on Environmental Physics; Janicke Consulting: Überlingen, Germany, 2023; Volume 11/1, Available online: https://www.janicke.de/data/bzu/bzu-011-01.pdf (accessed on 10 April 2024).
- Program System AUSTAL; Federal Environment Agency: Dessau-Roßlau, Germany, 2024. Available online: https://www.umweltbundesamt.de/en/topics/air/air-quality-control-in-europe/overview (accessed on 10 April 2024).
- TA Luft 2021. Neufassung der Ersten Allgemeinen Verwaltungsvorschrift zum Bundes-Immissionsschutzgesetz (Technische Anleitung zur Reinhaltung der Luft—TA Luft) [New Version of the First General Administrative Regulation to the Federal Immission Control Act (Technical Instructions on Air Quality Control—TA Luft)], GMBl No. 48-54, 1050-1192. 2021. Available online: https://www.verwaltungsvorschriften-im-internet.de/bsvwvbund_18082021_IGI25025005.htm (accessed on 10 April 2024).
- Janicke, U.; Fleuti, E.; Fuller, I. LASPORT—A model system for airport-related source systems based on a Lagrangian particle model. In Proceedings of the 11th International Conference on Harmonization within Atmospheric Dispersion Modeling for Regulatory Purposes, Cambridge, UK, 2–5 July 2007; Available online: https://www.harmo.org/Conferences/Proceedings/_Cambridge/publishedSections/Op352-356.pdf (accessed on 10 April 2024).
- Program System LASPORT. Janicke Consulting. Available online: https://www.janicke.de/en/lasport.html (accessed on 10 April 2024).
- VDI 3783 Part 18. Environmental Meteorology; Photolysis Frequencies for Calculating Pollutant Concentrations in the Atmosphere; Beuth: Berlin, Germany, 2017; Available online: https://www.vdi.de/en/home/vdi-standards/details/vdi-3783-blatt-18-environmental-meteorology-photolysis-frequencies-for-calculating-pollutant-concentrations-in-the-troposphere (accessed on 10 April 2024).
- Janicke, L. Particle simulation of inhomogeneous turbulent diffusion. In Air Pollution Modeling and Its Application II; De Wispelaere, C., Ed.; Springer: Boston, MA, USA, 1983; pp. 527–535. Available online: https://link.springer.com/chapter/10.1007/978-1-4684-7941-6_31 (accessed on 10 April 2024).
- VDI 3945 Part 3. Environmental Meteorology; Atmospheric Dispersion Models; Particle Model; Beut: Berlin, Germany, 2020; Available online: https://www.vdi.de/en/home/vdi-standards/details/vdi-3945-blatt-3-environmental-meteorology-atmospheric-dispersion-models-particle-model (accessed on 10 April 2024).
- Janicke, U.; Janicke, L. Lagrangian Particle Modeling for Regulatory Purposes; A Survey of Recent Developments in Germany. In Proceedings of the 11th International Conference on Harmonization within Atmospheric Dispersion Modeling for Regulatory Purposes, Cambridge, UK, 2–5 July 2007; Available online: https://www.harmo.org/Conferences/Proceedings/_Cambridge/publishedSections/Op109-113.pdf (accessed on 10 April 2024).
- Middleton, D.; Jones, A.; Redington, A.; Thomson, D.; Sokhi, R.; Luhana, L.; Fisher, B. Lagrangian modelling of plume chemistry for secondary pollutants in large industrial plumes. Atmos. Environ. 2008, 42, 415–427. [Google Scholar] [CrossRef]
- Dabdub, D.; Seinfeld, J.H. Extrapolation techniques used in the solution of stiff ODEs associated with chemical kinetics of air quality models. Atmos. Environ. 1995, 29, 403–410. [Google Scholar] [CrossRef]
- VDI 3783 Part 8. Environmental Meteorology; Turbulence Parameters for Dispersion Models Supported by Measurement Data; Beuth: Berlin, Germany, 2017; Available online: https://www.vdi.de/en/home/vdi-standards/details/vdi-3783-blatt-8-environmental-meteorology-turbulence-parameters-for-dispersion-models-supported-by-measurement-data (accessed on 25 February 2024).
- Diegmann, V.; Pfäfflin, F.; Tautz, F.; Wursthorn, H.; Baier, M.; Uhrner, U. Update RLuS. Technical Publication, Research Project 02.0375; Federal Highway Research Institute: Bergisch Gladbach, Germany, 2021. [Google Scholar]
- Lorentz, H.; Schmidt, W.; Hellebrandt, P.; Ketzel, M.; Jakobs, H.; Janicke, U. Einfluss eines Grossflughafens auf zeitliche und räumliche Verteilungen der Aussenluftkonzentrationen von Ultrafeinstaub [Influence of a Major Airport on Temporal and Spatial Distributions of Outdoor Air Concentrations of Ultrafine Particulate Matter]; Report 14/2021; German Federal Environment Agency: Dessau-Roßlau, Germany, 2021. Available online: https://www.umweltbundesamt.de/en/press/pressinformation/ground-level-engine-emissions-are-greatest-source (accessed on 10 April 2024).
- Janicke, U.; Montreuil, E.; Ghedhaïfi, W.; Terrenoire, E. Time resolved aircraft dispersion modelling. In Proceedings of the 3rd ECATS Conference, Online, 13–15 October 2020. [Google Scholar]
- ICAO Environmental Report 2010. International Civil Aviation Organisation. Available online: https://www.icao.int/environmental-protection/pages/envreport10.aspx (accessed on 10 April 2024).
- ICAO Document 9889: Airport Air Quality Manual, 2nd ed.; International Civil Aviation Organisation: Montreal, QC, Canada, 2020; Available online: https://www.icao.int/publications/pages/publication.aspx?docnum=9889 (accessed on 10 April 2024).
- Arunachalam, S.; Blanchard, C.; Henry, R.; Tombach, I. LAX Air Quality and Source Apportionment Study; Final Report, Prepared and Submitted to Los Angeles World Airports; Tetra Tech Inc.: Pasadena, CA, USA, 2013. [Google Scholar]
- UK Department for Transport. Project for the Sustainable Development of Heathrow; Air Quality Technical Report; Department for Transport: London, UK, 2006.
- Durdina, L. Results from Aircaft Engine Measurements; Private Communication; ZHAW School of Engineering: Winterthur, Switzerland, 2023. [Google Scholar]
- European Commission. EU Air Quality Standards. Available online: https://environment.ec.europa.eu/topics/air/air-quality/eu-air-quality-standards_en (accessed on 10 April 2024).
- US Environmental Protection Agency. Criteria Air Pollutants, NAAQS Table. Available online: https://www.epa.gov/criteria-air-pollutants/naaqs-table (accessed on 10 April 2024).
- European Commission. Revision of the Ambient Air Quality Directives. Available online: https://environment.ec.europa.eu/topics/air/air-quality/revision-ambient-air-quality-directives_en (accessed on 10 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).