Application of Lattice Boltzmann Approach for Teaching a Rock Mass Seepage Mechanics Course

Abstract

The technology of CO₂ geological storage and CH₄ intensive mining (CO₂-ECBM) in coal seams integrates greenhouse gas emission reduction and new fossil energy development and has great development prospects. The CO₂ injection, CO₂ sequestration mechanism and storage capacity, and CH₄ stimulation effect constitute the core content of the effectiveness of CO₂-ECBM, among which CO₂ injection is the most critical. Traditional seepage analysis methods often struggle to tackle flow-related issues influenced by microscale effects and intricate channels. This paper highlights the advantages of employing lattice Boltzmann (LBM) numerical simulations to study CO₂ seepage behaviors when teaching a Rock Mass Seepage Mechanics Course. This course primarily covers topics such as the pore structure of rock, unstable liquid seepage, gas seepage theory and related subjects. Its goal is to provide students with a solid theoretical foundation to address the complexities of fluid seepage in pours media encountered in practical scenarios. A novel LBM-based methodology was employed to estimate the CO₂ seepage capacity by incorporating the effects of different concentrations of [Bmin]Cl solution (0 wt%, 1 wt%, 3 wt%, and 5 wt%). The CO₂ velocity distribution cloud map of each coal sample was simulated; the average velocity distribution curve of each coal sample was obtained; and the velocity profile of the seepage channel of each coal sample was described. This study can provide theoretical guidance for the technology of CO₂ geological storage and CH₄ intensive mining in coal seams.

1. Introduction

The technology of CO₂ geological storage and CH₄ intensive mining (CO₂-ECBM) in coal seams integrates greenhouse gas emission reduction and new energy development and has great development prospects, but its effectiveness, economy, sustainability, and safety are still the main theoretical and technical problems facing CO₂-ECBM at present. The core aspect of the effectiveness of CO₂-ECBM is CO₂ injection. This topic is closely related to the seepage mechanism in porous media.

Universities have responded to this demand by introducing courses such as “Rock Mass Seepage Mechanics” for students majoring in fields like petroleum engineering and safety engineering. These courses aim to enhance students’ understanding of professional knowledge. Specifically, they cover the fundamental concepts of rock mass seepage mechanics, the basic laws governing it, mathematical models, and practical applications. By introducing students to the principles of seepage mechanics and mathematical models, these courses provide a solid foundation for solving complex fluid seepage problems in porous media. Currently, the prevalent format of domestic rock mass seepage mechanics courses typically presents traditional theoretical methods or simulation approaches. However, the complex pore and fissure structures found in extensively mined unconventional rock masses introduce multiscale effects into fluid diffusion, rendering traditional seepage theoretical analyses inadequate for comprehensively addressing these intricate flow phenomena [1,2]. While practical laboratory sessions enhance students’ comprehension of fluid flow in rock masses, certain limitations are inherent in the teaching of rock mass seepage mechanics experiments. These limitations include the need for specialized equipment, complex experimental procedures, potential data inaccuracies, and the inability to fully replicate real-world underground seepage conditions. To address these challenges, the introduction of advanced theoretical analysis techniques is necessary to provide students with a more intuitive and accurate understanding of seepage laws and mechanisms.

The extensively exploited unconventional rock masses exhibit complexity, making the lattice Boltzmann (LBM) simulation method increasingly prevalent in addressing microscale seepage issues and intricate channel networks [3,4,5,6,7,8,9,10,11,12,13,14,15]. The LBM approach offers flexibility in handling fluid–boundary interactions, a feat challenging for traditional numerical methods. LBM’s porous media flow model is composed of pore-scale and representational volume element (REV)-scale models, suited to different simulation scales. This simulation method obviates the need for detailed knowledge of fluid flow within pores, focusing on macro-physical parameters (e.g., porosity and permeability) after volume averaging, compensating for the limited simulation scope of the pore-scale LBM model. Wang et al. provided a comprehensive synthesis of multiscale transport phenomena encompassing desorption, nanopore diffusion, micropore infiltration, convection, and mass flow within mesoscopic pores. Their work culminated in the proposal of a shale gas production capacity model [16]. Li’s work focused on summarizing recent advancements in the multiphase lattice Boltzmann method, specifically emphasizing its application in elucidating heat transfer phenomena during boiling and condensation phase transitions [17]. Addressing the complexities inherent in actual environments and intricate structures, Chai delved into nonlinear percolation using the lattice Boltzmann method. This research introduced a lattice Boltzmann model to solve the Poisson equation by incorporating proposed rebound-Maxwell diffuse reflection combined boundary conditions and boundary discretization effects [18]. Zhao employed the LBM method to investigate pore structure and seepage characteristics in reservoirs, offering deeper insights into the pore structure traits and microscopic flow behavior within dense oil reservoirs [19]. Zhou et al. established a two-dimensional LBM model that facilitated the implementation of kinetic concentration boundary conditions during the interfacial mass transfer process. Their simulation effectively replicated the adsorption process within porous media at both pore-scale and mesoscopic levels [20]. Tackling water vapor adsorption in complex nanometer porous media, Zhang et al. proposed a pseudo-potential LBM method to study water seepage behavior, aiming to address this specific challenge [21]. Lastly, Zhao simulated nanopore flow dynamics using the LBM method and established an empirical formula tailored to different geometries and wettability conditions [22].

This paper aims to incorporate the LBM seepage simulation technique to investigate the effectiveness of CO₂ injection in CO₂-ECBM during the Rock Mass Seepage Mechanics Course.

2. Methodology

2.1. Present Situation of the Rock Mass Seepage Mechanics Course

Presently, extensively exploited unconventional rock masses exhibit complex fracture structures, and the fluid diffusion process—from pore desorption to fracture seepage—manifests multiscale effects. Traditional seepage analysis methods, relying on simplistic assumptions, are inadequate for analytical or semi-analytical flow modeling, particularly for scenarios characterized by significant microscale effects and intricate channel networks. These conventional methods struggle to accurately depict the fluid flow patterns in cross-scale rock masses transitioning from “microscopic pores” to “mesoscopic fractures” [23,24,25]. Thus, this course exists the problem of “Knowledge Obsolescence”.

2.2. The LBM Numerical Simulation Method

In recent years, computer simulation technology has significantly advanced, with numerical simulation techniques playing a pivotal role in the teaching of rock mass seepage mechanics. In this field, the primary focus is simulating fluid movement within porous media. The fundamental concept behind the LBM involves modeling fluids as composed of countless microscopic particles that interact within a grid framework. LBM simulates macroscopic fluid flow by tracking the collective behavior of these fluid particles, offering discrete macroscopic representation and continuous microscopic modeling. The underlying equation for solving fluid flow in LBM is the Boltzmann equation, and due to the discrete nature of the method, it boasts robust computational efficiency and supports parallel computing to accelerate calculations.

The general steps of LBM to address flow problems entail first establishing a grid within the flow field. Subsequently, a particle distribution function is defined within each grid cell to characterize the distribution of various particles within that cell. The particle distribution function within each cell is then calculated based on a collision model, culminating in simulation results obtained through continuous iterative computations. LBM enables precise simulations of complex flow phenomena, such as liquid infiltration through porous media, flow within tiny conduits, and interactions within multiphase flows.

In comparison to traditional Computational Fluid Dynamics (CFD) methods, LBM excels in terms of parallel computing efficiency, the capability to handle intricate boundary issues, and its innate capacity to manage multiphase flows seamlessly. This makes it highly promising in the realm of micro- and cross-scale research applications. LBM’s discrete nature makes it exceptionally suited for simulating particulate flow within rock mass pores. Unlike traditional CFD methods, LBM excels at capturing seepage within the intricate pores of coal bodies, providing accurate simulations for highly irregular pore structures.

When applied to the classroom teaching of rock mass seepage mechanics, LBM offers a vivid depiction of the physical characteristics and structures of rock mass. Furthermore, simulation technology is user-friendly, yields intuitive results, and serves as a powerful tool for increasing students’ interest in scientific research. It broadens students’ perspectives on scientific inquiry, fostering a positive learning environment, thus significantly optimizing the course on rock mass seepage mechanics.

LBM describes the evolution law of particles through the collision and migration of particles and takes the velocity distribution function f as the basic variable:

$$\frac{\partial f}{\partial t}+u·\nabla f=\mathsf{\Omega }$$

(1)

The velocity distribution function is a function of spatial location x, particle velocity ξ, and time t, namely f(x, ξ, t), which represents the density of particles with velocity ξ at spatial point x at time t.

The discretized lattice Boltzmann equation (LBE) is given as follows:

$$f_i(x+\xi \delta t,t+\delta t)-f_i(x,t)={\mathsf{\Omega }}_i$$

(2)

where the collision term Ω_i is the source of the complexity of the lattice Boltzmann equation. In order to simplify the LBE, the LBGK model with single relaxation was developed. The collision term in the model is expressed by the relaxation time:

$${\mathsf{\Omega }}_i=\frac{\delta t}{\tau }[f_i(x,t)-f_i^{eq}(x,t)]+\delta t{F}_i$$

(3)

The evolution equation of the LBGK model is given by:

$$\begin{array}{c}{f}_i\left(x+e_i{\delta }_t,t+{\delta }_t\right)-f_i\left(x,t\right)=-\frac{{\delta }_t}{\tau }\left[f_i\left(x,t\right)-f_i^{eq}\left(x,t\right)\right]+{\delta }_t{F}_i\end{array}$$

(4)

where $f_i\left(x,t\right)$ is the particle distribution function of x in the direction i at time t, τ is the non-dimensional relaxation time, and $f_i^{eq}\left(\mathit{x},t\right)$ is the equilibrium distribution function. The equilibrium distribution function can be uniformly expressed as:

$$\begin{array}{c}{f}_i^{eq}={\omega }_i\rho \left[1+\frac{3}{c^2}\left(e_i·u\right)+\frac{9}{2c^4}{\left(e_i·u\right)}^2-\frac{3}{2c^2}{u}^2\right]\end{array}$$

(5)

Here, ${\omega }_i$ is the weight coefficient, and ${\mathit{e}}_i$ is the discrete velocity. For different lattice types, ${\omega }_i$ and ${\mathit{e}}_i$ have different values, and the parameters of ${\omega }_i$ and ${\mathit{e}}_i$ in the D2Q9 model are used in this paper.

The fluid density and velocity expressions are defined as follows:

$$\begin{array}{c}\rho ={\displaystyle \sum _i}{f}_i,\rho u={\displaystyle \sum _i}{c}_i{f}_{i}v\end{array}$$

(6)

In this paper, by introducing the seepage resistance caused by the porous medium and other external forces, a fluid transport LBM model considering the influence of the wetting degree of the coal wall is established. The external forces include the seepage resistance of the porous medium and the force between the fluid and the solid wall. The expression of the seepage resistance caused by the medium is given in Equation (7):

$$F_b^{\sigma }=-\frac{\epsilon v}{K}u-\frac{\epsilon F_s}{\sqrt{K}}\left|u\right|u+\epsilon G$$

(7)

where $\epsilon$ is the porosity, $v$ is the viscosity coefficient of the fluid, K is the permeability, G is the external volume force, and $F_s$ is the structure function.

The expression for the force between the fluid phase and the solid wall is:

$${\mathrm{F}}_{\mathrm{a}\mathrm{d}\mathrm{s}}^{\sigma }(\mathrm{x})=-g_{\sigma \mathrm{w}}\psi (\mathrm{x})\sum _{i=1}^{N}w\left({\left|{\mathrm{e}}_i\right|}^2\right)\psi \left({\rho }_{\mathrm{w}}\right)s(\mathrm{x}+{\mathrm{e}}_i){\mathrm{e}}_i$$

(8)

Here, g_σw is the strength coefficient of the interaction force between the fluid phase and the solid wall, and ρ_w is the virtual velocity of the solid wall. In practice, g_σw and ρ_w can be adjusted, respectively, to obtain different sizes of contact angles. When the value of g_σw is negative, the contact angle between the fluid and the solid wall is less than 90°, and the fluid tends to wet the solid surface. When the value of g_σw is positive, the contact angle between the fluid and the solid wall is greater than 90°, and the fluid tends to alienate the solid surface. s is the indicator function, where s = 1 represents the solid wall and s = 0 represents the fluid phase.

3. Results and Discussions

3.1. Analysis of Coal Pore Surface Morphology

The SEM images of the original coal and the coal body treated with different concentrations of [Bmin]Cl solution are shown in Figure 1. According to Figure 1a, the surface of the coal body has the adhesion of other minerals, has smaller superficial pores, and is smoother, which indicates that the matrix of the coal has not been dissolved yet. Figure 1b shows a coal sample treated with a 1% [Bmin]Cl solution, which does not affect the coal very much due to its insufficient concentration. Figure 1c shows a coal sample treated with a 3% [Bmin]Cl solution, where the pores on the surface of the coal increased and the roughness was further increased. Figure 1d shows a coal sample treated with a 5% [Bmin]Cl solution, where morphological changes can be clearly seen with severe surface corrosion, increased roughness, and an increased number of pores. It can be seen that with the increase in concentration, the number of coal pores becomes larger, generating new cracks, enhancing the space for fluid seepage, and improving the permeability of the coal.

3.2. Analysis of Wetting Ability

The contact angle characteristics of the coal samples after treatment with raw coal and [Bmin]Cl solution are shown in Figure 2. The contact angles of the coal samples decreased continuously with the increase in [Bmin]Cl solution concentration, which were 82.6°, 72.0°, 67.9°, and 62.3°, respectively. It can be seen that the wettability of the coal samples before and after ionic liquid modification was continuously enhanced along with the increase in [Bmin]Cl solution concentration.

3.3. Modeling of the Random Pore Structure of the Coal Body

Using QSGS, it is possible to establish the pore distribution characteristics with the same core distribution probability (Pc), but with different porosity and different pore growth angles. It can be seen in Figure 3 that the homocore-type distribution with different porosity and pore growth angle has a unique pore structure, where the black area indicates the coal body and the white area indicates the pores, and the structure size in the figure is 20 × 20 μm².

The pore structure of the coal seam was established according to the above method with porosity settings of 46.7194%, 46.4635%, 47.0289%, and 47.2471% with increasing concentration, and the same Pc value (0.005) was taken for reconstruction. As can be seen in Figure 3, the number of pores increases with the increase in porosity at the same Pc value. It can be concluded that with the increase in [Bmin]Cl solution concentration, the pore number of coal samples modified with different concentrations of [Bmin]Cl increased significantly.

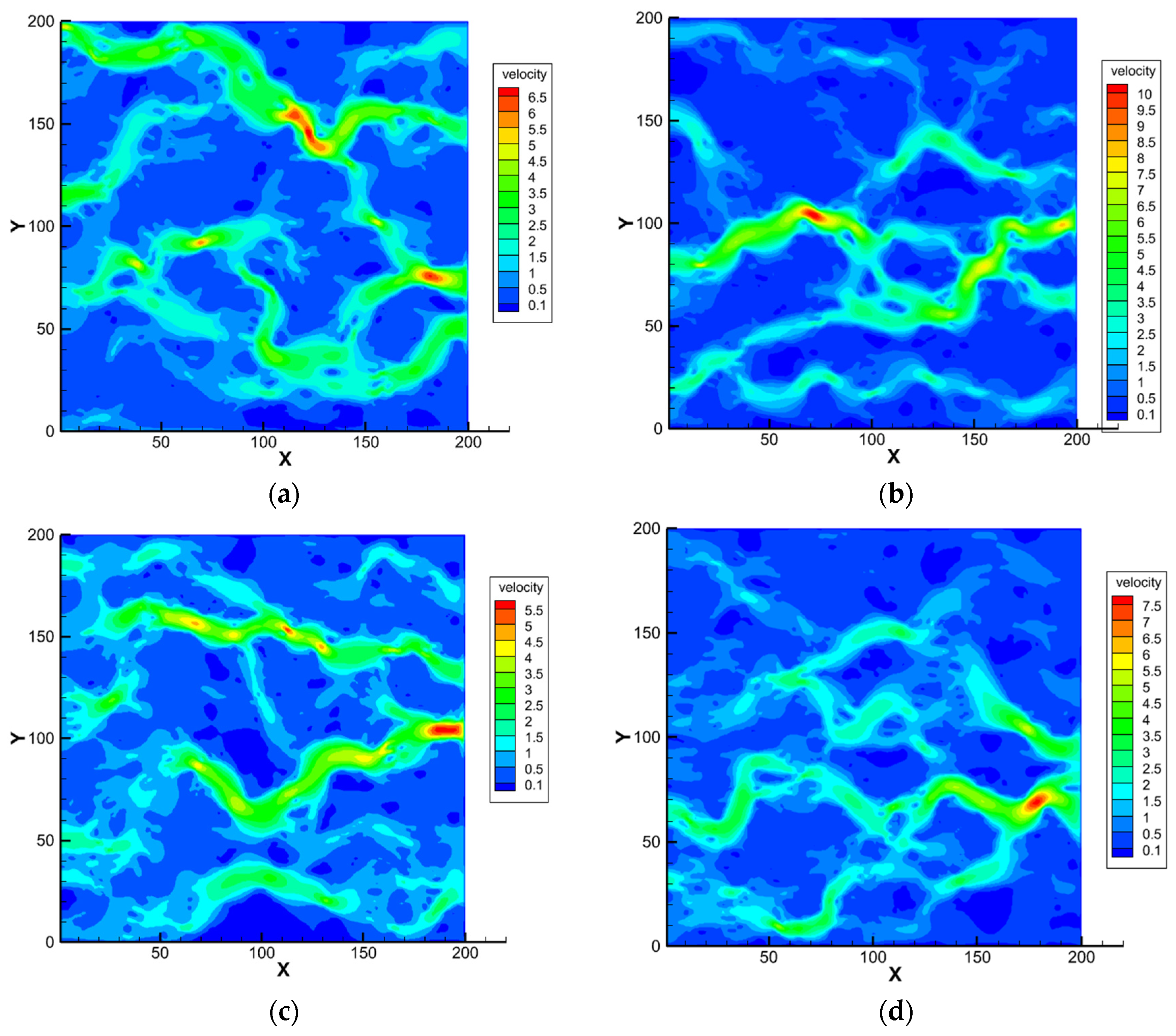
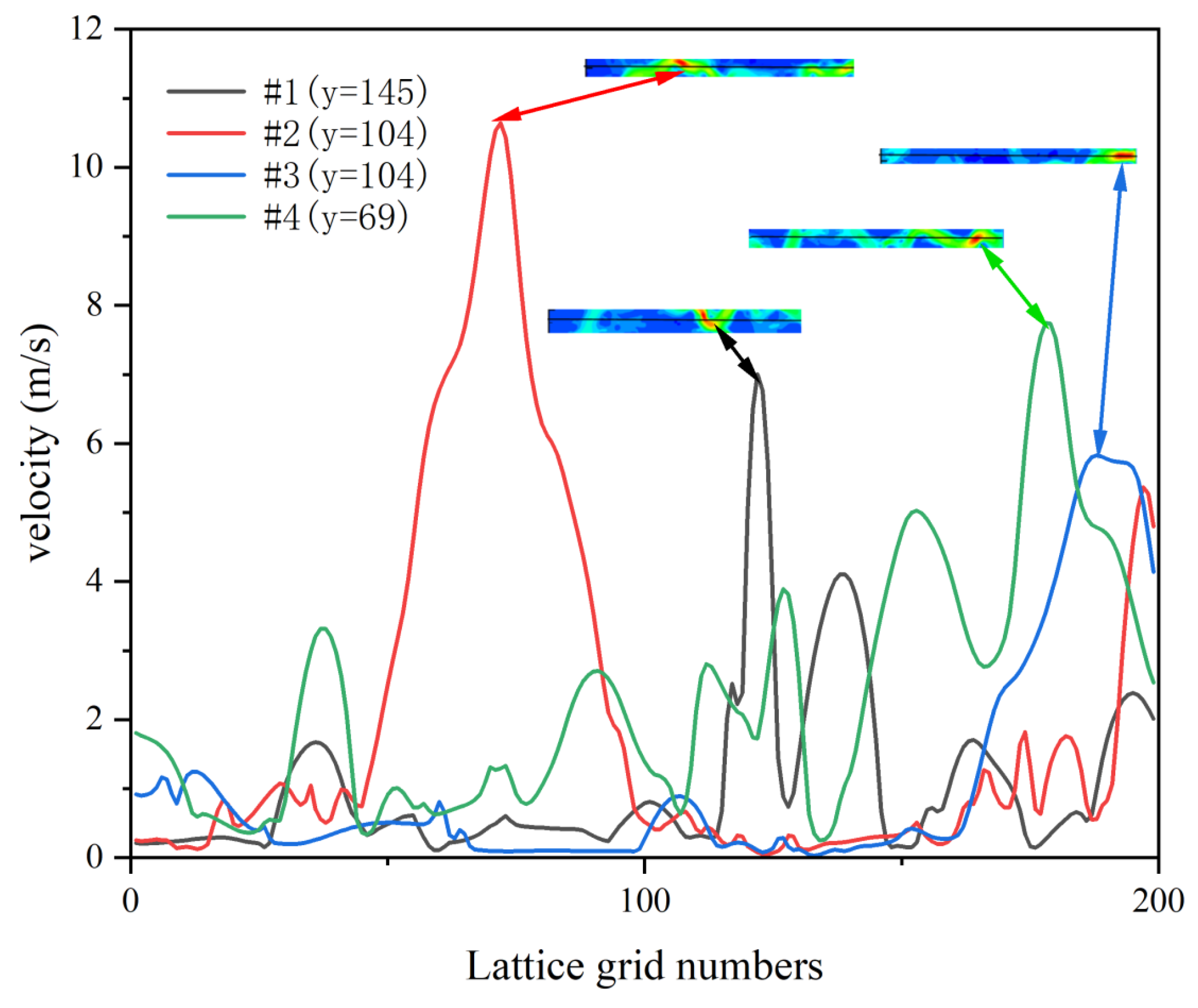
3.4. LBM Simulation Results of Coal Velocity Distribution

Figure 4a–d shows the LBM simulation results of the velocity field distribution of coal samples modified by 0 wt% [Bmin]Cl, 1 wt% [Bmin]Cl, 3 wt% [Bmin]Cl, and 5 wt% [Bmin]Cl with four different surfactant solutions, respectively. Figure 5 describes the average velocity distribution curve of each coal sample, and Figure 6 presents the velocity profile of the seepage channel of each coal sample.

From these figures, it can be seen that: (1) 1 wt% [Bmin]Cl modified coal samples have the highest velocity, which is caused by the joint effect of contact angle and porosity. Firstly, its porosity is the lowest, which leads to better connectivity, so the velocity is higher; secondly, the contact angle is reduced, which improves the wettability of the coal sample. (2) The difference in velocity between the coal sample treated with 3 wt% and 5 wt% [Bmin]Cl solution is smaller, and even the average velocity of the coal sample treated with 5 wt% [Bmin]Cl solution is higher than that of the coal sample treated with 3 wt% [Bmin]Cl solution in several places. This is because it is easy to see in the velocity distribution cloud diagram that the pores in the coal sample treated with a 3 wt% [Bmin]Cl solution are denser, so there are more flow channels, i.e., the average velocity is higher. (3) The velocity in the raw coal sample is lower than that in the coal sample treated with a 1 wt% [Bmin]Cl solution. This is because the flow channels in the raw coal sample solution are wider compared to the other three samples, resulting in a lower flow velocity.

4. Concluding Remarks

(1) The Lattice Boltzmann Method has demonstrated its suitability for classroom instruction in rock mass seepage mechanics. Compared to traditional teaching methods reliant on formula derivations, the LBM method offers a more vivid representation of the physical characteristics and structure of rock masses. (2) LBM’s simulation technology is user-friendly, delivering intuitive and comprehensible results. This not only ignites students’ interest in scientific research but also broadens their horizons in the field, fostering a positive learning environment and atmosphere. It represents a significant improvement in the delivery of the rock mass seepage mechanic’s course.