Next Article in Journal
An Assessment of the Coupled Weather Research and Forecasting Hydrological Model on Streamflow Simulations over the Source Region of the Yellow River
Previous Article in Journal
Research on Frequency Matching Correction Techniques for South China Precipitation Ensemble Forecast Based on the GRAPES Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 15
Issue 4
10.3390/atmos15040467
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

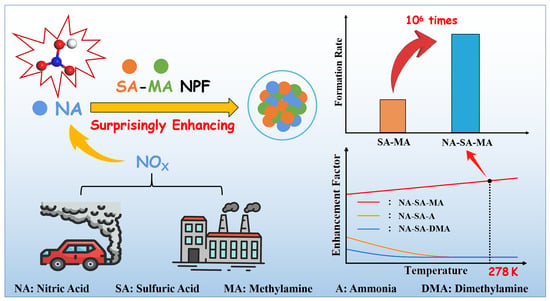
A Surprisingly High Enhancing Potential of Nitric Acid in Sulfuric Acid–Methylamine Nucleation

by
Fukang Qiao
,
Rongjie Zhang
,
Qiaojing Zhao
,
Fangfang Ma
,
Jingwen Chen
and
Hong-Bin Xie
*
Key Laboratory of Industrial Ecology and Environmental Engineering (Ministry of Education), School of Environmental Science and Technology, Dalian University of Technology, Dalian 116024, China
*
Author to whom correspondence should be addressed.
Atmosphere 2024, 15(4), 467; https://doi.org/10.3390/atmos15040467
Submission received: 10 March 2024 / Revised: 29 March 2024 / Accepted: 4 April 2024 / Published: 10 April 2024
(This article belongs to the Topic Atmospheric Chemistry, Aging, and Dynamics)
Browse Figures
Versions Notes

Abstract

:
Nitric acid (NA) has recently been found to enhance sulfuric acid (SA)-driven new particle formation (NPF) at low temperatures (≤240 K). However, studies on the role of NA in atmospheric NPF remain limited. Herein, we explored the enhancement effect of NA on binary SA–methylamine (MA) nucleation by investigating the mechanism and kinetics of (NA)x(SA)y(MA)z (0 ≤ x, 0 ≤ y, x + y ≤ 3, 0 ≤ z ≤ 3) clusters using quantum chemical calculations and cluster dynamics simulations. We found that the mixed ternary NA-SA-MA clusters have lower evaporation rates compared to the corresponding NA-SA–dimethylamine (DMA) and NA-SA–ammonia (A) clusters, indicating the stronger binding ability of NA with respect to SA-MA clusters. At atmospheric conditions (T ≥ 278.15 K), NA can enhance the cluster formation rate of SA-MA by about six orders of magnitude, demonstrating a surprisingly high enhancing potential. Moreover, NA acts as an important participant in the cluster growth pathways of the NA-SA-MA system, as opposed to the “bridging” role of NA in the previously studied NA-SA-A system. This study proposes the first case of NA efficiently enhancing SA–amine nucleation at ambient temperature, suggesting a larger impact of NA in atmospheric NPF than previously expected.

Graphical Abstract

1. Introduction

Atmospheric particulate matter poses a serious threat to global climate and air quality [1,2,3,4,5,6]. New particle formation (NPF) plays a pivotal role as an important contributor to atmospheric particulate matter, which can contribute over 50% of the global aerosol budget [1,2,3,4,5,6,7,8,9,10,11,12]. Therefore, a comprehensive understanding of NPF is essential for evaluating the impacts of particulate matter and devising effective control strategies.
The most important nucleation precursor of atmospheric NPF is thought to be sulfuric acid owing to its exceptionally low volatility and strong acidity [3,6,13,14,15,16,17,18,19,20,21,22,23,24]. Atmospheric bases, such as ammonia (A, NH3) and amines, can efficiently nucleate with SA via acid–base proton transfer reactions and the formation of hydrogen bonds [3,6,13,14,18,19,25,26,27,28,29,30,31]. Despite large differences in concentrations, amines have been found to more efficiently enhance SA particle formation compared with A [13,14,24,28,32]. However, the binary SA–base nucleation mechanisms fall short of explaining the high rates of NPF observed under realistic atmospheric conditions [33,34,35]. This implies that other potential gaseous precursors may participate in and further enhance binary SA–base nucleation.
Nitric acid (NA, HNO3) is an abundant inorganic acid in the troposphere, with a broad variety of sources and a wide range of distributions [36,37,38,39,40,41,42]. The tropospheric concentration of NA can be up to 1 × 1012 molecules cm−3, significantly exceeding that of SA by a factor of four to seven orders of magnitude [40,43,44,45]. Considering the high atmospheric abundance of NA, some recent investigations have concentrated on the enhancing effect of NA on SA–base nucleation [46,47,48,49,50,51]. Wang et al. and Liu et al. pointed out that NA can effectively enhance both SA-DMA and SA-A nucleation at low temperatures (≤240 K), but NA had a negligible enhancing effect at temperatures commonly encountered in the atmospheric boundary layer (280 K) [46,47,48]. In addition, Knattrup et al. found that NA can increase the cluster formation rate by studying mixed-acid–mixed-base clusters containing at most one NA molecule [49,50]. Amines cover a wide variety of species in the atmosphere with different basicities and structures, implying that the enhancing effect of NA may be different for different SA–amine systems. However, except for DMA and A, the enhancement effect of NA on SA–other amine nucleation has not been studied in detail, which hinders a comprehensive assessment of the role of NA in NPF processes. Therefore, it is essential to explore the enhancing effect of NA on SA–other amine nucleation in detail.
Methylamine (MA) has a higher global emission than DMA and a stronger basicity than A [52]. In addition, MA has the structural characteristics of a lower steric hindrance than DMA and the capability of forming one more hydrogen bond. Previous studies have shown that basicity, hydrogen-bonding capacity and steric hindrance jointly influence the clustering ability of a given amine with acids [53,54,55,56]. This implies that the enhancing effect of NA on SA-MA nucleation is not easy to predict simply based on the enhancing effect of NA on the previously studied SA-DMA and SA-A systems. Here, we conducted a systematic investigation of NA’s enhancing effect on SA-MA nucleation by exploring the thermodynamics and kinetics of the ternary NA-SA-MA system using quantum chemical calculations with simulations using the Atmospheric Cluster Dynamic Code (ACDC) [57]. Additionally, we chose the previously studied NA-SA-DMA and NA-SA-A systems as references to analyze and compare the enhancing role of NA in these three systems [47,48].

2. Materials and Methods

2.1. Configurational Sampling

Similar to our previous studies [53,58,59,60], a multi-step sampling approach was utilized to explore the most stable configurations of the clusters in the ternary NA-SA-MA system, including (NA)1-3(MA)1-3 and (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) clusters. The configurations of the remaining clusters in the ternary NA-SA-MA system ((SA)0-3(MA)0-3 and homomolecular (NA)1-3) were derived from previous research [48,61]. In order to obtain the most stable configurations, the ABCluster program was first employed to generate 6000 initial guess structures for each cluster type [62,63]. The CHARMM36 force field was applied for the simulation of all molecules in the ABCluster program. Based on the initial guess structures, four sequential calculation steps were performed to gradually screen for the global minimum. The specific details of the multi-step sampling approach and the employed calculation methods are presented in Appendix A. In brief, the configuration exhibiting the lowest Gibbs free energy value (G) was identified as the most stable configuration for a given cluster type. The binding free energy (ΔG) was derived from the subtraction of the individual G of the constituent monomers from the overall G of the studied cluster at a temperature of 298.15 K. All calculations utilizing the PM6 and ωB97X-D methods were performed through the GAUSSIAN 09 software [64], while the DLPNO-CCSD(T)/aug-cc-pVTZ computations were carried out by the ORCA 4.0.0 software [65]. In addition, all the cluster configurations for the ternary NA-SA-DMA and NA-SA-A systems, as reported in earlier research [47,48], were adopted and subsequently recalculated at the theoretical levels utilized in the current investigation.

2.2. Atmospheric Cluster Dynamics Code Simulations

ACDC was utilized to investigate the time evolution of cluster concentrations and growth pathways. For more details about the theory behind ACDC, see Appendix A [57,66]. Here, the simulated ternary NA-SA-MA system can be characterized as a “3 × 3” box involving (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (NA)0-3(MA)0-3 and (SA)0-3(MA)0-3 clusters. The choice of boundary clusters was guided by their stability at the specific temperatures examined, as detailed in Appendix A. Within the simulations, the SA concentration [SA] was fixed in the range of 106 to 107 cm−3, the NA concentration [NA] was adjusted between 108 and 1012 cm−3, and the MA concentration [MA] was set between 108 and 109 cm−3, which values correspond to their usual ambient concentrations [3,24,39]. The simulations were conducted at 238.15 K to 298.15 K, and the coefficient for the coagulation sink was established at 2 × 10−2 s−1, which corresponds to the typical value for polluted urban atmospheres [3]. As a comparison, the NA-SA-DMA and NA-SA-A systems were also simulated, with the DMA concentration [DMA] between 108 and 109 cm−3 and the A concentration [A] at 1010 cm−3. The simulation system for both the NA-SA-DMA and the NA-SA-A systems also consisted of a “3 × 3” box, and the selection of the boundary clusters can be seen in Appendix A. All other conditions were set the same as those used for the simulation of the NA-SA-MA system.

3. Results and Discussion

3.1. Cluster Structures

Given that (SA)1-3(MA)1-3 clusters have been extensively discussed in earlier studies [24,26,66], here, we primarily concentrate on the binary (NA)1-3(MA)1-3 and mixed ternary (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) clusters. The most stable conformations of the (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) clusters are shown in Figure 1, and the most stable conformations of the (NA)1-3(MA)1-3 clusters are displayed in Figure S1. Proton transfers from NA to MA occur in all the binary (NA)1-3(MA)1-3 clusters except (NA)1(MA)1, and these acid–base clusters are stabilized through electrostatic interactions between positively and negatively charged ions and intermolecular hydrogen bonds. The (NA)1(MA)1 cluster is the exception, as there is no proton transfer; it is only stabilized by hydrogen bonds. For all the mixed ternary (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) clusters, proton transfer and the formation of a complex hydrogen bond network are observed. When y ≥ z, all MA molecules undergo protonation by accepting a proton from SA, such as (NA)1(SA)1(MA)1, (NA)1(SA)2(MA)1, (NA)2(SA)1(MA)1 and (NA)1(SA)2(MA)2. When y < z, both SA and NA can transfer a proton to the MA molecules. Thus, the proton transfer process from SA to MA is comparatively more advantageous compared to the transfer from NA to MA in the case of all the mixed ternary NA-SA-MA clusters. This phenomenon is likely caused by the higher acidity of SA compared to NA. In addition, only one proton can be transferred to MA from SA molecules in all the acid–base clusters, and therefore no formation of SO42− is observed.
We then compared the number of hydrogen bonds within the mixed ternary (NA)x(SA)y(MA)z cluster with the numbers in the (NA)x(SA)y(DMA)z and (NA)x(SA)y(A)z clusters (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) (see Table 1), since the hydrogen bond is a vital structural factor for stabilizing clusters. It was found that the numbers of hydrogen bonds in all the (NA)x(SA)y(MA)z clusters were greater than or equal to those in the corresponding (NA)x(SA)y(DMA)z clusters, except for the case of (NA)1(SA)1(MA)1 and (NA)1(SA)1(MA)2. This is related to the presence of more hydrogen bond formation sites in MA than DMA, as it has one more methyl group. In addition, the numbers of hydrogen bonds in the (NA)x(SA)y(MA)z clusters are comparable to those in the (NA)x(SA)y(A)z clusters. Hence, the observed numbers of hydrogen bonds in the mixed ternary (NA)x(SA)y(MA)z clusters suggest that they are likely more stable.

3.2. Evaporation Rates

The evaporation rate of a cluster represents the rate at which molecules or smaller clusters escape from the original cluster, and therefore it can be used to infer the stability of the cluster. The evaporation rate of a mother cluster is relevant to the collision rate coefficient of its two daughter clusters or monomers and the difference in formation free energy between the mother cluster and its two possible daughter clusters or monomers (detailed in Equation (A3) in Appendix A). Since the difference between the collision rate coefficients for various systems is minor, the evaporation rate of a mother cluster mostly depends on the relative formation free energy of the mother cluster with respect to its possible daughter clusters or monomers. In general, clusters with lower evaporation rates are considered to be more stable [58,59,60]. Since we are mainly concerned with the enhancement effect of NA on SA-MA nucleation, here, we primarily focus on the evaporation rate based on the ΔG values (Figure S2) of the mixed ternary NA-SA-MA clusters (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3). Figure 2A shows the evaporation rates for the mixed ternary NA-SA-MA clusters at 278.15 K, while Figure 2B provides the evaporation rates for the binary SA-MA clusters as a comparison. For the ternary NA-SA-MA system, the evaporation rates of the four clusters (NA)1(SA)2(MA)3, (NA)2(SA)1(MA)3, (NA)1(SA)2(MA)2 and (NA)1(SA)1(MA)2 are on the order of 10−3–10−2 s−1. These are significantly lower than those of the other ternary NA-SA-MA clusters, which have evaporation rates higher than 101 s−1. Under atmospheric conditions, these four clusters may be considered to possess stability. Such a wide variation in the evaporation rate for various clusters is understandable, since the relative formation free energies of mother clusters with respect to their daughter clusters or monomers differ greatly. In comparison with the binary SA-MA clusters, we found that ternary NA-SA-MA clusters with equal acid and base molecule numbers, i.e., (NA)1(SA)2(MA)3, (NA)2(SA)1(MA)3 and (NA)1(SA)1(MA)2, have lower evaporation rates than the corresponding binary SA-MA clusters. This suggests that the addition of NA enhances the stability of these three clusters, and there is a strong possibility that they can participate in the main cluster growth pathways of the NA-SA-MA system.
A comparison was also conducted between the evaporation rates of the ternary NA-SA-MA clusters and those of the ternary NA-SA-DMA and NA-SA-A clusters (see Figure 2C,D). A common feature in all three systems is that the evaporation rates for clusters with equivalent numbers of acidic and basic molecules, i.e., (NA)1(SA)1(base)2, (NA)2(SA)1(base)3 and (NA)1(SA)2(base)3, are lower than those for the other ternary clusters. This is consistent with many previous studies [61,67]. Moreover, the evaporation rates of all the ternary NA-SA-MA clusters are lower compared to the corresponding ones in the NA-SA-DMA system, except for the (NA)1(SA)1(MA)2 and (NA)1(SA)2(MA)3 clusters. It has been observed that the evaporation rate for the (NA)1(SA)2(MA)2 cluster is significantly lower compared to that of the (NA)1(SA)2(DMA)2 cluster. Similarly, the evaporation rates for each of the ternary NA-SA-MA clusters are lower than those for the related NA-SA-A clusters. Therefore, the lower evaporation rates suggest that ternary NA-SA-MA clusters have greater stability when compared to the ternary NA-SA-DMA and NA-SA-A clusters.

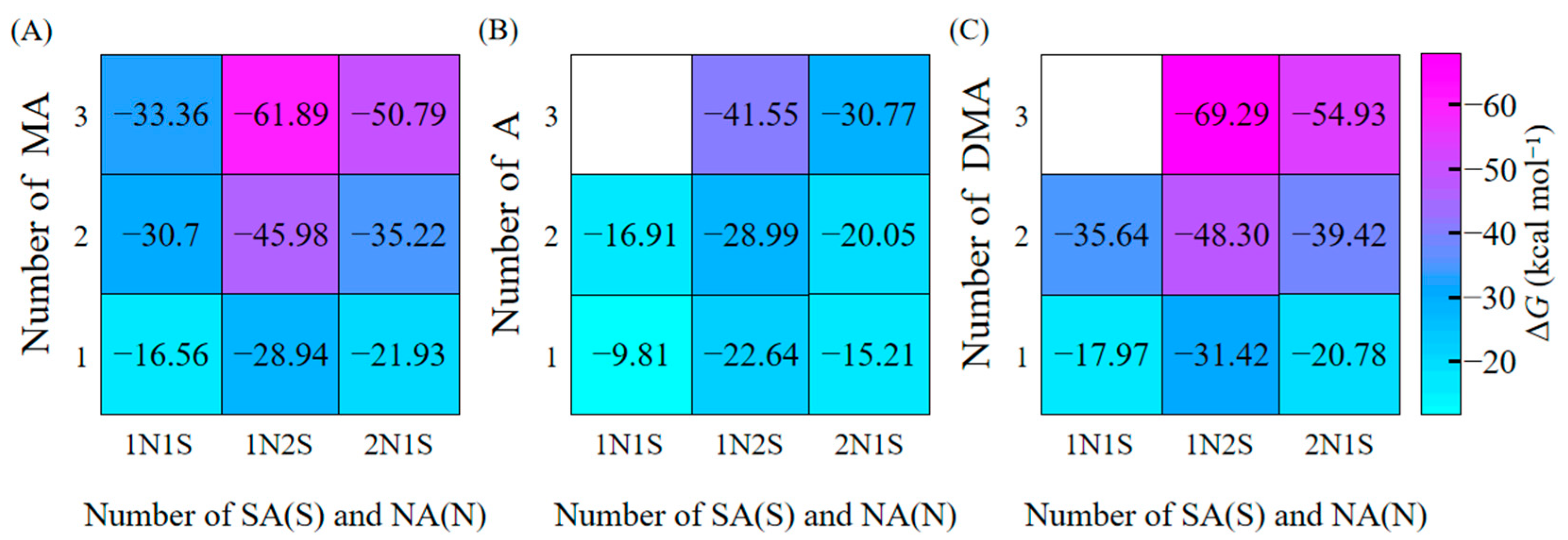
3.3. Addition Free Energies of NA to the Clusters

We employed the addition free energy of NA (ΔGadd) as an important parameter to evaluate the binding ability of NA to the binary SA–base clusters. Herein, ΔGadd values for the binary SA-MA, SA-DMA and SA-A clusters were calculated to compare the preferences for the uptake of NA between these three binary SA–base systems (Figure 3). The ΔGadd for each ternary (NA)x(SA)y(base)z cluster was calculated as follows:
ΔGadd = G(NA)x(SA)y(base)z − G(SA)y(base)z − GNA × x
where G(NA)x(SA)y(base)z, G(SA)y(base)z and GNA are the Gibbs free energies of the ternary (NA)x(SA)y(base)z cluster, the binary (SA)y(base)z cluster and NA monomers, respectively. As shown in Figure 3A, the ∆Gadd values for all the ternary NA-SA-MA clusters are highly negative, and therefore the addition of NA to the clusters is thermodynamically favorable. Furthermore, when the number of SA molecules stays constant, there is a clear trend that the ∆Gadd values of the (NA)x(SA)y(MA)z clusters decrease with an increase in the number of base molecules, suggesting that the greater number of bases in the cluster makes it more favorable to attract NA molecules. It is noteworthy that the ∆Gadd values for all the ternary NA-SA-MA clusters are lower than those for the corresponding ternary NA-SA-DMA and NA-SA-A clusters, signifying that NA binding with SA-MA clusters is more advantageous compared to the SA-DMA and SA-A clusters. We speculate that the introduction of NA leads to a change in the topological structure of the binary SA-MA clusters, resulting in stronger binding of NA with SA-MA clusters and more hydrogen bonds in the formed ternary NA-SA-MA clusters.

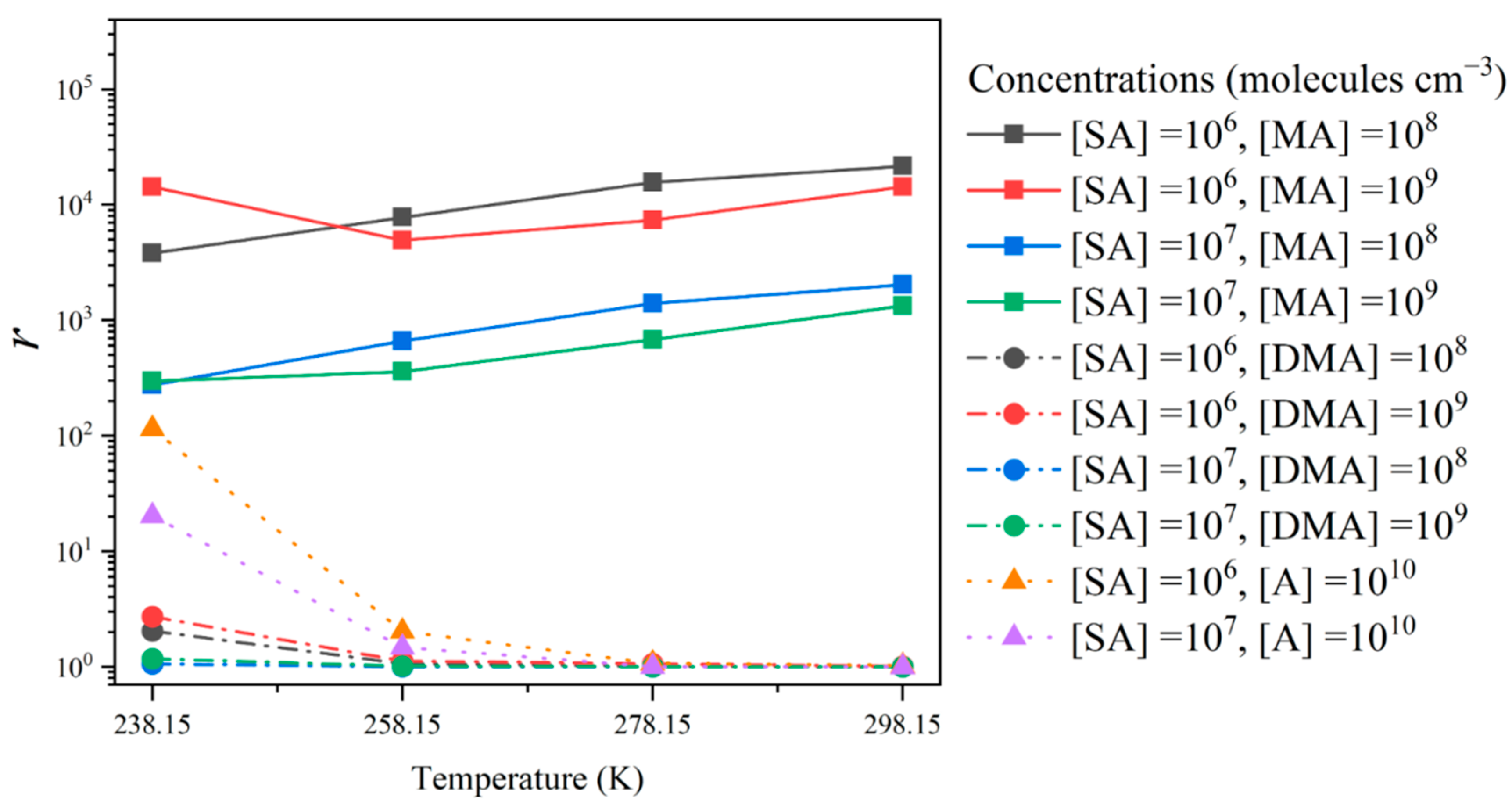
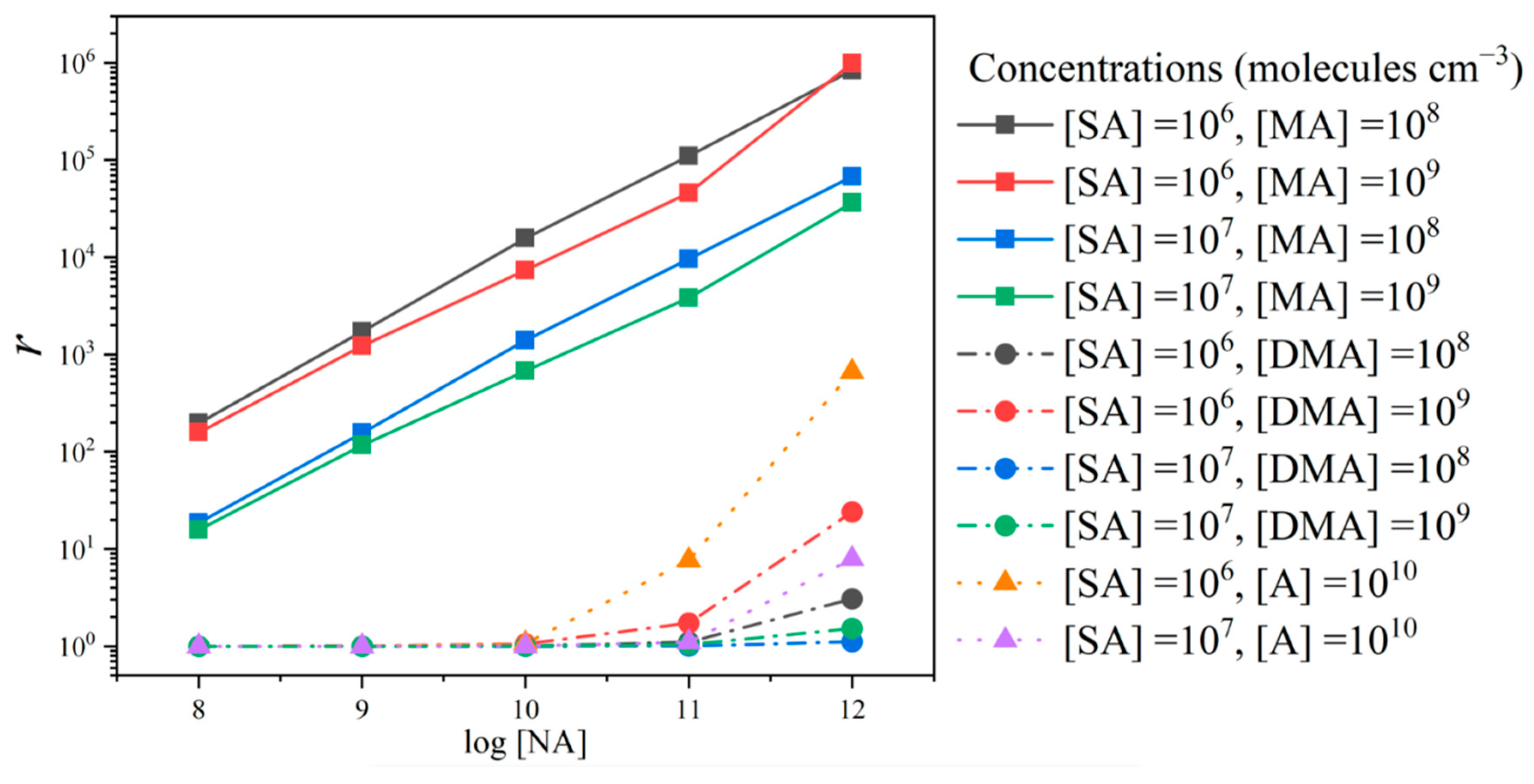
3.4. Enhancement Effect of NA on Cluster Formation Rates

Here, we further investigated the enhancing effect of NA on SA-MA nucleation by comparing the cluster formation rates before and after adding NA to the binary SA-MA system. We also compared it with the enhancing effect of NA on SA-DMA nucleation and SA-A nucleation (cluster formation rates of these nucleation systems are shown in Tables S1–S3). The enhancing effect of NA on binary SA–base nucleation is quantified by the enhancement factor (r):
r = J ( [ S A ] = x , [ b a s e ] = y , [ N A ] = z ) J ( [ S A ] = x , [ b a s e ] = y , [ N A ] = 0 )
where J ([SA] = x, [base] = y, [NA] = z) and J ([SA] = x, [base] = y, [NA] = 0) indicate the cluster formation rate of the ternary NA-SA–base system and the binary SA–base system without NA, respectively. Under realistic atmospheric conditions, precursor concentration and temperature are both important factors influencing the nucleation rate. Therefore, we examined r at different precursor concentrations and temperatures.
The effect of temperature on r when [NA] = 1010 cm−3 and T = 238.15 K–298.15 K is displayed in Figure 4. It is observable that NA always has a significant enhancing effect on SA-MA nucleation, with the r value ranging from 276 to 14370 under the considered conditions. The overall trend shows that the r value increases with increasing temperature, except for the case with the conditions of [SA] = 106 cm−3 and [MA] = 109 cm−3, where the r value initially decreases and then increases with increasing temperature. Furthermore, the r value under the lower SA concentration (106 cm−3) is higher than that under the higher SA concentration (107 cm−3), indicating that NA can cause stronger enhancement of SA-MA nucleation when the SA is scarce. Furthermore, for the NA-SA-DMA and NA-SA-A systems, the r value increases with decreasing temperature, and NA only has a prominent enhancing effect on binary SA-DMA/A nucleation at temperatures below 258.15 K. However, the r value of NA in the binary SA-DMA/A nucleation is much lower than that in the binary SA-MA nucleation under our considered conditions, which confirms the significantly high enhancement effect of NA on SA-MA nucleation.
Figure 5 shows the effect of NA concentration on r at 278.15 K. It can be seen that for three NA-SA-base systems, r shows a positive dependence on [NA] and the r value under the lower SA concentration (106 cm−3) is higher than that under the higher SA concentration (107 cm−3). For the NA-SA-MA system, r increases from 16 to about 106 as the NA concentration increases from 108 cm−3 to 1012 cm−3, reflecting the high enhancing effect of NA for the SA-MA system at 278.15 K. However, for the NA-SA-DMA and NA-SA-A systems, an enhancing effect of NA was only observed when NA > 1010 cm−3 at 278.15 K, which is still much lower than the r value for the NA-SA-MA system at the same NA concentration.
As discussed above, our results indicate that even under environmental conditions with high temperatures, such as at noon, NA can still efficiently enhance SA-MA nucleation to a surprisingly high degree, in contrast to the negligible enhancing effect of NA on binary SA-DMA or SA-A nucleation above 278.15 K presented in previous studies [46,47,48].

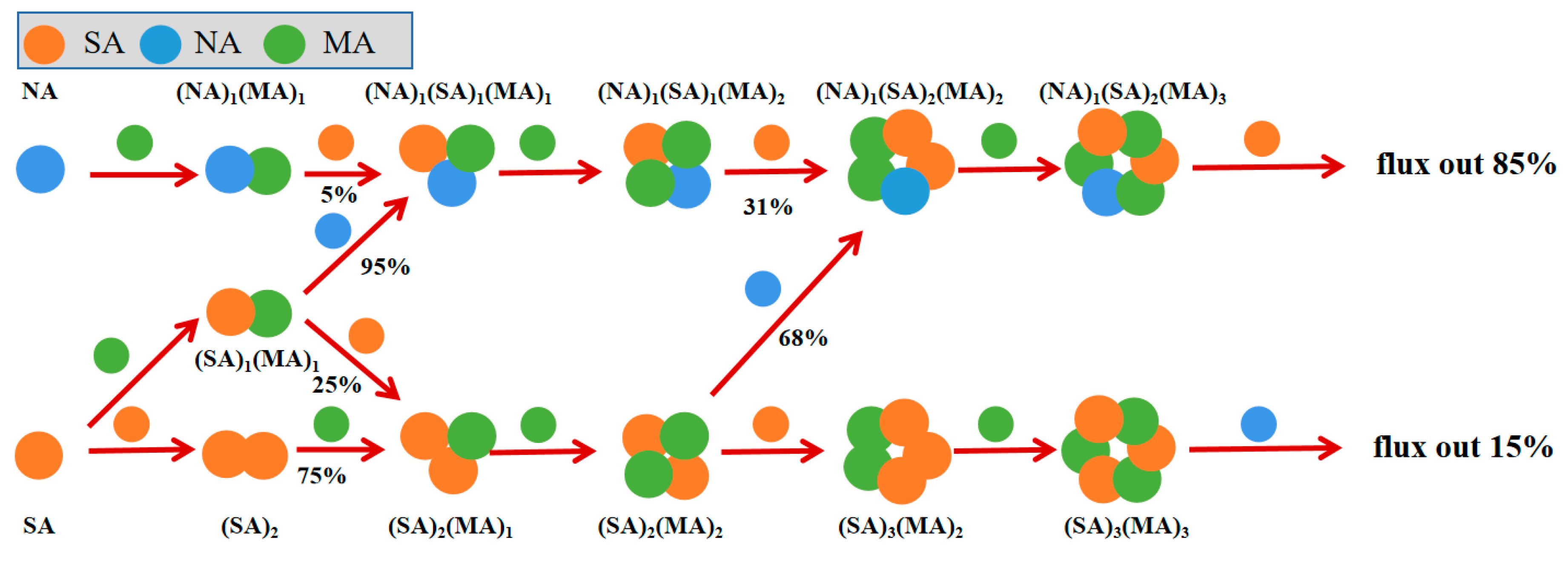
3.5. Mechanism of the NA-SA-MA Nucleation System

ACDC simulations can keep track of the fluxes between clusters, which makes analysis of the cluster formation mechanism easy. Herein, the cluster growth pathway within the NA-SA-MA system at 278.15 K, [NA] = 1010 cm−3, [SA] = 106 cm−3 and [MA] = 108 cm−3 is displayed in Figure 6. Under these conditions, NA led to an enhancement factor of about 15,000 for SA-MA nucleation. As shown in Figure 6, the cluster growth mainly proceeds through two channels. One is the binary SA-MA channel, which is initiated by the collision of two SA molecules or the collision between SA and MA molecules. The other is the NA-participated channel, which is initiated by the collision of NA and MA molecules. In addition, the two channels are linked by the addition of one NA molecule to the (SA)1(MA)1 and (SA)2(MA)2 clusters to form the (NA)1(SA)1(MA)1 and (NA)1(SA)2(MA)2 clusters, respectively. Both channels subsequently grow through collisions with monomers, ultimately producing the (SA)3(MA)3 and (NA)1(SA)2(MA)3 clusters, respectively. It is noted that the ternary NA-SA-MA clusters that participate in the growth pathways contain at most one NA molecule. Finally, (SA)3(MA)3 and (NA)1(SA)2(MA)3 clusters can directly collide with NA and SA molecules, respectively, to form the (NA)1(SA)3(MA)3 cluster, which grows out of the “3 × 3 box”, with the two paths contributing 15% and 85% of the cluster formation rates, respectively.
We also tested the influence of temperature and [NA] on the cluster growth pathway of the NA-SA-MA system. Figure S3 presents the cluster growth pathway at a lower temperature (238.15 K, Figure S3A) and a higher [NA] (1012 cm−3, Figure S3B). As shown in Figure S3, the main growth pathway is slightly more complicated than that at 278.15 K and [NA] = 1010 cm−3. The cluster growth pathway is still mainly divided into the SA-MA channel and the NA-participated channel. However, at 238.15 K or [NA] = 1012 cm−3, the two channels can also be connected by an extra route via the evaporation of a NA molecule: (NA)1(SA)1(MA)1 → (NA)1(SA)2(MA)1 → (SA)2(MA)1. Another difference is that the finally formed (NA)1(SA)2(MA)3 cluster can collide not only with an SA monomer but also with the (NA)1(MA)1 dimer cluster to grow out of the “3 × 3 box” at 238.15 K or [NA] = 1012 cm−3. Additionally, at 238.15 K, (NA)1(SA)1(MA)2 can also collide with itself to form the (NA)2(SA)2(MA)4 cluster growing out of the “3 × 3 box”.
Overall, the growth pathways under the three conditions are generally similar; the NA-participated clusters contribute almost 100% to the cluster formation rate, indicating the importance of the participation and enhancement of NA in SA-MA nucleation. This is different from the case in which NA mainly acts as a “bridge” joining the smaller and larger binary SA-A clusters in the cluster growth pathways of the NA-SA-A system [47].

4. Implications and Conclusions

This study is the first to point out the surprisingly high enhancing effect of NA on the nucleation of the binary SA-MA system at ambient temperature. For example, at [NA] = 1010 cm−3 and T = 278.15 K–298.15 K, a common concentration and normal temperature range in the troposphere, NA can efficiently enhance the cluster formation rate of the binary SA-MA system by about 104-fold. Moreover, the enhancing role of NA could be even more pronounced in local regions with higher concentrations of NA and near emission sources of MA. However, previous studies reported that only at lower temperatures (≤240 K) could NA efficiently enhance binary SA-DMA or SA-A nucleation [47,48]. Thus, the enhancing effect of NA on the investigated binary SA–base nucleation systems does not simply adhere to the sequence of gas basicity among the bases (DMA > MA > A) [68], although acid–base reactions occur between NA and bases in ternary NA-SA–base nucleation. This implies that the enhancing effect of NA on binary SA–base nucleation is related not only to the basicity of the atmospheric bases but also to their structural factors, e.g., their hydrogen-bonding capacity. Therefore, the contribution of NA to nucleation involving SA and other bases warrants further study to comprehensively expand the current understanding of the role of NA in atmospheric NPF.
The enhancing potential of MA in SA-driven nucleation is lower than that of the other typically observed alkyl amines, i.e., DMA and trimethylamine (TMA) [24]. However, recent studies showed that MA can synergistically enhance SA-driven nucleation with other amines [69,70]. Considering the high enhancing effect of NA on SA-MA nucleation, it is likely that NA could significantly enhance the nucleation of SA–multiple amines containing MA in realistic atmospheres. It is important to mention that a recent investigation has revealed that NA can increase the nucleation rate of complex mixed-acid–mixed-base systems (e.g., the quaternary NA-SA-MA-DMA system), but the multi-component clusters in this study only include one NA molecule [50]. Such an NA-enhanced multi-component nucleation mechanism containing more NA and base molecules may explain the intense NPF events in the urban atmosphere, which deserve more concern in the future.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos15040467/s1, Figure S1: Lowest Gibbs free energy conformations of the (NA)1-3(MA)1-3 clusters; Figure S2: Formation free energy (ΔG) of (A) (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (B) (NA)x(SA)y(A)z (x ≥ 1, y ≥ 1, 1 ≤ z ≤ x + y ≤ 3) and (C) (NA)x(SA)y(DMA)z (x ≥ 1, y ≥ 1, 1 ≤ z ≤ x + y ≤ 3) clusters at 298.15 K; Figure S3: Cluster growth pathways for the NA-SA-MA system at (A) 238.15 K, [NA] = 1010 molecules cm−3, [SA] = 106 molecules cm−3 and [MA] = 108 molecules cm−3 and (B) 278.15 K, [NA] = 1012 molecules cm−3, [SA] = 106 molecules cm−3 and [MA] = 108 molecules cm−3; Table S1: Cluster formation rates (J, cm−3 s−1) of the NA-SA-MA system and the SA-MA system, and the enhancement factor (r) at different temperatures (K) and precursor concentrations (molecules cm−3); Table S2: Cluster formation rates (J, cm−3 s−1) of the NA-SA-DMA system and the SA-DMA system, and the enhancement factor (r) at different temperatures (K) and precursor concentrations (molecules cm−3); Table S3: Cluster formation rates (J, cm−3 s−1) of the NA-SA-A system and the SA-A system, and the enhancement factor (r) at different temperatures (K) and precursor concentrations (molecule cm−3); Table S4: Coordinates of all optimized (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (NA)x(SA)y(DMA)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) and (NA)x(SA)y(A)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) clusters; Table S5: Single-point energies (kcal mol−1) at the DLPNO-CCSD(T)/aug-cc-pVTZ level and the corresponding Gibbs free energy correction Gcorr (kcal mol−1) and Gibbs free energy G (kcal mol−1) at 298.15 K for all the most stable configurations of the NA-SA-MA, NA-SA-DMA and NA-SA-A systems.

Author Contributions

Conceptualization, F.Q. and H.-B.X.; methodology, F.Q. and Q.Z.; formal analysis, F.Q. and R.Z.; investigation, F.Q.; writing—original draft preparation, F.Q.; writing—review and editing, F.Q., Q.Z., R.Z., H.-B.X., F.M. and J.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China (2022YFC3701000, Task1) and the National Natural Science Foundation of China (22236004 and 22176022).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in Supplementary Materials of this article.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Appendix A.1. Specific Details of Multi-Step Sampling Approach and Employed Calculation Methods

The multi-step sampling approach was employed to search for the most stable configurations of the clusters in the ternary NA-SA-MA system, including (NA)1-3(MA)1-3 and (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) clusters. First, the ABCluster program was employed to generate 6000 initial guess structures for each cluster type. The CHARMM36 force field was applied for the simulation of all molecules in the ABCluster program. Based on the initial guess structure, four sequential calculation steps were performed, including preliminary geometry optimization at the PM6 level of theory, followed by a single-point energy calculation at the ωB97X-D/6-31+G(d,p) level. Subsequently, a more precise geometry optimization and vibrational frequency analysis were conducted at the ωB97X-D/6-31++G(d,p) level of theory. The final step involved a single-point energy calculation at the DLPNO-CCSD(T)/aug-cc-pVTZ level of theory using the keywords “tightscf”, “tightpno”, “GRID4” and “nofinalgrid”. The Gibbs free energy (G) for each cluster was calculated by combining the single-point energy at the DLPNO-CCSD(T)/aug-cc-pVTZ theoretical level with a correction term for the Gibbs free energy derived from the ωB97X-D/6-31++G(d,p) level of theory. The configuration exhibiting the lowest G value was identified as the most stable configuration for a given cluster type. The binding free energy (ΔG) was derived from the subtraction of the individual G of the constituent monomers from the overall G of the studied cluster at a temperature of 298.15 K. ΔG values at different temperatures were obtained on the premise that both the enthalpy (ΔH) and entropy (ΔS) changes were held constant across the range of temperatures considered, which spanned from 238.15 K to 298.15 K. The coordinates of all the optimized (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (NA)x(SA)y(DMA)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) and (NA)x(SA)y(A)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) clusters can be seen in Table S4. Additionally, the single-point energies at the DLPNO-CCSD(T)/aug-cc-pVTZ level and the corresponding Gibbs free energy correction (Gcorr) and Gibbs free energy (G) values at 298.15K for all the most stable configurations of the NA-SA-MA, NA-SA-DMA and NA-SA-A systems can be seen in Table S5.

Appendix A.2. Physical Principles of ACDC

In short, the core of ACDC is to use the birth–death equation (Equation (A1)) to describe the time-dependent cluster distributions:
d c i dt = 1 2 ∑ j < i β j , ( i − j ) c j c ( i − j ) + ∑ j γ ( i + j ) → i c i + j − ∑ j β i , j c i c j − 1 2 ∑ j < i γ i → j c i   + Q i − S i
where subscripts (i, j, i − j, and i + j) represent different clusters or monomers in the system. ci represents the number concentration of i. βi,j denotes the collision rate coefficient between i and j, and γ(i+j)→i denotes the evaporation rate of a cluster i + j into smaller clusters, (or monomers) i and j. Qi represents an additional outside source term of i, and Si represents other sink terms for i. The collision rate coefficient (βi,j) between clusters i and j is calculated using the hard-sphere kinetic gas theory as follows:
β i , j = 3 4 π 1 6   6 k B T m i + 6 k B T m j 1 2 V i   1   3 + V j   1   3 2
where kB is the Boltzmann constant, T is the temperature, and mi and Vi are the mass and volume of i, respectively. The evaporation rate (γ(i+j)→i) is obtained from the corresponding collision rate coefficient and the binding free energy.
γ ( i + j ) → i = β i , j c ref exp ⁡ Δ G i + j −   Δ G i −   Δ G j k B T
where ΔG is the binding free energy of the cluster and cref is the reference monomer concentration at 1 atm, which is the pressure at which ΔG was calculated.

Appendix A.3. Selection of Boundary Clusters

The boundary clusters fluxing out of the simulation box are required to be sufficiently stable (low evaporation rates). As shown in Figure 2, for the studied “3 × 3 box” NA-SA-MA system, binary (SA)3(MA)2-3 clusters and mixed ternary (NA)1(SA)1(MA)2 and (NA)1(SA)2(MA)2-3 and (NA)2(SA)1(MA)3 clusters have relatively low evaporation rates on the order of 10−4 s−1~10−2 s−1. Therefore, (SA)4(MA)3, (SA)4(MA)4, (NA)1(SA)3(MA)3, (NA)1(SA)3(MA)4, (NA)2(SA)2(MA)4 and (NA)3(SA)1(MA)4 clusters were defined as boundary clusters in the ACDC simulation. For the NA-SA-DMA system, binary (SA)1(DMA)1, (SA)2(DMA)1-2 and (SA)3(DMA)2-3 clusters and mixed ternary (NA)1(SA)1(DMA)2, (NA)1(SA)2(DMA)3 and (NA)2(SA)1(DMA)3 clusters have relatively low evaporation rates on the order of 10−5 s−1~10−1 s−1. Therefore, we selected (SA)4(DMA)3, (SA)4(DMA)4, (NA)1(SA)3(DMA)4, (NA)2(SA)2(DMA)4 and (NA)3(SA)1(DMA)4 clusters as the boundary clusters in the ACDC simulation. For the NA-SA-A system, binary (SA)3(A)2-3 clusters and mixed ternary (NA)1(SA)2(A)3 and (NA)2(SA)1(A)3 clusters have relatively low evaporation rates on the order of 10−1 s−1~101 s−1. This allowed us to select (SA)4(A)3, (SA)4(A)4, (NA)1(SA)3(A)4, (NA)2(SA)2(A)4 and (NA)3(SA)1(A)4 as the boundary clusters for the NA-SA-A system in the ACDC simulation.

References

  1. Wang, M.; Kong, W.; Marten, R.; He, X.-C.; Chen, D.; Pfeifer, J.; Heitto, A.; Kontkanen, J.; Dada, L.; Kürten, A.; et al. Rapid Growth of New Atmospheric Particles by Nitric Acid and Ammonia Condensation. Nature 2020, 581, 184–189. [Google Scholar] [CrossRef] [PubMed]
  2. Riccobono, F.; Schobesberger, S.; Scott, C.E.; Dommen, J.; Ortega, I.K.; Rondo, L.; Almeida, J.; Amorim, A.; Bianchi, F.; Breitenlechner, M.; et al. Oxidation Products of Biogenic Emissions Contribute to Nucleation of Atmospheric Particles. Science 2014, 344, 717–721. [Google Scholar] [CrossRef] [PubMed]
  3. Yao, L.; Garmash, O.; Bianchi, F.; Zheng, J.; Yan, C.; Kontkanen, J.; Junninen, H.; Mazon, S.B.; Ehn, M.; Paasonen, P.; et al. Atmospheric New Particle Formation from Sulfuric Acid and Amines in A Chinese Megacity. Science 2018, 361, 278–281. [Google Scholar] [CrossRef] [PubMed]
  4. Zhang, R.; Khalizov, A.; Wang, L.; Hu, M.; Xu, W. Nucleation and Growth of Nanoparticles in the Atmosphere. Chem. Rev. 2012, 112, 1957–2011. [Google Scholar] [CrossRef] [PubMed]
  5. Zu, H.; Zhang, S.; Liu, L.; Zhang, X. The vital role of sulfuric acid in iodine oxoacids nucleation: Impacts of urban pollutants on marine atmosphere. Environ. Res. Lett. 2024, 19, 014076. [Google Scholar] [CrossRef]
  6. Kirkby, J.; Curtius, J.; Almeida, J.; Dunne, E.; Duplissy, J.; Ehrhart, S.; Franchin, A.; Gagné, S.; Ickes, L.; Kürten, A.; et al. Role of Sulphuric Acid, Ammonia and Galactic Cosmic Rays in Atmospheric Aerosol Nucleation. Nature 2011, 476, 429–433. [Google Scholar] [CrossRef] [PubMed]
  7. Feketeová, L.; Bertier, P.; Salbaing, T.; Azuma, T.; Calvo, F.; Farizon, B.; Farizon, M.; Märk, T.D. Impact of A Hydrophobic Ion on the Early Stage of Atmospheric Aerosol Formation. Proc. Natl. Acad. Sci. USA 2019, 116, 22540–22544. [Google Scholar] [CrossRef] [PubMed]
  8. Chen, H.; Finlayson-Pitts, B.J. New Particle Formation from Methanesulfonic Acid and Amines/Ammonia as a Function of Temperature. Environ. Sci. Technol. 2017, 51, 243–252. [Google Scholar] [CrossRef] [PubMed]
  9. Rose, C.; Zha, Q.; Dada, L.; Yan, C.; Lehtipalo, K.; Junninen, H.; Mazon, S.B.; Jokinen, T.; Sarnela, N.; Sipilä, M.; et al. Observations of Biogenic Ion-induced Cluster Formation in the Atmosphere. Sci. Adv. 2018, 4, eaar5218. [Google Scholar] [CrossRef]
  10. Liu, L.; Zhong, J.; Vehkamäki, H.; Kurtén, T.; Du, L.; Zhang, X.; Francisco, J.S.; Zeng, X.C. Unexpected Quenching Effect on New Particle Formation from the Atmospheric Reaction of Methanol with SO3. Proc. Natl. Acad. Sci. USA 2019, 116, 24966–24971. [Google Scholar] [CrossRef]
  11. Kirkby, J.; Duplissy, J.; Sengupta, K.; Frege, C.; Gordon, H.; Williamson, C.; Heinritzi, M.; Simon, M.; Yan, C.; Almeida, J.; et al. Ion-induced Nucleation of Pure Biogenic Particles. Nature 2016, 533, 521–526. [Google Scholar] [CrossRef] [PubMed]
  12. Schobesberger, S.; Junninen, H.; Bianchi, F.; Lonn, G.; Ehn, M.; Lehtipalo, K.; Dommen, J.; Ehrhart, S.; Ortega, I.K.; Franchin, A.; et al. Molecular Understanding of Atmospheric Particle Formation from Sulfuric Acid and Large Oxidized Organic Molecules. Proc. Natl. Acad. Sci. USA 2013, 110, 17223–17228. [Google Scholar] [CrossRef] [PubMed]
  13. Almeida, J.; Schobesberger, S.; Kurtén, A.; Ortega, I.K.; Kupiainen-Maatta, O.; Praplan, A.P.; Adamov, A.; Amorim, A.; Bianchi, F.; Breitenlechner, M.; et al. Molecular Understanding of Sulphuric Acid-amine Particle Nucleation in the Atmosphere. Nature 2013, 502, 359–363. [Google Scholar] [CrossRef] [PubMed]
  14. Kurtén, T.; Loukonen, V.; Vehkamäki, H.; Kulmala, M. Amines Are Likely to Enhance Neutral and Ion-induced Sulfuric Acid-water Nucleation in the Atmosphere More Effectively than Ammonia. Atmos. Chem. Phys. 2008, 8, 4095–4103. [Google Scholar] [CrossRef]
  15. Murphy, S.M.; Sorooshian, A.; Kroll, J.H.; Ng, N.L.; Chhabra, P.; Tong, C.; Surratt, J.D.; Knipping, E.; Flagan, R.C.; Seinfeld, J.H. Secondary Aerosol Formation from Atmospheric Reactions of Aliphatic Amines. Atmos. Chem. Phys. 2007, 7, 2313–2337. [Google Scholar] [CrossRef]
  16. Smith, J.N.; Barsanti, K.C.; Friedli, H.R.; Ehn, M.; Kulmala, M.; Collins, D.R.; Scheckman, J.H.; Williams, B.J.; McMurry, P.H. Observations of Aminium Salts in Atmospheric Nanoparticles and Possible Climatic Implications. Proc. Natl. Acad. Sci. USA 2010, 107, 6634–6639. [Google Scholar] [CrossRef] [PubMed]
  17. Loukonen, V.; Kurtén, T.; Ortega, I.K.; Vehkamäki, H.; Pádua, A.A.H.; Sellegri, K.; Kulmala, M. Enhancing Effect of Dimethylamine in Sulfuric Acid Nucleation in the Presence of Water-A Computational Study. Atmos. Chem. Phys. 2010, 10, 4961–4974. [Google Scholar] [CrossRef]
  18. Zhao, J.; Smith, J.N.; Eisele, F.L.; Chen, M.; Kuang, C.; McMurry, P.H. Observation of Neutral Sulfuric Acid-amine Containing Clusters in Laboratory and Ambient Measurements. Atmos. Chem. Phys. 2011, 11, 10823–10836. [Google Scholar] [CrossRef]
  19. Lehtipalo, K.; Rondo, L.; Kontkanen, J.; Schobesberger, S.; Jokinen, T.; Sarnela, N.; Kuerten, A.; Ehrhart, S.; Franchin, A.; Nieminen, T.; et al. The Effect of Acid-base Clustering and Ions on the Growth of Atmospheric Nano-particles. Nat. Commun. 2016, 7, 11594. [Google Scholar] [CrossRef]
  20. Chen, M.; Titcombe, M.; Jiang, J.; Jen, C.; Kuang, C.; Fischer, M.L.; Eisele, F.L.; Siepmann, J.I.; Hanson, D.R.; Zhao, J.; et al. Acid-base Chemical Reaction Model for Nucleation Rates in the Polluted Atmospheric Boundary Layer. Proc. Natl. Acad. Sci. USA 2012, 109, 18713–18718. [Google Scholar] [CrossRef]
  21. Erupe, M.E.; Viggiano, A.A.; Lee, S.H. The Effect of Trimethylamine on Atmospheric Nucleation Involving H2SO4. Atmos. Chem. Phys. 2011, 11, 4767–4775. [Google Scholar] [CrossRef]
  22. Lv, S.-S.; Miao, S.-K.; Ma, Y.; Zhang, M.-M.; Wen, Y.; Wang, C.-Y.; Zhu, Y.-P.; Huang, W. Properties and Atmospheric Implication of Methylamine-Sulfuric Acid-Water Clusters. J. Phys. Chem. A 2015, 119, 8657–8666. [Google Scholar] [CrossRef] [PubMed]
  23. Sipila, M.; Berndt, T.; Petaja, T.; Brus, D.; Vanhanen, J.; Stratmann, F.; Patokoski, J.; Mauldin, R.L.; Hyvarinen, A.P.; Lihavainen, H.; et al. The Role of Sulfuric Acid in Atmospheric Nucleation. Science 2010, 327, 1243–1246. [Google Scholar] [CrossRef] [PubMed]
  24. Olenius, T.; Halonen, R.; Kurtén, T.; Henschel, H.; Kupiainen-Määttä, O.; Ortega, I.K.; Jen, C.N.; Vehkamäki, H.; Riipinen, I. New Particle Formation from Sulfuric Acid and Amines: Comparison of Monomethylamine, Dimethylamine, and Trimethylamine. J. Geophys. Res. Atmos. 2017, 122, 7103–7118. [Google Scholar] [CrossRef]
  25. Nadykto, A.B.; Yu, F.; Jakovleva, M.V.; Herb, J.; Xu, Y. Amines in the Earth’s Atmosphere: A Density Functional Theory Study of the Thermochemistry of Pre-Nucleation Clusters. Entropy 2011, 13, 554–569. [Google Scholar] [CrossRef]
  26. Nadykto, A.; Herb, J.; Yu, F.; Xu, Y.; Nazarenko, E. Estimating the Lower Limit of the Impact of Amines on Nucleation in the Earth’s Atmosphere. Entropy 2015, 17, 2764–2780. [Google Scholar] [CrossRef]
  27. Nadykto, A.B.; Herb, J.; Yu, F.; Xu, Y. Enhancement in the Production of Nucleating Clusters due to Dimethylamine and Large Uncertainties in the Thermochemistry of Amine-enhanced Nucleation. Chem. Phys. Lett. 2014, 609, 42–49. [Google Scholar] [CrossRef]
  28. Jen, C.N.; McMurry, P.H.; Hanson, D.R. Stabilization of Sulfuric Acid Dimers by Ammonia, Methylamine, Dimethylamine, and Trimethylamine. J. Geophys. Res. Atmos. 2014, 119, 7502–7514. [Google Scholar] [CrossRef]
  29. Qiu, C.; Zhang, R.Y. Multiphase Chemistry of Atmospheric Amines. Phys. Chem. Chem. Phys. 2013, 15, 5738–5752. [Google Scholar] [CrossRef]
  30. Zhang, R.; Wang, L.; Khalizov, A.F.; Zhao, J.; Zheng, J.; McGraw, R.L.; Molina, L.T. Formation of Nanoparticles of Blue Haze Enhanced by Anthropogenic Pollution. Proc. Natl. Acad. Sci. USA 2009, 106, 17650–17654. [Google Scholar] [CrossRef]
  31. Xu, W.; Zhang, R.Y. A Theoretical Study of Hydrated Molecular Clusters of Amines and Dicarboxylic Acids. J. Chem. Phys. 2013, 139, 064312. [Google Scholar] [CrossRef] [PubMed]
  32. Myllys, N.; Elm, J.; Halonen, R.; Kurtén, T.; Vehkamäki, H. Coupled Cluster Evaluation of the Stability of Atmospheric Acid-Base Clusters with up to 10 Molecules. J. Phys. Chem. A 2016, 120, 621–630. [Google Scholar] [CrossRef] [PubMed]
  33. Yu, H.; Ren, L.; Kanawade, V.P. New Particle Formation and Growth Mechanisms in Highly Polluted Environments. Curr. Pollut. Rep. 2017, 3, 245–253. [Google Scholar] [CrossRef]
  34. Lee, S.H.; Gordon, H.; Yu, H.; Lehtipalo, K.; Haley, R.; Li, Y.; Zhang, R. New Particle Formation in the Atmosphere: From Molecular Clusters to Global Climate. J. Geophys. Res. Atmos. 2019, 124, 7098–7146. [Google Scholar] [CrossRef]
  35. Cai, R.; Yan, C.; Yang, D.; Yin, R.; Lu, Y.; Deng, C.; Fu, Y.; Ruan, J.; Li, X.; Kontkanen, J.; et al. Sulfuric acid-Amine Nucleation in Urban Beijing. Atmos. Chem. Phys. 2021, 21, 2457–2468. [Google Scholar] [CrossRef]
  36. Brown, S.S.; Ryerson, T.B.; Wollny, A.G.; Brock, C.A.; Peltier, R.; Sullivan, A.P.; Weber, R.J.; Dubé, W.P.; Trainer, M.; Meagher, J.F.; et al. Variability in Nocturnal Nitrogen Oxide Processing and Its Role in Regional Air Quality. Science 2006, 311, 67–70. [Google Scholar] [CrossRef] [PubMed]
  37. Vayenas, D.V.; Takahama, S.; Davidson, C.I.; Pandis, S.N. Simulation of the Thermodynamics and Removal Processes in the Sulfate-Ammonia-Nitric acid system during Winter: Implications for PM2.5 Control Strategies. J. Geophys. Res. Atmos. 2005, 110, D07S14. [Google Scholar] [CrossRef]
  38. Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics from Air Pollution to Climate Change, 3rd ed.; Wiley: New York, NY, USA, 2016. [Google Scholar]
  39. Kumar, M.; Zhong, J.; Zeng, X.C.; Francisco, J.S. Reaction of Criegee Intermediate with Nitric Acid at the Air-Water Interface. J. Am. Chem. Soc. 2018, 140, 4913–4921. [Google Scholar] [CrossRef]
  40. Acker, K.; Möller, D.; Auel, R.; Wieprecht, W.; Kalaß, D. Concentrations of Nitrous acid, Nitric acid, Nitrite and Nitrate in the Gas and Aerosol Phase at a Site in the Emission Zone During ESCOMPTE 2001 Experiment. Atmos. Res. 2005, 74, 507–524. [Google Scholar] [CrossRef]
  41. Mezuman, K.; Bauer, S.E.; Tsigaridis, K. Evaluating Secondary Inorganic Aerosols in Three Dimensions. Atmos. Chem. Phys. 2016, 16, 10651–10669. [Google Scholar] [CrossRef]
  42. Song, C.H.; Carmichael, G.R. A Three-Dimensional Modeling Investigation of the Evolution Processes of Dust and Sea-Salt Particles in East Asia. J. Geophys. Res. Atmos. 2001, 106, 18131–18154. [Google Scholar] [CrossRef]
  43. Zhang, R.; Sun, X.; Shi, A.; Huang, Y.; Yan, J.; Nie, T.; Yan, X.; Li, X. Secondary Inorganic Aerosols Formation During Haze Episodes at an Urban Site in Beijing, China. Atmos. Environ. 2018, 177, 275–282. [Google Scholar] [CrossRef]
  44. Ding, J.; Zhao, P.; Su, J.; Dong, Q.; Du, X.; Zhang, Y. Aerosol pH and Its Driving Factors in Beijing. Atmos. Chem. Phys. 2019, 19, 7939–7954. [Google Scholar] [CrossRef]
  45. Fairlie, T.D.; Jacob, D.J.; Dibb, J.E.; Alexander, B.; Avery, M.A.; van Donkelaar, A.; Zhang, L. Impact of Mineral Dust on Nitrate, Sulfate, and Ozone in Transpacific Asian Pollution Plumes. Atmos. Chem. Phys. 2010, 10, 3999–4012. [Google Scholar] [CrossRef]
  46. Wang, M.; Xiao, M.; Bertozzi, B.; Marie, G.; Rörup, B.; Schulze, B.; Bardakov, R.; He, X.-C.; Shen, J.; Scholz, W. Synergistic HNO3-H2SO4-NH3 Upper Tropospheric Particle Formation. Nature 2022, 605, 483–489. [Google Scholar] [CrossRef]
  47. Liu, L.; Li, H.; Zhang, H.; Zhong, J.; Bai, Y.; Ge, M.; Li, Z.; Chen, Y.; Zhang, X. The Role of Nitric Acid in Atmospheric New Particle Formation. Phys. Chem. Chem. Phys. 2018, 20, 17406–17414. [Google Scholar] [CrossRef]
  48. Liu, L.; Yu, F.; Du, L.; Yang, Z.; Francisco, J.S.; Zhang, X. Rapid Sulfuric Acid-Dimethylamine Nucleation Enhanced by Nitric Acid in Polluted Regions. Proc. Natl. Acad. Sci. USA 2021, 118, e2108384118. [Google Scholar] [CrossRef]
  49. Knattrup, Y.; Elm, J. Clusteromics IV: The Role of Nitric Acid in Atmospheric Cluster Formation. ACS Omega 2022, 7, 31551–31560. [Google Scholar] [CrossRef] [PubMed]
  50. Knattrup, Y.; Kubečka, J.; Elm, J. Nitric Acid and Organic Acids Suppress the Role of Methanesulfonic Acid in Atmospheric New Particle Formation. J. Phys. Chem. A 2023, 127, 7568–7578. [Google Scholar] [CrossRef]
  51. Wang, S.; Peng, Y.; Zhang, Q.; Wang, W.; Wang, Q. Mechanistic Understanding of Rapid H2SO4-HNO3-NH3 Nucleation in the Upper Troposphere. Sci. Total. Environ. 2023, 883, 163477. [Google Scholar] [CrossRef]
  52. Schade, G.W.; Crutzen, P.J. Emission of Aliphatic Amines from Animal Husbandry and Their Reactions: Potential Source of N2O and HCN. J. Atmos. Chem. 1995, 22, 319–346. [Google Scholar] [CrossRef]
  53. Xie, H.B.; Elm, J.; Halonen, R.; Myllys, N.; Kurten, T.; Kulmala, M.; Vehkamaki, H. Atmospheric Fate of Monoethanolamine: Enhancing New Particle Formation of Sulfuric Acid as an Important Removal Process. Environ. Sci. Technol. 2017, 51, 8422–8431. [Google Scholar] [CrossRef] [PubMed]
  54. Chen, H.; Varner, M.E.; Gerber, R.B.; Finlayson-Pitts, B.J. Reactions of Methanesulfonic Acid with Amines and Ammonia as a Source of New Particles in Air. J. Phys. Chem. B 2016, 120, 1526–1536. [Google Scholar] [CrossRef] [PubMed]
  55. Waller, S.E.; Yang, Y.; Castracane, E.; Racow, E.E.; Kreinbihl, J.J.; Nickson, K.A.; Johnson, C.J. The Interplay between Hydrogen Bonding and Coulombic Forces in Determining the Structure of Sulfuric Acid-Amine Clusters. J. Phys. Chem. Lett. 2018, 9, 1216–1222. [Google Scholar] [CrossRef] [PubMed]
  56. Yang, Y.; Waller, S.E.; Kreinbihl, J.J.; Johnson, C.J. Direct Link between Structure and Hydration in Ammonium and Aminium Bisulfate Clusters Implicated in Atmospheric New Particle Formation. J. Phys. Chem. Lett. 2018, 9, 5647–5652. [Google Scholar] [CrossRef]
  57. McGrath, M.J.; Olenius, T.; Ortega, I.K.; Loukonen, V.; Paasonen, P.; Kurtén, T.; Kulmala, M.; Vehkamäki, H. Atmospheric Cluster Dynamics Code: A Flexible Method for Solution of the Birth-death Equations. Atmos. Chem. Phys. 2012, 12, 2345–2355. [Google Scholar] [CrossRef]
  58. Zhang, R.; Xie, H.B.; Ma, F.; Chen, J.; Iyer, S.; Simon, M.; Heinritzi, M.; Shen, J.; Tham, Y.J.; Kurten, T.; et al. Critical Role of Iodous Acid in Neutral Iodine Oxoacid Nucleation. Environ. Sci. Technol. 2022, 56, 14166–14177. [Google Scholar] [CrossRef]
  59. Cai, R.; Yin, R.; Li, X.; Xie, H.-B.; Yang, D.; Kerminen, V.-M.; Smith, J.N.; Ma, Y.; Hao, J.; Chen, J.; et al. Significant Contributions of Trimethylamine to Sulfuric Acid Nucleation in Polluted Environments. Npj Clim. Atmos. Sci. 2023, 6, 75. [Google Scholar] [CrossRef]
  60. Ma, F.; Xie, H.-B.; Zhang, R.; Su, L.; Jiang, Q.; Tang, W.; Chen, J.; Engsvang, M.; Elm, J.; He, X.-C. Enhancement of Atmospheric Nucleation Precursors on Iodic Acid-Induced Nucleation: Predictive Model and Mechanism. Environ. Sci. Technol. 2023, 57, 6944–6954. [Google Scholar] [CrossRef]
  61. Elm, J. Elucidating the Limiting Steps in Sulfuric Acid-Base New Particle Formation. J. Phys. Chem. A 2017, 121, 8288–8295. [Google Scholar] [CrossRef]
  62. Zhang, J.; Dolg, M. ABCluster: The Artificial Bee Colony Algorithm for Cluster Global Optimization. Phys. Chem. Chem. Phys. 2015, 17, 24173–24181. [Google Scholar] [CrossRef] [PubMed]
  63. Zhang, J.; Dolg, M. Global Optimization of Clusters of Rigid Molecules using the Artificial Bee Colony Algorithm. Phys. Chem. Chem. Phys. 2016, 18, 3003–3010. [Google Scholar] [CrossRef] [PubMed]
  64. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  65. Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  66. Olenius, T.; Kupiainen-Määttä, O.; Ortega, I.K.; Kurtén, T.; Vehkamäki, H. Free Energy Barrier in the Growth of Sulfuric Acid-Ammonia and Sulfuric Acid-Dimethylamine clusters. J. Chem. Phys. 2013, 139, 084312. [Google Scholar] [CrossRef] [PubMed]
  67. Kupiainen-Määttä, O.; Olenius, T.; Kurtén, T.; Vehkamäki, H. CIMS Sulfuric Acid Detection Efficiency Enhanced by Amines Due to Higher Dipole Moments: A Computational Study. J. Phys. Chem. A 2013, 117, 14109–14119. [Google Scholar] [CrossRef] [PubMed]
  68. Temelso, B.; Morrison, E.F.; Speer, D.L.; Cao, B.C.; Appiah-Padi, N.; Kim, G.; Shields, G.C. Effect of Mixing Ammonia and Alkylamines on Sulfate Aerosol Formation. J. Phys. Chem. A 2018, 122, 1612–1622. [Google Scholar] [CrossRef] [PubMed]
  69. Elm, J. Clusteromics I: Principles, Protocols, and Applications to Sulfuric Acid-Base Cluster Formation. ACS Omega 2021, 6, 7804–7814. [Google Scholar] [CrossRef]
  70. Kubečka, J.; Neefjes, I.; Besel, V.; Qiao, F.; Xie, H.-B.; Elm, J. Atmospheric Sulfuric Acid-Multi-Base New Particle Formation Revealed through Quantum Chemistry Enhanced by Machine Learning. J. Phys. Chem. A 2023, 127, 2091–2103. [Google Scholar] [CrossRef]
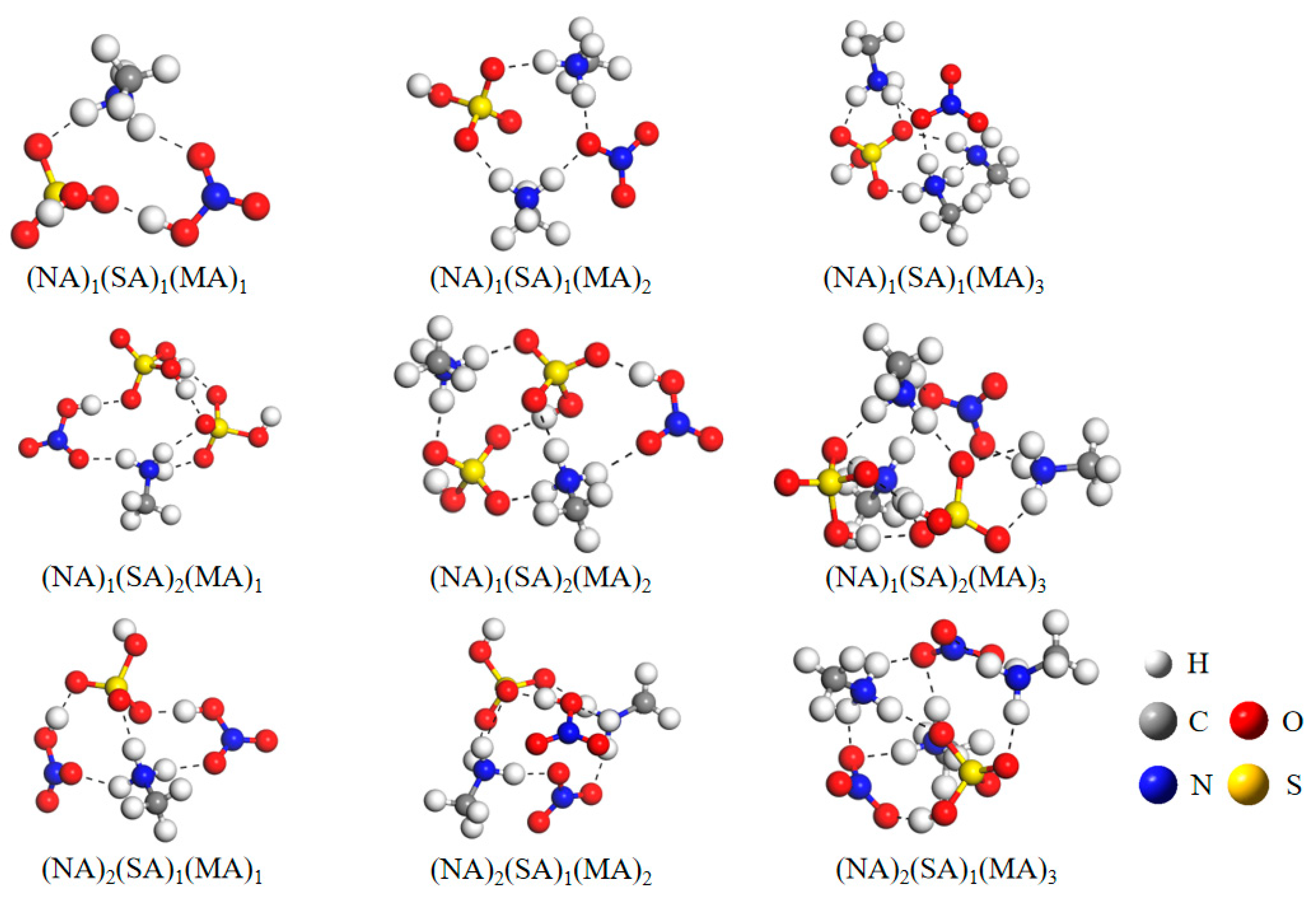
Atmosphere 15 00467 g001
Figure 1. The most stable configurations of the (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) clusters calculated at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory at 298.15 K. The dashed black lines represent hydrogen bonds.
Figure 1. The most stable configurations of the (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3) clusters calculated at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory at 298.15 K. The dashed black lines represent hydrogen bonds.
Atmosphere 15 00467 g001
Atmosphere 15 00467 g002
Figure 2. Evaporation rates of the (A) (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (B) (SA)1-3(MA)1-3, (C) (NA)x(SA)y(DMA)z (x ≥ 1, y ≥ 1, 1 ≤ z ≤ x + y ≤ 3) and (D) (NA)x(SA)y(A)z (x ≥ 1, y ≥ 1, 1 ≤ z ≤ x + y ≤ 3) clusters at 278.15 K.
Figure 2. Evaporation rates of the (A) (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (B) (SA)1-3(MA)1-3, (C) (NA)x(SA)y(DMA)z (x ≥ 1, y ≥ 1, 1 ≤ z ≤ x + y ≤ 3) and (D) (NA)x(SA)y(A)z (x ≥ 1, y ≥ 1, 1 ≤ z ≤ x + y ≤ 3) clusters at 278.15 K.
Atmosphere 15 00467 g002
Atmosphere 15 00467 g003
Figure 3. Addition free energy of NA (ΔGadd) for the (A) (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (B) (NA)x(SA)y(DMA)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) and (C) (NA)x(SA)y(A)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) clusters calculated at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory at 298.15 K and 1 atm.
Figure 3. Addition free energy of NA (ΔGadd) for the (A) (NA)x(SA)y(MA)z (1 ≤ x, 1 ≤ y, x + y ≤ 3, 1 ≤ z ≤ 3), (B) (NA)x(SA)y(DMA)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) and (C) (NA)x(SA)y(A)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) clusters calculated at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory at 298.15 K and 1 atm.
Atmosphere 15 00467 g003
Atmosphere 15 00467 g004
Figure 4. Enhancement factor (r) of NA in SA-MA, SA-DMA and SA-A nucleation at varying temperatures and precursor concentrations. The concentration of NA is fixed at 1010 cm−3. The solid black, red, blue and green lines represent the NA-SA-MA system; the dashed–dotted black, red, blue and green lines represent the NA-SA-DMA system; and the dotted orange and purple lines represent the NA-SA-A system.
Figure 4. Enhancement factor (r) of NA in SA-MA, SA-DMA and SA-A nucleation at varying temperatures and precursor concentrations. The concentration of NA is fixed at 1010 cm−3. The solid black, red, blue and green lines represent the NA-SA-MA system; the dashed–dotted black, red, blue and green lines represent the NA-SA-DMA system; and the dotted orange and purple lines represent the NA-SA-A system.
Atmosphere 15 00467 g004
Atmosphere 15 00467 g005
Figure 5. Enhancement factor (r) of NA in SA-MA, SA-DMA and SA-A nucleation at 278.15 K and with varying concentrations of NA (from 108 to 1012 cm−3). The solid black, red, blue and green lines represent the NA-SA-MA system; the dashed–dotted black, red, blue and green lines represent the NA-SA-DMA system; and the dotted orange and purple lines represent the NA-SA-A system.
Figure 5. Enhancement factor (r) of NA in SA-MA, SA-DMA and SA-A nucleation at 278.15 K and with varying concentrations of NA (from 108 to 1012 cm−3). The solid black, red, blue and green lines represent the NA-SA-MA system; the dashed–dotted black, red, blue and green lines represent the NA-SA-DMA system; and the dotted orange and purple lines represent the NA-SA-A system.
Atmosphere 15 00467 g005
Atmosphere 15 00467 g006
Figure 6. Cluster growth pathways for the NA-SA-MA system at 278.15 K, [NA] = 1010 cm−3, [SA] = 106 cm−3 and [MA] = 108 cm−3.
Figure 6. Cluster growth pathways for the NA-SA-MA system at 278.15 K, [NA] = 1010 cm−3, [SA] = 106 cm−3 and [MA] = 108 cm−3.
Atmosphere 15 00467 g006
Table 1. The numbers of hydrogen bonds (n) in (NA)x(SA)y(MA)z, (NA)x(SA)y(DMA)z and (NA)x(SA)y(A)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) clusters.
Table 1. The numbers of hydrogen bonds (n) in (NA)x(SA)y(MA)z, (NA)x(SA)y(DMA)z and (NA)x(SA)y(A)z (1 ≤ x, 1 ≤ y, 1 ≤ z ≤ x + y ≤ 3) clusters.
ClustersnClustersnClustersn
(NA)1(SA)1(MA)13(NA)1(SA)1(DMA)14(NA)1(SA)1(A)13
(NA)1(SA)1(MA)24(NA)1(SA)1(DMA)25(NA)1(SA)1(A)25
(NA)2(SA)1(MA)15(NA)2(SA)1(DMA)15(NA)2(SA)1(A)15
(NA)2(SA)1(MA)27(NA)2(SA)1(DMA)26(NA)2(SA)1(A)28
(NA)2(SA)1(MA)310(NA)2(SA)1(DMA)37(NA)2(SA)1(A)39
(NA)1(SA)2(MA)16(NA)1(SA)2(DMA)15(NA)1(SA)2(A)16
(NA)1(SA)2(MA)27(NA)1(SA)2(DMA)27(NA)1(SA)2(A)28
(NA)1(SA)2(MA)311(NA)1(SA)2(DMA)38(NA)1(SA)2(A)310
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Qiao, F.; Zhang, R.; Zhao, Q.; Ma, F.; Chen, J.; Xie, H.-B. A Surprisingly High Enhancing Potential of Nitric Acid in Sulfuric Acid–Methylamine Nucleation. Atmosphere 2024, 15, 467. https://doi.org/10.3390/atmos15040467

AMA Style

Qiao F, Zhang R, Zhao Q, Ma F, Chen J, Xie H-B. A Surprisingly High Enhancing Potential of Nitric Acid in Sulfuric Acid–Methylamine Nucleation. Atmosphere. 2024; 15(4):467. https://doi.org/10.3390/atmos15040467

Chicago/Turabian Style

Qiao, Fukang, Rongjie Zhang, Qiaojing Zhao, Fangfang Ma, Jingwen Chen, and Hong-Bin Xie. 2024. "A Surprisingly High Enhancing Potential of Nitric Acid in Sulfuric Acid–Methylamine Nucleation" Atmosphere 15, no. 4: 467. https://doi.org/10.3390/atmos15040467

APA Style

Qiao, F., Zhang, R., Zhao, Q., Ma, F., Chen, J., & Xie, H. -B. (2024). A Surprisingly High Enhancing Potential of Nitric Acid in Sulfuric Acid–Methylamine Nucleation. Atmosphere, 15(4), 467. https://doi.org/10.3390/atmos15040467

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop