Evaluation of Two Momentum Control Variable Schemes in Radar Data Assimilation and Their Impact on the Analysis and Forecast of a Snowfall Case in Central and Eastern China
Abstract
1. Introduction
2. Data and Methods
2.1. Observations
2.2. Methodologies
2.2.1. 3DVAR DA Method
2.2.2. Radar Observation Operator
2.2.3. Verification Methods
3. Experimental Design and Case Overview
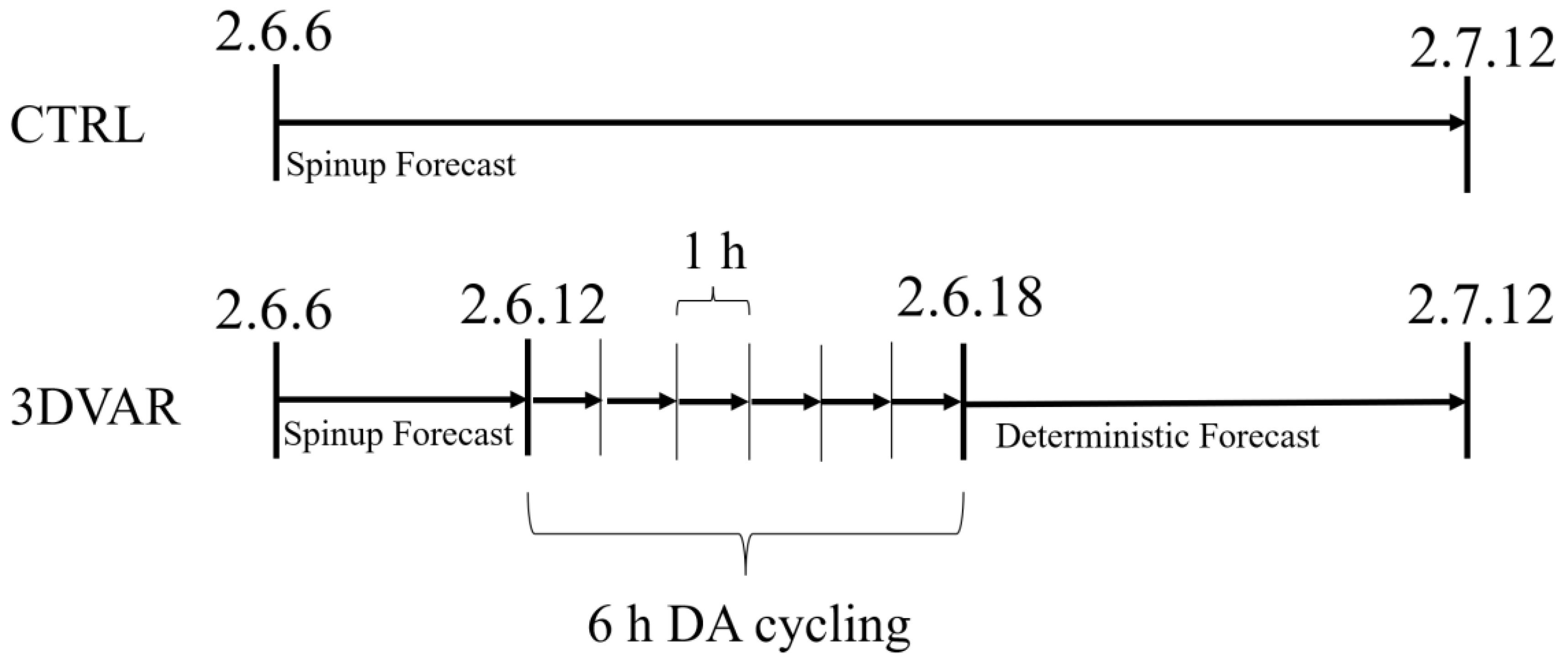
3.1. Model Configuration and Experiment Design
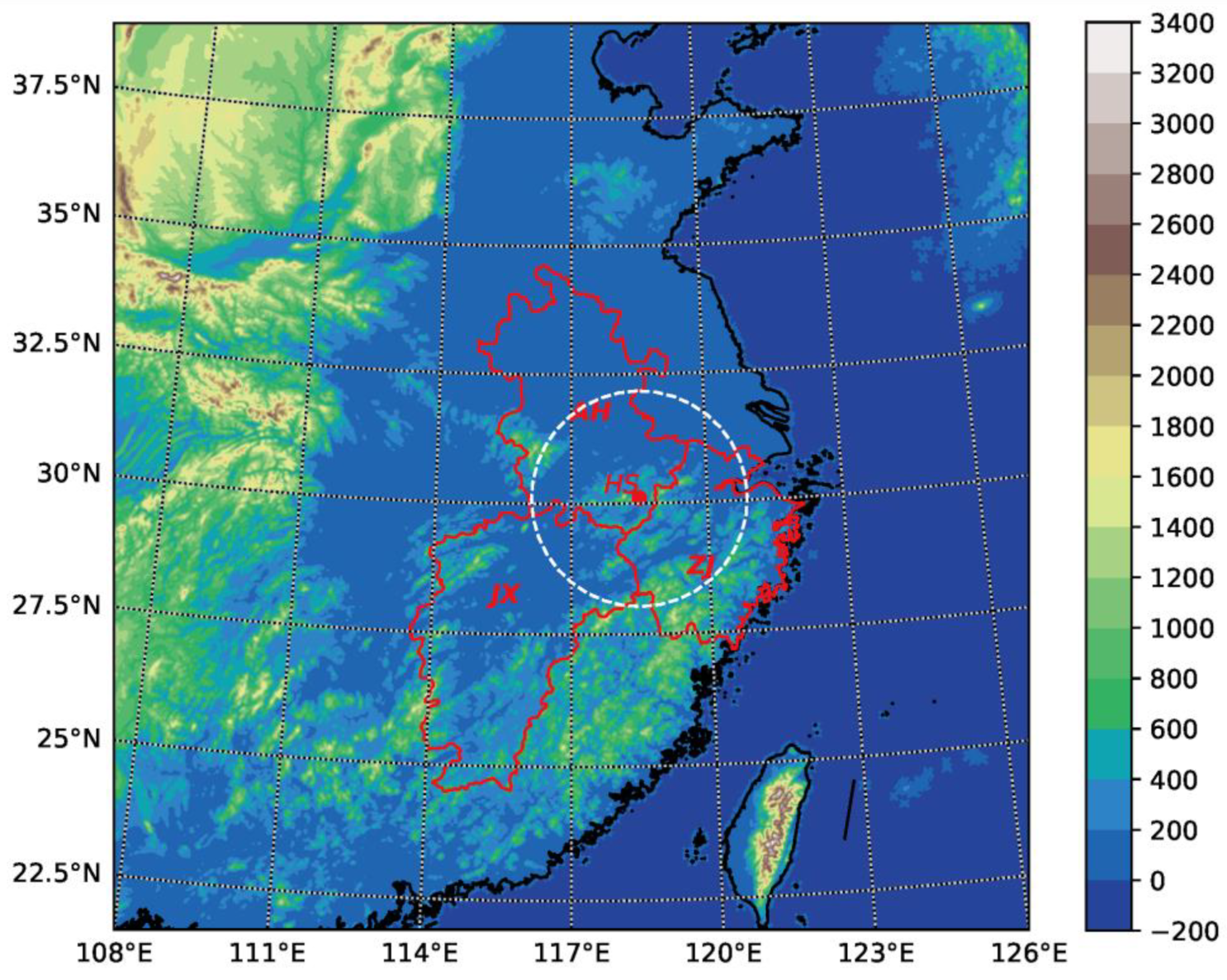
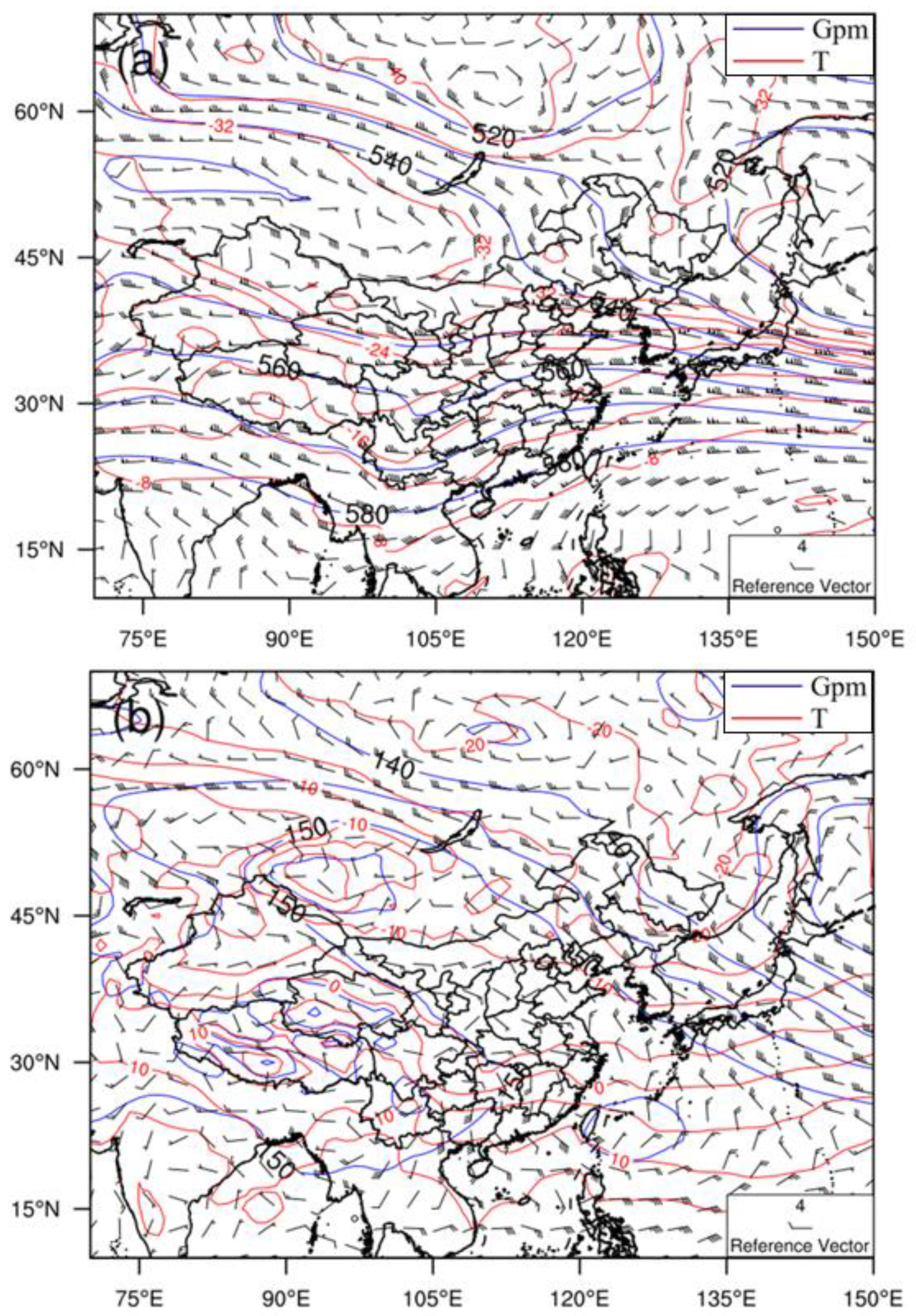
3.2. Synoptic Overview
4. Result
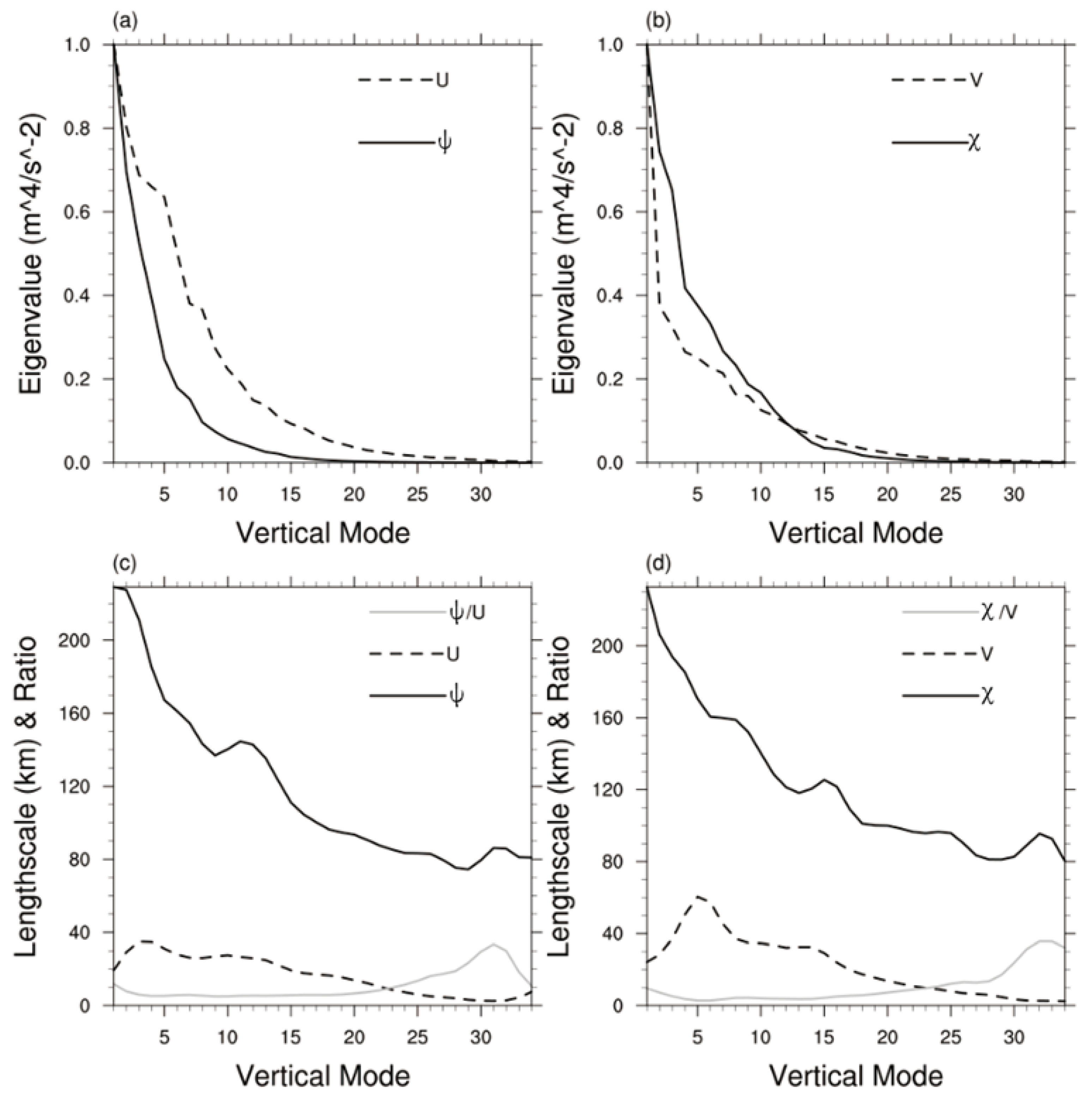
4.1. Comparison of the Background Error Statistics
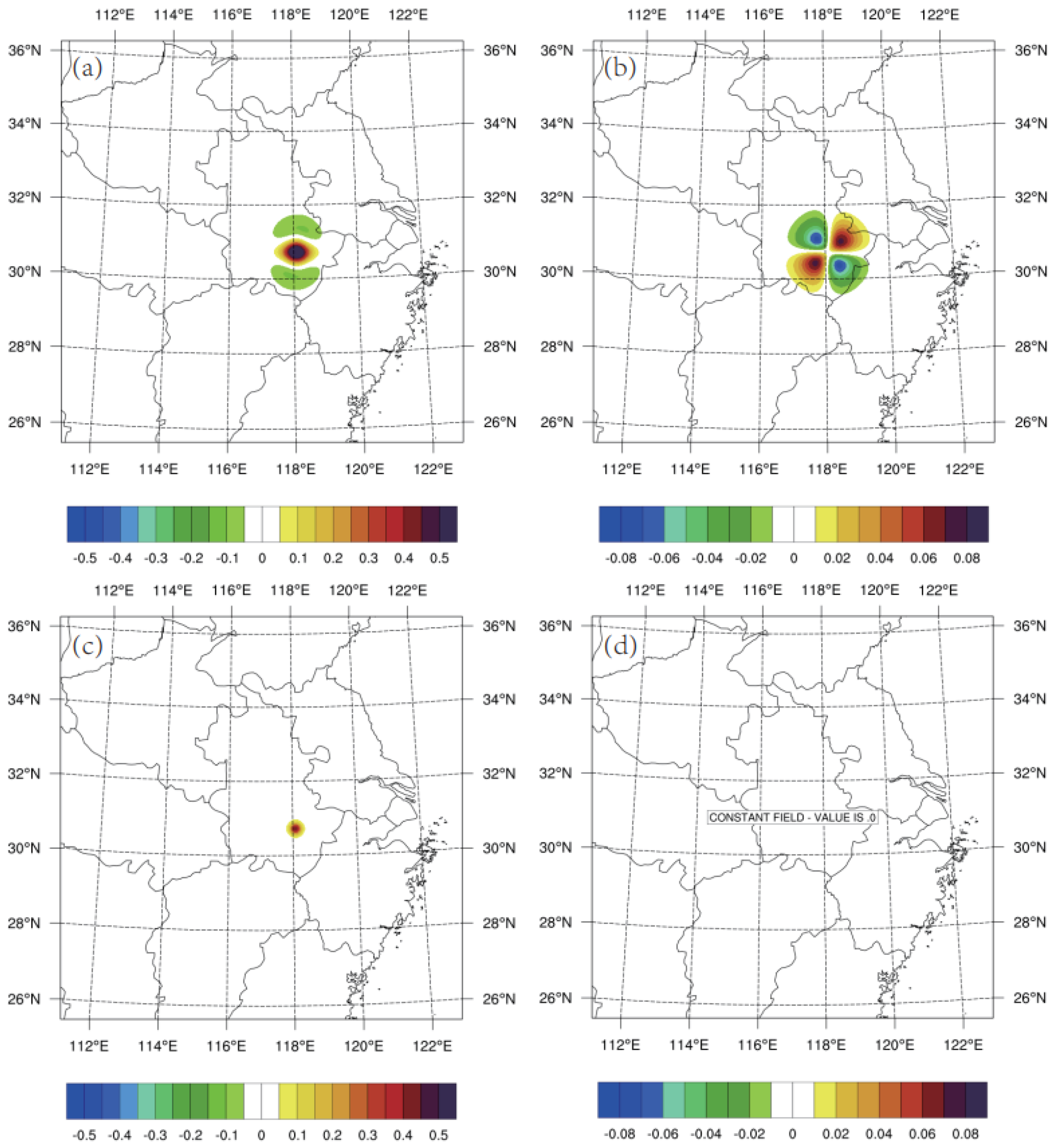
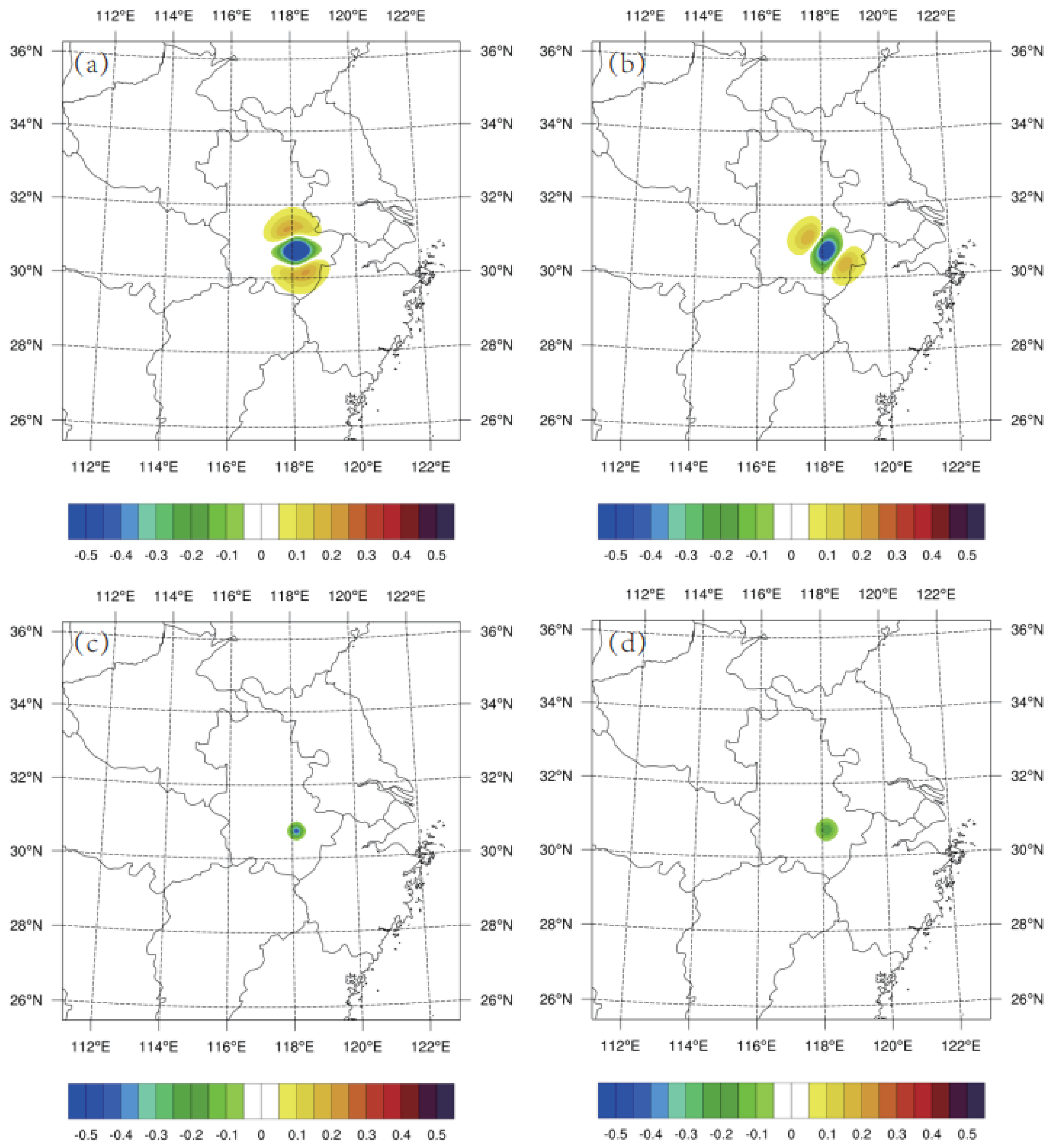
4.2. Single Observation Tests
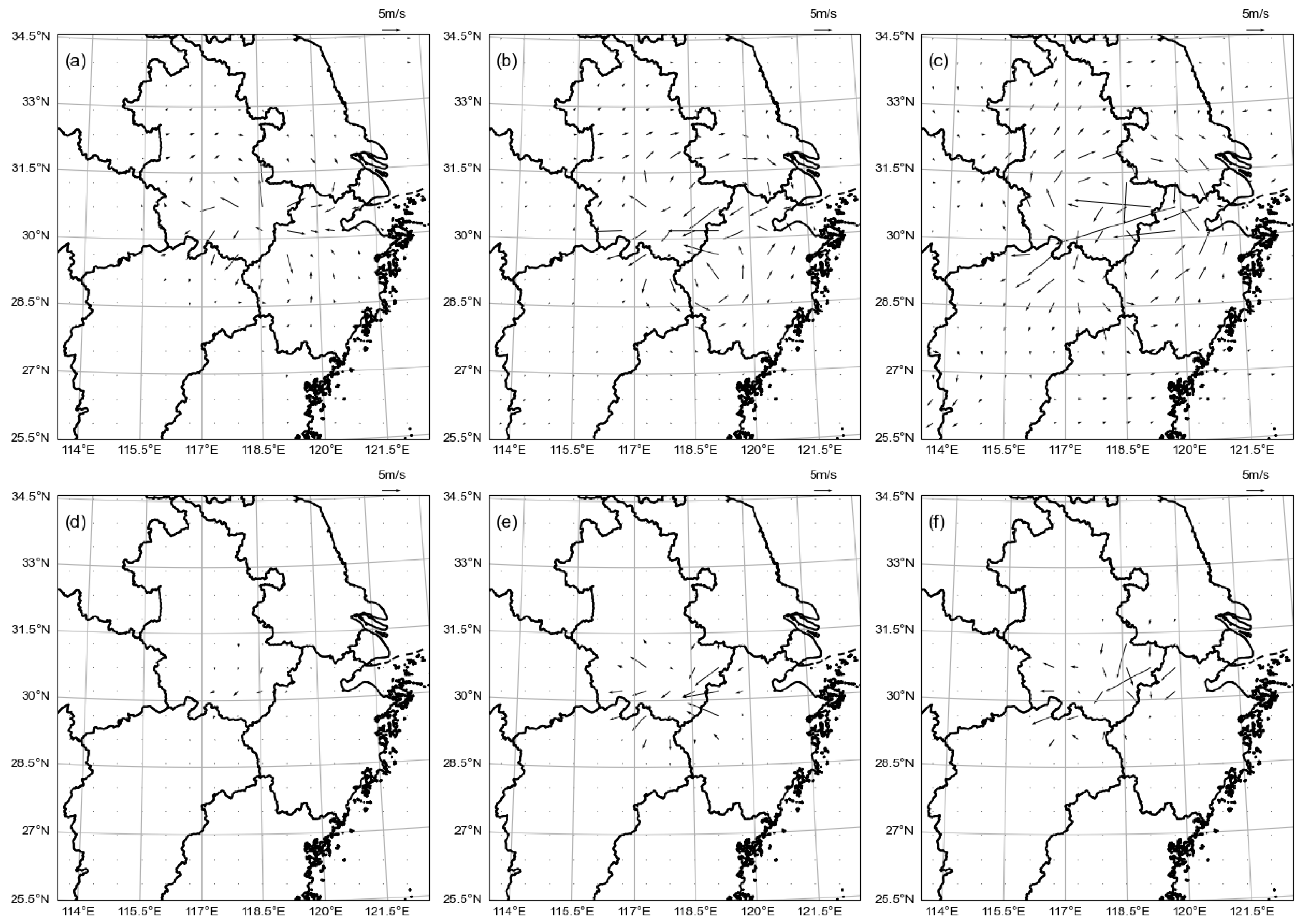
4.3. Wind Increment
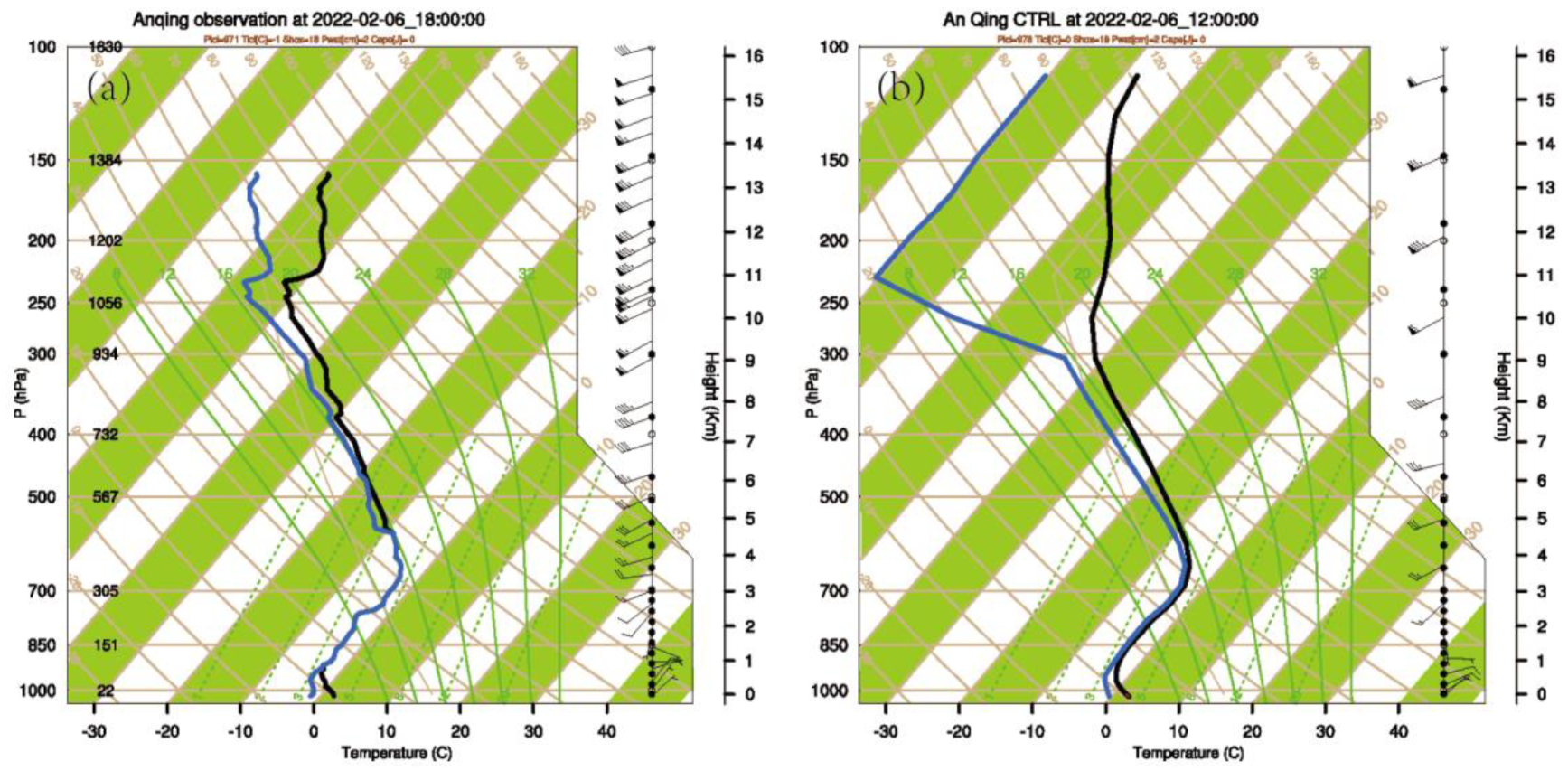
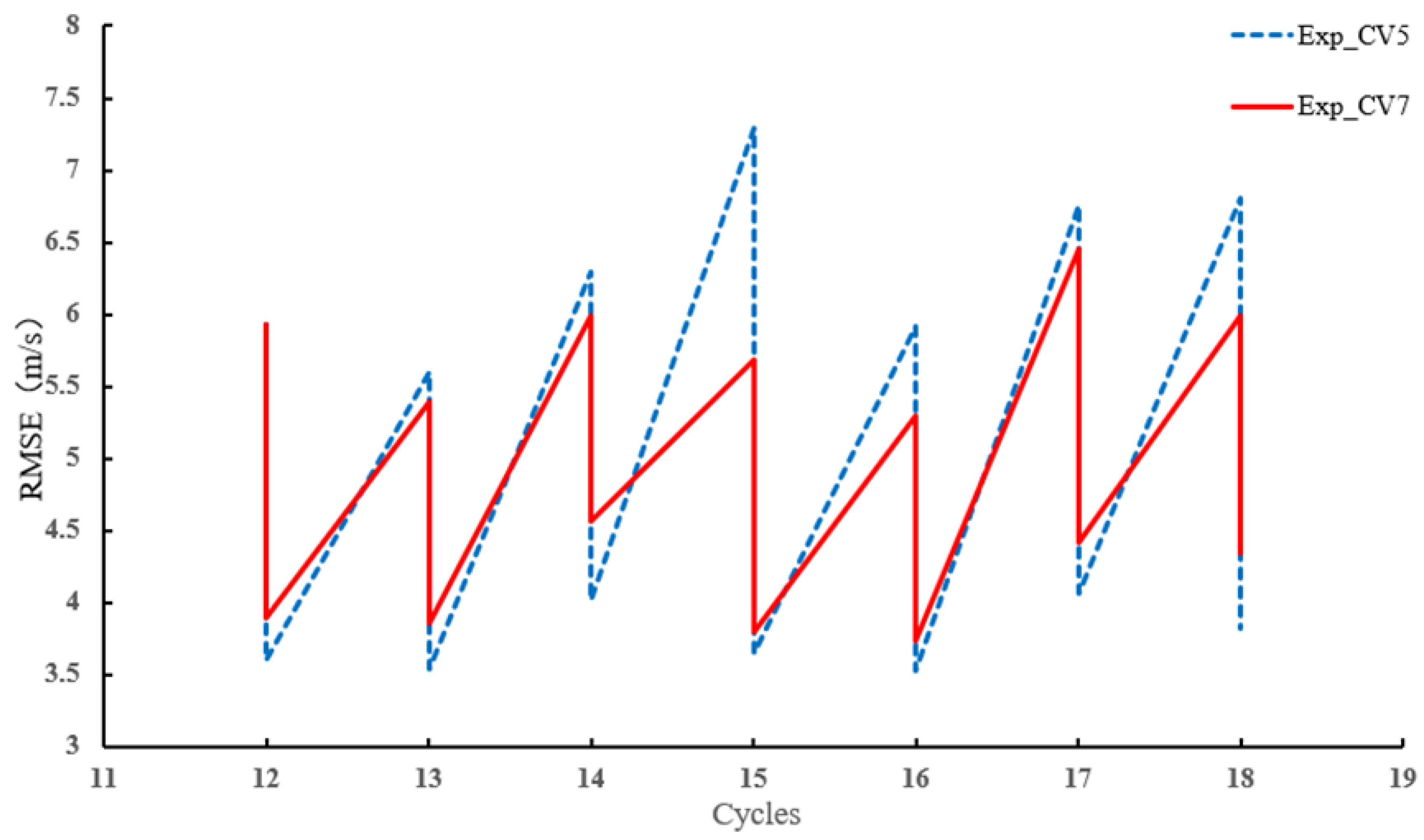
4.4. Analyses during DA Cycles
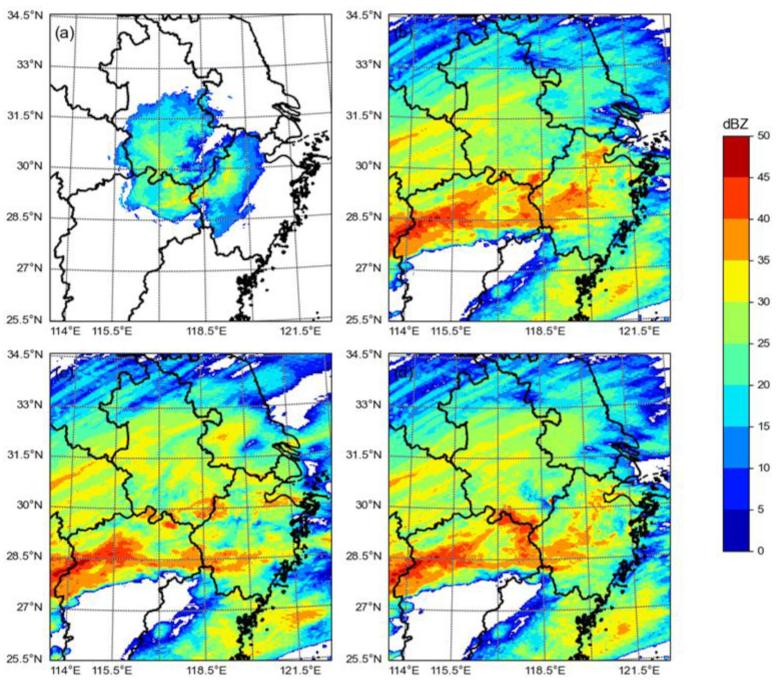
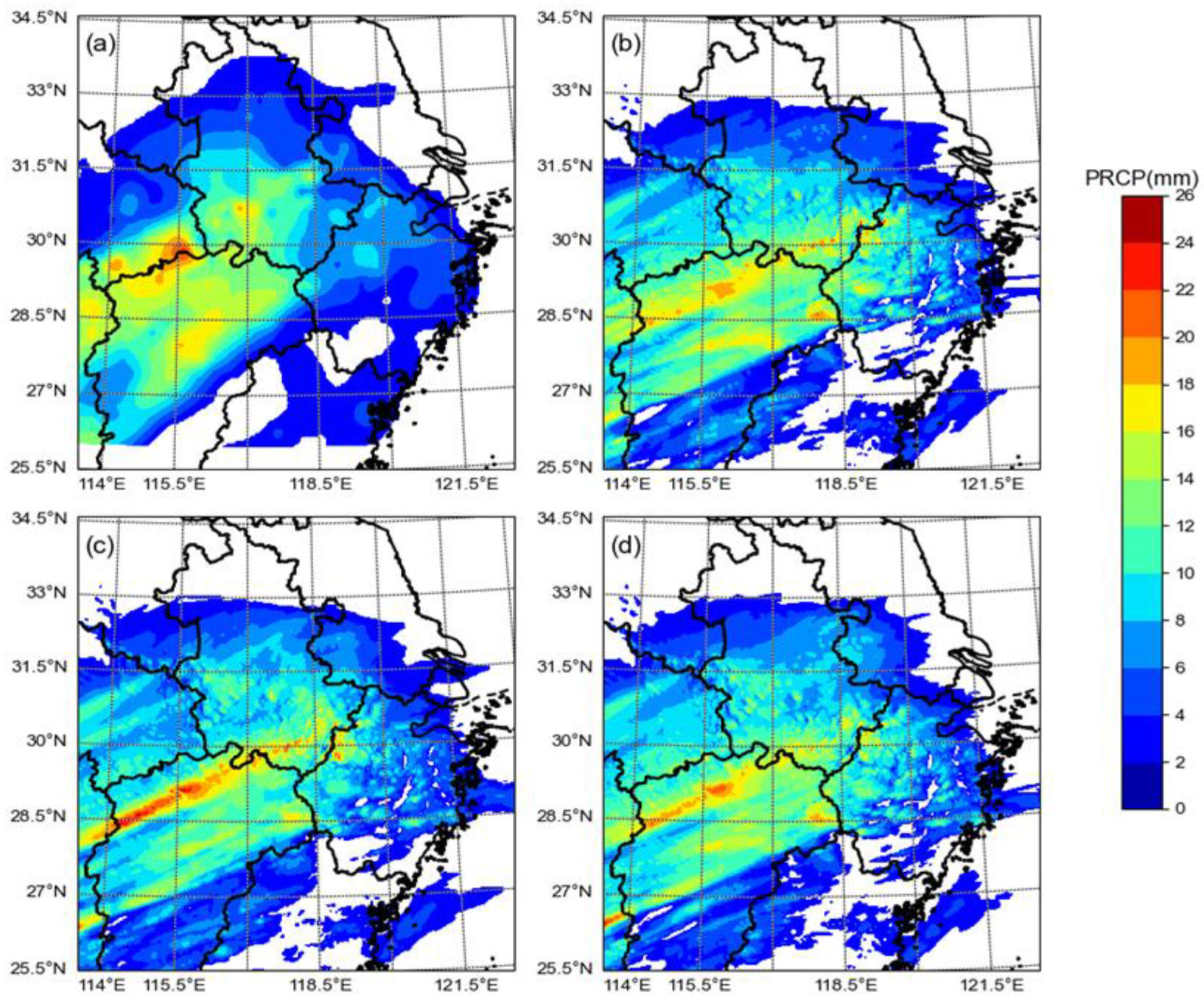
4.5. Forecasts
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Ping, F.; Meng, X.; Li, Y. Numerical Simulation of a Large-Scale Snowstorm Process in Northern China Using Different Cloud Microphysical Parameterization Schemes. Chin. J. Atmos. Sci. 2022, 46, 599–620. (In Chinese) [Google Scholar]
- Min, K.-H.; Chung, K.-S.; Lee, J.-W.; You, C.-R.; Lee, G. Intercomparing radar data assimilation systems for ICE-POP 2018 snowfall cases. Geosci. Model Dev. Discuss. 2022, 1–32. [Google Scholar] [CrossRef]
- Huang, H.; Tao, R.; Zhao, K.; Wen, L.; Chu, Z. Potential of snowfall nowcasting using polarimetric radar data and its link to ice microphysics: Study of two snowstorms in East China. J. Geophys. Res. Atmos. 2023, 128, e2022JD037654. [Google Scholar] [CrossRef]
- Gao, J.; Xue, M.; Shapiro, A.; Droegemeier, K.D. A variational method for the analysis of three-dimensional wind fields from two Doppler radars. Mon. Weather Rev. 1999, 127, 2128–2142. [Google Scholar] [CrossRef]
- Xu, D.; Shen, F.; Min, J. Effect of background error tuning on assimilating radar radial velocity observations for the forecast of hurricane tracks and intensities. Meteorol. Appl. 2020, 27, e1820. [Google Scholar] [CrossRef]
- Talagrand, O.; Courtier, P. Variational assimilation of meteorological observations with the adjoint vorticity equation I: Theory. Q. J. R. Meteorol. Soc. 1987, 113, 1311–1328. [Google Scholar] [CrossRef]
- Sun, J.; Flicker, D.W.; Lilly, D.K. Recovery of three-dimensional wind and temperature fields from single Doppler radar data. Atmos. Sci. 1991, 48, 876–890. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H. Radar data assimilation with WRF-4DVar: Part II. Comparison with WRF-3DVar. Mon. Weather Rev. 2013, 141, 2245–2264. [Google Scholar] [CrossRef]
- Zhang, F.; Snyder, C.; Sun, J. Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter. Mon. Weather Rev. 2002, 132, 1238–1253. [Google Scholar] [CrossRef]
- Xu, X.; Liu, L.; Zheng, G. Numerical Experiment of Assimilation of Doppler Radar Data with an Ensemble Kalman Filter. Chin. J. Atmos. Sci. 2006, 30, 712–728 (In Chinese). (In Chinese) [Google Scholar]
- Snook, N.; Xue, M.; Jung, Y. Multiscale EnKF assimilation of radar and conventional observations an ensemble forecasting for a tornadic mesoscale convective system. Mon. Weather Rev. 2015, 143, 1035–1057. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xue, M. Assimilation of radar velocity data with the WRF hybrid ensemble-3DVAR system for the prediction of hurricane Ike (2008). Mon. Weather Rev. 2012, 140, 3507–3524. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Some observing system simulation experiments with a hybrid 3DEnVAR system for storm-scale radar data assimilation. Mon. Weather Rev. 2014, 142, 3326–3346. [Google Scholar] [CrossRef]
- Shen, F.; Xu, D.; Xue, M.; Min, J. A comparison between EDA-EnVar and ETKF-EnVar data assimilation techniques using radar observations at convective scales through a case study of Hurricane Ike (2008). Meteorol. Atmos. Phys. 2018, 130, 649–666. [Google Scholar] [CrossRef]
- Courtier, P.; Thepaut, J.N.; Hollingsworth, A. A strategy for operational implementation of 4D-Var, using an incremental approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Xie, Y.; MacDonald, A.E. Selection of momentum variables for a three-dimensional variational analysis. Pure Appl. Geophys. 2012, 169, 335–351. [Google Scholar] [CrossRef]
- Xiao, Q.; Sun, J. Multiple-radar data assimilation and short-range quantitative precipitation forecasting of a squall line observed during IHOP. Mon. Weather Rev. 2007, 135, 3381–3404. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Fan, S. Indirect assimilation of radar reflectivity with WRF 3D-Var and its impact on prediction of four summertime convective events. J. Appl. Meteorol. Climatol. 2013, 52, 889–902. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D. Assimilation of reflectivity data in a convective-scale, Cycled 3DVar framework with hydrometeor classification. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Tong, W.; Zhang, Y.; Lin, C.-Y.; Xu, D. Comparison of the impacts of momentum control variables on high-resolution variational data assimilation and precipitation forecasting. Mon. Weather Rev. 2016, 144, 149–169. [Google Scholar] [CrossRef]
- Li, X.; Zeng, M.; Wang, Y.; Wang, W.; Wu, H.; Mei, H. Evaluation of two Momentum Control Variable Schemes and their Impact on the Variational Assimilation of Radar Wind Data: Case Study of a Squall Line. Adv. Atmos. Sci. 2016, 33, 1143–1157. [Google Scholar] [CrossRef]
- Lu, C.; Chen, Y.; Meng, D. Comparative analysis of two dynamical control variables and their impacts on typhoon assimilation and prediction. Trans. Atmos. Sci. 2019, 42, 916–925. [Google Scholar]
- Xu, D.; Yang, G.; Wu, Z.; Shen, F.; Li, H.; Zhai, D. Evaluate Radar Data Assimilation in Two Momentum Control Variables and the Effect on the Forecast of Southwest China Vortex Precipitation. Remote Sens. 2022, 14, 3460. [Google Scholar] [CrossRef]
- Shen, F.; Song, L.; Li, H.; He, Z.; Xu, D. Effects of different momentum control variables in radar data assimilation on the analysis and forecast of strong convective systems under the background of northeast cold vortex. Atmos. Res. 2022, 280, 106415. [Google Scholar] [CrossRef]
- Xiao, Q.; Kuo, Y.; Sun, J.; Lee, W.-C.; Lim, E.; Guo, Y.; Barker, D.M. Assimilation of Doppler radar observation with a regional 3DVar system: Impact of Doppler velocities on forecasts of a heavy rainfall case. J. Appl. Meteorol. 2005, 44, 768–788. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments. J. Atmos. Sci. 1997, 54, 1642–1661. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Huang, X.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Notes; UCAR: Boulder, CO, USA, 2008. [Google Scholar]
- Lim, K.-S.S.; Hong, S.-Y. Development of an effective double-moment cloud microphysics scheme with prognostic cloud condensation nuclei (CCN) for weather and climate models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Hong, S.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction; American Meteorological Society: Seattle, WA, USA, 2004. [Google Scholar]

| Experiment | DA Scheme |
|---|---|
| CTRL | No DA |
| Exp_CV5 | DA with CV5 scheme |
| Exp_CV7 | DA with CV7 scheme |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, S.; Shen, F.; Chen, J.; Liu, L.; Dong, D.; He, Z. Evaluation of Two Momentum Control Variable Schemes in Radar Data Assimilation and Their Impact on the Analysis and Forecast of a Snowfall Case in Central and Eastern China. Atmosphere 2024, 15, 342. https://doi.org/10.3390/atmos15030342
Wan S, Shen F, Chen J, Liu L, Dong D, He Z. Evaluation of Two Momentum Control Variable Schemes in Radar Data Assimilation and Their Impact on the Analysis and Forecast of a Snowfall Case in Central and Eastern China. Atmosphere. 2024; 15(3):342. https://doi.org/10.3390/atmos15030342
Chicago/Turabian StyleWan, Shen, Feifei Shen, Jiajun Chen, Lin Liu, Debao Dong, and Zhixin He. 2024. "Evaluation of Two Momentum Control Variable Schemes in Radar Data Assimilation and Their Impact on the Analysis and Forecast of a Snowfall Case in Central and Eastern China" Atmosphere 15, no. 3: 342. https://doi.org/10.3390/atmos15030342
APA StyleWan, S., Shen, F., Chen, J., Liu, L., Dong, D., & He, Z. (2024). Evaluation of Two Momentum Control Variable Schemes in Radar Data Assimilation and Their Impact on the Analysis and Forecast of a Snowfall Case in Central and Eastern China. Atmosphere, 15(3), 342. https://doi.org/10.3390/atmos15030342






