Abstract
Fibrous air filters are common devices used to remove airborne particles. Their performance is typically measured through their resistance to airflow and captured particle mass. Models describing the evolution of filter performance have been heavily researched; however, the need for improvement remains. Experimental work is irreplaceable in the development of high-fidelity models, yet the estimation of necessary variables is not trivial and may be influenced by selected measurement instruments and analysis methodologies. Therefore, the purpose of this work is to propose a framework to investigate the response of common aerosol measurement instruments, their corresponding analysis methodologies, and the application of their data. A Scanning Mobility Particle Sizer (SMPS) and Laser Aerosol Spectrometer (LAS) were selected for consideration, and their recorded data were compared against baseline measurements. The results of the experiments indicated that the SMPS and LAS yielded a ratio of estimated mass concentrations to the baseline mass concentrations of approximately 1.175 and 0.749, respectively. Regarding the SMPS, it was suggested that the measurable size range, application of a coverage factor, dynamic shape factor, and association between the curve fits and histograms were influential in the final estimates. For the LAS, the application of a curve fit, its association to the histograms, and the selection of the sampling periods were influential. Considering the results, the impact of these factors may not be considered negligible and may skew reproducibility between studies and fossilize confounding factors. Therefore, the proposed methodologies are useful in addressing potential errors in data collection and analysis.
1. Introduction
Fibrous air filters are commonplace air cleaning devices used to remove airborne particles from the environment. Their performance is measured by their resistance to airflow as well as their particle capture efficiency. Specifically, an ideal filter will have the highest capture efficiency possible, while simultaneously providing the lowest resistance to airflow possible. The realistic performance of a fibrous air filter is a complex relationship between the physical attributes of the filtration media, such as filter thickness and mean fiber diameter, and environmental characteristics, such as the air properties and challenge particle characteristics. Predictive models provide insight into realistic filter performance, providing useful information for designing and maintaining an HVAC system and ensuring the proper functionality of not only the filter, but of the larger system of which the filter is part of as well. Models for analyzing and predicting the performance of fibrous air filters have been sought for decades. Many of these are based upon Darcy’s Law for depth loading, and the Kozeny-Carman Equation (Ergun Equation) for surface loading. However, neither of these models fully describe the loading process of a filter. Bergman et al. [1] proposed a model considering captured particles as newly formed fibers, using Davies’ equation [2] and the Kozeny-Carman equation. Novick et al. [3] circumvented traditionally difficult variable estimates by assuming the depth loading of a HEPA filter was negligible, and correlated the airflow resistance of particle cake to the aerosol’s mass median diameter (MMD). Thomas et al. [4] combined a modified version of Bergman’s model with Novick’s model and provided a robust framework to describe the full life cycle of filtration media, benefiting from the strengths of both models. Berry et al. [5] provided a more thorough review of the loading models given above, as well as other relevant loading models.
The purpose of conventional filter loading models may be reduced to the relationship between the number of captured particles, their size and shape, and the induced airflow resistance. This is typically accounted for by considering known phenomena and their impact, such as the development of a particle cake and its porosity. Models tend to be unique in the specific ways that they describe filter performance, yielding varying degrees of success. However, knowing both the size distribution of the particles and their total concentration allows for the estimation of these necessary variables that are irreplaceable within both theoretical and empirical models. Yet, attaining the necessary data with confidence is no trivial task, and the produced results may easily be skewed by implicit errors contained within the data collection and analysis methodology. For example, Figure 1 illustrates results yielded by a simulation based upon the Thomas model for particle size distributions with different geometric mean diameters. When considering the maximum pressure drop prescribed by the US DOE for nuclear grade HEPA filters, the magnitude of the differences becomes problematic as even small deviations in the geometric mean diameter result in a predicted difference of more than 1 in. WC, representing a liberal estimate of 20% of the filter’s expected life. Due to the necessity of empirical data for theoretical model validation, and the prevalence of empirical models, effort must be made to quantify and address possible sources of error within experimental instrumentation operation and data analysis methodology. Therefore, the purpose of this work is to establish a framework to evaluate the response of commonly used aerosol measurement instruments, their corresponding data analysis methodologies, and the application of their data.
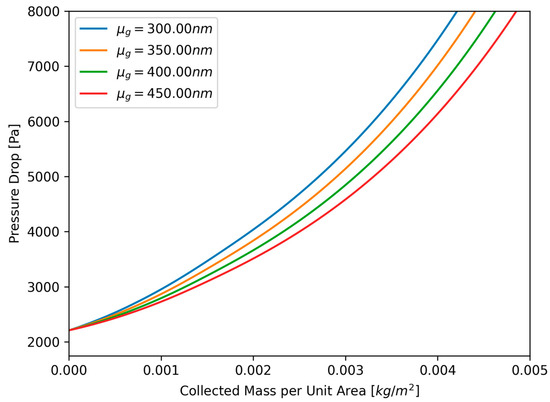
Figure 1.
Comparison of the Loading Curve Estimates Based Upon Different Geometric Mean Diameters.
This present work focuses on two instruments: (1) the Scanning Mobility Particle Sizer (SMPS) (Model 3936, TSI Inc., Shoreview, MN, USA), and (2) the Laser Aerosol Spectrometer (LAS) (Model 3340, TSI Inc.). These were selected based upon their prevalence in current research and utilization in standards, such as the ASME AG-1 standard [4,6,7,8]. However, these instruments operate in fundamentally different ways, resulting in observable differences in collected data and the use of distinct procedures to analyze and reduce the data. Yanoksy et al. [9] compared a DustTrak (TSI Inc.) and an Aerodynamic Particle Sizer (APS, TSI Inc.) to the Federal Reference Method (FRM), and reported systematic bias when comparing averaged data from the APS units. It was suggested that improper component calibration within the instruments could be responsible; however, it is reasonable to extrapolate these results to other instrument types as well. This suggests that even instruments of the same type should not be blindly trusted to yield the same data results. When considering how these errors will affect the interpretation and synthesis of the collected data, it is important to first establish how the data is expected to be used. For the current work, the anticipated application of the collected data is in conjunction with filter loading models–for example, as validation of a proposed model, or as a conceptual exploration using an established model. Therefore, errors relating to the instruments, which will manifest in the parameters of the size distributions, may be expected to affect the estimated pressure drop per unit of loaded mass in a corresponding filter loading curve.
At a base level, an SMPS measures the electrical mobility diameter of particles by charging them through a bipolar diffusion charging process and passing them through an electric field of successively increasing intensity, thereby influencing the velocity of the particles based upon their size [10]. Although considered an accurate and reliable instrument [11], the SMPS is also susceptible to errors, given known operational characteristics. Liu and Deshler [12] compared an SMPS to a standalone CPC by investigating the SMPS’s inlet impactor sampling flow rate, the efficacy of the SMPS neutralizer, and the temperature difference between the CPC saturators and condensers, and achieved strong agreement between the instruments after addressing the errors. Van Gulijk et al. [13] compared the response of an Electrical Low Pressure Impactor (ELPI) and SMPS when subjected to diesel soot, and hypothesized that the SMPS may underestimate the measurement of larger particles which circumvent its impactor due to their high mobilities. These particles are likely to be multiply charged due to their size and shape [14] and therefore it is plausible that they would behave as smaller particles in the DMA, potentially skewing the size distribution. However, Rogak and Flagan [15] addressed this by investigating the difference between the electrical mobility diameter and the mobility (aerodynamic) equivalent diameter of spherical particles and aerosol agglomerates within an appropriate size range. The authors concluded that the DMA data inversion procedure yielded acceptable agreement for particles of equivalent mobility diameters. Although the literature cited above cannot be described as a comprehensive investigation into the inner workings of an SMPS, they do provide reasonable insight into potential sources of error given an operational knowledge of the instrument.
Unlike an SMPS, an LAS measures the geometrical diameter of particles in real time. Particles are focused into a sample stream and passed through a laser, producing pulses of scattered light sensed by a pair of detectors [16]. The instrument interprets the size of the particles from the amplitude of the scattered light pulses, which is a function of particle size, and the number of particles from the number of received pulses. However, in addition to the dependence of light scattering methods on a particle’s size, they are also sensitive to a particle’s refractive index and shape [17]. Therefore, these characteristics must be addressed if the measured particles are not similar to those used in calibration. As an optical particle counter, an LAS will also suffer from particle coincidence at sufficiently high concentrations, resulting in the mischaracterization of the particle size distribution and total particle count [18]. Thus, it is often necessary to dilute the sampled aerosol, adding additional error and possibly altering the particle size distribution being measured. Contrasting the potential errors from particle coincidence and dilution, the counting efficiency of an LAS for particles which are sufficiently large (approximately ≥0.1 µm) is very good, and may be considered as approximately 100% efficient [16,18]. Finally, similar to the aforementioned errors of the SMPS, each LAS may also suffer from errors due to manufacturing tolerances and calibration procedures [18]. This supports the argument that each instrument should be evaluated beyond factory calibration, especially considering the use of particles different from the calibrating particle type. Again, the literature cited above is not a comprehensive description of the operating principles of an LAS, but provide a useful platform for the analysis and critique of collected data and potential error sources.
Although the previous paragraphs suggest that different instruments are capable of yielding reasonably similar results, it is important to examine the operating principles and specifically the utilized data analysis methodologies in order to identify their weaknesses and possible sources of error. In order to establish a framework for aerosol measurement instrument response, an investigation of corresponding data analysis methodologies for estimating the mass concentration with a focus on the implications for filtration model development and validation is included. Baseline measurements are established by collecting particle mass on HEPA filters to estimate the error for each instrument test based upon known particle characteristics and the developed analysis methodologies. The remaining sections in the current work detail the experimental setup and analysis methodologies and discuss the influence these may have on similarly gathered data regarding loading model analysis and development.
2. Experimental Setup
To accomplish the goals of the present work, a test stand capable of performing filter particle loading experiments was utilized. Its use ensured that the data was collected in an applicable manner as compared to how the instruments would be used in a particle loading test, allowing for the collection of instrument data and representative pressure drop data across HEPA filter test articles due to particle loading. The remainder of this section provides a description of the experimental setup employed to collect the instrument data. This includes the physical configuration of the test stand, the selected challenge particle type, as well as the configuration of the instruments and apparatuses.
Figure 2 shows the experimental setup for both the SMPS and LAS configurations. The configurations were similar, differentiated solely by the instruments themselves and their specific requirements. The test stand was built from a horizontal pipe used to contain and transport the test aerosol supplied from the particle generator and charge neutralizer. Air for the test stand was supplied from the ambient lab environment, maintained at standard conditions and passed through a pre-filter to ensure the removal of any ambient particles. A thin-walled probe was used to sample a small portion of the flow from the test stand to be transported to the aerosol measurement instruments, simulating realistic filtration experiments as they would normally operate. Flow from the probe was then split using an isokinetic flow splitter, and the divided flow was routed to each instrument. Transport losses were considered as negligible in this work due to the short length of tubing required to reach the instruments, as well as the short amount of time required to transport the particles to the instruments given the known sampling flow rates.
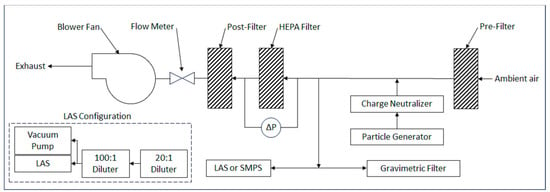
Figure 2.
Experimental Setup of the SMPS and LAS Configurations.
2.1. Dust Generation and Particle Morphology
Aluminum Trihydroxide (Al(OH)3) particles were selected as the challenge particle type, and the aerosol was generated from a Dust Aerosol Generator (model 3410U, TSI Inc.). A Kr-85 aerosol neutralizer (model 3054A, TSI Inc.) was connected in series between the aerosol generator and the test stand to neutralize any charge accumulated by the particles. The particle morphology was investigated using SEM images, given the sensitivity of the SMPS to particle shape. These images were generated by impinging particles onto carbon tape, as well as creating samples using partially loaded pieces of filter media. The shape of the particles was confirmed as irregular, shown in Figure 3. From inspection, it may be seen that the individual particles typically take the shape of platelets, which is consistent with commonly used production processes for manufacturing Al(OH)3 particles [19]. However, it must be noted that the work of Endo et al. [20] asserted a nearly spherical shape for the same particle type. The difference in the current particle morphology and the cited literature was not reconciled within the current work; however, it may be speculated that the method of aerosol generation was the differentiating factor. The previous literature utilized a fluidized bed generator, whereas the generator used in the current work dispersed the powder using a nozzle and compressed air which suctioned the powder using the venturi effect. The authors speculate two reasonable possibilities for this difference: (1) the method of particle generation used in the current work may have effectively broken aggregated particles and reduce the aerosol to the powder’s primary particles, and (2) aerosol generation of Al(OH)3 particles by fluidized beds generators may promote the formation of aggregated particles. The present work considers the particles as individual platelets and assumes that particle agglomeration was negligible. However, it is a reasonable assumption that alternative test particles may be used in different experiments which may have less severe or more severe morphological characteristics. For example, NaCl particles with cubic morphology or soot particles with fractal morphology resulting from agglomerated primary particles are both commonly employed particle types for filtration experiments that may be expected to behave differently than the Al(OH)3 particles. These differences may be expected to manifest not only in the instrumentation, as discussed earlier, but also in the evolution of filter performance. Specifically, agglomerated particles, due in part to their large dynamic shape factor, have the potential to skew the modeling of a filter if not properly considered. This may be attributed to an increase in particle mobility, interception parameter, and impact towards particle dendrite formation. However, the opposite is also reasonable to assume, given particles with a smaller dynamic shape factor. Therefore, the reader is cautioned to consider the impact of particle morphology, especially regarding particles with the potential for agglomeration.

Figure 3.
SEM images of collected Al(OH)3 particles.
Ultimately, particle shapes will affect the SMPS and the LAS differently. Regarding the SMPS, neglecting the dynamic shape factor will yield the correct electrical mobility equivalent particle diameter, but an estimation of this variable is required to correctly convert from the electrical mobility diameter to the volumetric equivalent diameter. Cheng et al. [21] state that the dynamic shape factor of talc particles, which are also plate-like, is 1.88. Given the similarities in the shape of the Al(OH)3 particles and talc particles, the same shape factor is assumed for the present work. Therefore, a value of 1.88 is estimated as the dynamic shape factor for the Al(OH)3 particles. The influence of the dynamic shape factor on the results is discussed more in Section 4.
2.2. SMPS Preparation and Configuration
The SMPS was configured with a sampling flow rate of 0.3 L/min and a total sampling period of 150 s, including the time for rescanning and purging. This allowed for the instrument to scan over a diameter range from 25.0 nm to 1000 nm with a resolution of 103 bins of equal width on a logarithmic scale. A small amount of vacuum grease was applied to the inlet impactor to mitigate particle bounce. Data collected from the SMPS utilized the instrument’s automatic distribution corrections, which account for particle charging, coincidence, and other known errors, such as transport losses. A custom long-column DMA with an effective length of 95 cm, fabricated by and purchased from the University of Minnesota, was installed onto the instrument. The purpose of this piece was to allow for more precision with smaller sampling sizes. The SMPS was connected to the test stand via an isokinetic flow splitter, with the other leg of the splitter transporting the sample flow to the mass collection filter. The instrument was operated using a factory calibration.
2.3. LAS Preparation and Configuration
The LAS was configured with a total sampling time of 150 s and a flow rate of 0.05 L/min. Although the LAS was capable of providing true real-time particle measurements, the choice to record multiple samples was made in order to provide parity with the SMPS sampling procedure and to investigate the influence of sampling periods. Particle diameters were measured over a range of 0.09 µm to 7.5 µm with a resolution of 99 bins of equal logarithmic widths. Prior to each test, the optics voltage and inlet flowrate were confirmed to be within acceptable levels to avoid the possibility of operational errors. Two diluters (model 3302A, TSI Inc.) were connected in series upstream of the LAS to provide an acceptable particle concentration for the instrument. One diluter was configured with a 20:1 dilution ratio, and the other with a 100:1 dilution ratio, for a combined nominal ratio of 2000:1. Given that the diluters required a flow rate of 5 L/min, an additional vacuum pump and flow controller (model MC-5SLPM-D, Alicat, Tucson, AZ, USA) were employed downstream of the diluters to allow for additional airflow to be induced beyond what the LAS was capable of providing. The vacuum pump was configured in parallel to the LAS, and the flow was divided using an isokinetic flow splitter. The reader may note that the term isokinetic would technically be incorrect in this situation, given the different flow rates through each leg of the splitter. However, the concentrations resulting from the different flow rates through each leg of the flow splitter were investigated, confirming that the particle number distribution and concentration were not influenced. This investigation was accomplished by using the SMPS to measure the concentration from one leg of the splitter while inducing a series of flow rates through the other leg of the splitter. None of the tests indicated that the concentration or size distribution of the measured particles was influenced, and therefore the use of the flow splitter was considered acceptable for operation with different flow rates through each leg. The diluters were connected to the test stand similarly to the SMPS with an additional isokinetic flow splitter, dividing the flow for the instrument and the mass collection filter. The instrument was operated using a factory calibration.
As previously mentioned, physical differences between the selected challenge particle type and the calibration particle type can be a source of error. Thus, it was necessary to consider these effects in order to determine if any corrections were necessary. The factory calibration of the LAS utilized Polystyrene Latex (PSL) spheres, which is in accordance with standard calibration procedures. Given that the LAS is an optical particle counter, the refractive index (RI) of PSL and Al(OH)3 had to be compared. The RI of Al(OH)3 is approximately between 1.568 and 1.587, whereas the RI of PSL spheres is approximately between 1.623 and 1.66 [22,23]. Due to the closeness of these values, the expected difference in the reported results was assumed to be negligible. Next, the difference in particle morphology was also addressed. Given that the wavelength of the laser used in this instrument was stated as 633 nm [16], the measurement of irregular particles much smaller than this could be considered as a volume effect [18], and therefore the instrument was expected to report the volumetric equivalent diameter. However, for irregular particles larger than the wavelength, the probability of light scattered by external reflection should be approximately equivalent to that of large spherical particles, since the average angle of scattering has similar probabilities [18]. It should be noted that irregular shapes could lead to a larger probability of internal reflection as well. Therefore, given that the particles were not porous, the reported geometric diameter may be considered as equivalent to the volumetric equivalent diameter. Thus, the differences between the challenge particle and the calibration particle, specifically the RI and particle morphology, were assumed to be negligible.
Prior to testing, each diluter was characterized to estimate their corresponding dilution factors. The characterization process used the LAS to record five diluted samples and five undiluted samples for both the 20:1 and 100:1 diluters. The particle counts for each set of five samples were averaged, and the individual dilution factors were estimated as the ratio of the sum of the recorded particle counts without dilution to the sum of particle counts with dilution. Finally, to properly determine the curve fit parameters, the recorded data was normalized using the bin boundaries exported with the LAS data. The bins were spaced evenly on a logarithmic scale, and the midpoints were calculated as the geometric means between the bin boundaries. For the current work, a size range of 0.09 µm to 7.5 µm was selected to ensure that the entirety of the particle size distribution was recorded, where 0.09 µm represents the smallest particle size the LAS is capable of measuring and 7.5 µm represents the largest.
2.4. Mass Collection Filter Preparation
A simple apparatus to hold HEPA filter media was used in parallel with both the SMPS and LAS to provide the baseline measurements for the particle mass concentration estimates. The media holder consisted of two separate, concentric pieces where the mass collection filter was inset into the bottom piece and affixed into place by inserting the topmost piece over it. The top piece was sealed with a rubber O-ring and moderate amount of vacuum grease, ensuring a leak-proof seal and smooth disassembly. Given the ease with which the mass collection filter was able to be removed from the holder apparatus, particulate mass loss from rough handling was readily avoidable. The filter media was supported by a coarse wire mesh to provide strength and prevent possible media failure. An analytical balance (model XPE205DR, Mettler-Toledo, Columbus, OH, USA) was used to weigh the filter media before and after each test to determine the amount of collected mass. Finally, the flow through the apparatus was induced using a vacuum pump and mass flow controller (model MCP-20SLPM-D, Alicat), and set at a volumetric flow rate of either 1.2 L/min or 5.0 L/min corresponding to the SMPS and LAS, respectively.
3. Methodology
The process for analyzing the instrument data followed the same general procedure for both instruments. However, both instruments necessitated specific supporting steps to address their individual traits. The mass concentration reported by each instrument was estimated using the recorded particle count data and integrated with respect to the particle diameter, shown in Equation (1).
where Cm and C represent the total particle mass and count concentrations for all particle sizes, respectively, f(dp) represents the function describing the particle size distribution, dp represents the particle diameters, and represents the density of the particles. Given the known characteristics of the challenge particle, the size distribution was assumed to be lognormal, given by Equation (2), where µg is the geometric mean diameter and is the geometric standard deviation.
The parameters for the lognormal distributions were estimated by curve fitting the reported normalized particle count data from the instruments. Given that the gravimetric filter cannot provide real-time data, the estimated mass concentrations from each instrument sample were averaged to provide a single distribution comparable to the gravimetric data. It is worth mentioning that the average concentration was equivalent to considering the total collected mass over the total amount of volumetric flow. However, the recorded counts cannot simply be averaged over each sample to curve fit a single distribution, as this neglects transient effects regarding derived loading curves.
3.1. Scanning Mobility Particle Sizer
The SMPS records electrical mobility diameter, which must be converted into the volumetric equivalent diameter to estimate the mass concentration. This conversion was accomplished using Equation (3), which was solved iteratively.
where dV represents the volumetric equivalent diameter, dee represents the electrical mobility equivalent diameter, χ represents the dynamic shape factor, and Cc represents the Cunningham correction factor. The use of the Cunningham correction factor was necessary given the size range of the particles, in order to account for aerodynamic slip for particles under 1 µm, and was calculated using Equation (4) [24].
where represents the mean free path of the gas molecules. Given that the distribution of particle sizes extended beyond the range that the SMPS was capable of measuring, the reported total number concentration was less than the true concentration due to the portion of the distribution curve that was neglected. Thus, the SMPS did not account for the total number of particles that was expected. Therefore, a coverage factor (CF) was applied in order to correct the measured concentration and account for the neglected fraction. This was accomplished by estimating the fraction of the distribution measured by the SMPS, which was then applied to the reported concentration to estimate the true concentration. A representative sample from the SMPS illustrates this in Figure 4, showing the portion of the distribution measured by the SMPS and the portion that was neglected. The CF was estimated by utilizing the fit lognormal function of the data for each sample, and integrating over the SMPS measurement range, shown in Equation (5), where dmax represents the maximum diameter reported by the SMPS.
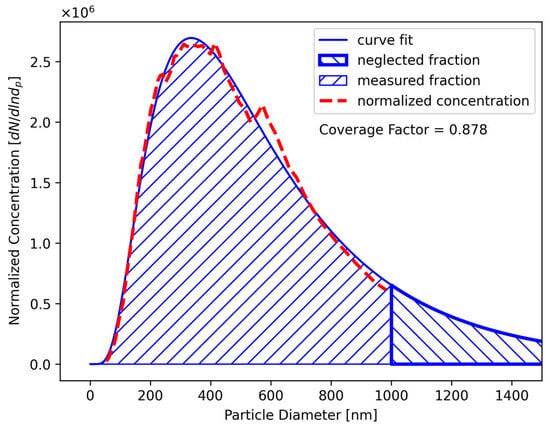
Figure 4.
Illustration of the measured and neglected fractions from representative SMPS data.
It should be noted here that the electrical mobility equivalent diameters were used with the particle size distribution instead of the volumetric equivalent diameters. This was because of the operational characteristics of the SMPS, specifically regarding the upper size limit for each bin. The value of dmax should increase for larger midpoint sizes given that each bin has equivalent logarithmic widths. Therefore, it is more conceptually consistent to use the electrical mobility equivalent diameter that the instrument bases the particle count binning on. This is due to the measured particle concentration being a function of the uppermost bin limit, not the largest bin midpoint, and therefore using the larger value represents a more correct estimate of the CF. The nominal concentration reported by the instrument was corrected using Equation (6).
where represents the corrected sample concentration, and represents the original reported sample concentration from the instrument. The corrected concentration was then used with Equation (1) to estimate the mass concentration of each sample. The individual sample mass concentrations were averaged according to Equation (7) for the comparison to the baseline measurement.
where represents the average concentration of the samples, and n represents the number of collected samples.
3.2. Laser Aerosol Spectrometer
As previously mentioned, the LAS required the use of two diluters operated in series, using Equation (8) to estimate the dilution factor.
where DF represents the dilution factors corresponding to the total, 20:1, and 100:1 dilution factors, respectively. Given that the particle size distributions were not truncated as with the SMPS, it was not necessary to estimate the coverage factor for the LAS, and the mass concentration was estimated using Equation (9).
where represents the estimated number concentration, represents the number of particles per bin, m represents the number of bins, represents the sampling volumetric flow rate, and t represents the sampling time. The average mass concentration was calculated using Equation (7).
3.3. Mass Collection Filter Procedure
As the mass collection filter lacked any ability to fractionate based upon particle size, a single value of the overall particle mass concentration was yielded for each test. This was accomplished by weighing the filtration media before and after each test. Since HEPA media was used for the mass collection, it is assumed that 100% of the particles were captured. Each of the mass measurements were repeated five times to generate reasonable confidence in the estimates. Finally, the mass concentration itself was calculated using Equation (10).
where and represent the pre- and post-weights relative to particle collection, j represents the number of weight measurements, and the total sampling time, i.e., the test duration.
4. Results and Discussion
Six methodologies for the SMPS were explored, along with four methodologies for the LAS, in order to investigate the proposed methodologies. Consideration was applied for how the results may vary given different assumed values or analysis procedures. These methods are termed S1–S6 and L1–L4 for the SMPS and LAS experiments, respectively. The mass concentration ratio results from Methods S1 and L1 are products of the proposed data collection and analysis methodologies and assumptions outlined in the preceding sections. The authors believe that these represent the correct procedures and values for the estimation of the mass concentrations and related variables. SMPS methods S2–S6 correspond to methodologies considering the effects of the dynamic shape factor, measured size range, and application of the coverage factor to investigate their effects on the reduced data, respectively. Likewise, LAS methods L2–L4 consider and investigate the effects of the number of collected samples and the use of curve fitting or histograms to estimate the mass concentrations, respectively.
Table 1 and Table 2 show the experimental results for the SMPS and LAS for the prescribed methodologies. It may be seen that the instruments estimated systematically different mass concentrations relative to the baseline results, given by the average ratio values. A reasonable amount of scatter was present, as is expected from empirical data. However, it is noteworthy that the scatter present within the SMPS is greater in magnitude than that present within the LAS. Furthermore, the LAS yielded a significantly lower ratio of estimated mass concentration to baseline mass concentration than the SMPS, implying more precision, but less accuracy.

Table 1.
SMPS estimated results from analysis methodologies.

Table 2.
LAS estimated results from analysis methodologies.
4.1. Influence of the Dynamic Shape Factor
The selected dynamic shape factor of the challenge particle played a significant role in the SMPS results, as illustrated in Table 1, Methods S1–S3. Upon inspection, it may be seen that not only do the ratios increase, but the scatter present between the individual ratios increases as well. Furthermore, it is interesting that as the selected dynamic shape factor increases, the scatter decreases, trending toward lower magnitudes. The average and median slopes of a loading curve derived from a representative test are useful to facilitate an understanding of the implications of these results. It may be seen that the average and median slope of the curves increases with an increasing dynamic shape factor, indicating that less mass is being estimated as collected and therefore that each unit of collected mass results in a greater induced pressure drop. Since the same data is used to produce each curve, the trend may be attributed solely to the influence of the dynamic shape factor on the calculated volumetric equivalent diameters. This result is logical given that the volume of a particle is proportional to the cubed diameter. Thus, a reduction in the reported diameters resulting from the electrical equivalent mobility to volumetric equivalent diameter conversion is expected to significantly decrease the estimated mass concentration from the instrument. It is therefore exceedingly important to consider the dynamic shape factor of the challenge particles, given the magnitude of impact that this single variable will have on the estimated results.
4.2. Influence of the SMPS Size Range
The possible theoretical size range for SMPS measurements is based upon the aerosol sampling flow rate and the specific DMA in operation [10]. Although the flow rates and hardware for the current work were constant, it is reasonable to expect that other scenarios may require different configurations. Given that the current configuration offers the largest possible range, it is logical to question what influence a smaller measurable size range would have. This was investigated in the current work by curve fitting the collected data over a smaller portion of the available size range, simulating the results from a different configuration for an identical test. However, it should be noted that this is not entirely representative, given that alternate configurations would be expected to have different responses and histograms from the same aerosol inputs. Table 1, Methods S1, S4, and S5 illustrate the results between loading curves generated from the collected test stand data using the prescribed methodology and different SMPS size ranges. It is interesting to note that the simulated decreasing size ranges resulted in an overall increase in the average ratio and scatter present within the reduced data, manifesting in the loading curve as a decreasing slope corresponding with the smaller size ranges. This may be seen in Figure 5, which shows the estimated loading curves corresponding to the full range, 80% of the full range, and 60% of the full range. As in the previous subsection, it may be asserted that the increase in the estimated mass concentrations results in an increase in the estimated airflow resistance per unit of loaded mass.
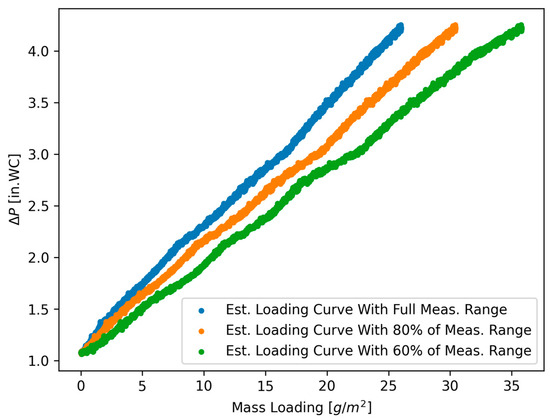
Figure 5.
Illustration of the measured and neglected fractions from representative SMPS data.
The implication of these results highlights an artifact present within the data from the curve of the histogram representing the measured particle size range. This is illustrated in Figure 4, where it may be seen that although the fit is good, there are clear deviations between it and the data. Specifically considering the upper range of particle sizes, the curve fit underestimates the particle concentration at around 600 nm, and overestimates the concentration at around 1000 nm, with the switch occurring between 700 nm and 800 nm. Thus, given the prescribed data analysis methodology, it is likely that a combination between the different concentrations calculated from the smaller size ranges and the coverage factor estimated from the curve fit were responsible for the estimated increase in mass concentrations. For the sake of conceptual consistency, it must be noted here that the current methodology using the maximum size range may be influenced in a similar way to the smaller simulated size ranges, since the entire size range of the challenge particle is not measured. However, the known shape of the particle distribution and the given closeness of the sample curve fits offers reasonable support for the current methodology.
4.3. Influence of the SMPS Coverage Factor
Given that the SMPS was not capable of measuring the full range of particle sizes, the application of a coverage factor was necessary. This stems from the operational characteristics of the instrument and the use of an impactor to prevent particles over the acceptable size range from potentially skewing the data, effectively truncating the original particle size distribution. However, it is not enough to simply curve fit the remainder of the distribution and apply the measured concentration. Since the CPC will measure the concentration of the fractionated particles from the DMA, the total number concentration estimated for the distribution by the instrument is reduced by the removal of the larger fraction of particles. Thus, given that the size distribution of the challenge particles is known, it is logical to correct the underestimated reported concentration. However, it is also worth investigating the possible outcome for a methodology that does not incorporate the coverage factor. Table 1, Methods S1 and S6, illustrate the resulting ratios and representative loading curve slopes calculated with and without the coverage factor correction. As is expected, the ratio and loading curves representing no coverage correction estimate lower mass concentrations, and therefore a lower amount of collected mass by the test stand filter. Furthermore, it is worth noting that the scatter present in the data without the coverage factor is less, implying that its inclusion increases the scatter, although this is likely attributable to the curve fitting procedure. Thus, the impact of the coverage factor and its corresponding concentration correction becomes greater for particle size distributions of which the SMPS and its measurement range cover a smaller fraction. It is worth noting, given the potentially shorter measurement ranges for the SMPS, that this concept would be applicable to those scenarios as well. Furthermore, it is also worth mentioning that this methodology is predicated upon prior knowledge of the particle size distribution, and therefore somewhat limited in its overall application if the shape of the distribution is unknown. However, this may be easily remedied by an initial investigation of the data prior to the analysis.
Upon inspection of Table 1, it may be seen that the average mass concentration given by the prescribed methodology (S1) is approximately 17.5% higher than the baseline measurements. On the other hand, the method which neglects the coverage factor (S6) gives an average mass concentration approximately 1.2% larger than the baseline measurements. Referencing the coverage factor from method S1, it is conspicuous that the coverage factor is in the same relative vicinity as the average overestimation between the SMPS and baseline mass concentrations. However, the authors believe that the closeness of the results derived without using the coverage factor are coincidental, since the SMPS does not automatically correct for the eliminated number of particles from its impactor. Therefore, conceptually, the correction of the particle number concentration offered by the coverage factor is sound, and neglecting it based upon the closeness of the results from estimating the ratios without the correction factor would impart bias upon the methodology.
4.4. Influence of the LAS Curve Fitting
In contrast to the SMPS, the measurable size range of the LAS exceeded the largest particle size and was nearly able to measure the minimum particle size as well. On the surface, this could alleviate the necessity of curve fitting the particle size distribution in order to account for the full range of sizes, although this would neglect the lower end of the distribution. However, since particle mass calculations are dependent upon the cubed diameter, this would likely be a negligible difference and would be overshadowed by errors present within the data acquisition process. Yet, given the available measurement resolution provided by the number of histogram bins, it is worthwhile to investigate the influence that the curve fitting process has on the estimated results. Table 2, methods L1 and L4, illustrate the differences in the calculated ratios using the curve fits versus the histogram data, where it may be seen that the histograms provide significantly higher estimations than the curve fits. It is worth noting that the mass concentrations using the histograms were simply estimated by calculating the volumes associated with each bin and multiplying by the number of recorded particles to yield the overall particle volume associated with that size. Likewise, loading curve slopes derived from representative data also show that the histogram slope is not as steep. This is concerning, given that the utilization of a continuous function to estimate the mass concentration is expected to differ from estimates resulting from a discrete histogram, but not at the observed magnitude. In the interest of determining where the difference originates, it is logical to consider the curve fit itself and how closely it represents the collected data. Figure 6 illustrates a representative LAS histogram and its corresponding curve fit from the data collected in the present work, where the overall closeness of the fit to the data is excellent, except for a few areas towards the upper end of the size range. Comparing a particle with a diameter of 800 nm to that of a particle with a diameter of 500 nm as an example, one may note that the ratio of particle volumes is equal to 4.096, indicating that larger particle is approximately 4 times as massive as the smaller particles. Thus, it is reasonable to attribute the larger mass concentration estimated using the histogram instead of the curve fit to the observed deviation between the two. The methodology in the current work considers the curve fit to be the more accurate method, given the known particle size distribution and the consistency with which recorded LAS samples deviated from the shape of the distribution at the same particle sizes.
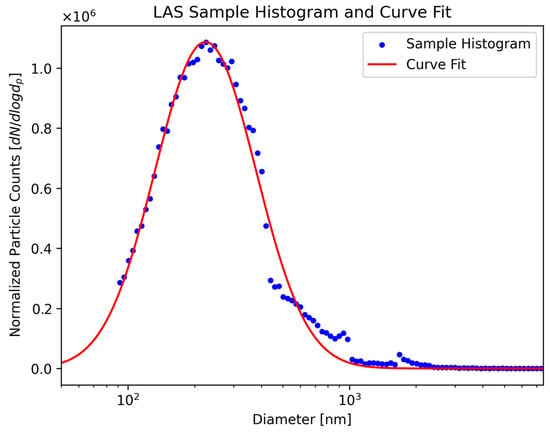
Figure 6.
A representative curve fit of an LAS sample.
The LAS uses two pairs of collection optics to detect the scattered light from the particles, where one pair measures light from smaller particles, and the other from larger particles [16]. This hardware configuration creates four gain stages in the process of converting the signal related to the measured particles, essentially separating the size distribution into four stages. From an inspection of the data in Figure 6, it may be seen that the measured size distribution may be divided into four distinct regions based upon the discontinuity of the lognormal shape. Thus, it is logical to attribute these deviations to the processing of the particle signal, where the overlap between the different collection optics appears to influence the accuracy of the collected data. However, these deviations do not appear significant enough in magnitude to warrant discarding the data. Given the known shape of the particle size distribution for the challenge particle, this supports the utilization of a curve fit for the estimation of the mass concentration, as it is robust against the observed deviations found in the collected data from the instrument.
4.5. Influence of the LAS Sample Period
It is interesting to note that the resulting loading curves derived from LAS data were much smoother than those derived from SMPS data, as may be seen by comparing Figure 5 and Figure 7. This was attributed to the real-time nature of the LAS data acquisition, where particle counts are added to the histogram as they are measured, whereas the SMPS adds the counts sequentially for each bin as it scans across the measurement range. Thus, the LAS appears to provide more consistent data as it can incorporate the time-dependent characteristics of the test stand, namely that the concentration does not seem to be entirely steady with respect to time. The authors attribute this to the nature of the DAG and the selected powder, which can clump and stick to surfaces, resulting in a somewhat inconsistent particle feed rate. An aerosol generator or particle type which may be expected to provide a more consistent feed rate, such as NaCl particles generated using an atomizer or nebulizer, would likely avoid this phenomenon.
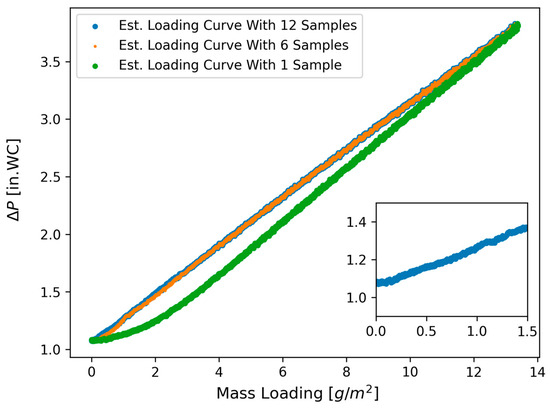
Figure 7.
Loading curves considering different sampling periods for the LAS.
Given that the LAS sampled over a user-defined period, it is worth investigating the effects of the sampling time on the derived data. To define this idea, consider an LAS which collects two samples over a period, . Since the LAS provides real-time data and a high degree of particle counting accuracy, it is reasonable to assume that the sum of the counts attributed to both samples would be equivalent to a single sample taken over a period of twice as long, or .Thus, the benefit of decreasing the number of samples, and therefore the analytical expense, should be considered. For the current work, the impact of this was investigated simply by taking each LAS sample and creating an aggregate representation of the entire test by summing the counts of the corresponding size bins to create an overall distribution. This aggregate distribution was then fit to a curve and followed the same procedure as for the individual samples. Table 2, Methods L1, L2, and L3 shows the estimated ratios for different numbers of considered samples, where it may be noted that the difference between the final results is essentially negligible. This is an expected result, since the same number of particles are being considered regardless of how they are divided. However, the resulting loading curves, shown in Figure 7, illustrate an important difference. The unique curve resulting from the single sample appears to be the consequence of applying what is equivalent to the average mass concentration of all the recorded samples. Thus, the conclusion may be drawn that the difference between the derived loading curves can be attributed to the transient output of the dust generator and therefore the fluctuating particle concentrations within the test stand. However, it is also interesting that the different curves show an overall good agreement toward the end of the test, which is consistent with the results from Table 2. It is logical to attribute this to the fact that the same number of particles were considered in both methods, and therefore the total mass loading and corresponding pressure drop at the end of the test should be very similar. Nonetheless, the reader should note that the extrapolation of these curves to higher mass loadings from the present data would cause deviations since the slopes of the curves are not the same. However, referencing the corresponding average and median slopes from Table 2 appears misleading in terms of this interpretation when compared against the observed slopes in Figure 7. This is attributed to the scatter present within the data and its influence on the numerical derivative used to calculate the values of the slopes.
In conclusion to this section, it is worth addressing the shape of the curves derived from the single aggregate sample and multiple sample methods. The curve for the single aggregate sample method does portray the ideal shape of a loading curve, with seemingly clear depth, transition, and loading regimes. It may be seen from Figure 7 that the loading regimes using the prescribed method do exist, but the transition from depth loading to surface loading was very rapid with respect to the collected mass. This is reasonable for HEPA media at the conditions and velocities used in this work, and is supported by the work of Novick et al. [3]. Thus, the rapid and almost imperceptible transition from depth loading to surface loading is not a cause for concern regarding the validity of the proposed methodology. Furthermore, the difference in the shape of the curve derived from the single aggregate sample may be attributed to incorporating time-dependent influences into the loading curves as a confounding factor. This is reasonable, as the mass concentration does not change with respect to time for the single aggregate sample, and therefore would behave as if considering an average mass concentration for each time step. Therefore, utilizing a single sample to cover the entirety of the filter loading process for a concentration that changes with respect to time would skew the derived data with time-dependent phenomena.
4.6. Impact towards the Development and Validation of Filtration Loading Models
Accounting for the previous sections and the potential skewing of reduced data from the analysis methodologies, it is important to acknowledge the impact that this may have on the creation and validation of filtration loading models. A simple way to approach this is by considering Darcy’s Law, given in Equation (11).
where represents the pressure drop, represents the air viscosity, L represents the media thickness, A represents the filtration area, and represents the permeability. From inspection, it may be seen that the pressure drop is inversely proportional to the permeability, which will decrease as more particle mass is deposited onto a filter due to the increase in induced drag. For the data corresponding to tests S1 and S6, the slope of the loading curves at each data point yield average and media values of and , respectively, for the loading curve with the applied CF, and and , respectively, for the curve without the applied CF. These results represent a difference of approximately 15% between the averages, and approximately 14% between the medians. Clearly, the results ascertained from the different methodologies yield tangibly different outcomes regarding the slope of the curves. One may notice that these do not directly represent permeability as defined by Darcy’s Law. However, they may be interpreted through the definition of permeability nonetheless as they are conceptually encompassed by it, where the permeability is typically a function of the independent variables, such as the collected mass, and the resulting dependent variables. From the slope of the loading curves, it is inferred that the permeability is decreasing and that a difference in the slopes will directly result in a difference in the variables comprising the permeabilities. Thus, the difference between values derived from data using either methodology would not be negligible. Therefore, care must be taken when considering the analysis methodologies used and the implications involved in their application to filtration loading model development and validation.
5. Conclusions
The purpose of this work was to propose an experimental framework and analysis methodologies to address potential errors and their impacts in the application of filtration modeling. Given the intended and direct application of the present work, these impacts may cause serious differences in models developed and validated using the different instrument configurations and analysis methodologies presented within this work. This is problematic in relation to the development and publication of reproduceable results, as each of the discussed configurations and methodologies can result in processes, data, and derived values that may deviate from study to study. This work focused on the application of the collected data from two common aerosol instruments and data analysis to contribute to the development and validation of aerosol filtration loading models. However, this should not imply that the results should be constrained in the scope of their potential application to filter loading analysis alone, as they apply to any work seeking to measure the shape of particle size distribution and concentration of airborne particles.
Considering the SMPS data collection and analysis methodology, several specific factors were investigated. The dynamic shape factor of the particles was identified as heavily influential on the estimated results, and therefore its selection should be carefully considered. Given that the maximum particle size the SMPS was capable of measuring did not fully encapsulate the particle size distribution, a coverage factor was used in order to correct the reported particle concentration by calculating the fraction of the measured distribution. Furthermore, the configuration of the SMPS hardware and flow rate determined the measurable size range, which was estimated to influence the resulting mass concentration yielded from the analysis. This was attributed to confounding factors inherent to the curve fitting process and the calculation of the nominal total particle concentrations, which decreased with a decreasing considered size range. Each of these concepts influenced the estimated mass concentration resulting from analysis of the SMPS data, and therefore would influence work related to loading models based upon it.
The prescribed LAS data collection and analysis methodology was similar to that of the SMPS but contained differences which were influential. Unlike the SMPS, the LAS is a true real-time instrument, which implies that particle measurements are recorded regardless of the sampling period. However, the impact of considering a single sample versus multiple samples suggested that the loss of time-variant information resulted in the implicit incorporation of the transient change in particle concentration within the test stand. Thus, a confounding factor would be introduced if the data were to be considered on a mass basis instead of a time basis. Also, the application of curve fitting process to the LAS data was investigated, where it was noted that its incorporation yielded a lower mass concentration estimate than simply calculating the mass concentration from the instrument histogram. This was attributed to the instrument’s hardware and signal processing, which appeared to cause fluctuations in measurements, resulting in the overestimation of the number of larger particles and therefore an overestimation of the mass concentration. However, given the known size distribution of the particles, this did not represent a catastrophic result, as the curve fits adequately addressed this and provided a reasonable estimate.
Considering the results from the investigation of the two instruments and their associated data analysis methodologies, their influence in the development and validation of filtration loading models should not be neglected. Using Darcy’s Law and the overall filter permeability as a metric, the present study strongly inferred that a significant difference in the final calculated mass concentration results stemmed from the different methodologies, and therefore may potentially cause significant differences in estimated filter loading curves. This in itself is not notable given the direct relationship between the aerosol mass concentration and the mass a filter is expected to collect. However, given the reasonable nature of the different methodologies on the surface, it is likely that their incorporation would fossilize confounding factors into reduced datasets used to develop and validate filtration models, impacting reproducibility and overall accuracy and application.
Overall, the results from both sets of tests indicate that each instrument yielded systematically higher mass concentration estimates than the corresponding results from the mass collection filters. Thus, the authors propose that, for future tests with the specific setup and instrument configurations included within the present work, their results may be corrected by the average ratio calculated between the estimated concentrations from the instruments and the collection filter. It is reasonable to assert that the corrected estimates are likely closer to the actual mass concentration present within the test stand than an uncorrected estimate. Furthermore, it is important to note that each unique test stand apparatus and aerosol measurement instrument should undergo a similar analysis to that presented in this work as opposed to utilizing the included results. This is conceptually consistent with calibrating each instrument separately and addressing the individual quirks and facets of the instruments and test stands that are known to be unique for each experimental setup.
Author Contributions
Conceptualization G.B., I.B. and H.C.; Investigation and Formal Analysis G.B.; Original draft G.B.; Content review and editing G.B., A.K., I.B. and H.C.; Project Oversight A.K. and H.C.; Funding A.K. and H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the U.S. Department of Energy Office of Environmental Management under Scope of Work Number: G-SOW-A-02284.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author due to permission requirements from the U.S. Department of Energy.
Acknowledgments
The authors would like to acknowledge the contributions made by Ethan Schuetzle and Will McKelvey in support of this work.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that have influenced the work reported in this paper.
Disclaimer
The corresponding author contributed to this work in a personal capacity. This work was not funded or endorsed by the U.S. Army Engineer Research and Development Center (ERDC). Any opinions, findings, conclusions, or recommendations expressed herein do not necessarily reflect the views of ERDC.
Nomenclature
| A | Filtration Area [m2] |
| C | Particle Number Concentration [m−3] |
| CF | Coverage Factor [dimensionless] |
| CCF | Corrected Particle Number Concentration [m−3] |
| Cc | Cunningham correction factor [dimensionless] |
| Cm | Particle Mass Concentration [kg m−3] |
| Average Particle Mass Concentration [kg m−3] | |
| C0 | Original Sample Number Concentration [m−3] |
| counts | Number of Particles Per Bin [dimensionless] |
| DFtotal | Total Dilution Factor [dimensionless] |
| DF20 | 20:1 Dilution Factor [dimensionless] |
| DF100 | 100:1 Dilution Factor [dimensionless] |
| dee | Electrical Mobility Equivalent Diameter [m] |
| dmax | Maximum Measured Diameter [m] |
| dp | Particle Diameter [m] |
| dV | Volumetric Equivalent Diameter [m] |
| f | Particle Size Distribution [dimensionless] |
| j | Number of Measurements [dimensionless] |
| L | Thickness [m] |
| m | Number of Histogram bins [dimensionless] |
| n | Number of Collected Samples [dimensionless] |
| tsample | Sampling Time [s] |
| Volumetric Flow Rate [m3 s−1] | |
| Wpre | Filter Pre-Weight [kg] |
| Wpost | Filter Post-Weight [kg] |
| χ | Dynamic Shape Factor [dimensionless] |
| ∆P | Airflow Resistance [Pa] |
| κ | Permeability [dimensionless] |
| µ | Viscosity [Pa s] |
| µg | Geometric Mean Diameter [m] |
| σg | Geometric standard deviation [dimensionless] |
References
- Bergman, W. HEPA Filter Particle Loading; International Society for Nuclear Air Treatment Technologies: Cincinnati, OH, USA, 2006. [Google Scholar]
- Davies, C.N. The Separation of Airborne Dust and Particles. Proc. Inst. Mech. Eng. Part B Manag. Eng. Manuf. 1953, 1, 185–213. [Google Scholar] [CrossRef]
- Novick, V.J.; Monson, P.R.; Ellison, P.E. The Effect of Solid Particle Mass Loading on the Pressure Drop of HEPA Filters. J. Aerosol Sci. 1992, 23, 657–665. [Google Scholar] [CrossRef]
- Thomas, D.; Penicot, P.; Contal, P.; Leclerc, D.; Vendel, J. Clogging of Fibrous Filters by Solid Aerosol Particles Experimental and Modelling Study. Chem. Eng. Sci. 2001, 56, 3549–3561. [Google Scholar] [CrossRef]
- Berry, G.; Beckman, I.; Cho, H. A Comprehensive Review of Particle Loading Models of Fibrous Air Filters. J. Aerosol Sci. 2023, 167, 106078. [Google Scholar] [CrossRef]
- ASME. ASME AG-1-2017 Code on Nuclear Air and Gas Treatment; The American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Bémer, D.; Callé, S. Evolution of the Efficiency and Pressure Drop of a Filter Media with Loading. Aerosol Sci. Technol. 2000, 33, 427–439. [Google Scholar] [CrossRef]
- Kim, S.C.; Wang, J.; Shin, W.G.; Scheckman, J.H.; Pui, D.Y.H. Structural Properties and Filter Loading Characteristics of Soot Agglomerates. Aerosol Sci. Technol. 2009, 43, 1033–1041. [Google Scholar] [CrossRef]
- Yanosky, J.D.; Williams, P.L.; MacIntosh, D.L. A Comparison of Two Direct-Reading Aerosol Monitors with the Federal Reference Method for PM2.5 in Indoor Air. Atmos. Environ. 2002, 36, 107–113. [Google Scholar] [CrossRef]
- TSI Incorporated. Model 3936 Scanning Mobility Particle SizerTM (SMPSTM) Spectrometer Operation and Service Manual; TSI Incorporated: Shoreview, MN, USA, 2010. [Google Scholar]
- Khlystov, A.; Stanier, C.; Pandis, S.N. An Algorithm for Combining Electrical Mobility and Aerodynamic Size Distributions Data When Measuring Ambient Aerosol Special Issue of Aerosol Science and Technology on Findings from the Fine Particulate Matter Supersites Program. Aerosol Sci. Technol. 2004, 38, 229–238. [Google Scholar] [CrossRef]
- Liu, P.S.K.; Deshler, T. Causes of Concentration Differences Between a Scanning Mobility Particle Sizer and a Condensation Particle Counter. Aerosol Sci. Technol. 2003, 37, 916–923. [Google Scholar] [CrossRef]
- Van Gulijk, C.; Marijnissen, J.C.M.; Makkee, M.; Moulijn, J.A.; Schmidt-Ott, A. Measuring Diesel Soot with a Scanning Mobility Particle Sizer and an Electrical Low-Pressure Impactor: Performance Assessment with a Model for Fractal-like Agglomerates. J. Aerosol Sci. 2004, 35, 633–655. [Google Scholar] [CrossRef]
- Flagan, R.C. Electrical Techniques. In Aerosol Measurement: Principles, Techniques, and Applications; Wiley-InterScience, Inc.: Hoboken, NJ, USA, 2001; ISBN 0-471-35636-0. [Google Scholar]
- Rogak, S.N.; Flagan, R.C. Bipolar Diffusion Charging of Spheres and Agglomerate Aerosol Particles. J. Aerosol Sci. 1992, 23, 693–710. [Google Scholar] [CrossRef]
- TSI Incorporated. Laser Aerosol Spectrometer Model 3340 Operation and Service Manual; TSI Incorporated: Shoreview, MN, USA, 2014. [Google Scholar]
- Pratte, P.; Cosandey, S.; Goujon-Ginglinger, C. A Scattering Methodology for Droplet Sizing of E-Cigarette Aerosols. Inhal. Toxicol. 2016, 28, 537–545. [Google Scholar] [CrossRef] [PubMed]
- Gebhart, J. 15-Optical Direct-Reading Techniques: Light Intensity Systems. In Aerosol Measurement: Principles, Techniques, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001; pp. 419–454. [Google Scholar]
- Souza, A.D.V.; Arruda, C.C.; Fernandes, L.; Antunes, M.L.P.; Kiyohara, P.K.; Salomão, R. Characterization of Aluminum Hydroxide (Al(OH)3) for Use as a Porogenic Agent in Castable Ceramics. J. Eur. Ceram. Soc. 2015, 35, 803–812. [Google Scholar] [CrossRef]
- Endo, Y.; Chen, D.-R.; Pui, D.Y.H. Effects of Particle Polydispersity and Shape Factor during Dust Cake Loading on Air Filters. Powder Technol. 1998, 98, 241–249. [Google Scholar] [CrossRef]
- Cheng, Y.-S.; Yeh, H.-C.; Allen, M.D. Dynamic Shape Factor of a Plate-Like Particle. Aerosol Sci. Technol. 1988, 8, 109–123. [Google Scholar] [CrossRef]
- Wefers, K.; Chanakya, M. Oxides and Hydroxides of Aluminum; Alcoa Laboratories: Pittsburgh, PA, USA, 1987; p. 100. [Google Scholar]
- Marx, E.; Mulholland, G.W. Size and Refractive Index Determination of Single Polystyrene Spheres. J. Res. Natl. Bur. Stan. 1983, 88, 321. [Google Scholar] [CrossRef] [PubMed]
- Hinds, W.C. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999; ISBN 978-0-471-19410-1. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).