Comparison of Cold Pool Characteristics of Two Distinct Gust Fronts over Bohai Sea Bay in China
Abstract
1. Introduction
- (1)
- Why do GF gales occur in some environments but not in others? What environmental parameters determine the potential for GF gales?
- (2)
- What is the relationship between strength in GFs and cold pools? What is the potential role of cold pools in the evolution of GFs?
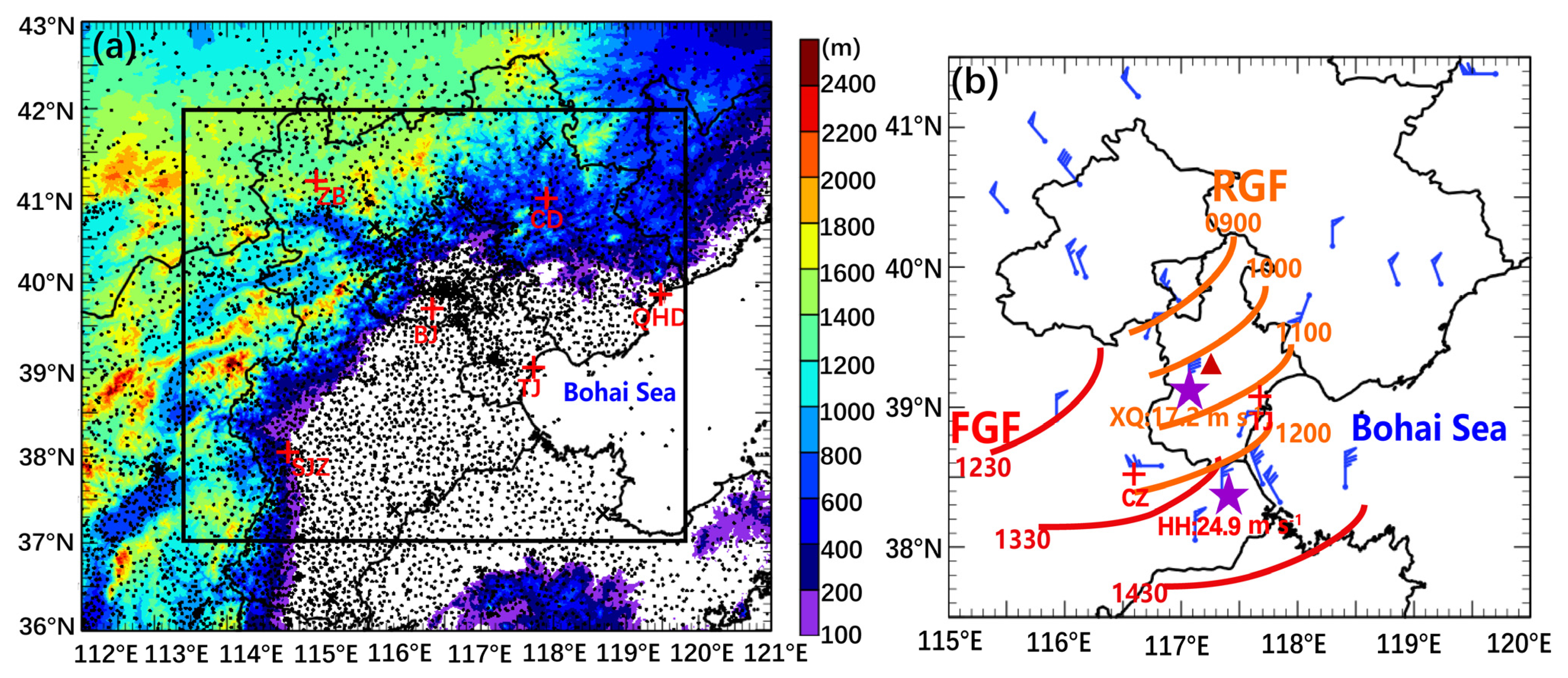
2. Data and Methods
2.1. Reanalyzed and Observation Data
2.2. Description of VDRAS
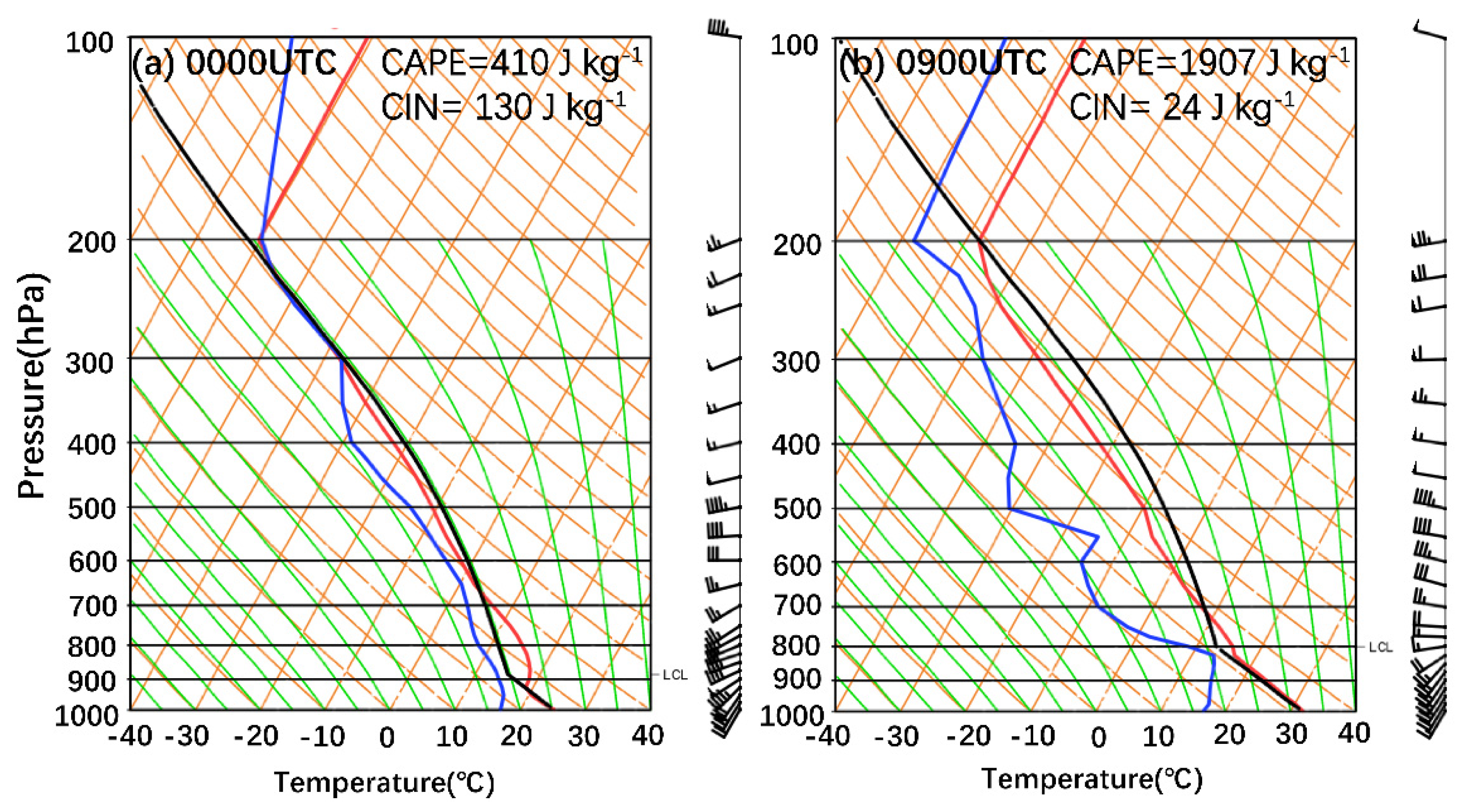
3. Synoptic Conditions and Environment Conditions
4. Comparison of Evolution Characteristics of Cold Pools and GFs
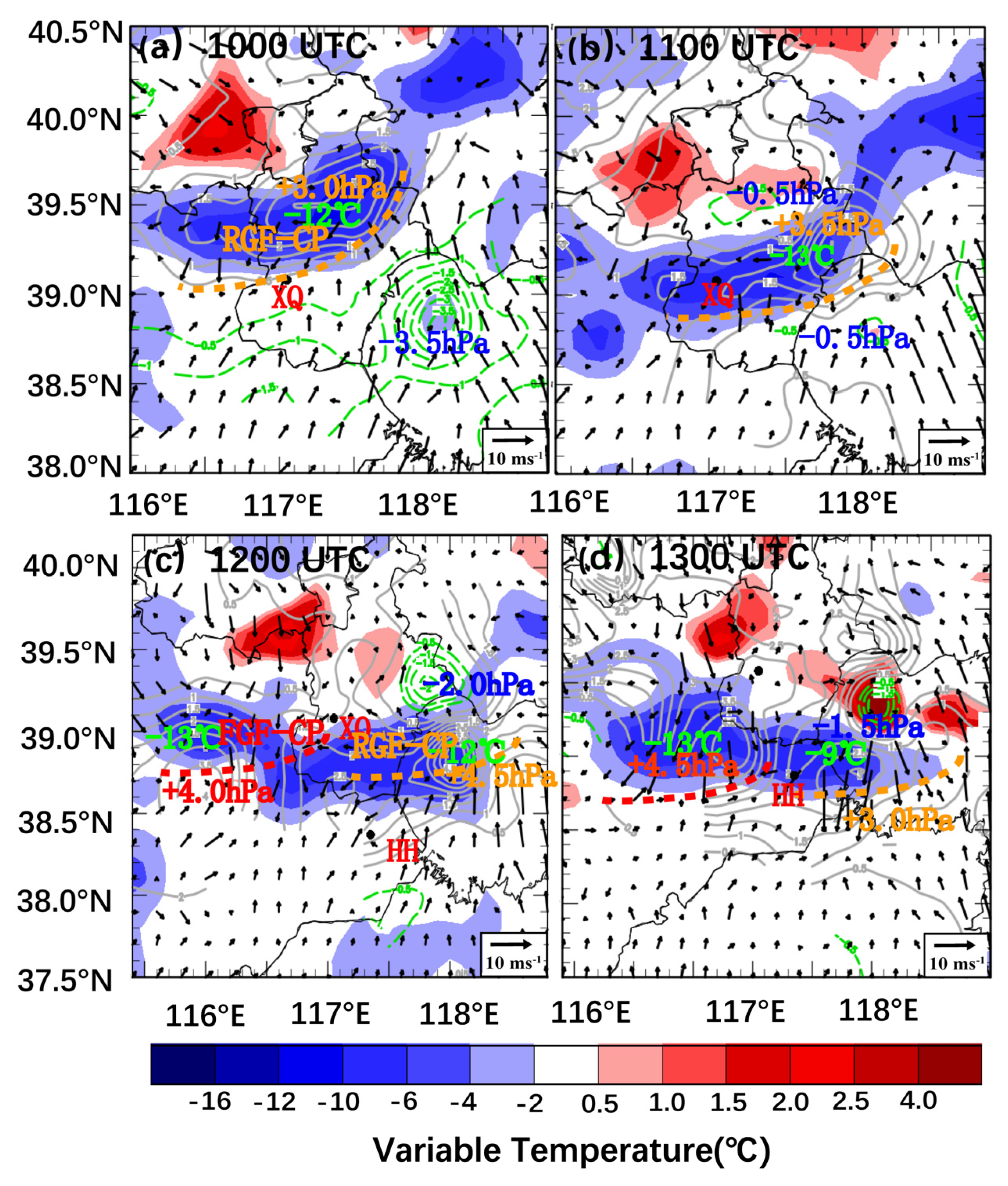
4.1. Comparison of Surface Thermal Fields
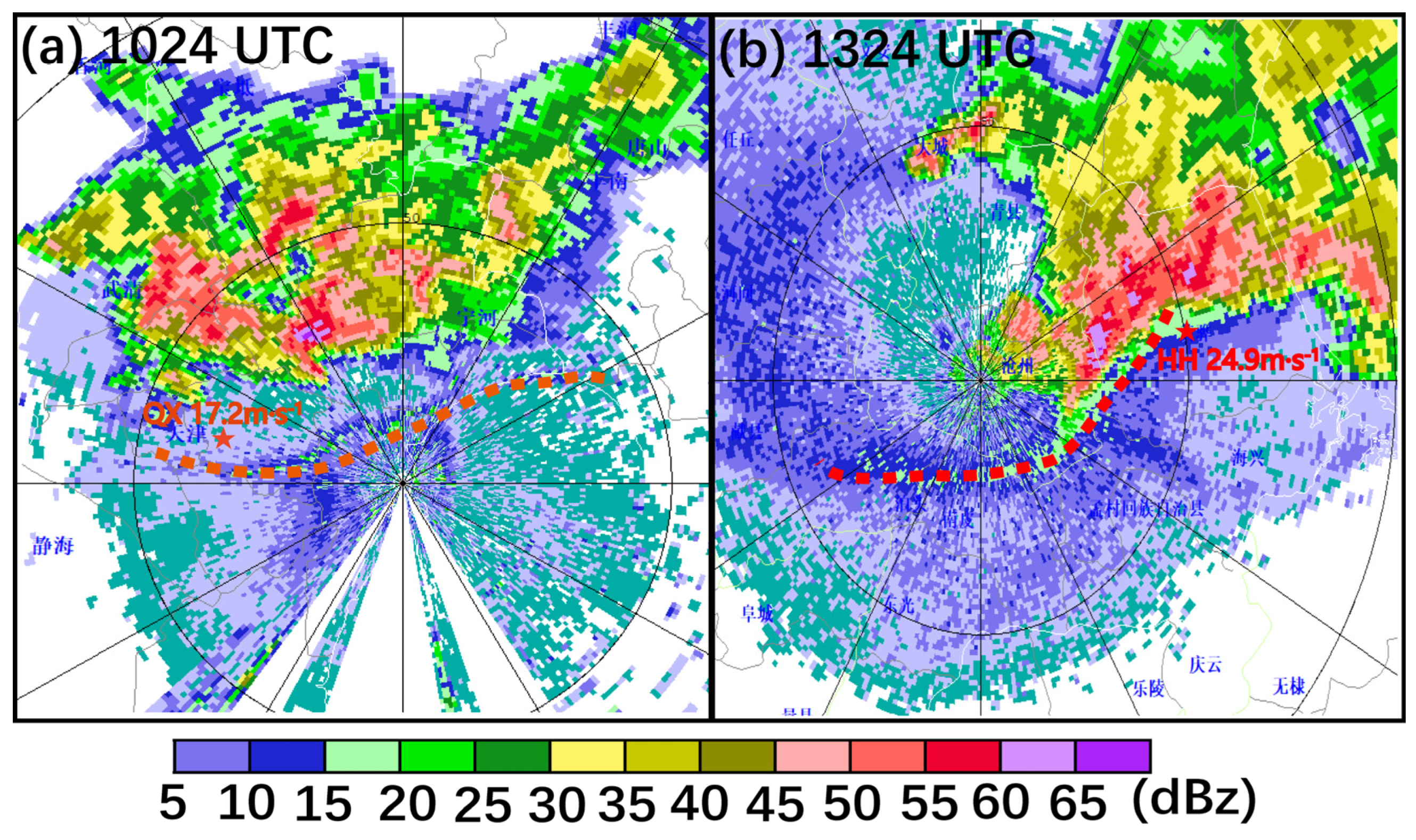
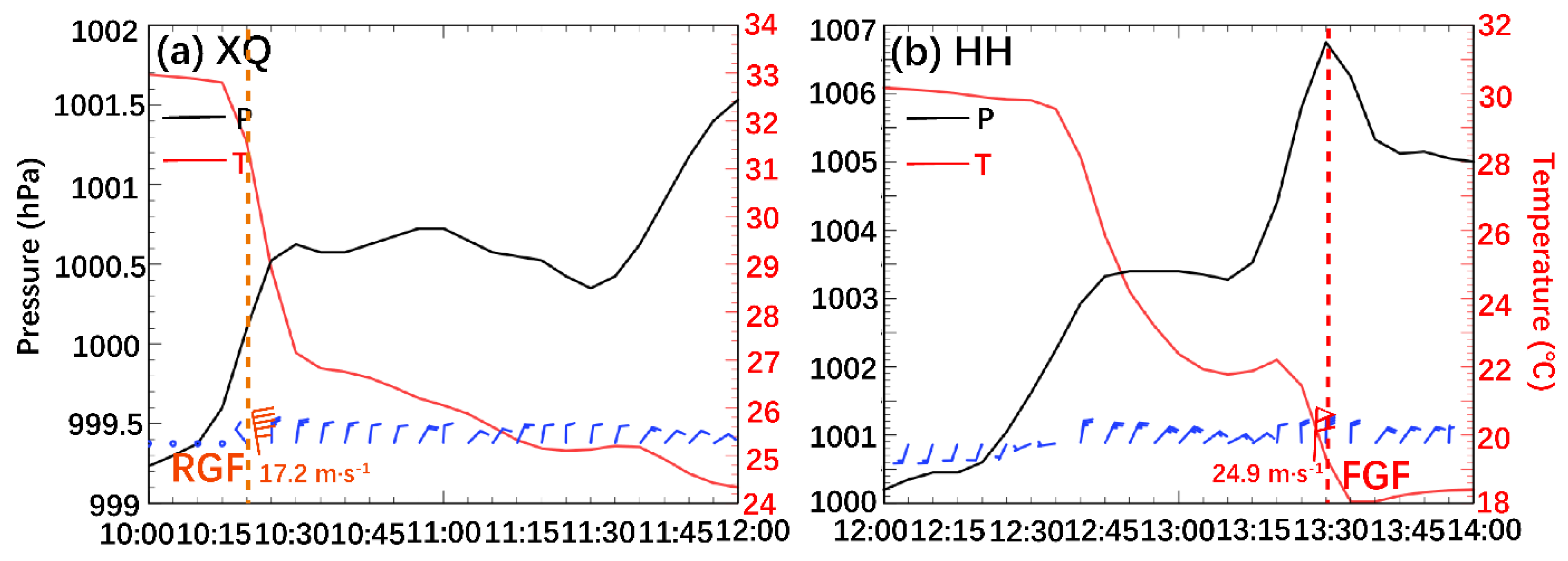
4.2. Comparison of Evolution Characteristics of Cold Pool GFs
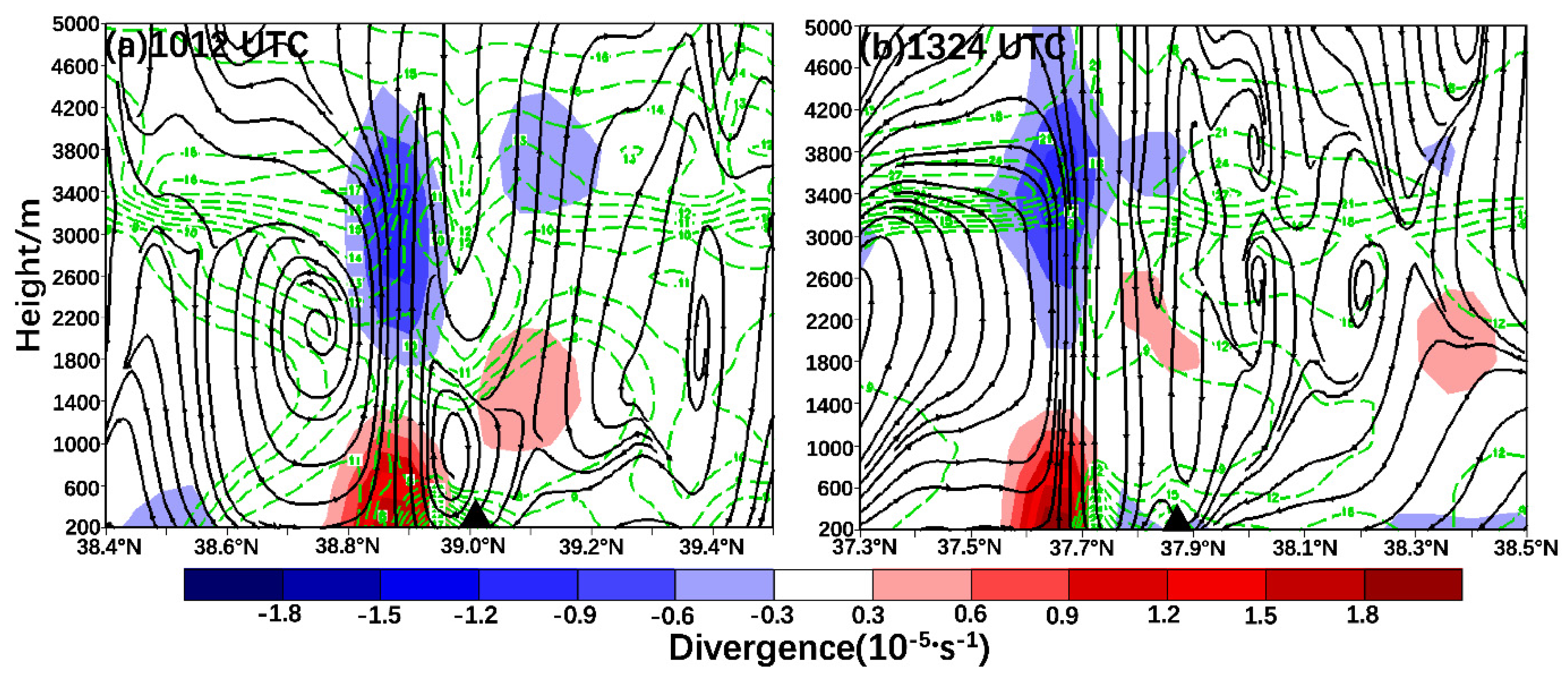
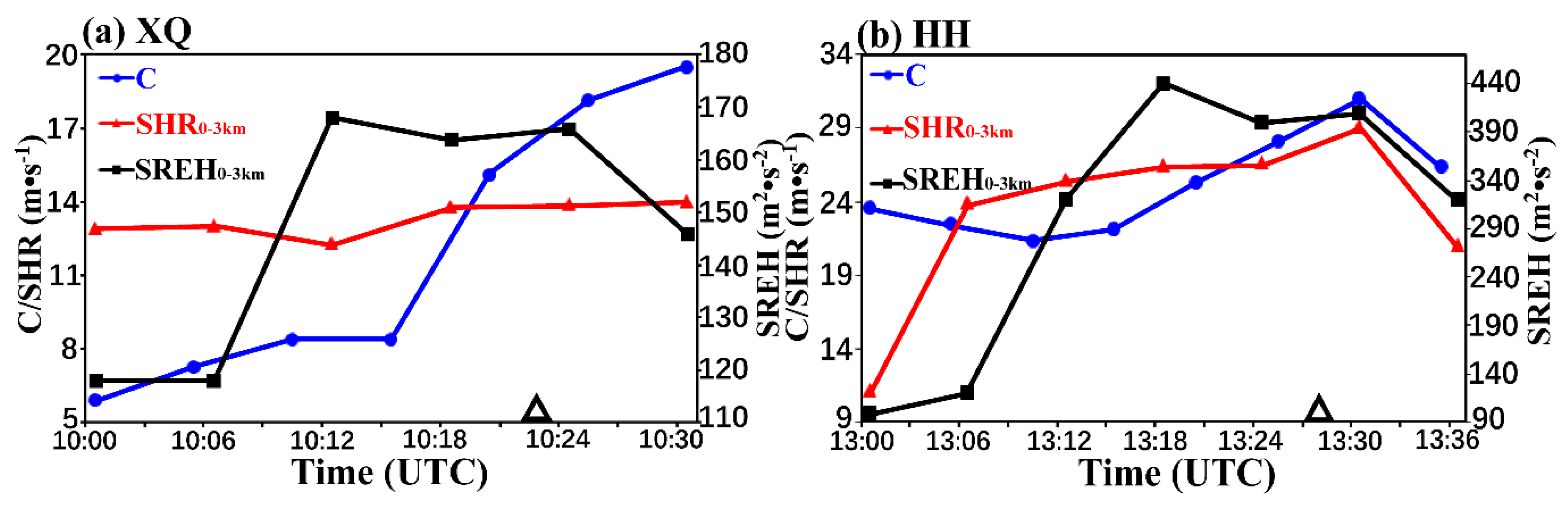
5. Implications of Cold Pools on the GFs
5.1. Intensity of GFs
5.2. Intensity of Cold Pools
5.3. Depth of Cold Pools
5.4. Propagation Speed of Cold Pools
5.5. Implications of Cold Pools on the GFs
6. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GFs | Gust fronts |
| RGF | Rearward gust front |
| FGF | Frontward gust front |
| QLCS | Quasi-linear convective system |
| BE | Bow echo |
| CCs | Convective cells |
| MVs | Meso-γ-scale vortices |
| VDRAS | Variational Doppler Radar Data Assimilation System |
| 4DVAR | Four-dimensional variational data assimilation |
| RKW88 | Rotunno–Klemp–Weisman [26] |
| KHI | Kelvin–Helmholtz instability |
| IG | Internal gravity |
| LECP | Leading edge of the cold pool |
| BSB | Bohai Sea Bay |
| CI | Convection initiation |
| MCS | Mesoscale convection system |
| WRF | Weather Research and Forecast |
| AWS | Automatic weather station |
| AGL | Above ground level |
| CINRADs | China New-Generation Radars |
| CAPE | Convective available potential energy |
| CIN | Convective inhibition |
| LCL | Lifting condensation level |
| SREH | Storm-relative environmental helicity |
References
- Wilson, J.W.; Roberts, R.D. Lake Victoria thunderstorms: Radar-observed initiation and storm evolution modes. Mon. Weather Rev. 2022, 150, 2485–2502. [Google Scholar] [CrossRef]
- Ma, R.Y.; Sun, J.H.; Yang, X.L. A 7-yr climatology of the initiation, decay, and morphology of severe convective storms during the warm season over North China. Mon. Weather Rev. 2021, 149, 2599–2612. [Google Scholar] [CrossRef]
- Hurlbut, M.; Cohen, A. Environments of northeast U.S. severe thunderstorm events from 1999 to 2009. Weather Forecast. 2014, 29, 3–22. [Google Scholar] [CrossRef][Green Version]
- Richter, H.; Peter, J.; Collis, S. Analysis of a destructive wind storm on 16 November 2008 in Brisbane, Australia. Mon. Weather Rev. 2014, 142, 3038–3060. [Google Scholar] [CrossRef]
- Fritsch, J.M.; Vislocky, R.L. Enhanced depiction of surface weather features. Bull. Am. Meteorol. Soc. 1996, 77, 491–506. [Google Scholar] [CrossRef]
- Bai, L.Q.; Meng, Z.Y.; Huang, Y.; Zhang, Y.; Niu, S.; Su, T. Convection initiation resulting from the interaction between a quasi-stationary dryline and intersecting gust fronts: A case study. J. Geophys. Res. Atmos. 2019, 124, 2379–2396. [Google Scholar] [CrossRef]
- Cui, X.Y.; Chen, M.X.; Qin, R.; Li, C.; Han, L. The roles of surface convergence line and upper-level forcing on convection initiation ahead of a gust front: A case study. J. Geophys. Res. Atmos. 2023, 128, e2022JD036921. [Google Scholar] [CrossRef]
- Knupp, K.R. Observational analysis of a gust front to bore to solitary wave transition within an evolving nocturnal boundary layer. J. Atmos. Sci. 2006, 63, 2016–2035. [Google Scholar] [CrossRef]
- Luo, X.; Xue, M.; Fei, J.F. Simulation and analysis of the initiation of a squall line within a Meiyu front system in East China. Atmosphere 2018, 9, 183. [Google Scholar] [CrossRef]
- Waniha, P.F.; Roberts, R.D.; Wilson, J.W.; Kijazi, A.; Katole, B. Dual-polarization radar observations of deep convection over Lake Victoria Basin in East Afica. Atmosphere 2019, 10, 706. [Google Scholar] [CrossRef]
- Marsham, J.H.; Parker, D.J. Secondary initiation of multiple bands of cumulonimbus over southern Britain. II: Dynamics of secondary initiation. Q. J. R. Meteorol. Soc. 2006, 132, 1053–1072. [Google Scholar] [CrossRef]
- Zheng, J.; Abulikemu, A.; Wang, Y.; Kong, M.; Liu, Y. Convection initiation associated with the merger of an immature sea-breeze front and a gust front in Bohai Bay Region, North China: A case study. Atmosphere 2022, 13, 750. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Y.; Lin, X. Mesoscale observational analysis of isolated convection associated with the interaction of the sea breeze front and the gust front in the context of the urban heat humid island effect. Atmosphere 2022, 13, 603. [Google Scholar] [CrossRef]
- Friedrich, K.; Kingsmill, D.E.; Young, C.R. Misocyclone characteristics along Florida gust fronts during CaPE. Mon. Weather Rev. 2005, 133, 3345–3367. [Google Scholar] [CrossRef]
- Wakimoto, R.M.; Murphey, H.V.; Davis, C.A.; Atkins, N.T. High winds generated by bow echoes. Part II: The relationship between the mesovortices and damaging straight-line winds. Mon. Weather Rev. 2006, 134, 2813–2829. [Google Scholar] [CrossRef]
- Xu, X.; Xue, M.; Wang, Y. Mesovortices within the 8 May 2009 bow echo over the central United States: Analyses of the characteristics and evolution based on Doppler radar observations and a high-resolution model simulation. Mon. Weather Rev. 2015, 143, 2266–2290. [Google Scholar] [CrossRef]
- Goff, R.C. Vertical structure of thunderstorm outflows. Mon. Weather Rev. 1976, 104, 1429–1440. Available online: https://journals.ametsoc.org/doi/pdf/10.1175/1520-0493%281976%29104%3C1429%3AVSOTO%3E2.0.CO%3B2 (accessed on 11 February 2024). [CrossRef]
- Luchetti, N.T.; Friedrich, K.; Rodell, C.E.; Lundquist, J.K. Characterizing thunderstorm gust fronts near complex terrain. Mon. Weather Rev. 2020, 148, 3267–3286. [Google Scholar] [CrossRef]
- Luchetti, N.T.; Friedrich, K.; Rodell, C.E. Evaluating thunderstorm gust fronts in New Mexico and Arizona. Mon. Weather Rev. 2020, 148, 4943–4956. [Google Scholar] [CrossRef]
- Wakimoto, R.M. The life cycle of thunderstorm gust fronts as viewed with Doppler radar and rawinsonde data. Mon. Weather Rev. 1982, 110, 1060–1082. [Google Scholar] [CrossRef]
- Klingle, D.L.; Smith, D.R.; Wolfson, M.M. Gust front characteristics as detected by Doppler radar. Mon. Weather Rev. 1987, 115, 905–918. [Google Scholar] [CrossRef]
- Harrison, S.J.; Mecikalski, J.R.; Knupp, K.R. Analysis of outflow boundary collisions in north-central Alabama. Weather Forecast. 2009, 24, 1680–1690. [Google Scholar] [CrossRef]
- Karan, H.; Knupp, K. Radar and profiler analysis of colliding boundaries: A case study. Mon. Weather Rev. 2009, 137, 2203–2222. [Google Scholar] [CrossRef]
- May, P.T. Thermodynamic and vertical velocity structure of two gust fronts observed with a wind Profile/RASS during MCTEX. Mon. Weather Rev. 1999, 127, 1796–1807. [Google Scholar] [CrossRef]
- Cotton, W.R.; Bryan, G.; Van den Heever, S.C. Storm and Cloud Dynamics; Academic Press: Cambridge, MA, USA, 2011; Volume 99, 820p. [Google Scholar]
- Martner, B.E. Vertical velocities in a thunderstorm gust front and outflow. J. Appl. Meteorol. 1997, 36, 615–622. [Google Scholar] [CrossRef]
- Thorpe, A.J.; Miller, M.J.; Moncrieff, M.W. Two-dimensional convection in non-constant shear: A model of midlatitude squall lines. Q. J. R. Meteorol. Soc. 1982, 108, 739–762. [Google Scholar] [CrossRef]
- Rotunno, R.; Klemp, J.B.; Weisman, M.L. A theory for strong, long-lived squall lines. J. Atmos. Sci. 1988, 45, 463–485. [Google Scholar] [CrossRef]
- Weisman, M.L.; Klemp, J.B.; Rotunno, R. Structure and evolution of numerically simulated squall lines. J. Atmos. Sci. 1988, 45, 1900–2013. [Google Scholar] [CrossRef]
- Weisman, M.L.; Rotunno, R. The use of vertical wind shear versus helicity in interpreting supercell dynamics. J. Atmos. Sci. 2000, 57, 1452–1472. [Google Scholar] [CrossRef]
- Weckwerth, T.M.; Wakimoto, R.M. The initiation and organization of convective cells atop a cold-air outflow boundary. Mon. Weather Rev. 1992, 120, 2169–2187. [Google Scholar] [CrossRef]
- Kingsmill, D.E. Convection initiation associated with a sea-breeze front, a gust front, and their collision. Mon. Weather Rev. 1995, 123, 2913–2933. [Google Scholar] [CrossRef]
- Weisman, M.L.; Trapp, R.J. Low-level mesovortices within squall lines and bow echoes. Part I: Overview and dependence on environmental shear. Mon. Weather Rev. 2003, 131, 2779–2803. [Google Scholar] [CrossRef][Green Version]
- Trapp, R.J.; Weisman, M.L. Low-level mesovortices within squall lines and bow echoes. Part II: Their genesis and implications. Mon. Weather Rev. 2003, 131, 2804–2823. [Google Scholar] [CrossRef]
- Atkins, N.T.; Laurent, M.S. Bow echo mesovortices. Part I: Processes that influence their damaging potential. Mon. Weather Rev. 2009, 137, 1497–1513. [Google Scholar] [CrossRef]
- Kirsch, B.; Ament, F.; Hohenegger, C. Convective cold pools in long-term boundary layer mast observations. Mon. Weather Rev. 2021, 149, 811–820. [Google Scholar] [CrossRef]
- Provod, M.; Marsham, J.H.; Parker, D.J.; Birch, C.E. A characterization of cold pools in the West African Sahel. Mon. Weather Rev. 2016, 144, 1923–1934. [Google Scholar] [CrossRef]
- Hiris, Z.A.; Gallus, W.A., Jr. On the relationship of cold pool and bulk shear magnitudes on upscale convective growth in the Great Plains of the United States. Atmosphere 2021, 12, 1019. [Google Scholar] [CrossRef]
- Parker, M.D. Self-organization and maintenance of simulated nocturnal convective systems from PECAN. Mon. Weather Rev. 2021, 149, 999–1022. [Google Scholar] [CrossRef]
- Squitieri, B.J.; Gallus, W.A. On the changes in convection-allowing WRF forecasts of MCS evolution due to decreases in model horizontal and vertical grid spacing. Part I: Changes in cold pool evolution. Weather Forecast. 2022, 37, 1903–1923. [Google Scholar] [CrossRef]
- Xue, M. Density currents in shear flows: Effects of rigid lid and cold-pool internal circulation, and application to squall line dynamics. Q. J. R. Meteorol. Soc. 2002, 128, 47–73. [Google Scholar] [CrossRef]
- Borque, P.; Nesbitt, S.W.; Trapp, R.J.; Trapp, S.L.; Que, M. Observational study of the thermodynamics and morphological characteristics of a midlatitude continental cold pool event. Mon. Weather Rev. 2020, 148, 719–737. [Google Scholar] [CrossRef]
- Meyer, B.; Haerter, J.O. Mechanical forcing of convection by cold pools: Collisions and energy scaling. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002281. [Google Scholar] [CrossRef]
- Hirt, M.; George, C.C.; Sophia, A.K.S.; Julien, S.; Rieke, H. Cold-pool-driven convective initiation: Using causal graph analysis to determine what convection-permitting models are missing. Q. J. R. Meteorol. Soc. 2020, 146, 2205–2227. [Google Scholar] [CrossRef]
- Abulikemu, A.; Wang, Y.; Gao, R.; Wang, Y.; Xu, X. A numerical study of convection initiation associated with a gust front in Bohai Bay region, North China. J. Geophys. Res. Atmos. 2019, 124, 13843–13860. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N.A. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments. J. Atmos. Sci. 1997, 54, 1642–1661. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N.A. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part II: Retrieval experiments of an observed Florida convective storm. J. Atmos. Sci. 1998, 55, 835–852. [Google Scholar] [CrossRef]
- Friedrich, K.; Kalina, E.A.; Aikins, J.; Gochis, D.; Rasmussen, R. Precipitation and cloud structures of intense rain during the 2013 Great Colorado Flood. J. Hydrometeorol. 2015, 17, 22–27. [Google Scholar] [CrossRef]
- Tai, S.L.; Liou, Y.C.; Sun, J.; Chang, S.F. The development of a terrain-resolving scheme for the forward model and its adjoint in the four-dimensional Variational Doppler Radar Analysis System (VDRAS). Mon. Weather Rev. 2016, 145, 289–306. [Google Scholar] [CrossRef]
- Crook, A.; Sun, J. Analysis and forecasting of the low-level wind during the Sydney 2000 Forecast Demonstration Project. Weather Forecast. 2004, 19, 151–167. [Google Scholar] [CrossRef]
- Sun, J.; Chen, M.; Wang, Y. A frequent-updating analysis system based on radar, surface, and mesoscale model data for the Beijing 2008 forecast demonstration project. Weather Forecast. 2010, 25, 1715–1735. [Google Scholar] [CrossRef]
- Sun, J. Convective-scale assimilation for radar data: Progress and challenges. Q. J. R. Meteorol. Soc. 2006, 131, 3439–3463. [Google Scholar] [CrossRef]
- Chen, M.X.; Xiao, X.; Gao, F.; Lei, L.; Wang, Y.C.; Sun, J.Z. A case study and batch verification on high resolution numerical simulations of severe convective events using an analysis system based on rapid-refresh 4-D variational radar data assimilation. Acta Meteorol. Sin. 2016, 74, 421–441. (In Chinese) [Google Scholar] [CrossRef]
- Xiao, X.; Sun, J.Z.; Chen, M.X.; Qie, X.S.; Ying, Z.M.; Wang, Y.C.; Ji, L. Comparison of environmental and mesoscale characteristics of two types of mountain-to-plain precipitation systems in the Beijing Region, China. J. Geophys. Res. Atmos. 2019, 124, 6856–6872. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, J.Z.; Ying, Z.; Xue, L.; Chen, D.; Lin, W. Effects of local-scale orography and urban heat island on the initiation of a record-breaking rainfall event. J. Geophys. Res. Atmos. 2021, 126, e2021JD034839. [Google Scholar] [CrossRef]
- Zhang, L.N.; Sun, J.Z.; Ying, Z.M.; Xian, X. Initiation and development of a squall line crossing Hangzhou Bay. J. Geophys. Res. Atmos. 2021, 126, e2020JD032504. [Google Scholar] [CrossRef]
- Xiao, X.; Sun, J.; Ji, L.; Zhang, L.; Ying, Z.; Chen, Z. A study on local-scale thermal and dynamical mechanisms in the initiation of a squall line under weak forcing. J. Geophys. Res. Atmos. 2022, 127, e2021JD035561. [Google Scholar] [CrossRef]
- Mahoney, W.P. Gust front characteristics and the kinematics associated with interacting thunderstorm outflows. Mon. Weather Forecast Rev. 1988, 116, 1474–1491. [Google Scholar] [CrossRef]
- Bryan, G.H.; Rotunno, R. Gravity currents in a deep anelastic atmosphere. J. Atmos. Sci. 2008, 65, 536–566. [Google Scholar] [CrossRef]
- Atkins, N.T.; Laurent, M.S. Bow echo mesovortices. Part II: Their genesis. Mon. Weather Rev. 2009, 137, 1514–1532. [Google Scholar] [CrossRef]
- Marion, G.R.; Trapp, R.J. The dynamical coupling of convective updrafts, downdrafts, and cold pools in simulated supercell thunderstorms. J. Geophys. Res. Atmos. 2019, 124, 664–683. [Google Scholar] [CrossRef]
- Hutson, A.; Weiss, C.; Bryan, G. Using the translation speed and vertical structure of gust fronts to infer buoyancy deficits within thunderstorm outflow. Mon. Weather Rev. 2019, 147, 3575–3594. [Google Scholar] [CrossRef]
- Weisman, M.L. The genesis of severe, long-lived bow echoes. J. Atmos. Sci. 1993, 50, 645–670. [Google Scholar] [CrossRef]
- Weisman, M.L.; Rotunno, R. “A theory for strong long-lived squall lines” revisited. J. Atmos. Sci. 2004, 61, 361–382. [Google Scholar] [CrossRef]
- Davies-Jones, R.P. Streamwise vorticity: The origin of updraft rotation in supercell storms. J. Atmos. Sci. 1984, 41, 2991–3006. [Google Scholar] [CrossRef]
- Maddox, R.A. An evaluation of tornado proximity wind and stability data. Mon. Weather Rev. 1976, 104, 133–142. [Google Scholar] [CrossRef]





| Element Features | RGF | FGF | ||||
|---|---|---|---|---|---|---|
| Representative station gust wind (m·s−1) | Xiqing 17.2 | Huanghua 24.9 | ||||
| Evolution time (UTC) | 1012 | 1036 | 1054 | 1312 | 1324 | 1342 |
| Intensity of GFs (10−5·s−1) | 2.4 | 2.4 | 2.0 | 3.6 | 4.0 | 4.4 |
| Intensity of cold pools (°C·(10 km) −1) | 24 | 22 | 22 | 26 | 32 | 28 |
| Depth of cold pools (m) | 600 | 900 | 800 | 1400 | 1450 | 1600 |
| Propagation speed of cold pools (m·s−1) | 8.4 | 18.1 | 19.5 | 21.3 | 28.2 | 31.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Xiao, X. Comparison of Cold Pool Characteristics of Two Distinct Gust Fronts over Bohai Sea Bay in China. Atmosphere 2024, 15, 247. https://doi.org/10.3390/atmos15030247
Xu C, Xiao X. Comparison of Cold Pool Characteristics of Two Distinct Gust Fronts over Bohai Sea Bay in China. Atmosphere. 2024; 15(3):247. https://doi.org/10.3390/atmos15030247
Chicago/Turabian StyleXu, Changyi, and Xian Xiao. 2024. "Comparison of Cold Pool Characteristics of Two Distinct Gust Fronts over Bohai Sea Bay in China" Atmosphere 15, no. 3: 247. https://doi.org/10.3390/atmos15030247
APA StyleXu, C., & Xiao, X. (2024). Comparison of Cold Pool Characteristics of Two Distinct Gust Fronts over Bohai Sea Bay in China. Atmosphere, 15(3), 247. https://doi.org/10.3390/atmos15030247





