Abstract
Many applications rely on a correct estimation of the convective boundary layer (CBL) depth over mountainous terrain, but often these applications use numerical model simulations. Although models inevitably smooth terrain, the amount of smoothing depends on grid spacing. We investigate the behavior of the CBL in coarse- and fine-grid models applied to mountainous terrain by using output from an operational mesoscale modeling system and by performing quasi-idealized simulations. We investigate different areas in different climate zones using different CBL top derivation methods, grid spacing ratios, planetary boundary layer (PBL) schemes, and terrain smoothing. We find that when compared to fine-grid simulations, CBL depths are systematically larger in coarse domains over mountaintops, and to a lesser extent in valleys. On average, differences between coarse- and fine-domains over mountaintops could reach around 10%. In certain locations, differences could be as high as 25%. We attribute the result to terrain smoothing. Similarly, when using a coarse-grid CBL height (relative to mean sea level) interpolated using fine-grid terrain information, there is good agreement with fine-grid CBL depths over mountaintops and less agreement in valleys. Our results have implications for applications that use output from coarse model grids in mountainous terrain. These include inverse modeling studies (e.g., greenhouse gas budget estimations or integrated water vapor transport), PBL evaluation studies, climate research, air quality applications, planning and executing prescribed burns, and studies associated with precipitation over mountainous terrain.
1. Introduction
The planetary boundary layer (PBL) is a key component of the soil–atmosphere continuum as it is one control on exchanges of heat, moisture, and trace gases between the Earth’s surface and the atmosphere. Many applications rely on a correct estimation of the PBL depth, including climate, air pollution, and PBL model evaluation studies. Often these applications use model simulations, which inevitably smooth mountainous terrain. The PBL behavior is additionally determined by the parameterization of turbulence and many studies show that the simulated PBL depth can depend significantly on the selected turbulence parameterization scheme [1,2,3,4]. For flat terrain [5], and for a mixture of flat and mountainous terrain in Utah, [6], hereafter D17, showed that differences in simulated convective boundary layer (CBL) depths on fair weather days between coarse and fine domains exist even if the physical parameterizations are identical. They found that CBL depths are larger in the coarse domain than in the fine domain, and are largest over mountaintops by more than 10%. They found that differences between coarse and fine domains can be reduced by using CBL heights or by using high-resolution terrain information to interpolate CBL depth. The differences between the coarse and fine domains are the smallest for interpolated CBL depths. Their study was based on a comparison between model domains with 3.3 and 10 km grid spacing for one single domain in mountainous terrain.
We aim to generalize the results of D17 by investigating whether the differences in CBL depths and heights between models at different grid spacings found in D17 are dependent on terrain smoothing, CBL derivation methods, or model parameters, including PBL parameterizations, grid spacing ratio, and vertical resolution. This is conducted by performing quasi-idealized simulations. We also investigate how consistent the differences in CBL depths and heights are between coarse- and fine-grid simulations across multiple mountain areas in the western USA. To this end, we use the output from the same operational forecast system as used by D17 but for two more mountainous regions, and we use an additional model domain with 30 km grid spacing for the three regions. The regions differ in their mountainous and climate characteristics. For these investigations, we perform quasi-idealized simulations with the Weather Research and Forecasting (WRF) model [7].
The main objective is to investigate the importance of terrain smoothing on CBL depths across multiple mountainous terrains. An enhanced understanding of the impact of terrain smoothing on CBL characteristics might lead to a better understanding of CBL development in mountainous terrain, in general, and ultimately to a parameterization that incorporates subgrid-scale effects on CBL depths for climate and inverse model applications.
The study is organized as follows: Section 2 introduces the numerical models and data used. Section 3 discusses the approach to compare coarse- and fine-grid models, the PBL schemes and methods used to determine the CBL depth, and introduces the numerical experiments to isolate terrain smoothing in our results. Section 4 discusses the influence of PBL parameterization (Section 4.1), the influence of terrain smoothing (Section 4.2), the sensitivity in three mountainous regions over two years (Section 4.3), and the sensitivity to grid spacing and aspect ratio (Section 4.4). We then expand our results to investigate the use of CBL depths (relative to terrain elevation), CBL heights (relative to mean sea level), and the interpolated CBL depths across the three mountainous terrains (Section 4.5). Potential implications and conclusions of this study are given in Section 5.
2. Numerical Model
2.1. Two-Year Output from WRF-4DWX
We use the output from the 4DWX system which is run operationally by the US Army Test and Evaluation Command for several US Army test ranges and provides four to eight (depending on the test range) daily runs with hourly model output [8,9]. 4DWX is based on the Advanced Research core of the WRF numerical model [7] and operates with a grid spacing of 1.1 km or 3.3 km in the innermost domain, depending on the test range. For our study, we focus on three different test ranges located in complex mountainous terrain (Figure 1): Dugway Proving Ground (DPG, Figure 1b,c); Yuma Proving Ground (YPG, Figure 1d,e) and White Sands Missile Range (WSMR, Figure 1f,g). 4DWX is run in a one-way nested grid configuration, and we use hourly output from domains with a grid spacing of 30 km, 10 km, and 3.3 km for a two-year period from 1 July 2012 to 30 June 2014. D17 used the same time period but limited their investigations to DPG. For YPG and DPG a 1.1 km grid also is used in daily operations. Domains with grid spacings on the order of 1 km are generally small and cover only a few mountains or valleys (see, e.g., Figure 2a). By focusing on coarser domains that are larger, we are able to investigate processes related to terrain smoothing in a more statistical way because these domains include many more mountains of different sizes, as opposed to a smaller domain with a single mountain or valley which could lead to biased results. Moreover, as the scale of mountaintops and valleys relates to the grid cell size, it is more straightforward to express terrain features in relatively simple metrics such as a Laplacian when using coarser domains. The domains for the three test ranges differ not only in location and size (Table 1), but also in orographical characteristics, as will be shown in more detail in Section 3.1. All areas are steppe or desert climates [10]. DPG and WSMR are in arid steppe climates with warm summers and cold winters with snow cover, and YPG is in a hot desert climate.
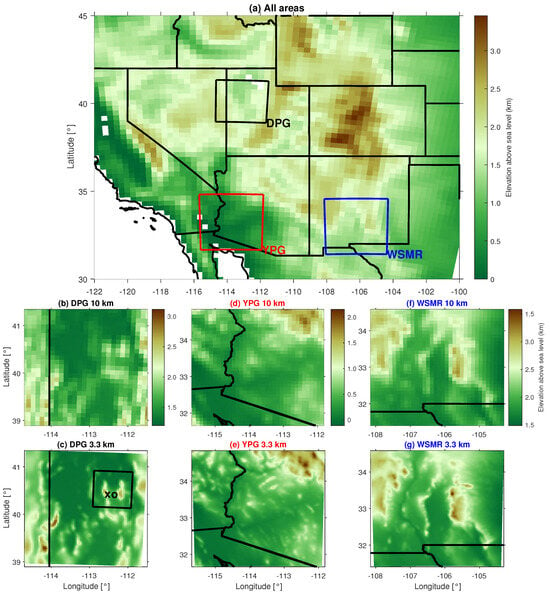
Figure 1.
Study areas with terrain elevation for different model domains. (a) 30 km domain with the extent of the 3.3 km domains for DPG (black), YPG (red), and WSMR (blue). Panels (b–g) show the 10 and 3.3 km terrain elevation for DPG, YPG, and WSMR, where the color bars apply on both coarse and fine domains. The domain in (c) marks the boundaries for Figure 2a, the ‘x’ and ‘o’ mark the mountaintop and valley locations mentioned elsewhere in the text.
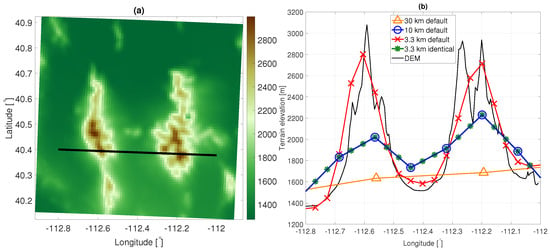
Figure 2.
(a) Representation of mountainous terrain elevation in Utah on 1.1 km grid spacing (see Figure 1c for the location), (b) the effect of terrain smoothing on terrain elevation when using different grid spacings (indicated in the legend) along the cross-section indicated by the black line in (a). For reference, a digital elevation model (DEM) based on Google Earth Pro is shown.

Table 1.
Details of the different domains per investigated area.
The used parameterization schemes in 4DWX include the Yonsei University (YSU) scheme for the PBL [11], the Noah land-surface model [12], the Monin–Obukhov surface-layer scheme [13], the Dudhia scheme for shortwave radiation [14], Rapid Radiative Transfer Model for longwave radiation [15], the updated Kain–Fritsch cumulus scheme in the two outer domains only [16], and the Thompson microphysics scheme [17]. More background on the use of YSU and other PBL schemes in mountainous terrain is given in Section 3.2.
The outermost domain in 4DWX is initialized using the Global Forecast System from the National Center of Environmental Prediction, and is run with a resolution of 1°. Vertical grid spacing ranges from around 40 m near the surface to about 450 m at 4 km AGL and is the same for all domains. The terrain data come from the USGS database at a horizontal resolution of 3 arcseconds and are interpolated by taking all source data points that are the closest to a specific model grid point.
2.2. Data Selection for Two-Year Output
Our analysis focuses on CBL depths. Therefore, we only select fair-weather days for which CBL depths are well-defined, and deploy the same strategy as in D17. The criteria are based on the minimum daily integrated which must be higher than 70% of the maximum daily integrated value for a specific month. In addition, quartile differences and standard deviation cannot exceed 100 W m−1 for more than 3 h. These criteria remove days with substantial cloud cover in all or parts of the domains, yet ensure a sufficient number of days for a statistically robust analysis.
Applying the criteria for the 10–3.3 km domain comparisons results in the selection of more than 75% of the days in winter, spring, and autumn for YPG, more than 50% for WSMR, and around 40–50% for DPG (Table 2). The monsoon period with a higher probability of clouds and deep convection is the most important limitation to days available for analysis in summer. Additionally, there are fewer available days in the finest domains in summer, which is explained by enhanced cloud development in these domains over the more highly resolved mountainous terrain (e.g., compare 10–3.3 km and 30–3.3 km domains). The fewer fair-weather days in the 30 km domain than in the smaller domains is explained by the higher probability of synoptic weather systems passing through the larger domain (e.g., compare 10–3.3 km with 30–10 km domains).

Table 2.
Number of available days per season in the period of July 2012 to June 2014 for each of the coarse and fine domain combinations after selection for fair-weather days. Both coarse and fine domains are considered for selection criteria, leading to a single value for available days in each domain comparison. DJF, MAM, JJA, and SON stand for winter (December, January, February), spring (March, April, May), summer (June, July, August), and fall (September, October, November) months, respectively. See text for further explanation.
2.3. Quasi-Idealized Simulations
We use quasi-idealized simulations (30, 10, and 3.3 km domains) of case studies to investigate the impact of terrain smoothing and of PBL parameterizations on the differences in CBL depths across the domains. We use the same setup as 4DWX but with a newer version of WRF (version 3.8.1). To investigate the impact of terrain smoothing in the quasi-idealized simulations, the terrain elevation from the coarse domain is interpolated to the fine domain. We do this for the DPG domain only because, from all the domains investigated, this domain has the widest representation of mountainous terrain, including an abundance of mountaintops (Table 3). More details are provided in Section 3.3.

Table 3.
Terrain properties for different terrain types in the indicated domains as determined by with the respective fine domain as reference.
During days with strong surface heating, differences in CBL depths between the coarse and fine domains are largest, leading to low correlation r between terrain elevation and the maximum daily PBL height relative to mean sea level, i.e., a weakly terrain following PBL height [18,19]. At DPG, the lowest correlations are found in summer (D17) and we, therefore, selected a summer day (1 July 2013, r = 0.44) as our primary case study day to investigate the impact of terrain smoothing on our results (see Section 3.2 and Section 3.3 for additional details). The CBL depth differences between coarse and fine domains over mountaintops and valleys on this day compare well to the 2-yr climatology. An additional case study was simulated for another summer (10 July 2013; r = 0.53). We focus our analysis on the time period between 06:00 and 22:00 MST, with the simulations initialized at 11:00 MST on the previous day.
3. Methods
3.1. Aggregation Approach and Subgrid Terrain Properties
For the comparison of simulated CBL depths and other variables among domains with different grid spacings, we use the ’aggregation approach’ from D17. In this approach, we aggregate the fine grid points centered on every coarse grid point. For example, when comparing domains with a grid-spacing ratio of 1:3, we aggregate nine fine grid points for every one coarse grid point; with a grid-spacing ratio of 1:9, we aggregate 81 fine grid points for every one coarse grid point. Besides CBL depth, the variables we aggregate include terrain elevation, surface sensible heat flux H, wind speed, and at the vertical model levels.
Terrain properties are quantified using the laplacian wherein is the terrain elevation in the finer domain. These terrain properties are considered subgrid relative to the coarser grid and will, therefore, be referred to as subgrid terrain properties. Subgrid terrain properties are separated into pre-defined areas of interest: flat terrain (values around zero of ), mountaintops and ridges (negative values of ), and valleys (positive values of ). Table 3 defines the thresholds and the variability of the subgrid terrain properties in the different study areas. In general, YPG and WSMR include more flat terrain than DPG, and DPG has higher mountaintops (Table 3). We further note that in all domains, mountaintops are flattened more than valleys are filled. This is a consequence of the generally larger horizontal scale of valleys than of mountaintops and is also demonstrated in Figure 2b.
In the case of a 1:3 grid ratio, we find a smooth transition from negative values of associated with underestimated terrain elevation in the coarse domain, to positive values of associated with overestimated terrain elevation (for more details about DPG, see in D17 their Figure 4b). This is a general feature of mountainous terrain when comparing domains with different grid spacings and thus, similar features are found for YPG and WSMR (Table 3).
3.2. PBL Parameterization and CBL Top Derivation
D17 did not investigate the role of PBL parameterization in their study. We expand on the study of D17 by exploring the role of PBL schemes in the comparison of coarse and fine domains using a one-day case study. The PBL parameterization scheme includes the representation of the vertical transport of heat, momentum, and moisture due to turbulent mixing, which affects CBL development. Differences in the representation of these processes in PBL parameterization schemes at different spatial scales can, therefore, have a large impact on CBL depth. If differences in CBL depths between coarse and fine domains in mountainous terrain remain similar for a variety of grid spacings and PBL schemes, it might indicate that CBL differences are not due to differences in the representation of physical processes at different spatial scales. On the other hand, if differences in CBL depths between coarse and fine domains vary with the choice of PBL scheme, this might indicate that parameterizing certain processes in mountainous terrain is more appropriate at some grid spacings than others.
To investigate the role of PBL parameterization schemes, we select five of them (see Table 4): the YSU scheme [11], a first-order nonlocal scheme that includes a countergradient term for the nonlocal mixing and resolves entrainment explicitly; the Asymmetrical Convective Model version 2 (ACM2) scheme, a nonlocal scheme that combines nonlocal upward mixing and local downward mixing, with their relative contribution depending upon the stability [20]; the Mellor–Yamada–Janjic (MYJ) scheme [21]; the Mellor–Yamada–Nakanishi–Niino Level 2.5 (MYNN2.5) scheme [22] and the Quasi-Normal Scale Elimination (QNSE) scheme [23]. The latter three schemes use a 1.5-order turbulent kinetic energy (TKE) closure scheme and are based on solving the TKE equation prognostically, but differ in length scales and eddy diffusivity coefficients [24]. For each PBL scheme, the recommended surface layer scheme was used (Table 4).

Table 4.
Overview of model settings used to study sensitivity to PBL parameterizations.
D17 only used one CBL depth detection method based on the WRF 4DWX output, which is based on the YSU scheme. This scheme uses the bulk Richardson () method [28] to estimate CBL depth. Herein, we use several other CBL depth detection methods, including the parcel method [29], the vertical gradient [5], and a 1.5 K increase in the minimum mixed-layer temperature [30]. Although the methods result in different absolute values of the CBL depth, differences between coarse and fine domains with the different PBL parameterization schemes are relatively minimal (see Appendix A). Therefore, we use only the method to derive the CBL top in all simulations, independent of PBL parameterization. The method evaluates the first model level, starting from the surface to the level where exceeds a critical value . A final CBL depth is calculated by linear interpolation between this model level and the level below it. We use 0.25 for , a value that has been widely used in observational and modeling studies [31,32,33]. CBL depths are first calculated for each individual profile, and then these CBL depths are aggregated according to the procedure explained in Section 3.1.
3.3. Influence of Terrain Smoothing
In flat terrain simulations, based on a single case study, and comparing 9 km to 1 km grid cells, ref. [5] found slightly larger CBL depths in coarse vs. fine domains on the order of 5% (see their Table 6). They attributed this mostly to the differences in the shape of vertical profiles of temperature. D17 found that over mountainous terrain, based on two years of data, CBL depth differences between 10 km and 3.3 km domains were much larger than over flat terrain, reaching higher than 10%, while over flat terrain the differences were minimal. The smoothing of mountainous terrain in domains using coarse grid spacings leads to changes in the characteristics (scale and intensity) of terrain-driven circulations (dynamic effects) and changes in the height of the CBL top above the terrain (static effects). To quantify the contributions of these two effects, we performed quasi-idealized simulations at different grid spacings but with the identical (coarsest) terrain resolution, interpolating the terrain elevation of the coarse domain to the grid points of the fine domain. This approach is shown in Figure 2b. We performed this approach for paired 30 and 10 km, and 10 and 3.3 km domains, but for our analysis, we focus just on the latter. We call these the “interpolated-terrain simulations” hereafter. These simulations attempt to eliminate the effect of terrain smoothing and isolate the effect of PBL representation at different resolutions. An overview of our research foci is shown in Table 5.

Table 5.
Overview of areas, domains, and periods used for the different research foci.
4. Results and Interpretation
4.1. Sensitivity to PBL Parameterization
D17 showed that based on 4DWX output at DPG, larger CBL depths are simulated in coarse domains than in fine domains, especially in mountainous terrain. The 4DWX output alone does not allow an investigation of the influence of physical parameterizations since it only uses the nonlocal YSU scheme. We, therefore, perform quasi-idealized simulations for the same area (DPG) with WRF at 10 and 3.3 km grid spacing (using the five widely used PBL parameterization schemes mentioned above) during a summer day, on 1 July 2013. With values of r = 0.44, defined as the correlation between terrain elevation and the maximum daily CBL height (relative to mean sea level), this day was representative of days with typical CBL growth, and thus the simulated differences between coarse and fine domains are similar to those in the 2-yr climatology. Other details of these simulations are given in Section 2.3 and Section 3.2.
All simulations using different PBL schemes show clear convective PBL evolution leading to maximum CBL depths at 15:00 MST (Figure 3a). The nonlocal schemes YSU and ACM2 simulate maximum CBL depths of around 2750 m, whereas the local schemes MYJ, QNSE, and MYNN2.5 simulate CBL depths in the range of around 2300–2500 m. This is in line with previous studies that also showed that nonlocal schemes simulate deeper CBLs than local schemes over both flat and complex terrains [1,3,4].
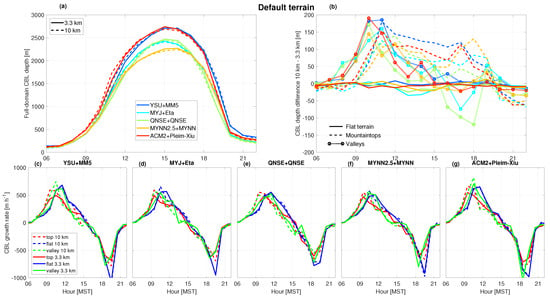
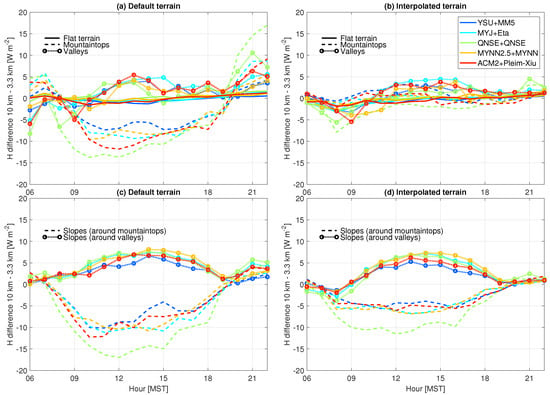
Figure 3.
Hourly evolution at DPG on 1 July 2013 of (a) domain-averaged CBL depths expressed by medians for the indicated domains, (b) differences in CBL depths over flat terrain (solid lines), mountaintops (dashed lines), and valleys (dotted lines) for various PBL schemes, and (c–g) absolute CBL growth rates in the 10 km and 3.3 km domains over mountaintops, valleys, and flat terrain (colors). The colors of the legend in (a) apply to (b). The CBL depth is determined using the method with = 0.25.
Over flat terrain, the differences in CBL depths between the coarse and fine domains are minimal and around zero throughout the day among all PBL schemes (solid lines in Figure 3b). This is in line with the 2-year climatology of D17, and smaller than reported by [5]. Over mountaintops (recall there are 53 available grid cells in the domain; see Table 3) and valleys (28 available grid cells) a clear tendency for larger CBL depths in the coarse domain was simulated (dashed lines in Figure 3b). Over mountaintops, CBL depths remain larger in the coarse domain throughout the day, with a maximum difference between coarse and fine domains of around 150 m. Differences are about 5–10% larger in the coarse domain, relative to the CBL depths in the fine domain. At the time of maximum CBL depth (15:00 MST), the difference is around 100 m across all PBL schemes. In the valleys, differences in CBL depths between the coarse and fine domains gradually decrease to a minimum at around 15:00 MST. Although the differences in CBL depths in this one-day case study are slightly smaller than reported for the two-year comparison by D17, our comparisons show that PBL parameterization itself is not critical in explaining the differences between coarse and fine domains in mountainous terrain.
The differences in morning CBL depths between the coarse and fine domain increase more rapidly in valleys than over mountaintops (circled lines vs. dashed lines, resp., in Figure 3b). In our simulations, this effect is evident for all PBL parameterization schemes as shown by CBL growth rates in Figure 3c–g. Slower CBL growth in the morning transition period in a resolved valley has been related to cold-air pool formation and increased morning stability in the resolved valley (D17). Also over mountaintops, all PBL schemes simulate a faster CBL growth during the morning in the coarse domain (Figure 3c–g). In general, stability is weaker in the atmosphere above the mountaintops in the coarse domain compared to the fine domain, making it easier to heat the nocturnal boundary layer in the morning. Moreover, a mountaintop in a fine domain is better resolved, with surrounding grid cells on different azimuth angles, whereas a coarse domain “mountaintop” has a flatter surface and processes at the surface would react differently to solar heating to which subsequent CBL growth responds. Additionally, over more resolved terrain, smaller-scale terrain-driven flows will develop resulting in more pronounced cold-air advection from lower terrain, thereby counteracting CBL growth. In contrast to mountainous terrain, the differences in CBL growth over flat terrain (blue lines) are minimal at all times (Figure 3c–g).
The patterns and values apparent in this one-day case study are similar to the findings of D17 (see Figure 8c in D17). We thus conclude that differences in CBL depths between domains with different grid spacings tend not to depend on the specific PBL physics parameterization among those we tested. As mentioned previously in Section 3.2, we also investigated the influence of different CBL top derivation methods on our results, but CBL depths remained larger in coarse-grid domains, irrespective of the method used (see Appendix A). Since in our simulations physical parameterization and CBL top derivation method can be excluded as relevant drivers of differences between coarse and fine domains in complex terrain, we now focus our investigation on the influence of terrain smoothing.
4.2. Sensitivity to Terrain Smoothing
We investigate the role of terrain smoothing directly on simulated CBL depths using the same case study as in the previous subsection. Our approach consists of replacing the terrain elevation on the fine grid (3.3 km) with the terrain elevation from the coarse grid, as described in Section 3.3 and illustrated in Figure 2b. We refer to these as interpolated-terrain simulations. Smoothing of the mountainous terrain in coarse domains leads to changes in the characteristics (scale and intensity) of terrain-driven circulations (dynamic effects) and changes in the height of the CBL top above the terrain (static effects). By keeping terrain elevation constant while everything else varies between coarse and fine domains, we can further attempt to eliminate the effect of terrain smoothing and isolate the effect of PBL representation at different grid spacings. We expect differences in CBL depths between coarse and fine domains over mountainous terrains to reduce to values similar to those over flat terrain, hence around zero. This would indicate that sub-grid scale processes affect the simulated CBL depth over mountainous terrain.
Indeed, the CBL depth differences between coarse and fine domains reduce largely to around zero in mid-afternoon, when CBLs are highest, over mountaintops and in valleys across all PBL schemes (dashed and circled lines in Figure 4b). The effect is clearest over mountaintops, where CBL depth differences are reduced from around 100 m in the default terrain simulations (Figure 3b), to around zero in the interpolated-terrain simulations in the cases of most PBL schemes (Figure 4b). An exception is the QNSE scheme, which produces negative differences in CBL depths in valleys and over mountaintops from around noon. We obtain similar results using larger grid spacing comparisons (i.e., 30- and 10 km grid spacing, see Supplemental Material Figure S1).
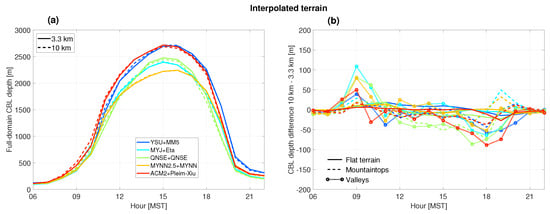
Figure 4.
(a,b) Same as Figure 3a,b but from simulations where the coarse (10 km) and the fine domain (3.3 km) have the same terrain elevation, also called interpolated-terrain simulations.
Note, that the CBL depth differences are not completely reduced to zero. We consider at least three reasons. First, this is a consequence of using and comparing models on different grid spacings. Even over flat terrain, differences in CBL depths among models at different grid spacings exist see, e.g., [5] and Figure 3b. Thus, in our simulations that use and compare models with identical—but mountainous—terrains, differences between coarse and fine domains are still to be expected. In convective situations, [5] found this effect to be more apparent for TKE-based schemes, and related this to a larger grid spacing dependency compared to nonlocal schemes. We also find the largest differences result from the TKE-based schemes (compare, e.g., Figure 3b and Figure 4b).
A second factor that might explain CBL depth differences between coarse and fine domains is the consequence of using the aggregation approach to compare domains of different resolutions over mountainous terrain. Averaging the eight surrounding grid cells around a mountaintop or a valley on a fine grid does not necessarily lead to precisely the same values that are on a coarse grid, even though terrain elevations at the locations common to both domains are identical (see Figure 2b). Similarly, aggregated CBL depths might also lead to small differences between domains. This was also pointed out by [5], who found that minor terrain elevation differences can lead to larger CBL depths in coarse domains.
Third, finer domains improve the simulation of terrain-driven flows, including slope flows [34]. Since these flows have an impact on CBL depths, differences in CBL depths between the coarse and fine domains are expected. We explore this impact on CBL depth differences over slopes next. We define two different types of slopes: slopes surrounding mountaintops, and slopes surrounding valleys (Table 3). In the default terrain simulations, the differences in CBL depths between coarse and fine domains are slightly larger over slopes than over flat terrain (Figure 5). The differences in CBL depths over slopes are, however, smaller than over mountaintops and in valleys (compare Figure 3b and Figure 5a). For interpolated-terrain simulations, CBL depth differences over slopes surrounding mountaintops decrease mostly to around zero, whereas the CBL depth differences over slopes surrounding valleys increase relative to default terrain. Notably, over the slopes surrounding valleys, we find larger CBLs in the morning and smaller in the late afternoon, similar to the interpolated terrain simulations of valleys (Figure 4b).
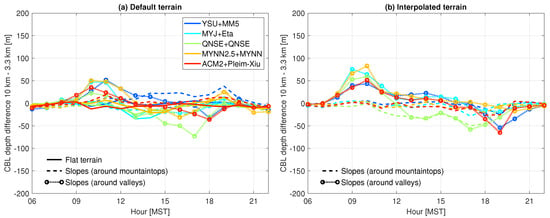
Figure 5.
(a) Same as Figure 3b but over sloping terrain, and (b) same as (a) but from the interpolated-terrain simulations.
Because wind speed and H are major factors affecting CBL growth, we investigate their role in causing these CBL depth differences between the simulations, see Figure 6 and Figure 7 for absolute differences, and Supplemental Figures S2 and S3 for relative differences. We find lower values of H and wind speeds over mountaintops in coarse vs. fine domains (Figure 6a and Figure 7a). The differences diminish when terrain is interpolated (Figure 6b and Figure 7b, resp.). Better-resolved terrain enhances winds over mountaintops but reduces winds in valleys due to increased sheltering, also affecting H.
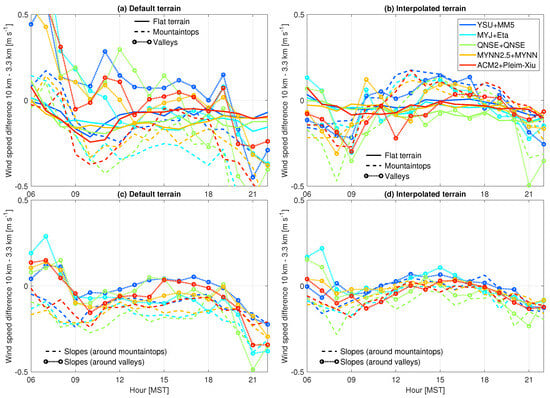
Figure 7.
Same as Figure 6 but for surface wind speed.
We find larger differences in H over slopes surrounding mountaintops and valleys (Figure 6c), than over mountaintops and in valleys themselves (Figure 6a), persisting in interpolated-terrain simulations (Figure 6d). In contrast, we find smaller differences in wind speed over slopes surrounding mountaintops and valleys (Figure 7c), than over mountaintops and in valleys (Figure 7a), but the differences are virtually zero when the terrain is the same in both domains (Figure 7d). This result implies that the ability to resolve slopes has a large impact on the magnitude of the simulated winds. Nevertheless, the differences in H in default terrain settings clearly do not explain the differences in CBL depths between coarse and fine domains, as was also noted by D17.
4.3. CBL Evolution in Three Study Areas
To investigate whether the CBL depth differences depend on the geographical area, we expand our investigation to three different areas with different terrain and climates (see Figure 2). Diurnal PBL evolution is similar among the three different domains, with the deepest CBLs at WSMR (Figure 8). CBLs are shallowest at DPG, except for during summer when YPG has the lowest afternoon CBL depths, corresponding with the earlier onset of the monsoon season in Arizona [32,35]. Maximum afternoon CBL depths in summer range from ∼1700 m at YPG to ∼2300 m at WSMR (Figure 8). CBL depths are very small in winter at DPG, which has a colder climate and is subject to more snow cover than the other areas. The geographical and temporal (seasonal and diurnal) variability of the CBL is consistent with other studies of CBL depths over the same areas [32,36].
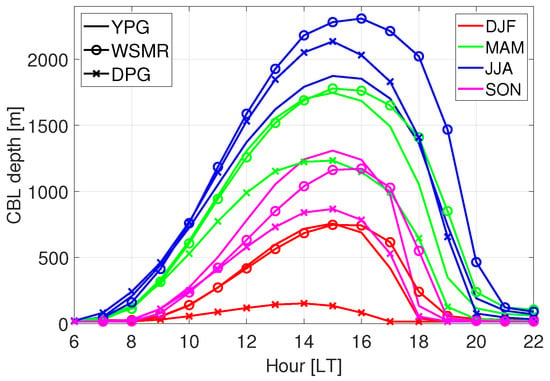
Over flat terrain, the differences in CBL depths between the coarse and fine domains are small during all seasons and at all locations (Figure 9a and Figure 10a–d). The CBL depths tend to be somewhat smaller (by ∼1%) in the coarse domain in the early afternoon, but somewhat larger (by ∼2%) in the late afternoon (maximum value is around 2% for WSMR at 18:00 LT in summer months, Figure 9a). These minor differences are consistent with the findings of [5], and in agreement with D17, who compared CBL depths at DPG only. Relative to maximum CBL depths (Figure 8), the mean differences in CBL depths between coarse and fine domains are minimal, however, (Figure 10a–d). Although variances in CBL depth differences between coarse and fine domains are higher in summer than in winter (as a consequence of the larger variability of CBL depths in summer), they are equally spread around zero (Figure 10a–d), which is similar to the findings of D17.
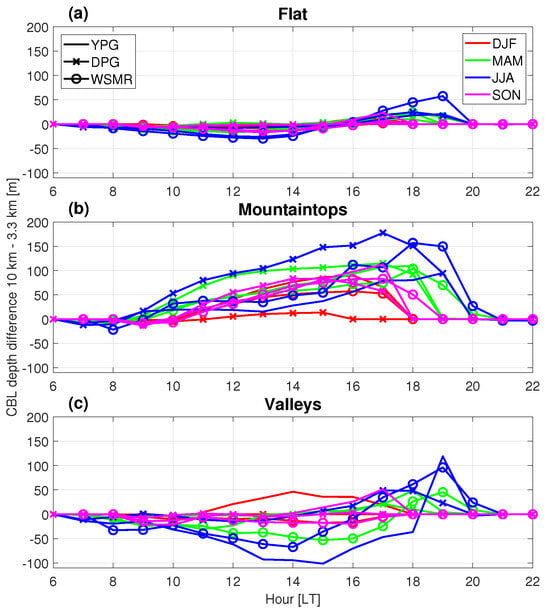
Figure 9.
Hourly and seasonal medians of CBL depth difference between the coarse (10 km) and fine (3.3 km) domains for the indicated terrain types. See Table 3 for the number of aggregated grid cells used per indicated terrain type, and Table 2 for the number of available days per season per area. The legends in (a) apply to all panels. See Table 2 for definition of seasons.
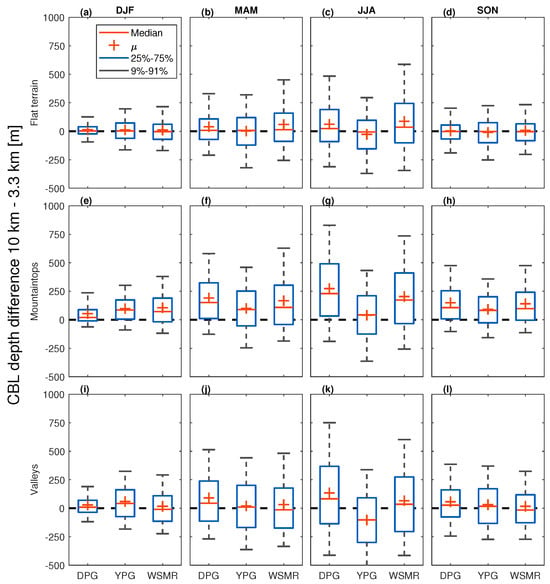
Figure 10.
Differences in CBL depths between coarse and fine domains based on daily maximum depths (coarse minus fine) during all seasons over indicated terrain types for (a–d) flat terrain, (e–h) mountaintops, and (i–l) valleys. See Table 2 for definition of seasons.
CBL depth differences between coarse and fine domains are larger in parts of a domain that are mountainous (Figure 9b,c and Figure 10e–l). Generally, the largest differences in CBL depths are found over mountaintops in all geographical areas, throughout the day, and peak during the late afternoon in all seasons (Figure 9b and Figure 10e–h). An exception is at YPG in summer, where the differences in CBL depths between coarse and fine domains over mountaintops are comparable to those over flat terrain (Figure 10g). Differences in CBL depths also tend to be larger in summer than in winter when they reach relative maximum differences of about 10%, but in some locations these relative differences can become larger than 25% (see Figure S4 in Supplemental Material). Mountaintops were selected based on −40 m, as explained in Section 3.1; see also Table 3. For subselections of steeper and higher mountaintops, the differences in CBL depths are larger in all areas (see Figure S5 in Supplemental Material).
The results are less clear in valleys than over mountaintops, with both positive and negative differences in CBL depths between the coarse and fine domains (Figure 9c). D17 related this to the ability of fine-grid simulations to resolve subsidence over the valley, cold-air pools, and upslope flows. The net result of these processes is a slower CBL growth in fine domains. In addition, valley orientation might play a role. All these factors might lead to a less straightforward signal in the comparison of CBL depths between coarse and fine domains in valleys than over mountaintops. The spread in the differences in CBL depths between coarse and fine domains does not depend on terrain, but it does depend on season in all three areas (Figure 10), which is consistent with the findings of D17.
4.4. Sensitivity to Grid Spacing and Grid Spacing Ratios
D17 focused on CBL depth differences between 10 km and 3 km domains. Herein, we also examine the 30 km domain to explore the role of coarse grids that are more comparable to climate models, which nevertheless are often compared with observations at individual points (e.g., radiosoundings). The DPG, YPG and WSMR areas include a mixture of both complex and flat terrain, which is suitable for this investigation (see Figure 1). For simplicity, we focus here on DPG only, because results are similar at YPG and WSMR (see Supplemental Material Figures S6 and S7, resp.). We compare the 30, 10 and 3.3 km domains for the same 2-yr period. The terrain properties and number of available grid cells over flat terrain, mountaintops, and valleys are shown in Table 3.
Simulations tend to produce larger CBL depths in coarse vs. fine domains, with the largest differences over mountaintops, followed by valleys and flat terrain (Figure 11a–c). There is a delay in the decay of the CBL in the late afternoon in the coarser domains. This is related to the late-afternoon transition, which in general, is later for models run on coarser grids.
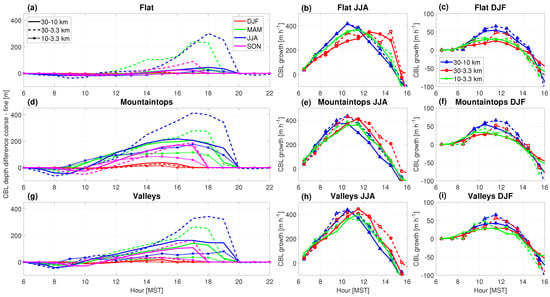
Figure 11.
(a–c) Same as Figure 9 but for multiple grid spacing comparisons (indicated in the legend), and for DPG only; (b,e,h) summer and (c,f,i) winter CBL growth rates for indicated terrain types. See Table 2 for the data availability per season, and Table 3 for the definition of the terrain types and the number of available grid cells. Legend in (a) applies to (d,g), legend in (c) apply to all (b,e,f,h,i) panels. See Table 2 for definition of seasons.
The differences between coarse and fine domains during morning and afternoon transition periods are quite apparent in the CBL growth rate (Figure 11d–i). As was shown by D17 in their comparison of the 10 km and 3.3 km simulations, the largest differences in CBL growth rates between coarse and fine domains in summer are found over mountaintops (Figure 11e). In valleys, the differences in CBL growth rates between coarse and fine domains are largest in the early morning but are also considerable in the early afternoon after 12:00 MST (Figure 11h). Over flat terrain, the differences in CBL growth rates are similar between all compared coarse and fine domains in summer (Figure 11b) and winter (Figure 11c). In winter, differences occur later in the morning than during the summer, related to the typical later onset of CBL growth in winter (Figure 11c,f,i).
Although at WSMR and YPG there are different delays and values for growth rates compared to DPG, the largest differences between coarse and fine domains are over mountaintops, followed by valleys (see Figures S6 and S7 in Supplemental Material). This is also evident from the differences between daily maximum CBL depths in the course and fine domains (see Figure S8 in Supplemental Material). However, part of the differences in daily maximum CBL depths over mountainous terrain (Figure S8e–l) appears to depend on the grid spacing itself (and not necessarily different terrain smoothing), because differences in CBL depths between the 30 and 10 km domains are also larger over flat terrain at all locations in all seasons (Figure S8a–d in Supplemental Material).
4.5. CBL Depths, Heights, and Interpolation in Mountainous Terrain
We investigated CBL depth evolution for simulations with different grid spacings where the same mountainous terrain is represented by resolved mountaintops (3.3 km grid spacing), lower mountaintops and shallower valleys (10 km grid spacing), to sloping terrain (30 km grid spacing), see Figure 2b. Of particular interest in the current study is the CBL behavior over mountaintops and in valleys. We select a single mountaintop and valley to answer more directly the following questions. What are the implications if CBL depths over mountaintops are different in simulations with different grid spacings? And do CBL depths in coarse simulations converge toward CBL depths in fine simulations if we correct information on the coarse grid to account for sub-grid scale terrain? The mountaintop and valley locations were selected because they exhibit a gradual transition from fine to coarse grid spacing (Figure 2b). The selected case study is the same as for previous subsections (1 July 2013).
Over mountaintops, the coarse domain exhibits more rapid CBL development, but also delays in CBL onset and decay, compared to the fine domain (Figure 12a). Conversely, in valleys, the fine domain exhibits a delayed onset and earlier decay of the CBL compared to the coarse domain (Figure 12b). Daily maximum CBL depths are more similar in valleys than over mountaintops due to more consistent terrain elevation in valleys across the different grid spacings (Figure 2b).
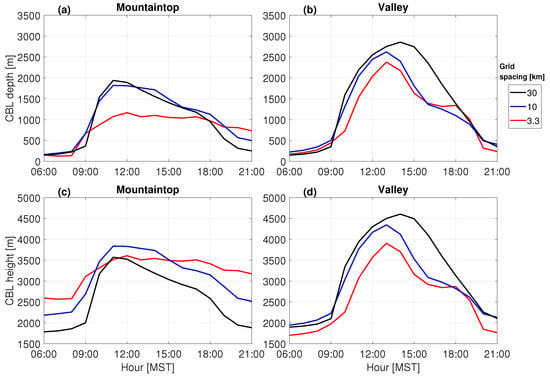
Figure 12.
(a) Mountaintop, (b) valley CBL depths, and (c) mountaintop, (d) valley CBL heights on 1 July 2013 (r = 0.44) in simulations at 3.3 km, 10 km and 30 km grid spacing. CBL tops are estimated by using the -method ( = 0.25). Mountaintop and valley locations are marked by ‘x’ and ‘o’, resp., in Figure 1c.
An interesting aspect of the deepening afternoon CBL is its increasing independence on underlying terrain [19]. Correcting for subgrid terrain variability by using CBL height, rather than depth, enhances the agreement between coarse and fine domains (Figure 12c). This means that CBL depth estimates from the coarse domain can be improved by correcting for the subgrid terrain variability. This is especially valid over unresolved mountaintops but not so much in unresolved valleys, where CBL heights and depths are similar (compare Figure 12b and Figure 12d), in agreement with the results of D17. We simulated another case study (10 July 2013) with slightly different CBL characteristics, but the conclusions remain similar: CBL growths and depths differ between coarse and fine domains, but using the CBL height and correcting for subgrid terrain variability increases the similarity between results on coarse and fine grids (see Figure S9 in Supplemental Material).
Building on the method proposed by D17, we interpolate CBL heights from coarse to fine domains and subsequently subtract fine-domain terrain elevations. This ’interpolated CBL depth’ approach assumes similar CBL heights in both domains, which is especially effective when deep CBLs occur. Application to different mountainous regions reveals correlations between coarse-domain CBL depth (x-axis) and the differences in CBL depths between the coarse and fine domains over mountaintops, especially at DPG and WSMR (Figure 13a,e). At YPG, the differences in CBL depths between coarse and fine domains appear less correlated with the CBL depth (Figure 13c). We further find greater seasonality in the maximum CBL depths (x-axis) at DPG (smaller CBLs in winter than in summer) than at YPG and WSMR (more seasonal spread of CBLs).
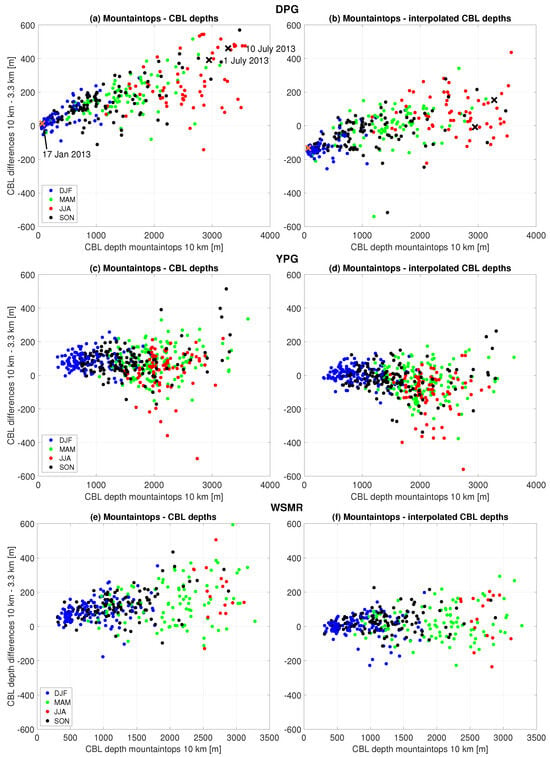
Figure 13.
Daily average of (a,c,e) CBL depth and (b,d,e) interpolated CBL depth differences between coarse and fine domains as a function of the averaged daily CBL depth of the coarse domain over the selected grid cells over mountaintops at (a,b) DPG, (c,d) YPG, and (e,f) WSMR. Colors indicate the season. Each dot represents the average of the available grid cells. See Table 2 for definition of seasons.
However, the approach shows limitations in valleys, with varying success in different regions (Figure 14). This interpolated approach is valuable for regions with sufficiently deep and relatively level CBLs, where the CBL depth exceeds a certain terrain length scale. This length scale could be linked, for example, to the regionally averaged mountain elevation and to the grid spacing used in a model. Negative comparisons might arise for shallower CBLs, such as in the early morning, late evening, or winter. In valleys there is generally a larger scatter than over mountaintops, so careful consideration is required when applying the interpolation method (Figure 14). Hence this correction is particularly effective during late spring, summer, and early fall when convection is strongest (D17).
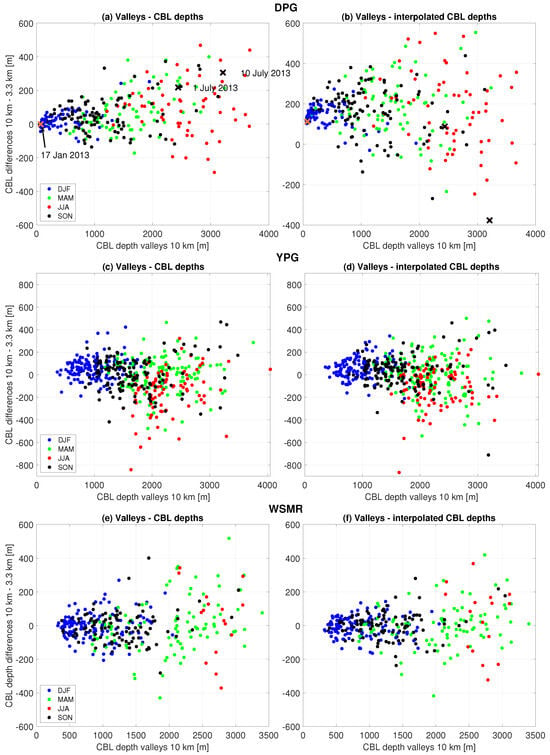
Figure 14.
Same as Figure 13 but for valley terrains.
5. Conclusions and Potential Implications
We investigated the behavior of simulated CBL depths as a function of model resolution in mountainous terrain by using mesoscale model output and by performing quasi-idealized simulations. We found that when compared to fine-domain simulations, CBL depths are systematically larger in coarse-domain simulations over mountaintops, and to a lesser extent in valleys. Over mountaintops, an average difference in CBL depths between coarse- and fine-domains of around 10% was found. In some locations during summer, however, differences could be as large as 25%. We attributed this directly to the terrain smoothing in coarse domains. The results are robust across all parameters (location, PBL parameterization, and CBL derivation method) that we investigated. The differences in CBL depths among simulations are eliminated only when terrain elevations are identical in both coarse and fine domains.
A direct comparison of simulated CBLs over the same mountaintop but with different grid spacings (ranging from 3.3 to 30 km) further revealed not only that different grid spacings lead to different CBL depths, but also to different CBL growth rates and different delays in CBL onset and decay over mountaintops and in valleys. The differences in CBL growth rates and timing are likely a result of terrain-induced flows and other feedback mechanisms absent in the coarse domains.
We then investigated the applicability of using CBL height (relative to mean sea level) from the coarse domain, interpolating to the fine domain. This method was referred to as the interpolated CBL depth. It showed better applicability over mountaintops than in valleys. For the method to work, the CBL depth should be larger than the dominant length scale of the underlying topography.
The general conclusion is that CBL depths in numerical simulations are likely to vary artificially with the horizontal coarseness of the computational grid when smoothing of terrain depends on grid spacing. Our results are important for many applications that rely on the correct estimation of the CBL depth in mountainous terrain. For example:
- PBL evaluation studies:Studies that use coarse domains (i.e., grid spacing on the order of several 10 s km) typically neglect analysis over mountainous terrain [32,33,37]. Ref. [32] showed that coarse models overestimate PBL depths when compared to observations (their Figure 8). Part of the overestimation in complex terrain can be directly attributed to the terrain smoothing on the coarse grid. PBL evaluation studies in situations with deep CBLs would clearly benefit from including subgrid terrain variability for improved estimates of CBL depths.
- Climate studies:Many climate studies use global circulation models to investigate future and past states of the climate. An example is the category of research that aims to correctly project the impact of anthropogenic forcing onto future climate. Models that are used for these studies typically have grid spacings on the order of 10 s of km. From our study, we conclude that such configurations might lead to artificially deep CBLs in mountainous terrain. Through feedback mechanisms in the boundary layer (e.g., enhanced entrainment through deeper CBLs), one could expect different projections for e.g., surface temperature as a consequence of deeper CBLs.
- Trace gas transport modeling: Coarse models, often used in inverse modeling for greenhouse gas (GHG) emission estimates, may present challenges when assimilating mountaintop GHG observations; therefore, such data are typically not incorporated [38,39,40]. However, an increasing number of GHG concentration observations are located at mountaintops [41,42,43,44,45]. Ref. [46] suggested to include mountaintop GHG concentration observations in atmospheric inversion models through assimilation in coarse models during the afternoon, rather than during the night [47]. A systemic overestimation of CBL depth in coarse models can potentially have serious consequences when GHG concentrations are assimilated in mountainous terrain. D17 found that, using a simplified boundary layer model, a difference of 10% in CBL depth would lead to a difference in CO2 CBL concentration of 1 ppm which can result in large differences in carbon emission estimates. Adjusting for elevation mismatches, as suggested by [46], is effective mainly in the afternoon when CBLs are highly convective. For shallow CBL scenarios (e.g., winter or early morning), this adjustment might actually result in even larger overestimates of the CBL depth, especially if the CBL follows small-scale terrain features in reality. Our findings underscore the importance of considering the time of day and year for GHG concentration assimilation, reinforcing the need for finer grid spacing in simulating atmospheric CO2 transport for more accurate simulation of CBL depth. Similarly, studies that investigate integrated water vapor transport (IWVT) to determine atmospheric moisture sources and sinks, rely on the PBL depth as the separation between the moister boundary layer and the drier, free atmosphere in a similar way as in inverse modeling approaches. These studies use grid spacing of 10 km or higher [48,49]. Unlike inverse modeling approaches, IWVT studies deal with active tracers, thereby complicating the significance of the PBL depth signal in the final outcome, as surface water vapor concentration has less correlation with the PBL depth, for instance.
- Air pollution studies: A realistic CBL depth is important to air pollution studies for two main reasons: first, pollutant concentrations are fairly well-mixed within the CBL, and therefore, inversely related to the depth of the CBL. A CBL that is too deep—as expected in coarse-grid models in mountainous terrain—would lead to an underestimation of critical values for pollutant concentration. Second, misplacing the entrainment zone too high might introduce different background air into the CBL, introducing a bias in air pollutant concentration. This, in turn, could lead to different estimates of pollutant concentrations when atmospheric stability is high, for example at night. The degree to which different CBL depths play a role in calculating pollutant concentration as a consequence of terrain smoothing has yet to be determined. Nevertheless, a 10% difference in CBL depth could lead to large errors in pollution concentrations in the PBL, either below or above a certain threshold value for air pollution warnings.
- Planning and executing prescribed burns: Predicting the behavior of intentionally ignited fires and the smoke they release depends on several factors, including the CBL depth. We have shown that coarse models often simulate larger CBL depths compared to finer models. Since larger CBL depths generally create more favorable conditions for prescribed burning, relying on a coarse model for CBL depth in complex terrain could incorrectly indicate acceptable conditions. Thus, models that excessively smooth terrain are unsuitable for accurate decision-making in this context.
- Orographic precipitation studies: One result of our study is that coarse models tend to unrealistically advance the morning heating of the boundary layer. Ref. [50] showed from observations that this advanced heating enhances convective initiation, which in turn could lead to premature cloud formation, precipitation, and thunderstorm development in mountainous terrain when coarse-grid models are used. Other processes affected by grid spacing include stability [51] and mechanical and thermal forcings [52]. Whether early convective initiation due to coarser grid spacing affects cloud evolution and precipitation characteristics, has yet to be determined.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos15020145/s1. Figure S1: (a–c) same as Figure A1a–c in Appendix A of the main manuscript but for 30 km and 10 km grid spacing comparisons, (d–f) same as Figure A1e–g in Appendix A of the main manuscript but for 30 km and 10 km grid spacing comparisons, and (g–i) same as (d–f) but for interpolated terrain simulations; Figure S2: Same as Figure 6 in main manuscript but for relative differences; Figure S3: Same as Figure 7 in main manuscript but for relative differences; Figure S4: Same as Figure 10 in main manuscript but for relative differences; Figure S5: Hourly and seasonal medians of CBL depth difference between the coarse (10 km) and fine (3.3 km) domains for the DPG area for steeper and higher mountains in the DPG area than shown in Figure 9b in main manuscript. Each panel title indicates the laplacian range for this subselection of and the mean terrain elevation difference between coarse and fine grid domains of the selected grid cells. See Table 2 in main manuscript for the number of available days per season per area; Figure S6: Same as Figure 11 in main manuscript but for WSMR area; Figure S7: Same as Figure 11 in main manuscript but for YPG area; Figure S8: Same as Figure 10 in main manuscript but for the comparison of 30 and 10 km grid spacing domains; Figure S9: Same as Figure 12 in main manuscript but for 10 July 2013, r = 0.54.
Author Contributions
Conceptualization, G.-J.D. and S.F.J.D.W.; methodology, G.-J.D. and S.F.J.D.W.; software, S.F.J.D.W. and J.C.K.; validation, G.-J.D.; formal analysis, G.-J.D.; investigation, G.-J.D.; data provision, J.C.K.; data curation, G.-J.D.; writing—original draft preparation, G.-J.D.; writing—review and editing, G.-J.D., S.F.J.D.W. and J.C.K.; visualization, G.-J.D.; supervision, S.F.J.D.W.; project administration, S.F.J.D.W.; funding acquisition, S.F.J.D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded partly by National Oceanic and Atmospheric Administration award Grant NA13OAR4310065.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
We used the Weather Research and Forecasting model to generate the output for the quasi-idealized simulations. The 4DWX output can be made available upon request due to technical restrictions. 4DWX output used for the study is too large to share directly in a public repository, and thus is not directly available to the public, but could be made available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 4DWX | Four-Dimensional Weather System |
| ACM2 | Asymmetrical Convective Model version 2 |
| AGL | above ground level |
| CBL | Convective Boundary Layer |
| D17 | Duine and De Wekker (2017) |
| DPG | Dugway Proving Ground |
| GHG | Greenhouse Gas |
| IWVT | Integrated Water Vapor Transport |
| MST | Mountain Standard Time |
| MYJ | Mellor–Yamada–Janic |
| MYNN2.5 | Mellory-Yamada-Nakanishi-Niino Level 2.5 |
| PBL | Planetary Boundary Layer |
| QNSE | Quasi-Normal Scale Elimination |
| TKE | Turbulent Kinetic Energy |
| USGS | United States Geological Survey |
| YPG | Yuma Proving Ground |
| YSU | Yonsei University |
| WRF | Weather Research and Forecasting model |
| WSMR | White Sands Missile Range |
Appendix A. Sensitivity to CBL Derivation Method and Vertical Resolution
Other important aspects that could influence our results are the CBL derivation methods and vertical resolution. We investigated this by using the same day as the quasi-idealized case study presented in the main part of the paper (1 July 2013). We selected four widely used methods to derive the top of a convective PBL, including the -method, the parcel method, the +1.5K method [30], and the 2 K km−1 (or fixed-threshold) method [5]. The parcel method showed very similar results as the -method, and so were omitted in this analysis. We show the results of simulations using five different PBL parameterization schemes.
By using the method, a more comparable pattern in diurnal CBL development is estimated for all schemes than focusing on the internally calculated PBLs (Figure A1a,b). The local and nonlocal schemes are separated into two groups: the nonlocal schemes YSU and ACM2 show maximum CBL depths of around 2750 m, whereas the local TKE-based schemes (MYJ, QNSE, and MYNN2.5) show CBL depths in the range of around 2300–2500 m. Using the +1.5K method leads to very comparable CBL depths for all PBL schemes (Figure A1c), which was found in earlier research [5,30]. Using this method we also find deeper CBLs for nonlocal than for local schemes [1,3]. The 2 K km−1 (fixed-threshold) method shows a consistent pattern for CBL depths among all schemes, with the largest values of around 3200 m (Figure A1d). This method, however, seems to be biased by vertical grid spacing, as will be discussed in the next paragraph.
Despite the similarities for domain-averaged absolute CBL depths between coarse- and fine-grid domains, over mountaintops, there is a clear tendency for larger CBL depths in the coarse-grid than in the fine-grid domain for all PBL schemes, even by applying the different CBL derivation methods (solid lines in Figure A1e–g). We note a scattered behavior, however, for internally calculated CBL depths for mountaintops (solid lines in Figure A1e), with only a slight tendency for larger CBL depths in the coarse-grid domain. For mountaintops, larger CBL depths are found for all schemes in the coarse-grid domain (Figure A1e), whereas the full-domain averaged CBL depths in the coarse-grid domain are lower. Using and comparing single methods, a clearer pattern is found for simulating larger CBL depths in the coarse-grid domains over mountaintops. For example, using the -method (solid lines in Figure A1f), all PBL schemes simulate larger CBL depths for coarse- than for fine grids. They remain larger in the coarse-grid domain throughout the day, with a maximum difference of around 100 m. This pattern is similar to the 2-yr climatology (see Figure 9), and confirms that our one-day case study is representative of the two-yr climatology. When using the +1.5K method, we find similar differences as for the method (solid lines in Figure A1g). The 2 K km−1 method shows reduced differences for CBL depths (solid lines in Figure A1h). This method, however, is not well suited for an analysis based on simulations for one day, as the found value for a fixed threshold would be assigned directly to distinct model levels. This is demonstrated by increasing the vertical grid spacing in the innermost domain only [53], where indeed larger CBL depths are simulated in the coarse-grid domain (see marked lines in Figure A1h). Therefore, we conclude that the 2 K km−1 method is unsuitable when it comes to our analysis based on one day.
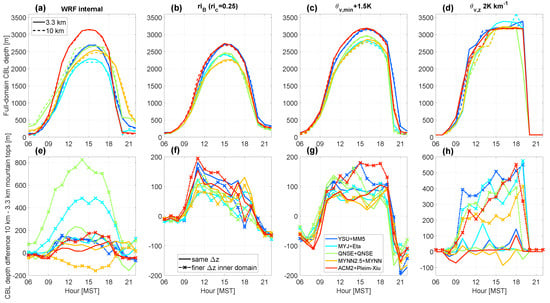
Figure A1.
Hourly evolution of domain-averaged CBL depths expressed in medians with 10 km (dashed lines) and 3.3 km (solid lines) grid spacing domains (a–d), and differences over mountaintops (e–g) on 1 July 2013, DPG area, for different PBL schemes. The solid lines in (e–h) represent default run, the ‘x’ marked lines in (e–h) represent differences between the coarse- and fine-grid domains, but with nested vertical grid spacing. Note the different y-axis for the panel of (e–h). The legend in (a) applies on all upper panels, the legends in (f) on all lower panels, and the colors from the legend in (g) apply on all panels.
Applying the nested vertical grid spacing simulations to the other CBL derivation methods (‘x’ marked lines in Figure A1e–g), we note that CBL depths for the increased vertical grid spacing become slightly larger in the coarse-grid than in the fine-grid domain than for simulations without vertical grid nesting. Interestingly, the schemes that derive a CBL using a TKE threshold (MYJ and QNSE), show much larger values in the coarse-grid domain. As only the fine-grid domain has been changed in the settings in combination with the one-way nesting approach, we conclude that the minimum threshold for TKE is reached at lower levels in models with finer grid spacings, hence in the finer-grid spacing domain that resolves the terrain better. This means that less TKE is transported vertically for increasing vertical grid spacing. However, for the other CBL derivation methods, the differences are similar or slightly larger in comparison with the default grid spacing. This leads to the conclusion that vertical grid spacing itself is not the driving factor for larger CBL depths in the coarse-grid domain. More importantly, we have shown in this appendix that irrespective of the PBL parameterizations used, CBL depths are always larger over mountaintops in coarse than in fine-grid domains.
References
- García-Díez, M.; Fernández, J.; Fita, L.; Yagüe, C. Seasonal dependence of WRF model biases and sensitivity to PBL schemes over Europe. Q. J. Roy. Meteor. Soc. 2013, 139, 501–514. [Google Scholar] [CrossRef]
- Cohen, A.E.; Cavallo, S.M.; Coniglio, M.C.; Brooks, H.E. A review of planetary boundary layer parameterization schemes and their sensitivity in simulating southeastern US cold season severe weather environments. Weather Forecast 2015, 30, 591–612. [Google Scholar] [CrossRef]
- Kalverla, P.; Duine, G.J.; Steeneveld, G.J.; Hedde, T. Evaluation of the Weather Research and Forecasting model for contrasting diurnal cycles in the Durance Valley complex terrain during the KASCADE field campaign. J. Appl. Meteorol. Clim. 2016, 55, 861–882. [Google Scholar] [CrossRef]
- Duine, G.J.; Jones, C.; Carvalho, L.M.; Fovell, R.G. Simulating Sundowner Winds in Coastal Santa Barbara: Model Validation and Sensitivity. Atmosphere 2019, 10, 155. [Google Scholar] [CrossRef]
- LeMone, M.A.; Tewari, M.; Chen, F.; Dudhia, J. Objectively determined fair-weather CBL depths in the ARW-WRF model and their comparison to CASES-97 observations. Mon. Weather Rev. 2013, 141, 30–54. [Google Scholar] [CrossRef]
- Duine, G.J.; De Wekker, S. The effects of horizontal grid spacing on simulated daytime boundary layer depths in an area of complex terrain in Utah. Environ. Fluid Mech. 2020, 20, 1313–1331. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Davis, C.; Warner, T.; Astling, E.; Bowers, J. Development and application of an operational, relocatable, mesogamma-scale weather analysis and forecasting system. Tellus A 1999, 51, 710–727. [Google Scholar] [CrossRef]
- Liu, Y.; Warner, T.T.; Bowers, J.F.; Carson, L.P.; Chen, F.; Clough, C.A.; Davis, C.A.; Egeland, C.H.; Halvorson, S.F.; Huck, T.W., Jr.; et al. The operational mesogamma-scale analysis and forecast system of the US Army Test and Evaluation Command. Part I: Overview of the modeling system, the forecast products, and how the products are used. J. Appl. Meteorol. Climatol. 2008, 47, 1077–1092. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Janjić, Z.I. Nonsingular implementation of the Mellor–Yamada level 2.5 scheme in the NCEP Meso model. NCEP Off. Note 2002, 437, 61. [Google Scholar]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res.-Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Thompson, G.; Rasmussen, R.M.; Manning, K. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part I: Description and sensitivity analysis. Mon. Weather Rev. 2004, 132, 519–542. [Google Scholar] [CrossRef]
- Kalthoff, N.; Binder, H.J.; Kossmann, M.; Vögtlin, R.; Corsmeier, U.; Fiedler, F.; Schlager, H. Temporal evolution and spatial variation of the boundary layer over complex terrain. Atmos. Environ. 1998, 32, 1179–1194. [Google Scholar] [CrossRef]
- De Wekker, S.F.; Kossmann, M. Convective boundary layer heights over mountainous terrain—A review of concepts. Front. Earth Sci. 2015, 3, 77. [Google Scholar] [CrossRef]
- Pleim, J.E. A combined local and nonlocal closure model for the atmospheric boundary layer. Part I: Model description and testing. J. Appl. Meteorol. Clim. 2007, 46, 1383–1395. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor–Yamada level-3 model: Its numerical stability and application to a regional prediction of advection fog. Bound.-Lay. Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Sukoriansky, S.; Galperin, B.; Perov, V. Application of a new spectral theory of stably stratified turbulence to the atmospheric boundary layer over sea ice. Bound.-Lay. Meteorol. 2005, 117, 231–257. [Google Scholar] [CrossRef]
- Kleczek, M.A.; Steeneveld, G.J.; Holtslag, A.A. Evaluation of the weather research and forecasting mesoscale model for GABLS3: Impact of boundary-layer schemes, boundary conditions and spin-up. Bound.-Lay. Meteorol. 2014, 152, 213–243. [Google Scholar] [CrossRef]
- Beljaars, A. The parametrization of surface fluxes in large-scale models under free convection. Q. J. Roy. Meteor. Soc. 1995, 121, 255–270. [Google Scholar]
- Janjic, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Pleim, J.E. A simple, efficient solution of flux-profile relationships in the atmospheric surface layer. J. Appl. Meteorol. Clim. 2006, 45, 341–347. [Google Scholar] [CrossRef]
- Vogelezang, D.; Holtslag, A. Evaluation and model impacts of alternative boundary-layer height formulations. Bound.-Lay. Meteorol. 1996, 81, 245–269. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; 666p. [Google Scholar]
- Nielsen-Gammon, J.W.; Powell, C.L.; Mahoney, M.J.; Angevine, W.M.; Senff, C.; White, A.; Berkowitz, C.; Doran, C.; Knupp, K. Multisensor estimation of mixing heights over a coastal city. J. Appl. Meteorol. Clim. 2008, 47, 27–43. [Google Scholar] [CrossRef]
- Seibert, P.; Beyrich, F.; Gryning, S.E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Seidel, D.J.; Zhang, Y.; Beljaars, A.; Golaz, J.C.; Jacobson, A.R.; Medeiros, B. Climatology of the planetary boundary layer over the continental United States and Europe. J. Geophys. Res.-Atmos. 2012, 117, D17106. [Google Scholar] [CrossRef]
- Koffi, E.; Bergamaschi, P.; Karstens, U.; Krol, M.; Segers, A.; Schmidt, M.; Levin, I.; Vermeulen, A.; Fisher, R.; Kazan, V.; et al. Evaluation of the boundary layer dynamics of the TM5 model over Europe. Geosci. Model Dev. 2016, 9, 3137. [Google Scholar] [CrossRef]
- Wagner, J.S.; Gohm, A.; Rotach, M.W. The impact of horizontal model grid resolution on the boundary layer structure over an idealized valley. Mon. Weather Rev. 2014, 142, 3446–3465. [Google Scholar] [CrossRef]
- Bright, D.R.; Mullen, S.L. The sensitivity of the numerical simulation of the southwest monsoon boundary layer to the choice of PBL turbulence parameterization in MM5. Weather Forecast 2002, 17, 99–114. [Google Scholar] [CrossRef]
- Holzworth, G.C. Estimates of mean maximum mixing depths in the contiguous United States. Mon. Weather Rev. 1964, 92, 235–242. [Google Scholar] [CrossRef]
- Davy, R. The Climatology of the Atmospheric Boundary Layer in Contemporary Global Climate Models. J. Climate 2018, 31, 9151–9173. [Google Scholar] [CrossRef]
- Rödenbeck, C. Estimating CO2 Sources and Sinks from Atmospheric Mixing Ratio Measurements Using a Global Inversion of Atmospheric Transport; MPI-BGC: Jena, Germany, 2005; 53p. [Google Scholar]
- Geels, C.; Gloor, M.; Ciais, P.; Bousquet, P.; Peylin, P.; Vermeulen, A.; Dargaville, R.; Aalto, T.; Brandt, J.; Christensen, J.; et al. Comparing atmospheric transport models for future regional inversions over Europe–Part 1: Mapping the atmospheric CO2 signals. Atmos. Chem. Phys. 2007, 7, 3461–3479. [Google Scholar] [CrossRef]
- Peters, W.; Krol, M.; Van Der Werf, G.; Houweling, S.; Jones, C.; Hughes, J.; Schaefer, K.; Masarie, K.; Jacobson, A.; Miller, J.; et al. Seven years of recent European net terrestrial carbon dioxide exchange constrained by atmospheric observations. Glob. Chang. Biol. 2010, 16, 1317–1337. [Google Scholar] [CrossRef]
- Keeling, C.D.; Bacastow, R.B.; Bainbridge, A.E.; Ekdahl, C.A., Jr.; Guenther, P.R.; Waterman, L.S.; Chin, J.F. Atmospheric carbon dioxide variations at Mauna Loa observatory, Hawaii. Tellus 1976, 28, 538–551. [Google Scholar] [CrossRef]
- Forrer, J.; Rüttimann, R.; Schneiter, D.; Fischer, A.; Buchmann, B.; Hofer, P. Variability of trace gases at the high-Alpine site Jungfraujoch caused by meteorological transport processes. J. Geophys. Res-Atmos. 2000, 105, 12241–12251. [Google Scholar] [CrossRef]
- De Wekker, S.F.; Ameen, A.; Song, G.; Stephens, B.B.; Hallar, A.G.; McCubbin, I.B. A preliminary investigation of boundary layer effects on daytime atmospheric CO2 concentrations at a mountaintop location in the Rocky Mountains. Acta Geophys. 2009, 57, 904–922. [Google Scholar] [CrossRef]
- Lee, T.R.; De Wekker, S.F.; Pal, S.; Andrews, A.E.; Kofler, J. Meteorological controls on the diurnal variability of carbon monoxide mixing ratio at a mountaintop monitoring site in the Appalachian Mountains. Tellus B Chem. Phys. Meteorol. 2015, 67, 25659. [Google Scholar] [CrossRef]
- Zhu, C.S.; Cao, J.J.; Xu, B.Q.; Huang, R.J.; Wang, P.; Ho, K.F.; Shen, Z.X.; Liu, S.X.; Han, Y.M.; Tie, X.X.; et al. Black carbon aerosols at Mt. Muztagh Ata, a high-altitude location in the western Tibetan Plateau. Aerosol Air Qual. Res 2016, 16, 752–763. [Google Scholar] [CrossRef]
- Lin, J.C.; Mallia, D.V.; Wu, D.; Stephens, B.B. How can mountaintop CO2 observations be used to constrain regional carbon fluxes? Atmos. Chem. Phys. 2017, 17, 5561–5581. [Google Scholar] [CrossRef]
- Peters, W.; Jacobson, A.R.; Sweeney, C.; Andrews, A.E.; Conway, T.J.; Masarie, K.; Miller, J.B.; Bruhwiler, L.M.; Pétron, G.; Hirsch, A.I.; et al. An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker. Proc. Natl. Acad. Sci. USA 2007, 104, 18925–18930. [Google Scholar] [CrossRef]
- Yang, Z.; Dominguez, F. Investigating land surface effects on the moisture transport over South America with a moisture tagging model. J. Clim. 2019, 32, 6627–6644. [Google Scholar] [CrossRef]
- Insua-Costa, D.; Miguez-Macho, G. A new moisture tagging capability in the Weather Research and Forecasting model: Formulation, validation and application to the 2014 Great Lake-effect snowstorm. Earth Syst. Dynam. 2018, 9, 167–185. [Google Scholar] [CrossRef]
- Henkes, A.; Fisch, G.; Toledo Machado, L.A.; Chaboureau, J.P. Morning boundary layer conditions for shallow to deep convective cloud evolution during the dry season in the central Amazon. Atmos. Chem. Phys. Discuss. 2021, 2021, 1–29. [Google Scholar] [CrossRef]
- Kirshbaum, D.J.; Adler, B.; Kalthoff, N.; Barthlott, C.; Serafin, S. Moist orographic convection: Physical mechanisms and links to surface-exchange processes. Atmosphere 2018, 9, 80. [Google Scholar] [CrossRef]
- Göbel, M.; Serafin, S.; Rotach, M.W. Adverse impact of terrain steepness on thermally-driven initiation of orographic convection. Weather Clim. Dyn. 2023, 2023, 1–28. [Google Scholar] [CrossRef]
- Daniels, M.H.; Lundquist, K.A.; Mirocha, J.D.; Wiersema, D.J.; Chow, F.K. A new vertical grid nesting capability in the Weather Research and Forecasting (WRF) Model. Mon. Weather Rev. 2016, 144, 3725–3747. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).