The Roles of the Eastern Atlantic Niño and Central Atlantic Niño in ENSO Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results
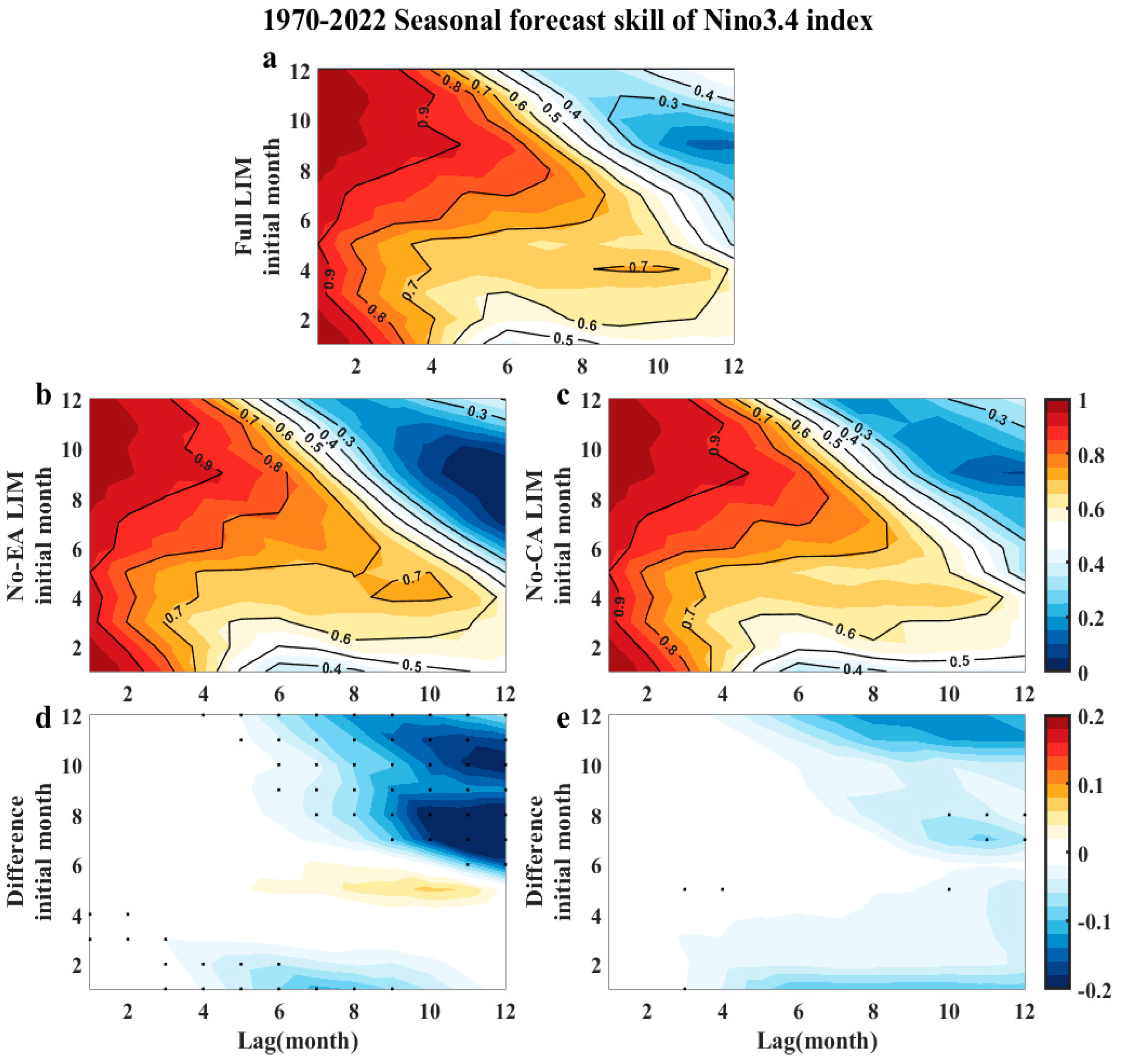
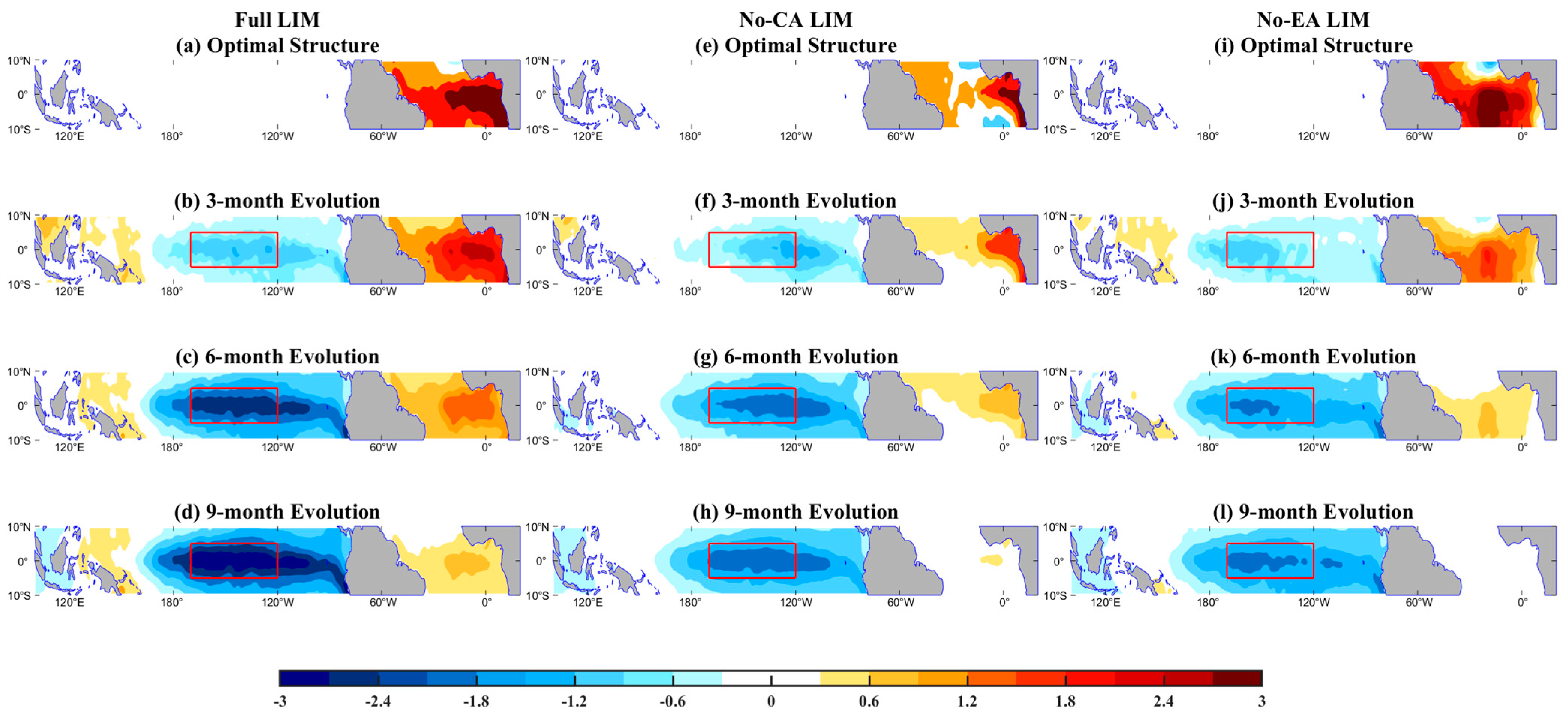
3.1. The Impact of the Two Atlantic Niño Modes on ENSO Prediction
3.2. The Role of the EA/CA Mode in ENSO Diversity Predictability
3.3. The Interdecadal Role of EA and CA Niño in ENSO Prediction
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alexander, M.A.; Blade, I.; Newman, M.; Lanzante, J.R.; Lau, N.; Scott, J.D. The Atmospheric Bridge: The Influence of ENSO Teleconnections on Air—Sea Interaction over the Global Oceans. J. Clim. 2002, 15, 2205–2231. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Cobb, K.M.; Furtado, J.C.; Schneider, N.; Anderson, B.T.; Bracco, A.; Alexander, M.A.; Vimont, D.J. Central Pacific El Nino and decadal climate change in the North Pacific Ocean. Nat. Geosci. 2010, 3, 762–765. [Google Scholar] [CrossRef]
- Liu, Z.; Di Lorenzo, E. Mechanisms and Predictability of Pacific Decadal Variability. Curr. Clim. Chang. Rep. 2018, 4, 128–144. [Google Scholar] [CrossRef]
- Cai, W.; Wu, L.; Lengaigne, M.; Li, T.; McGregor, S.; Kug, J.; Yu, J.; Stuecker, M.F.; Santoso, A.; Li, X.; et al. Pantropical climate interactions. Science 2019, 363, eaav4236. [Google Scholar] [CrossRef] [PubMed]
- Capotondi, A.; Deser, C.; Phillips, A.S.; Okumura, Y.; Larson, S.M. ENSO and Pacific Decadal Variability in the Community Earth System Model Version 2. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002022. [Google Scholar] [CrossRef]
- Kane, R.P. Extremes of the ENSO phenomenon and Indian summer monsoon rainfall. Int. J. Climatol. 1998, 18, 775–791. [Google Scholar] [CrossRef]
- Kripallani, R.H.; Kulkarni, A. Rainfall variability over South-east Asia—Connections with Indian monsoon and ENSO extremes: New perspectives. Int. J. Climatol. 1998, 17, 1155–1168. [Google Scholar] [CrossRef]
- Dutta, U.; Hazra, A.; Chaudhari, H.S.; Saha, S.K.; Pokhrel, S.; Verma, U. Unraveling the Global Teleconnections of Indian Summer Monsoon Clouds: Expedition from CMIP5 to CMIP6. Glob. Planet. Chang. 2022, 215, 103873. [Google Scholar] [CrossRef]
- Capotondi, A.; Sardeshmukh, P.D. Optimal precursors of different types of ENSO events. Geophys. Res. Lett. 2015, 42, 9952–9960. [Google Scholar] [CrossRef]
- Capotondi, A.; Ricciardulli, L. The influence of pacific winds on ENSO diversity. Sci. Rep. 2021, 11, 18672. [Google Scholar] [CrossRef] [PubMed]
- Tseng, Y.H.; Huang, J.H.; Chen, H.C. Improving the Predictability of Two Types of ENSO by the Characteristics of Extratropical Precursors. Geophys. Res. Lett. 2022, 49, e2021GL097190. [Google Scholar] [CrossRef]
- Chen, H.; Jin, Y.; Liu, Z.; Sun, D.; Chen, X.; McPhaden, M.J.; Capotondi, A.; Lin, X. Central-Pacific El Niño-Southern Oscillation less predictable under greenhouse warming. Nat. Commun. 2024, 15, 4370. [Google Scholar] [CrossRef]
- Jin, F. An Equatorial Ocean Recharge Paradigm for ENSO. Part I: Conceptual Model. J. Atmos. Sci. 1997, 54, 811–829. [Google Scholar] [CrossRef]
- Jin, F. An Equatorial Ocean Recharge Paradigm for ENSO. Part II: A Stripped-Down Coupled Model. J. Atmos. Sci. 1997, 54, 830–847. [Google Scholar] [CrossRef]
- Meinen, C.S.; McPhaden, M.J. Observations of Warm Water Volume Changes in the Equatorial Pacific and Their Relationship to El Niño and La Niña. J. Clim. 2000, 13, 3551–3559. [Google Scholar] [CrossRef]
- Vecchi, G.A.; Harrison, D.E. Tropical Pacific Sea Surface Temperature Anomalies, El Niño, and Equatorial Westerly Wind Events. J. Clim. 2000, 13, 1814–1830. [Google Scholar] [CrossRef]
- McPhaden, M.J. Evolution of the 2002/03 El Niño. Bull. Am. Meteorol. Soc. 2004, 85, 677–696. [Google Scholar] [CrossRef]
- Capotondi, A.; Sardeshmukh, P.D.; Ricciardulli, L. The Nature of the Stochastic Wind Forcing of ENSO. J. Clim. 2018, 31, 8081–8099. [Google Scholar] [CrossRef]
- Zhao, Y.; Jin, Y.; Li, J.; Capotondi, A. The Role of Extratropical Pacific in Crossing ENSO Spring Predictability Barrier. Geophys. Res. Lett. 2022, 49, e2022GL099488. [Google Scholar] [CrossRef]
- Zhao, Y.; Jin, Y.; Capotondi, A.; Li, J.; Sun, D. The Role of Tropical Atlantic in ENSO Predictability Barrier. Geophys. Res. Lett. 2023, 50, e2022GL101853. [Google Scholar] [CrossRef]
- Jin, Y.; Meng, X.; Zhang, L.; Zhao, Y.; Cai, W.; Wu, L. The Indian Ocean Weakens the ENSO Spring Predictability Barrier: Role of the Indian Ocean Basin and Dipole Modes. J. Clim. 2023, 36, 8331–8345. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, R.; Liu, T.; Duan, W.; Yang, D.; Zheng, F.; Ren, H.; Lian, T.; Gao, C.; Chen, D.; et al. Progress in ENSO prediction and predictability study. Natl. Sci. Rev. 2018, 5, 826–839. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, Y.; Rong, X. Theory for the Seasonal Predictability Barrier: Threshold, Timing, and Intensity. J. Clim. 2019, 32, 423–443. [Google Scholar] [CrossRef]
- Jin, Y.; Lu, Z.; Liu, Z. Controls of Spring Persistence Barrier Strength in Different ENSO Regimes and Implications for 21st Century Changes. Geophys. Res. Lett. 2020, 47, e2020GL088010. [Google Scholar] [CrossRef]
- Webster, P.J.; Yang, S. Monsoon and Enso: Selectively Interactive Systems. Q. J. R. Meteorol. Soc. 1992, 118, 877–926. [Google Scholar] [CrossRef]
- Xue, Y.; Cane, M.A.; Zebiak, S.E.; Blumenthal, M.B. On the prediction of ENSO: A study with a low- order Markov model. Tellus Ser. A-Dyn. Meteorol. Oceanol. 1994, 46, 512–528. [Google Scholar] [CrossRef]
- Jin, E.K.; Kinter, J.L.; Wang, B.; Park, C.K.; Kang, I.S.; Kirtman, B.P.; Kug, J.S.; Kumar, A.; Luo, J.J.; Schemm, J.; et al. Current status of ENSO prediction skill in coupled ocean–atmosphere models. Clim. Dyn. 2008, 31, 647–664. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, Z.; Lu, Z.; He, C. Seasonal Cycle of Background in the Tropical Pacific as a Cause of ENSO Spring Persistence Barrier. Geophys. Res. Lett. 2019, 46, 13371–13378. [Google Scholar] [CrossRef]
- Wu, R.; Kirtman, B.P.; van den Dool, H. An Analysis of ENSO Prediction Skill in the CFS Retrospective Forecasts. J. Clim. 2009, 22, 1801–1818. [Google Scholar] [CrossRef]
- Hou, M.; Duan, W.; Zhi, X. Season-dependent predictability barrier for two types of El Niño revealed by an approach to data analysis for predictability. Clim. Dyn. 2019, 53, 5561–5581. [Google Scholar] [CrossRef]
- Keenlyside, N.S.; Latif, M. Understanding Equatorial Atlantic Interannual Variability. J. Clim. 2007, 20, 131–142. [Google Scholar] [CrossRef]
- Polo, I.; Rodríguez-Fonseca, B.; Losada, T.; García-Serrano, J. Tropical Atlantic Variability Modes (1979–2002). Part I: Time-Evolving SST Modes Related to West African Rainfall. J. Clim. 2008, 21, 6457–6475. [Google Scholar] [CrossRef]
- Polo, I.; Martin-Rey, M.; Rodriguez-Fonseca, B.; Kucharski, F.; Mechoso, C.R. Processes in the Pacific La Niña onset triggered by the Atlantic Niño. Clim. Dyn. 2015, 44, 115–131. [Google Scholar] [CrossRef]
- Rodríguez Fonseca, B.; Polo, I.; García Serrano, J.; Losada, T.; Mohino, E.; Mechoso, C.R.; Kucharski, F. Are Atlantic Niños enhancing Pacific ENSO events in recent decades? Geophys. Res. Lett. 2009, 36, L20705. [Google Scholar] [CrossRef]
- Ding, H.; Keenlyside, N.S.; Latif, M. Impact of the Equatorial Atlantic on the El Niño Southern Oscillation. Clim. Dyn. 2012, 38, 1965–1972. [Google Scholar] [CrossRef]
- Martín-Rey, M.; Polo, I.; Rodriguez-Fonseca, B.; Kucharski, F. Changes in the interannual variability of the tropical Pacific as a response to an equatorial Atlantic forcing. Sci. Mar. 2012, 76, 105–116. [Google Scholar] [CrossRef]
- Martín-Rey, M.; Rodríguez-Fonseca, B.; Polo, I.; Kucharski, F. On the Atlantic–Pacific Niños connection: A multidecadal modulated mode. Clim. Dyn. 2014, 43, 3163–3178. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kug, J.S.; Park, J.Y. Two distinct roles of Atlantic SSTs in ENSO variability: North Tropical Atlantic SST and Atlantic Niño. Geophys. Res. Lett. 2013, 40, 4012–4017. [Google Scholar] [CrossRef]
- Keenlyside, N.S.; Ding, H.; Latif, M. Potential of equatorial Atlantic variability to enhance El Niño prediction. Geophys. Res. Lett. 2013, 40, 2278–2283. [Google Scholar] [CrossRef]
- Wang, L.; Yu, J.Y.; Paek, H. Enhanced biennial variability in the Pacific due to Atlantic capacitor effect. Nat. Commun. 2017, 8, 14887. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Li, T. Impacts of Tropical North Atlantic and Equatorial Atlantic SST Anomalies on ENSO. J. Clim. 2021, 34, 1–58. [Google Scholar] [CrossRef]
- Ham, Y.; Kug, J.; Park, J.; Jin, F. Sea surface temperature in the north tropical Atlantic as a trigger for El Nino/Southern Oscillation events. Nat. Geosci. 2013, 6, 112–116. [Google Scholar] [CrossRef]
- Chang, P.; Fang, Y.; Saravanan, R.; Ji, L.; Seidel, H. The cause of the fragile relationship between the Pacific El Niño and the Atlantic Niño. Nature 2006, 443, 324–328. [Google Scholar] [CrossRef]
- Lübbecke, J.F.; McPhaden, M.J. On the Inconsistent Relationship between Pacific and Atlantic Niños. J. Clim. 2012, 25, 4294–4303. [Google Scholar] [CrossRef]
- Tokinaga, H.; Richter, I.; Kosaka, Y. ENSO Influence on the Atlantic Niño, Revisited: Multi-Year versus Single-Year ENSO Events. J. Clim. 2019, 32, 4585–4600. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Han, W.; McPhaden, M.J.; Hu, A.; Xing, W. Emergence of the Central Atlantic Niño. Sci. Adv. 2023, 9, eadi5507. [Google Scholar] [CrossRef]
- Tokinaga, H.; Xie, S. Weakening of the equatorial Atlantic cold tongue over the past six decades. Nat. Geosci. 2011, 4, 222–226. [Google Scholar] [CrossRef]
- Prigent, A.; Lübbecke, J.F.; Bayr, T.; Latif, M.; Wengel, C. Weakened SST variability in the tropical Atlantic Ocean since 2000. Clim. Dyn. 2020, 54, 2731–2744. [Google Scholar] [CrossRef]
- Losada, T.; Rodríguez-Fonseca, B. Tropical atmospheric response to decadal changes in the Atlantic Equatorial Mode. Clim. Dyn. 2016, 47, 1211–1224. [Google Scholar] [CrossRef]
- Lübbecke, J.F.; Rodríguez Fonseca, B.; Richter, I.; Martín Rey, M.; Losada, T.; Polo, I.; Keenlyside, N.S. Equatorial Atlantic variability—Modes, mechanisms, and global teleconnections. Wires Clim. Chang. 2018, 9, e527. [Google Scholar] [CrossRef]
- Penland, C.; Matrosova, L. A Balance Condition for Stochastic Numerical Models with Application to the El Niño-Southern Oscillation. J. Clim. 1994, 7, 1352–1372. [Google Scholar] [CrossRef]
- Penland, C.; Sardeshmukh, P.D. The Optimal Growth of Tropical Sea Surface Temperature Anomalies. J. Clim. 1995, 8, 1999–2024. [Google Scholar] [CrossRef]
- Newman, M.; Alexander, M.A.; Scott, J.D. An empirical model of tropical ocean dynamics. Clim. Dyn. 2011, 37, 1823–1841. [Google Scholar] [CrossRef]
- Newman, M.; Sardeshmukh, P.D. Are we near the predictability limit of tropical Indo-Pacific sea surface temperatures? Geophys. Res. Lett. 2017, 44, 8520–8529. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108, 4407. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.S.; Alexander, M.A. Twentieth century tropical sea surface temperature trends revisited. Geophys. Res. Lett. 2010, 37, 10. [Google Scholar] [CrossRef]
- Kug, J.; Jin, F.; An, S. Two Types of El Niño Events: Cold Tongue El Niño and Warm Pool El Niño. J. Clim. 2009, 22, 1499–1515. [Google Scholar] [CrossRef]
- Hasselmann, K. Stochastic climate models Part I. Theory. Tellus 1976, 28, 473–485. [Google Scholar]
- Takahashi, K.; Montecinos, A.; Goubanova, K.; Dewitte, B. ENSO regimes: Reinterpreting the canonical and Modoki El Niño: Reinterpreting Enso Modes. Geophys. Res. Lett. 2011, 38, L10704. [Google Scholar] [CrossRef]
- Vimont, D.J.; Alexander, M.A.; Newman, M. Optimal growth of Central and East Pacific ENSO events. Geophys. Res. Lett. 2014, 41, 4027–4034. [Google Scholar] [CrossRef]
- Zhang, L.; Han, W. Barrier for the Eastward Propagation of Madden-Julian Oscillation Over the Maritime Continent: A Possible New Mechanism. Geophys. Res. Lett. 2020, 47, 2020GL090211. [Google Scholar] [CrossRef]
- Steiger, J.H. Tests for comparing elements of a correlation matrix. Psychol. Bull. 1980, 87, 245–251. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, Y.; Shen, X.; Jin, Y.; Rao, Z.; Pang, Y.; Huang, S. The Roles of the Eastern Atlantic Niño and Central Atlantic Niño in ENSO Prediction. Atmosphere 2024, 15, 1433. https://doi.org/10.3390/atmos15121433
Gan Y, Shen X, Jin Y, Rao Z, Pang Y, Huang S. The Roles of the Eastern Atlantic Niño and Central Atlantic Niño in ENSO Prediction. Atmosphere. 2024; 15(12):1433. https://doi.org/10.3390/atmos15121433
Chicago/Turabian StyleGan, Yuzhi, Xingchen Shen, Yishuai Jin, Zhengxiang Rao, Yiqun Pang, and Shouyou Huang. 2024. "The Roles of the Eastern Atlantic Niño and Central Atlantic Niño in ENSO Prediction" Atmosphere 15, no. 12: 1433. https://doi.org/10.3390/atmos15121433
APA StyleGan, Y., Shen, X., Jin, Y., Rao, Z., Pang, Y., & Huang, S. (2024). The Roles of the Eastern Atlantic Niño and Central Atlantic Niño in ENSO Prediction. Atmosphere, 15(12), 1433. https://doi.org/10.3390/atmos15121433






