A Sensitivity Study of a Bayesian Inversion Model Used to Estimate Emissions of Synthetic Greenhouse Gases at the European Scale
Abstract
1. Introduction
2. Materials and Methods
2.1. Inversion Modelling
2.1.1. Observations
2.1.2. A Priori Emission Field
2.1.3. Footprint/Emission Sensitivity Maps
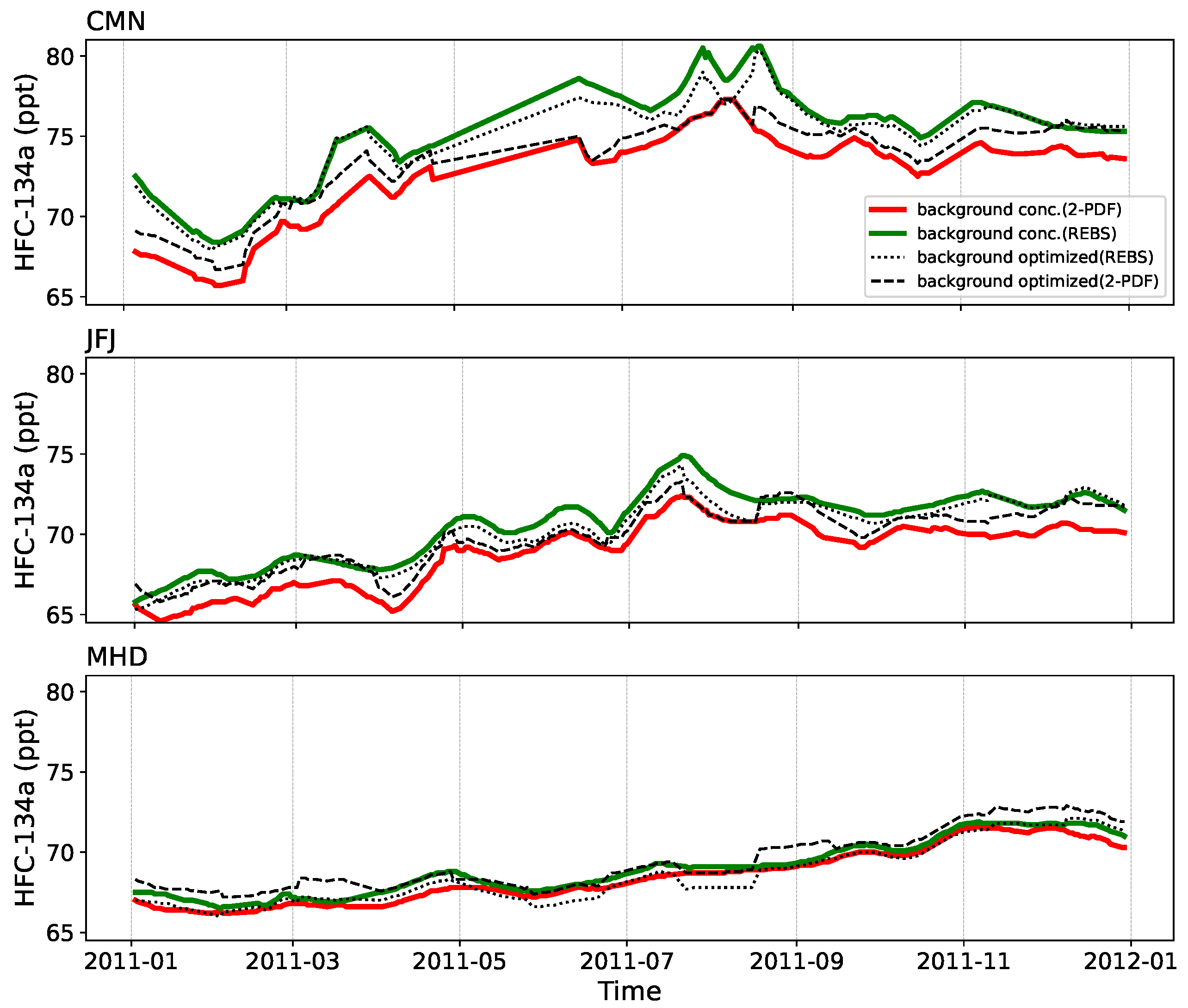
2.1.4. Background Mixing Ratios
2.1.5. Aggregated Grid
2.2. Sensitivity Tests
- Simulations S_CMN, S_JFJ, and S_MHD are inversions that exclusively use data from the CMN, JFJ, and MHD stations, respectively.
- Similarly, the simulations S_CJ, S_CM, and S_JM combine observations from the CMN and JFJ, CMN and MHD, and JFJ and MHD sites, respectively.
3. Results
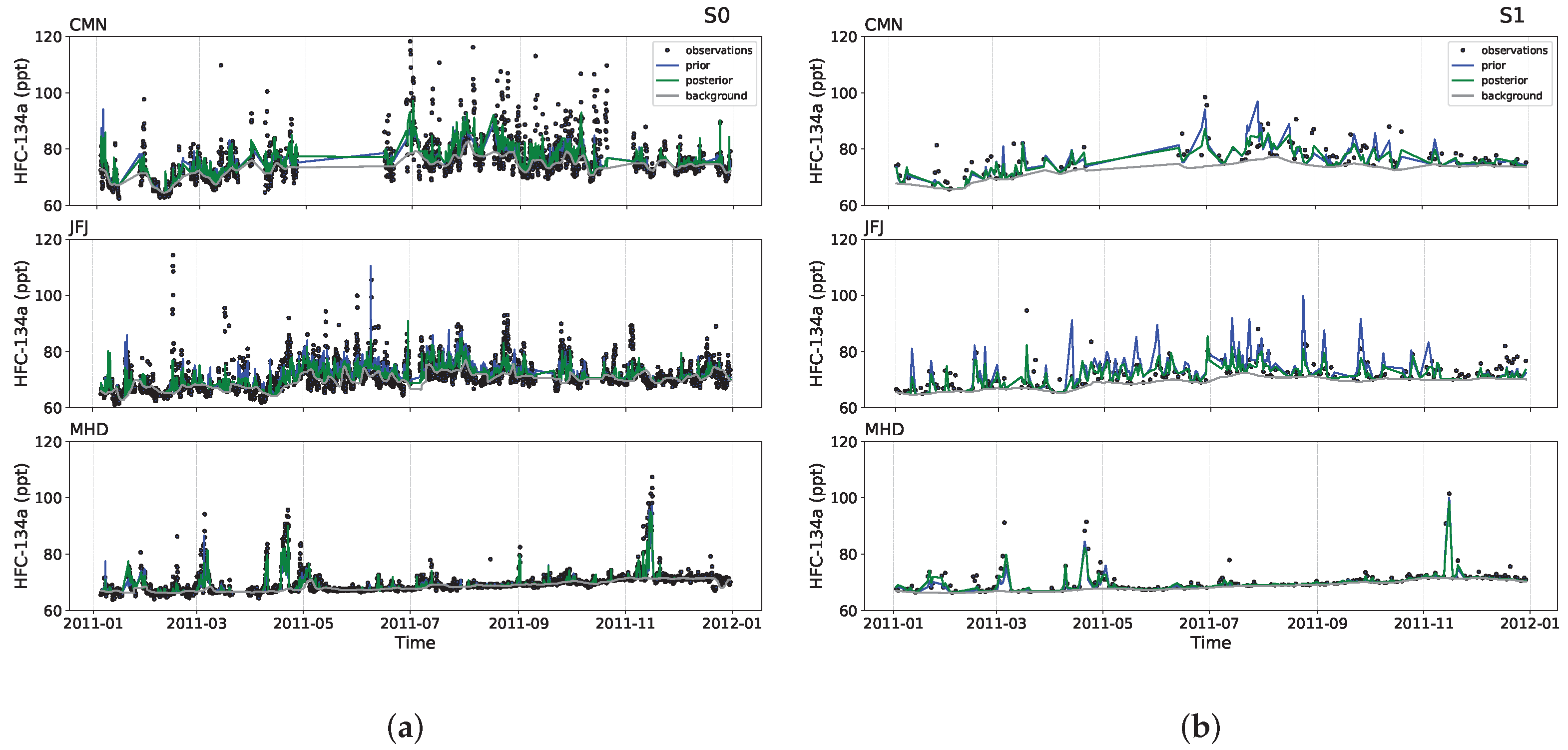
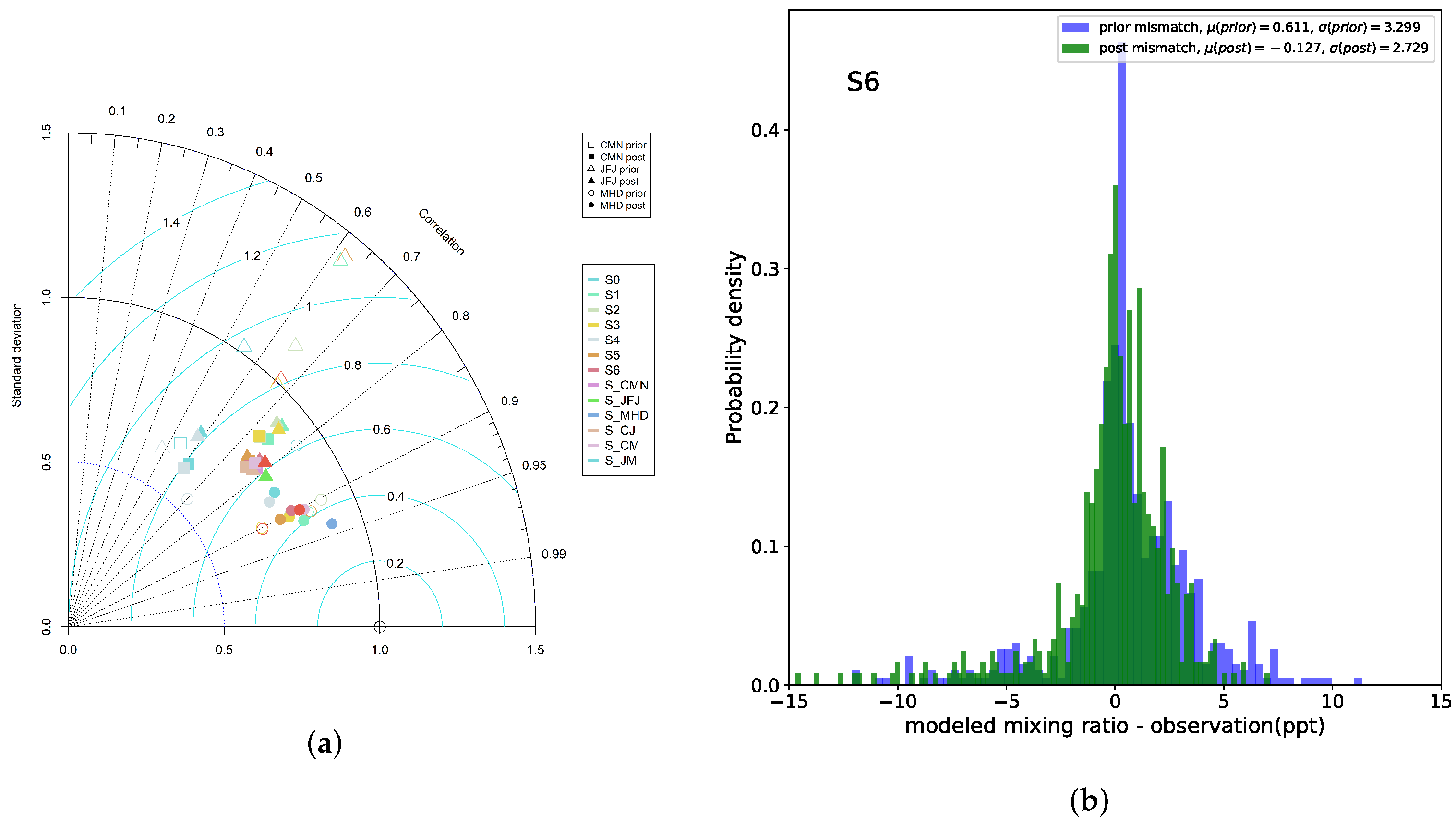
3.1. Simulated Time Series
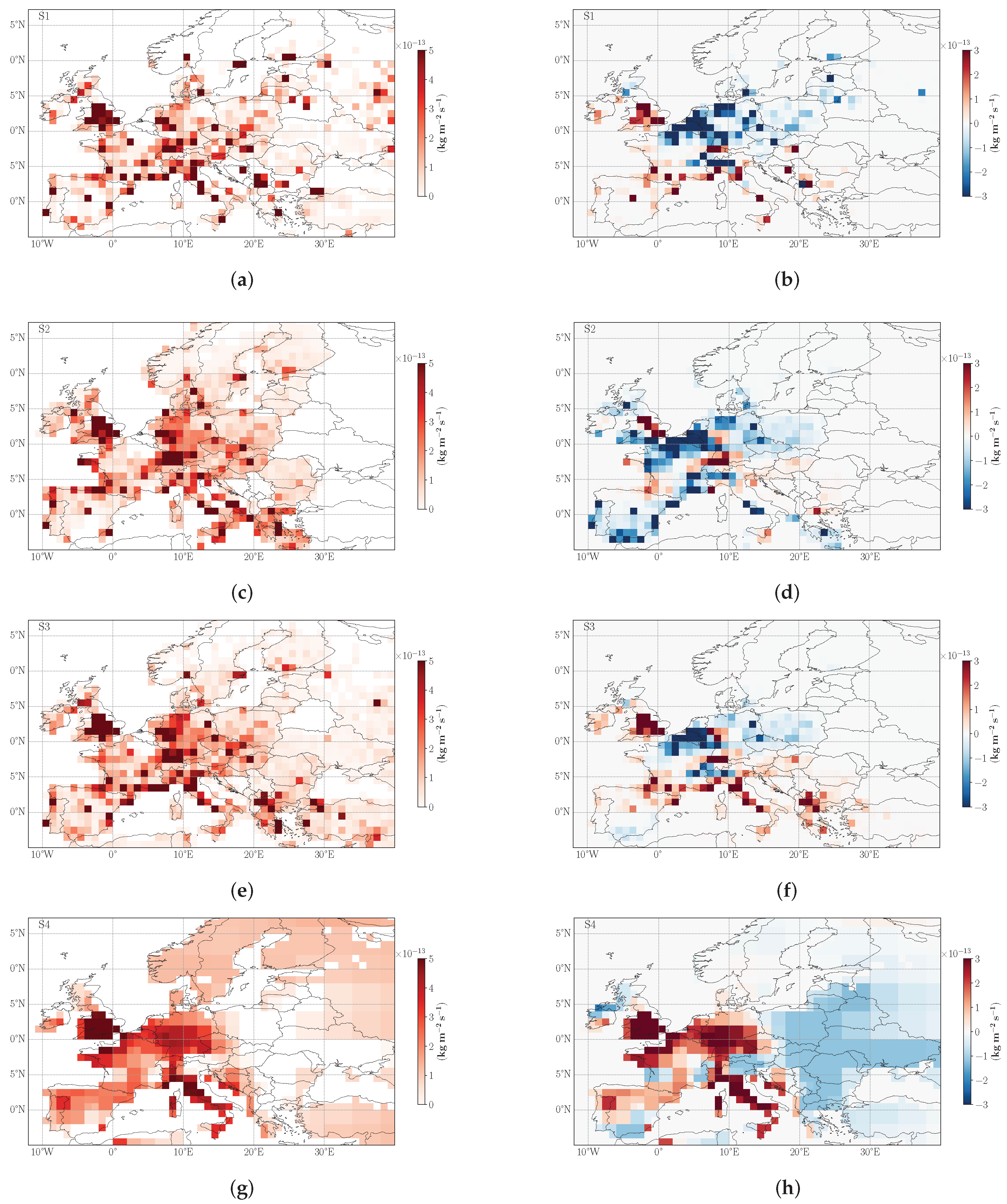
3.2. Emissions Fluxes
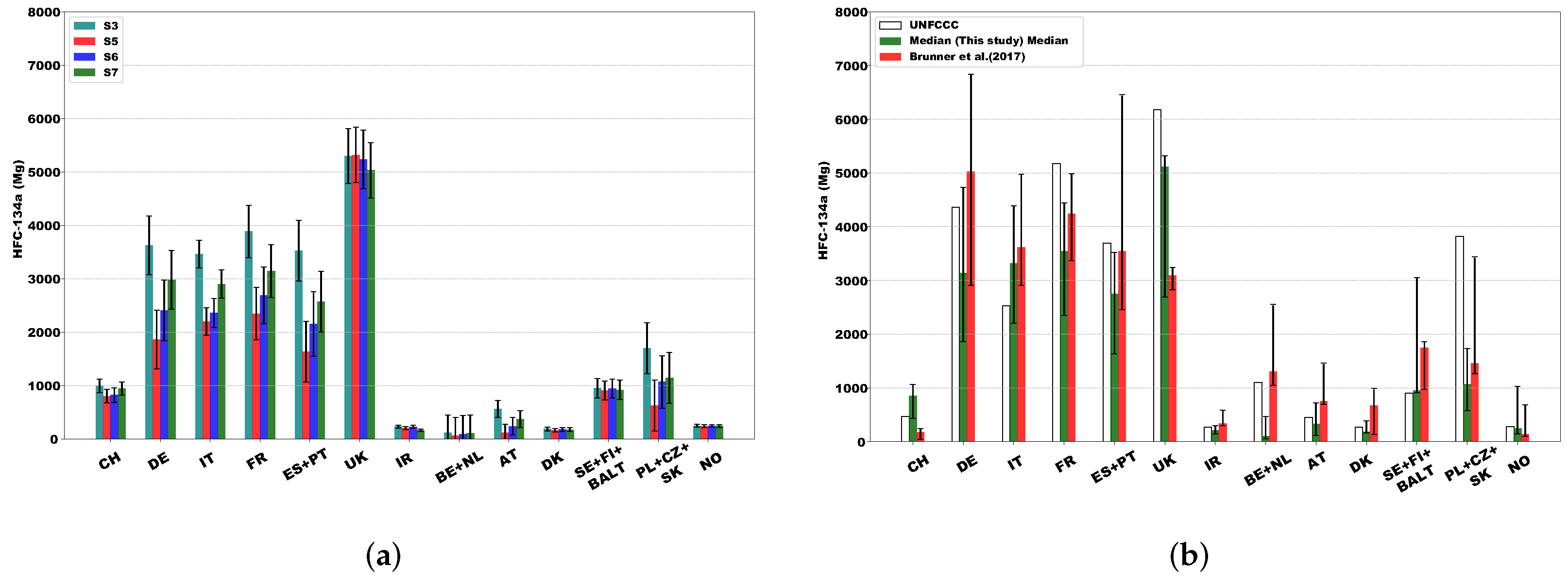
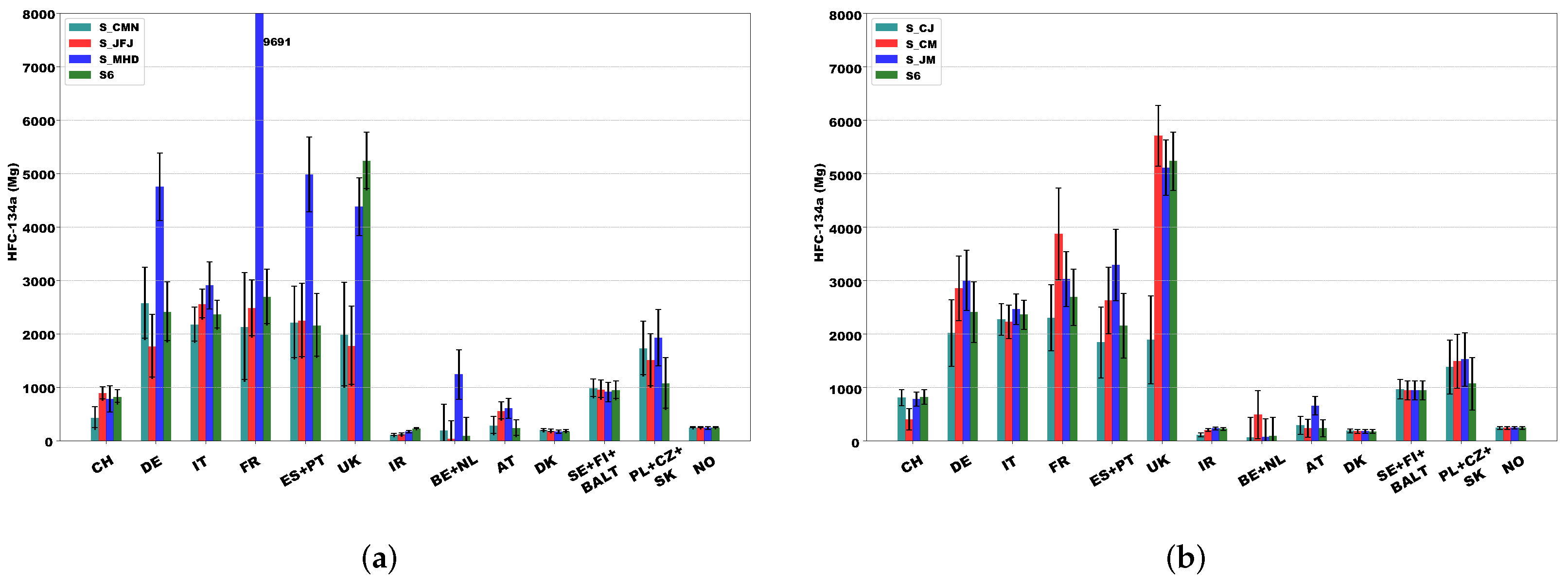
3.3. Country-Aggregated Emissions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2021—The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- IPCC. 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories—IPCC; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Enting, I.G. Inverse Problems in Atmospheric Constituent Transport; Medium: Electronic Resource; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2002. [Google Scholar]
- Berchet, A.; Sollum, E.; Thompson, R.L.; Pison, I.; Thanwerdas, J.; Broquet, G.; Chevallier, F.; Aalto, T.; Berchet, A.; Bergamaschi, P.; et al. The Community Inversion Framework v1.0: A unified system for atmospheric inversion studies. Geosci. Model Dev. 2021, 14, 5331–5354. [Google Scholar] [CrossRef]
- Katharopoulos, I.; Rust, D.; Vollmer, M.K.; Brunner, D.; Reimann, S.; O’Doherty, S.J.; Young, D.; Stanley, K.M.; Schuck, T.; Arduini, J.; et al. Impact of Transport Model Resolution and a Priori Assumptions on Inverse Modeling of Swiss F-gas Emissions. Atmos. Chem. Phys. 2023, 23, 14159–14186. [Google Scholar] [CrossRef]
- Stell, A.C.; Bertolacci, M.; Zammit-Mangion, A.; Rigby, M.; Fraser, P.J.; Harth, C.M.; Krummel, P.B.; Lan, X.; Manizza, M.; Mühle, J.; et al. Modelling the growth of atmospheric nitrous oxide using a global hierarchical inversion. Atmos. Chem. Phys. 2022, 22, 12945–12960. [Google Scholar] [CrossRef]
- Lian, J.; Lauvaux, T.; Utard, H.; Bréon, F.M.; Broquet, G.; Ramonet, M.; Laurent, O.; Albarus, I.; Chariot, M.; Kotthaus, S.; et al. Can we use atmospheric CO2 measurements to verify emission trends reported by cities? Lessons from a 6-year atmospheric inversion over Paris. Atmos. Chem. Phys. 2023, 23, 8823–8835. [Google Scholar] [CrossRef]
- Petrescu, A.M.R.; Qiu, C.; McGrath, M.J.; Peylin, P.; Peters, G.P.; Ciais, P.; Thompson, R.L.; Tsuruta, A.; Brunner, D.; Kuhnert, M.; et al. The consolidated European synthesis of CH4 and N2O emissions for the European Union and United Kingdom: 1990–2019. Earth Syst. Sci. Data 2023, 15, 1197–1268. [Google Scholar] [CrossRef]
- Miller, S.M.; Michalak, A.M.; Detmers, R.G.; Hasekamp, O.P.; Bruhwiler, L.M.P.; Schwietzke, S. China’s Coal Mine Methane Regulations Have Not Curbed Growing Emissions. Nat. Commun. 2019, 10, 303. [Google Scholar] [CrossRef]
- Yao, B.; Fang, X.; Vollmer, M.K.; Reimann, S.; Chen, L.; Fang, S.; Prinn, R.G. China’s Hydrofluorocarbon Emissions for 2011–2017 Inferred from Atmospheric Measurements. Environ. Sci. Technol. Lett. 2019, 6, 479–486. [Google Scholar] [CrossRef]
- Velders, G.J.M.; Andersen, S.O.; Daniel, J.S.; Fahey, D.W.; McFarland, M. The importance of the Montreal Protocol in protecting climate. Proc. Natl. Acad. Sci. USA 2007, 104, 4814–4819. [Google Scholar] [CrossRef]
- Stohl, A.; Seibert, P.; Arduini, J.; Eckhardt, S.; Fraser, P.; Greally, B.R.; Lunder, C.; Maione, M.; Mühle, J.; O’Doherty, S.; et al. An analytical inversion method for determining regional and global emissions of greenhouse gases: Sensitivity studies and application to halocarbons. Atmos. Chem. Phys. 2009, 9, 1597–1620. [Google Scholar] [CrossRef]
- Hu, L.; Montzka, S.A.; Miller, J.B.; Andrews, A.E.; Lehman, S.J.; Miller, B.R.; Thoning, K.; Sweeney, C.; Chen, H.; Godwin, D.S.; et al. U.S. emissions of HFC-134a derived for 2008–2012 from an extensive flask-air sampling network. J. Geophys. Res. Atmos. 2015, 120, 801–825. [Google Scholar] [CrossRef]
- Lunt, M.F.; Rigby, M.; Ganesan, A.L.; Manning, A.J.; Prinn, R.G.; O’Doherty, S.; Mühle, J.; Harth, C.M.; Salameh, P.K.; Arnold, T.; et al. Reconciling reported and unreported HFC emissions with atmospheric observations. Proc. Natl. Acad. Sci. USA 2015, 112, 5927–5931. [Google Scholar] [CrossRef] [PubMed]
- Simmonds, P.G.; Rigby, M.; Manning, A.J.; Lunt, M.F.; O’Doherty, S.; McCulloch, A.; Fraser, P.J.; Henne, S.; Vollmer, M.K.; Mühle, J.; et al. Global and regional emissions estimates of 1,1-difluoroethane (HFC-152a, CH3CHF2) from in situ and air archive observations. Atmos. Chem. Phys. 2016, 16, 365–382. [Google Scholar] [CrossRef]
- Brunner, D.; Arnold, T.; Henne, S.; Manning, A.; Thompson, R.L.; Maione, M.; O’Doherty, S.; Reimann, S. Comparison of four inverse modelling systems applied to the estimation of HFC-125, HFC-134a, and SF6 emissions over Europe. Atmos. Chem. Phys. 2017, 17, 10651–10674. [Google Scholar] [CrossRef]
- Graziosi, F.; Arduini, J.; Furlani, F.; Giostra, U.; Cristofanelli, P.; Fang, X.; Hermanssen, O.; Lunder, C.; Maenhout, G.; O’Doherty, S.; et al. European emissions of the powerful greenhouse gases hydrofluorocarbons inferred from atmospheric measurements and their comparison with annual national reports to UNFCCC. Atmos. Environ. 2017, 158, 85–97. [Google Scholar] [CrossRef]
- Manning, A.J.; Redington, A.L.; Say, D.; O’Doherty, S.; Young, D.; Simmonds, P.G.; Vollmer, M.K.; Mühle, J.; Arduini, J.; Spain, G.; et al. Evidence of a recent decline in UK emissions of hydrofluorocarbons determined by the InTEM inverse model and atmospheric measurements. Atmos. Chem. Phys. 2021, 21, 12739–12755. [Google Scholar] [CrossRef]
- Kim, J.; Thompson, R.; Park, H.; Bogle, S.; Mühle, J.; Park, M.K.; Kim, Y.; Harth, C.M.; Salameh, P.K.; Schmidt, R.; et al. Emissions of Tetrafluoromethane (CF4) and Hexafluoroethane (C2F6) From East Asia: 2008 to 2019. J. Geophys. Res. Atmos. 2021, 126, e2021JD034888. [Google Scholar] [CrossRef]
- Redington, A.L.; Manning, A.J.; Henne, S.; Graziosi, F.; Western, L.M.; Arduini, J.; Ganesan, A.L.; Harth, C.M.; Maione, M.; Mühle, J.; et al. Western European emission estimates of CFC-11, CFC-12 and CCl4 derived from atmospheric measurements from 2008 to 2021. Atmos. Chem. Phys. 2023, 23, 7383–7398. [Google Scholar] [CrossRef]
- Say, D.; Manning, A.J.; O’Doherty, S.; Rigby, M.; Young, D.; Grant, A. Re-Evaluation of the UK’s HFC-134a Emissions Inventory Based on Atmospheric Observations. Environ. Sci. Technol. 2016, 50, 11129–11136. [Google Scholar] [CrossRef]
- Keller, C.A.; Hill, M.; Vollmer, M.K.; Henne, S.; Brunner, D.; Reimann, S.; O’Doherty, S.; Arduini, J.; Maione, M.; Ferenczi, Z.; et al. European Emissions of Halogenated Greenhouse Gases Inferred from Atmospheric Measurements. Environ. Sci. Technol. 2012, 46, 217–225. [Google Scholar] [CrossRef]
- Prinn, R.G.; Weiss, R.F.; Arduini, J.; Arnold, T.; DeWitt, H.L.; Fraser, P.J.; Ganesan, A.L.; Gasore, J.; Harth, C.M.; Hermansen, O.; et al. History of chemically and radiatively important atmospheric gases from the Advanced Global Atmospheric Gases Experiment (AGAGE). Earth Syst. Sci. Data 2018, 10, 985–1018. [Google Scholar] [CrossRef]
- EU. EUR-Lex-32014R0517-EN-EUR-Lex, 2014. Doc ID: 32014R0517 Doc Sector: 3 Doc Title: Regulation (EU) No 517/2014 of the European Parliament and of the Council of 16 April 2014 on Fluorinated Greenhouse Gases and Repealing Regulation (EC) No 842/2006 Text with EEA Relevance. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex%3A32014R0517 (accessed on 1 September 2023).
- Thompson, R.L.; Stohl, A. FLEXINVERT: An atmospheric Bayesian inversion framework for determining surface fluxes of trace species using an optimized grid. Geosci. Model Dev. 2014, 7, 2223–2242. [Google Scholar] [CrossRef]
- Evangeliou, N.; Thompson, R.L.; Eckhardt, S.; Stohl, A. Top-down estimates of black carbon emissions at high latitudes using an atmospheric transport model and a Bayesian inversion framework. Atmos. Chem. Phys. 2018, 18, 15307–15327. [Google Scholar] [CrossRef]
- Jia, M.; Evangeliou, N.; Eckhardt, S.; Huang, X.; Gao, J.; Ding, A.; Stohl, A. Black Carbon Emission Reduction Due to COVID-19 Lockdown in China. Geophys. Res. Lett. 2021, 48, e2021GL093243. [Google Scholar] [CrossRef] [PubMed]
- Prinn, R.G.; Weiss, R.F.; Fraser, P.J.; Simmonds, P.G.; Cunnold, D.M.; Alyea, F.N.; O’Doherty, S.; Salameh, P.; Miller, B.R.; Huang, J.; et al. A history of chemically and radiatively important gases in air deduced from ALE/GAGE/AGAGE. J. Geophys. Res. Atmos. 2000, 105, 17751–17792. [Google Scholar] [CrossRef]
- Janssens-Maenhout, G.; Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E. Emissions Database for Global Atmospheric Research; Version Version 4.2 (Time-Series); European Commission, Joint Research Centre (JRC): Brussels, Belgium, 2011. [Google Scholar]
- Ferrario, F.M.; Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Vullo, E.L.; Solazzo, E.; Olivier, J.; Vignati, E. EDGAR v6.0 Greenhouse Gas Emissions; European Commission, Joint Research Centre (JRC): Brussels, Belgium, 2021. [Google Scholar]
- Commission, E.; Centre, J.R.; Olivier, J.G.J.; Guizzardi, D.; Schaaf, E.; Solazzo, E.; Crippa, M.; Vignati, E.; Banja, M.; Muntean, M.; et al. GHG Emissions of All World: 2021 Report; Publications Office of the European Union: Luxembourg, 2021. [Google Scholar]
- Stohl, A.; Forster, C.; Frank, A.; Seibert, P.; Wotawa, G. Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 2005, 5, 2461–2474. [Google Scholar] [CrossRef]
- Seibert, P.; Frank, A. Source-receptor matrix calculation with a Lagrangian particle dispersion model in backward mode. Atmos. Chem. Phys. 2004, 4, 51–63. [Google Scholar] [CrossRef]
- Stohl, A.; Hittenberger, M.; Wotawa, G. Validation of the lagrangian particle dispersion model FLEXPART against large-scale tracer experiment data. Atmos. Environ. 1998, 32, 4245–4264. [Google Scholar] [CrossRef]
- Seibert, P. Iverse Modelling with a Lagrangian Particle Disperion Model: Application to Point Releases Over Limited Time Intervals. In Air Pollution Modeling and Its Application XIV; Gryning, S.E., Schiermeier, F.A., Eds.; Springer: Boston, MA, USA, 2001; pp. 381–389. [Google Scholar] [CrossRef]
- Cesari, R.; Paradisi, P.; Allegrini, P. Source identification by a statistical analysis of backward trajectories based on peak pollution events. Int. J. Environ. Pollut. 2014, 55, 94–103. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service. Complete ERA5 Global Atmospheric Reanalyis. 2023. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.143582cf?tab=overview (accessed on 1 September 2023).
- Tipka, A.; Haimberger, L.; Seibert, P. Flex_extract v7.1.2—A software package to retrieve and prepare ECMWF data for use in FLEXPART. Geosci. Model Dev. 2020, 13, 5277–5310. [Google Scholar] [CrossRef]
- Giostra, U.; Furlani, F.; Arduini, J.; Cava, D.; Manning, A.J.; O’Doherty, S.J.; Reimann, S.; Maione, M. The determination of a “regional” atmospheric background mixing ratio for anthropogenic greenhouse gases: A comparison of two independent methods. Atmos. Environ. 2011, 45, 7396–7405. [Google Scholar] [CrossRef]
- Ruckstuhl, A.F.; Henne, S.; Reimann, S.; Steinbacher, M.; Vollmer, M.K.; O’Doherty, S.; Buchmann, B.; Hueglin, C. Robust extraction of baseline signal of atmospheric trace species using local regression. Atmos. Meas. Tech. 2012, 5, 2613–2624. [Google Scholar] [CrossRef]
- Pérez, I.A.; Sánchez, M.L.; García, M.A. CO2 dilution in the lower atmosphere from temperature and wind speed profiles. Theor. Appl. Clim. 2012, 107, 247–253. [Google Scholar] [CrossRef]
- Griffiths, A.D.; Conen, F.; Weingartner, E.; Zimmermann, L.; Chambers, S.D.; Williams, A.G.; Steinbacher, M. Surface-to-mountaintop transport characterised by radon observations at the Jungfraujoch. Atmos. Chem. Phys. 2014, 14, 12763–12779. [Google Scholar] [CrossRef]
- Fang, S.X.; Tans, P.P.; Steinbacher, M.; Zhou, L.X.; Luan, T. Comparison of the regional CO2 mole fraction filtering approaches at a WMO/GAW regional station in China. Atmos. Meas. Tech. 2015, 8, 5301–5313. [Google Scholar] [CrossRef]
- Maione, M.; Graziosi, F.; Arduini, J.; Furlani, F.; Giostra, U.; Blake, D.R.; Bonasoni, P.; Fang, X.; Montzka, S.A.; O’Doherty, S.J.; et al. Estimates of European emissions of methyl chloroform using a Bayesian inversion method. Atmos. Chem. Phys. 2014, 14, 9755–9770. [Google Scholar] [CrossRef][Green Version]
- Graziosi, F.; Arduini, J.; Bonasoni, P.; Furlani, F.; Giostra, U.; Manning, A.J.; McCulloch, A.; O’Doherty, S.; Simmonds, P.G.; Reimann, S.; et al. Emissions of carbon tetrachloride from Europe. Atmos. Chem. Phys. 2016, 16, 12849–12859. [Google Scholar] [CrossRef]
- Henne, S.; Brunner, D.; Oney, B.; Leuenberger, M.; Eugster, W.; Bamberger, I.; Meinhardt, F.; Steinbacher, M.; Emmenegger, L. Validation of the Swiss methane emission inventory by atmospheric observations and inverse modelling. Atmos. Chem. Phys. 2016, 16, 3683–3710. [Google Scholar] [CrossRef]
- Vollmer, M.K.; Mühle, J.; Trudinger, C.M.; Rigby, M.; Montzka, S.A.; Harth, C.M.; Miller, B.R.; Henne, S.; Krummel, P.B.; Hall, B.D.; et al. Atmospheric histories and global emissions of halons H-1211 (CBrClF2), H-1301 (CBrF3), and H-2402 (CBrF2CBrF2). J. Geophys. Res. Atmos. 2016, 121, 3663–3686. [Google Scholar] [CrossRef]
- Schoenenberger, F.; Henne, S.; Hill, M.; Vollmer, M.K.; Kouvarakis, G.; Mihalopoulos, N.; O’Doherty, S.; Maione, M.; Emmenegger, L.; Peter, T.; et al. Abundance and sources of atmospheric halocarbons in the Eastern Mediterranean. Atmos. Chem. Phys. 2018, 18, 4069–4092. [Google Scholar] [CrossRef]
- Vojta, M.; Plach, A.; Thompson, R.L.; Stohl, A. A comprehensive evaluation of the use of Lagrangian particle dispersion models for inverse modeling of greenhouse gas emissions. Geosci. Model Dev. 2022, 15, 8295–8323. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Corazza, M.; Karstens, U.; Athanassiadou, M.; Thompson, R.L.; Pison, I.; Manning, A.J.; Bousquet, P.; Segers, A.; Vermeulen, A.T.; et al. Top-down estimates of European CH4 and N2O emissions based on four different inverse models. Atmos. Chem. Phys. 2015, 15, 715–736. [Google Scholar] [CrossRef]
- UN Environment Programme. Emissions Gap Report 2023: Broken Record—Temperatures Hit New Highs, yet World Fails to Cut Emissions (Again). Available online: https://wedocs.unep.org/20.500.11822/43922 (accessed on 1 September 2023).


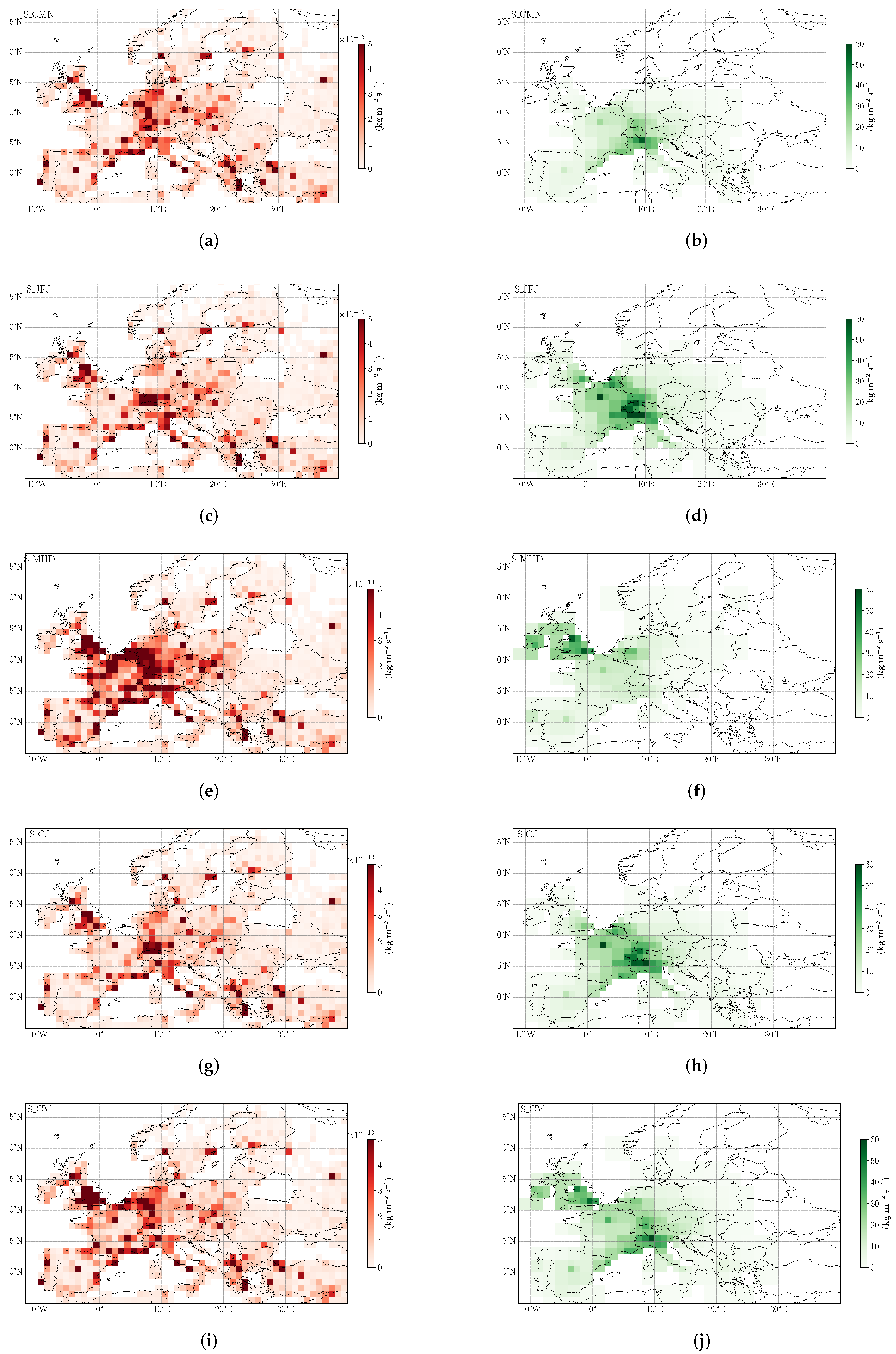
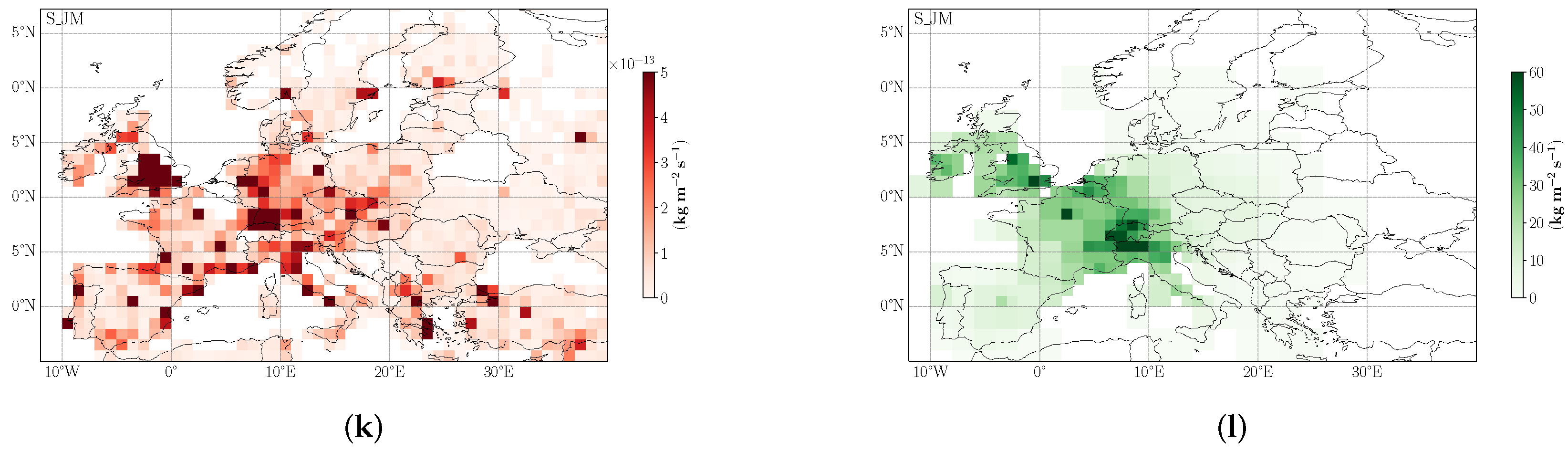

| Station | Primary Scale Accuracy (%) | Scale Propagation Uncertainty | Precision | Average Total Uncertainty (2σ%) |
|---|---|---|---|---|
| CMN | 1 | 0.7%/0.48 ppt | 0.6%–0.44 ppt | 3.0 |
| JFJ | 1 | 0.3%/0.16 ppt | 0.3%–0.22 ppt | 2.2 |
| MHD | 1 | 0.2%/0.15 ppt | 0.3%–0.22 ppt | 2.1 |
| Parameter | Value/Remarks |
|---|---|
| Horizontal resolution of the meteorological fields | 0.28° × 0.28° |
| temporal resolution of the meteorological fields | 3 h |
| Horizontal resolution of simulation domain | 1° × 1° |
| Backwards trajectories lengths | 5 days |
| Receptor release height at CMN | 2000 m |
| Receptor release height at JFJ | 3000 m |
| Receptor release height at MHD | 26 m |
| TEST_ID | Baseline Treatment | Releases | Prior Inventory |
|---|---|---|---|
| S0 | REBS | AA* | EDGAR v7.0 |
| S1 | 2-PDF | 1 | EDGAR v4.2 |
| S2 | 2-PDF | 1 | EDGAR v6.0 |
| S3 | 2-PDF | 1 | EDGAR v7.0 |
| S4 | REBS | AA* | flat prior |
| S5 | REBS | 1 | EDGAR v7.0 |
| S6 | REBS (optimized) | 1 | EDGAR v7.0 |
| S7 | 2-PDF (optimized) | 1 | EDGAR v7.0 |
| S_CMN | REBS (optimized) | 1 | EDGAR v7.0 |
| S_JFJ | REBS (optimized) | 1 | EDGAR v7.0 |
| S_MHD | REBS (optimized) | 1 | EDGAR v7.0 |
| S_CJ | REBS (optimized) | 1 | EDGAR v7.0 |
| S_CM | REBS (optimized) | 1 | EDGAR v7.0 |
| S_JM | REBS (optimized) | 1 | EDGAR v7.0 |
| Test | R | RMSE | NSD | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior | Posterior | Prior | Posterior | Prior | Posterior | |||||||||||||
| CMN | JFJ | MHD | CMN | JFJ | MHD | CMN | JFJ | MHD | CMN | JFJ | MHD | CMN | JFJ | MHD | CMN | JFJ | MHD | |
| S0 | 0.57 | 0.54 | 0.84 | 0.62 | 0.58 | 0.86 | 7.11 | 4.34 | 2.17 | 6.81 | 3.99 | 2.03 | 0.56 | 0.82 | 0.71 | 0.61 | 0.71 | 0.73 |
| S1 | 0.68 | 0.62 | 0.86 | 0.75 | 0.75 | 0.89 | 4.37 | 4.62 | 2.52 | 3.73 | 2.9 | 2.22 | 1.04 | 1.38 | 0.75 | 0.87 | 0.91 | 0.74 |
| S2 | 0.71 | 0.67 | 0.88 | 0.76 | 0.76 | 0.89 | 3.87 | 3.39 | 2.19 | 3.73 | 2.83 | 2.27 | 0.86 | 1.02 | 0.76 | 0.82 | 0.86 | 0.68 |
| S3 | 0.7 | 0.67 | 0.86 | 0.74 | 0.76 | 0.89 | 4.18 | 3.35 | 2.66 | 3.77 | 2.83 | 2.1 | 0.8 | 0.98 | 0.64 | 0.85 | 0.9 | 0.75 |
| S4 | 0.57 | 0.49 | 0.7 | 0.61 | 0.58 | 0.86 | 7.22 | 4.3 | 2.8 | 6.85 | 3.99 | 1.97 | 0.46 | 0.62 | 0.54 | 0.61 | 0.71 | 0.75 |
| S5 | 0.72 | 0.67 | 0.86 | 0.77 | 0.77 | 0.88 | 3.88 | 3.66 | 2.48 | 3.39 | 2.67 | 2.26 | 0.85 | 1 | 0.64 | 0.77 | 0.76 | 0.7 |
| S6 | 0.72 | 0.67 | 0.86 | 0.77 | 0.77 | 0.88 | 3.88 | 3.66 | 2.48 | 3.42 | 2.64 | 2.23 | 0.85 | 1 | 0.64 | 0.76 | 0.78 | 0.74 |
| S7 | 0.7 | 0.67 | 0.86 | 0.75 | 0.78 | 0.88 | 4.18 | 3.35 | 2.66 | 3.55 | 2.62 | 2.19 | 0.8 | 0.98 | 0.64 | 0.77 | 0.81 | 0.73 |
| Simulation | DE (Mg·yr−1) | IT (Mg·yr−1) | FR (Mg·yr−1) | UK (Mg·yr−1) | ES + PT (Mg·yr−1) |
|---|---|---|---|---|---|
| S0 | |||||
| S1 | |||||
| S2 | |||||
| S3 | |||||
| S4 | |||||
| S5 | |||||
| S6 | |||||
| S7 | |||||
| S_CMN | |||||
| S_JFJ | |||||
| S_MHD | |||||
| S_CJ | |||||
| S_CM | |||||
| S_JM | |||||
| Median * | 3140 | 3318 | 3542 | 5118 | 2747 |
| Range * | 1861–4735 | 2199–4384 | 2346–4439 | 2686–5319 | 1636–3523 |
| UNFCCC 2011 | 4357 | 2523 | 5171 | 6178 | 3695 |
| EDGARv4.2 | 6663 | 3723 | 5464 | 3832 | 2471 |
| EDGARv6.0 | 4673 | 5135 | 6081 | 4315 | 5282 |
| EDGARv7.0 | 4198 | 2188 | 4956 | 3334 | 3202 |
| Median ** | 5026 | 3613 | 4237 | 3090 | 3545 |
| Range ** | 2909–6823 | 2909–4958 | 3367–4970 | 2827–3227 | 2453–6437 |
| EMPA ** | |||||
| UKMO ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Annadate, S.; Falasca, S.; Cesari, R.; Giostra, U.; Maione, M.; Arduini, J. A Sensitivity Study of a Bayesian Inversion Model Used to Estimate Emissions of Synthetic Greenhouse Gases at the European Scale. Atmosphere 2024, 15, 51. https://doi.org/10.3390/atmos15010051
Annadate S, Falasca S, Cesari R, Giostra U, Maione M, Arduini J. A Sensitivity Study of a Bayesian Inversion Model Used to Estimate Emissions of Synthetic Greenhouse Gases at the European Scale. Atmosphere. 2024; 15(1):51. https://doi.org/10.3390/atmos15010051
Chicago/Turabian StyleAnnadate, Saurabh, Serena Falasca, Rita Cesari, Umberto Giostra, Michela Maione, and Jgor Arduini. 2024. "A Sensitivity Study of a Bayesian Inversion Model Used to Estimate Emissions of Synthetic Greenhouse Gases at the European Scale" Atmosphere 15, no. 1: 51. https://doi.org/10.3390/atmos15010051
APA StyleAnnadate, S., Falasca, S., Cesari, R., Giostra, U., Maione, M., & Arduini, J. (2024). A Sensitivity Study of a Bayesian Inversion Model Used to Estimate Emissions of Synthetic Greenhouse Gases at the European Scale. Atmosphere, 15(1), 51. https://doi.org/10.3390/atmos15010051





