Abstract
Profound research on the characteristics of the long-term persistence of wind is greatly significant for understanding the characteristics of wind speed mechanisms as well as for avoiding disasters caused by wind. In the current study, we selected the hourly 10 min wind speed series between 2017 and 2021 from 105 nation-level meteorological stations in Xinjiang and investigated the spatiotemporal variations in the long-term persistence of wind speed in different regions of Xinjiang and in different seasons using detrended fluctuation analysis. The main findings are as follows: (1) The wind speed in Xinjiang shows noticeable annual and seasonal variations, exhibiting satisfactory long-term sustainability. Winter has the best long-term sustainability, followed sequentially by spring, autumn, and summer because of wind speed stability. (2) The long-term persistence of hourly wind speed in Xinjiang exhibits remarkable regionality, with regions with strong wind superior to the remaining regions. (3) The long-term persistence of wind speed within the same season is primarily associated with wind speed magnitude and the dispersion degree between 90% and 100% of the wind speed numerical values. A higher wind speed indicates better long-term persistence. At the same speed, the more discrete the numerical values in the 90–100% distribution range, the better the persistence.
1. Introduction
As the global energy crisis has emerged, the development of renewable energy has received widespread attention [1]. Wind energy, as an important component of renewable energy, has become a hotspot of research. Wind functions as a fundamental element in describing atmospheric motion and is closely related to weather phenomena, such as precipitation and strong convection [2]. Its speed can exhibit such noticeable characteristics as nonlinearity [3], intermittency, and long-term persistence [4]. Thorough research on these changes, which are manifested in wind, is of great significance for gaining a comprehensive understanding of wind speed mechanisms and avoiding possible harm caused by wind [5,6].
The long-term persistence of wind speed can be defined as the characteristics of patterns of change, where the maximum wind speed tends to occur after a high wind speed, whereas the minimum wind speed is likely to occur after a low wind speed [7]. Long-term persistence refers to the similarity exhibited on the time axis in the field of nonlinear science, which means that the current or past climate state has an impact on future climate evolution over a period; it is a feature of climate state memory based on time and is manifested by a characteristic or state that can persist for a long time and that does not easily change [8]. Any given climate series can be divided into two parts: synoptic-scale disturbance and long-term cumulative signals [9]; that is, the current wind speed state is determined by both factors.
In recent years, a series of studies on the long-term persistence of wind speed series in different regions and temporal resolutions has been carried out. Hourly average wind speed exhibits long-term memory in the United States, Italy, and Turkey [10,11,12,13]. In Brazil, the maximum wind speed exhibits a similar long-term power correlation, whose performance, however, differs under complex terrain conditions [14]. In China, the daily average wind speed series in the Huaihe River region, the hourly wind speed series in the Northeast region, and the 10 min average wind speed series in Yunnan Province all display noticeable autocorrelation and long-term sustainability [15,16,17]. Li et al. [5] conducted research on the wind speed time series measured from wind towers and found that wind speed time series at different heights at the same observation point share consistent scaling behavior, exhibiting strong long-range persistence.
Determined fluctuation analysis (DFA) is a simple and fast nonlinear analysis method for studying the long-term persistence of time series that was first proposed by Peng et al. [18] for analyzing DNA sequences, which provides an effective tool for analyzing the scaling characteristics of nonstationary, long-range power-law related time series by fitting and eliminating local trend terms. DFA overcomes the nonlinear influence of the original data sequence and is able to provide the true scaling law of physical variables in the time series. Therefore, it has been extensively applied in the meteorological field [19,20,21,22,23,24].
Xinjiang is located in the hinterland of the Eurasian continent, where mountains and basins are alternately arranged. The basins are surrounded by high mountains, which are known as “three mountains sandwiched by two basins”. The Altai Mountains rise in the north, and the Kunlun Mountains rise in the south, with the Tianshan Mountains lying in the middle, which divides Xinjiang into two halves: the Tarim Basin in the south and the Junggar Basin in the north. The region to the south of the Tianshan Mountains is customarily named Southern Xinjiang, and that to the north is Northern Xinjiang, and the Hami and Turpan Basins are in Eastern Xinjiang. The terrains of Xinjiang are diverse and include high mountains, basins, river valleys, plateaus, and deserts. The unique landforms bring about diversity in wind speeds across Xinjiang and result in nine major wind energy reserve zones, i.e., the Alashankou, Erzis River Valley, Laofengkou, Dabancheng, Santanghu, southeastern Hami, Thirteen Rooms, Robpo, and Xiaocaohu wind zones.
The current study aimed to investigate the characteristics of the long-term persistence of wind speed in different seasons and regions of Xinjiang based on the 10 min average wind speed after the punctual time point during a period of five years reported by 105 national meteorological observation stations. The characteristics of the long-term persistence of wind speed in Xinjiang were compared at different timescales and spatial scales, i.e., from overall to local and from year to season, and the factors influencing the long-term persistence of hourly wind speed were also explored.
2. Materials and Methods
2.1. Study Region and Data Source
The data are sourced from the Xinjiang Meteorological Information Center. Observation data of the 10 min average wind speed from the punctual time point from 2017 to 2021 reported by 105 national ground-based meteorological observation stations were selected (Figure 1). This selection was based on the consideration of long continuous observation records to exclude the possible impacts of a missing high rate and poor continuity of wind speed series upon DFA results. All data underwent systematic quality control, which included a cutoff check, extreme value check, internal consistency check, spatiotemporal consistency check, and manual intervention check.
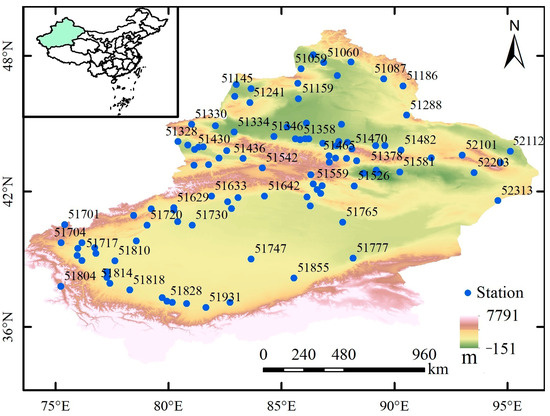
Figure 1.
Spatial distribution of the national ground observation stations in Xinjiang. (The blue dots represent the location and ID number of station).
2.2. Methodology
2.2.1. DFA
DFA was performed in accordance with the following procedures [25]:
(1) For an original sequence with a given length ( = 1, 2, …, ), a new recombinant sequence was constructed:
where represents the average of the original sequence .
(2) The new sequence was sectioned into number of windows (), which had the same time length S but did not overlap with each other. As the sequence length may not be evenly divided by , another window partitioning was performed from the tail of the sequence to ensure the integrity of the sequence. Similarly, another nonoverlapping Ns window was obtained, and thus, a total of 2Ns windows were obtained. The windows were labeled with v.
(3) Within each window, designated with , the sequence was subjected to -order polynomial regression fitting to obtain a local fluctuating trend sequence (the use of -order polynomial fitting to remove trends is termed -order DFA, and the value of was 2 in this study). Within each window, the fitted sequence was subtracted from the sequence to obtain a detrended sequence :
(4) For the detrended sequence, the variance function within each window was calculated as follows:
(5) The variance functions obtained from the 2Ns number of windows were accumulated, and the square root was calculated to obtain the wave function as follows:
In DFA, the wave function increases as the window size s increases. If the original sequence is associated with long-term conditions, the function and the size of the window s should follow a power-law scaling relation, as follows:
where 0.5 indicates that the time sequence is negatively correlated with the long term; = 0.5 means that the sequence is scale-invariant and thus represents an independent random process (corresponding to white noise); > 0.5 indicates that the observed values are not independent of each other and that the system presents a positive correlation with the long term; 1 indicates a process of 1/f fluctuation; and 1.5 indicates a Brownian signal, which is a highly correlated signal sequence.
2.2.2. Discreteness Analysis
Discreteness analysis is a method for measuring the dispersion degree of a set of data. To eliminate the impact of the level of data values on the measurement of dispersion, the relative dispersion degree is often measured by calculating the dispersion coefficient. For a data sequence with a given length of n (i = 1, 2, …, n), the dispersion coefficient is as follows:
where represents the average of the data, and S represents the standard deviation of the data, which is calculated as follows:
The dispersion coefficient is primarily used to compare the dispersion degrees among multiple sets of data. A larger dispersion coefficient indicates a higher dispersion degree, and vice versa.
3. Results
3.1. Seasonal Distribution Characteristics
The 10 min wind speeds of each punctual time point observed by the 105 stations were averaged, and the hourly wind speed sequence between 2017 and 2021 was obtained. To verify the relationship between the distribution of the wind speed sequence and the time sequence, the wind speed sequence was randomly reordered and then compared with the original sequence. Figure 2a shows the distribution of the average wind speed at different times before and after the disordering, with the x-axis representing cumulative hours and the y-axis representing wind speed; the blue curve indicates the disordered wind speed sequence and the red curve indicates the original sequence. Figure 2b shows the log–log curves of the variation in the function of the fluctuation in the wind speed time sequence according to timescale s, where the x-axis represents the logarithm of accumulated hours of wind speed, the y-axis represents the logarithm of wind speed, and the red and blue curves are the distribution curves of the wind speed before and after randomization based on DFA (shown to remove trends for each window with a quadratic polynomial), respectively, and the gray curve is the white noise curve. The scaling exponent of each of the curves could satisfactorily reflect the long-term persistence of the wind speed sequence at the designated timescale (1–1500 d).
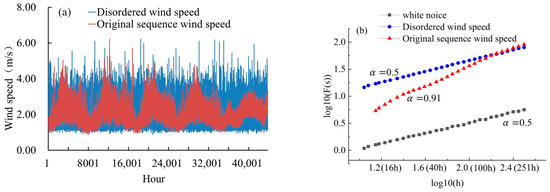
Figure 2.
The average wind speed sequences in Xinjiang. (a) shows the distribution of average wind speed before and after random disruption, and (b) shows the double logarithmic curve of wind speed over time.
In terms of the pattern in the wind speed variation, the hourly wind speed was characterized by annual amplitudes, with higher wind speeds in spring and summer and lower wind speeds in autumn and winter, which was consistent with that reported in the literature [26]. According to the DFA results, the average scaling exponent was 0.5 after the hourly wind speed sequence was disordered, indicating white noise. In contrast, before the treatment, the average scaling exponent was 0.91, exhibiting strong long-term persistence; this exponent indicated that the wind speed sequence in Xinjiang exhibited long-term persistence, which was caused by the fractal nature of the time sequence. A slight fluctuation of the scaling exponent was observed at 40 h (log10(h) = 1.6), and the exponent before it was more stable than that after it.
Figure 3 shows the distribution of the hourly wind speed sequence in spring, summer, autumn, and winter from 2017 to 2021, as well as the corresponding DFA outcomes. The x-axis in the left figure represents cumulative hours, while the y-axis represents wind speed. According to this figure, the wind speed in each season exhibited a noticeable annual cycle: the wind speed gradually increased in spring, followed by a gradual decrease in summer and autumn, and then a slight upward trend in winter (the variation in winter was the smallest). The scaling exponents in the four seasons are summarized in Table 1. The exponents in autumn and winter were higher than those in spring and summer, with the highest value observed in winter (up to 0.94), which indicated the best long-term persistence, and the lowest value in summer (0.75).
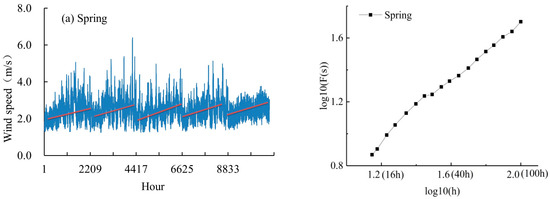
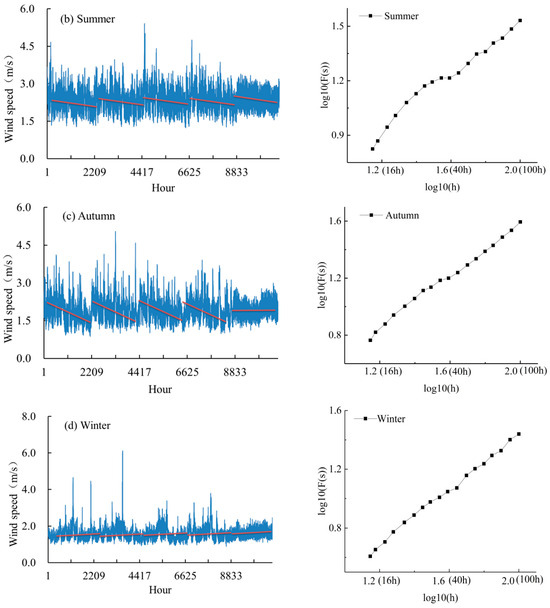
Figure 3.
Wind speed data and DFA analysis in (a) Spring, (b) Summer, (c) Autumn, and (d) Winter.

Table 1.
Distribution of the key wind speed elements in each season.
On the right side of Figure 3, the x-axis represents the logarithm of the accumulated hours of wind speed, while the y-axis represents the logarithm of wind speed. Slight fluctuations in the scaling exponent were also observed at approximately 40 h in each season (Figure 3), which was consistent with the annual distribution. This finding indicated that the wind speed was controlled by different dominant factors at different scales, and the scale also changed accordingly. At a small timescale, the wind speed was greatly affected by the small eddy motion of atmospheric turbulence and featured nonstationary signals, which were similar to molecular motion; at a large timescale, wind speed was mainly affected by large eddy motion and exhibited excellent long-term persistence. After disorderly treatment, the scaling exponent of the wind speech sequence at either timescale was the same as that of the white nose sequence, i.e., α = 0.5.
Further exploration of the characteristics of the wind speed values in each season revealed that the average minimum wind speed occurred in winter, with the smallest number of strong wind days—that is, days on which the instantaneous wind speed reaches or exceeds 17.0 m·s−1 or is visually estimated as reaching or exceeding level 8—whereas the largest number of strong wind days and the highest wind speed gustiness were observed in summer. This finding indicates that the long-term persistence of the hourly wind speed sequence may be linked with wind speed stability. The hourly wind speed distribution in each season was calculated, and the violin plot of the hourly wind speeds in different seasons is shown in Figure 4. The wind speed in winter was stable, and the values were concentrated between 1.4 m/s and 1.5 m/s. The wind speed distributions in spring and summer were more even than those in autumn and winter; that is, the differences in the frequency of various wind speeds in spring and summer were significantly smaller than those in autumn and winter. Although the boxplots of the wind speed distribution characteristics in spring and autumn were similar to that in summer, the performances of the long-term persistence in these seasons differed. It is reasonable to presume that long-term persistence represents a continuous change in data, which may be related to the degree of data concentration as well as the internal structure of the data themselves. Therefore, further analysis of the spatiotemporal differences in wind speed variation needs to be performed.
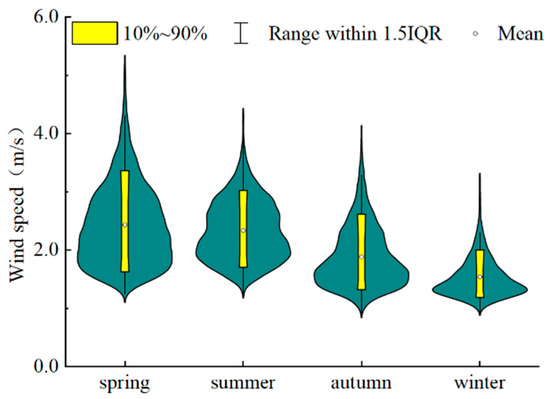
Figure 4.
Wind speed distributions in different seasons (IQR represents the interquartile difference).
3.2. Characteristics of the Spatiotemporal Distribution
According to the hourly wind speed data observed by the 105 stations, the patterns of variation in the wind speed were basically consistent across the stations, which was manifested by greater variations in spring and summer and the smallest variation in winter (Figure 5a). The x-axis in Figure 5a represents the meteorological station numbers, while the y-axis represents the average wind speed. Analysis of the variation in the function of the fluctuation in the hourly wind speed sequence at each station according to the timescale S showed that there were three states in the wind speed-scaling index distribution. The first state included slight fluctuations in the scaling index that occurred at approximately 63 h (log10(h) = 1.8), and such phenomena occurred more frequently at the stations with a relatively high average wind speed. The second state included slight fluctuations in the scaling index that occurred at approximately 25 h (log10(h) = 1.4), and such phenomena occurred more frequently at the stations with a relatively low average wind speed. The third state included no significant change in the scaling index, which often occurred at the stations where the wind speed was close to the average wind speed of the entire Xinjiang region. Before each of the time point fluctuations, the scaling exponent was larger than 1.1, while the value after it was smaller than 0.8; that is, the scaling exponent behaved as the “1/f fluctuation” on the small scale, while on the large scale, the value was approximately 0.8, exhibiting long-term memory. Therefore, given the same stability, the higher the wind speed is, the better the long-term persistence.
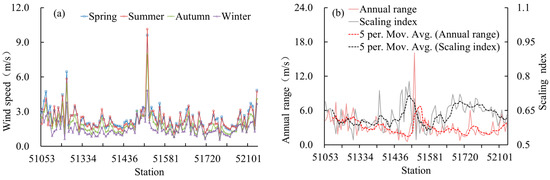
Figure 5.
Average wind speed and annual ranges. (a) shows the average wind speed in different seasons at each station, and (b) shows the annual range and slope distribution of wind speed at each station.
The spatial distribution of the hourly wind speed sequence in Xinjiang between 2017 and 2021 was analyzed using DFA, and the results are shown in Figure 6. In terms of the annual scale, the scaling exponent of the wind speed sequence in all of Xinjiang was much higher than 0.5. The long-term persistence of the East Xinjiang tuyere centered around Thirteen Rooms, the North Xinjiang tuyere centered around Alashankou, the northern mountainous areas of North Xinjiang, and the western mountainous areas of South Xinjiang [27] were noticeably superior to other regions, and the Taklamakan Desert and Kumtag Desert regions also exhibited strong long-term wind speed persistence. In these areas, the nine major wind zones had high wind speeds and unique desert environments, which often experienced strong storm weather, indicating a good relationship between the magnitude and long-term persistence of wind speed. In the surrounding mountainous areas, however, variations in the wind speed were more complex, and the long-term persistence was relatively weak due to the influence of mountainous terrain. Taking the area along the Tianshan Mountains in northern Xinjiang as an example, the overall wind speed is relatively low due to the blocking effect of mountain ranges, and there are many intermittent weather events, so the long-term sustainability of the wind speed is relatively weak.
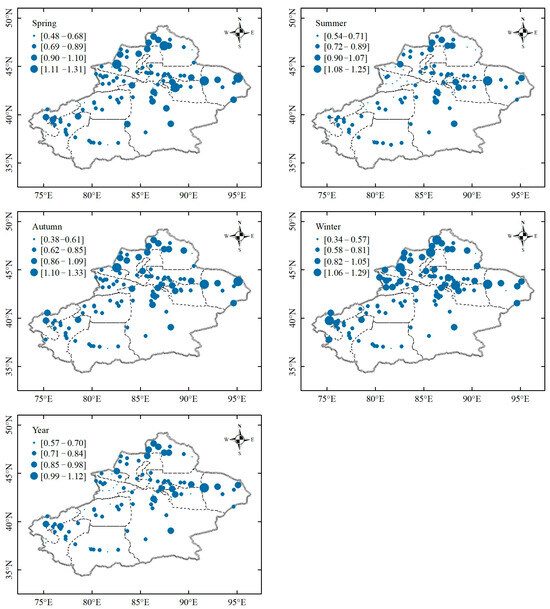
Figure 6.
Seasonal spatial distribution of the long-term persistence of wind speed.
From a seasonal perspective, the long-term persistence at different stations differed according to season. In spring and summer, the long-term persistence was basically the same, while in the remaining seasons, particularly in winter, great differences were observed. In spring, the scaling exponent of the wind speed sequences in the entire Xinjiang region showed a stronger long-term correlation compared with those in other seasons. The wind speed in Hotan was low in winter, exhibiting poor long-term persistence. In summer, the average wind speed in Ili was lower than that in other regions. In the meantime, during this season, strong winds frequently occurred in this region with strong gusts, and therefore, the long-term persistence performance was also poor.
The correlation between the wind speed and the scaling exponent was analyzed, as shown in Figure 5b. The x-axis represents the meteorological station area number, while the y-axis represents the annual range and scale index. For each station, the annual correlation was poor, which indicated great seasonal differences in the wind speed. Further analysis of the relationship between the annual range and long-term persistence of the wind speed at each station showed that the stations with great variation in the annual wind speed exhibited weak long-term persistence (Figure 5b). In the same season, the station with a higher wind speed exhibited better long-term persistence (according to a test level of 0.05) (Figure 7, the marked positions of each station are shown in Figure 1). In addition, analysis of the correlations among the average wind speeds, scaling exponents, and the dispersion degrees of the wind speed values within the distribution range of 90-100% at each station showed that stations with high dispersion coefficients outperformed other stations in hourly wind speed persistence (Figure 8, the marked positions of each station are shown in Figure 1). For convenient comparison, all data shown in this figure underwent dimensionless processing.
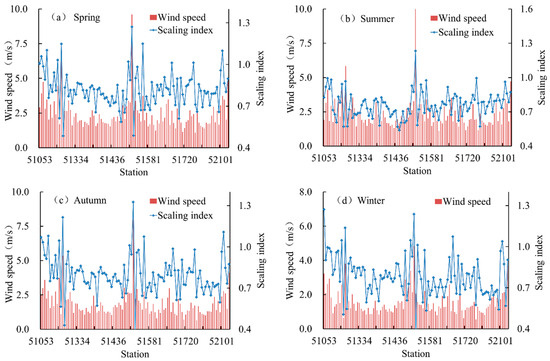
Figure 7.
The seasonal average wind speed and long-term persistence at different stations in (a) Spring, (b) Summer, (c) Autumn, and (d) Winter.
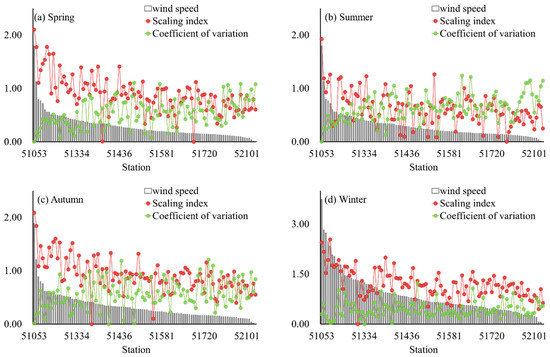
Figure 8.
The relationship between the long-term persistence and the dispersion degree of the 90–100% wind speed range at different stations in (a) Spring, (b) Summer, (c) Autumn, and (d) Winter.
Based on the abovementioned results, the long-term persistence of the wind speed in a given area was based on two factors: the magnitude and stability of the wind speed. When the stability in the same season was comparable, the higher magnitude of the wind speed indicated better long-term persistence; when the average wind speed was comparable, the station with a more stable wind speed exhibited better long-term persistence. However, for the stations with an even wind speed distribution, the more discrete the values within the 90–100% distribution range of the wind speed are, the better the long-term persistence. Therefore, due to unique climate conditions, a variety of subtle changes were observed in the wind speed of Xinjiang. When conducting long-term persistence analysis, the finer the time frequency of the data is, the better it captures the details of future development and changes.
4. Discussion and Conclusions
Wind speed depends on the meteorological laws of nature and is influenced by a variety of factors, such as temperature, atmospheric motion, air humidity, and environmental conditions; wind speed is a typical nonlinear nonstationary signal [28]. Studies on its long-term persistence characteristics can reveal the complexity of its temporal and spatial structure more clearly and provide a deeper understanding of the sustained changes and gust characteristics of the wind speed. Better long-term persistence means a greater proportion of the predictable component is derived from the “product” effect of persistence in future actual changes, which has important reference significance for forecasting. In this study, the hourly wind speed time sequence in Xinjiang showed noticeable long-term persistence, with seasonal characteristics mainly related to the stability of wind speed: winter was the best season for long-term persistence, followed by spring and autumn, and then summer. The most remarkable feature of the spatial distribution of wind speed was that strong wind zones outperformed other zones in long-term persistence. According to the analysis of the long-term persistence of wind speed in the same season, the main factors affecting the long-term memory of hourly wind speed in a certain area were the magnitude of the wind speed and the dispersion degree of the numerical values within the wind speed distribution range of 90–100%. A higher wind speed resulted in better long-term persistence. When the wind speed was the same, a higher dispersion degree of the values within the wind speed distribution range of 90–100% led to better persistence.
Research on wind speed data has mostly focused on spatiotemporal changes and the analysis of extreme wind speed values, with less attention paid to the internal structural connections of wind speed time series. In terms of long-range persistence, Ka et al. found in their energy spectrum studies of atmospheric turbulence that there exists a wide range of inertial sub-ranges between the scales of energy injection and dissipation, spanning at least 30 years. As the resolution increases, the effective small-scale dissipation rate decreases. This phenomenon exists in orbits of the same resolution and can also be observed at the planetary scale [29,30]. Research has shown that wind speed has significant long-term persistence, but these studies have been mostly qualitative research in different regions and at different heights. Most previous research on wind speed has focused on spatiotemporal changes and extreme value analysis, with less attention given to the internal structural connections of the wind speed time sequence. For studies on long-term persistence, most were qualitative in nature. This study set out to investigate the characteristics of the long-term persistence of wind speed in Xinjiang and made attempts to conduct an analysis of its influential factors, and its results could disclose the close correlation between wind speed changes and internal structure more clearly. Based on the different manifestations of the long-term persistence of wind speeds in different regions, this study found that future wind speed was closely related to the wind speed in a certain period and was greatly affected by long-term variations in the regional wind speed. Research conducted by long-term persistence studies has extensive application prospects in predicting wind speed at tuyeres, and the results may provide a scientific basis and decision-making reference for wind forecasting, energy planning, power system operation, and wind disaster prevention. This study also found that when the wind speeds were the same, a higher dispersion degree of the numerical values within the same wind speed distribution range of 90% to 100% led to better persistence. Nevertheless, a sufficient theoretical basis to explain this phenomenon is lacking, which constitutes the main content of the next stage of research.
Author Contributions
Conceptualization, X.W. and Q.L.; data curation, X.W. and X.L.; formal analysis, X.W., X.L. and Q.L.; funding acquisition, X.W.; investigation, H.Z. and C.L.; methodology, X.W. and Q.L.; project administration, X.W.; resources, X.W., Q.L. and X.L.; software, X.W., H.Z. and X.Z.; supervision, X.L. and Q.L.; validation, X.W. and X.Z.; visualization, X.W., X.L., Q.L., C.L. and X.Z.; writing—original draft, X.W., X.L. and H.Z.; writing—review and editing, X.W. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Third Xinjiang Scientific Expedition Program (grant number 2021xjkk1300) and the Desert Meteorological Science Research Foundation of China (grant number Sqj2021009).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the data sharing policy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, H.; Peng, Y.X.; Niu, D. WRF simulation of near ground wind field in complex terrain regions. J. China Inst. Water Resour. Hydropower Res. 2018, 16, 98–104. (In Chinese) [Google Scholar]
- Xiong, M. Climate regionalization and characteristics of surface winds over China in recent 30 years. Plateau Meteorol. 2015, 34, 39–49, (In Chinese with an English Abstract). [Google Scholar]
- Liu, Y.; Li, H.; Ma, Z.; Xin, W. The nonlinear characteristics analysis of wind speed time series. J. North China Electr. Power Univ. 2008, 35, 99–102, (In Chinese with an English abstract). [Google Scholar]
- Li, Q.; Li, C.; Yang, Y. Application of wind speed self-similarity and fractal dimension in wind field analysis. Chin. J. Power Eng. 2016, 36, 914–919, (In Chinese with an English Abstract). [Google Scholar]
- Scarrott, C.; Macdonald, A. A review of extreme value threshold estimation and uncertainty quantification. REVSTAT 2012, 10, 33–60. [Google Scholar]
- Hu, X.; Fang, G.; Yang, J.; Zhao, L.; Ge, Y. Simplified models for uncertainty quantification of extreme events using Monte Carlo technique. Reliab. Eng. Syst. Saf. 2023, 230, 108935. [Google Scholar] [CrossRef]
- Li, Q.; Chen, L.; Zhang, Z.; Liu, W. Research on Long-Range Persistence of Tower Wind Speed Based on DFA Method. Meteorol. Sci. Technol. 2023, 51, 262–268, (In Chinese with an English Abstract). [Google Scholar]
- Lei, Y.D. Long-Term Persistence of Precipitation Sequences in Southern China. Master’s thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2018. (In Chinese). [Google Scholar]
- Yuan, N.; Fu, Z.; Liu, S. Long-term memory in climate variability: A new look based on fractional integral techniques. J. Geophys. Res. Atmos. 2013, 118, 12–962. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Nagarajan, R. Evidence of crossover phenome-na in wind-speed data. IEEE Trans. Circuits Syst. 2004, 51, 2255–2262. [Google Scholar] [CrossRef]
- Kavasseri, R.; Nagarajan, R. A multifractal description of wind speed records. Chaos Solitons Fractals 2005, 24, 165–173. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Nagarajan, R. A qualitative description of boundary layer wind speed records. Fluct. Noise Lett. 2006, 6, 201–213. [Google Scholar] [CrossRef]
- Kocak, K. Examination of persistence properties of wind speed records using detrended fluctuation analysis. Energy 2009, 34, 1980–1985. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Kanevski, M. Power spectrum and multifractal detrended fluctuation analysis of high-frequency wind measurements in mountainous regions. Appl. Energy 2016, 162, 1052–1601. [Google Scholar] [CrossRef]
- Li, Q.; Fu, Z.; Yuan, N.; Xie, F. Effects of non-stationarity on the magnitude and sign scaling in the multi-scale vertical ve-locity increment. Phys. A Stat. Mech. Appl. 2014, 410, 9–16. [Google Scholar] [CrossRef]
- Sun, B.; Yao, H.T. Multi-fractal detrended fluctuation analysis of wind speed time series in wind farm. CES Trans. Electr. Mach. Syst. 2014, 29, 204–210, (In Chinese with an English Abstract). [Google Scholar]
- Wang, X.; Mei, Y.; Li, W.; Kong, Y.; Cong, X. Influence of sub-daily variation on multi-fractal detrended fluctuation analysis of wind speed time series. PLoS ONE 2016, 11, e0146284. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Zhang, F.; Yang, Q.; Zhang, J.; Liu, R. Long-term memory behaviors for outgoing longwave radiation in the tropics. J. Trop. Meteorol. 2017, 33, 426–432, (In Chinese with an English Abstract). [Google Scholar]
- Zhao, S.; He, W. Evaluation of the performance of the Beijing Climate Centre Climate System Model1.1(m) to simulate precipitation across China based on long-range correlation characteristics. J. Geophys. Res. Atmos. 2015, 120, 12576–12588. [Google Scholar] [CrossRef]
- He, W.; Zhao, S.; Liu, Q.; Jiang, Y.; Deng, B. Long-range correlation in the drought and flood index from 1470 to 2000 in eastern China. Int. J. Climatol. 2016, 36, 1676–1685. [Google Scholar] [CrossRef]
- Yuan, N.; Ding, M.; Huang, Y.; Fu, Z.; Xoplaki, E.; Luterbacher, J. On the long-term climate memory in the surface air temperature records over Antarctica: A nonnegligible factor for trend evaluation. J. Clim. 2015, 28, 5922–5934. [Google Scholar] [CrossRef]
- He, W.; Zhao, S. Assessment of the quality of NCEP-2 and CFSR reanalysis daily temperature in China based on long-range correlation. Clim. Dyn. 2018, 50, 493–505. [Google Scholar] [CrossRef]
- Varotsos, C.; Kirk-Davidof, F.D. Long-memory processes in ozone and temperature variations at the region 60 S-60 N. Atmos. Chem. Phys. 2006, 6, 4093–4100. [Google Scholar] [CrossRef]
- Yuan, Q.; Yang, Y.; Li, C.; Kan, W.; Ye, K. Research of wind speed time series based on the Hurst exponent. Appl. Math. Mech. 2018, 39, 798–810, (In Chinese with an English Abstract). [Google Scholar]
- Jia, S.; Chen, X.; Song, Y.; Li, S. Analysis of characteristics of wind speed change in Xinjiang from 1970 to 2013. Ludong Univ. J. 2019, 35, 352–359, (In Chinese with an English Abstract). [Google Scholar]
- Tuniyazi, N.; Rezvagu, Z.; Meng, F.X. Analysis on forecasting of a winter gale in west of southern Xinjiang. Arid. Meteorol. 2018, 36, 1003–1011, (In Chinese with an English Abstract). [Google Scholar]
- Dong, K.H. Evaluation of Non-Stationary Wind and Its Impact on Structural Wind Loads. Master’s thesis, Beijing Jiaotong University, Beijing, China, 2015. (In Chinese). [Google Scholar]
- Tung, K.K.; Orlando, W.W. The k-3 and k-5/3 Energy Spectrum of Atmospheric Turbulence: Quasigeostrophic Two-Level Model Simulation. J. Atmos. Sci. 2003, 60, 824–835. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Kovadlo, P.G. Estimation of mean energy characteristics of atmospheric turbulence at various heights from reanalysis data. Earth Environ. Sci. 2018, 211, 012023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).