Abstract
Near-surface PM2.5 estimates remain a global scientific research challenge due to their effect on human fitness and atmospheric environmental quality. However, practical near-surface PM2.5 estimates are impeded by the incomplete monitoring data. In this study, we propose the trigonometric polynomial fitting (TPF) method to estimate near-surface PM2.5 concentrations in south-central China during 2015. We employ 10-fold cross-validation (CV) to assess the reliability of TPF in estimating practical PM2.5 values. When compared to alternative methods such as the orthogonal polynomial fitting (OBF) method based on Chebyshev basis functions, Kriging interpolation, and radial basis function (RBF) interpolation, our results show that utilizing TPF31, with a maximum order of 3 in the direction and a maximum order of 1 in the
direction, leads to superior efficiency through error minimization. TPF31 reduces MAE and RMSE by 1.93%, 24%, 6.96% and 3.6%, 23.07%, 10.43%, respectively, compared to the other three methods. In addition, the TPF31 method effectively reconstructs the spatial distribution of PM2.5 concentrations in the unevenly distributed observation stations of Inner Mongolia and the marginal regions of the study area. The reconstructed spatial distribution is remarkably smooth. Despite the non-uniform distribution of observation stations and the presence of missing data, the TPF31 method demonstrates exceptional effectiveness in accurately capturing the inherent physical attributes of spatial distribution. The theoretical and experimental results emphasize that the TPF method holds significant potential for accurately reconstructing the spatial distribution of PM2.5 in China.
1. Introduction
Driven by the Sustainable Development Goals (SDGs), the problem of PM2.5 pollution has increasingly attracted the attention of all sectors of society [1]. PM2.5 pollution is closely related to several SDGs because long-term exposure to a PM2.5-polluted environment poses a great threat to the health of citizens. At the same time, the adverse effects of PM2.5 pollution on the environment and climate change will further affect people’s lifestyle, quality of life, and, ultimately, global economic and social development [2,3,4,5,6,7]. From a health perspective, PM2.5 can enter the alveolar region via the respiratory tract, causing damage to the human respiratory system as well as the lungs [8,9], and excessive exposure to high levels of PM2.5 increases the incidence of stroke, ischemic heart disease, cancer, and other related diseases. The World Health Organization reports that 90% of the global population resides in hazardous environments enveloped by PM2.5, which is strongly linked to cardiovascular, cerebrovascular, and respiratory ailments [10]. Global disease data show that China has the world’s third-largest risk factor for premature death due to PM2.5, which is responsible for up to 2 million deaths annually [11,12,13]. Furthermore, in terms of climate and ecosystem, PM2.5 is intricately linked to air quality and visibility, cloud formation, and precipitation processes. By scattering and absorbing solar radiation, PM2.5 modifies the impact of surface temperature on the amount of radiation that reaches Earth’s surface. It directly affects the climate by scattering and absorbing sunlight and indirectly affects the climate by serving as cloud condensation nuclei. This, in turn, impacts optical properties, the lifetime of clouds, and precipitation [14].
Specifically, China has witnessed a surge in PM2.5 pollution levels over the past few decades, due to the rapid pace of urbanization and industrialization [15,16,17]. The concentration of PM2.5 exceeds the standards set by the World Health Organization. According to the 2022 Report on the State of China’s Environment, only 21.6% (73 out of 338) of cities at or above the prefecture level meet environmental air quality standards, while a staggering 78.4% (265 cities) exceed them. Fine particulate matter, specifically PM2.5 and PM10, are primary pollutants that surpass standard levels for over 80% of the measured days. According to the “2022 China Ecological Environment Status Report” (https://www.gov.cn), among the nation’s 339 cities at the prefecture level and above in 2022, 213 met the air quality standards, accounting for 62.8%, while 126 cities exceeded the environmental quality standards, accounting for 37.2%. Among these 126 cities, 25.4% had PM2.5 levels exceeding the standard. The average concentration of PM2.5 in the Beijing–Tianjin–Hebei region was 44 micrograms per cubic meter—a 2.3% increase from 2021. In the Fenwei Plain, PM2.5 had an average concentration of 46 micrograms per cubic meter—a 9.5% increase from 2021. This demonstrates that PM2.5 remains a major air pollutant in China. To effectively manage air pollution and accurately measure PM2.5 concentration, China has established monitoring stations at all levels across various regions to comprehensively evaluate ambient air quality.
However, China’s air-quality monitoring station network was established relatively late and is unevenly distributed across the country, with most stations concentrated in three typical city clusters in eastern China—the Beijing–Tianjin–Hebei region, the Yangtze River Delta, and the Pearl River Delta [10]. Therefore, it is imperative to estimate PM2.5 concentration data, particularly in central and southern China, as this is crucial for comprehending the genesis and management of air pollution in China and gauging the impact of industrial development on environmental quality. The Sustainable Development Goals (SDGs) contain ten targets with a specific focus on reducing the adverse per capita environmental impacts of cities, including a special focus on air quality and municipal and other waste management. One of the SDGs’ indicators is the annual average level of PM2.5, which aims to assess the impact of PM2.5 pollution on the health of the population. In the context of the implementation of the sustainable development agenda, research related to PM2.5 pollution is of great relevance and practical value [18,19]. Ground-based monitoring station data are the most fundamental and direct means of studying the spatial and temporal distribution characteristics and transport mechanisms of PM2.5. However, individual station measurements may not provide information on the spatial variation of regional PM2.5 concentrations [11]. Moreover, the geography of China is complex, which may pose challenges in aligning remote-sensing data with actual locations [20]. Remote-sensing technology can result in missing data due to problems such as cloud cover [21]. Despite these challenges, ground-based monitoring stations provide more accurate data than remote sensing on a spatial scale, as most changes in PM2.5 are regional.
Accurately describing the spatial and temporal distribution characteristics and transmission mechanism of PM2.5 based solely on fixed-point observation data obtained from ground-based detection stations is challenging. Spatial interpolation methods, widely employed in atmospheric studies and other fields, offer a solution by mitigating the impact of insufficient ground-based observation data on accurately characterizing the spatial and temporal distribution characteristics of PM2.5. These methods include spatiotemporal statistical models based on Kriging interpolation, spatial and temporal regression models based on Kriging interpolation integrated with remote-sensing AOD data, neural network models based on RBF interpolation, and 3D RBF interpolation for hydrological structure analysis [22,23,24,25,26,27,28,29,30].
A spatiotemporal statistical model based on Kriging interpolation has been utilized to estimate and forecast the distribution of PM2.5 over land in the United States, resulting in more accurate estimates near monitoring stations and laying a foundation for PM2.5 prediction at any spatial location [22,23]. Meanwhile, the spatial and temporal regression model based on Kriging interpolation can be utilized to accurately simulate PM2.5 concentrations by integrating high-resolution remote-sensing AOD data with ground-based PM2.5 observations [25]. In 2023, Amini et al. combined Kriging interpolation with a GMDH-type neural network model to minimize errors in groundwater salinity estimation at unsampled sites and to significantly improve the accuracy and reliability of groundwater salinity estimation [26]. Zheng Haiming and Shang Xiaoxiao developed a neural network model based on RBF interpolation, which exhibits superior predictive performance compared to traditional backpropagation models and offers distinct advantages in PM2.5 prediction [28]. A study of the hydrological structure in the ECS by applying 3D RBF interpolation was carried out by Gao et al. in 2022, which showed that 3D RBF successfully reconstructed a reasonable 3D hydrological structure in the ECS shelf [29]. In 2023, Li Yuhan et al. employed the RBF interpolation method to calculate the density of fracture distribution. They established a DFN model under the multi-level constraints of seismic data and lithology data. This method significantly reduced the uncertainty of simulating and predicting discrete fractures between wells [30].
Even if high-precision simulation or prediction data can be obtained, the Kriging and RBF interpolation methods still exhibit some limitations in their application. When characterizing the spatial structure of data and estimating variance, Kriging interpolation requires the computation of the inverse matrix to fully describe spatial variation in terms of the variogram. However, this process can be both time-consuming and tedious [31]. The primary advantage of the RBF method lies in its ability to effectively extract pertinent information from discrete point data, resulting in a smoother and more natural magnified image. The radial basis function (RBF) interpolation method is known for its computational efficiency, making it a favorable choice when compared to other interpolation methods [32,33,34]. One of its valuable features is the ability to address the limitation of uniform grids by distributing discrete nodes in irregular regions for constructing the grid model. However, it is more susceptible to noise and outliers, necessitating the determination of both the number and type of radial basis functions. Therefore, the pursuit of interpolation schemes that balance accuracy and efficiency remains a primary focus of scientific research.
Orthogonal polynomial fitting is a highly precise and efficient technique for modeling intricate data, which has been extensively applied in various fields including artificial intelligence, image processing, and marine science [31,32,33,34,35,36]. Li et al. [31] utilized the Chebyshev polynomial fitting technique to derive the temporal–spatial distribution of PM2.5 in central and southern regions of China, followed by analysis thereof. Experimental findings demonstrated that selecting an appropriate degree for polynomials could yield highly precise computation outcomes. Wang et al. [13] proposed a methodology integrating adjoint assimilation models with the orthogonal polynomial fitting (OPF) method based on the Chebyshev basis functions approach to determine tidal harmonic constants within shallow waters of the Bohai Sea and Yellow Sea regions. The outcomes revealed that OPF exhibited exceptional resolution within shallow water zones, thereby enabling the acquisition of more accurate co-tidal diagrams congruent with four distinct modeling simulations.
The aims of this paper were to analyze the spatial distribution characteristics and trends of PM2.5 concentrations in south-central China using the orthogonal polynomial-based trigonometric polynomial fitting (TPF) method and to estimate the PM2.5 concentrations in this region using the proposed TPF method. Section 2 describes the required materials as well as the methodology, and introduces the PM2.5 concentration data and various polynomial fitting methods, including the trigonometric polynomial basis function, the Chebyshev polynomial basis function (referred to as the Chebyshev polynomial fitting method), the Kriging interpolation method, and the RBF interpolation method. Section 3 presents the experimental analysis. Section 4 and Section 5 provide discussion and conclusions, respectively.
2. Materials and Methods
2.1. Study Region and Data
The study area for this research is located in central and southern China, specifically focusing on three typical urban agglomerations located in eastern China’s Pearl River Delta (PRD) region. These urban agglomerations are characterized by high levels of human activity and developed economies. With continuous scientific planning and the reasonable construction of ground-based PM observation networks, over 1400 air-quality monitoring stations were distributed throughout the districts of 337 cities in 2022. The study region is equipped with a total of 235 monitoring stations, the data from which have been utilized in this study. The PM2.5 concentration data provided by these monitoring stations are sourced from the China National Environmental Monitoring Center (CNEMC). The CNEMC provides online access to near real-time data on PM2.5 concentrations; however, there is no direct interface for downloading the data [37]. Due to equipment costs and limited resources, PM2.5 monitoring is limited to a selected number of stations, leading to incomplete spatial coverage. As a result, obtaining comprehensive three-dimensional information poses challenges [17]. We employed web crawling technology, utilizing methods identical to those described in [38], to acquire PM2.5 concentration data from multiple cities during 2015. Meanwhile, due to either the inadequacy of web crawler technology or the CNEMC’s failure to release data during that period, this study presents observations from all hours in 2015 except for those between 0:00 a.m. on 1 January and 0:00 a.m. on 2 January, resulting in a total of 8760 h of data. The average of the hourly measurements was determined to obtain the PM2.5 concentration of each monitoring station on a certain day in a year. Additionally, in the event of multiple PM2.5 monitoring stations within a single city, all available measurements were averaged to provide an accurate representation. The spatial distribution of the 235 monitoring stations is illustrated in Figure 1. The color shade of each point represents the size of the annual average PM2.5 concentration at that site in 2015.
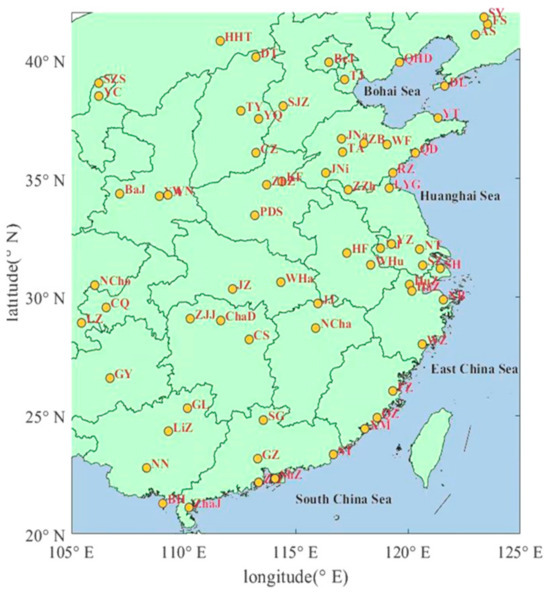
Figure 1.
Distribution of locations of 235 monitoring stations across south-central China. Each point on the map represents the location of a city where a monitoring station is situated, along with the corresponding city name.
2.2. Methodology
The trigonometric polynomial fitting method was employed to estimate the PM2.5 concentrations at unknown locations, while the Chebyshev polynomial fitting method, the RBF interpolation method, and the Kriging interpolation methods were utilized for comparative analysis. These methods, discussed below, are commonly used for the estimation of scattered point data.
2.2.1. Trigonometric Polynomial Fitting Method
The accuracy of the results in the polynomial fitting method theoretically increases with the increase of the polynomial order when there is sufficient observation data. However, in practice, the available data for analysis are limited, so the selection of the polynomial order needs to be based on the amount of data. In this paper, we controlled the order of TPF between 0 and 8.
The PM2.5 datasets are represented by , where and denote rectangular coordinates obtained through the conversion of longitudes and latitudes using stereographic map projection, represents the observed PM2.5 concentration, and signifies the total number of data points.
The distribution of PM2.5 concentrations calculated by the TPF method are:
where
, , , and are constant coefficients that can also be determined through the least square method [39].
2.2.2. Chebyshev Polynomial Fitting Method
The orthogonal polynomial fitting (OPF) method based on Chebyshev basis functions is described as follows (the order of the OPF method can be adjusted within the range of 0 to 8):
where are the points in the coordinate, is the order of polynomials in the direction, are the Chebyshev polynomials when the orders are from to , and the coefficient of the Chebyshev polynomials is denoted by . The calculation formula is as follows:
where is the th coefficient of the -order polynomial. is the PM2.5 concentration distribution, which can be fitted as:
A more comprehensive elucidation of the Chebyshev polynomial fitting method (OPF) can be found in Li et al.’s seminal work published in 2019 [31].
2.2.3. Interpolation Methods
The radial basis function (RBF) method is an exact interpolation method, and in this paper, we chose the three-dimensional RBF method for the subsequent experiments. If is the number of data points, and represent the horizontal and vertical coordinates, separately, and the input vector is , and is set as the Euclidean norm, then the PM2.5 concentration distribution can be represented as:
where is the RBF interpolation method and are the coefficients. The linear algebraic equation solved using the situ observation data yields the coefficients in the above equation:
where and
The RBF interpolation method has been widely applied in hydrological analysis. The functions of RBF interpolation methods include Gaussian functions, multi-quadratic functions, inverse quadratic functions, and thin-plate splines. Among these, the RBF interpolation method combining cubic and thin-plate spline functions has proven to be an effective approach for reconstructing ECS shelf temperature and salinity with minimal errors [29]. Therefore, we chose the thin-plate spline RBF interpolation method for subsequent experiments.
The Kriging interpolation method has been extensively employed in the investigation of atmospheric pollution [19,20,21,22,23,24,25]. In this study, we adopted a spherical semivariogram model as the basis for the Kriging interpolation method, with a specified range and threshold value.
It can be represented as:
where is the weight coefficient. This model represents the contribution of the observed value at each spatial sample point to its estimated value . The key to the Kriging interpolation method is to solve the weight coefficients.
2.3. Experimental Design and Process
The estimation results in this study were assessed using a 10-fold random cross-validation [31]. The observed PM2.5 dataset was randomly divided into ten subsets, with nine subsets assigned to set A and one subset assigned to set B. Set A data was utilized for interpolation, while the accuracy of estimation was evaluated using the data from set B. The average estimation errors resulting from the 10-fold random cross-validation were utilized to evaluate the efficacy and precision of the aforementioned methods.
First, the 10-fold random cross-validation was performed to determine the optimal fitting orders ( and ) for both the TPF and OPF methods. Each set of order combinations ( and ) was tested, using the TPF and OPF methods to fit the PM2.5 values. The random cross-validation was repeated 64 times for each of the two fitting methods. Additionally, the 10-fold random cross-validation was employed to evaluate the fitting and interpolation results. By calculating the average error of the interpolated outcomes across all the cross-validation, we assessed the effectiveness and accuracy of the aforementioned interpolation methods. Furthermore, these four methods were utilized to estimate the average spatial distribution of PM2.5 concentration in south-central China during 2015. This allowed us to evaluate the performance of different approaches in obtaining the average field.
2.4. Statistical Analysis
To assess the fitting and interpolation validity, the mean absolute error (MAE) and the root mean square error (RMSE) were selected as the criteria for selecting the most appropriate fitting method for this study. The MAE serves as a natural and unambiguous measure of the average discrepancy between estimations and observations, making it an essential metric for quantifying estimation accuracy. However, the MAE does not exhibit sensitivity toward significant deviations. The RMSE, being more sensitive to large errors, is computed as the square root of the sum of squared errors. Even small amounts of very large errors can significantly increase the RMSE. By employing both the MAE and the RMSE as indicators, the accuracy and stability of the estimated results could be validated comprehensively. However, experiments yielding MAE or RMSE values exceeding 100 or negative correlation coefficients were excluded from our study.
where represents the total number of test data and and are the simulated and observed values of PM2.5 concentration. and represent the mean of the simulated and observed values of PM2.5 concentration, respectively.
3. Results
The determination of the maximum degrees of the basis function in both the horizontal and vertical directions is crucial for the TPF method. The MAE and the RMSE for each order combination ( and ) were calculated, and these are shown in Table 1 and Table 2.

Table 1.
MAEs of TPF method. The unit is μg·m−3. The bolded data in the table are the best realized.

Table 2.
RMSEs of TPF method. The unit is μg·m−3. The bolded data in the table are the best realized.
Table 1 and Table 2 reveal that the MAEs follow an upward trend as the degrees of the basis function ( and ) increased. Notably, the fitting results displayed MAE or RMSE values that became excessively high when . This limitation can be attributed to the inherent nature of the polynomial function itself.
The MAEs in the reasonable crossover experiments for TPF were primarily concentrated within the range of 8–13. Notably, the lowest MAEs were observed when the orders were set to their respective values (TPF31). Table 2 demonstrates that the RMSEs exhibited similar patterns to the MAEs across all order combinations in the 10-fold random cross-validation. Comparing the RMSE values in Table 2 enabled us to evaluate the performance of TPF31 and to identify the most accurate and stable model that aligned best with the PM2.5 results. As a result, TPF31 was consistently selected for subsequent experiments using the TPF method.
For the OPF method, all combinations of polynomial orders ( and ) were tested during the 10-fold random cross-validation. The corresponding statistical parameters are presented in Table 3 and Table 4. The statistical data indicated that the choice of polynomial order had minimal impact on the MAE and RMSE values observed in the 64 group experiments, as their values exhibited limited fluctuations. In this study’s dataset, the fitting results remained unaffected by larger errors resulting from extensive polynomial coefficient calculations, due to polynomial order amplification. This can be attributed to the availability of sufficient observation data, despite their uneven distribution, which enhanced the accuracy of fitting when employing high-order OPF. This finding supports an observation presented in a previous study by Li [31]. The order of the Chebyshev polynomial fitting method was determined by selecting the group that exhibited the minimum errors (OPF73).

Table 3.
MAEs of OPF method. The unit is μg·m−3. The bolded data in the table are the best realized.

Table 4.
RMSEs of OPF method. The unit is μg·m−3. The bolded data in the table are the best realized.
We show the results of the 10-fold cross-validation experiment error for the four methods in Figure 2 and Table 5. As shown in Figure 2, the crossover experiments indicated that TPF31 outperformed the other three methods. The results of the two fitting methods, TPF31 and OPF73, were highly similar, and the difference in the MAE of each cross-experiment did not exceed 1 μg·m−3. In six sets of experiments (CV1, CV5, CV6, CV8, CV9, and CV10), TPF31 outperformed OPF73, and in CV2, CV3, CV4, and CV7, TPF31 slightly outperformed OPF73. In terms of mean error, RBF yielded the least favorable results. In all the crossover experiments, the error results of RBF were always the highest, with the MAE 31.82% higher than that of TPF31, and the RMSE 30.03% higher than that of TPF31. The trend between the MAE values obtained by OPF73 and TPF31 was the closest, but most of the MAE values obtained by using TPF31 were in the range of 7–9 μg·m−3, and the smallest MAE value among the four interpolation methods was about 6.2 μg·m−3.
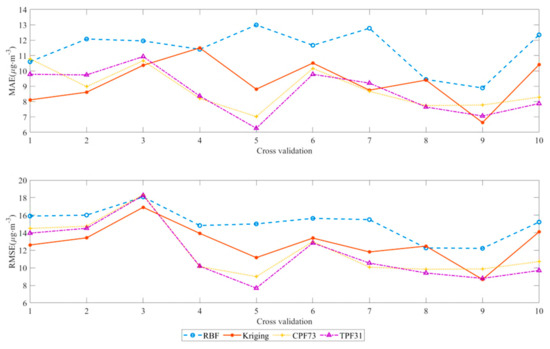
Figure 2.
MAE and RMSE of the corresponding methods for 10-fold cross-validations. (Blue dashed line: the RBF interpolation method; solid red line: the Kriging interpolation method; yellow dashed line: OPF73; purple dashed line: TPF31).

Table 5.
MAE and RMSE of each method in the 10-fold cross-validation. The unit is μg·m−3. The bolded data in the table are the best realized.
Figure 3 presents a scatterplot depicting the match between interpolated and detected values, considering all estimates of the detected locations in the 10-fold cross-validation. The red dashed lines represent boundaries where the deviation was less than 20. The estimates obtained from TPF31 demonstrated a better match with the observed values, with 93.48% of the values falling within the line where the deviation was less than 20. The interpolations from OPF73 and Kriging were closely aligned, with 90.87% and 89.2% of the values, respectively, falling within this range. Notably, the RBF interpolated values appeared to be more dispersed, exhibiting relatively large deviations between observed and estimated values. A total of 41 sites, accounting for 17.83% of all observations, exhibited a significant discrepancy (i.e., the deviation between the observed value and the estimated value was more than 20) between the observed and simulated PM2.5 concentrations. The occurrence of such high errors can be attributed to the overfitting of the RBF method at the edges of the study area. These problematic sites were mainly concentrated in Inner Mongolia, Ningxia, Gansu, Sichuan, Chongqing, and Liaoning, which constituted the boundary regions of the study area. The limited vegetation coverage in Ningxia and Gansu, coupled with the presence of valleys surrounding Sichuan and Chongqing, contributed to the heightened aggregation of PM2.5 particles in these areas. Furthermore, the prevalence of heavy industries in Liaoning Province exacerbates the severity of PM2.5 pollution. Consequently, these regions stood out as the most heavily impacted by PM2.5 pollution.
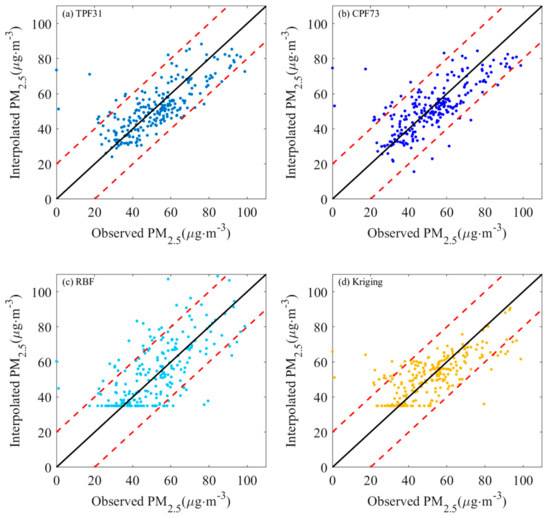
Figure 3.
Scatterplots of the matchups between the estimated and observed PM2.5 concentrations. The black line is the 1:1 line and the red dashed lines are the cut-off lines for deviations less than 20 μg·m−3. ((a) TPF31, (b) OPF73, (c) the RBF interpolation method, and (d) the Kriging interpolation method).
Furthermore, Figure 4 presents the distribution of absolute errors. Among all the methods’ results, the Kriging interpolation method yielded the highest percentage of absolute-error value distributions of 0 to 5 (43.04% of the values). However, the percentage of absolute-error values in the interval greater than 25 was considerably higher for Kriging (10.87% of the values) compared to TPF31 (6.52% of the values). In terms of absolute-error values below 10, RBF had approximately 55% of the values, Kriging had 65%, OPF73 had 64%, and TPF31 had 66%. The proportion of absolute-error values greater than 25 for TPF31 was only 2%. Analysis revealed that most of the errors in TPF31 fell within the range of 0 to 10, which was a significant advantage over the other three methods.
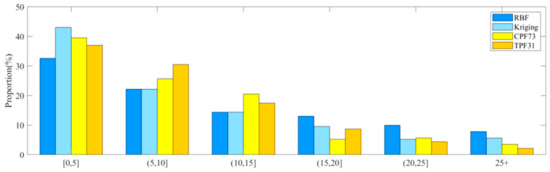
Figure 4.
The component of absolute error of the three interpolation methods. (Blue: the RBF interpolation method; cyan: the Kriging interpolation method; yellow: OPF73; orange: TPF31).
In all the cross-validation procedures, TPF31 consistently delivered superior results compared to OPF73, RBF interpolation, and Kriging interpolation. (The mean errors for all points to be estimated were 8.66 μg·m−3 and 11.59 μg·m−3, respectively).
Figure 5 displays the annual average PM2.5 concentrations in 2015 at the 235 monitoring stations within the study area. Each point’s color shade represents the magnitude of the PM2.5 concentration at that location. Subsequently, we applied the four methods to analyze the reconstructed PM2.5 spatial distribution in south-central China, and the corresponding outcomes are depicted in Figure 6. Among the four methods, TPF31 resulted in smoother spatial distributions of concentrations, which aligned with the observations shown in Figure 5. Furthermore, the spatial distributions obtained from TPF31 strongly coincided with those obtained by Wei et al. (2021) for the year 2015 [10].
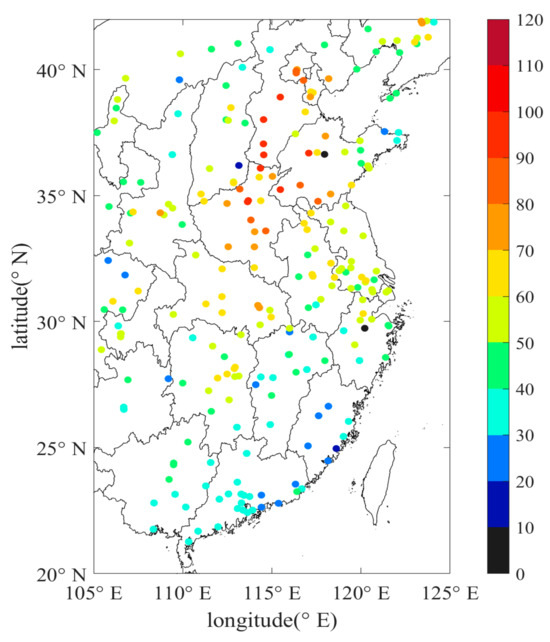
Figure 5.
Annual average PM2.5 concentrations at 235 monitoring stations in south-central China in 2015. The color shade of each point represents the size of the PM2.5 annual average concentration at that point in 2015.
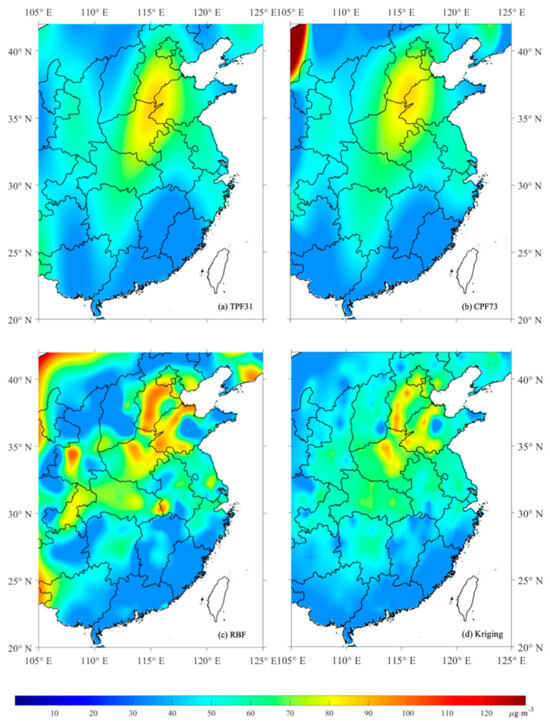
Figure 6.
PM2.5 concentrations of experiments calculated by (a) TPF31, (b) OPF73, (c) the RBF interpolation method, and (d) the Kriging interpolation method.
While CPF73 also exhibited satisfactory error performance, it demonstrated slightly inferior smoothness compared to TPF31 in accurately reflecting real-world phenomena. However, an obvious anomalous bulge appeared in the south-central region of Inner Mongolia in the spatial distribution of PM2.5 concentration when using CPF73 (Figure 6b). The average PM2.5 concentration in this region, estimated by CPF73, was approximately 103.92 μg·m−3, and the fitted values of PM2.5 were significantly higher than the observed values, as shown in Figure 5. This indicated the occurrence of overfitting in the south-central region of Inner Mongolia when utilizing CPF73.
The RBF method exhibited residual overfitting at the boundary locations of the study area, as observed in Figure 6c. In contrast, Kriging interpolation provided a more accurate representation of the spatial distribution of PM2.5 concentrations, closely reflecting real-world phenomena. However, in the Beijing–Tianjin–Hebei region, Kriging interpolation produced concentration values that were excessively high and not sufficiently smooth, as shown in Figure 6d. Although Kriging interpolation achieved good results, its smoothness slightly lagged behind that of TPF31. Consequently, the PM2.5 distributions calculated by TPF31 were closer to the observed values compared to the other three methods. Considering the analyses conducted, it can be concluded that TPF31 was the most suitable interpolation method for simulating PM2.5 concentrations in this study, as supported by cross-validation.
4. Discussion
This study aimed to evaluate the effectiveness of the trigonometric polynomial fitting (TPF) method in modeling atmospheric pollutant distributions, specifically in scenarios involving irregular and limited observation station distribution. By harnessing the flexibility and adaptability of the TPF framework, we aimed to gain valuable insights into its performance in capturing the spatial variations and patterns of pollutant concentrations across diverse regions. To assess the TPF method’s capability, we simulated the PM2.5 concentrations in China’s central and southern regions during 2015. Remarkably, the TPF method demonstrated strong predictive accuracy, with impressive cross-validation MAE and RMSE values of 8.66 μg·m−3 and 11.59 μg·m−3, respectively This high level of accuracy highlighted the method’s ability to effectively model and predict PM2.5 concentrations under conditions of unevenly distributed observation stations, further supporting its utility in environmental research. Furthermore, the TPF method performed superiorly in accurately representing the spatial patterns and variations of PM2.5 concentrations, outperforming alternative interpolation techniques such as OPF, RBF, and Kriging. Although these widely used techniques yielded satisfactory results in general environmental data interpolation, they were less effective in capturing uneven pollutant distributions. In contrast, the TPF method excelled in capturing the unique characteristics of the region, leading to a more faithful reproduction of the spatial distribution of PM2.5 concentrations when compared to alternative approaches.
The use of interpolation and fitting techniques for simulating atmospheric pollutant concentrations has been a consistent focus of research. The accuracy and precision of interpolation have always been key considerations in these studies [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. In the study by Li et al. [31], the results indicated that the optimal polynomial fitting (OPF) method accurately reconstructed PM2.5 fields. The estimated PM2.5 concentrations obtained from the OPF method closely aligned with observations on 27 December 2017 [31]. Additionally, the successful application of the TPF method for accurately modeling Arctic sea-ice depth prompted us to explore its potential in the field of atmospheric-pollution modeling [39]. Therefore, we chose to apply the TPF method to investigate the PM2.5 concentrations during the entire year of 2015. Comparative analysis of the simulation results revealed that the TPF method exhibited the lowest simulation error in cross-validation experiments, displaying superior performance compared to other methods.
In particular, the TPF method demonstrated exceptional performance in simulating areas characterized by unevenly distributed observation stations, limited observation stations, and marginal regions within the simulation area. In the southeastern region of Inner Mongolia, which is characterized by unevenly distributed observation stations, both the CPF method and RBF interpolation showed noticeable overfitting phenomena. The observed concentrations in the southeastern part of Inner Mongolia were around 50 μg·m−3, but the simulated average of OPF in this region was 103.92 μg·m−3 and the simulated average of RBF in this region was 71.89 μg·m−3. Furthermore, in the marginal areas of the study region, when comparing simulated values to observed data and examining provincial boundaries on a map, RBF interpolation also exhibited significant issues with overestimation. Observed concentrations at the edge of the study area ranged from 50 to 55 μg·m−3, but the RBF averaged 67.82 μg·m−3 for the simulation in this area. The Kriging interpolation offered a comprehensive analysis of the spatial structure and variance estimation of data, relying on the variogram to characterize the spatial variation of the property being studied. However, this method can be time-consuming and complex, due to the requirement of calculating inverse matrices [40,41,42].
On the contrary, when analyzing the reconstructed spatial distribution maps, it became apparent that the TPF method performed well even in regions with unevenly distributed observation stations, areas with higher observed concentration values, and along the boundaries of the study area.
The reason behind this behavior is attributed to the definition of the interpolation methods used. In our simulation scenario for the entire year of 2015, the larger dataset was more sensitive to the effects of unevenly distributed observation stations. The TPF method, based on trigonometric functions, effectively fitted data with higher fluctuations or sparse observations. As a result, the TPF method achieved higher accuracy in simulation, while other methods suffered from overfitting, due to their definitions or their computationally intensive nature, or exhibited overfitting issues along the boundaries [29,40].
In this study, we focused solely on the analysis of observation station data. However, it is important to recognize that observation station data can be influenced by various factors, such as the geographical location, meteorological conditions, seasonal variations, and economic composition. China has a complex geography and a long coastline, so different geographic locations may affect the level of data from monitoring stations in those areas. For example, the Sichuan and Chongqing regions may have high PM2.5 concentrations due to the high valleys around them, so the PM2.5 data from the stations in these regions may be higher, while the southern coastal cities are close to the ocean, so the data from the stations in this region may be relatively lower [12]. Meteorological factors are the external conditions for the formation of PM2.5 pollution, and precipitation, wind speed, temperature, and humidity all have an effect on PM2.5. Precipitation has a scouring effect on the dust particles in PM2.5, temperature and wind speed have a significant effect on their dispersion, and high humidity favors the formation of PM2.5 [42]. In the north, long winters and high demand for indoor heating make the concentration of PM2.5 in the air higher. Beijing–Tianjin–Hebei, North China, and the Yangtze River Delta have high population densities and a high degree of industrialization, so motor vehicle emissions and industrial activities in these regions are likely to have some impact on the monitoring results in these regions. During field observations, large amounts of data were lost due to a variety of unforeseen factors (e.g., instrument failures, power interruptions, and network outages), which may have resulted in significant data gaps in the archived data [38].
While our paper specifically highlights the efficacy of the trigonometric polynomial fitting (TPF) method for simulating PM2.5 concentrations, we intend to further investigate its application to simulate PM2.5 data from multiple sources in future research. Additionally, we plan to extend this method to the study of other atmospheric pollutants. By utilizing this approach, we aim to capture the complex interactions between atmospheric dynamics, emission sources, and dispersion patterns, particularly when faced with non-uniform observation station distributions. This research direction holds promise for overcoming challenges associated with limited data availability and incorporating comprehensive spatial information. It is important to note that in this study, the PM2.5 data were only fitted for south-central China in 2015. It remains uncertain whether the best-fitting function (TPF31) performs well in other regions. While TPF31 enables obtaining the spatial distribution of PM2.5 concentrations with high resolution, it does not account for temporal changes in monitoring PM2.5 concentrations. To gain a more comprehensive understanding of PM2.5 concentrations, further studies are necessary to evaluate the performance of different interpolation methods in capturing the fitting effect.
5. Conclusions
Long-term exposure to PM2.5 pollution not only jeopardizes human health, but also hinders the sustainable development of cities [43]. Therefore, this paper took “PM2.5” as the research object and proposed a trigonometric polynomial fitting (TPF) method for estimating PM2.5 concentration in south-central China. The core of the TPF method lies in choosing a reasonable polynomial order, and the optimal order chosen will depend on the utilized data information. Based on PM2.5 data collected in 2015 from central and southern regions of China, the optimal order of TPF and OPF was determined through a 10-fold cross-validation procedure.
TPF method demonstrated an increasing trend in statistical errors as the degrees of the basis function ( and ) increased. However, there was a large deviation between the fitting results and the observed data, when . This indicated unreliability in accurately representing the actual situation. The limitations arose from the inherent structure of the polynomial function. The optimal orders of the TPF method in the x and y directions were determined as 3 and 1, respectively.
For the OPF method, the fitting results remained unaffected by the larger errors resulting from extensive polynomial coefficient calculations, due to the polynomial order amplification in this study. The relatively sufficient observation data, although unevenly distributed, enhanced the accuracy of fitting when employing high-order OPF. The optimal orders of the OPF method in the x and y directions were determined as 7 and 3, respectively.
The statistical parameters comparison showed that TPF31 yielded superior outcomes compared to OPF73, RBF interpolation, and Kriging interpolation. OPF73 performed better than the other two interpolations. RBF interpolation performed worst, due to the substantial computational burden when processing extensive datasets.
TPF31 more accurately reproduced the spatial distribution of PM2.5 concentration in the south-central region of China, and the accuracy of TPF31 was higher than that of OPF73, the Kriging interpolation method, and the RBF interpolation method. Compared with the study by Li et al. (2019) [31], the computational results of the trigonometric polynomial fitting method proposed in this paper were more in line with the spatial and temporal variation patterns of the annual average PM2.5 concentration in the south-central region of China in 2015 (Wei et al., 2021 [10]) and did not produce overfitting in the boundary region. The Kriging interpolation method and the RBF interpolation method failed to accurately reconstruct the spatial distribution of PM2.5 concentration in south-central China in 2015, owing to significant errors and a non-smooth simulated spatial pattern exhibited by these two methods. In summary, the trigonometric polynomial fitting method proposed in this paper has more significant advantages in characterizing the spatial distribution of PM2.5, which can provide strong support for estimating the regional PM2.5 concentration data.
In this study, we only fitted the annual average PM2.5 concentration data in 2015, and we will subsequently validate the effectiveness of the method on other temporal and spatial scales and explore its applicability, as well as the effectiveness of its use in PM2.5 transport modeling.
With the continuous development of society and the economy, people’s concern for PM2.5 has been elevated from “concern for public health” to “concern for the ecological environment”, which means that the focus of China’s ecological environmental protection work has fundamentally changed. Although there are limitations to our study, it can provide a strong scientific basis for estimating regional PM2.5 concentration data, which can be used as an important reference for formulating effective policies and enforcing effective regulations. In addition, based on the results of this study, effective measures can be taken to improve air quality, reduce pollutant emissions, and better promote the SDGs. This plays a positive role in promoting China’s development in the SDG process.
Author Contributions
Conceptualization, N.L.; methodology, N.L. and M.X.; software, Y.C. and X.L.; formal analysis, Y.C.; writing—original draft preparation, N.L.; writing—review and editing, N.L.; supervision, X.L.; funding acquisition, W.S. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 41806219, the Central Guidance on Local Science and Technology Development Fund of Dalian City (“Research on marine dynamic in-situ monitoring technology for risk warning of coastal nuclear power cold source blockage risk in Dalian”).
Institutional Review Board Statement
This study did not involve humans or animals.
Informed Consent Statement
Not applicable.
Data Availability Statement
The PM2.5 data in this paper were hourly data in 2015 sourced from China National Environmental Monitoring Center (CNEMC) (http://www.cnemc.cn/, accessed on 30 October 2023).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jia, N.; Li, Y.; Chen, R.; Yang, H. A review of global PM2.5 exposure research trends from 1992 to 2022. Sustainability 2023, 15, 10509. [Google Scholar] [CrossRef]
- Pineda AA, L.; Cano, J.A. Assessment of air quality in the Aburrá Valley (Colombia) using composite indices: Towards comprehensive sustainable development planning. Urban Clim. 2021, 39, 100942. [Google Scholar] [CrossRef]
- Ramanathan, V.; Feng, Y. Air pollution, greenhouse gases and climate change: Global and regional perspectives. Atmos. Environ. 2009, 43, 37–50. [Google Scholar] [CrossRef]
- Gibson, J. Air pollution, climate change, and health. Lancet Oncol. 2015, 16, e269. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Guo, J.; Ding, A.; Liao, H.; Liu, J.; Sun, Y.; Wang, T.; Xue, H.; Zhang, H.; Zhu, B. Aerosol and boundary-layer interactions and impact on air quality. Natl. Sci. Rev. 2017, 4, 810–833. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, M.; Wang, L.; Qin, W.; Li, J. Aerosol radiative effects from observations and modelling over the Yangtze River Basin, China from 2001 to 2015. Int. J. Climatol. 2019, 39, 3476–3491. [Google Scholar] [CrossRef]
- Song, Y.; Huang, B.; He, Q.; Chen, B.; Wei, J.; Mahmood, R. Dynamic assessment of PM2.5 exposure and health risk using remote sensing and geo-spatial big data. Environ. Pollut. 2019, 253, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Zhang, N.; Yan, X.; Wang, M.; Wang, J. The effect of ambient fine particulate matter (PM 2.5) on respiratory diseases in China: A systematic review and meta-analysis. Stoch. Environ. Res. Risk Assess. 2020, 34, 593–610. [Google Scholar] [CrossRef]
- Yao, F.; Si, M.; Li, W.; Wu, J. A multidimensional comparison between MODIS and VIIRS AOD in estimating ground-level PM2.5 concentrations over a heavily polluted region in China. Sci. Total Environ. 2018, 618, 819–828. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Sun, L.; Xue, W.; Ma, Z.; Liu, L.; Fan, T.; Cribb, M. Extending the EOS long-term PM2.5 data records since 2013 in China: Application to the VIIRS deep blue aerosol products. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Jing, Y.; Pan, L.; Sun, Y. Estimating PM2.5 concentrations in a central region of China using a three-stage model. Int. J. Digit. Earth 2023, 16, 578–592. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, L. High-precision estimation of hourly PM2.5 concentration based on a grid scale of satellite-derived products. Atmos. Pollut. Res. 2023, 14, 101724. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Shi, Z.; Sun, J.; Gong, K.; Li, J.; Qin, M.; Wei, J.; Li, T.; Kan, H.; et al. Effects of using different exposure data to estimate changes in premature mortality attributable to PM2.5 and O3 in China. Environ. Pollut. 2021, 285, 117242. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Liu, Y.; Lv, X.; Zhang, J.; Fu, K. The High Order Conservative Method for the Parameters Estimation in a PM2.5 transport adjoint model. Adv. Meteorol. 2017, 2017, 4626585. [Google Scholar] [CrossRef]
- He, K.; Huo, H.; Zhang, Q. Urban air pollution in China: Current status, characteristics, and progress. Annu. Rev. Energy Environ. 2002, 27, 397–431. [Google Scholar] [CrossRef]
- Sun, L.; Wei, J.; Duan, D.H.; Guo, Y.M.; Yang, D.X.; Jia, C.; Mi, X.T. Impact of Land-Use and Land-Cover Change on urban air quality in representative cities of China. J. Atmos. Sol. Terr. Phys. 2016, 142, 43–54. [Google Scholar] [CrossRef]
- Li, C.C.; Mao, J.T.; Lau, A.K.; Yuan, Z.; Wang, M.; Liu, X. Application of MODIS aerosol product in the study of air pollution in Beijing. Sci. China Ser. D Earth Sci. 2005, 35, 177–186. [Google Scholar]
- Xu, J.; Gao, C.; Lee, J.K.W.; Zhao, J. PM2.5: A barrier to fitness and health promotion in China. J. Sport Health Sci. 2017, 6, 292–294. [Google Scholar] [CrossRef]
- Dong, J.; Wang, Y.; Wang, L.; Zhao, W.; Huang, C. Assessment of PM2.5 exposure risk towards SDG indicator 11.6. 2—A case study in Beijing. Sustain. Cities Soc. 2022, 82, 103864. [Google Scholar] [CrossRef]
- Kumar, N. What can affect AOD–PM2.5 association? Environ. Health Perspect. 2010, 118, A109–A110. [Google Scholar] [CrossRef]
- Lang, S.L.; Fang, H.L.; Chen, M.Z. Atmospheric correction of Landsat ETM—Land surface imagery. l. Methods. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2490–2498. [Google Scholar] [CrossRef]
- Physick, W.L.; Cope, M.E.; Lee, S.; Hurley, P.J. An approach for estimating exposure to ambient concentrations. J. Expo. Sci. Environ. Epidemiol. 2007, 17, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.J.; Serre, M.L.; van Donkelaar, A.; Martin, R.V.; Burnett, R.T.; Jerrett, M. Comparison of geostatistical interpolation and remote sensing techniques for estimating long-term exposure to ambient PM2.5 concentrations across the continental United States. Environ. Health Perspect. 2012, 120, 1727–1732. [Google Scholar] [CrossRef]
- Sampson, P.D.; Richards, M.; Szpiro, A.A.; Bergen, S.; Sheppard, L.; Larson, T.V.; Kaufman, J.D. A regionalized national universal kriging model using Partial Least Squares regression for estimating annual PM2.5 concentrations in epidemiology. Atmos. Environ. 2013, 75, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Hu, Z.; Zhong, K.; Xu, J.; Zhang, F.; Zhao, Y.; Wu, P. Satellite-based high-resolution mapping of ground-level PM2.5 concentrations over East China using a spatiotemporal regression kriging model. Sci. Total Environ. 2019, 672, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Amini, H.; Ashrafzadeh, A.; Khaledian, M. Enhancing groundwater salinity estimation through integrated GMDH and geostatistical techniques to minimize Kriging interpolation error. Earth Sci. Inform. 2023, 1–15. [Google Scholar] [CrossRef]
- Chang, J.H.; Hart, D.R.; Munroe, D.M.; Curchitser, E.N. Bias correction of ocean bottom temperature and salinity simulations from a regional circulation model using regression kriging. J. Geophys. Res. Ocean. 2021, 126, e2020JC017140. [Google Scholar] [CrossRef]
- Zheng, H.; Shang, X. Study on prediction of atmospheric PM2.5 based on RBF neural network. In Proceedings of the 2013 Fourth International Conference on Digital Manufacturing & Automation, Qingdao, China, 29–30 June 2013; pp. 1287–1289. [Google Scholar]
- Gao, Y.; Guo, J.; Wang, J.; Lv, X. Assessment of Three-Dimensional Interpolation Method in Hydrologic Analysis in the East China Sea. J. Mar. Sci. Eng. 2022, 10, 877. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Li, C.; Xie, J.; Wu, R. Fracture modeling of carbonate rocks via radial basis interpolation and discrete fracture network. Carbonates Evaporites 2023, 38, 85. [Google Scholar] [CrossRef]
- Li, B.; Liu, Y.; Wang, X.; Fu, Q.; Lv, X. Application of the orthogonal polynomial fitting method in estimating PM2.5 concentrations in central and southern regions of China. Int. J. Environ. Res. Public Health 2019, 16, 1418. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, R.; Peng, C.; Yan FE, N.G.; Wang, X.F.; Xiang, W.U.; Cai, Z.Y. Effect of elevated-temperature annealing on microstructure and properties of Cu–0.15 Zr alloy. Trans. Nonferrous Met. Soc. China 2021, 31, 3772–3784. [Google Scholar] [CrossRef]
- Preethi, R.; Sathiyapriya, G.; Shanthi, S.A. Radial basis function bipolar fuzzy neural network. Mater. Today Proc. 2023, 80, 389–394. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Y.; Wang, Y.; Xu, M.; Lv, X. Fitting Cotidal Charts of Eight Major Tidal Components in the Bohai Sea, Yellow Sea Based on Chebyshev Polynomial Method. J. Mar. Sci. Eng. 2022, 10, 1219. [Google Scholar] [CrossRef]
- Li, Z.L.; Niu, Y.P. Application of Orthogonal Polynomial Fitting Method to Extract Gravity Wave Signals from AIRS Data Related to Typhoon Deep Convection. Earth Space Sci. 2022, 9, e2022EA002408. [Google Scholar] [CrossRef]
- Guorong, S.; Mingkun, L.; Yan, L.; Yungchun, L.; Bin, W.; Cunfu, H. Application of Legendre orthogonal polynomial method in calculating reflection and transmission coefficients of multilayer plates. Wave Motion 2019, 84, 32–45. [Google Scholar] [CrossRef]
- Zhou, H.; Pan, H.; Li, S.; Lv, X. Application of Empirical Orthogonal Function Interpolation to Reconstruct Hourly Fine Particulate Matter Concentration Data in Tianjin, China. Complexity 2020, 2020, 9724367. [Google Scholar] [CrossRef]
- Bai, K.; Li, K.; Guo, J.; Yang, Y.; Chang, N.-B. Filling the gaps of in situ hourly PM2.5 concentration data with the aid of empirical orthogonal function analysis constrained by diurnal cycles. Atmos. Meas. Tech. 2020, 13, 1213–1226. [Google Scholar] [CrossRef]
- Nie, Y.; Wang, Y.; Lv, X. Acquiring the arctic-scale spatial distribution of snow depth based on AMSR-E snow depth product. J. Atmos. Ocean. Technol. 2019, 36, 1957–1965. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Chevalier, C.; Bect, J.; Ginsbourger, D.; Vazquez, E.; Picheny, V.; Richet, Y. Fast parallel kriging-based stepwise uncertainty reduction with application to the identification of an excursion set. Technometrics 2014, 56, 455–465. [Google Scholar] [CrossRef]
- Lu, D.; Xu, J.; Yang, D.; Zhao, J. Spatio-temporal variation and influence factors of PM2.5 concentrations in China from 1998 to 2014. Atmos. Pollut. Res. 2017, 8, 1151–1159. [Google Scholar] [CrossRef]
- Wang, L.; Niu, D.; Fan, H.; Long, X. Urban configuration and PM2.5 concentrations: Evidence from 330 Chinese cities. Environ. Int. 2022, 161, 107129. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).