Numerical Investigation of the Impact of Tall Buildings on Pollutant Dispersion during Stable Stratification
(This article belongs to the Section Air Pollution Control)
Abstract
:1. Introduction
2. Numerical Method
3. Simulation Setting
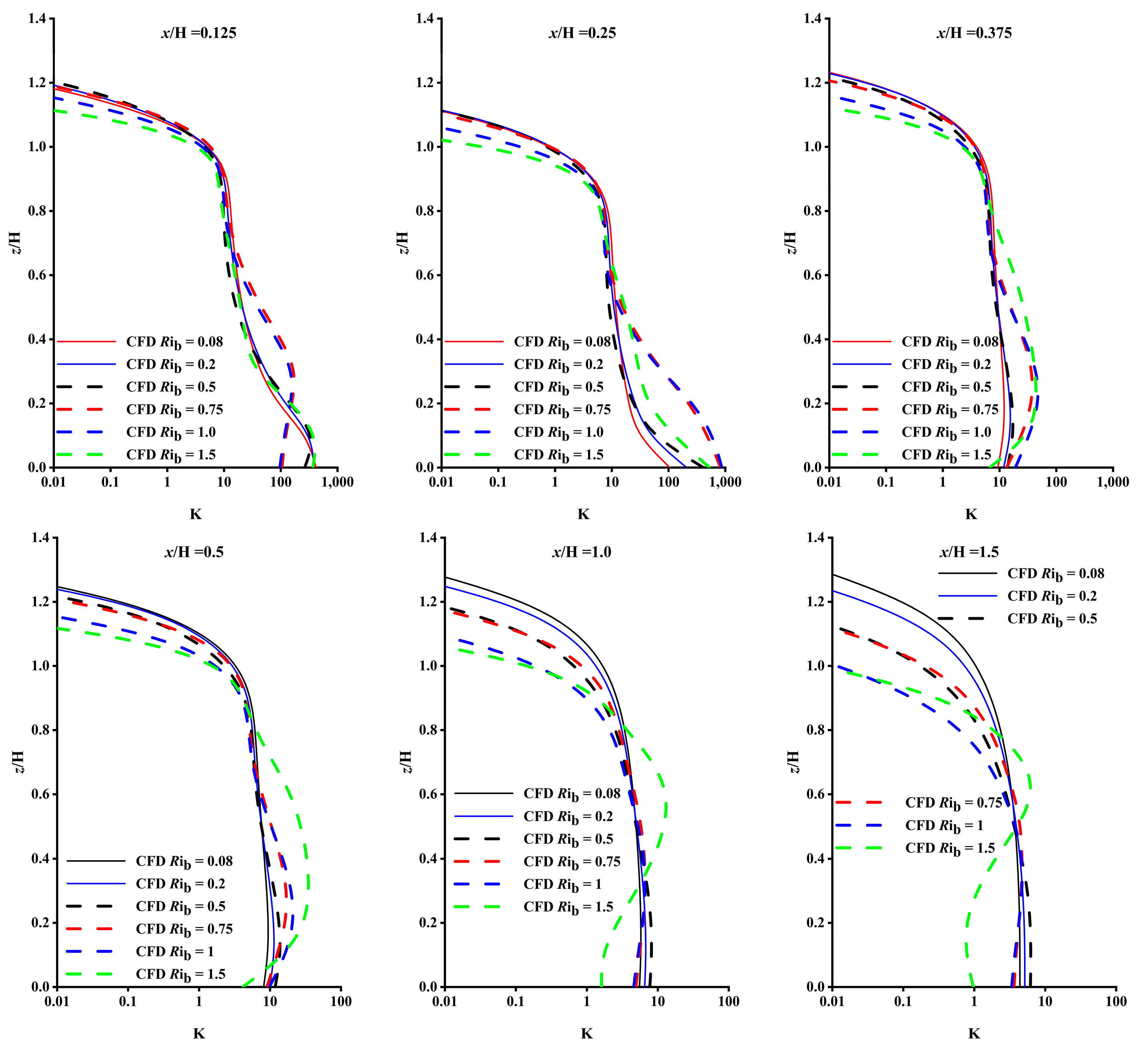
4. Model Validity Analysis
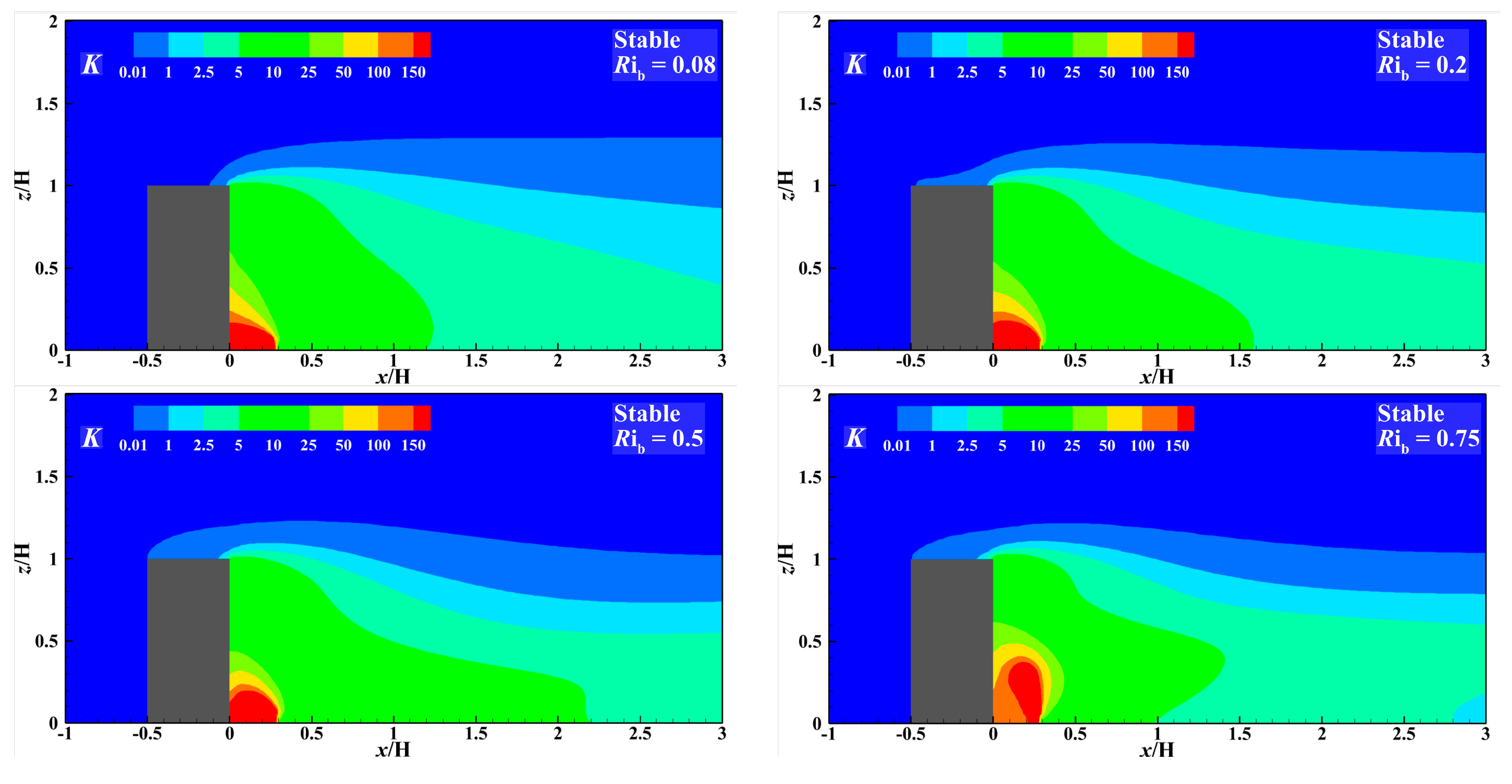
5. Results and Discussion
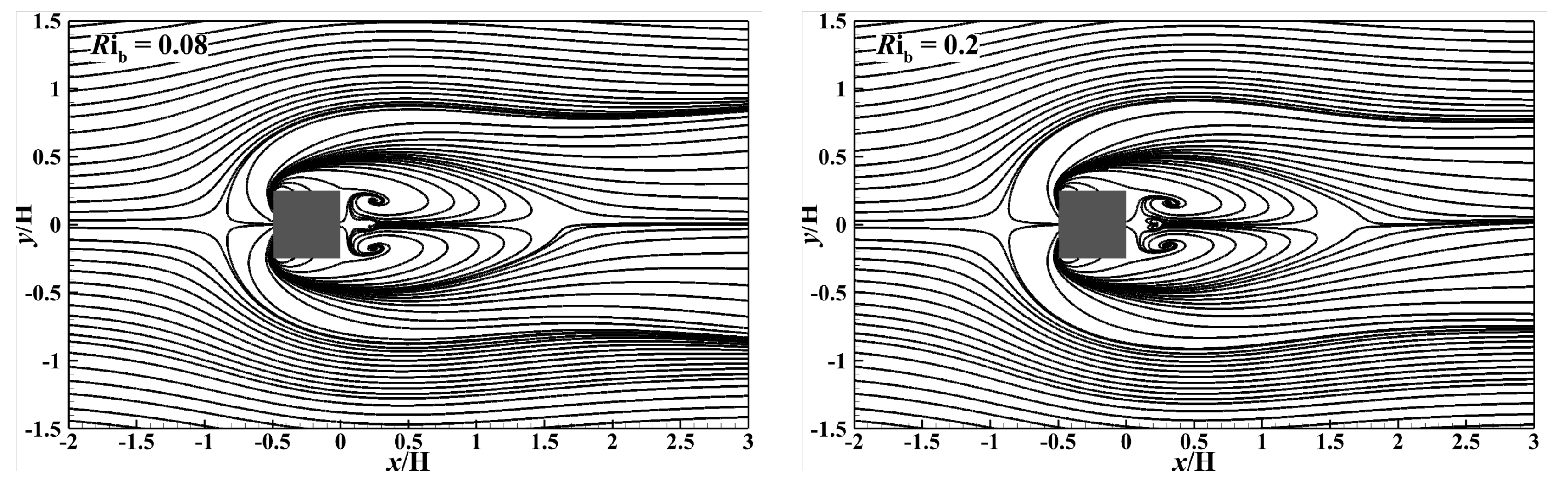
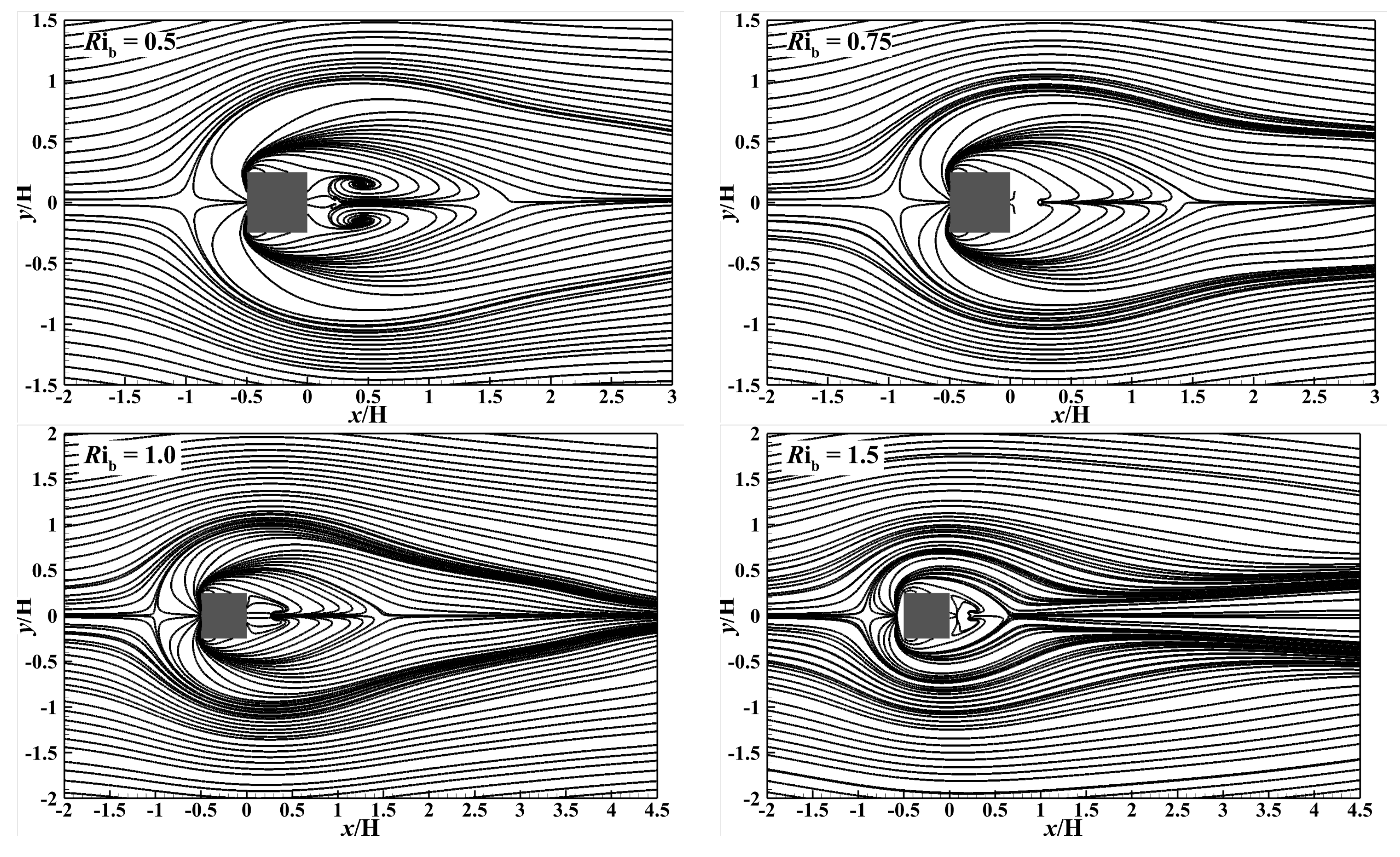
5.1. Flow Field
5.1.1. Distribution of the Mean Longitudinal Velocity
5.1.2. Distribution of the Mean Vertical Velocity
5.1.3. Flow Pattern
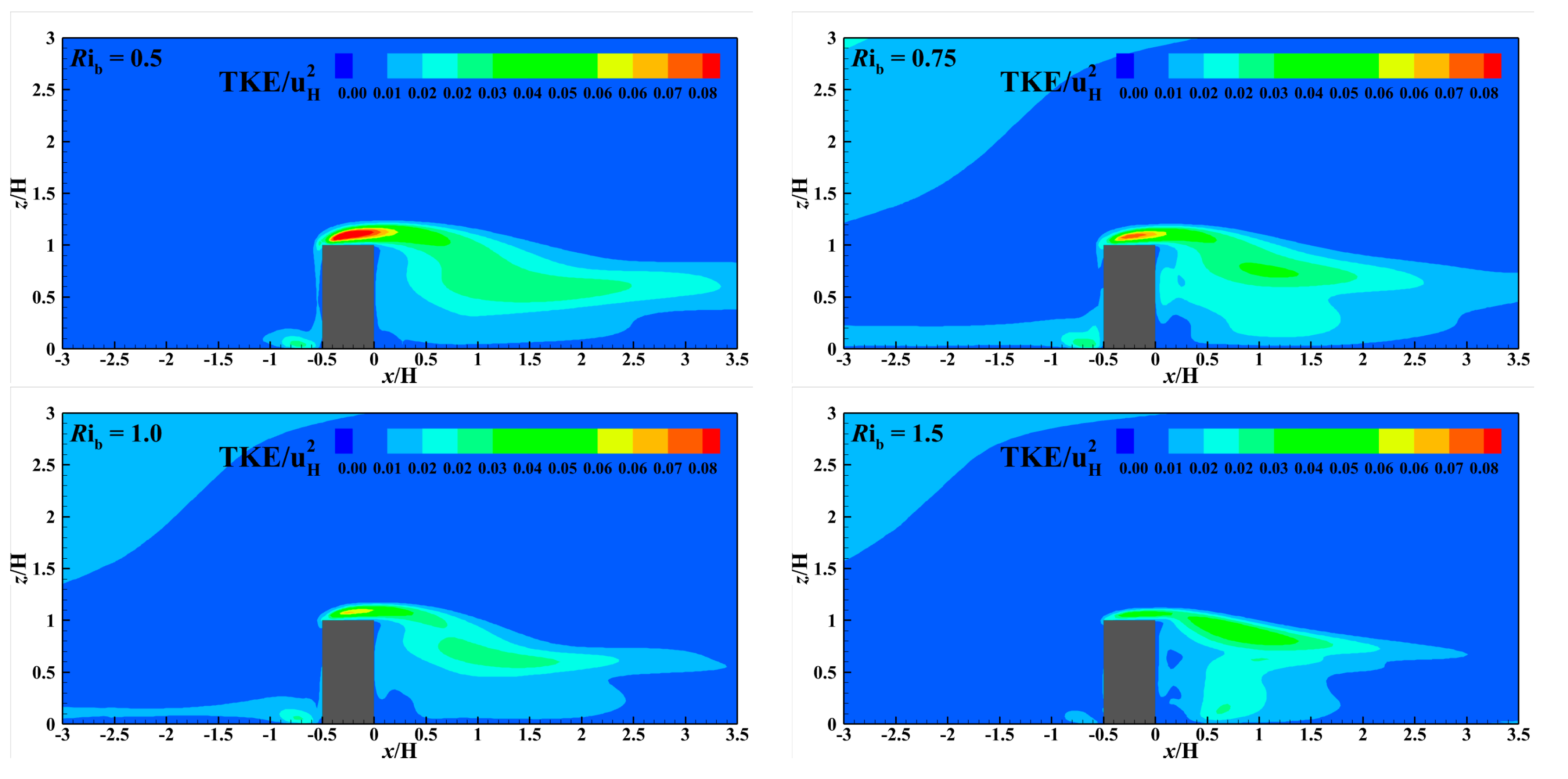
5.2. Turbulent Kinetic Energy TKE/uH2
5.3. Concentration Field
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| velocity vector | viscous stress tensor | ||
| density | specific heat at a constant pressure | ||
| pressure | thermal conductivity | ||
| mass fraction | diffusion coefficient of | ||
| temperature | Velocity | ||
| friction velocity | height | ||
| ground roughness | reference height | ||
| potential temperature | Monin–Obukhov length | ||
| temperature scale | ground sensible heat flux | ||
| average flow velocity at the reference height | kinematic viscosity coefficient |
References
- White, B.R.; Stein, W. Wind-tunnel studies of variable stack heights for a low-profile building. J. Wind. Eng. Ind. Aerodyn. 1990, 36, 675–687. [Google Scholar] [CrossRef]
- Wilson, D.J.; Fabris, I.; Ackerman, M.Y. Measuring adjacent building effects on laboratory exhaust stack design. Trans.-Am. Soc. Heat. Refrig. Air Cond. Eng. 1998, 104, 1012–1030. [Google Scholar]
- Chavez, M.; Hajra, B.; Stathopoulos, T.; Bahloul, A. Near-field pollutant dispersion in the built environment by CFD and wind tunnel simulations. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 330–339. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD simulation of near-field pollutant dispersion in the urban environment: A review of current modeling techniques. Atmos. Environ. 2013, 79, 716–730. [Google Scholar] [CrossRef]
- Vardoulakis, S.; Fisher, B.E.A.; Pericleous, K.; Gonzalez-Flesca, N. Modeling air quality in street canyons: A review. Atmos. Environ. 2003, 37, 155–182. [Google Scholar] [CrossRef]
- Yassin, M.F. A wind tunnel study on the effect of thermal stability on flow and dispersion of rooftop stack emissions in the near wake of a building. Atmos. Environ. 2013, 65, 89–100. [Google Scholar] [CrossRef]
- Mavroidis, I.; Griffiths, R.F.; Hall, D.J. Field and wind tunnel investigations of plume dispersion around single surface obstacles. Atmos. Environ. 2003, 37, 2903–2918. [Google Scholar] [CrossRef]
- Uehara, K.; Murakami, S.; Oikawa, S.; Wakamatsu, S. Wind tunnel experiments on how thermal stratification affects flow in and above urban street canyons. Atmos. Environ. 2000, 34, 1553–1562. [Google Scholar] [CrossRef]
- Ohya, Y. Wind-tunnel study of atmospheric stable boundary layers over a rough surface. Bound.-Layer. Meteorol. 2001, 98, 57–82. [Google Scholar] [CrossRef]
- Ohya, Y.; Nakamura, R.; Uchida, T. Intermittent bursting of turbulence in a stable boundary layer with low-level jet. Bound.-Layer. Meteorol. 2008, 126, 349–363. [Google Scholar] [CrossRef]
- Olvera, H.A.; Choudhuri, A.R. Numerical simulation of hydrogen dispersion in the vicinity of a cubical building in stable stratified atmospheres. Int. J. Hydrogen Energy 2006, 31, 2356–2369. [Google Scholar] [CrossRef]
- Nakamura, Y.; Oke, T.R. Wind, temperature and stability conditions in an east-west oriented urban canyon. Atmos. Environ. 1988, 22, 2691–2700. [Google Scholar] [CrossRef]
- Rotach, M.W. Profiles of turbulence statistics in and above an urban street canyon. Atmos. Environ. 1995, 29, 1473–1486. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, X.; Tominaga, Y.; Gu, M. CFD simulation of flow fields and pollutant dispersion around a cubic building considering the effect of plume buoyancies. Build. Environ. 2022, 208, 108640. [Google Scholar] [CrossRef]
- Jeong, S.J.; Kim, A.R. CFD Study on the influence of atmospheric stability on near-field pollutant dispersion from rooftop emissions. Asian J. Atmos. Environ. 2018, 12, 47–58. [Google Scholar] [CrossRef]
- Guo, D.; Wang, R.; Zhao, P.; Li, Y.; Yao, R.; Liu, Y. Numerical simulation of the influence of flow field around buildings under temperature formation. Radiat. Prot. 2020, 40, 290–300. [Google Scholar]
- Guo, D.; Yang, F.; Shi, X.; Li, Y.; Yao, R. Numerical simulation and wind tunnel experiments on the effect of a cubic building on the flow and pollutant diffusion under stable stratification. Build. Environ. 2021, 205, 108222. [Google Scholar] [CrossRef]
- Shi, X.; Guo, D.; Li, Y.; Yao, R. Numerical simulation of the influence of building objects on flow field under stable stratification. Radiat. Prot. 2022, 42, 317–325. [Google Scholar]
- Bazdidi-Tehrani, F.; Gholamalipour, P.; Kiamansouri, M.; Jadidi, M. Large eddy simulation of thermal stratification effect on convective and turbulent diffusion fluxes concerning gaseous pollutant dispersion around a high-rise model building. J. Build. Perform. Simul. 2019, 12, 97–116. [Google Scholar] [CrossRef]
- Rahmatmand, A.; Yaghoubi, M.; Rad, E.G.; Tavakol, M.M. 3D experimental and numerical analysis of wind flow around domed-roof buildings with open and closed apertures. Build. Simulat. 2014, 7, 305–319. [Google Scholar] [CrossRef]
- Tavakol, M.M.; Yaghoubi, M.; Motlagh, M.M. Air flow aerodynamic on a wallmounted hemisphere for various turbulent boundary layers. Exp. Therm. Fluid. Sci. 2010, 34, 538–553. [Google Scholar] [CrossRef]
- Ntinas, G.K.; Zhang, G.; Fragos, V.P.; Bochtis, D.D.; Nikita-Martzopoulou, C. Airflow patterns around obstacles with arched and pitched roofs: Wind tunnel measurements and direct simulation. Eur. J. Mech. B Fluid. 2014, 43, 216–229. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical simulation of dispersion around an isolated cubic building: Comparison of various types of k–ɛ models. Atmos. Environ. 2009, 43, 3200–3210. [Google Scholar] [CrossRef]
- Santos, J.M.; Reis, N.C., Jr.; Goulart, E.V.; Mavroidis, I. Numerical simulation of flow and dispersion around an isolated cubical building: The effect of the atmospheric stratification. Atmos. Environ. 2009, 43, 5484–5492. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Arya, S.P.; Snyder, W.H. A comparison of numerical and physical modeling of stable atmospheric flow and dispersion around a cubical building. Atmos. Environ. 1996, 30, 1327–1345. [Google Scholar] [CrossRef]
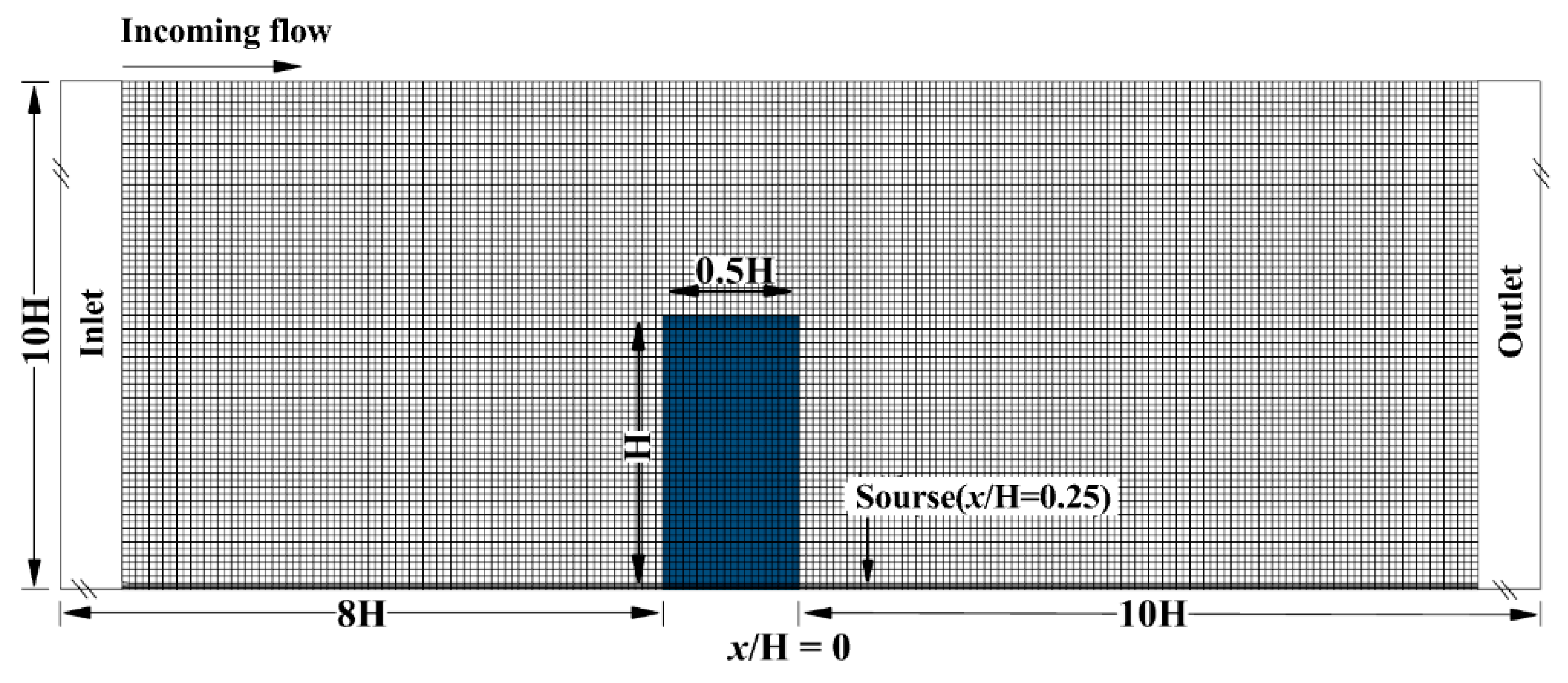
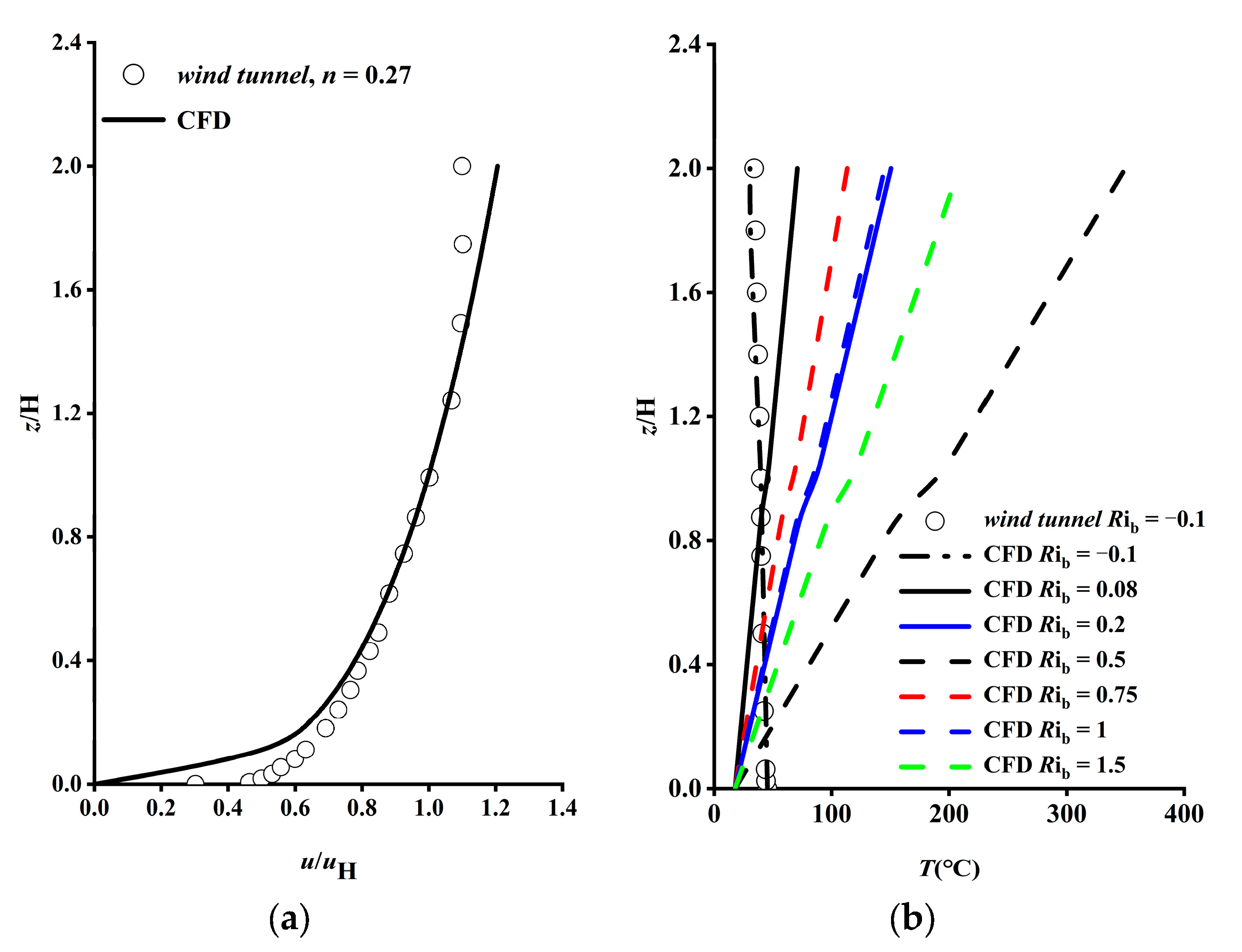
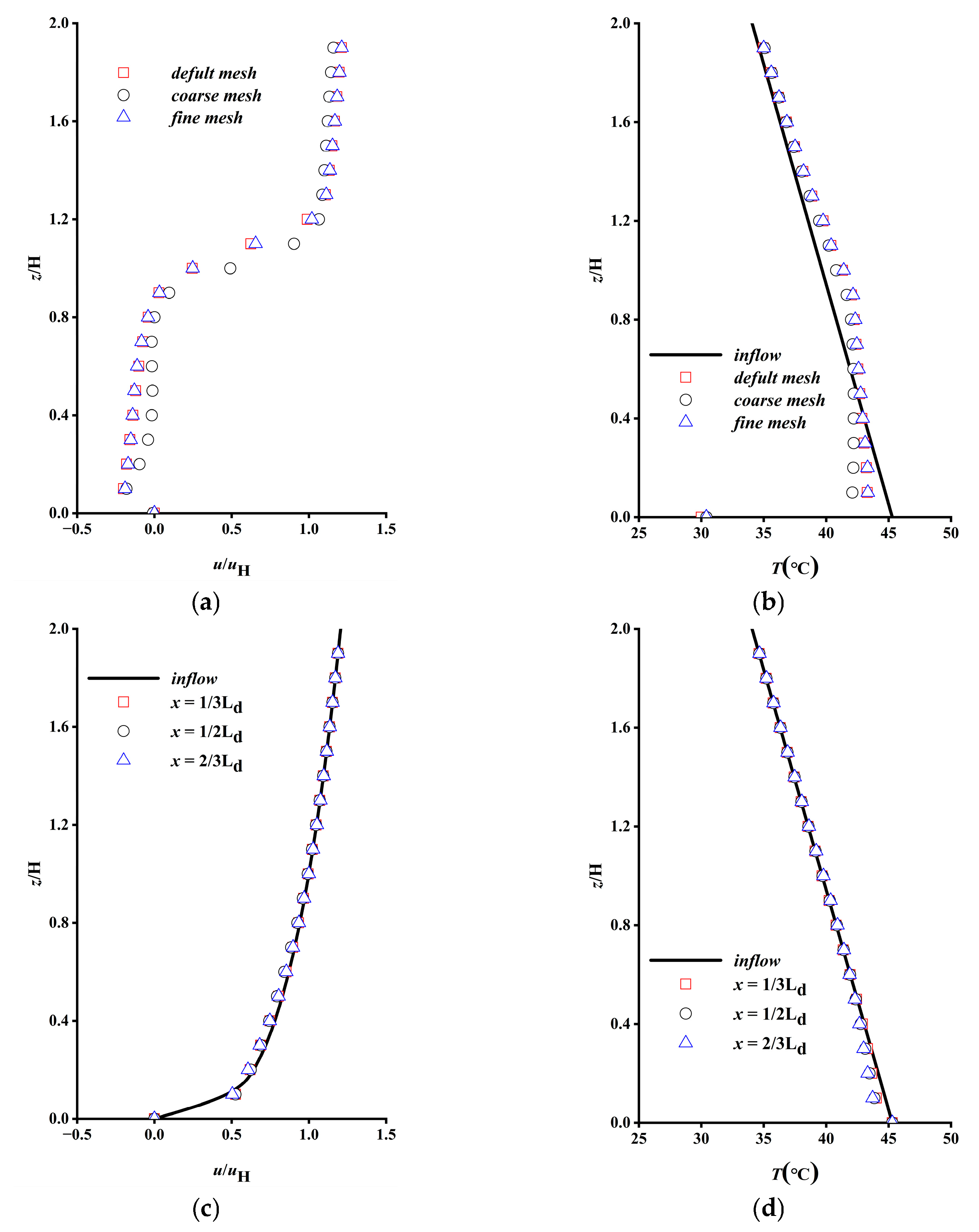
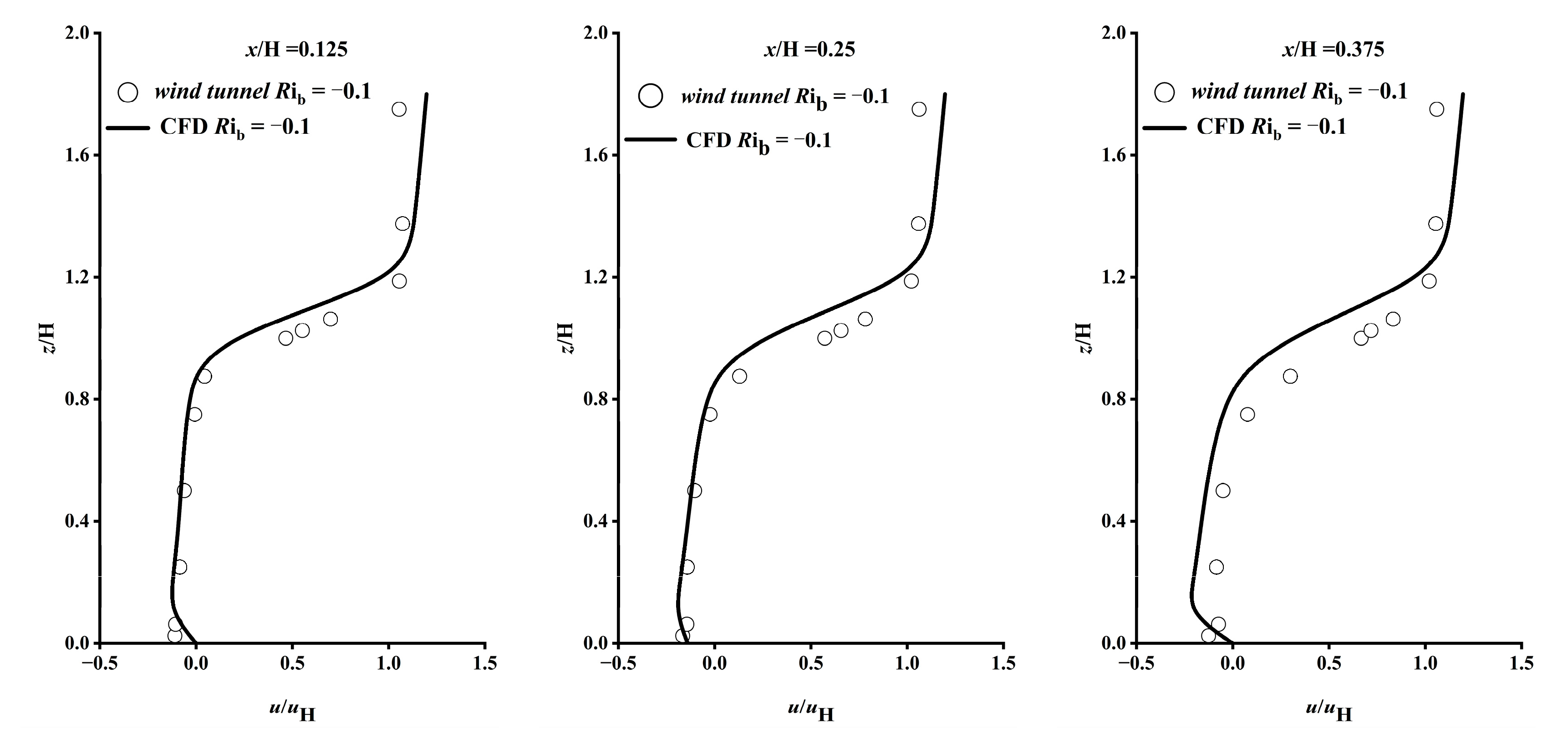
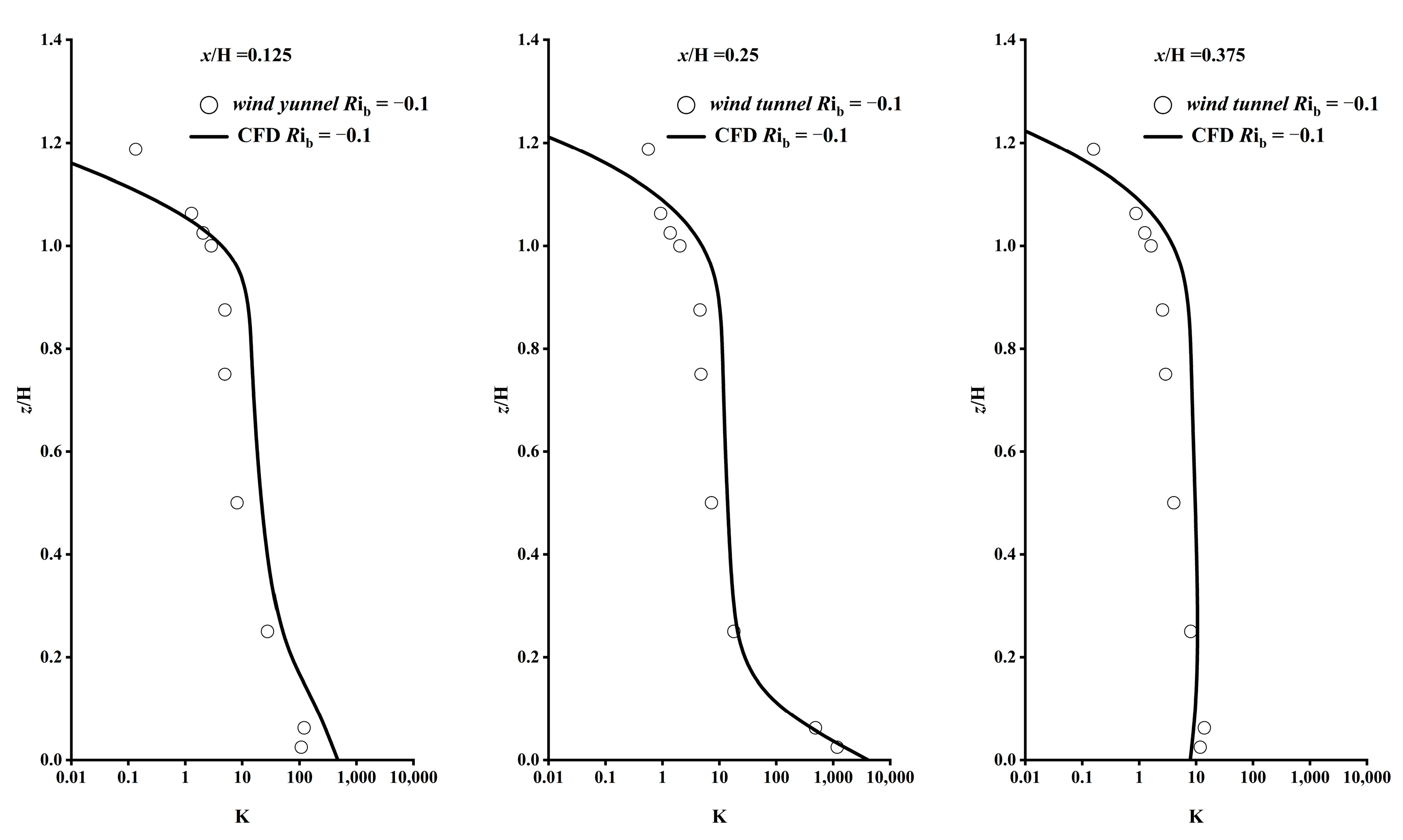
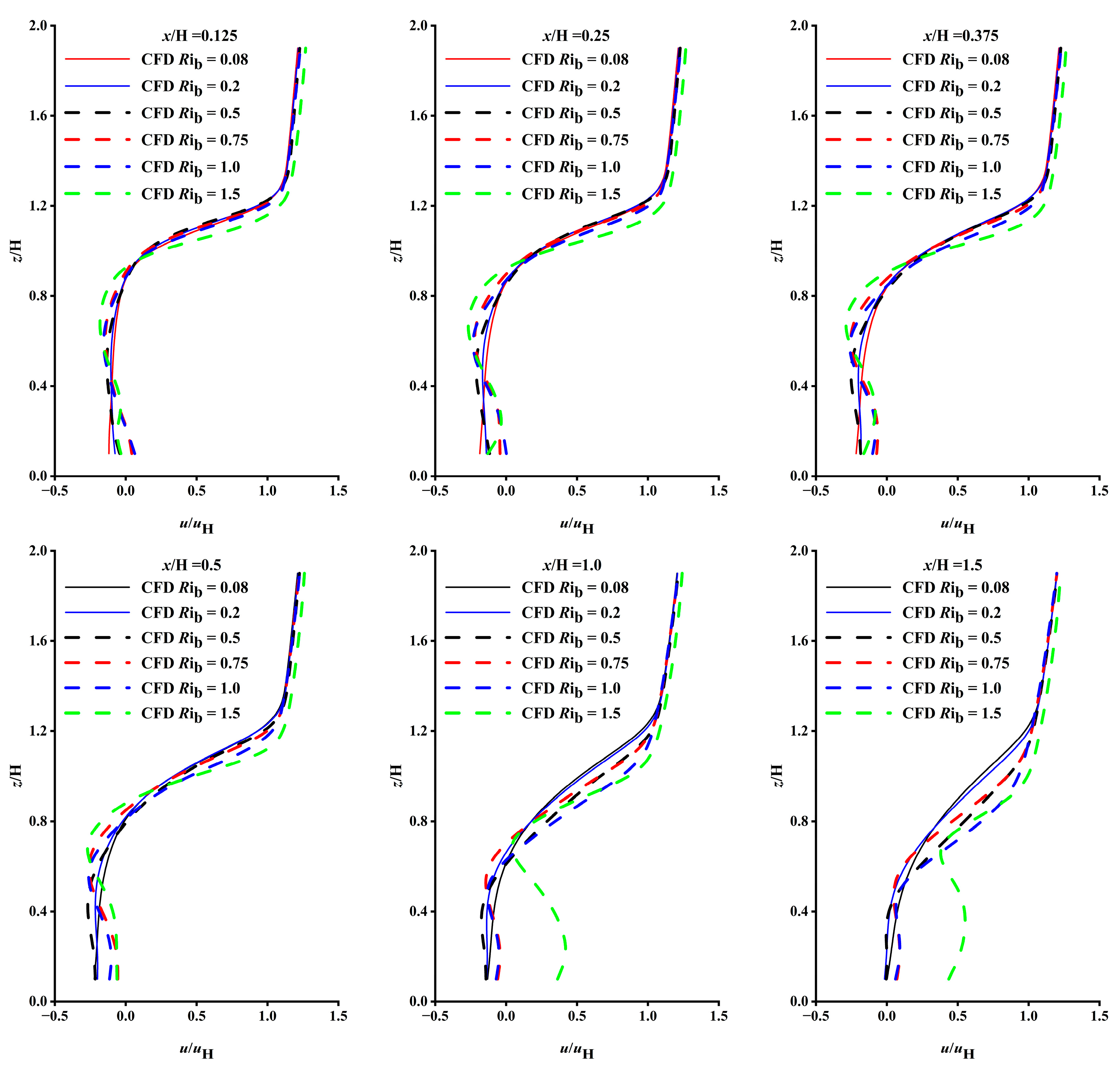
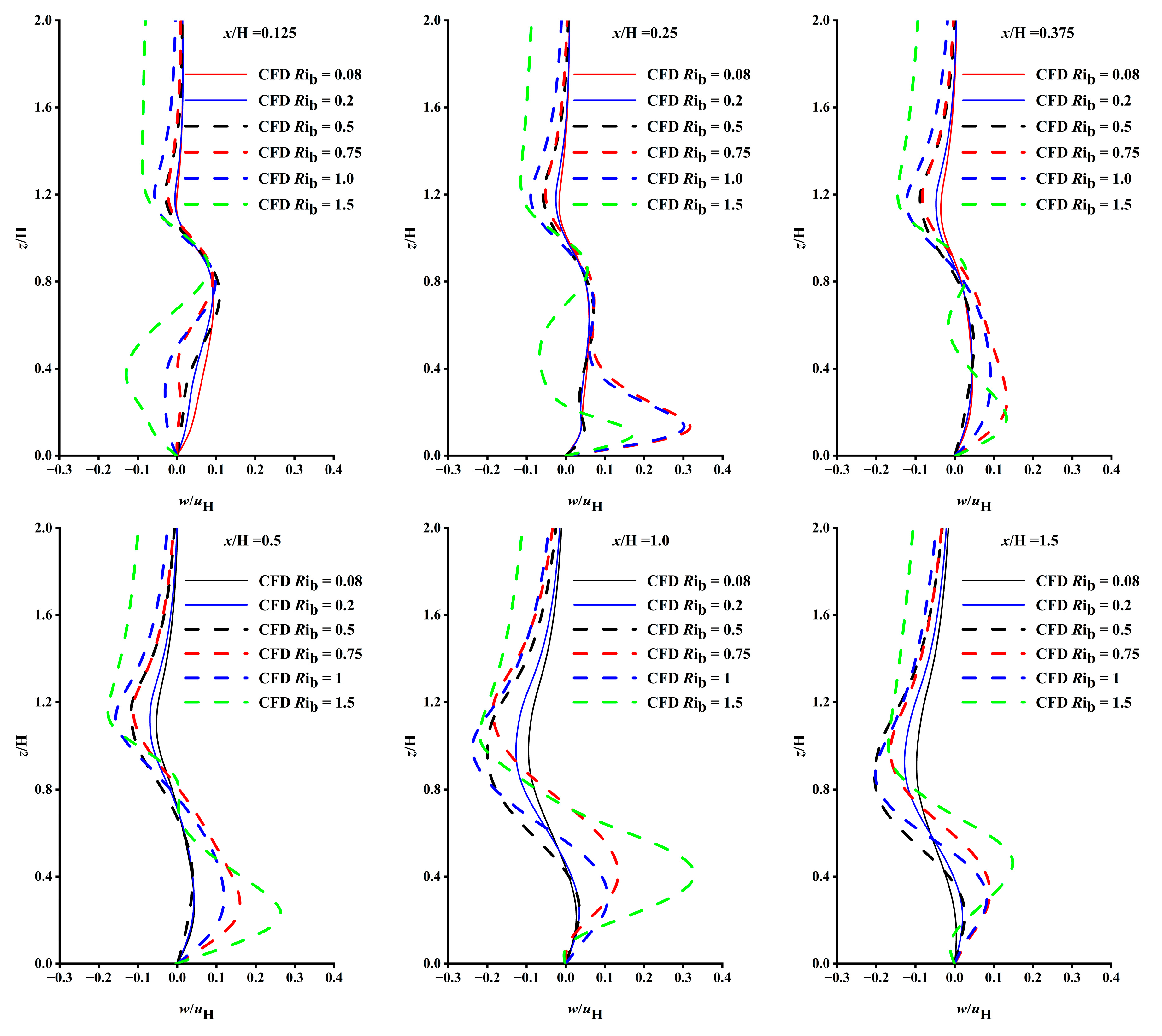
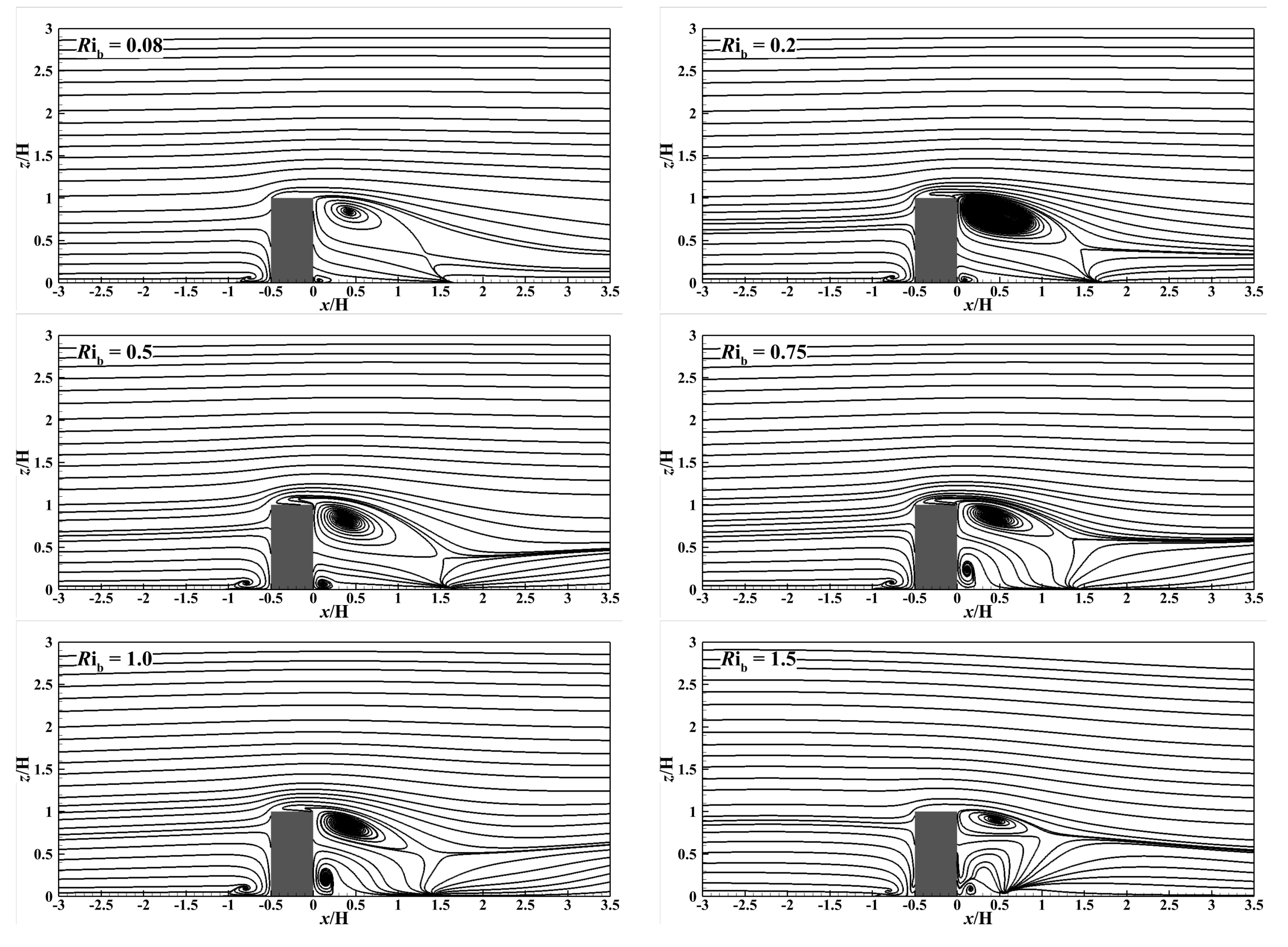



| Stability | Rib | uH | Re | n | TW (°C) | TH (°C) | |
|---|---|---|---|---|---|---|---|
| Wind tunnel | Unstable | −0.1 | 1.37 | 14,613 | 0.27 | 45.3 | 11.3 |
| CFD | Unstable | −0.1 | 1.37 | 14,613 | 0.27 | 45.3 | 11.3 |
| Stable | 0.08 | 17.7 | 45.5 | ||||
| 0.2 | 1.37 | 14,613 | 0.27 | 17.7 | 87.3 | ||
| 0.5 | 17.7 | 191.7 | |||||
| 0.75 | 0.6 | 6400 | 17.7 | 67.7 | |||
| 1.0 | 0.27 | 17.7 | 84.4 | ||||
| 1.5 | 17.7 | 117.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, R.; Guo, D.; Wang, D.; Pan, Y.; Zhang, J.; Yao, R. Numerical Investigation of the Impact of Tall Buildings on Pollutant Dispersion during Stable Stratification. Atmosphere 2024, 15, 16. https://doi.org/10.3390/atmos15010016
Li Y, Li R, Guo D, Wang D, Pan Y, Zhang J, Yao R. Numerical Investigation of the Impact of Tall Buildings on Pollutant Dispersion during Stable Stratification. Atmosphere. 2024; 15(1):16. https://doi.org/10.3390/atmos15010016
Chicago/Turabian StyleLi, Yunpeng, Ruojie Li, Dongpeng Guo, Dezhong Wang, Yanhui Pan, Junfang Zhang, and Rentai Yao. 2024. "Numerical Investigation of the Impact of Tall Buildings on Pollutant Dispersion during Stable Stratification" Atmosphere 15, no. 1: 16. https://doi.org/10.3390/atmos15010016
APA StyleLi, Y., Li, R., Guo, D., Wang, D., Pan, Y., Zhang, J., & Yao, R. (2024). Numerical Investigation of the Impact of Tall Buildings on Pollutant Dispersion during Stable Stratification. Atmosphere, 15(1), 16. https://doi.org/10.3390/atmos15010016





