The Robustness of the Derived Design Life Levels of Heavy Precipitation Events in the Pre-Alpine Oberland Region of Southern Germany
Abstract
:1. Introduction
2. Materials and Methods
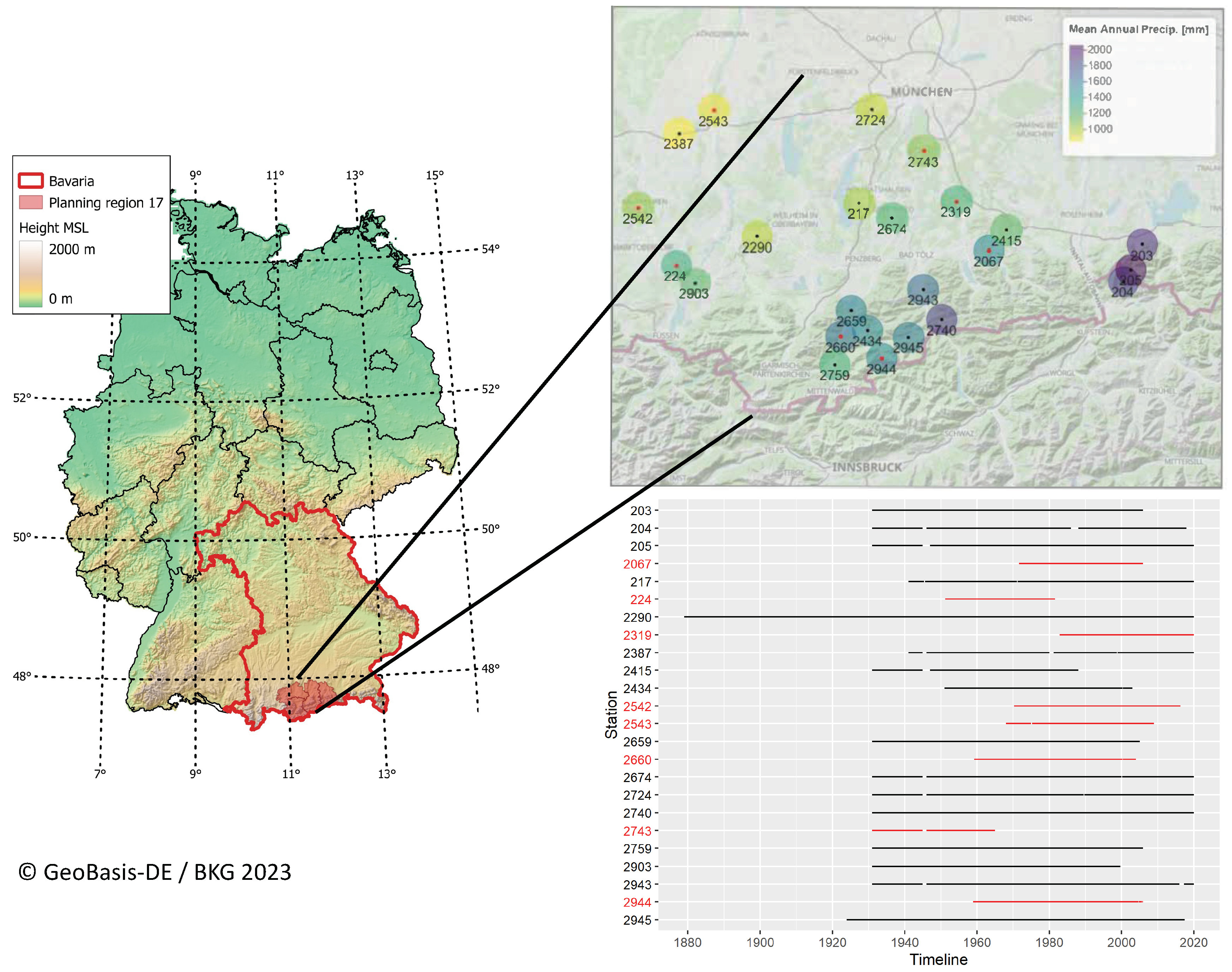
2.1. Study Region
2.2. Data
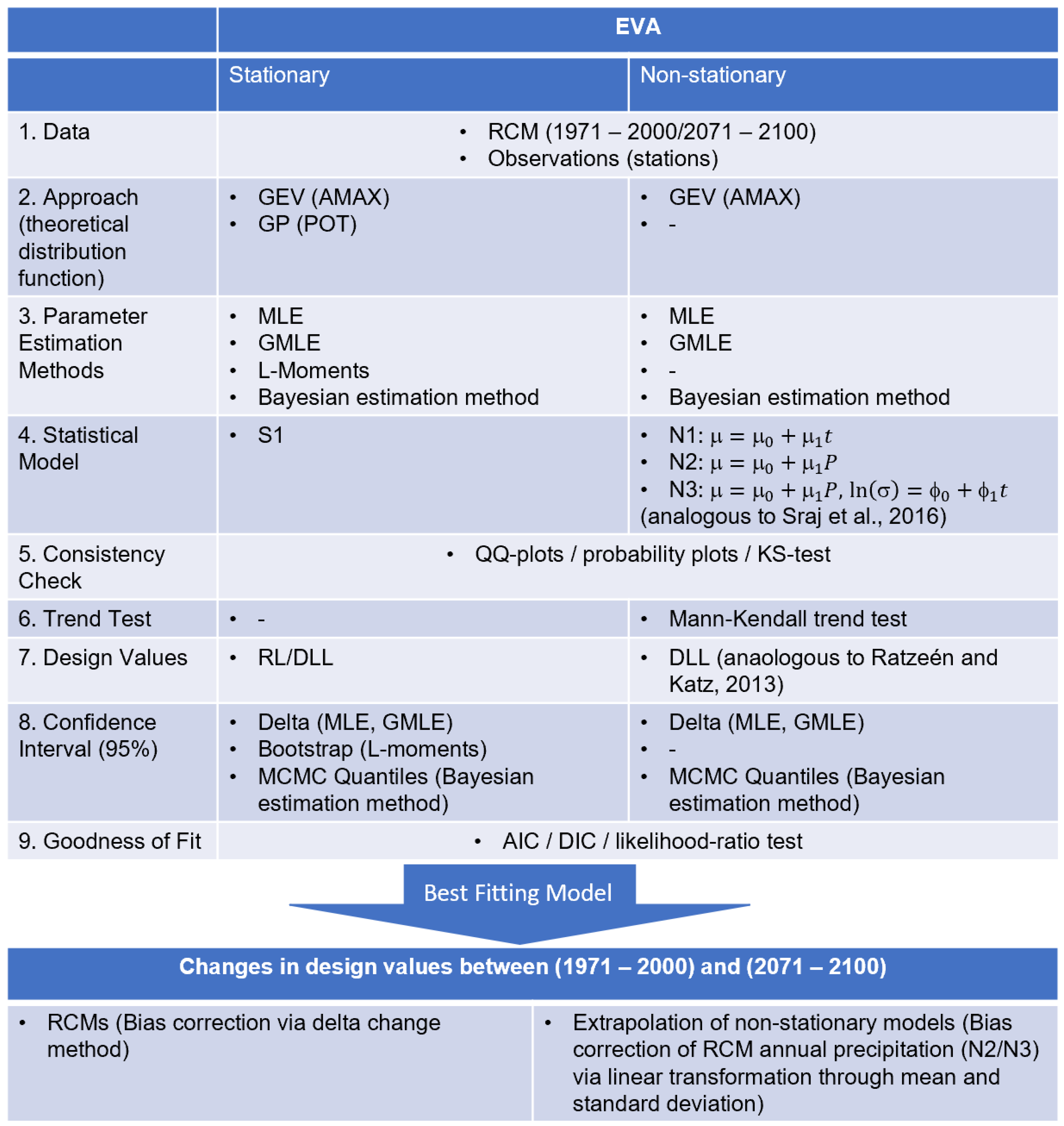
2.3. Methods
2.3.1. Theoretical Extreme Distribution Functions
2.3.2. Parameter Estimation Methods (PEMs)
Maximum Likelihood Estimation (MLE)
Method of Moments
Generalized Maximum Likelihood Estimation (GMLE)
Bayesian Inference
2.3.3. Goodness-of-Fit Test
2.3.4. Implementation of Non-Stationarity
- N1: non-stationary model (1) with location parameter being a function of time: (t) = + t;
- N2: non-stationary model (2) with location parameter being a function of annual precipitation: (t) = + P;
- N3: non-stationary model (3) with location parameter being a function of annual precipitation and parameter being a function of time: (t) = + P, ln((t)) = + t.
2.3.5. Equivalent Design Life Level
2.3.6. Usage of Regional Climate Models
3. Results
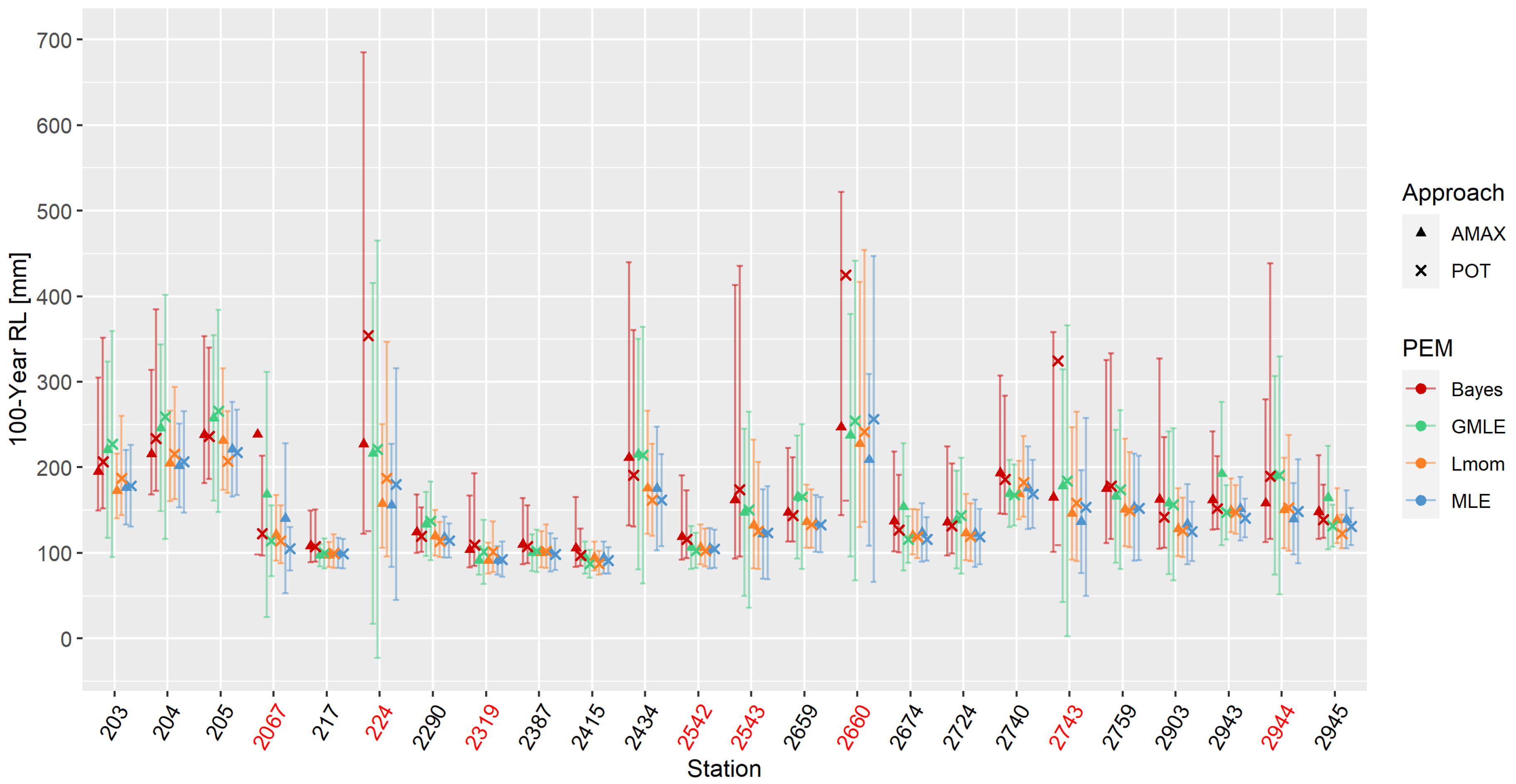
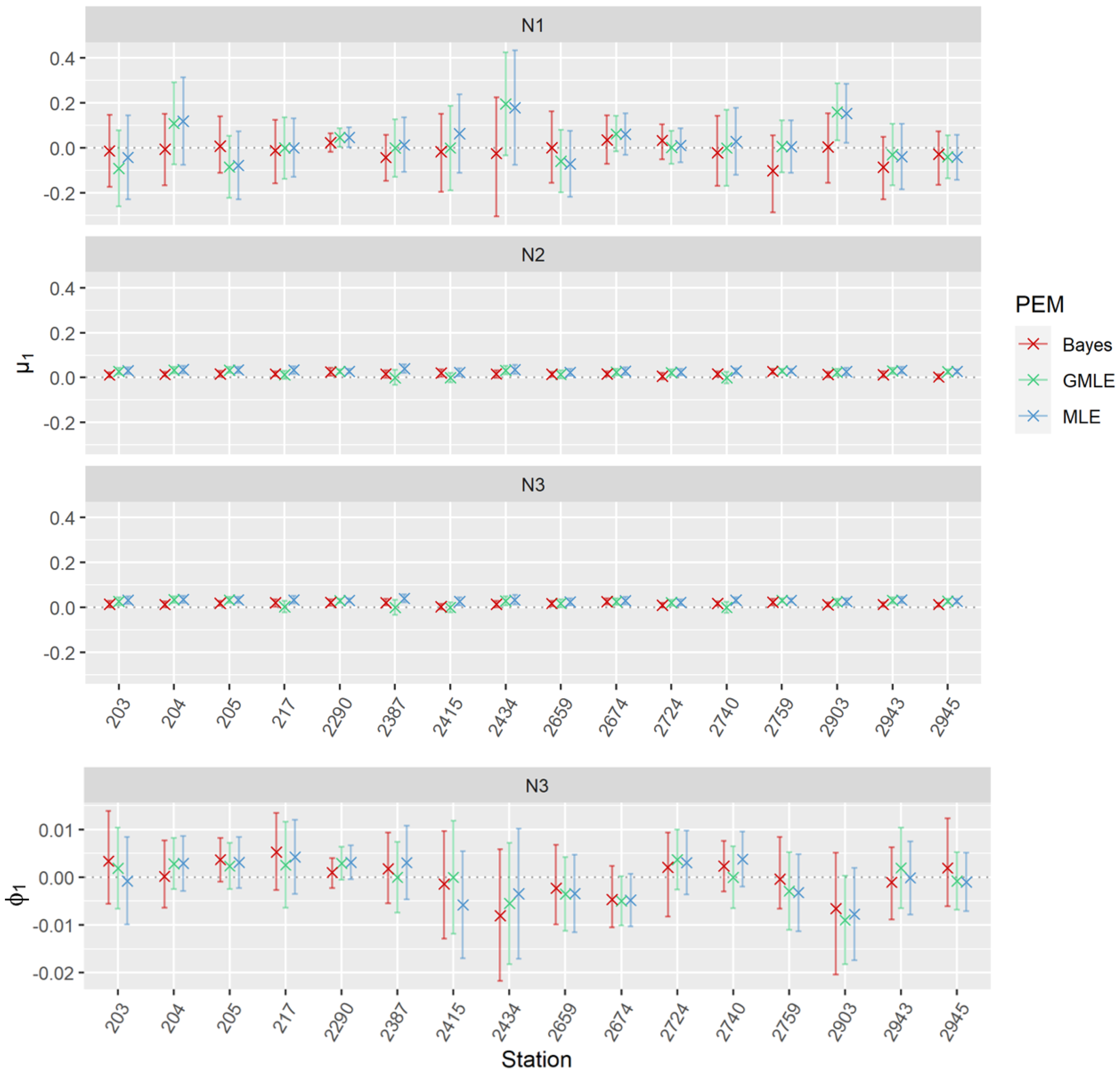
3.1. Theoretical Distributions and Parameter Estimation Methods
3.2. Justification and Evaluation of Non-Stationary EVA
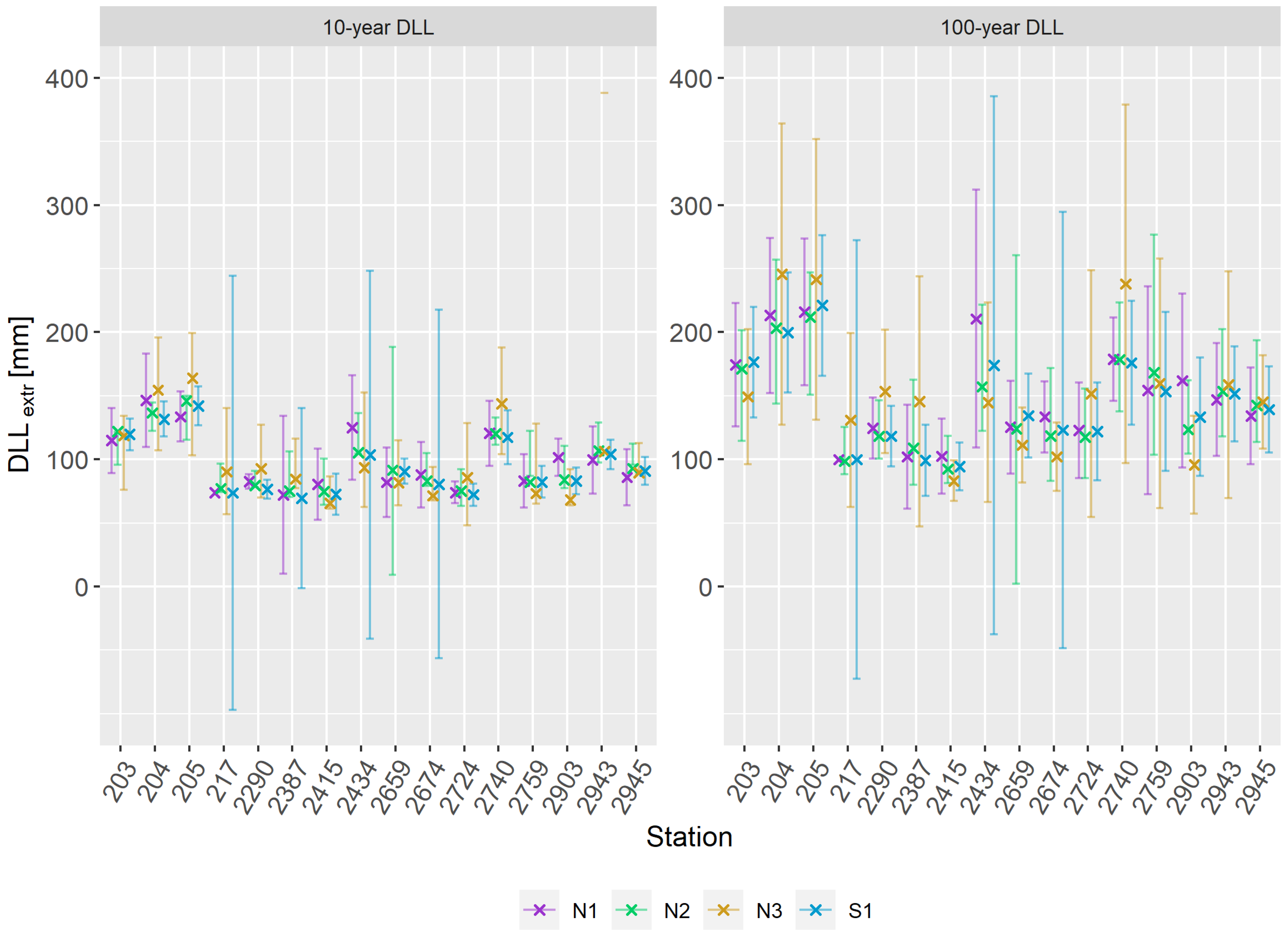
3.3. Changes in Design Life Levels
3.3.1. Extrapolation of Non-Stationary Models
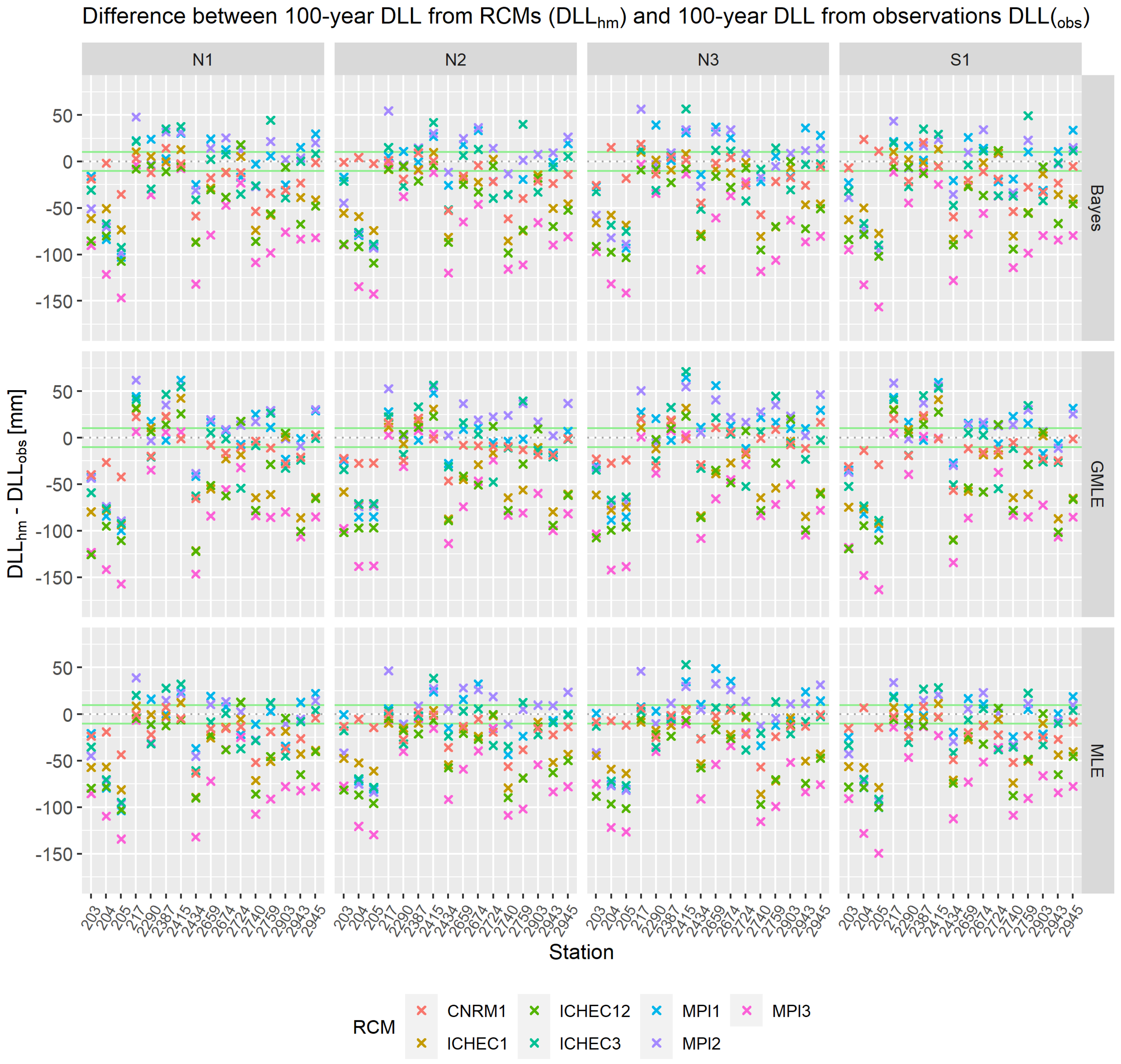
3.3.2. Non-Stationary EVA Using Regional Climate Model Output
4. Discussion
5. Conclusions
- For the end of this century in the Oberland region, there is no robust tendency towards increased precipitation extremes expressed as DLLs, even under the assumption of the high-impact RCP8.5 emission scenario. This is confirmed following approaches based on extrapolated observation data and RCM output.
- It is further concluded that, in practice, non-stationary EVA is not necessarily needed. Non-stationary EVA potentially offers an added value in cases when long series of observations (in the order of 100 years) are available and robust trends of extremes can be derived.
- As observation data are often not sufficient in practice, RCM data driven by Reanalysis data provide an alternative for filling data gaps in space and time.
- RCMs also provide potential options for non-stationary EVA under future climate conditions; however, additional uncertainties such as the unknown future emissions as well as uncertainties from different large-scale forcing (i.e., different GCMs) and RCM parameterizations must be considered.
- Despite all of the methodological uncertainties, EVA currently provides a sound solution to derive hydrometeorological design values for infrastructure that has to withstand extreme events.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swiss Re. Natural Catastrophes in 2021: The Floodgates Are Open; Technical Report; Swiss Re Institute: Zürich, Switzerland, 2022. [Google Scholar]
- Junghänel, T.; Bissolli, P.; Daßler, J.; Fleckenstein, R.; Imbery, F.; Janssen, W.; Kaspar, F.; Lengfeld, K.; Leppelt, T.; Rauthe, M.; et al. Hydro-Klimatologische Einordnung der Stark-und Dauerniederschläge in Teilen Deutschlands im Zusammenhang mit dem Tiefdruckgebiet “Bernd” vom 12. bis 19. Juli 2021; Technical Report; Deutscher Wetterdienst: Offenbach am Main, Germany, 2021. [Google Scholar]
- Lehmkuhl, F.; Schüttrumpf, H.; Schwarzbauer, J.; Brüll, C.; Dietze, M.; Letmathe, P.; Völker, C.; Hollert, H. Assessment of the 2021 summer flood in Central Europe. Environ. Sci. Eur. 2022, 34, 107. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Yang, C.; Leah, G.; Gomis, M.I.; Matthews, J.B.R.; Berger, S.; et al. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 3–32. [Google Scholar] [CrossRef]
- Pörtner, H.-O.; Roberts, D.C.; Tignor, M.M.B.; Poloczanska, E.; Mintenbeck, K.; Alegría, A.; Craig, M.; Langsdorf, S.; Löschke, S.; Möller, V.; et al. (Eds.) Climate Change 2022: Impacts, Adaptation and Vulnerability; Working Group II Contribution to the IPCC Sixth Assessment Report; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022. [Google Scholar]
- van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Madakumbura, G.D.; Thackeray, C.W.; Norris, J.; Goldenson, N.; Hall, A. Anthropogenic influence on extreme precipitation over global land areas seen in multiple observational datasets. Nat. Commun. 2021, 12, 3944. [Google Scholar] [CrossRef] [PubMed]
- Martinkova, M.; Kysely, J. Overview of observed clausius-clapeyron scaling of extreme precipitation in midlatitudes. Atmosphere 2020, 11, 786. [Google Scholar] [CrossRef]
- Dingman, S.L. Physical Hydrology; Waveland Press, Inc.: Long Grove, IL, USA, 2015. [Google Scholar]
- Salas, J.D.; Obeysekera, J.; Vogel, R.M. Techniques for assessing water infrastructure for nonstationary extreme events: A review. Hydrol. Sci. J. 2018, 63, 325–352. [Google Scholar] [CrossRef]
- Slater, L.J.; Anderson, B.; Buechel, M.; Dadson, S.; Han, S.; Harrigan, S.; Kelder, T.; Kowal, K.; Lees, T.; Matthews, T.; et al. Nonstationary Weather and Water Extremes: A Review of Methods for Their Detection, Attribution, and Management. Hydrol. Earth Syst. Sci. 2021, 25, 3897–3935. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Stephenson, A.; Tawn, J. Bayesian Inference for Extremes: Accounting for the Three Extremal Types; Springer Science + Business Media, Inc.: Dordrecht, The Netherlands, 2004; pp. 291–307. [Google Scholar]
- Wi, S.; Valdés, J.B.; Steinschneider, S.; Kim, T.W. Non-stationary frequency analysis of extreme precipitation in South Korea using peaks-over-threshold and annual maxima. Stoch. Environ. Res. Risk Assess. 2016, 30, 583–606. [Google Scholar] [CrossRef]
- Scarrott, C.; Macdonald, A. A Review of Extreme Value Threshold Estimation And Uncertainty Quantification. REVSTAT Stat. J. 2012, 10, 33–60. [Google Scholar]
- Beirlant, J.; Goegebeur, Y.; Teugels, J.; Segers, J.; De Waal, D.; Ferro, C. Statistics of Extremes: Theory and Applications; John Wiley & Sons Ltd.: Chichester, UK, 2004. [Google Scholar]
- Martins, E.S.; Stedinger, J.R. Generalized maximum likelihood Pareto-Poisson estimators for partial duration series. Water Resour. Res. 2001, 37, 2551–2557. [Google Scholar] [CrossRef]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Martins, E.S.; Stedinger, J.R. Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour. Res. 2000, 36, 737–744. [Google Scholar] [CrossRef]
- Reis, D.S.; Stedinger, J.R. Bayesian MCMC flood frequency analysis with historical information. J. Hydrol. 2005, 313, 97–116. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- Mehmood, A.; Jia, S.; Mahmood, R.; Yan, J.; Ahsan, M. Non-Stationary Bayesian Modeling of Annual Maximum Floods in a Changing Environment and Implications for Flood Management in the Kabul River Basin, Pakistan. Water 2019, 11, 1246. [Google Scholar] [CrossRef]
- Feldmann, D.; Laux, P.; Heckl, A.; Schindler, M.; Kunstmann, H. Near surface roughness estimation: A parameterization derived from artificial rainfall experiments and two-dimensional hydrodynamic modelling for multiple vegetation coverages. J. Hydrol. 2023, 617, 128786. [Google Scholar] [CrossRef]
- Villarini, G.; Taylor, S.; Wobus, C.; Vogel, R.; Hecht, J.; White, K.; Baker, B.; Gilroy, K.; Olsen, J.R.; Raff, D. Floods and Nonstationarity: A Review; Technical Report, CWTS 2018-01; U.S. Army Corps of Engineers: Washington, DC, USA, 2018. [Google Scholar]
- Rootzén, H.; Katz, R.W. Design Life Level: Quantifying risk in a changing climate. Water Resour. Res. 2013, 49, 5964–5972. [Google Scholar] [CrossRef]
- Cooley, D. Return Periods and Return Levels Under Climate Change. In Extremes in a Changing Climate: Detection, Analysis and Uncertainty; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 97–114. [Google Scholar] [CrossRef]
- Šraj, M.; Viglione, A.; Parajka, J.; Blöschl, G. The influence of non-stationarity in extreme hydrological events on flood frequency estimation. J. Hydrol. Hydromech. 2016, 64, 426–437. [Google Scholar] [CrossRef]
- Katz, R.W. Statistical Methods for Nonstationary Extremes. In Extremes in a Changing Climate: Detection, Analysis and Uncertainty; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 15–37. [Google Scholar] [CrossRef]
- Wunsch, C. The Interpretation of Short Climate Records, with Comments on the North Atlantic and Southern Oscillations. Bull. Am. Meteorol. Soc. 1999, 80, 245–256. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Climate change, the Hurst phenomenon, and hydrological statistics. Hydrol. Sci. J. 2003, 48, 3–24. [Google Scholar] [CrossRef]
- Matalas, N.C. Comment on the Announced Death of Stationarity. J. Water Resour. Plan. Manag. 2012, 138, 311–312. [Google Scholar] [CrossRef]
- Bayazit, M. Nonstationarity of Hydrological Records and Recent Trends in Trend Analysis: A State-of-the-art Review. Environ. Process. 2015, 2, 527–542. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Negligent killing of scientific concepts: The stationary case. Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Hu, Y.; Liang, Z.; Singh, V.P.; Zhang, X.; Wang, J.; Li, B.; Wang, H. Concept of Equivalent Reliability for Estimating the Design Flood under Non-stationary Conditions. Water Resour. Manag. 2018, 32, 997–1011. [Google Scholar] [CrossRef]
- Emeis, S. Analysis of decadal precipitation changes at the northern edge of the alps. Meteorol. Z. 2021, 30, 285–293. [Google Scholar] [CrossRef]
- Nissen, K.M.; Ulbrich, U.; Leckebusch, G.C. Vb cyclones and associated rainfall extremes over central Europe under present day and climate change conditions. Meteorol. Z. 2013, 22, 649–660. [Google Scholar] [CrossRef]
- Peristeri, M.; Ulrich, W.; Smith, R.K. Genesis conditions for thunderstorm growth and the development of a squall line in the northern Alpine foreland. Meteorol. Atmos. Phys. 2000, 72, 251–260. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Nonstationarity versus scaling in hydrology. J. Hydrol. 2006, 324, 239–254. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G.R. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 239–254. [Google Scholar]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Mascaro, G.; Viola, F.; Deidda, R. Evaluation of Precipitation From EURO-CORDEX Regional Climate Simulations in a Small-Scale Mediterranean Site. J. Geophys. Res. Atmos. 2018, 123, 1604–1625. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Jungclaus, J.; Reick, C.H.; Legutke, S.; Bader, J.; Böttinger, M.; Brovkin, V.; Crueger, T.; Esch, M.; Fieg, K.; et al. Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J. Adv. Model. Earth Syst. 2013, 5, 572–597. [Google Scholar] [CrossRef]
- Nolan, P.; Mckinstry, A. EC-Earth Global Climate Simulations-Ireland’s Contributions to CMIP6; Technical Report; Environmental Protection Agency: Wexford, Ireland, 2020. [Google Scholar]
- Laux, P.; Rötter, R.P.; Webber, H.; Dieng, D.; Rahimi, J.; Wei, J.; Faye, B.; Srivastana, A.; Bliefernicht, J.; Adeyeri, O.; et al. To bias correct or not to bias correct? An agricultural impact modelers’ perspective on regional climate model data. Agric. For. Meteorol. 2021, 304–305, 108406. [Google Scholar] [CrossRef]
- Pickands, J. Statistical Inference Using Extreme Order Statistics. Source Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Gilleland, E.; Katz, R.W. ExtRemes 2.0: An extreme value analysis package in R. J. Stat. Softw. 2016, 72, 1–39. [Google Scholar] [CrossRef]
- Anagnostopoulou, C.; Tolika, K. Extreme precipitation in Europe: Statistical threshold selection based on climatological criteria. Theor. Appl. Climatol. 2012, 107, 479–489. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Coles, S.G.; Dixon, M.J. Likelihood-Based Inference for Extreme Value Models. Extremes 1999, 2, 5–23. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions using Linear Combinations of Order Statistics. Source J. R. Stat. Soc. Ser. Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Parameter and Quantile Estimation for the Generalized Pareto Distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Neath, A.A. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. Wiley Interdiscip. Rev. Comput. Stat. 2019, 11, e1460. [Google Scholar] [CrossRef]
- Hawkins, E.; Osborne, T.M.; Ho, C.K.; Challinor, A.J. Calibration and bias correction of climate projections for crop modelling: An idealised case study over Europe. Agric. For. Meteorol. 2013, 170, 19–31. [Google Scholar] [CrossRef]
- Navarro-Racines, C.; Tarapues, J.; Thornton, P.; Jarvis, A.; Ramirez-Villegas, J. High-resolution and bias-corrected CMIP5 projections for climate change impact assessments. Sci. Data 2020, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Dang, Q.; Laux, P.; Kunstmann, H. Future high- and low-flow estimations for Central Vietnam: A hydro-meteorological modelling chain approach. Hydrol. Sci. J. 2017, 62, 1867–1889. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Müller, C.; Voigt, M.; Iber, C.; Sauer, T. Starkniederschläge: Entwicklung in Vergangenheit und Zukunft; Technical Report; KLIWA: Offenbach, Germany, 2019. [Google Scholar]
- Coles, S.G.; Powell, E.A. Bayesian Methods in Extreme Value Modelling: A Review and New Developments. Int. Stat. Rev. 1996, 64, 119–136. [Google Scholar] [CrossRef]
- Lengfeld, K.; Kirstetter, P.E.; Fowler, H.J.; Yu, J.; Becker, A.; Flamig, Z.; Gourley, J. Use of radar data for characterizing extreme precipitation at fine scales and short durations. Environ. Res. Lett. 2020, 15, 085003. [Google Scholar] [CrossRef]
- Junghänel, T.; Ertel, H.; Deutschländer, T.; Wetterdienst, D.; Hydrometeorologie, A. Bericht zur Revision der Koordinierten Starkregenregionalisierung und-Auswertung des Deutschen Wetterdienstes in der Version 2010; Technical Report; Deutscher Wetterdienst Abteilung Hydrometeorologie: Offenbach am Main, Germany, 2017. [Google Scholar]
- Poschlod, B.; Ludwig, R.; Sillmann, J. Ten-year return levels of sub-daily extreme precipitation over Europe. Earth Syst. Sci. Data 2021, 13, 983–1003. [Google Scholar] [CrossRef]
- Maity, R.; Suman, M.; Laux, P.; Kunstmann, H. Bias correction of zero-inflated RCM precipitation fields: A copula-based scheme for both mean and extreme conditions. J. Hydrometeorol. 2019, 20, 595–611. [Google Scholar] [CrossRef]
- Warscher, M.; Wagner, S.; Marke, T.; Laux, P.; Smiatek, G.; Strasser, U.; Kunstmann, H. A 5 km resolution regional climate simulation for Central Europe: Performance in high mountain areas and seasonal, regional and elevation-dependent variations. Atmosphere 2019, 10, 682. [Google Scholar] [CrossRef]
- Ban, N.; Schmidli, J.; Schär, C. Heavy precipitation in a changing climate: Does short-term summer precipitation increase faster? Geophys. Res. Lett. 2015, 42, 1165–1172. [Google Scholar] [CrossRef]
- Kyselý, J.; Rulfová, Z.; Farda, A.; Hanel, M. Convective and stratiform precipitation characteristics in an ensemble of regional climate model simulations. Clim. Dyn. 2016, 46, 227–243. [Google Scholar] [CrossRef]
- Berthou, S.; Kendon, E.J.; Chan, S.C.; Ban, N.; Leutwyler, D.; Schär, C.; Fosser, G. Pan-European climate at convection-permitting scale: A model intercomparison study. Clim. Dyn. 2020, 55, 35–59. [Google Scholar] [CrossRef]





| Driving Model (GCM) | RCM | Ensemble | ||
|---|---|---|---|---|
| ICHEC-EC-Earth | COSMO-crCLIM-v1-1 | r1i1p1 | 1950–2005 | 2006–2100 |
| ICHEC-EC-Earth | COSMO-crCLIM-v1-1 | r3i1p1 | 1950–2005 | 2006–2100 |
| ICHEC-EC-Earth | COSMO-crCLIM-v1-1 | r12i1p1 | 1950–2005 | 2006–2100 |
| MPI-M-MPI-ESM-LR | COSMO-crCLIM-v1-1 | r1i1p1 | 1949–2005 | 2006–2100 |
| MPI-M-MPI-ESM-LR | COSMO-crCLIM-v1-1 | r2i1p1 | 1949–2005 | 2006–2100 |
| MPI-M-MPI-ESM-LR | COSMO-crCLIM-v1-1 | r3i1p1 | 1949–2005 | 2006–2100 |
| CNRM-CERFACES-CNRM-CM5 | COSMO-crCLIM-v1-1 | r1i1p1 | 1951–2005 | 2006–2100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laux, P.; Weber, E.; Feldmann, D.; Kunstmann, H. The Robustness of the Derived Design Life Levels of Heavy Precipitation Events in the Pre-Alpine Oberland Region of Southern Germany. Atmosphere 2023, 14, 1384. https://doi.org/10.3390/atmos14091384
Laux P, Weber E, Feldmann D, Kunstmann H. The Robustness of the Derived Design Life Levels of Heavy Precipitation Events in the Pre-Alpine Oberland Region of Southern Germany. Atmosphere. 2023; 14(9):1384. https://doi.org/10.3390/atmos14091384
Chicago/Turabian StyleLaux, Patrick, Elena Weber, David Feldmann, and Harald Kunstmann. 2023. "The Robustness of the Derived Design Life Levels of Heavy Precipitation Events in the Pre-Alpine Oberland Region of Southern Germany" Atmosphere 14, no. 9: 1384. https://doi.org/10.3390/atmos14091384
APA StyleLaux, P., Weber, E., Feldmann, D., & Kunstmann, H. (2023). The Robustness of the Derived Design Life Levels of Heavy Precipitation Events in the Pre-Alpine Oberland Region of Southern Germany. Atmosphere, 14(9), 1384. https://doi.org/10.3390/atmos14091384







