Advances of Phase-Field Model in the Numerical Simulation of Multiphase Flows: A Review
Abstract
:1. Introduction
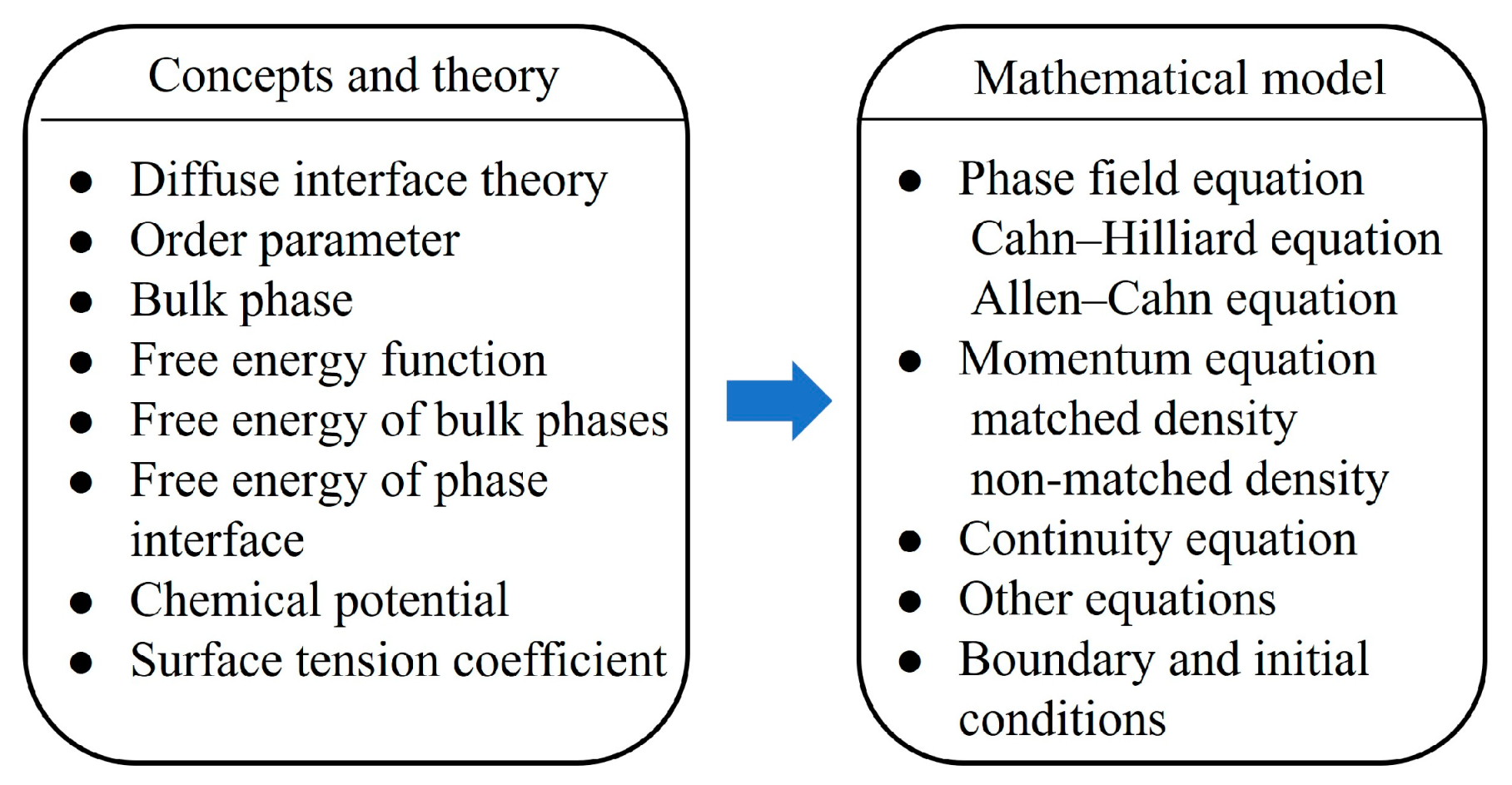
2. Theory and Mathematical Models
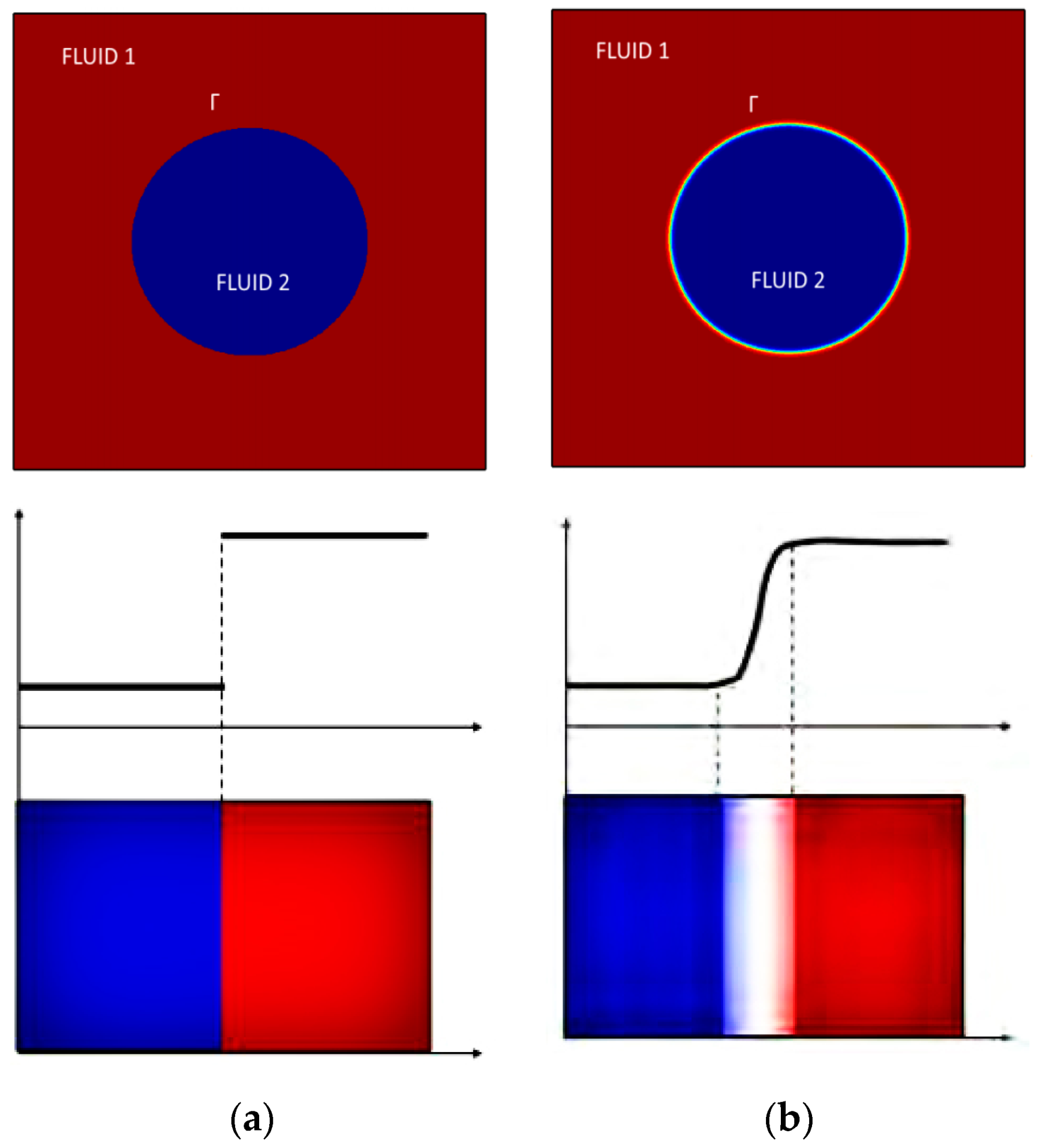
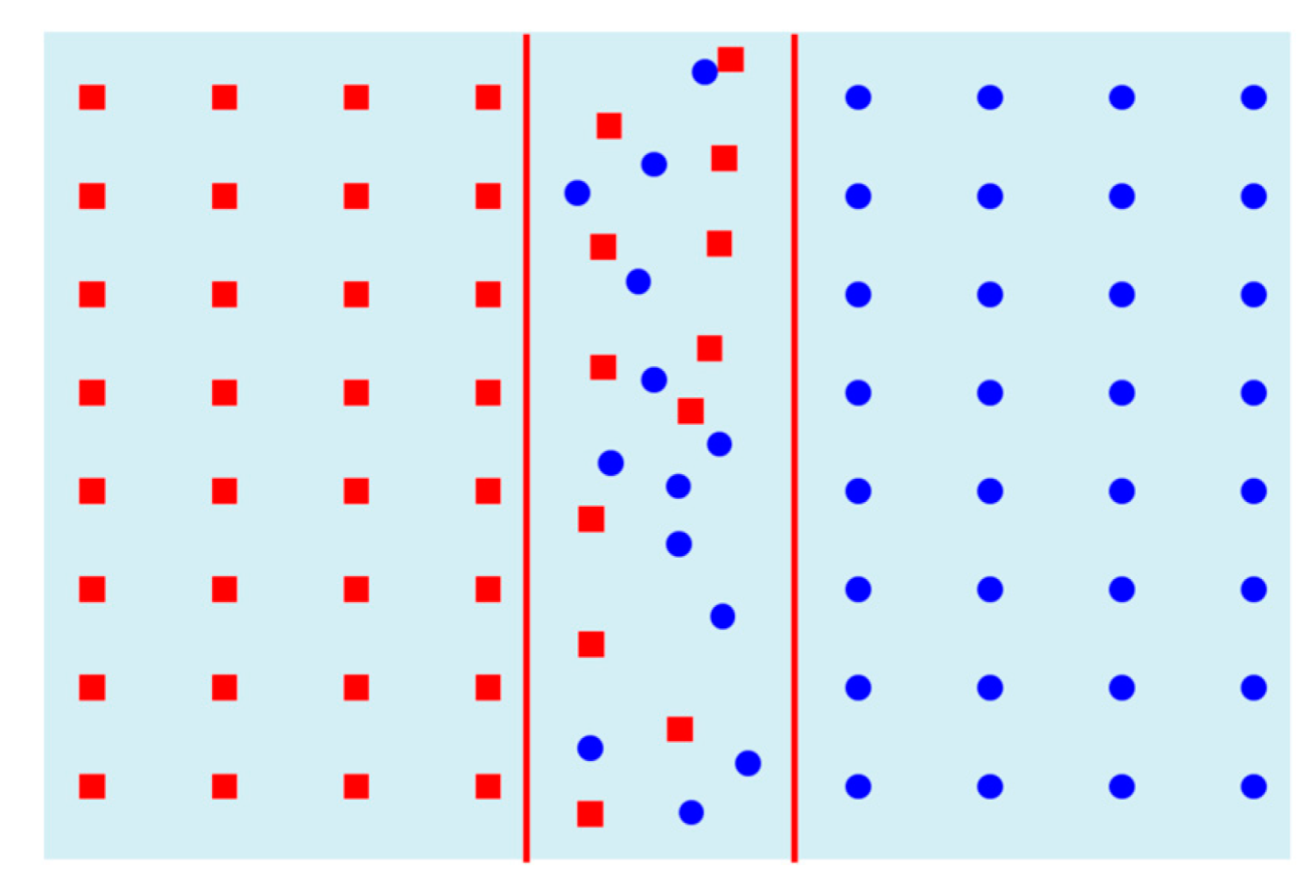
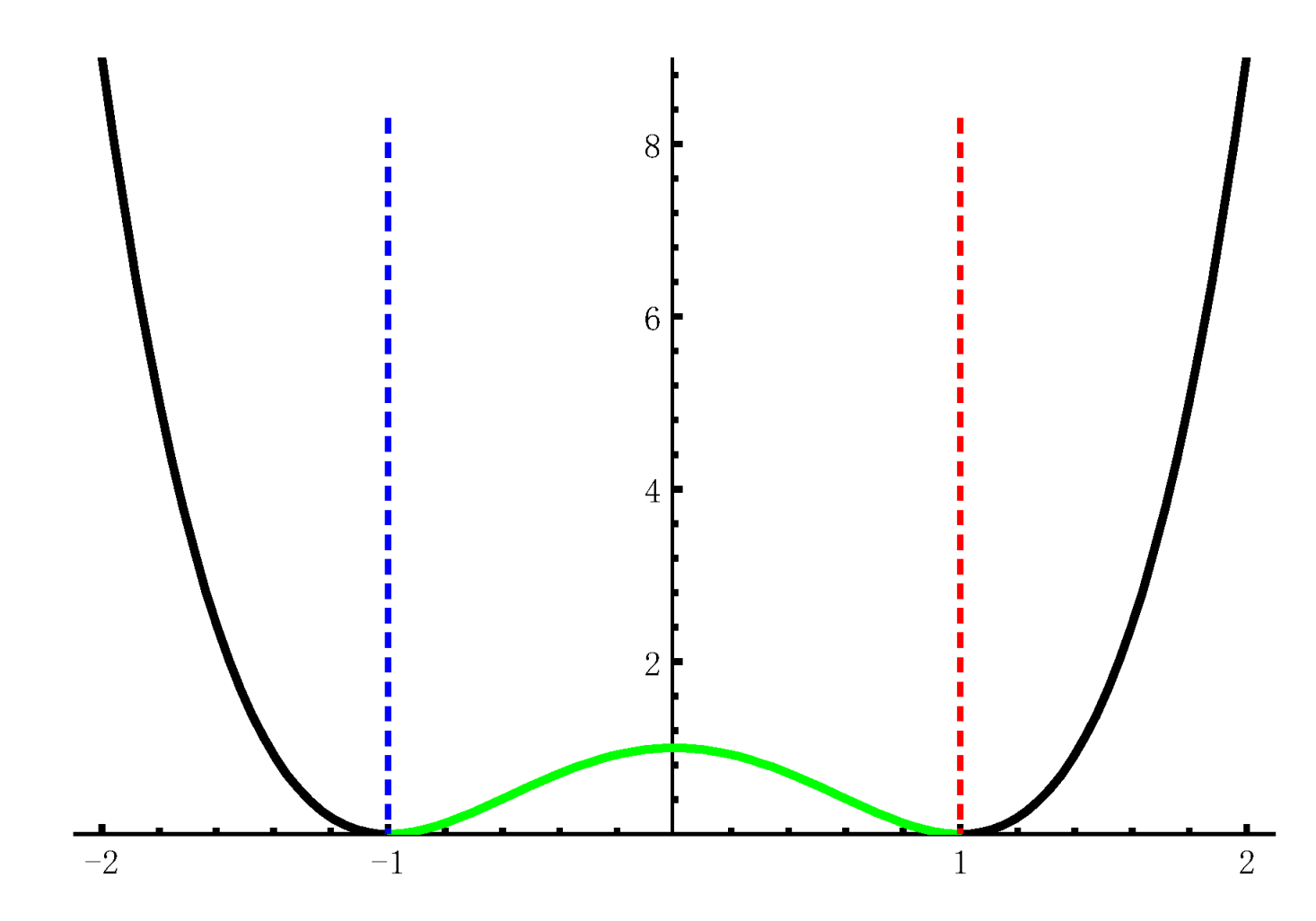
2.1. Fundamental Theory
2.2. Mathematical Models
2.2.1. Phase-Field Equation
2.2.2. Momentum Equation
- (1)
- Matched density;
- (2)
- Non-matched density with a small density difference;
- (3)
- Non-matched density with a large density difference.
2.2.3. Continuity Equation
2.2.4. Boundary Condition and Initial Condition
3. Numerical Methods
3.1. Discretization of Governing Equation
3.2. Multiphase Flows with Large Density and Viscosity Contrasts
3.3. Multiphase Flows in Complex/Irregular Domains
3.4. Multiphase Flow at Microscale
3.5. Multi-Component Multiphase Flows
3.6. Others
4. Applications
4.1. Application of PFM in Fluid Mechanics
4.2. Application of PFM in Material Science
4.3. Other Interesting Applications
5. Conclusions and Future Work
- (1)
- PFM is relatively mature in either fundamental theories or mathematical models. By coupling the commonly used phase-field models (Cahn–Hilliard or Allen–Cahn equations) or its modified versions with the momentum equation, the multiphase system of fluid/solid mixtures with large density and viscosity contrasts can be well modeled. However, it is also worth noting that classical PFM is always restricted to isothermal conditions without considering the influence of temperature variation, which needs more to pay attention to more effects in future study.
- (2)
- In terms of numerical methods, the discretization of the fourth-order term of order parameter and the numerical algorithm of multiphase flows with large density and viscosity ratios have been well developed. At present, the PFM is capable of dealing with multiphase flow problems with large differences in physical properties. However, the primary challenge of PFM in the numerical simulation is still to develop the robust, high-accurate and energy-stable numerical algorithms or schemes with mass conservation and thermodynamic consistency, especially to be applicable to the conditions of large density and viscosity ratios at a high Reynolds number. In addition, due to the limitation of computing capability, PFM now is most widely used in mechanism investigations, and its application in engineering practice is still at an initial stage. Thus, a stable and efficient numerical method for PFM is still a research hotspot for future work.
- (3)
- With respect to the application, PFM has been widely applied in various scientific and engineering fields such as fluid mechanics, material science, computer science, petroleum engineering, chemical engineering, biomedicine and astrophysics, etc. However, the application of PFM primarily remains on the mechanism study on simple or/and regular geometries; applications in practical engineering problems in complex/irregular domains are in initial stage and still need more effort. Thus, extending PFM to the real complex or large-scale engineering problems is still a research trend in the near future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brennen, C.E. Fundamentals of Multiphase Flow, 1st ed.; Cambridge University Press: London, UK, 2005; pp. 1–368. [Google Scholar]
- Nazeer, M. Multiphase flow development in gravitational and magnetic fields. Waves Random Complex Media 2023. [Google Scholar] [CrossRef]
- Blunt, M.J. Multiphase Flow in Permeable Media: A Pore-Scale Perspective, 1st ed.; Cambridge University Press: London, UK, 2017; pp. 1–500. [Google Scholar]
- Fuster, D.; Agbaglah, G.; Josserand, C.; Popinet, S.; Zaleski, S. Numerical simulation of droplets, bubbles and waves: State of the art. Fluid Dyn. Res. 2009, 41, 065001. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y.J. A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Zolfaghari, H.; Izbassarov, D.; Muradoglu, M. Simulations of viscoelastic two-phase flows in complex geometries. Comput. Fluids 2017, 156, 548–561. [Google Scholar] [CrossRef]
- Feng, X.Y. Study on the Direct Numerical Simulation of Droplet and Bubble Motion in Two-Phase Flow in Tank; China University of Petroleum: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Herrmann, M. A balanced force refined level set grid method for two-phase flows on unstructured flow solver grids. J. Comput. Phys. 2008, 227, 2674–2706. [Google Scholar] [CrossRef]
- Kirkpatick, M.P.; Armfield, S.W.; Kent, J.H. A representation of curved boundaries for the solution of the Navier–Stokes equations on a staggered three-dimensional Cartesian grid. J. Comput. Phys. 2003, 184, 1–36. [Google Scholar] [CrossRef]
- O’brien, A.; Bussmann, M. A volume-of-fluid ghost-cell immersed boundary method for multiphase flows with contact line dynamics. Comput. Fluids 2018, 165, 43–53. [Google Scholar] [CrossRef]
- Akhlaghi, M.; Mohammadi, V.; Nouri, N.M.; Taherkhani, M.; Karimi, M. Multi-fluid VOF model assessment to simulate the horizontal air-water intermittent flow. Chem. Eng. Res. Des. 2019, 152, 48–59. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E.G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef]
- Enright, D.; Fedkiw, R.; Ferziger, J.; Mitchell, I. A hybrid particle level set method for improved interface capturing. J. Comput. Phys. 2002, 183, 83–116. [Google Scholar] [CrossRef]
- Sun, D.L.; Tao, W.Q. A coupled volume-of-fluid and level set (VOSET) method for computing incompressible two-phase flows. Int. J. Heat Mass Transf. 2010, 53, 645–655. [Google Scholar] [CrossRef]
- Lord, R. On the theory of surface forces.—II. Compressible fluids. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1892, 33, 209–220. [Google Scholar]
- Waals, J.D.V.D. The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density. J. Stat. Phys. 1979, 20, 200–244. [Google Scholar] [CrossRef]
- Galdi, P.; Joseph, D.D.; Preziosi, L.; Rionero, S. Mathematical problems for miscible, incompressible fluids with Korteweg stresses. Eur. J. Mech. B Fluids 1991, 10, 253–267. [Google Scholar]
- Sun, S.Y.; Zhang, T. Reservoir Simulations: Machine Learning and Modeling, 1st ed.; Gulf Professional Publishing: Houston, TX, USA, 2020; pp. 1–330. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. III. nucleation in a two component incompressible fluid. J. Chem. Phys. 1959, 31, 688–699. [Google Scholar] [CrossRef]
- Shen, J. Modeling and numerical approximation of two-phase incompressible flows by a phase-field approach. Multiscale Model. Anal. Mater. Simul. 2011, 22, 147–195. [Google Scholar]
- Anderson, D.M.; McFadden, G.B.; Wheeler, A.A. Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 1998, 30, 139–165. [Google Scholar] [CrossRef]
- Lamorgese, A.G.; Molin, D.; Mauri, R. Phase field approach to multiphase flow modeling. Milan J. Math. 2011, 79, 597–642. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, X.; Liang, H.; Chai, Z.; Shi, B. A brief review of the phase-field-based lattice Boltzmann method for multiphase flows. Capillarity 2019, 2, 33–52. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Beckermann, C.; Diepers, H.J.; Steinbach, I.; Karma, A.; Tong, X. Modeling melt convection in phase-field simulations of solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Wheeler, A.A.; Boettinger, W.J.; McFadden, G.B. Phase-field model for isothermal phase transitions in binary alloys. Phys. Rev. A 1992, 45, 7424–7439. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.G.; Kim, W.T.; Suzuki, T. Phase-field model for binary alloys. Phys. Rev. E 1999, 60, 7186–7197. [Google Scholar] [CrossRef] [PubMed]
- Guermond, J.L.; Quartapelle, L. A projection fem for variable density incompressible flows. J. Comput. Phys. 2000, 165, 167–188. [Google Scholar] [CrossRef]
- Abels, H.; Garcke, H.; Grün, G.; Metzger, S. Diffuse interface models for incompressible two-phase flows with different densities. In Transport Processes at Fluidic Interfaces; Springer: Cham, Switzerland, 2017; Volume 22, pp. 203–229. [Google Scholar]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Lowengrub, J.; Truskinovsky, L. Quasi-incompressible Cahn–Hilliard fluids and topological transitions. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 1998, 454, 2617–2654. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, J.; Wang, Q. An energy stable algorithm for a quasi-incompressible hydrodynamic phase-field model of viscous fluid mixtures with variable densities and viscosities. Comput. Phys. Commun. 2017, 219, 20–34. [Google Scholar] [CrossRef]
- Shokrpour Roudbari, M.; Simsek, G.; van Brummelen, E.H. Diffuse-interface two-phase flow models with different densities: A new quasi-incompressible form and a linear energy-stable method. Math. Models Methods Appl. Sci. 2018, 28, 733–770. [Google Scholar] [CrossRef]
- Tao, W.Q. Numerical Heat Transfer, 2nd ed.; Xi’an Jiaotong University Press: Xi’an, China, 2001; pp. 1–566. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: New York, NY, USA, 2007; pp. 1–520. [Google Scholar]
- Eyre, D.J. Unconditionally gradient stable time marching the Cahn-Hilliard equation. MRS Online Proc. Libr. 1998, 529, 39–46. [Google Scholar] [CrossRef]
- Shin, J.; Lee, H.G.; Lee, J.Y. Convex splitting Runge-Kutta methods for phase-field models. Comput. Math. Appl. 2017, 73, 2388–2403. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X.F. Decoupled, energy stable schemes for phase-field models of two-phase incompressible flows. SIAM J. Numer. Anal. 2015, 53, 279–296. [Google Scholar] [CrossRef]
- Rainer, B.; Steven, M.W.; Marco, S.; Voigt, A. Convexity splitting in a phase field model for surface diffusion. Int. J. Numer. Anal. Mod. 2019, 16, 192–209. [Google Scholar]
- Chen, Y.; Lowengrub, J.; Shen, J.; Wang, C.; Wise, S. Efficient energy stable schemes for isotropic and strongly anisotropic Cahn-Hilliard systems with willmore regularization. J. Comput. Phys. 2018, 365, 56–73. [Google Scholar] [CrossRef]
- Liu, X.; He, Z.K.; Chen, Z.X. A fully discrete virtual element scheme for the Cahn-Hilliard equation in mixed form. Comput. Phys. Commun. 2020, 246, 106870. [Google Scholar] [CrossRef]
- Bu, L.L.; Mei, L.Q.; Hou, Y. Stable second-order schemes for the space-fractional Cahn-Hilliard and Allen-Cahn equations. Comput. Math. Appl. 2019, 78, 3485–3500. [Google Scholar] [CrossRef]
- Aboelenen, T.; Ei-hawary, H.M. A high-order nodal discontinuous Galerkin method for a linearized fractional Cahn-Hilliard equation. Comput. Math. Appl. 2017, 73, 1197–1217. [Google Scholar] [CrossRef]
- Zhao, X.P.; Wang, Q. A second order fully-discrete linear energy stable scheme for a binary compressible viscous fluid model. J. Comput. Phys. 2019, 395, 382–409. [Google Scholar] [CrossRef]
- Yang, J.X.; Kim, J. An unconditionally stable second-order accurate method for systems of Cahn-Hilliard equations. Commun. Nonlinear Sci. Numer. Simul. 2020, 87, 105276. [Google Scholar] [CrossRef]
- Ahammad, M.J.; Alam, J.M.; Rahman, M.A.; Butt, S.D. Numerical simulation of two-phase flow in porous media using a wavelet based phase-field method. Chem. Eng. Sci. 2017, 173, 230–241. [Google Scholar] [CrossRef]
- Alam, J.M. A wavelet based numerical simulation technique for two-phase flows using the phase field method. Comput. Fluids 2017, 146, 143–153. [Google Scholar] [CrossRef]
- Ding, H.; Spelt, P.D.M.; Shu, C. Differ interface model for incompressible two-phase flows with large density ratios. J. Comput. Phys. 2007, 226, 2078–2095. [Google Scholar] [CrossRef]
- Kay, D.; Welford, R. Efficient numerical solution of Cahn-Hilliard-Navier-Stokes fluids in 2D. Siam. J. Sci. Comput. 2007, 29, 2241–2257. [Google Scholar] [CrossRef]
- Abels, H. On a diffuse interface model for two-phase flows of viscous, incompressible fluids with matched densities. Arch. Ration. Mech. Anal. 2009, 194, 463–506. [Google Scholar] [CrossRef]
- Abels, H.; Terasawa, Y. Non-homogeneous Navier-Stokes systems with order-parameter-dependent stresses. Math. Methods Appl. Sci. 2010, 33, 1532–1544. [Google Scholar] [CrossRef]
- Song, B.; Plana, C.; Lopez, J.M.; Avila, M. Phase-field simulation of core-annular pipe flow. Int. J. Multiph. Flow 2019, 117, 14–24. [Google Scholar] [CrossRef]
- Dong, S. On imposing dynamic contact-angle boundary conditions for wall-bounded liquid-gas flows. Comput. Methods Appl. Mech. Eng. 2012, 247, 179–200. [Google Scholar] [CrossRef]
- Gao, M.; Wang, X.P. An efficient scheme for a phase field model for the moving contact line problem with variable density and viscosity. J. Comput. Phys. 2014, 272, 704–718. [Google Scholar] [CrossRef]
- Yu, H.J.; Yang, X.F. Numerical approximations for a phase-field moving contact line model with variable densities and viscosities. J. Comput. Phys. 2017, 334, 665–686. [Google Scholar] [CrossRef]
- Yang, Z.R.; Zhong, C.W.; Zhuo, C.S. Phase-field method based on discrete unified gas-kinetie scheme for large-density-ratio two-phase flows. Phys. Rev. E 2019, 99, 043302. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.W.; Wu, J.; Lin, X.J. An improved diffuse interface method for three-dimensional multiphase flows with complex interface deformation. Int. J. Numer. Methods Fluids 2020, 92, 976–991. [Google Scholar] [CrossRef]
- Joshi, V.; Jaiman, R.K. A positivity preserving and conservative variational scheme for phase-field modeling of two-phase flows. J. Comput. Phys. 2018, 360, 137–166. [Google Scholar] [CrossRef]
- Wang, Z.C.; Dong, S.C.; Triantafyllou, M.S.; Constantinides, Y.; Karniadakis, G.E. A stabilized phase-field method for two-phase flow at high Reynolds number and large density/viscosity ratio. J. Comput. Phys. 2019, 397, 108832. [Google Scholar] [CrossRef]
- Huang, Z.; Lin, G.; Ardekani, A.M. A consistent and conservative Phase-Field method for multiphase incompressible flows. J. Comput. Appl. Math. 2022, 408, 114116. [Google Scholar] [CrossRef]
- Kwak, S.; Yang, J.; Kim, J. A conservative Allen–Cahn equation with a curvature-dependent Lagrange multiplier. Appl. Math. Lett. 2022, 126, 107838. [Google Scholar] [CrossRef]
- Feng, X.; Qiao, Z.; Sun, S.; Wang, X. An energy-stable Smoothed Particle Hydrodynamics discretization of the Navier-Stokes-Cahn-Hilliard model for incompressible two-phase flows. J. Comput. Phys. 2023, 479, 111997. [Google Scholar] [CrossRef]
- Li, Y.B.; Choi, J.; Kim, J. Multi-component Cahn-Hilliard system with different boundary conditions in complex domains. J. Comput. Phys. 2016, 323, 1–16. [Google Scholar] [CrossRef]
- Luo, L.; Wang, X.P.; Cai, X.C. An efficient finite element method for simulation of droplet spreading on a topologically rough surface. J. Comput. Phys. 2017, 349, 233–252. [Google Scholar] [CrossRef]
- Li, Y.B.; Qi, X.L.; Kim, J. Direct discretization method for the Cahn-Hilliard equation on an evolving surface. J. Sci. Comput. 2018, 77, 1147–1163. [Google Scholar] [CrossRef]
- Li, Y.B.; Luo, C.J.; Xia, B.H.; Kim, J. An efficient linear second order unconditionally stable direct discretization method for the phase-field crystal equation on surfaces. Appl. Math. Model. 2019, 67, 477–490. [Google Scholar] [CrossRef]
- Zimmermann, C.; Toshniwal, D.; Landis, C.M.; Hughes, T.J.R.; Mandadapu, K.K.; Sauer, R.A. An isogeometric finite element formulation for phase transitions on deforming surfaces. Comput. Methods Appl. Mech. Eng. 2019, 351, 441–477. [Google Scholar] [CrossRef]
- Guo, Z.L.; Yu, F.; Lin, P.; Wise, S.; Lowengrub, J. A diffuse domain method for two-phase flows with large density ratio in complex geometries. J. Fluid Mech. 2021, 907, A38. [Google Scholar] [CrossRef]
- Fakhari, A.; Rahimian, M.H. Phase-field modeling by the method of lattice Boltzmann equations. Phys. Rev. E 2010, 81, 036707. [Google Scholar] [CrossRef] [PubMed]
- Banari, A.; Janben, C.F.; Grilli, S.T. An efficient lattice Boltzmann multiphase model for 3D flows with large density ratios at high Reynolds numbers. Comput. Math. Appl. 2014, 68, 1819–1843. [Google Scholar] [CrossRef]
- Liang, H. Lattice Boltzmann Method for Multiphase Fluid Flows in Complex Microchannels; Huazhong University of Science and Technology: Wuhan, China, 2015. [Google Scholar]
- Geier, M.; Fakhari, A.; Lee, T. Conservative phase-field lattice Boltzmann model for interface tracking equation. Phys. Rev. E 2015, 91, 063309. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.N.; Liu, H.H.; Zhang, C.H. Three-dimensional phase-field lattice Boltzmann model for incompressible multiphase flows. J. Comput. Sci. 2016, 17, 340–356. [Google Scholar] [CrossRef]
- Fakhari, A.; Geier, M.; Lee, T. A mass-conserving lattice Boltzmann method with dynamic grid refinement for immiscible two-phase flows. J. Comput. Phys. 2016, 315, 434–457. [Google Scholar] [CrossRef]
- Fakhari, A.; Bolster, D. Diffuse interface modeling of three-phase contact line dynamics on curved boundaries: A lattice Boltzmann model for large density and viscosity ratios. J. Comput. Phys. 2017, 334, 620–638. [Google Scholar] [CrossRef]
- Su, T.; Li, Y.; Liang, H.; Xu, J. Numerical study of single bubble rising dynamics using the phase field lattice Boltzmann method. Int. J. Mod. Phys. C 2018, 29, 1850111. [Google Scholar] [CrossRef]
- Zhang, C.J.; Fakhari, A.; Li, J.; Luo, L.S.; Qian, T.Z. A comparative study of interface-conforming ALE-FE scheme and diffuse interface AMR-LB scheme for interfacial dynamics. J. Comput. Phys. 2019, 395, 602–619. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, J.; Wu, H. Phase-field lattice Boltzmann model for two-phase flows with large density ratio. Phys. Rev. E 2022, 105, 015304. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.Y.; Zu, Y.Q. A lattice Boltzmann method for incompressible two-phase flows on partial wetting surface with large density ratio. J. Comput. Phys. 2007, 227, 763–775. [Google Scholar] [CrossRef]
- Li, Y.; Su, T.; Liang, H.; Rong, X.J. Phase field lattice Boltzmann model for two-phase flow coupled with additional interfacial force. Acta Phys. Sin. 2018, 67, 224701. (In Chinese) [Google Scholar]
- Wang, X.; Yang, B.X. Polymer crystallization by phase field method coupling with lattice Boltzmann method. J. Chem. Ind. Eng. 2018, 69, 193–199. (In Chinese) [Google Scholar]
- Yuan, X.; Shi, B.; Zhan, C.; Chai, Z. A phase-field-based lattice Boltzmann model for multiphase flows involving N immiscible incompressible fluids. Phys. Fluids 2022, 34, 023311. [Google Scholar] [CrossRef]
- Hu, Y.; Li, D.C.; Niu, X.D.; Shu, S. A diffuse interface lattice Boltzmann model for thermocapillary flows with large density ratio and thermophysical parameters contrasts. Int. J. Heat Mass Transf. 2019, 138, 809–824. [Google Scholar] [CrossRef]
- Ambrus, V.E.; Busuioc, S.; Wagner, A.J.; Paillusson, F.; Kusumaatmaja, H. Multicomponent flow on curved surfaces: A vielbein lattice Boltzmann approach. Phys. Rev. E 2019, 100, 063306. [Google Scholar] [CrossRef]
- Alpak, F.O.; Zacharoudiou, I.; Berg, S.; Dietderich, J.; Saxena, N. Direct simulation of pore-scale two-phase visco-capillary flow on large digital rock images using a phase-field lattice Boltzmann method on general-purpose graphics processing units. Comput. Geosci. 2019, 23, 849–880. [Google Scholar] [CrossRef]
- Nestler, B.; Choudhury, A. Phase-field modeling of multi-component systems. Curr. Opin. Solid State Mater. Sci. 2011, 15, 93–105. [Google Scholar] [CrossRef]
- Kim, J. Phase-field models for multi-component fluid flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar] [CrossRef]
- Santra, S.; Mandal, S.; Chakraborty, S. Phase-field modeling of multicomponent and multiphase flows in microfluidic systems: A review. Int. J. Heat Fluid Flow. 2021, 31, 3089–3131. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, X.P. Modeling and simulation of dynamics of three-component flows on solid surface. Jpn. J. Ind. Appl. Math. 2014, 31, 611–631. [Google Scholar] [CrossRef]
- Huang, Z.; Lin, G.; Ardekani, A.M. A consistent and conservative model and its scheme for N-phase-M-component incompressible flows. J. Comput. Phys. 2021, 434, 110229. [Google Scholar] [CrossRef]
- Far, K.E.; Gorakifard, M.; Fattahi, E. Multiphase phase-field lattice Boltzmann method for simulation of soluble surfactants. Symmetry 2021, 13, 1019. [Google Scholar]
- Hester, E.W.; Couston, L.A.; Favier, B.; Burns, K.J.; Vasil, G.M. Improved phase-field models of melting and dissolution in multi-component flows. Proc. R. Soc. A 2020, 476, 20200508. [Google Scholar] [CrossRef] [PubMed]
- Yang, J. Phase field modeling and computation of multi-component droplet evaporation. Comput. Methods Appl. Mech. Eng. 2022, 401, 115675. [Google Scholar] [CrossRef]
- Barrett, J.W.; Garcke, H.; Nürnberg, R. Phase field models versus parametric front tracking methods: Are they accurate and computationally efficient? Commun. Comput. Phys. 2014, 15, 506–555. [Google Scholar] [CrossRef]
- Egger, A.; Pillai, U.; Agathos, K.; Kakouris, E.; Chatzi, E.; Aschroft, I.A.; Triantafyllou, S.P. Discrete and phase field methods for linear elastic fracture mechanics: A comparative study and state-of-the-art review. Appl. Sci. 2019, 9, 2436. [Google Scholar] [CrossRef]
- Cervera, M.; Barbat, G.B.; Chiumenti, M.; Wu, J.Y. A Comparative review of XFEM, Mixed FEM and phase-field models for quasi-brittle cracking. Arch. Computat. Methods Eng. 2022, 29, 1009–1083. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Nguyen, H.T.; Abdullah Dönmez, A. Critical comparison of phase-field, peridynamics, and crack band model M7 in light of gap test and classical fracture tests. J. Appl. Mech. 2022, 89, 061008. [Google Scholar] [CrossRef]
- Diehl, P.; Lipton, R.; Wick, T.; Tyagi, M. A comparative review of peridynamics and phase-field models for engineering fracture mechanics. Comput. Mech. 2022, 69, 1259–1293. [Google Scholar] [CrossRef]
- Jain, S.S. Accurate conservative phase-field method for simulation of two-phase flows. J. Comput. Phys. 2022, 469, 111529. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, X.F.; Shen, J.; Wang, Q. A decoupled energy stable scheme for a hydrodynamic phase-field model of mixtures of nematic liquid crystals and viscous fluids. J. Comput. Phys. 2016, 305, 539–556. [Google Scholar] [CrossRef]
- Liu, J.Q. Calculation and Optimization of Multi-Field Coupled Phase-Field Model Based on Multi-GPU Parallel; Lanzhou University of Technology: Lanzhou, China, 2018. (In Chinese) [Google Scholar]
- Xu, S. Parallel Computation Based on Adaptive Finite Element of Multi-Field Coupling Phase Field Model Simulation; Lanzhou University of Technology: Lanzhou, China, 2019. [Google Scholar]
- Zahari, N.M.; Zawawi, M.H.; Sidek, L.M.; Mohamad, D.; Itam, Z.; Ramli, M.Z.; Syamsir, A.; Abas, A.; Rashid, M. Introduction of discrete phase model (DPM) in fluid flow: A review. AIP Conf. Proc. 2018, 2030, 020234. [Google Scholar]
- Xu, J.; Zhao, P.; Zhang, Y.; Wang, J.; Ge, W. Discrete particle methods for engineering simulation: Reproducing mesoscale structures in multiphase systems. Res. Chem. Mater. 2022, 1, 69–79. [Google Scholar] [CrossRef]
- He, M.; Zhao, B.; Xu, J.; Kong, L.; Wang, J. Assessment of kinetic theory for gas–solid flows using discrete particle method. Phys. Fluids 2022, 34, 093315. [Google Scholar] [CrossRef]
- Subramaniam, S.; Balachandar, S. Modeling Approaches and Computational Methods for Particle-Laden Turbulent Flows, 1st ed.; Academic Press: San Diego, CA, USA, 2022. [Google Scholar]
- Marchioli, C.; Zhao, L. Dispersed multiphase flows: Advances in measuring, simulation and modeling. Acta Mech. Sin. 2022, 38, 722900. [Google Scholar] [CrossRef]
- Nochetto, R.H.; Salgado, A.J.; Tomas, I. A diffuse interface model for two-phase ferrofluid flows. Comput. Methods Appl. Mech. Eng. 2016, 309, 497–531. [Google Scholar] [CrossRef]
- Li, J.Y.; Zeng, Z.; Qiao, L. Numerical simulation of droplets’ dynamics wetting process with the phase field method. Appl. Math. Mech. 2019, 40, 957–967. [Google Scholar]
- Feng, Q.H.; Zhao, Y.C.; Wang, S.; Zhang, Y.G.; Sun, Y.H.; Shi, S.B. Pore-scale oil-water two-phase flow simulation based on phase field method. Chin. J. Comput. Phys. 2020, 37, 439–447. [Google Scholar]
- Balashov, V.A.; Savenkov, E.B. Thermodynamically consistent spatial discretization of the one-dimensional regularized system of the Navier-Stokes-Cahn-Hilliard equations. J. Comput. Appl. Math. 2020, 372, 112743. [Google Scholar] [CrossRef]
- Subhedar, A.; Galenko, P.K.; Varnik, F. Thin interface limit of the double-sided phase-field model with convection. Philos. Trans. R. Soc. A 2020, 378, 20190540. [Google Scholar] [CrossRef] [PubMed]
- Conti, M.; Giorgini, A. Well-posedness for the Brinkman-Cahn-Hilliard system with unmatched viscosities. J. Differ. Equ. 2019, 268, 6350–6384. [Google Scholar] [CrossRef]
- Soligo, G.; Roccon, A.; Soldati, A. Breakage, coalescence and size distribution of surfactant-laden droplets in turbulent flow. J. Fluid Mech. 2019, 881, 244–282. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Liu, W.; Free, M.L. Phase-field modeling and simulation of gas bubble coalescence and detachment in a gas-liquid two-phase electrochemical system. J. Electrochem. Soc. 2020, 167, 013532. [Google Scholar] [CrossRef]
- Bonart, H.; Kahle, C.; Repke, J. Comparison of energy stable simulation of moving contact line problems using a thermodynamically consistent Cahn–Hilliard Navier–Stokes model. J. Comput. Phys. 2019, 399, 108959. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, Z.L. Spontaneous shrinkage of droplet on a wetting surface in the phase-field model. Phys. Rev. E 2019, 100, 061302. [Google Scholar] [CrossRef]
- Yang, J.; Li, Y.; Kim, J. Modified multi-phase diffuse-interface model for compound droplets in contact with solid. J. Comput. Phys. 2023, 491, 112345. [Google Scholar] [CrossRef]
- Zhou, S.W.; Zhuang, X.Y.; Rabczuk, T. Phase-field modeling of fluid-driven dynamic cracking in porous media. Comput. Methods Appl. Mech. Eng. 2019, 350, 169–198. [Google Scholar] [CrossRef]
- Xia, L.; Yvonnet, J.; Ghabezloo, S. Phase field modeling of hydraulic fracturing with interfacial damage in highly heterogeneous fluid-saturated porous media. Eng. Fract. Mech. 2017, 186, 158–180. [Google Scholar] [CrossRef]
- Li, P.F.; Zhu, Q.Z.; Gu, S.T.; Tao, N. A phase field method to simulate crack nucleation and crack prorogation in rock-like materials. Eng. Mech. 2018, 35, 41–48. [Google Scholar]
- Ambati, M.; Gerasimov, T.; De, L.L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Makvandi, R.; Duczek, S.; Juhre, D. A phase-field fracture model based on strain gradient elasticity. Eng. Fract. Mech. 2019, 220, 106648. [Google Scholar] [CrossRef]
- Goswami, S.; Anitescu, C.; Rabczuk, T. Adaptive phase field analysis with dual hierarchical meshes for brittle fracture. Eng. Fract. Mech. 2019, 218, 106608. [Google Scholar] [CrossRef]
- Zhu, M.X.; Li, J.C.; Song, H.G.; Chen, J.M. A phase field model for the propagation of electrical tree in nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 336–342. [Google Scholar] [CrossRef]
- Wang, C.T.; Cai, J.J. CFD studies on a single Taylor bubble rising behaviors in liquid LBE based on diffuse-interface method. Nucl. Sci. Eng. 2019, 39, 363–372. (In Chinese) [Google Scholar]
- Zhang, B.; Zhao, Y.H.; Wang, H.; Chen, W.P.; Hou, H. Three-dimensional phase field simulation of dendritic morphology of Al-Si alloy. Rare Met. Mater. Eng. 2019, 48, 2835–2840. (In Chinese) [Google Scholar]
- Pinomaa, T.; Yashchuk, I.; Lindroos, M.; Andersson, T.; Laukkanen, A. Process-structure-properties-performance modeling for selective laser melting. Metals 2019, 9, 1138. [Google Scholar] [CrossRef]
- Riahinasab, S.T.; Keshavarz, A.; Melton, C.N.; Elbaradei, A.; Warren, G.I.; Selinger, R.L.B.; Stokes, B.J.; Hirst, L.S. Nanoparticle-based hollow microstructures formed by two-stage nematic nucleation and phase separation. Nat. Commun. 2019, 10, 894. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yang, X.F. Numerical approximations for a new L2-gradient flow based Phase field crystal model with precise nonlocal mass conservation. Comput. Phys. Commun. 2019, 243, 51–67. [Google Scholar] [CrossRef]
- Balakrishna, A.R.; Carter, W.C. Combining phase-field crystal methods with a Cahn-Hilliard model for binary alloys. Phys. Rev. E 2018, 97, 043304. [Google Scholar] [CrossRef] [PubMed]
- Bosch, J.; Kay, D.; Stoll, M.; Wathen, A.J. Fast solvers for Cahn-Hilliard inpainting. SIAM J. Imaging Sci. 2014, 7, 67–97. [Google Scholar] [CrossRef]
- Kvamme, B.; Qasim, M.; Baig, K.; Kivelä, P.H.; Bauman, J. Hydrate phase transition kinetics from phase field theory with implicit hydrodynamics and heat transport. Int. J. Greenh. Gas Control 2014, 29, 263–278. [Google Scholar] [CrossRef]
- Lee, H.G.; Park, J.; Yoon, S.; Lee, C.; Kim, J. Mathematical model and numerical simulation for tissue growth on bioscaffolds. Appl. Sci. 2019, 9, 4058. [Google Scholar] [CrossRef]
- Faghihi, D.; Feng, X.Z.; Lima, E.A.B.F.; Oden, J.T.; Yankeelov, T.E. A coupled mass transport and deformation theory of multi-constituent tumor growth. J. Mech. Phys. Solids 2020, 139, 103936. [Google Scholar] [CrossRef]
- Guan, G.; Kuang, X.; Tang, C.; Zhang, L. Comparison between phase-field model and coarse-grained model for characterizing cell-resolved morphological and mechanical properties in a multicellular system. Commun. Nonlinear Sci. Numer. Simul. 2023, 117, 106966. [Google Scholar] [CrossRef]
- Zhang, T.; Cogan, N.; Wang, Q. Phase-field models for biofilms II. 2D numerical simulations of biofilm-flow interaction. Commun. Comput. Phys. 2008, 4, 72–101. [Google Scholar]
- Tremaine, S. On the origin of irregular structure in Saturn’s rings. Astron. J. 2002, 125, 894–901. [Google Scholar] [CrossRef]

| No. | Classification | Representative Methods |
|---|---|---|
| 1 | interface modeling | interface-capturing method, interface-tracking method |
| 2 | fluid motion | Euler’s method, Lagrange method, hybrid method |
| . | … | … |
| Coupling Schemes | Representative Methods |
|---|---|
| All equations are solved simultaneously | Solving all variables simultaneously and globally; |
| Solving part of variables simultaneously and globally; | |
| Solving all variables simultaneously and locally. | |
| Equations are solved separately | Non-pressure-based approach; |
| Vorticity–stream function method, vorticity–velocity method, etc.; Pressure-based approach: Pressure-correction method, projection method, fractional step method, artificial compression method, pressure Poisson equation method, etc. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zheng, D.; Zhang, W. Advances of Phase-Field Model in the Numerical Simulation of Multiphase Flows: A Review. Atmosphere 2023, 14, 1311. https://doi.org/10.3390/atmos14081311
Li J, Zheng D, Zhang W. Advances of Phase-Field Model in the Numerical Simulation of Multiphase Flows: A Review. Atmosphere. 2023; 14(8):1311. https://doi.org/10.3390/atmos14081311
Chicago/Turabian StyleLi, Jingfa, Dukui Zheng, and Wei Zhang. 2023. "Advances of Phase-Field Model in the Numerical Simulation of Multiphase Flows: A Review" Atmosphere 14, no. 8: 1311. https://doi.org/10.3390/atmos14081311
APA StyleLi, J., Zheng, D., & Zhang, W. (2023). Advances of Phase-Field Model in the Numerical Simulation of Multiphase Flows: A Review. Atmosphere, 14(8), 1311. https://doi.org/10.3390/atmos14081311






