Abstract
Resonance fluorescence scattering is the physical mechanism with which lidar detects atmospheric metal layers. The resonance fluorescence scattering cross section is an important parameter for lidar data processing. In this work, the resonance fluorescence backscattering cross sections of most detectable metal atoms and ions in the atmosphere were calculated. The calculated maximum backscattering cross section of Na at the D2 line is 7.38 × 10−17 m2/sr; K at the D1 line is 7.37 × 10−17 m2/sr; Fe at the 372 nm line is 7.53 × 10−18 m2/sr; Fe at the 374 nm line is 6.98 × 10−18 m2/sr; Fe at the 386 nm line is 3.75 × 10−18 m2/sr; Ni at the 337 nm line is 4.05 × 10−18 m2/sr; and Ni at the 341 nm line is 2.05 × 10−17 m2/sr; Ca is 3.06 × 10−16 m2/sr; Ca+ is 1.12 × 10−16 m2/sr. The influence of the laser linewidth on the effective scattering cross section was discussed. If the laser linewidth is lower than 2 GHz to detect Na, the laser center frequency locked at the D2a line is a better option than the D2 line in order to obtain greater signals. If an unlocked lidar is used to detect Na, the frequency at D2a should be used as the laser center frequency when the effective scattering cross section of Na was calculated, because the absorption cross section of Na atom has two local maxima. This work proposes a quantifiable comparative method for assessing the observation difficulty of different metal particles by comparing their relative uncertainties in lidar observation. It is assumed that under the same observation conditions, the detectability of different metal atoms and ions is compared. Using Na as a basis for comparison, the relative uncertainty of Ni at 337 nm is the highest, about a factor of 21 larger than that of Na, indicating that it is the most difficult to be detected. The purpose of this work is to present a quantifiable comparison method for the detection difficulty of the metal particles by lidar in the middle and upper atmosphere, which has great significance for the design of the lidar system.
1. Introduction
There are a large number of metal atoms and ions in the middle and upper atmosphere at 80 to 110 km, which make up the well-known atmospheric metal layer [1]. These atoms and ions absorb photons of specific energies and then emit them. This physical process is known as resonance fluorescence scattering [2]. Therefore, people can detect these atoms and ions with the resonance fluorescence scattering mechanism, and treat them as tracers to study the physical and chemical processes in the middle and upper atmosphere. At present, it has been confirmed that the detectable metal atoms mainly include sodium [3,4], potassium [5], iron [6,7], nickel [8,9] and calcium [10,11], and the detectable ions include calcium ions [11,12] and magnesium ions [13,14]. Calcium ions are currently the only metal ions that can be detected by the ground-based instrument [15,16].
Resonance fluorescence scattering lidar is an important means of detecting metal layers in the middle and upper atmosphere. Its basic principle is to adjust the wavelength of the laser to the resonance fluorescence wavelength of the atoms and ions to be observed, and then emit photons to the target area [17]. Resonance fluorescence scattering occurs after atoms and ions absorb photons, and the telescope of the ground-based lidar system receives the backscattered photons. Finally, the density of particles can be measured in the target area according to the number of received photons [18]. The lidar observation of metal particles is of great significance to the study of the law of middle and upper atmosphere motion and the change in the space weather environment.
In 1969, Bowman used lidar with continuously tunable narrow-band organic dye laser to detect Na atoms in the middle and upper atmosphere for the first time [1,19]. Granier used lidar with a Nd:YAG pumped dye laser to generate 423 nm and 393 nm wavelengths for detecting calcium atoms and ions in 1985 [11]. Since then, lidar has become an important tool for studying the middle and upper atmosphere. The species of metal particles detected using lidar are also increasing. Von Zahn reported the first observation of K density and temperature profiles in 1996 with a solid-state laser system [5]. Gelbwachs developed the dual-wavelength Iron Boltzmann factor lidar in 1994 [20]; this kind of lidar can detect temperature of middle and upper atmosphere by using the Maxwell-Boltzmann relationship from the ratio of Fe atoms excited at 372 and 374 nm. Collins and Gerding observed Ni atoms with different lidar systems in 2015 and 2019, respectively [8,21]. However, their detection results differed by an order of magnitude. The development of lidar system is rapid, and the means to generate specific resonance fluorescence wavelengths are also varied. More than six species of metal particles have been observed by ground-based lidar in the past decades. However, the relative detection difficulties of these particles cannot be specifically known from these different works. It is necessary to propose a quantifiable method to evaluate the detection difficulty of different metal particles.
During the lidar data processing, it is essential to invert the raw photon number collected by the lidar to the number density of particles used during the study, in which the effective backscattering cross section is a key parameter. The effective backscattering cross section is obtained by convolving the resonance fluorescence scattering cross section of the particle with the normalized laser line shape [1]. The value of the effective backscattering cross section can be affected by both the laser linewidth and the laser line shape. Therefore, the calculation of the resonance fluorescence scattering cross section of each particle is very important to the data inversion [22]. However, there is a lack of a summary of calculation results of the resonance fluorescence scattering cross sections of metal particles that can be detected by ground-based lidar. Different metal particles have different detectability. The comparison of the detectability of the different metal particles is also rare.
This work proposes a quantifiable comparative method for assessing the observation difficulty of different metal particles in the middle and upper atmosphere by comparing their relative uncertainties in lidar observation. The relative uncertainty of observation is primarily influenced by the particle’s resonance fluorescence wavelength, resonance fluorescence scattering cross section, and the abundance in the middle and upper atmosphere. The calculation of the resonance fluorescence scattering cross section of each metal atom and ion is import in this comparative method. Firstly, the calculation method of resonance fluorescence scattering cross section is introduced. After considering the hyperfine structure, the resonance fluorescence scattering cross section of the metal atoms and ions are calculated. Then, the variations in the effective scattering cross section of different atoms and ions with the laser linewidth are discussed. In particular, when detecting sodium atoms, it is found that setting the center frequency of the laser at different values will have a significant impact on the results of the effective backscattering cross section. Finally, assuming under the same observation conditions, the detectability of each metal atom and ion are compared. The purpose of this work is to present a quantifiable comparison method for the detection difficulty of the metal particles by lidar in the middle and upper atmosphere, which has great significance for the design of the lidar system.
2. Resonance Fluorescence Scattering Cross Section
2.1. Calculation Method of Resonance Fluorescence Scattering Cross Section
Metal atoms and ions transition to a higher energy level after absorbing incident photons. The higher energy level is unstable and has a short effective lifetime. The excited atom will eventually fall back to the original energy level and scatter resonance fluorescent photons at the same time. All the absorbed photons will eventually be scattered. This process is called resonance fluorescence scattering [2]. The probability of an incident photon being absorbed by atoms and ions is called the absorption cross section. The absorption cross section at the peak is given by:
where is the electron charge; is the vacuum permittivity; is the electron mass; is the speed of light; and is the oscillator strength of metal atoms or ions. Atoms and ions are always moving. Different velocities of the motion result in different Doppler shifts, then the cumulative effect is the Doppler broadening [23]. is the RMS width of the Doppler broadening, and it is written as:
where is the resonance fluorescence center frequency of atoms or ions; is the Boltzmann constant; is the absolute temperature; is the absolute mass of atoms or ions. Since the atmospheric metal layer is located in the mesopause and low thermosphere, the temperature, , is usually taken as 200 K. Then, the absorption cross section formula for the incident photon frequency is:
Since the resonance fluorescence scattering of metal atoms and ions occurs immediately after absorbing photons, and the number of the scattered photons is equal to the number of the absorbed photons during the integration time, the absorption cross section of atoms and ions is equivalent to their scattering cross section. The probability of the resonance fluorescence scattering of atoms and ions in all directions is the same. The following equation can be used to calculate the maximum backscattering cross section:
In this equation, the maximum backscattering cross sections of atoms and ions can be calculated. The detailed parameters of metal atoms and ions calculated in this work are given in Table 1.

Table 1.
Detailed parameters of several metal atoms and ions.
2.2. Calculation of Scattering Cross Sections of Metal Atoms and Ions
Na has a total of six transition spectral lines of the hyperfine structure of its D2 line. Thus, the scattering cross sections of each spectral line need to be calculated separately. The detailed parameters of each transition spectral line are given in Table 2 [4].

Table 2.
Detailed parameters of the D2 line of Na [4].
The absorption cross section of Na is the sum of the absorption cross section of each transition line of its hyperfine structure:
where is the relative oscillator strength of the i-th transition spectrum line, is the absorption cross section of the i-th line. The total absorption cross sections of Na and its absorption cross sections of six hyperfine transition lines are shown in Figure 1.
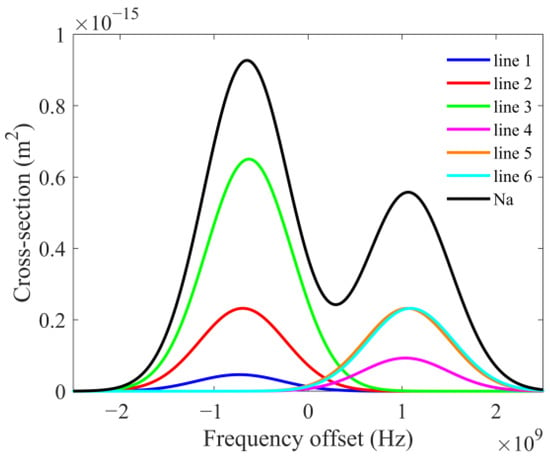
Figure 1.
The absorption cross section of Na and each spectral line of its hyperfine structure.
The calculation method for K is basically same for Na, but K has isotopes in nature, such as 39K, 40K and 41K. The abundance of 40K is extremely low, so it can be ignored. The abundance of 39K and 41K are 93.3% and 6.7%, respectively. Therefore, it is necessary to consider its isotope abundance when calculating the total absorption cross section for K. Then, its absorption section calculation formula is written as:
where is the isotope abundance, and if = 40, = 0. The detailed parameters of the D1 line of K are given in Table 3 [5].

Table 3.
Detailed parameters of the D1 line of K [5].
When calculating the scattering cross sections of Fe [6], Ni [8,9], Ca and Ca+ [10,12], the hyperfine spectral structure is not considered, so the relative oscillator strength is not considered in the calculation. According to the detailed parameters of each atom and ion given in the Table 1, the scattering cross sections of each atom and ion can be calculated, and their scattering cross sections are shown in Figure 2.
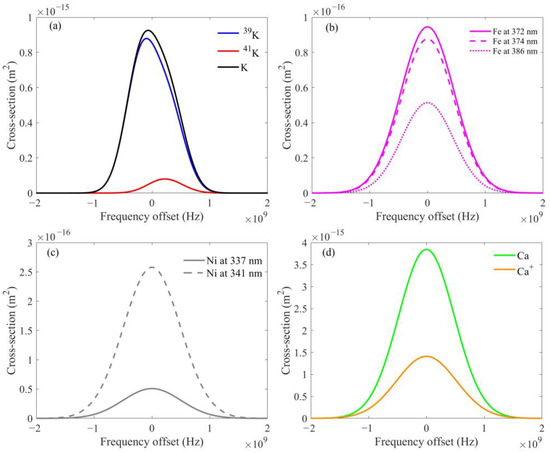
Figure 2.
The absorption cross sections of atoms and ions. (a) K and its isotopes; (b) Fe; (c) Ni; (d) Ca and Ca+.
Table 4 shows the calculation results of the maximum backscattering cross sections of metal atoms and ions, and compares them with the values in the references. The calculation results of Fe are at the 372 nm line, Fe at the 374 nm line, Fe at the 386 nm line, Ca and Ca+ are consistent with the references. However, the calculation results of the peak absorption cross section of Na and K are not close to the value of references [3], because the early calculation of the absorption cross section of Na and K did not consider their hyperfine structure. After considering the hyperfine structure, the calculation results of Na and K are close to the values read from the figures in the references [5,24]. Although Ni at the 337 nm line and the 341 nm line have no reference to give the value of peak absorption cross section, the effective backscattering cross section is calculated by using the laser linewidth (0.9547 GHz) given by the reference [25]. Ni at the 337 nm line is 3.14 × 10−18 m2/sr, and the 341 nm line is 1.58 × 10−17 m2/sr, which is consistent with the reference.

Table 4.
Comparison of peak absorption cross section of several metal atoms and ions with other’s work.
According to the calculated maximum backscattering cross sections of each atom and ion, the histogram is drawn as shown in Figure 3 for comparison. It is found that the maximum backscattering cross section of Ca is the largest among the metal particles calculated in this work, which is 75.56 times that of the smallest Ni at the 337 nm line. Ca and Ca+ are both higher than other metal particles, and Ca is higher than Ca+. Na is close to K. Ni at the 341 nm line is 5.06 times of Ni the 337 nm line. Fe at the 372 nm line is close to the 374 nm line. Fe at the 386 nm line is close to Ni at the 337 nm line.
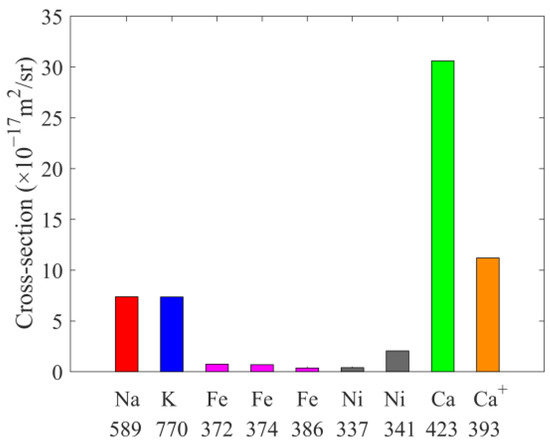
Figure 3.
Comparison of maximum backscattering cross sections of atoms and ions. The x-axis represents the names of particles and the number below the name is the resonance fluorescence wavelength in nanometers.
2.3. Variation in Effective Backscattering Cross Section with Laser Linewidth
The resonance fluorescence scattering cross section is an intrinsic property of atoms and ions. In actual observation, the line shape and linewidth of the laser are different due to the different lasers used by different lidar. Although the monochromatic nature of the laser is well, it is still quasi-monochromatic light with a certain linewidth. Thus, the maximum backscattering cross section cannot be used to calculate the atomic and ionic number density in the target area directly. It is necessary to convolute the resonance fluorescence scattering cross section with the normalized laser line shape to obtain an effective scattering cross section. Assuming that the laser line shape of the lidar is a Gaussian line shape, the normalization laser line shape is given by [1]:
where is the center frequency of the laser. is the RMS width of the Gaussian linear shape, and the formula of is:
where is the full width at half maximum of the laser. The effective scattering cross-section can be obtained by convolution of the absorption cross-section and the normalization laser line:
Since the resonance fluorescence scattering of atoms and ions is isotropic, the effective backscattering cross section is:
In actual observation, the stability of the laser linewidth has an impact on the effective backscattering cross section. This work studies the trend of the effective backscattering cross section with the laser linewidth under the temperature condition of 200 K. Figure 4 shows the effective backscattering cross section of each atom and ion at the center frequency with the laser linewidth. It is found that except for Na, the effective backscattering cross section is larger when the laser linewidth is narrower. The effective backscattering cross section of Na has a maximum value at the laser linewidth of 1.5 GHz, which is different from the changing trend of other atoms and ions. The specific reasons will be discussed in the next section.
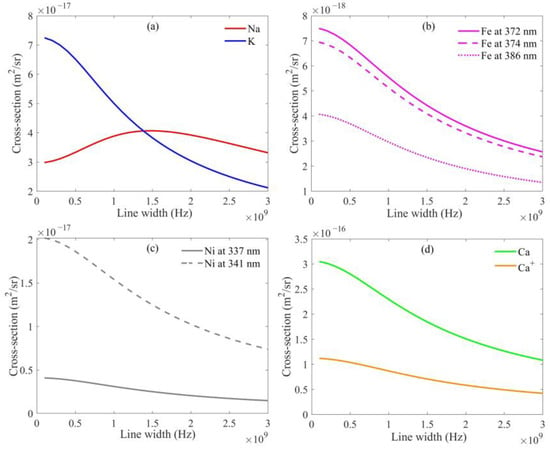
Figure 4.
Effective backscattering cross sections of atoms and ions as a function of the linewidth of the laser. (a) Na and K; (b) Fe; (c) Ni; (d) Ca and Ca+.
3. Discussion
3.1. Variation in Effective Backscattering Cross Section of Sodium Atom with Laser Linewidth
Since the absorption cross section of Na has two maxima and the two maxima are 1.68 GHz apart, the effective backscattering cross section does not show a similar trend to that of K as shown in Figure 4a, when the center frequency of the laser is at the center frequency of the D2 line of Na (wavelength is 589.1583 nm). Figure 5a shows the effective scattering cross section of Na when the laser linewidths are 0.5 GHz, 1.5 GHz and 3 GHz, respectively. It is found that when the linewidth is 0.5 GHz, the effective scattering cross section at the center of the D2 line is lower than that of 1.5 GHz. Similarly, when the laser linewidth is 3 GHz, the effective scattering cross section at the center of the D2 line is still less than that of 1.5 GHz. However, in the case of the center frequency of the laser at D2a line of Na (wavelength 589.1590 nm), the effective scattering cross section decreases with an increasing laser linewidth. It shows a similar change trend to other metal particles. Since the absorption cross section of Na atom has two peaks, the absorption cross section at the center of D2 is not the maximum. The effective scattering cross section is obtained by convolving the laser line shape with Na absorption cross section. The convolved result is influenced by the laser center frequency value, and it is evident that when the laser linewidth is less than 2 GHz, the effective scattering cross section value at the laser center frequency set at the maximum of D2a is greater than the value at the laser center frequency set at the maximum of D2.
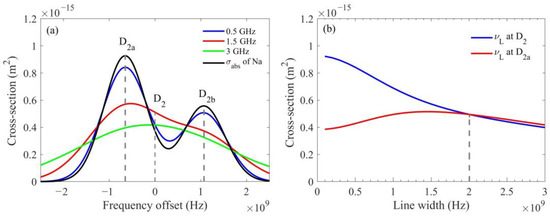
Figure 5.
Laser center frequencies set at D2 and D2a make different trends of effective scattering cross section with the linewidth of the laser due to the two peaks of absorption cross section of Na atoms. (a) Comparison of effective scattering cross sections of the sodium with different linewidths of the laser. Vertical dashed lines indicate the positions of D2a, D2 and D2b; (b) effective scattering cross section of the sodium with the linewidth of the laser at the different center frequencies of D2 and D2a. Vertical dashed line indicates the position of the intersection of two different trend curves.
Therefore, the effective backscattering cross section at D2a line of Na is recalculated as the laser linewidth changes. As shown in Figure 5b, it is found that when the laser center frequency is set to the frequency at D2a line of Na, the effective backscattering cross section of Na also shows a decreasing trend with the increasing laser linewidth.
As shown in Figure 5b, when the laser linewidth is lower than 2 GHz, the effective backscattering cross section of the laser center frequency set at the D2a line is greater than the effective backscattering cross section of the laser center frequency set at the D2 line; when the laser linewidth is higher than 2 GHz, the effective backscattering cross section of the laser center frequency set at the D2a line is lower than the effective backscattering cross section of the laser center frequency set at the D2 line. Therefore, the laser center frequency of the frequency-locked lidar should be locked at the D2a line to obtain the maximum echo signal of Na when the laser linewidth is lower than 2 GHz. If the frequency-unlocked lidar is used for observation, when calculating the effective backscattering cross section of Na, the frequency at the D2a line should be used as the laser center frequency to match the maximum echo signal received by the telescope. When the laser linewidth is higher than 2 GHz, the center frequency of the laser needs to be stable near the D2 line. In this case, the position of the center frequency of the laser has no great influence on the observation results.
3.2. Comparison of Detectability of Metal Atoms and Ions
The effective backscattering cross section is an important parameter for the lidar equation used to invert the density of atoms and ions in the mesopause region. With the support of the calculated effective scattering cross-section results obtained above, this work can propose the following methods to compare the detectability of different metallic particles. The signal received by the lidar includes the resonance fluorescence signal and the environmental background noise :
The general lidar equation is given by [17]:
where is the number of photons received by the lidar, is the laser emission power, is the integration time, is the Planck constant, is the laser wavelength, is the effective backscattering cross section, is the density of atoms and ions at the target height, is the distance between the target area and the observation point, is the spatial resolution, is the area of the telescope, is the optical efficiency of the lidar, is the geometric parameters of the lidar, is the product of atmospheric attenuation coefficients of laser emission and return. is the environmental background noise during the integration time.
Assuming the same set of lidar is used, with the same integration time and the same transmit power. Taking Na as a benchmark, the ratio of K signal to Na signal as an example can be written as:
In Equation (13), and are mainly affected by wavelengths. The resonance fluorescence wavelengths of the metal atoms and ions are basically in the visible light and near ultraviolet ranges. In this range, the change in wavelength has very little effect on [1]. In the echo signal at a height of 90 km, the resonance fluorescence signal is much larger than the background noise, assuming that the optical efficiency of the same set of lidar systems is also only slightly affected by wavelength changes in the visible light and near ultraviolet ranges. Equation (13) can be approximated by:
Then, the ratio of the number of photons received by K and Na under the same conditions is obtained.
In this work, the signal-noise ratio is used to analyze the lidar detection precision of metal particles. The signal refers to the resonance fluorescence scattering signal of the detected metal particles received by lidar, and the noise is the fluctuation noise of the photon number [27]. The detection precision increases with the increasing signal-noise ratio. Since the photon count of lidar obeys the Poisson distribution [28], the fluctuation noise of the photon number is , so the signal-noise ratio formula can be written as:
Similarly, it can be considered that in the echo signal at an altitude of 90 km, the resonance fluorescence signal is much larger than the ambient background noise, that is, , so the signal-noise ratio equation can be approximately by:
In order to characterize the detectability of each atom and ion, this work compared the relative uncertainty of the detection of each atom and ion. The detection precision decreases with the increasing relative uncertainty. Relative uncertainty is the ratio of absolute uncertainty to actual observed value [29]. It is the reciprocal of the signal-noise ratio:
Equations (14) and (17) are combined to simultaneous equations. The relative uncertainty of K was compared with the relative uncertainty of Na. The ratio of relative uncertainty can be written as:
It can be seen that the relative uncertainty ratio between metal particles and sodium atoms is mainly influenced by the resonant fluorescence wavelength, effective backscattering cross-section, and abundance in the middle and upper atmosphere. It can be obtained from the relative uncertainty ratio of various atoms and ions to Na. Table 5 shows the ratio of relative uncertainty of metal atoms and ions to Na at the same height of 90 km, the effective backscattering cross section of each atom and ion at a laser linewidth of 1.5 GHz, and the density of atoms and ions.

Table 5.
Ratio of relative uncertainty of metal atoms and ions to Na.
Ignoring the laser emission power required to observe different particles, the stability of the frequency, the quantum efficiency of the photomultiplier tube in the receiving system and other related technical difficulties, only the physical properties of metal atoms and ions and their concentrations in the atmosphere are considered. Because they have different resonance fluorescence wavelengths, scattering cross sections, and the abundances in the middle and upper atmosphere. The ratios of relative uncertainty of the detection of different metal atoms and ions are compared. It can be seen from Table 5 that the scattering cross sections of Na is close to K. However, the relative uncertainty of K is nearly an order of magnitude higher than Na. Because the concentration of K in the atmosphere is only about 1/80 of that of Na. Therefore, K is more difficult to detect than Na.
Fe at the 374 nm line has different densities in the atmosphere with the 372 nm line and the 386 nm line. Fe at 374 nm is a weak resonance line compared to the 372 nm line [20]. The density of Fe at the 372 nm and the 386 nm resonance line is much greater than the density of Fe at the 374 nm line. The effective backscattering cross section of Fe at the 372 nm line is one magnitude lower than that of Na. However, it has an extremely high concentration in the atmosphere, thus the relative uncertainty of Fe at the 372 nm line is low. While the scattering cross section of Fe at 374 nm line is close to the 372 nm line, the relative uncertainty is one magnitude higher than that of Na due to its low concentration. The scattering cross section of Fe at the 386 nm line is half of the 372 nm line. The density of Fe at the 386 nm line is close to the 372 nm line. Then, the relative uncertainty of Fe at 386 nm line is only greater than Na and Fe at the 372 nm line.
The scattering cross section of Ca is the largest among this work. However, Ca has the lowest concentration in the atmosphere, so its relative uncertainty is equivalent to that of K. The scattering cross section of Ca+ is lower than half of Ca, but its concentration is 6~7 times that of Ca. So, the relative uncertainty of Ca+ is lower than Ca. The first lidar detection of Ni shows that the number density of its 337 nm line is about 16,000 cm−3 [21], which is equivalent to that of Fe. However, the latest two detections both show that the concentration of Ni at the 337 nm line is equivalent to the concentration of the 341 nm line [8,25], and its density is about 300 cm−3. This work uses the latest detection results for comparison. Since the scattering cross section and the concentration in the atmosphere of Ni at the 337 nm line are both low, it is the particle with the highest relative uncertainty among all the particles compared in this work. The relative uncertainty of the 341 nm line of Ni is much smaller than the 337 nm line because its scattering cross section is one magnitude higher than the 337 nm line.
Since the relative uncertainty represents the detection precision of metal particles, the detection precision becomes lower with the increasing ratio of relative uncertainty to sodium atom. Therefore, under the premise assumed in this work, except for sodium atoms, the 372 nm line of Fe has the highest detection precision, while Ni has the lowest detection precision.
4. Conclusions
In this work, the resonance fluorescence scattering cross sections of each metal atom and ion are calculated. The maximum backscattering cross section of Na at the D2 line is 7.38 × 10−17 m2/sr; K at the D1 line is 7.37 × 10−17 m2/sr; Fe at the 372 nm line is 7.53 × 10−18 m2/sr; Fe at the 374 nm line is 6.98 × 10−18 m2/sr; Fe at the 386 nm line is 3.75 × 10−18 m2/sr; Ni at the 337 nm line is 4.05 × 10−18 m2/sr; Ni at the 341 nm line is 2.05 × 10−17 m2/sr; Ca is 3.06 × 10−16 m2/sr; Ca+ is 1.12 × 10−16 m2/sr. The scattering cross section of Ca is the largest in this work. Both Ca and Ca+ are higher than other metal particles, and Ca is higher than Ca+. The scattering cross section of Na and K atoms is close. The scattering cross section of Ni at the 337 nm line is the smallest.
Except for Na, the effective backscattering cross section of all metal particles at the center frequency decreases with the increasing laser linewidth. The effective backscattering cross section of Na increases first and then decreases with the increasing laser linewidth. Because the absorption cross section of Na atom has two maxima, the absorption cross section of the frequency at D2 is not the maxima. The laser center frequency of the frequency-locked lidar should be locked at the D2a line to obtain the maximum echo signal of Na when the laser linewidth is lower than 2 GHz. If the frequency-unlocked lidar is used for Na observation, when calculating the effective backscattering cross section of Na, the frequency at D2a should be used as the center frequency of the laser. When the measured linewidth of the laser is greater than 2 GHz, there is little difference between the two circumstances.
This work does not consider the different detection technology and the realization difficulty of the lasers with different wavelengths. It is obtained that the detection precision from high to low is Na, Fe at the 372 nm line, Fe at the 386 nm line, Ca+, Ca, K, Ni at the 341 nm line, Fe at the 374 nm line, and Ni at the 337 nm line. The detection precision of Ca+ is higher than that of Ca, and the detection precision of Ni at the 341 nm line is higher than that of the 337 nm line.
This work calculated the resonance fluorescence scattering cross section of different metal particles in atmosphere, and discussed the influence of laser linewidth on the effective scattering cross section. It also compared the detectability of different particles and different resonance lines of the same particle. It is helpful to have a deeper understanding of the detection difficulty of each metal particle. This is of great significance for optimizing and improving the detection efficiency of ground-based lidar. In the future, the metal layer lidar system parameters, such as the laser power, the temporal-spatial resolution, and the telescope diameter, will be designed based on the different detection difficulties of metal particles. We will also try to ascertain how to meet the detection requirements of different metal particles in the most reasonable way.
Author Contributions
Conceptualization, K.W., Z.W. and Y.X. (Yuchang Xun); Data curation, Z.W. and J.J.; Formal analysis, K.W., Y.W., Y.X. (Yuan Xia), Y.X. (Yuchang Xun) and L.D.; Funding acquisition, Z.W.; Investigation, K.W., Y.W. and F.W.; Methodology, K.W., Z.W., Y.W., F.W. and L.D.; Project administration, Z.W.; Resources, Z.W., Y.X. (Yuan Xia), Y.X. (Yuchang Xun), J.J. and L.D.; Software, K.W. and Y.W.; Supervision, Z.W.; Validation, Y.X. (Yuan Xia), Y.X. (Yuchang Xun), F.W., J.J. and L.D.; Visualization, K.W.; Writing—original draft, K.W.; Writing—review and editing, K.W., Z.W., Y.X. (Yuan Xia), Y.X. (Yuchang Xun), F.W. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Project Supported by the Specialized Research Fund for State Key Laboratories.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article. The data used in this study are from published references.
Acknowledgments
The authors thank the reviewers for their instructions and suggestions and the editors for their help. The authors also acknowledge the support of Chinese Meridian Project.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Megie, G. Laser measurements of atmospheric trace constituents. Laser Remote Chem. Anal. 1988, 333, 437–443. [Google Scholar]
- Astafiev, O.; Zagoskin, A.M.; Abdumalikov Jr, A.; Pashkin, Y.A.; Yamamoto, T.; Inomata, K.; Nakamura, Y.; Tsai, J.S. Resonance fluorescence of a single artificial atom. Science 2010, 327, 840–843. [Google Scholar] [CrossRef] [PubMed]
- Gardner, C.S. Sodium resonance fluorescence lidar applications in atmospheric science and astronomy. Proc. IEEE 1989, 77, 408–418. [Google Scholar] [CrossRef]
- She, C.; Yu, J.; Latifi, H.; Bills, R. High-spectral-resolution fluorescence light detection and ranging for mesospheric sodium temperature measurements. Appl. Opt. 1992, 31, 2095–2106. [Google Scholar] [CrossRef] [PubMed]
- von Zahn, U.; Höffner, J. Mesopause temperature profiling by potassium lidar. Geophys. Res. Lett. 1996, 23, 141–144. [Google Scholar] [CrossRef]
- Fuhr, J.; Martin, G.; Wlese, W.; Younger, S. Atomic transition probabilities for iron, cobalt, and nickel (a critical data compilation of allowed lines). J. Phys. Chem. Ref. Data 1981, 10, 305–566. [Google Scholar] [CrossRef]
- Gardner, C.S.; Papen, G.C.; Chu, X.; Pan, W. First lidar observations of middle atmosphere temperatures, Fe densities, and polar mesospheric clouds over the North and South Poles. Geophys. Res. Lett. 2001, 28, 1199–1202. [Google Scholar] [CrossRef]
- Gerding, M.; Daly, S.; Plane, J. Lidar soundings of the mesospheric nickel layer using Ni (3F) and Ni (3D) transitions. Geophys. Res. Lett. 2019, 46, 408–415. [Google Scholar] [CrossRef]
- Wu, F.; Chu, X.; Du, L.; Jiao, J.; Zheng, H.; Xun, Y.; Feng, W.; Plane, J.M.; Yang, G. First Simultaneous Lidar Observations of Thermosphere-Ionosphere Sporadic Ni and Na (TISNi and TISNa) Layers (~105–120 km) Over Beijing (40.42° N, 116.02° E). Geophys. Res. Lett. 2022, 49, e2022GL100397. [Google Scholar] [CrossRef]
- Smith, G.; Raggett, D. Oscillator strengths and collisional damping parameters for lines of neutral calcium. J. Phys. B At. Mol. Phys. 1981, 14, 4015. [Google Scholar] [CrossRef]
- Granier, G.; Jégou, J.-P.; Mégie, G. Resonant lidar detection of Ca and Ca+ in the upper atmosphere. Geophys. Res. Lett. 1985, 12, 655–658. [Google Scholar] [CrossRef]
- Alpers, M.; Höfffner, J.; von Zahn, U. Upper atmosphere Ca and Ca+ at mid-latitudes: First simultaneous and common-volume lidar observations. Geophys. Res. Lett. 1996, 23, 567–570. [Google Scholar] [CrossRef]
- Abreu, V.J. Wind measurements from an orbital platform using a lidar system with incoherent detection: An analysis. Appl. Opt. 1979, 18, 2992–2997. [Google Scholar] [CrossRef] [PubMed]
- Yeh, S.-D.; Browell, E.V. Shuttle lidar resonance fluorescence investigations. 2: Analysis of thermospheric Mg+ measurements. Appl. Opt. 1982, 21, 2373–2380. [Google Scholar] [CrossRef]
- Raizada, S.; Smith, J.; Lautenbach, J.; Aponte, N.; Perillat, P.; Sulzer, M.; Mathews, J. New lidar observations of Ca+ in the mesosphere and lower thermosphere over arecibo. Geophys. Res. Lett. 2020, 47, e2020GL087113. [Google Scholar] [CrossRef]
- Gerding, M.; Alpers, M.; Höffner, J.; Von Zahn, U. Sporadic Ca and Ca+ layers at mid-latitudes: Simultaneous observations and implications for their formation. In Annales Geophysicae; Springer: Berlin/Heidelberg, Germany, 2001; pp. 47–58. [Google Scholar]
- Fujii, T.; Fukuchi, T. Resonance fluorescence lidar for measurements of the middle and upper atmosphere. In Laser Remote Sensing; CRC Press: Boca Raton, FL, USA, 2005; pp. 197–450. [Google Scholar]
- Yi, F.; Zhang, S.; Zeng, H.; He, Y.; Yue, X.; Liu, J.; Lv, H.; Xiong, D. Lidar observations of sporadic Na layers over Wuhan (30.5° N, 114.4° E). Geophys. Res. Lett. 2002, 29, 1–4. [Google Scholar] [CrossRef]
- Bowman, M.; Gibson, A.; Sandford, M. Atmospheric sodium measured by a tuned laser radar. Nature 1969, 221, 456–457. [Google Scholar] [CrossRef]
- Gelbwachs, J.A. Iron Boltzmann factor LIDAR: Proposed new remote-sensing technique for mesospheric temperature. Appl. Opt. 1994, 33, 7151–7156. [Google Scholar] [CrossRef]
- Collins, R.; Li, J.; Martus, C. First lidar observation of the mesospheric nickel layer. Geophys. Res. Lett. 2015, 42, 665–671. [Google Scholar] [CrossRef]
- Kane, T.J.; Gardner, C.S. Lidar observations of the meteoric deposition of mesospheric metals. Science 1993, 259, 1297–1300. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Dulles, VA, USA, 1986. [Google Scholar]
- Bills, R.E.; Gardner, C.S.; She, C.Y. Narrowband lidar technique for sodium temperature and Doppler wind observations of the upper atmosphere. Opt. Eng. 1991, 30, 13–21. [Google Scholar] [CrossRef]
- Wu, F.; Zheng, H.; Yang, Y.; Cheng, X.; Li, F.; Du, L.; Wang, J.; Jiao, J.; Plane, J.M.; Feng, W. Lidar observations of the upper atmospheric nickel layer at Beijing (40° N, 116° E). J. Quant. Spectrosc. Radiat. Transf. 2021, 260, 107468. [Google Scholar] [CrossRef]
- Lautenbach, J.; Höffner, J. Scanning iron temperature lidar for mesopause temperature observation. Appl. Opt. 2004, 43, 4559–4563. [Google Scholar] [CrossRef] [PubMed]
- Hasinoff, S.W. Photon, Poisson Noise. Comput. Vis. A Ref. Guide 2014, 4, 16. [Google Scholar]
- Krueger, D.A.; She, C.-Y.; Yuan, T. Retrieving mesopause temperature and line-of-sight wind from full-diurnal-cycle Na lidar observations. Appl. Opt. 2015, 54, 9469–9489. [Google Scholar] [CrossRef]
- Meyer, V.R. Measurement uncertainty. J. Chromatogr. A 2007, 1158, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Gardner, C.S.; Kane, T.J.; Senft, D.C.; Qian, J.; Papen, G.C. Simultaneous observations of sporadic E, Na, Fe, and Ca+ layers at Urbana, Illinois: Three case studies. J. Geophys. Res. Atmos. 1993, 98, 16865–16873. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).