The 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Multistability, Multiscale Predictability, and Sensitivity in Numerical Models
Abstract
1. Introduction
- The validity of existing analogies and metaphors for butterfly effects.
- The insightful analysis of various Lorenz models reveals the role of monostability with single types of solutions and multistability with attractor co-existence in contributing to the multiscale predictability of weather and climate.
- The development of conceptual, theoretical, and real-world models to reveal fundamental physical processes and multiscale interactions that contribute to our understanding of the butterfly effect on the predictability of weather and climate.
- Innovative machine learning methods that (1) classify chaotic and non-chaotic processes and identify weather and climate systems at various spatial and temporal scales (e.g., sub-seasonal to seasonal time scales) and (2) detect computational chaos and saturation dependence on various types of solutions.
- The impact of tiny perturbations on emergent pattern formation with self-organization (e.g., stripes and rolls), the formation of high-impact weather (e.g., tornados and hurricanes), etc.
2. A Brief Review of Lorenz Models and Butterfly Effects
2.1. A Review of Lorenz Models
2.1.1. Lorenz Models in the 1960s
2.1.2. Lorenz Models between 1970 and 2008
2.1.3. Transitivity, Intransitivity, and Almost Intransitivity
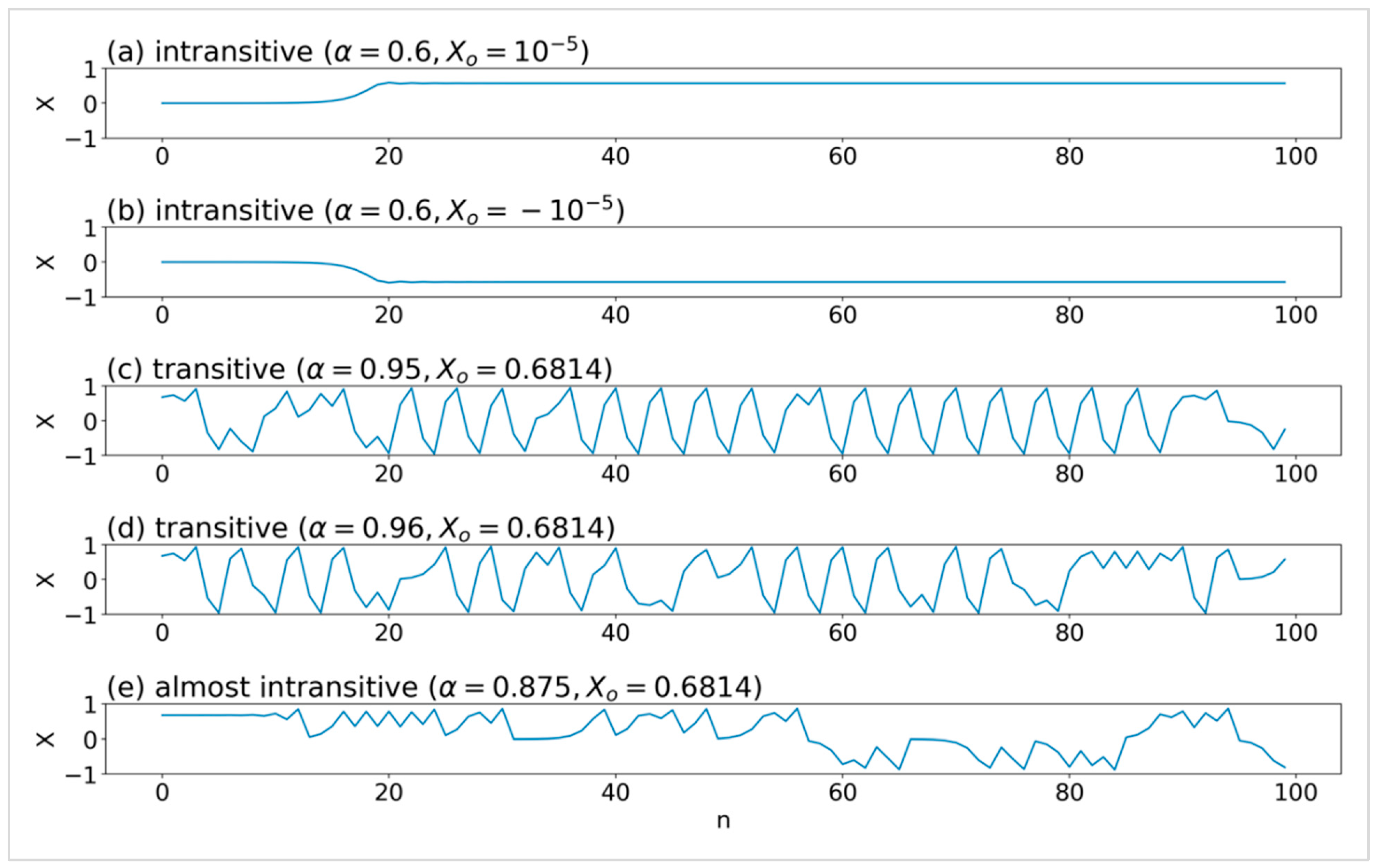
the intransitivity and the final state sensitivity (Grebogi et al. (1983) [82]; Table A1) are related. On the other hand, considering the presence of chaotic solutions within a transitive regime, such as those observed in the Lorenz 1963 model, whether or not “almost intransitivity” could manifest during a specific time period is an intriguing question.“There are two or more sets of long-term statistics, each of which has a greater-than-zero probability of resulting from randomly chosen initial conditions”
2.1.4. Analogues and Recurrence
“A flow with no transient component eventually comes arbitrarily close to assuming a state which it has assumed before, and the history following the latter occurrence remains arbitrarily close to the history following the former.”
“Analogues are two states of the atmosphere that exhibit resemblance to each other. Either state in a pair of analogues can be considered equivalent to the other state plus a small superposed ‘error’.”
2.1.5. Simplifications and Generalizations of Lorenz Models
2.1.6. Error Growth Analysis Using the First- and Second-Order ODEs
2.2. A Review of Butterfly Effects within Lorenz Models
- For want of a nail, the shoe was lost.
- For want of a shoe, the horse was lost.
- For want of a horse, the rider was lost.
- For want of a rider, the battle was lost.
- For want of a battle, the kingdom was lost.
- And all for the want of a horseshoe nail.
2.3. A Review of Lorenz’s Perspective on the Predictability Limit
- A.
- The Lorenz 1963 model qualitatively revealed the essence of finite predictability within a chaotic system, such as the atmosphere. However, the Lorenz 1963 model did not determine a precise limit for atmospheric predictability.
- B.
- In the 1960s, using real-world models, the two-week predictability limit was originally estimated based on a doubling time of 5 days. Since then, this finding has been documented in Charney et al. (1966) [143] and has become a consensus.
3. Overview of the Published Papers
3.1. (A) Butterfly Effects and Sensitivities
3.2. (B) Atmospheric Dynamics and the Application of Theoretical Models
3.3. (C) Predictability and Predictions
3.4. (D) Computational and Machine Learning Methods
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Lorenz (1960/1962) Model and the Lorenz (1996/2006) Model
Appendix B. The Logistic Map and Logistic ODE
Appendix C. Definitions of Selected Concepts in the Special Issue
| Name | Definitions | Recommendations |
|---|---|---|
| First kind of attractor co-existence | The co-existence of chaotic and steady-state solutions. | [7,8,9,160] |
| Second kind of attractor co-existence | The co-existence of nonlinear oscillatory and steady-state solutions. | [7,8,9] |
| Analogues | Analogues are two states of the atmosphere that exhibit resemblance to each other. | [21] |
| Attractor | The smallest attracting point set that, itself, cannot be decomposed into two or more subsets with distinct basins of attraction. | [8] |
| Butterfly effect (BE), general | The phenomenon in that a small alteration in the state of a dynamical system will cause subsequent states to differ greatly from the states that would have followed without the alteration. | [4] |
| BE of the first kind (BE1) | The sensitive dependence on initial conditions (SDICs). | [1,4,139] |
| BE of the second kind (BE2) | The capability of a small disturbance to create an organized circulation at large distances. | [2,4,139] |
| BE of the third kind (BE3) |
| [139,140,157] |
| BE in Saiki and Yorke (2023) | Instability in high-dimensional linear systems. | [155] |
| Chaos | Bounded aperiodic orbits exhibit a sensitive dependence on ICs. | [4,159] |
| Final state sensitivity | Nearby orbits settle to one of multiple attractors for a finite but arbitrarily long time. | [82] |
| Intransitivity | A specific type of solution lasts forever. | [52,72] |
| Monostability | The appearance of single-type solutions. | [159] |
| Multistability | A system with multistability contains more than one bounded attractor that only depends on ICs. | [159] |
| Quasi-periodicity | A quasi-periodic solution consists of two or more incommensurate frequencies, the ratios of which are irrational. | [91] |
| Recurrence | This refers to a trajectory returning to the vicinity of its previous location. | [92,93] |
| Sensitive dependence | The property characterizing an orbit if most other orbits that pass close to it at some point do not remain close to it as time advances. | [4] |
| Ventilation coefficient parameterization | A parameter used in numerical models of atmospheric convection to represent the effect of environmental wind on convective updrafts. | [156] |
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lorenz, E.N. Predictability: Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? In Proceedings of the 139th Meeting of AAAS Section on Environmental Sciences, New Approaches to Global Weather, GARP, AAAS, Cambridge, MA, USA, 29 December 1972; 5p. [Google Scholar]
- Gleick, J. Chaos: Making a New Science; Penguin: New York, NY, USA, 1987; 360p. [Google Scholar]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993; 227p. [Google Scholar]
- The Nobel Committee for Physics. Scientific Background on the Nobel Prize in Physics 2021 “For Groundbreaking Contributions to Our Understanding of Complex Physical Systems”; The Royal Swedish Academy of Sciences: Stockholm, Sweden, 2021. [Google Scholar]
- Fischer, K.H.; Hertz, J.A. Spin Glasses; Cambridge University Press: Cambridge, UK, 1993; ISBN 9780521447775. [Google Scholar]
- Shen, B.-W. Aggregated Negative Feedback in a Generalized Lorenz Model. Int. J. Bifurc. Chaos 2019, 29, 1950037. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is weather chaotic? Coexistence of chaos and order within a generalized Lorenz model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R.; Reyes, T.A. Is Weather Chaotic? Coexisting Chaotic and Non-Chaotic Attractors within Lorenz Models. In The 13th Chaos International Conference CHAOS 2020; Springer Proceedings in Complexity; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Shen, B.-W. Attractor Coexistence, Butterfly Effects, and Chaos Theory (ABC): A Review of Lorenz Models and a Generalized Lorenz Model. In Proceedings of the 16th Chaos International Conference CHAOS 2023, Heraklion, Greece, 13–16 June 2023; submitted. [Google Scholar]
- Chen, G.-R. Butterfly Effect and Chaos. 2020. Available online: https://www.ee.cityu.edu.hk/~gchen/pdf/Lorenz_T.pdf (accessed on 1 July 2023). (In Chinese).
- Lorenz, E.N. Maximum simplification of the dynamic equations. Tellus 1960, 12, 243–254. [Google Scholar] [CrossRef]
- Lewis, J.; Lakshmivarahan, S.; Dhall, S. Dynamic Data Assimilation: A Least Squares Approach; Cambridge University Press: Cambridge, UK, 2006; 654p. [Google Scholar]
- Lorenz, E.N. The statistical prediction of solutions of dynamic equations. In Proceedings of the International Symposium on Numerical Weather Prediction, Tokyo, Japan, 7–13 November 1962; pp. 629–635. [Google Scholar]
- Saltzman, B. Finite Amplitude Free Convection as an Initial Value Problem-I. J. Atmos. Sci. 1962, 19, 329–341. [Google Scholar] [CrossRef]
- Lakshmivarahan, S.; Lewis, J.M.; Hu, J. Saltzman’s Model: Complete Characterization of Solution Properties. J. Atmos. Sci. 2019, 76, 1587–1608. [Google Scholar] [CrossRef]
- Lewis, J.M.; Lakshmivarahan, S. Role of the Observability Gramian in Parameter Estimation: Application to Nonchaotic and Chaotic Systems via the Forward Sensitivity Method. Atmosphere 2022, 13, 1647. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Li, T.-Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Lorenz, E.N. The problem of deducing the climate from the governing equations. Tellus 1964, 16, 1–11. [Google Scholar] [CrossRef]
- Lorenz, E.N. Atmospheric predictability as revealed by naturally occurring analogues. J. Atmos. Sci. 1969, 26, 636–646. [Google Scholar] [CrossRef]
- Lorenz, E.N. Low-order models of atmospheric circulations. J. Meteor. Soc. Jpn. 1982, 60, 255–267. [Google Scholar] [CrossRef]
- Lorenz, E.N. Energy and numerical weather prediction. Tellus 1960, 12, 364–373. [Google Scholar] [CrossRef]
- Lorenz, E.N. Simplified dynamic equations applied to the rotating-basin experiments. J. Atmos. Sci. 1962, 19, 39–51. [Google Scholar] [CrossRef]
- Lorenz, E.N. The mechanics of vacillation. J. Atmos. Sci. 1963, 20, 448–464. [Google Scholar] [CrossRef]
- Lorenz, E.N. A study of the predictability of a 28-variable atmospheric model. Tellus 1965, 17, 321–333. [Google Scholar] [CrossRef]
- Lorenz, E.N. Atmospheric predictability experiments with a large numerical model. Tellus 1982, 34, 505–513. [Google Scholar] [CrossRef]
- Lorenz, E. The predictability of hydrodynamic flow. Trans. N. Y. Acad. Sci. 1963, 25, 409–432. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Lewis, J. Roots of ensemble forecasting. Mon. Weather Rev. 2005, 133, 1865–1885. [Google Scholar] [CrossRef]
- Nese, J.M. Quantifying local predictability in phase space. Phys. D Nonlinear Phenom. 1989, 35, 237–250. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Brown, R.; Kennel, M.B. Local Lyapunov exponents computed from observed data. J. Nonlinear Sci. 1992, 2, 343–365. [Google Scholar] [CrossRef]
- Eckhardt, B.; Yao, D. Local Lyapunov exponents in chaotic systems. Phys. D 1993, 65, 100–108. [Google Scholar] [CrossRef]
- Krishnamurthy, V. A predictability study of Lorenz’s 28-variable model as a dynamical system. J. Atmos. Sci. 1993, 50, 2215–2229. [Google Scholar] [CrossRef]
- Szunyogh, I.; Kalnay, E.; Toth, Z. A comparison of Lyapunov and optimal vectors in a low-resolution GCM. Tellus 1997, 49A, 200–227. [Google Scholar] [CrossRef]
- Yoden, S. Atmospheric Predictability. J. Meteorol. Soc. Jpn. 2007, 85B, 77–102. [Google Scholar] [CrossRef]
- Oseledec, V.I. A multiplicative ergodic theorem. Ljapunov characteristic numbers for dynamical systems. Trans. Mosc. Math. Sci. 1968, 19, 197–231. [Google Scholar]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Quart. J. Roy. Meteor. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Buizza, R.; Leutbecher, M.; Isaksen, L. Potential use of an ensemble of analyses in the ECMWF Ensemble Prediction System. Quart. J. Roy. Meteor. Soc. 2008, 134, 2051–2066. [Google Scholar] [CrossRef]
- Cui, J.; Shen, B.-W. A Kernel Principal Component Analysis of Coexisting Attractors within a Generalized Lorenz Model. Chaos Solitons Fractals 2021, 146, 110865. [Google Scholar] [CrossRef]
- Lorenz, E.N. Empirical Orthogonal Functions and Statistical Weather Prediction; Scientific Report No. 1, Statistical Forecasting Project; Air Force Research Laboratories, Office of Aerospace Research, USAF: Bedford, MA, USA, 1956. [Google Scholar]
- Pedlosky, J. Finite-amplitude baroclinic waves with small dissipation. J. Atmos. Sci. 1971, 28, 587–597. [Google Scholar] [CrossRef]
- Pedlosky, J. Limit cycles and unstable baroclinic waves. J. Atmos. Sci. 1972, 29, 53–63. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer: New York, NY, USA, 1987; p. 710. [Google Scholar]
- Pedlosky, J.; Frenzen, C. Chaotic and periodic behavior of finite-amplitude baroclinic waves. J. Atmos. Sci. 1980, 37, 1177–1196. [Google Scholar] [CrossRef]
- Shen, B.-W. Solitary Waves, Homoclinic Orbits, and Nonlinear Oscillations within the non-dissipative Lorenz Model, the inviscid Pedlosky Model, and the KdV Equation. In The 13th Chaos International Conference CHAOS 2020; Springer Proceedings in Complexity; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Leith, C.E. Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 1971, 28, 145–161. [Google Scholar] [CrossRef]
- Leith, C.E.; Kraichnan, R.H. Predictability of turbulent flows. J. Atmos. Sci. 1972, 29, 1041–1058. [Google Scholar] [CrossRef]
- Lorenz, E.N. Investigating the predictability of turbulent motion. Statistical Models and Turbulence. In Proceedings of the Symposium Held at the University of California, San Diego, CA, USA, 15–21 July 1971; Springer: Berlin/Heidelberg, Germany, 1972; pp. 195–204. [Google Scholar]
- Lorenz, E.N. Low-order models representing realizations of turbulence. J. Fluid Mech. 1972, 55, 545–563. [Google Scholar] [CrossRef]
- Lorenz, E.N. Nondeterministic theories of climatic change. Quat. Res. 1976, 6, 495–506. [Google Scholar] [CrossRef]
- Lorenz, E.N. Attractor sets and quasi-geostrophic equilibrium. J. Atmos. Sci. 1980, 37, 1685–1699. [Google Scholar] [CrossRef]
- Lorenz, E.N. On the existence of a slow manifold. J. Atmos. Sci. 1986, 43, 1547–1557. [Google Scholar] [CrossRef]
- Lorenz, E.N.; Krishnamurthy, V. On the nonexistence of a slow manifold. J. Atmos. Sci. 1987, 44, 29402950. [Google Scholar] [CrossRef]
- Lorenz, E.N. The slow manifold. What is it? J. Atmos. Sci. 1992, 49, 24492451. [Google Scholar] [CrossRef]
- McWilliams, J.C. A perspective on the legacy of Edward Lorenz. Earth Space Sci. 2019, 6, 336–350. [Google Scholar] [CrossRef]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Applied Mathematical Sciences; Springer: New York, NY, USA, 1982; 269p. [Google Scholar]
- Shen, B.-W. On periodic solutions in the non-dissipative Lorenz model: The role of the nonlinear feedback loop. Tellus A 2018, 70, 1471912. [Google Scholar] [CrossRef]
- Shen, B.-W. Homoclinic Orbits and Solitary Waves within the non-dissipative Lorenz Model and KdV Equation. Int. J. Bifurc. Chaos 2020, 30, 15. [Google Scholar] [CrossRef]
- Lorenz, E.N. Irregularity: A fundamental property of the atmosphere. Crafoord Prize Lecture, presented at the Royal Swedish Academy of Sciences, Stockholm, September 28, 1983. Tellus 1984, 36A, 98–110. [Google Scholar] [CrossRef]
- Lorenz, E.N. Can chaos and intransitivity lead to interannual variability? Tellus 1990, 42A, 378–389. [Google Scholar] [CrossRef]
- Pielke, R.A.; Zeng, X. Long-Term Variability of Climate. J. Atmos. Sci. 1994, 51, 155–159. [Google Scholar] [CrossRef]
- Van Veen, L.; Opsteegh, T.; Verhulst, F. Active and passive ocean regimes in a low-order climate model. Tellus A 2001, 53, 616–627. [Google Scholar] [CrossRef]
- Van Veen, L. Baroclinic Flow and the Lorenz-84 Model. Int. J. Bifurc. Chaos 2003, 13, 2117–2139. [Google Scholar] [CrossRef]
- Lorenz, E.N. Chaos, spontaneous climatic variations and detection of the greenhouse effect. In Greenhouse-Gas-Induced Climatic Change: A Critical Appraisal of Simulations and Observations; Schlesinger, M.E., Ed.; Elsevier Science Publishers B. V.: Amsterdam, The Netherlands, 1991; pp. 445–453. [Google Scholar]
- Lorenz, E.N. Predictability—A problem partly solved. In Proceedings of the Seminar on Predictability, Shinfield Park, Reading, UK, 4–8 September 1995; ECMWF: Reading, UK, 1996; Volume I. [Google Scholar]
- Lorenz, E.N. Predictabilitya problem partly solved. In Predictability of Weather and Climate; Palmer, T., Hagedorn, R., Eds.; Cambridge University Press: Cambridge, UK, 2006; pp. 40–58. [Google Scholar]
- Lorenz, E.N. Designing Chaotic Models. J. Atmos. Sci. 2005, 62, 1574–1587. [Google Scholar] [CrossRef]
- Lorenz, E.N. Regimes in simple systems. J. Atmos. Sci. 2006, 63, 2056–2073. [Google Scholar] [CrossRef][Green Version]
- Lorenz, E.N. Compound windows of the Hénon map. Phys. D 2008, 237, 1689–1704. [Google Scholar] [CrossRef]
- Lorenz, E.N. Climatic determinism. Meteor. Monographs, Amer. Meteor. Soc. 1968, 8, 1–3. [Google Scholar]
- Lorenz, E.N. Climatic Predictability; GARP Publications Series; GARP: Jersey City, NJ, USA, 1975; pp. 132–136. [Google Scholar]
- Lorenz, E.N. Some aspects of atmospheric predictability. European Centre for Medium Range Weather Forecasts, Seminar 1981. In Proceedings of the Problems and Prospects in Long and Medium Range Weather Forecasting, Reading, UK, 14–18 September 1982; pp. 1–20. [Google Scholar]
- Lorenz, E.N. Climate Is What You Expect; NCAR: Boulder, CO, USA, 1997; unpublished work; Available online: https://eapsweb.mit.edu/sites/default/files/Climate_expect.pdf (accessed on 1 July 2023).
- Holmes, P. A Nonlinear Oscillator with a Strange Attractor. Phil. Trans. R. Soc. 1979, A191, 419. [Google Scholar]
- May, R. The cubic map in theory and practice. Nature 1984, 311, 13–14. [Google Scholar] [CrossRef]
- De Oliveira, J.A.; Papesso, E.R.; Leonel, E.D. Relaxation to Fixed Points in the Logistic and Cubic Maps: Analytical and Numerical Investigation. Entropy 2013, 15, 4310–4318. [Google Scholar] [CrossRef]
- Grebogi, C.; Ott, E.; Yorke, J.A. Chaotic attractors in crisis. Phys. Rev. Lett. 1982, 48, 1507–1510. [Google Scholar] [CrossRef]
- Grebogi, C.; Ott, E.; Yorke, J.A. Crises, sudden changes in chaotic attractors, and transient chaos. Phys. D 1983, 7, 181–200. [Google Scholar] [CrossRef]
- Hirsch, M.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos, 3rd ed.; Academic Press: Waltham, MA, USA, 2013; 432p. [Google Scholar]
- Grebogi, C.; McDonald, S.W.; Ott, E.; Yorke, J.A. Final state sensitivity: An obstruction to predictability. Phys. Lett. A 1983, 99, 415–418. [Google Scholar] [CrossRef]
- Charney, J.G.; DeVore, J.G. Multiple flow equilibria in the atmosphere and blocking. J. Atmos. Sci. 1979, 36, 1205–1216. [Google Scholar] [CrossRef]
- Chen, Z.-M.; Xiong, X. Equilibrium states of the Charney-DeVore quasi-geostrophic equation in mid-latitude atmosphere. J. Math. Anal. Appl. 2016, 444, 1403–1416. [Google Scholar] [CrossRef]
- Faranda, D.; Masato, G.; Moloney, N.; Sato, Y.; Daviaud, F.; Dubrulle, B.; Yiou, P. The switching between zonal and blocked mid-latitude atmospheric circulation: A dynamical system perspective. Clim. Dyn. 2016, 47, 1587–1599. [Google Scholar] [CrossRef]
- Dorrington, J.; Palmer, T. On the interaction of stochastic forcing and regime dynamics. Nonlinear Process. Geophys. 2023, 30, 49–62. [Google Scholar] [CrossRef]
- Wikipedia. El Niño–Southern Oscillation—Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/El_Ni%C3%B1o%E2%80%93Southern_Oscillation (accessed on 1 July 2023).
- Wallace, J.M.; Battisti, D.S.; Thompson, D.W.J.; Hartmann, D.L. The Atmospheric General Circulation, 1st ed.; Cambridge University Press: Cambridge, UK, 2023; 456p. [Google Scholar]
- Van den Dool, H.M. A new look at weather forecasting trough analogues. Mon. Wea. Rev. 1989, 117, 2230–2247. [Google Scholar] [CrossRef]
- Van den Dool, H.M. Searching for analogues, how long must we wait? Tellus A 1994, 46, 314–324. [Google Scholar] [CrossRef]
- Faghih-Naini, S.; Shen, B.-W. Quasi-periodic orbits in the five-dimensional non-dissipative Lorenz model: The role of the extended nonlinear feedback loop. Int. J. Bifurc. Chaos 2018, 28, 1850072. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; p. 437. [Google Scholar]
- Reyes, T.; Shen, B.-W. A Recurrence Analysis of Chaotic and Non-Chaotic Solutions within a Generalized Nine-Dimensional Lorenz Model. Chaos Solitons Fractals 2019, 125, 1–12. [Google Scholar] [CrossRef]
- Reyes, T.; Shen, B.-W. A Recurrence Analysis of Multiple African Easterly Waves during Summer 2006. In Current Topics in Tropical Cyclone Research; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Lorenz, E.N. On the existence of extended range predictability. J. Appl. Meteor. 1973, 12, 543–546. [Google Scholar] [CrossRef]
- Lorenz, E.N. Three approaches to atmospheric predictability. Bull. Am. Meteor. Soc. 1969, 50, 345–351. [Google Scholar]
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Poincaré, H. Science et Méthode, Flammarion, 1908 ed.; English Translated; Maitland, F., Ed.; Thomas Nelson and Sons: London, UK, 1914. [Google Scholar]
- Curry, J.H. Generalized Lorenz systems. Commun. Math. Phys. 1978, 60, 193–204. [Google Scholar] [CrossRef]
- Curry, J.H.; Herring, J.R.; Loncaric, J.; Orszag, S.A. Order and disorder in two- and three-dimensional Benard convection. J. Fluid Mech. 1984, 147, 1–38. [Google Scholar] [CrossRef]
- Howard, L.N.; Krishnamurti, R.K. Large-scale flow in turbulent convection: A mathematical model. J. Fluid Mech. 1986, 170, 385–410. [Google Scholar] [CrossRef]
- Hermiz, K.B.; Guzdar, P.N.; Finn, J.M. Improved low-order model for shear flow driven by Rayleigh–Benard convection. Phys. Rev. E 1995, 51, 325–331. [Google Scholar] [CrossRef] [PubMed]
- Thiffeault, J.-L.; Horton, W. Energy-conserving truncations for convection with shear flow. Phys. Fluids 1996, 8, 1715–1719. [Google Scholar] [CrossRef]
- Musielak, Z.E.; Musielak, D.E.; Kennamer, K.S. The onset of chaos in nonlinear dynamical systems determined with a new fractal technique. Fractals 2005, 13, 19–31. [Google Scholar] [CrossRef]
- Roy, D.; Musielak, Z.E. Generalized Lorenz models and their routes to chaos. I. Energy-conserving vertical mode truncations. Chaos Solit. Fract. 2007, 32, 1038–1052. [Google Scholar] [CrossRef]
- Roy, D.; Musielak, Z.E. Generalized Lorenz models and their routes to chaos. II. Energyconserving horizontal mode truncations. Chaos Solit. Fract. 2007, 31, 747–756. [Google Scholar] [CrossRef]
- Roy, D.; Musielak, Z.E. Generalized Lorenz models and their routes to chaos. III. Energyconserving horizontal and vertical mode truncations. Chaos Solit. Fract. 2007, 33, 1064–1070. [Google Scholar] [CrossRef]
- Moon, S.; Han, B.-S.; Park, J.; Seo, J.M.; Baik, J.-J. Periodicity and chaos of high-order Lorenz systems. Int. J. Bifurc. Chaos 2017, 27, 1750176. [Google Scholar] [CrossRef]
- Paxson, W.; Shen, B.-W. A KdV-SIR Equation and Its Analytical Solutions for Solitary Epidemic Waves. Int. J. Bifurc. Chaos 2022, 32, 2250199. [Google Scholar] [CrossRef]
- Saiki, Y.; Sander, E.; Yorke, J. Generalized Lorenz equations on a three-sphere. Eur. Phys. J. Spec. Top. 2017, 226, 1751–1764. [Google Scholar] [CrossRef]
- Shen, B.-W. On the Predictability of 30-Day Global Mesoscale Simulations of African Easterly Waves during Summer 2006: A View with the Generalized Lorenz Model. Geosciences 2019, 9, 281. [Google Scholar] [CrossRef]
- Lawler, E.; Thye, S.; Yoon, J. Order on the Edge of Chaos Social Psychology and the Problem of Social Order; Cambridge University Press: Cambridge, UK, 2015; ISBN 9781107433977. [Google Scholar]
- Crutchfield, J.P. Between order and chaos. Nat. Phys. 2011, 8, 17–24. [Google Scholar] [CrossRef]
- Melby, P.; Kaidel, J.; Weber, N.; Hübler, A. Adaptation to the edge of chaos in the self-adjusting logistic map. Phys. Rev. Lett. 2000, 84, 5991–5993. [Google Scholar] [CrossRef]
- Palmer, T.N. Edward Norton Lorenz. 23 May 1917–16 April 2008. Biogr. Mem. Fellows R. Soc. 2009, 55, 139–155. [Google Scholar] [CrossRef]
- Emanuel, K. Edward Norton Lorenz (1917–2008); National Academy of Sciences: Washington, DC, USA, 2011; p. 4. [Google Scholar]
- Feldman, D. Chaos and Fractals: An Elementary Introduction; Oxford University Press: Oxford, UK, 2012; 408p. [Google Scholar]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 5, 346–349. [Google Scholar] [CrossRef]
- Nese, J.M.; Dutton, J.A.; Wells, R. Calculated attractor dimensions for low-order spectral models. J. Atmos. Sci. 1987, 44, 1950–1972. [Google Scholar] [CrossRef]
- Ruelle, D. Chaotic Evolution and Strange Attractors. In Lezioni Lincee; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar] [CrossRef]
- Zeng, X.; Pielke, R.A.; Eykholt, R. Estimate of the fractal dimension and predictability of the atmosphere. J. Atmos. Sci. 1992, 49, 649–659. [Google Scholar] [CrossRef]
- Kaplan, J.L.; Yorke, J.A. Chaotic behavior of multidimensional difference equations. In Functional Differential Equations and the Approximations of Fixed Points; Lecture Notes in Mathematics; Peitgen, H.O., Walther, H.O., Eds.; Springer: New York, NY, USA, 1979; Volume 730, pp. 228–237. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Shen, B.-W. Nonlinear feedback in a five-dimensional Lorenz model. J. Atmos. Sci. 2014, 71, 1701–1723. [Google Scholar] [CrossRef]
- Shen, B.-W. Nonlinear feedback in a six-dimensional Lorenz Model. Impact of an additional heating term. Nonlin. Process. Geophys. 2015, 22, 749–764. [Google Scholar] [CrossRef]
- Shen, B.-W. Hierarchical scale dependence associated with the extension of the nonlinear feedback loop in a seven-dimensional Lorenz model. Nonlin. Process. Geophys. 2016, 23, 189–203. [Google Scholar] [CrossRef]
- Shen, B.-W. On an extension of the nonlinear feedback loop in a nine-dimensional Lorenz model. Chaotic Model. Simul. (CMSIM) 2017, 2, 147–157. [Google Scholar]
- Nicolis, C. Probabilistic aspects of error growth in atmospheric dynamics. Quart. J. Roy. Meteorol. Soc. 1992, 118, 553–568. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, Y.Q.; Magnusson, L.; Buizza, R.; Lin, S.-J.; Chen, J.-H.; Emanuel, K. What is the predictability limit of midlatitude weather? J. Atmos. Sci. 2019, 76, 1077–1091. [Google Scholar] [CrossRef]
- Alligood, K.; Saucer, T.; Yorke, J. Chaos An Introduction to Dynamical Systems; Springer: New York, NY, USA, 1996; 603p. [Google Scholar]
- Meiss, J.D. Differential Dynamical Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; 412p. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westpress View: Boulder, CO, USA, 2015; 513p. [Google Scholar]
- Paxson, W.; Shen, B.-W. A KdV-SIR Equation and Its Analytical Solutions: An Application for COVID-19 Data Analysis. Chaos Solitons Fractals 2023, 173, 113610. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.; McKendrink, A. A contribution to the mathematical theory of epidemics. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Liu, H.-L.; Sassi, F.; Garcia, R.R. Error growth in a whole atmosphere climate model. J. Atmos. Sci. 2009, 66, 173–186. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Wu, M.-L. African Easterly Waves in 30-day High-resolution Global Simulations: A Case Study during the 2006 NAMMA Period. Geophys. Res. Lett. 2010, 37, L18803. [Google Scholar] [CrossRef]
- Shen, B.-W.; Atlas, R.; Oreale, O.; Lin, S.-J.; Chern, J.-D.; Chang, J.; Henze, C.; Li, J.-L. Hurricane Forecasts with a Global Mesoscale-Resolving Model: Preliminary Results with Hurricane Katrina (2005). Geophys. Res. Lett. 2006, 33, L13813. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Atlas, R.; Lee, T.; Reale, O.; Chern, J.-D.; Lin, S.-J.; Chang, J.; Henze, C.; Li, J.-L. Hurricane Forecasts with a Global Mesoscale-resolving Model on the NASA Columbia Supercomputer. In Proceedings of the AGU 2006 Fall Meeting, San Francisco, CA, USA, 11–16 December 2006. [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Atlas, R. Three Kinds of Butterfly Effects within Lorenz Models. Encyclopedia 2022, 2, 1250–1259. [Google Scholar] [CrossRef]
- Palmer, T.N.; Doring, A.; Seregin, G. The real butterfly effect. Nonlinearity 2014, 27, R123–R141. [Google Scholar] [CrossRef]
- Drazin, P.G. Nonlinear Systems; Cambridge University Press: Cambridge, UK, 1992; p. 333. [Google Scholar]
- Lorenz, E.N. The butterfly effect. In Premio Felice Pietro Chisesi E Caterina Tomassoni Award Lecture; University of Rome: Rome, Italy, 2008. [Google Scholar]
- Charney, J.G.; Fleagle, R.G.; Lally, V.E.; Riehl, H.; Wark, D.Q. The feasibility of a global observation and analysis experiment. Bull. Am. Meteor. Soc. 1966, 47, 200–220. [Google Scholar]
- GARP. GARP topics. Bull. Am. Meteor. Soc. 1969, 50, 136–141. [Google Scholar]
- Lorenz, E.N. How much better can weather prediction become? MIT Technol. Rev. 1969, 39–49. Available online: https://eapsweb.mit.edu/sites/default/files/How_Much_Better_Can_Weather_Prediction_1969.pdf (accessed on 1 July 2023).
- Lorenz, E.N. Studies of atmospheric predictability. In [Part 1] [Part 2] [Part 3] [Part 4] Final Report, February, Statistical Forecasting Project; Air Force Research Laboratories, Office of Aerospace Research, USAF: Bedford, MA, USA, 1969; 145p, Available online: https://eapsweb.mit.edu/about/history/publications/lorenz (accessed on 1 July 2023).
- Lorenz, E.N. Estimates of atmospheric predictability at medium range. In Predictability of Fluid Motions; Holloway, G., West, B., Eds.; American Institute of Physics: New York, NY, USA, 1984; pp. 133–139. [Google Scholar]
- Lorenz, E.N. The growth of errors in prediction. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Società Italiana di Fisica: Bologna, Italy, 1985; pp. 243–265. [Google Scholar]
- Smagorinsky, J. Problems and promises of deterministic extended range forecasting. Bull. Amer. Meteor. Soc. 1969, 50, 286–312. [Google Scholar] [CrossRef]
- Lighthill, J. The recently recognized failure of predictability in Newtonian dynamics. Proc. R. Soc. Lond. A 1986, 407, 35–50. [Google Scholar]
- Rotunno, R.; Snyder, C. A generalization of Lorenz’s model for the predictability of flows with many scales of motion. J. Atmos. Sci. 2008, 65, 1063–1076. [Google Scholar] [CrossRef]
- Durran, D.; Gingrich, M. Tmospheric predictability: Why atmospheric butterflies are not of practical importance. J. Atmos. Sci. 2014, 71, 2476–2478. [Google Scholar] [CrossRef]
- Reeves, R.W. Edward Lorenz Revisiting the Limits of Predictability and Their Implications: An Interview from 2007. BAMS 2014, 95, 681–687. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Zeng, X. Lorenz’s View on the Predictability Limit. Encyclopedia 2023, 3, 887–899. [Google Scholar] [CrossRef]
- Saiki, Y.; Yorke, J.A. Can the Flap of a Butterfly’s Wings Shift a Tornado into Texas—Without Chaos? Atmosphere 2023, 14, 821. [Google Scholar] [CrossRef]
- Chou, Y.-L.; Wang, P.-K. An Expanded Sensitivity Study of Simulated Storm Life Span to Ventilation Parameterization in a Cloud Resolving Model. Atmosphere 2023, 14, 720. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. One Saddle Point and Two Types of Sensitivities Within the Lorenz 1963 and 1969 Models. Atmosphere 2022, 13, 753. [Google Scholar] [CrossRef]
- Zeng, X. Atmospheric Instability and Its Associated Oscillations in the Tropics. Atmosphere 2023, 14, 433. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Kesarkar, A.; Zeng, X.; Atlas, R. The Dual Nature of Chaos and Order in the Atmosphere. Atmosphere 2022, 13, 1892. [Google Scholar] [CrossRef]
- Yorke, J.; Yorke, E. Metastable chaos: The transition to sustained chaotic behavior in the Lorenz model. J. Stat. Phys. 1979, 21, 263–277. [Google Scholar] [CrossRef]
- Anthes, R.A. Predictability and Predictions. Atmosphere 2022, 13, 1292. [Google Scholar] [CrossRef]
- Wang, C.-C.; Tsai, C.-H.; Jou, B.J.-D.; David, S.J. Time-Lagged Ensemble Quantitative Precipitation Forecasts for Three Landfalling Typhoons in the Philippines Using the CReSS Model, Part I: Description and Verification against Rain-Gauge Observations. Atmosphere 2022, 13, 1193. [Google Scholar] [CrossRef]
- Tseng, J.C.-H. An ISOMAP Analysis of Sea Surface Temperature for the Classification and Detection of El Niño & La Niña Events. Atmosphere 2022, 13, 919. [Google Scholar] [CrossRef]
- Pielke, R., Sr. The Real Butterfly Effect. 2008. Available online: https://pielkeclimatesci.wordpress.com/2008/04/29/the-real-butterfly-effect/ (accessed on 9 July 2023).
- Anthes, R. Turning the Tables on Chaos: Is the Atmosphere More Predictable than We Assume? UCAR Magazine, Spring/Summer, 6 May 2011. Available online: https://news.ucar.edu/4505/turning-tables-chaos-atmosphere-more-predictable-we-assume (accessed on 9 July 2023).
- Zeng, X.; Pielke, R.A., Sr.; Eykholt, R. Chaos theory and its applications to the atmosphere. Bull. Am. Meteorol. Soc. 1993, 74, 631–644. [Google Scholar] [CrossRef]

| Year | 1960 | 1960/62 | 1963 | 1964 | 1965 | 1969 | 1969 |
|---|---|---|---|---|---|---|---|
| Equations | 3 ODEs, | 12 ODEs | 3 ODEs, | Logistic map | 28 variables | Logistic ODE | 21 2nd-order ODEs, |
| Origins | PDE; vorticity Eq | PDEs; a 2-layer, QG model | PDEs; convection | PDEs; a 2-layer, QG model | PDE; vorticity Eq | ||
| Features of Solutions | oscillatory solutions with elliptic functions | irregular fluctuations | chaos | steady, periodic, non-periodic | irregular solutions | error growth and saturation | ‘turbulence’ * |
| Year | 1972 | 1976 | 1980 | 1984 | 1986 | 1996/2006 | 2005 | 2008 |
|---|---|---|---|---|---|---|---|---|
| Equations | turbulence models | cubic map | low-order PE or QG (9 or 3) ODEs | 3 ODEs | 5 or 3 ODEs | N ODEs | N ODEs | Henon map |
| Origins | PDE based | PDE based | Not PDE based | PDE based, (the 1980 model) | Not PDE based | Not PDE based | ||
| Features of Solutions | turbulence | transitivity | (modified) shallow water Eqs. | general circulation, transitivity | slow manifolds (w elliptic functions) | chaos | chaos | chaos |
| The Lorenz (1986) Model | The Limiting Equations | The Non-Dissipative Lorenz Model | |
|---|---|---|---|
| References | Lorenz (1986) | Sparrow(1982) | Shen (2018) |
| Equations | |||
| Solutions | nonlinear periodic orbits | three types of solutions, including two types of periodic solutions and homoclinic orbits | |
| Remarks | See Shen (2018) for details | See Shen (2018) for details |
| Quasi-geostrophic (QG) System | 1962-8v, 1960/1962-12v, 1963-14v, 1965-28v |
| Conservative Vorticity Equation | 1960, 1969 |
| Rayleigh Benard Convection Equations | 1963 (& Generalized Lorenz Models) |
| Shallow Water Equations | 1980, 1986 |
| No PDEs | 1984, 1996, 2005 |
| (Discrete) Maps | 1964 (Logistic), 1976 (Cubic), 2008 (Henon) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. The 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere 2023, 14, 1279. https://doi.org/10.3390/atmos14081279
Shen B-W, Pielke RA Sr., Zeng X. The 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere. 2023; 14(8):1279. https://doi.org/10.3390/atmos14081279
Chicago/Turabian StyleShen, Bo-Wen, Roger A. Pielke, Sr., and Xubin Zeng. 2023. "The 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Multistability, Multiscale Predictability, and Sensitivity in Numerical Models" Atmosphere 14, no. 8: 1279. https://doi.org/10.3390/atmos14081279
APA StyleShen, B.-W., Pielke, R. A., Sr., & Zeng, X. (2023). The 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere, 14(8), 1279. https://doi.org/10.3390/atmos14081279








