Application of Functional Principal Component Analysis in the Spatiotemporal Land-Use Regression Modeling of PM_2.5

Abstract

Functional data are generally curves indexed over a time domain, and land-use regression (LUR) is a promising spatial technique for generating high-resolution spatial estimation of retrospective long-term air pollutants. We developed a methodology for the novel functional land-use regression (FLUR) model, which provides high-resolution spatial and temporal estimations of retrospective pollutants. Long-term fine particulate matter (PM_2.5) in the megacity of Tehran, Iran, was used as the practical example. The hourly measured PM_2.5 concentrations were averaged for each hour and in each air monitoring station. Penalized smoothing was employed to construct the smooth PM_2.5 diurnal curve using averaged hourly data in each of the 30 stations. Functional principal component analysis (FPCA) was used to extract FPCA scores from pollutant curves, and LUR models were fitted on FPCA scores. The mean of all PM_2.5 diurnal curves had a maximum of 39.58 µg/m³ at 00:26 a.m. and a minimum of 29.27 µg/m³ at 3:57 p.m. The FPCA explained about 99.5% of variations in the observed diurnal curves across the city using just three components. The evaluation of spatially predicted long-term PM_2.5 diurnal curves every 15 min provided a series of 96 high-resolution exposure maps. The presented methodology and results could benefit future environmental epidemiological studies.

1. Introduction

Air pollution is one of the most challenging health problems worldwide. In particular, airborne fine particulate matter (PM_2.5) is recognized as the main cause of nine million deaths at the global level [1]. Long-term exposure to a higher concentration of PM_2.5 is known to be associated with higher mortality from an all-natural cause of death, cardiovascular disease, respiratory disease, lung cancer, diabetes, dementia, asthma, and acute lower-respiratory infections such as pneumonia and bronchiolitis [2]. Moreover, it is associated with the onset of several diseases, most importantly, lung cancer and leukemia [3,4].

Scientific communities around the world have focused on studying the problem of air pollution from different aspects. Researchers considered modeling various pollutants to predict (or estimate) retrospective, real-time, or prospective concentrations as each of these goals has various implications. They used a number of statistical frameworks to spatially, temporally, or spatiotemporally model pollutant concentrations based on their goals, with different time and spatial scales for local, national, and continental study areas. Moreover, researchers tried to recognize and use the best set of predicting information based on their available resources. Examples of such studies are the spatiotemporal real-time prediction of hourly PM_2.5 concentration to build a novel short-distance route finder using the back-propagation neural network as the modeling technique [5]; the modeling of several air pollutants to build an early warning system based on the technique of fuzzy time series, where the goal was to temporally predict prospective air-pollutant concentrations [6]; the spatial prediction of the annual average of several air pollutants to be used in epidemiological studies of long-term exposure to air pollutants, where the goal was to spatially estimate retrospective concentrations of air pollutants in the residential addresses of citizens using data from around 30 fixed monitoring stations by applying the ordinary land-use regression (LUR) model [7,8]; the spatiotemporal modeling of the daily averages of PM_2.5 concentrations using a set of land-use predictors that provided high-resolution daily-exposure estimation maps for epidemiological studies of long-term air pollutant health effects [9]; and the spatial modeling of the annually averaged diurnal curve of nitrogen dioxides using an extension of the technique of ordinary kriging for functional data, which provided retrospective long-term estimation which is suitable for subsequent environmental epidemiological studies [10].

Land-use regression has been used extensively in environmental epidemiology to provide individual-level spatial estimation of long-term retrospective exposure data. Generally, it uses the averaged concentrations of an air pollutant over one or several years at a number of monitoring stations, uses land-use variables at the geo-location of monitoring stations as the predictors of the model and then uses the trained model to spatially predict retrospective long-term concentrations at all geo-points in the study area by employing high-resolution input maps of the model predictors [11,12,13,14].

To date, many LUR studies published focus on the spatial modeling of annual or seasonal means of pollutants [7,8,15,16] or the spatiotemporal modeling of a series of a pollutant’s averages at discrete time points, such as days [9] or hours [17]. To the best of our knowledge, none of the published LUR studies have modeled the long-term diurnal curves of a pollutant where the datum unit is a curve and not a scalar value. The only similar study that was recently published modeled the long-term diurnal curves of nitrogen dioxides using the functional extension of the ordinary kriging technique. Despite its novelty in terms of modeling continuous diurnal pollutant curves, it suffered from a lack of providing any land-use predictor and relied on kriging, which resulted in low-resolution and smoothed long-term-exposure estimation maps [10].

Functional data analysis (FDA) is a branch of modern statistics that deals with so-called functional data. Functional data are generally curves or surfaces that derive from the continuous measurements of a variable over time. However, functional data are usually observed at consecutive discrete time points, in most cases due to the design of measuring instruments, so a smoothing method is generally used to recover continuous functional data [18,19]. Spatiotemporal models for functional data have been recently proposed by [20] based on the EM algorithm, extending [21].

Epidemiological studies of the long-term effects of air pollution usually rely on LUR studies where high-resolution annual spatial estimations of a pollutant are extracted from LUR maps at the geographic location of participants’ residential addresses [22,23,24,25,26,27]. However, this exposure assessment has an important limitation: a person is usually exposed to the pollutant’s concentrations at several geographic locations (home, work, school, etc.) and at different periods during a typical day. Therefore, using estimated exposures at merely the geolocation of each person’s residential address could result in exposure misclassification. Even using a ratio of the estimated daily average of a pollutant concentration to the time spent by a person in the geographic location of his/her home and workplace maybe not be justifiable because, as highlighted in a recently published study, the pattern of changes in air-pollutant concentrations during the daily timeframe may vary in the study area [10]. Hence, we adopted the framework of the LUR model and extended it to FLUR to provide high-resolution spatial estimation for the annually averaged diurnal curves of PM_2.5 and not just the estimation of spatial annual averages without considering intra-day changes. The FLUR model is a spatiotemporal model with a continuous time dimension and the ability to produce a high-resolution spatial estimation of retrospective long-term pollutants. This model as an extension of the LUR model can foster epidemiological studies of long-term air pollutants.

The remainder of the paper is structured as follows: In Section 2, we provide a description of the study area and data, including an explanation of the ordinary LUR model, the basis expansion of functional data, the functional land-use regression model, and validation using an alternative model. Section 3 presents descriptive mean and standard deviation curves for long-term diurnal PM_2.5 curves in the study area, along with the estimated functional principal component curves and their corresponding estimated scores. We also discuss the results of LUR modeling of functional principal component scores, the estimated curves of the FLUR model coefficients, the result of comparison of the FLUR model and the alternative spatiotemporal model, as well as the estimated series of high-resolution prediction maps. In Section 4, we discuss the results, and Section 5 provides the conclusion.

2. Materials and Methods

In this section, we first describe the study area, response data, and predictors’ data. Then, we introduce the ordinary LUR model, followed by the basis expansion of functional data. Finally, we introduce the functional land-use regression model and its estimation procedure.

2.1. Description of the Study Area and Data

The study area is the megacity of Tehran, Iran, with 9 million urban residents and a daytime population of >10 million inhabitants due to diurnal migration. Tehran’s populated area covers approximately 613 km². The Alborz Mountains are located in the north of Tehran and a desert is located to the south. The elevation in Tehran is approximately 1800 m above sea level in the north and approximately 1000 m in the south. The prevailing winds blow from the west and north. The weather is predominantly sunny, and the mean cloud cover is approximately 30% [7,8,9]. The average temperature of Tehran in 2015 was 19 °C and the annual total precipitation was 205 mm [9].

Hourly data of Tehran’s airborne PM_2.5, which were measured at 30 fixed air quality-monitoring stations in 2015, were acquired from the Tehran Air Quality Control Company and the Iranian Department of Environment. These two agencies maintain the monitoring stations and regularly check the validation of data and calibrate measuring devices. The extent of the megacity of Tehran and the locations of monitoring stations are depicted in Figure 1. We calculated the mean of PM_2.5 data in the year 2015 at each monitoring station for each hour from 0 to 23 as the raw response data to be used in the modeling.

We employed the same set of predictors in a recent study of a PM_2.5 spatiotemporal daily LUR model in Tehran in 2015 to predict the spatial dimension of our model [9]. The predictors were the natural logarithm of distance to the nearest road (m), total population density in buffer radii of 2750 m (persons per km²), arid or undeveloped land-use area in buffer radii of 200 m (m²), and the residual of recognizable land-use areas in buffer radii of 400 m (m²), all of which were provided as fine-scale raster maps with a resolution of 5 m.

2.2. Ordinary LUR Model

An ordinary LUR model, in general, employs long-term averages of a measured air pollutant from a number of monitoring stations as the response of a regression model and a rich set of suitable high-resolution geographical information as the model predictors to spatially estimates the retrospective long-term averages of the air pollutant in all the geo-points in the study area.

The training or fitting model of the ordinary LUR model is as follows:

$$y_i={\alpha }_0+{{\displaystyle \sum }}_{j=1}^p{\alpha }_j{x}_{i,j}+{\epsilon }_i; i=1, \dots , n,$$

(1)

where $y_i$ is the long-term average of the measured pollutant concentrations at monitoring station $i$ and $x_{i,j}$ is the value of corresponding geographical predictor $j$ at the geo-location of that monitoring station, and ${\alpha }_j ; j=0,\dots ,p$ are coefficients to be estimated.

Hence, the resulting prediction model of the ordinary LUR is as follows:

$$\widehat{y_{\mathit{s}}}=\widehat{{\alpha }_0}+{{\displaystyle \sum }}_{j=1}^p\widehat{{\alpha }_j}{x}_{\mathit{s},j}; \mathit{s}\in S^2 ,$$

(2)

where $\widehat{y_{\mathit{s}}}$ is the estimate of the long-term average of pollutant concentrations at the geo-location $\mathit{s}$, $x_{\mathit{s},j}$ is the value of the corresponding geographical predictor $j$ at the same geo-location $\mathit{s}$, and $S^2$ is the study area. In addition, $\widehat{{\alpha }_j};j=0,\dots ,p$ are fixed values resulting from fitting the train model of Equation (1).

2.3. Basis Expansion of Functional Data

The basic philosophy of functional data analysis is to consider successive measurements of the quantity of interest, e.g., the concentration of an air pollutant, as realizations of an underlying continuous function are defined over that time domain [28]. Therefore, it is essential to first convert the pair of time and the corresponding concentration observed at that time, $\left(t_{ih},y_{ih}\right); h=0,\dots ,23$, to a smooth functional observation: $y_i\left(t\right); t \in \left(0,T\right]$, where $T=24$ is the diurnal period of our study. This was accomplished using smoothing techniques at each monitoring station ($i=1, \dots , n$).

The set of Fourier basis functions was employed for the smoothing and representation of functional observations. The Fourier basis expansion expresses functional data using the below formula:

$$y_i\left(t\right)=c_0+c_1\sin \left(\omega t\right)+c_2\cos \left(\omega t\right)+\dots +c_{k-1}\sin \left(\frac{k\omega t}{2}\right)+c_k\cos \left(\frac{k\omega t}{2}\right); i=1, \dots , n,$$

(3)

where $\omega =2\pi /T$ and the number of the used basis functions was k = 23, as this number provides a saturated model corresponding to the hourly data required for subsequent functional principal component analysis.

2.4. Functional Principal Component Analysis

Functional principal component analysis (FPCA) is an extension of ordinary principal component analysis. Although the aim of both methods is dimension reduction, their input data and the type of their estimated factors are different. The ordinary principal component analysis employs several variables as input scalar data to estimate a limited number of variables acting as underlying factors. The FPCA input data are functional data such as diurnal pollutant curves at different stations and the output to be estimated is a limited number of functional data, such as curves with the same domain of input curves, acting as underlying factors [18]. Assume that $y_i\left(t\right)$ is a functional datum, e.g., an observed diurnal PM_2.5 curve; the FPCA estimates a limited number of empirical orthogonal functions with the same time domain, of which approximates the functional datum as a linear expression of those estimated empirical basis functions. Therefore, each functional datum can be represented as follows:

$$y_i\left(t\right)=\overline{y}\left(t\right)+{{\displaystyle \sum }}_{r=1}^m\widetilde{c_{ir}}{\tilde{B}}_r\left(t\right); i=1, \dots , n,$$

(4)

where $\overline{y}\left(t\right)$ is the mean function which is the average of all functional data across monitoring stations; ${\tilde{B}}_r\left(t\right);r=1,\dots ,m$ are the estimated principal component basis functions that are independent on the monitoring station $i$; and $\widetilde{c_{ir}}$ are the corresponding functional principal component scores (FPCS) specific to station $i$. Details about FPCA can be found elsewhere [18].

2.5. Functional Land-Use Regression Model

We aim to develop functional fitting and prediction LUR models analogous to Equations (1) and (2) that can model and predict the diurnal curves of the pollutant instead of its diurnal scalar averages.

The fitting LUR model for the functional response of $y\left(t\right)$ is

$$y_i\left(t\right)={\alpha }_0\left(t\right)+{\displaystyle \sum }_{j=1}^p{\alpha }_j\left(t\right)x_{ij}+{\mathsf{\epsilon }}_i\left(t\right); i=1,\dots , n$$

(5)

Hence, the resulting prediction LUR model for the functional response of $y\left(t\right)$ is as follows:

$$\widehat{y_s\left(t\right)}=\widehat{{\alpha }_0\left(t\right)}+{\displaystyle \sum }_{j=1}^p\widehat{{\alpha }_j\left(t\right)}{x}_{sj}; \mathit{s}\in S^2$$

(6)

To estimate the functional coefficients of $\widehat{{\alpha }_j\left(t\right)} ; j=0,\dots ,p$ where $t \in \left(0,t\right]$, we need to fit the below regression models for scalar responses of $c_{ir}$ where $r$ is considered fixed in each model:

$$\widetilde{c_{ir}}={\alpha }_{0r}+{\displaystyle \sum }_{j=1}^p{\alpha }_{jr}{x}_{ij}+{ϵ}_{ir}; i=1, \dots , n; r=1, \dots , m$$

(7)

Therefore, $m$ independent multiple regression models with the same set of Equation (5) predictors are fitted. The response of each regression model is $c_{ir} ; i=1, \dots , n$ for a fixed $r=1, \dots , m$ corresponding to a vector of FPCS values resulting from Equation (4).

Then, by substituting Equation (7) into Equation (4), we obtain the below equation:

$$y_i\left(t\right)=\overline{y}\left(t\right)+{\displaystyle \sum }_{r=1}^m\left\{\left({\alpha }_{0r}+{\displaystyle \sum }_{j=1}^p{\alpha }_{jr}{x}_{ij}+{ϵ}_{ir}\right){\tilde{B}}_r\left(t\right)\right\}; i=1,\dots , n$$

(8)

The arrangement of Equation (6) results in the below equation, which resembles Equation (5):

$$y_i\left(t\right)=\left\{\overline{y}\left(t\right)+{\displaystyle \sum }_{r=1}^m\left\{{\alpha }_{0r}{\tilde{B}}_r\left(t\right)\right\}\right\}+{\displaystyle \sum }_{j=1}^p\left\{{\displaystyle \sum }_{r=1}^m\left\{{\alpha }_{jr}{\tilde{B}}_r\left(t\right)\right\}\right\}{x}_{ij}+{\displaystyle \sum }_{r=1}^m\left\{{ϵ}_{ir}{\tilde{B}}_r\left(t\right)\right\}; i=1,\dots , n$$

(9)

Comparing Equations (5) and (9) shows that:

$${\alpha }_0\left(t\right)=\overline{y}\left(t\right)+{\displaystyle \sum }_{r=1}^m\left\{{\alpha }_{0r}{\tilde{B}}_r\left(t\right)\right\}; {\alpha }_j\left(t\right)={\displaystyle \sum }_{r=1}^m\left\{{\alpha }_{jr}{\tilde{B}}_r\left(t\right)\right\}; {\epsilon }_i\left(t\right)={\displaystyle \sum }_{r=1}^m\left\{{ϵ}_{ir}{\tilde{B}}_r\left(t\right)\right\}$$

(10)

Hence, the estimation of $\widehat{{\alpha }_j\left(t\right)}; j=0,\dots ,p$ in Equation (6) is as follows:

$$\widehat{{\alpha }_0\left(t\right)}=\overline{y}\left(t\right)+{{\displaystyle \sum }}_{r=1}^m\left\{\widehat{{\alpha }_{0r}}{\tilde{B}}_r\left(t\right)\right\}; \widehat{{\alpha }_j\left(t\right)}={{\displaystyle \sum }}_{r=1}^m\left\{\widehat{{\alpha }_{jr}}{\tilde{B}}_r\left(t\right)\right\}; j=1,\dots ,p,$$

(11)

where $t \in \left(0,T\right]$ and ${\tilde{B}}_r\left(t\right) ; r=1,\dots ,m$ are the estimated functional principal component basis functions in Equation (4); $\widehat{{\alpha }_{jr}}$ is the estimated scalar coefficient resulting from fitting multiple regression models of Equation (7).

Alternatively, if the goal is to only spatially predict the resulting estimation maps at each time point and not the estimation of the functional regression coefficients curves of ${\alpha }_j\left(t\right);j=1,\dots ,p$, Equation (9) can be re-arranged to achieve a more parsimonious equation that relies on storing $m$ high-resolution, calculated, inter-mean spatial raster maps instead of $p$ high-resolution maps of predictors. This could facilitate the delivery of the estimated exposure values because the number of adequate functional principal components could be less than the number of geographic predictors of the FLUR model.

$$\widehat{y_s\left(t\right)}=\left\{\overline{y}\left(t\right)+{\displaystyle \sum }_{r=1}^m\left\{\widehat{{\alpha }_{0r}}{\tilde{B}}_r\left(t\right)\right\}\right\}+{\displaystyle \sum }_{r=1}^m\left\{{\displaystyle \sum }_{j=1}^p\left\{\widehat{{\alpha }_{jr}}{x}_s\right\}\right\}{\tilde{B}}_r\left(t\right); \mathit{s}\in S^2$$

(12)

Hence, Equation (12) can be represented using the simple formula below:

$$\widehat{y_s\left(t\right)}=\widehat{{\alpha }_0\left(t\right)}+{\displaystyle \sum }_{r=1}^m\widetilde{z_{rs}}{\tilde{B}}_r\left(t\right); \mathit{s}\in S^2 and \widetilde{z_{rs}}=\left\{{\displaystyle \sum }_{j=1}^p\left\{\widehat{{\alpha }_{jr}}{x}_s\right\}\right\};r=1,\dots ,m$$

(13)

Please note that $\widehat{{\alpha }_0\left(t\right)}$ and ${\tilde{B}}_r\left(t\right);r=1,\dots ,m$ are just simple time series where, even with the temporal resolution of a minute during the day, each would be a series of 1440 real numbers and $\widetilde{z_{rs}};r=1,\dots ,m;\mathit{s}\in S^2$ for each fixed $r$ is a calculated, high-resolution, inter-mean spatial raster map. The number of these inter-mean spatial maps are the same as the number of used functional principal components in the model.

Furthermore, please note that multiplying each principal component curve of ${\tilde{B}}_r\left(t\right)$, which is purely temporal to the corresponding calculated inter-mean map of $\widetilde{z_{rs}}; \mathit{s}\in S^2$ which is purely spatial, and summing the results of all these interaction terms in Equation (13), enables the FLUR model to be highly flexible in terms of accounting for complicated space and time interactions in the spatiotemporal modeling of the air pollutant.

Finally, the estimated long-term PM_2.5 maps were plotted for two sets of desirable time points over the study area. The selected time points were: (a) the start of each hour from 0 to 23 where the series of 24 estimation maps are presented as a figure, and (b) the start of each 15 min in the diurnal time domain where the series of 96 high-resolution estimation maps is presented as a Supplementary Video that highlights changes in the spatial pattern of long-term PM_2.5 concentrations in Tehran over the day.

All statistical analyses and mappings were performed in the freely available “R” statistical environment and its accompanying “fda” and “raster” packages [29,30,31].

2.6. Validation Using an Alternative Model

While the ordinary LUR model is a spatial model, the proposed FLUR model is a spatiotemporal model that provides spatial estimation at each arbitrary time point during the diurnal period. To check the validity of the proposed FLUR model, we used the D-STEM (Distributed Space–Time Expectation Maximization) spatiotemporal model [32] as an alternative modeling approach that provides spatial estimation at each hour in the diurnal period.

The equation of the D-STEM spatiotemporal model is as follows:

$$y\left(\mathit{s},t\right)={\alpha }_0+{\displaystyle \sum }_{j=1}^p{\alpha }_j{x}_{j\left(\mathit{s}\right)}+\rho \omega \left(\mathit{s},t\right)+z\left(t\right)+\epsilon \left(\mathit{s},t\right); \mathit{s}\in S^2$$

(14)

where ${\alpha }_j;j=0,\dots ,p$ are fixed-effect coefficients of the model, $x_{j\left(\mathit{s}\right)}$ are the same set of spatial predictors of the FLUR model, $\omega \left(\mathit{s},t\right)$ is a latent spatiotemporal variable with an exponential auto-correlation structure, $\rho$ is a scaling parameter, $z\left(t\right)$ is a latent temporal variable with a Markovian dynamic structure, and $\epsilon \left(\mathit{s},t\right)$ is the measurement error term.

3. Results

Figure 2 shows the mean ± 2SD of the PM_2.5 long-term diurnal curves of 30 monitoring stations in Tehran in 2015. The smoothed mean profile starts from 39.48 µg/m³ at 00:00, then shows a slight increase to 39.58 µg/m³ at 00:26 a.m., which is the maximum value of the mean profile. Then, it decreases to 34.5 µg/m³ at 06:45 a.m. and increases to 35.22 µg/m³ at 08:56 a.m. Thereafter, it decreases to 29.27 µg/m³ at 03:57 p.m., which is the minimum value of the mean profile; subsequently, the mean profile continuously increases until its end at 11:59 p.m., which is 39.47 µg/m³.

Figure 3 shows the estimated three main functional principal component curves of long-term PM_2.5 diurnal curves across 30 monitoring stations in Tehran, where 92.5%, 5%, and 2% of variations in the observed curves are explained by the first, second, and third functional principal component curves, respectively. These curves are ${\tilde{B}}_r\left(t\right);r=1,2,3$ in Equation (4).

Table 1. The estimated three main functional principal component scores (FPCS) of PM_2.5 diurnal curves for the 30 monitoring stations in Tehran.

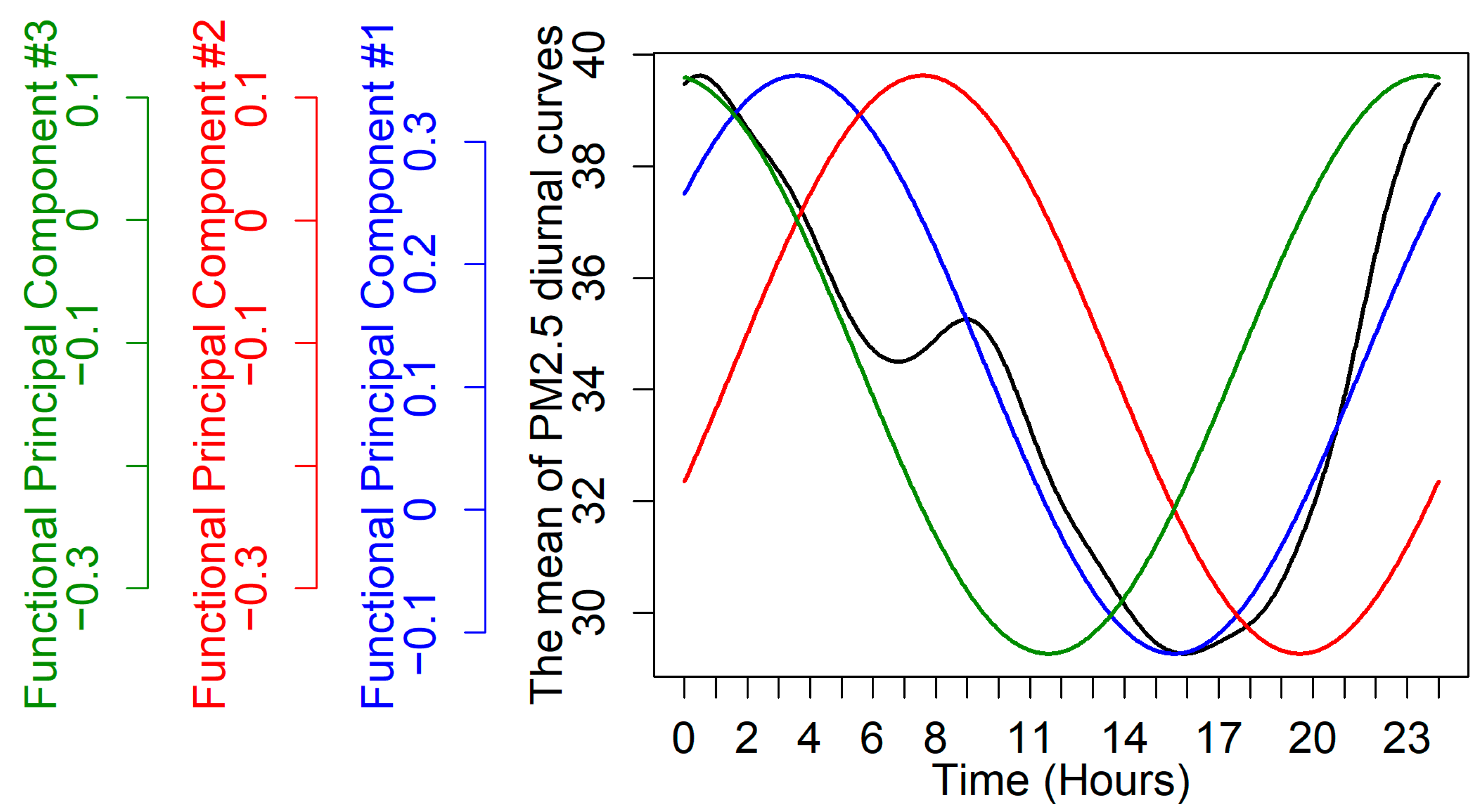
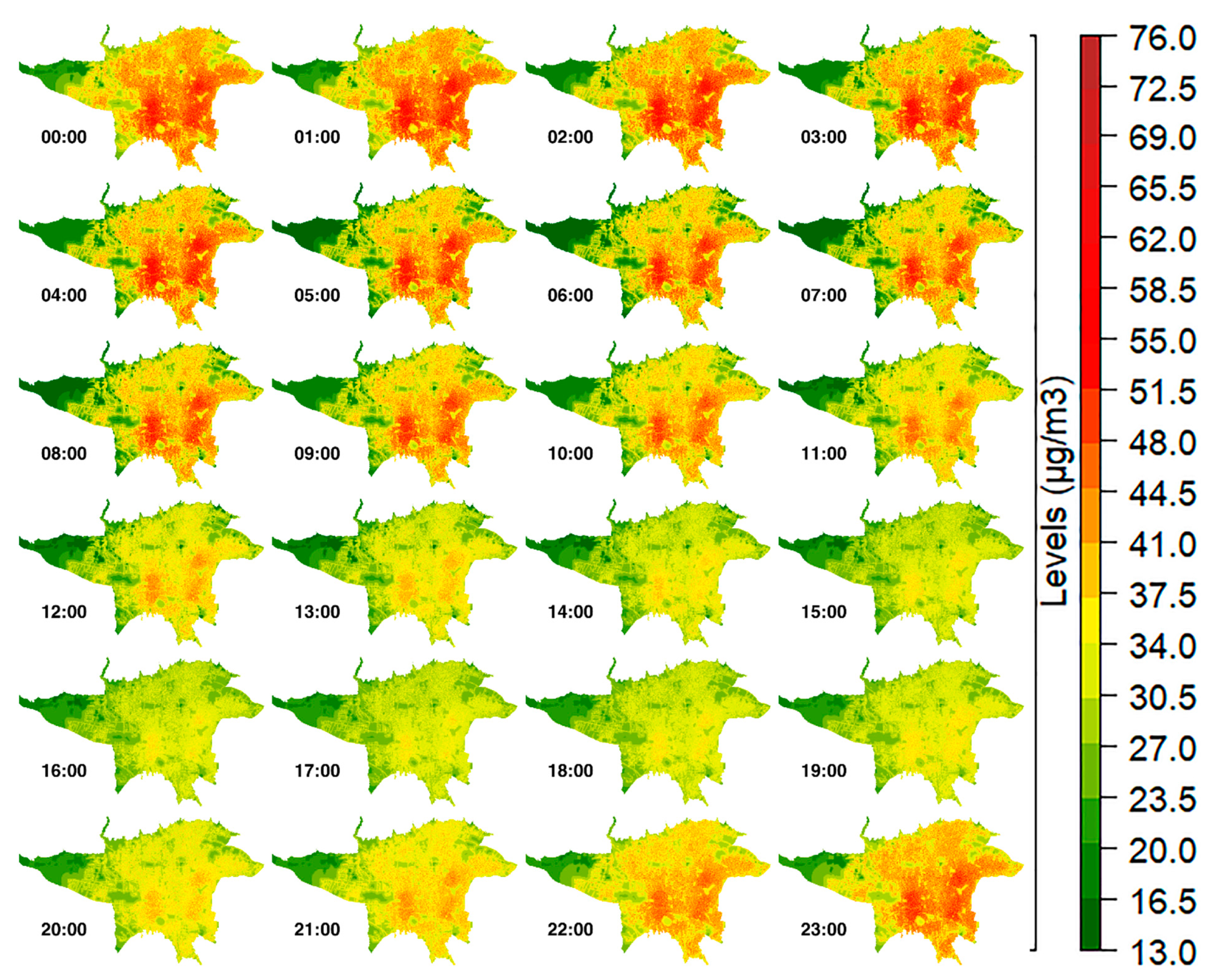
Station ID	Station Name	Latitude (N)	Longitude (E)	FPCS #1	FPCS #2	FPCS #3
1	Region 11	35.672980	51.389730	−5.83	1.57	7.25
2	Golbarg	35.731030	51.506130	−34.19	2.18	−0.06
3	Elmo Sanat	35.739811	51.511431	16.87	−4.74	−0.56
4	Tehran university	35.703356	51.397764	21.12	1.37	−3.73
5	Cheshme	35.752714	51.262824	−7.61	−12.57	4.76
6	Shokufe park	35.685736	51.450761	17.16	−3.61	6.50
7	Region 15	35.641076	51.479964	−12.29	13.55	−7.97
8	Setad	35.727080	51.431200	−0.01	−3.98	2.67
9	Atisaz	35.797161	51.522739	7.31	−22.75	3.48
10	Aghdasyeh	35.795870	51.484140	−27.26	−3.31	4.14
11	Beheshti	35.803375	51.395137	−36.75	−6.69	−1.69
12	Pasdaran	35.789664	51.473361	−40.13	17.48	2.53
13	Farmandary Rey	35.593005	51.427697	83.90	7.73	−8.86
14	Region 4	35.741820	51.506430	−27.95	−5.18	−6.73
15	Sharif University	35.702270	51.350940	24.79	−2.77	−7.59
16	Shad Abad	35.670050	51.297350	−15.74	3.15	−1.54
17	Poonak	35.762300	51.331680	−52.98	1.3	−2.46
18	Rose park	35.739890	51.267891	−17.40	−10.39	2.01
19	Salamat park	35.648900	51.356078	34.71	5.11	−5.78
20	Shahre Rey	35.603630	51.425710	7.14	6.94	−4.53
21	Ghaem park	35.658217	51.328228	71.56	13.01	15.79
22	Region 2	35.777089	51.368175	−43.33	−0.50	−3.51
23	Darous	35.769994	51.454160	25.66	−8.84	−4.47
24	Tarbiyat Modares university	35.717510	51.381570	−43.73	6.14	−1.08
25	Region 19	35.635210	51.362519	0.62	4.18	9.64
26	Razi park	35.670158	51.389386	79.87	−7.21	−2.85
27	Region 10	35.697480	51.358031	−7.97	4.92	2.82
28	Region 16	35.644584	51.397657	−9.95	5.75	2.96
29	Masoudiyeh	35.630030	51.499020	0.55	−1.81	−0.82
30	Tehransar	35.712960	51.214490	−8.15	−0.04	−0.33

shows the three vectors of FPCS values corresponding to the three functional principal component curves that are presented in Figure 3. These values are $\widetilde{c_{ir}};i=1,\dots ,30;r=1,2,3$ in Equation (4), which are station-specific scalar values. The difference between the station-specific curves and the overall mean curve of all the stations is the result of multiplying these values by the corresponding functional principal component curves of Figure 3.

Table 2. Estimated regression coefficients for the three main functional principal component scores (FPCS) as the responses of ordinary regression models.

Regression Intercept and Predictors	Estimated Coefficients for the Main FPCS
	FPCS #1	FPCS #2	FPCS #3
0. Intercept	2.908 × 101	−6.643 × 10−2	5.868 × 10−1
1. Residual of recognizable land-use areas in buffer radii of 400 m (m2)	−1.495 × 10−3	4.702 × 10−5	−3.206 × 10−5
2. Natural logarithm of distance to the nearest road (m)	−1.313 × 101	−1.202 × 100	−3.579 × 10−1
3. Total population density in buffer radii of 2750 m (persons per km2)	1.622 × 10−3	3.484 × 10−4	2.405 × 10−5
4. Arid or undeveloped land-use area in buffer radii of 200 m (m2)	−4.563 × 10−4	−1.220 × 10−4	7.129 × 10−5

shows the estimated coefficients resulting from fitting each column of the FPCS values of Table 1 to the set of four geographical predictors. The presented coefficients are the results of three independent fitting LUR models of Equation (7). These estimated scalar coefficients are needed in Equations (11) and (13) to then provide functional coefficients curves and spatiotemporal estimation of the retrospective long-term air pollutant, respectively.

Figure 4 depicts the estimated functional regression coefficients of the FLUR model. These estimated curves are $\widehat{{\alpha }_j\left(t\right)};j=0,1,2,3$ in Equation (11). The estimated functional coefficients show the time-varying effects of purely spatial predictors on the diurnal curve of long-term PM_2.5 concentrations. As expected, the estimated functional intercept curve in Figure 4 mimics the pattern of the diurnal mean curve in Figure 2. The estimated curves of functional coefficients number 1, 2, and 4 are negative, which correspond to predictors number 1, 2, and 4 in Table 2. However, the sign of the estimated curve of the third functional coefficient is positive. This figure emphasizes that the effect of land-use predictors on long-term particulate matter concentration is not constant throughout the day.

The black vertical axis meters the black curve which shows the estimated functional intercept of the model, and the blue axis meters the blue curve which shows the estimated first functional coefficient that corresponds to the predictor of recognizable land-use areas in buffer radii of 400 m (m²). The brown vertical axis meters the brown curve which shows the estimated second functional coefficient that corresponds to the predictor of the natural logarithm of distance to the nearest road (m). The red axis meters the red curve which shows the estimated third functional coefficient that corresponds to the predictor of total population density in buffer radii of 2750 m (persons per km²). The green vertical axis meters the green curve which shows the estimated fourth functional coefficient that corresponds to the predictor of arid or undeveloped land-use area in buffer radii of 200 m (m²).

The result of comparing the prediction of the FLUR model and the alternative D-STEM model is presented in

Table 3. Comparison of the introduced FLUR model and the alternative D-STEM model from different aspects (spatial, temporal, and spatiotemporal) using the R-Squared and RMSE metrics *.

Dimensions	FLUR Model Assessment		D-STEM Model Assessment
	R-Squared	RMSE	R-Squared	RMSE
Spatial	32.75%	5.6580	33.62%	5.6578
Temporal	99.99%	0.0041	99.44%	0.6727
Spatiotemporal	43.35%	6.0820	42.20%	6.1895

* A higher value of R-Squared and a lower value of RMSE means better prediction.

. Although the prediction error of the FLUR model in the spatial aspect was a bit more than the D-STEM model (5.6580 vs. 5.6578), the prediction error of the temporal aspect of the FLUR model was substantially less than the D-STEM model (0.0041 vs. 0.6727), and the prediction error of the spatiotemporal aspect of the FLUR model was also less than the D-STEM model (6.0820 vs. 6.1895).

Figure 5 displays the spatial estimation of a long-term retrospective PM_2.5 concentration with a resolution of 5 m for hours from 0 to 23, provided by the FLUR model. These maps result from the evaluation of Equation (13) on the start time point of each hour. Furthermore, the estimated diurnal curves of long-term PM_2.5 were evaluated on initial time points of every 15 min during the diurnal timeframe, which is presented in Video S1. It highlights that the level and spatial pattern of PM_2.5 long-term concentrations change with the hours of the day.

As shown in Figure 5 and in the Supplementary Video of estimation maps, the trend of changes in PM_2.5 concentrations was not constant in the diurnal period. For example, the west of Tehran had its cleanest conditions at the approximate hours of 5 a.m. to 8 a.m., while it seems the rest of Tehran had their less polluted conditions around the hours of 3 p.m. to 7 p.m. This result highlighted one of the important strengths of the FLUR model: it accounts for complicated space and time interactions in spatiotemporal estimations of the air pollutant.

4. Discussion

In this study, we estimated spatially resolved long-term retrospective diurnal curves of PM_2.5 in the megacity of Tehran. This is analogous to the spatiotemporal estimation of long-term retrospective PM_2.5 concentrations over a very fine temporal resolution in the daily timeframe.

The high concentrations of PM_2.5 concentrations at monitoring stations and at the estimated maps in Tehran are in line with previous studies. The estimated PM_2.5 concentrations were higher in the south, center, and east regions, while being lower in the west and north of Tehran—this is primarily related to population and traffic density [33].

The sign of estimated regression coefficients in the FLUR model presented in Figure 4 is the same as the sign of a corresponding, published, non-functional LUR model for PM_2.5 daily averages in Tehran [9]. Hence, the impact of the predictors’ effects on PM_2.5 concentrations during the day is the same as the whole day average that was previously published. Thanks to this functional data analysis extension of the ordinary LUR model, we can see that the effects of these geographical predictors are not fixed during the day. The fact that time-invariant geographical predictors have time-variant effects on PM_2.5 concentrations during the day is interesting, but interpreting the reasons behind these increases and decreases in the intensity of effects during the day is not simple. Possibly, diurnal variations in emissions of the sources of the predictors are representative (e.g., traffic for the road variable) and diurnal variations in meteorology (e.g., mixing height) play a role.

The trend of PM_2.5 concentrations changes during the day at the monitoring stations and at the estimated maps, as depicted in Figure 2 and Figure 5; they are tied with traffic regulations that restrict the commuting of heavy supply trucks in the megacity of Tehran to the hours between 10 p.m. and 6 a.m. [34,35]. A similar pattern for long-term diurnal changes in nitrogen dioxides was reported in a recently published paper, where the authors employed a functional extension of ordinary kriging [10]. Furthermore, this is in line with an emission inventory approach which showed that 85% of particle matter emissions in Tehran were sourced from heavy-duty vehicles [36].

The developed FLUR model provides spatiotemporal estimations of long-term PM_2.5 concentrations with a very high spatial resolution (5 m) in the continuous diurnal time domain. Theoretically, this can be seen as an infinite temporal resolution because the estimated diurnal curve can be evaluated at every desirable time point during the day, which is an advantage with respect to conventional spatiotemporal models for scalar responses that model air pollutants at discrete time points. Moreover, the developed FLUR model is parsimonious with respect to alternative approaches to modeling, such as fitting separate LUR models for spatial predicting at each desirable time point (such as the hours from 0 to 23); this is because, if separate LUR models are fitted, the resulting high-resolution maps for all those LUR models need to be stored. Meanwhile, here, we just needed to use three calculated inter-mean high-resolution spatial prediction maps, four time series resulting from the evaluation of the functional intercept of the FLUR model, and the three functional principal component curves that were evaluated at desirable time points (hourly/every 15 min/ or every minute during the daily timeframe) to provide the complete spatiotemporal prediction using Equation (13).

It is well known that ignoring hours in epidemiological studies of long-term exposure to air pollutants may result in exposure misclassification because people generally do not stay in just one geographic location (e.g., their residential address) during the whole day. On top of that, we showed that the spatial pattern of PM_2.5 is not constant during the day, so hour-specific exposure is not necessarily proportional to the corresponding daily average. This observed pattern is also in line with a recently published study of nitrogen dioxide modeling in Tehran [10].

On the other hand, although some previously published LUR studies predicted long-term hourly pollutant concentrations [37,38,39,40], none of them provided a finer time scale than hours. By employing functional data analysis methods, we succeeded in predicting the pollutant concentrations more practically, at a time scale of 15 min.

Furthermore, from a modeling point of view, to the best of our knowledge, this is the first LUR study with an underlying functional response model instead of using one of various predicting models for scalar data [18,19,30]. Therefore, we are the first group to spatially model the long-term diurnal curves of a pollutant using the LUR framework.

Finally, by comparing the prediction of the developed FLUR model (with continuous time scale) and the alternative model of D-STEM (with discrete time scale), we displayed comparable results which validate the estimation procedure of the proposed FLUR model. We also highlighted the strength of the FLUR model, which is based on semi-parametric methods of functional data analysis, resulting in flexibility when accounting for the temporal variation of the pollutant.

5. Conclusions

In this study, we developed a method for the land-use regression modeling of long-term diurnal curves of PM_2.5 at a high temporal and spatial resolution. The airborne PM_2.5 concentration data in the megacity of Tehran were used to fit the novel functional land-use regression (FLUR) model. The resulting estimation maps at a very high spatial and temporal resolution could benefit future epidemiological studies in this highly populated and polluted Middle Eastern megacity. The developed FLUR model demonstrated high flexibility in terms of accounting for complicated space and time interactions. Moreover, the described detailed procedure to predict curves by extending the ordinary LUR model can be adapted to other predicting techniques, such as machine learning to build models that predict curves instead of just scalar values. The environmental epidemiological studies of long-term air pollutants could benefit from the methodology and results of the FLUR model provided in this study, as the FLUR methodology provides high-resolution estimation maps of retrospective long-term air pollutants, and at the same time accounts for complex temporal variations and the interaction of spatial and temporal dimensions.