Study on NDVI Periodic Change Characteristics of Inner Mongolia Grassland Based on Variational Mode Decomposition Algorithm
Abstract
1. Introduction
2. Materials and Methods
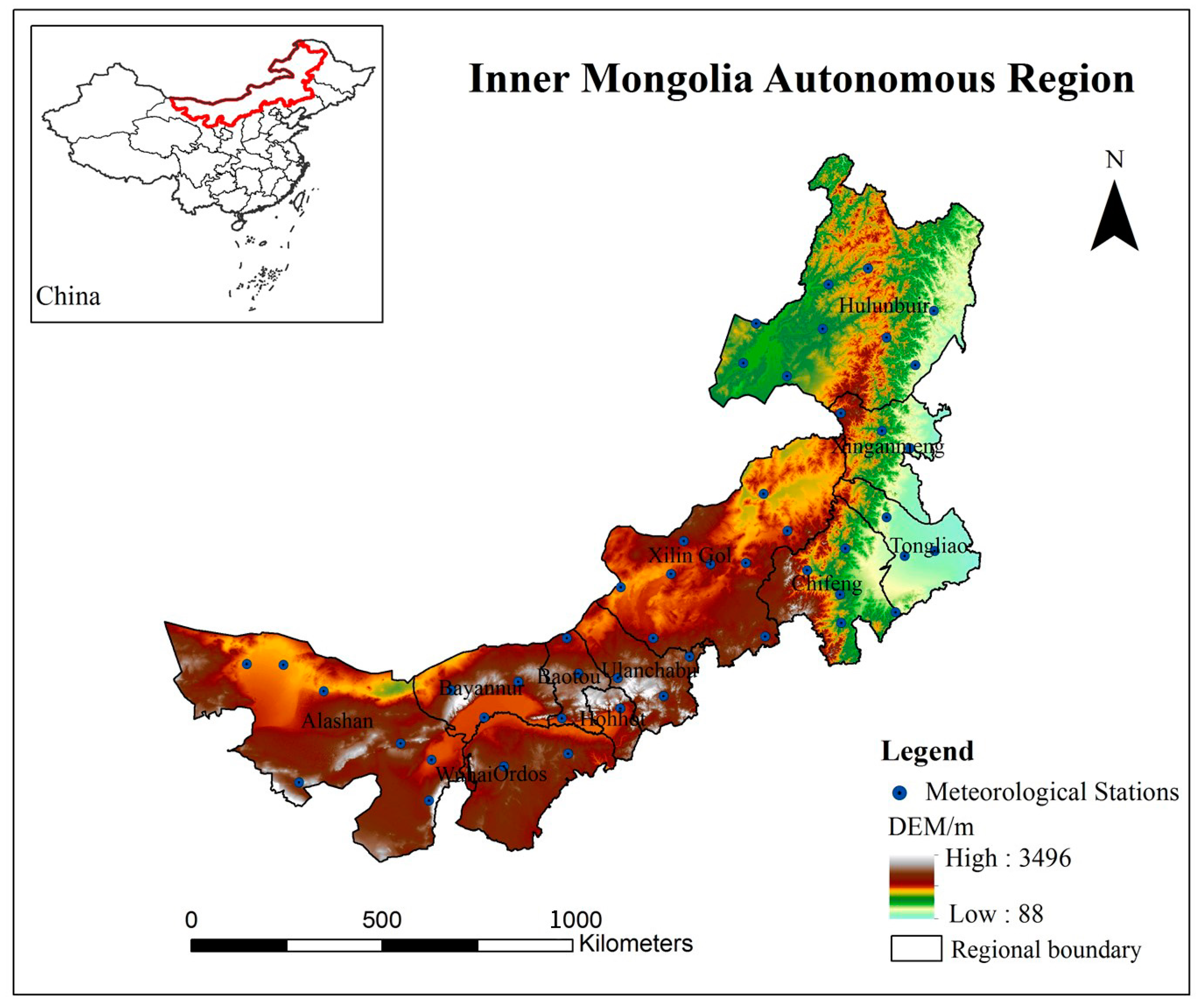
2.1. Study Area
2.2. Data Set
2.3. Research Method
3. Results and Analysis
3.1. Comparison and Analysis of EMD and VMD Algorithms
3.2. Analysis of Monthly Scale Periodic Change
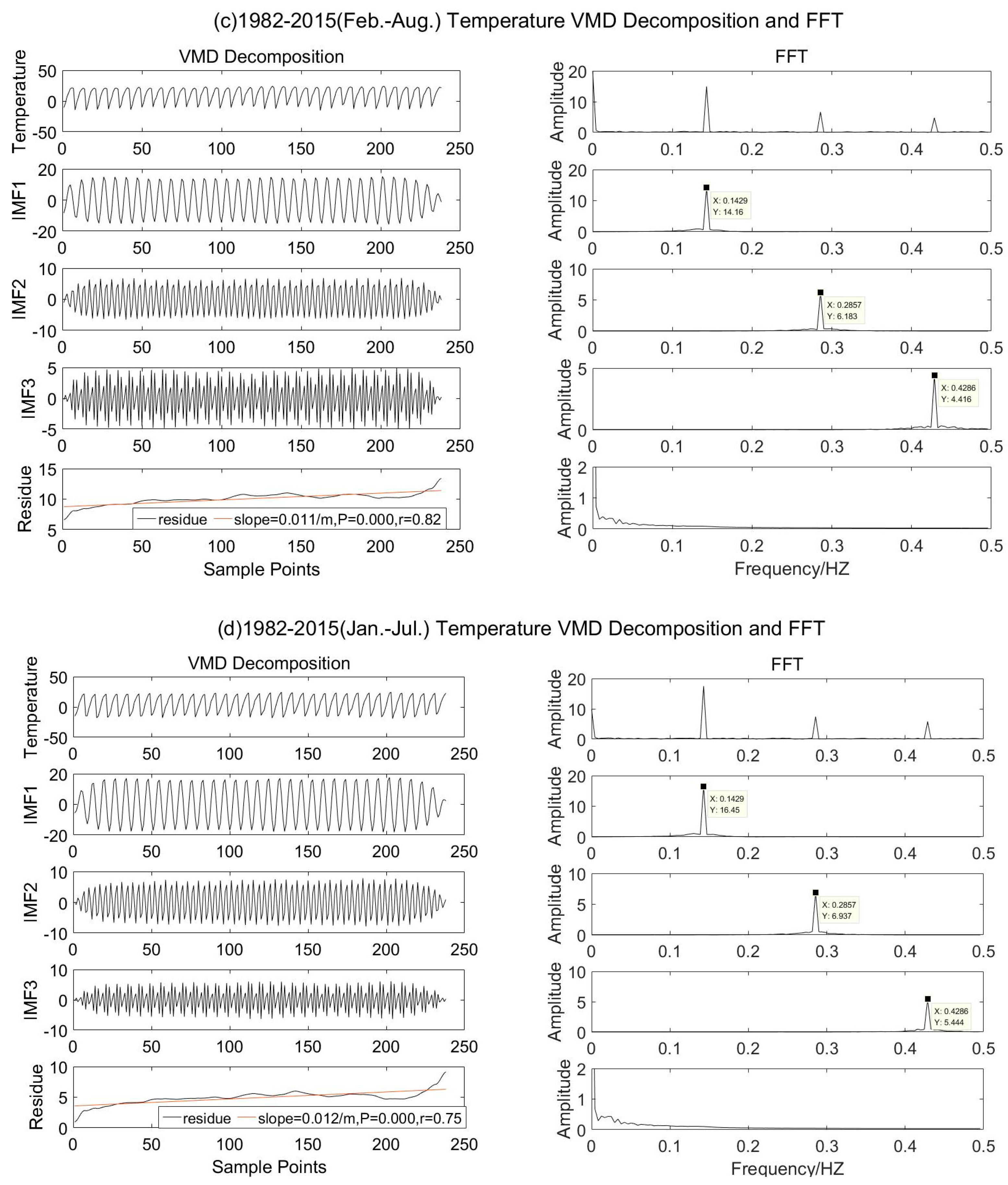
- From 1982 to 2015, the center frequencies of the modal components of NDVI and temperature IMF1 and IMF2 on the monthly scale from April to October were consistent, 0.143 HZ and 0.286 HZ, respectively, in which IMF1 showed a 6.99 month cycle and IMF2 showed a 3.49 month cycle.
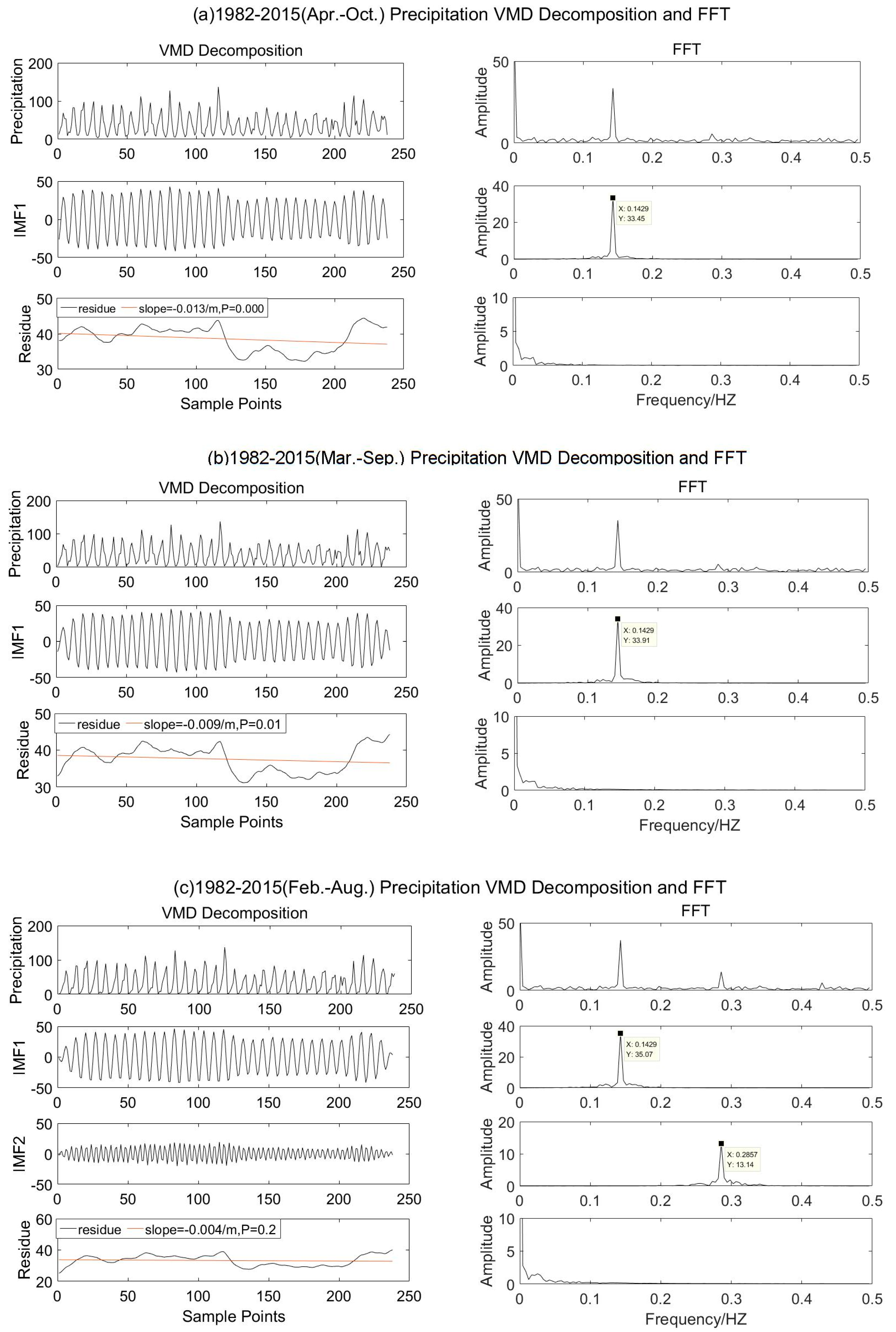
- From March to September, February to August, and January to July in 1982–2015, the monthly temperature had three IMF components, which are expressed as 6.99, 3.49, and 2.33 month fluctuation cycles.
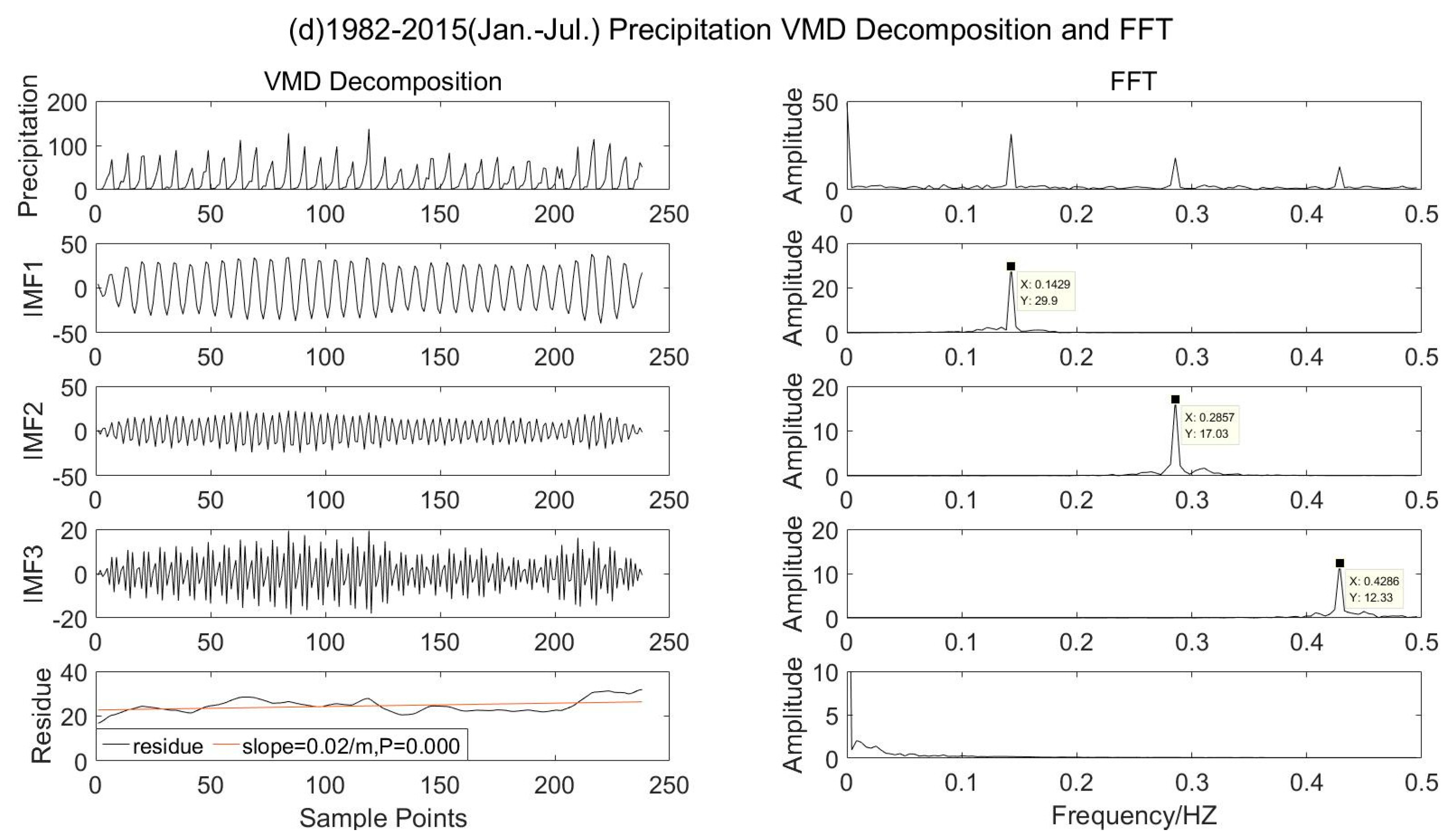
- From April to October, March to September, February to August, and January to July of each year from 1982 to 2015, the precipitation had a similar period of 6.99 months with the IMF1 modal component of NDVI in April to October in the same time period. In addition, the scale NDVI from April to October is consistent with the scale component IMF2 of precipitation from February to August and from January to July, showing a 3.49 month cycle change, which is half of the IMF1 cycle; the central frequency of precipitation IMF3 from January to July is 0.429 HZ, and the period is 2.33 months, which is one third of the oscillation period of IMF1.
- When the central frequency of IMF1 is the same, the average amplitude of monthly scale temperature from low to high is 8.56 (April to October), 10.51 (March to September), 14.16 (February to August), and 16.45 (January to July); the average amplitude of monthly precipitation from low to high is 29.9 (January to July), 33.45 (April to October), 33.91 (March to September), and 35.07 (February to August); when the central frequency of IMF2 is the same, the average amplitude of monthly scale temperature from low to high is 1.46 (April to October), 3.56 (March to September), 6.18 (February to August), and 6.94 (January to July); when the central frequency of IMF 3 is the same, the average amplitude of monthly scale temperature is 2.56 (March to September), 4.42 (February to August), and 5.44 (January to July) from low to high, showing that the amplitude increases with the increase of the lag period.
3.3. Annual Scale Periodicity Analysis
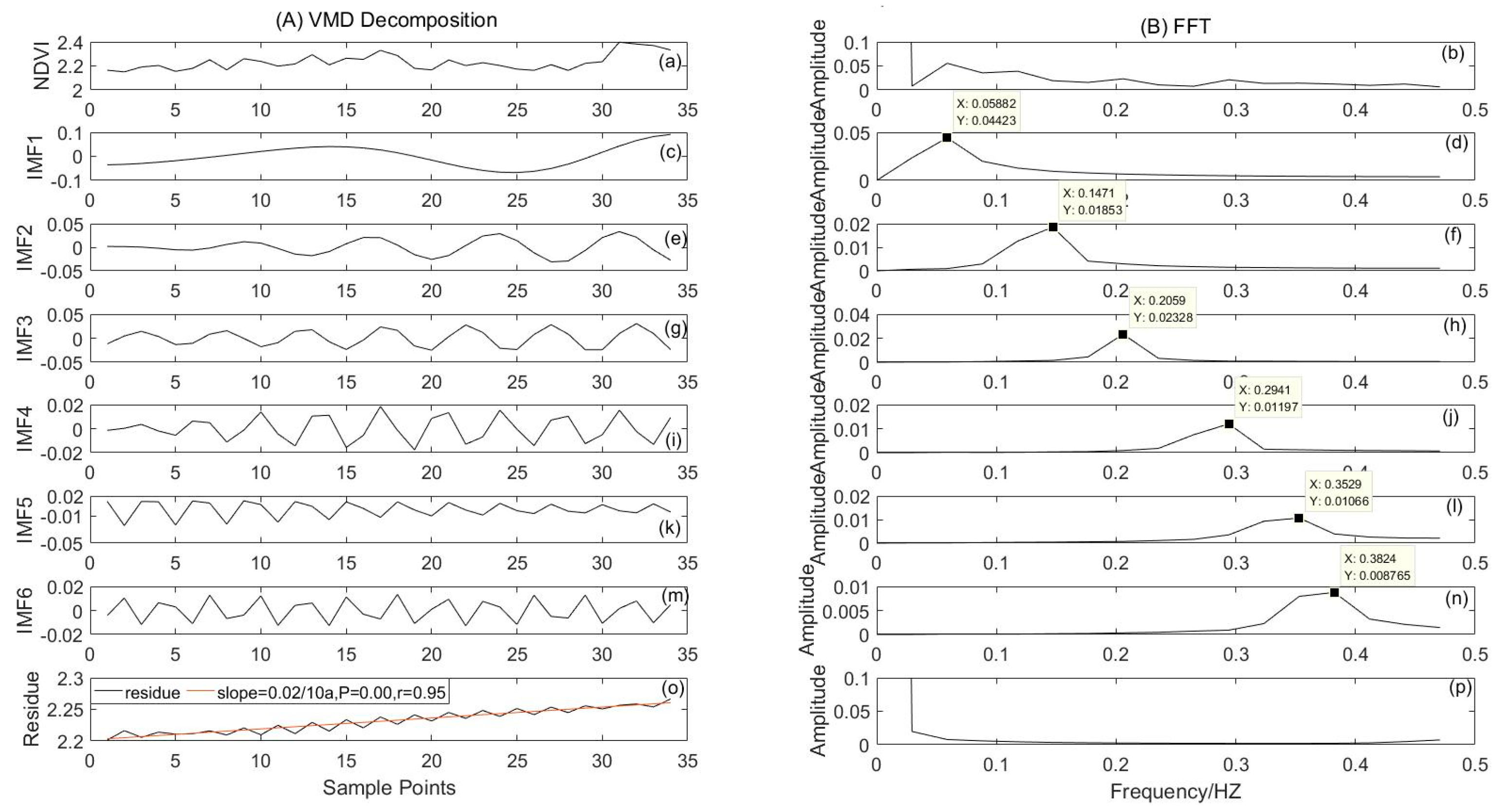
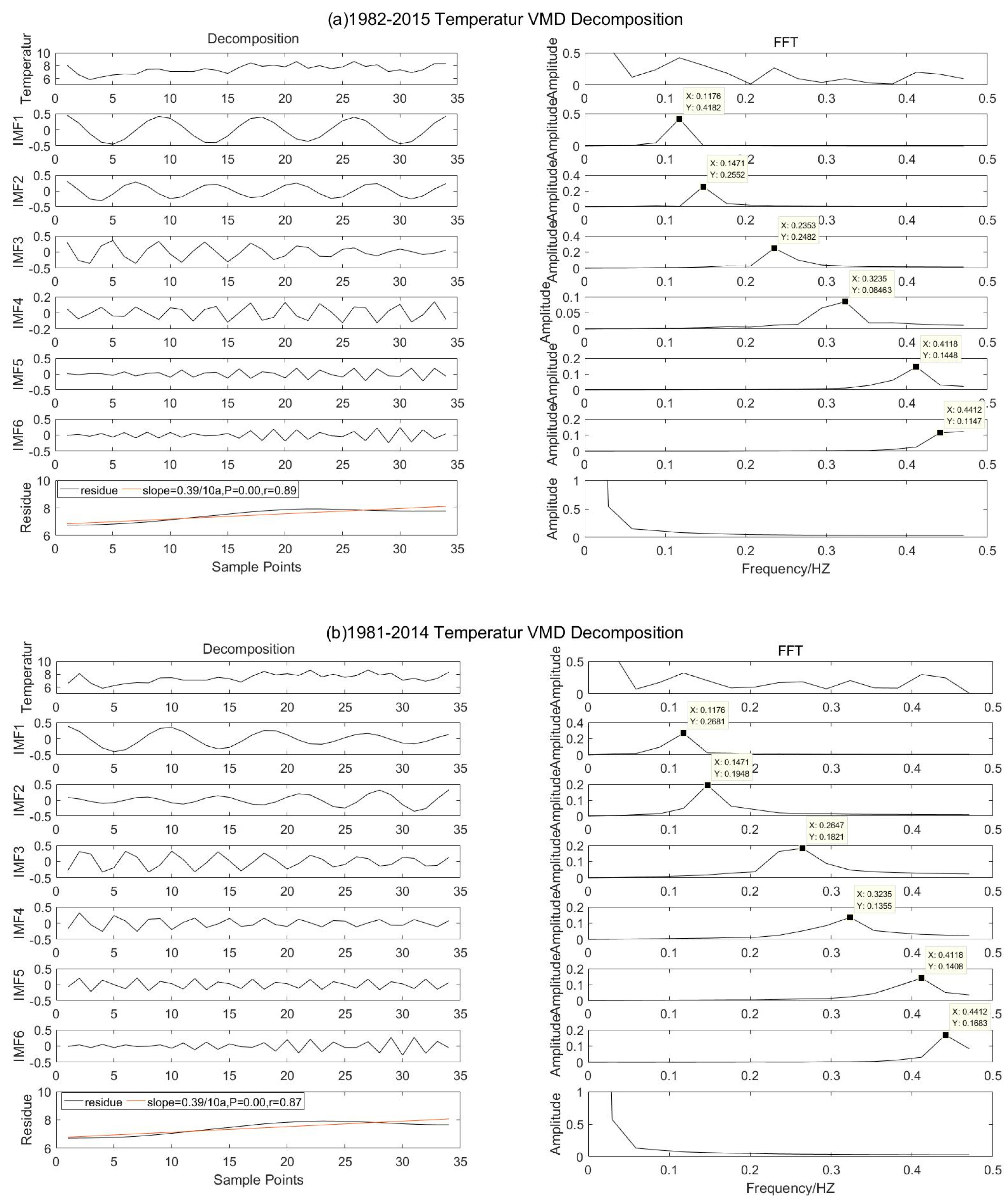
- There are several periods of NDVI on the scale of 1982–2015, which are about 16.95, 6.8a, 4.85a, 3.4a, 2.83a, and 2.61a, respectively; the scale temperature in 1982–2015, 1981–2014, 1980–2013, and 1979–2012 has the periodic characteristics of 8.47a, 6.8a, 3.09a, 2.43a, and 2.27a; and the corresponding precipitation periods are 16.95a, 6.8a, 4.85a, 3.09a, 2.43a, and 2.27a.
- The annual scale temperature IMF1 center frequency is 0.118 HZ, and the period is 8.47, which is half of the NDVI IMF1 period; the temperature is consistent with the cycle of NDVI IMF2.
- The periodic characteristics of NDVI in 1982–2015 are the same as the corresponding precipitation periods in 1982–2015, 1981–2014, and 1979–2012, which are 16.95a, 6.8a, and 4.85a, respectively.
- The center frequency of IMF1 and IMF4 components of precipitation in 1980–2013 is consistent with that of NDVI IMF1 and IMF3 in 1982–2015, which are 0.059 HZ and 0.147 HZ, respectively, and the period is 16.95a and 4.85a.
- In addition, the annual scale precipitation in 1982–2015, 1981–2014, 1980–2013, and 1979–2012 included a 2.43a oscillation period, and in 1982–2015, 1980–2013, and 1979–2012 also included a 3.09a fluctuation period.
4. Discussion and Conclusions
4.1. The Periodic Variation Characteristics of Meteorological Factors and Their Impact on Regional Vegetation
4.2. Vegetation NDVI Periodic Change Characteristics
4.3. Delay Analysis of Vegetation Caused by the Meteorological Factors
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Chen, X.Q.; Wang, H. Spatial and temporal variations of vegetation belts and vegetation cover degrees in Inner Mongolia from 1982 to 2003. Acta Geogr. Sin. 2009, 64, 84–94. [Google Scholar]
- Zhu, X.; Xiao, G.; Zhang, D.; Guo, L. Mapping abandoned farmland in China using time series MODIS NDVI. Sci. Total Environ. 2021, 755, 142651. [Google Scholar] [CrossRef]
- Sun, H.Y.; Wang, C.Y.; Zheng, N.; Bukhosor. Analysis of the vegetation cover change and the relationship between NDVI and environmental factors by using NOAA time series data. J. Remote Sens. 1998, 2, 204–210. [Google Scholar]
- Shen, B.B.; Wei, Y.B.; Ma, L.C.; Xu, D.W.; Ding, L.; Hou, L.L.; Qin, Q.; Xin, X.P. Spatiotemporal changes and drivers of fractional vegetation cover in Inner Mongolia grassland of China. Trans. CSAE 2022, 38, 118–126. [Google Scholar]
- Wu, L.L.; Wang, S.Y.; Ma, Y.X.; Yang, R.X.; Guan, Y.L.; Hai, K.; Liu, W.H. Response of vegetation to climate change in Central Asia with remote sensing and meteorological data. J. Remote Sens. 2022, 26, 2248–2267. [Google Scholar]
- Zhou, Y.K. Impacts of growth magnitude and length on long-term trends and interannual variation of vegetation productivity over Northeastern China. J. Remote Sens. 2021, 25, 8–19. [Google Scholar]
- Shen, B.; Fang, S.B.; Yu, W.G. Different correlations between NDVI and meteorological factors at temporal-time scales. J. Remote Sens. 2016, 20, 481–490. [Google Scholar]
- Joiner, J.; Yoshida, Y.; Anderson, M.; Holmes, T.; Hain, C.; Reichle, R.; Koster, R.; Middleton, E.; Zeng, F.W. Global relationships among traditional reflectance vegetation indices (NDVI and NDII), evapotranspiration (ET), and soil moisture variability on weekly timescales. Remote Sens. Environ. 2018, 219, 339–352. [Google Scholar] [CrossRef]
- Zhou, C.H.; Liang, J.Y.; Xie, Y.C. Investigating causal relationships between grassland deterioration and climate and socioeconomic changes through time-series computational learning. J. Clean. Prod. 2022, 366, 132963. [Google Scholar] [CrossRef]
- Zhou, C.H.; Xie, Y.C.; Zhang, A.B.; Liu, C.; Yang, J.Y. Spatiotemporal analysis of interactions between seasonal water, climate, land use, policy, and socioeconomic changes: Hulun-Buir Steppe as a Case Study. Water Res. 2022, 209, 117937. [Google Scholar] [CrossRef]
- Xu, X.; Ren, Z.Y.; Yang, R. The spatial and temporal dynamics of NDVI and its relation with climatic factors in Loess Plateau. J. Shaanxi Nor. Univ. 2012, 40, 82–87. [Google Scholar]
- Tu, Y.; Jiang, L.L.; Liu, R.; Xiao, Z.L.; Min, J. Spatiotemporal changes of vegetation NDVI and its driving forces in China during 1982–2015. Trans. CSAE 2021, 37, 75–84. [Google Scholar]
- Du, J.Q.; Zhao, C.X.; Jiaerheng, A.; Fang, S.F.; Xiang, B.; Yin, J.Q.; He, P.; Yuan, X.J.; Fang, G.L.; Shu, J.M. Analysis on spatio-temporal trends and drivers in monthly NDVI during recent decades in Xinjiang, China based two datasets. Trans. CSAE 2016, 32, 172–181. [Google Scholar]
- Yin, G.; Meng, X.Y.; Wang, H.; Hu, Z.Y.; Sun, Z.Q. Spatial-temporal variation of vegetation and its correlation with climate change in Central Asia during the period of 1982–2012. Acta Ecol. Sin. 2017, 37, 3149–3163. [Google Scholar]
- Wu, H.H.; Kuang, H.B.; Meng, B.; Feng, W.W. Study on the periodic characteristics of BDI index based on EMD-WA model. Syst. Eng-Theory Pract. 2018, 38, 1586–1598. [Google Scholar]
- Wang, X.L.; Zhang, Q.; Zhang, S.C. Periodic oscillation analysis of GPS water vapor time series using combined algorithm based on EMD and WD. Geo-Inform. Sci. Wuhan Univ. 2018, 43, 620–628. [Google Scholar]
- Han, H.; Ma, M.; Ping, Y.; Yi, S. Periodicity analysis of NDVI time series and its relationship with climatic factors in the Heihe River Basin in China. Remote Sens. Tech. Appl. 2011, 26, 554–560. [Google Scholar]
- Song, N.P.; Du, L.T.; Wang, L. Vegetation dynamics over 2000-2012 and its driving factors in Yanchi County, Ningxia Province. Acta Ecol. Sin. 2016, 35, 7377–7386. [Google Scholar]
- Chen, C.F.; Son, N.T.; Chang, L.Y.; Chen, C.C. Monitoring of soil moisture variability in relation to rice cropping systems in the Vietnamese Mekong delta using MODIS data. Appl. Geogr. 2011, 31, 463–475. [Google Scholar] [CrossRef]
- Liu, X.X.; Zhang, A.B.; Shi, C.M.; Wang, H.F. Filtering and multi-scale RBF prediction model of rainfall based on EMD method. In Proceedings of the First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009. [Google Scholar]
- Liu, H.X.; Zhang, A.B.; Jiang, T.; Zhao, A.Z.; Zhao, Y.L.; Wang, D.L. Response of vegetation productivity to climate change and human activities in the Shaanxi–Gansu–Ningxia region, China. J. Ndn. Soci. Remote Sens. 2018, 46, 1081–1092. [Google Scholar] [CrossRef]
- Liu, X.X.; Tian, Z.X.; Zhang, A.B.; Zhao, A.Z.; Liu, H.X. Impacts of climate on spatiotemporal variations in vegetation NDVI from 1982–2015 in Inner Mongolia, China. Sustainability 2019, 11, 768. [Google Scholar] [CrossRef]
- Zhao, A.Z.; Zhang, A.B.; Cao, S.; Liu, X.F.; Liu, J.H.; Cheng, D.Y. Responses of vegetation productivity to multi-scale drought in Loess Plateau, China. Catena 2018, 163, 165–171. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A-Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zhao, H.S.; Guo, S.W.; Gao, D. Fault feature extraction of bearing faults based on singular value decomposition and variational modal decomposition. J. Vib. Shock 2016, 35, 183–188. [Google Scholar]
- Chen, T.Y.; Xie, Y.C.; Liu, C.; Bai, Y.F.; Zhang, A.B.; Mao, L.S.; Fan, S.Y. Trend analysis of relationship between primary productivity, precipitation and temperature in Inner Mongolia. Int. J. Geo-Inf. 2018, 7, 214. [Google Scholar] [CrossRef]
- Hu, Y.Q.; Hu, L.; Sun, P.; Wen, Q.Z.; Feng, A.L.; Liu, W. Spatio-temporal evolution of drought events in Huaihe River Basin: A non-stationary standardized precipitation evapotranspiration index study. J. Beijing Nor. Univ. 2022, 58, 116–124. [Google Scholar]
- Zhang, G.Y.; Wu, Y.G.; Liu, Y.; Zhang, W.B. A contrastive analysis of EMD and EEMD on multiple time-scale characteristics of rainfall. China Rural Water Hydropower 2014, 8, 98–103. [Google Scholar]
- Jiang, T.; Liu, B.H.; Li, X.; Li, G.Q. Forced oscillation location in power systems using multiple empirical mode decomposition. Proc. CSEE 2022, 42, 8063–8074. [Google Scholar]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition a noise assisted data analysis method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P. On the influence of sampling on the empirical mode decomposition. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Toulouse, France, 14–19 May 2006. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Proc. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, C.L.; Wu, Y.J.; Zhen, C.G. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering. Proc. CSEE 2015, 35, 3358–3365. [Google Scholar]
- Tang, G.J.; Wang, X.L. Variational mode decomposition method and its application on incipient fault diagnosis of rolling bearing. J. Vib. Eng. 2016, 29, 638–648. [Google Scholar]
- Ma, Z.Q.; Li, Y.C.; Liu, Z.; Guang, C.J. Rolling bearing fault feature extraction based on variational mode decomposition and Teager energy operator. J. Vib. Shock 2016, 35, 134–139. [Google Scholar]
- Xia, J.Z.; Yu, M.Q.; Huang, C.; Wang, Z.A.; Lu, Q.P. Fault feature extraction of rolling element bearing based on VMD and Infogram. J. Vib. Shock 2017, 36, 111–117. [Google Scholar]
- Liang, Z.; Sun, G.Q.; Li, H.C.; Wei, Z.N.; Zang, H.X.; Zhou, Y.Z.; Chen, S. Short-term load forecasting based on VMD and PSO optimized deep belief network. Power Syst. Technol. 2018, 42, 598–606. [Google Scholar]
- Lei, F.; Wei, Z.N.; Li, H.J.; Kwok, W.C.; Son, G.Q.; Sun, Y.H. Short-term wind speed interval prediction based on VMD and BA-RVM algorithm. Electr. Power Autom. Equip. 2017, 37, 93–100. [Google Scholar]
- Yang, J.P.; Ding, Y.J.; Chen, R.S. Analysis on periodic variations of annual hydrologic and meteorological series in source regions of Yangtze and Yellow Rivers. J. Dzt. Res. 2005, 25, 351–355. [Google Scholar]
- Meng, M.; Zheng, N. Change characteristic of ndvi and its response to climate change in inner mongolia over the past 30 years. Remote Sens. Technol. Appl. 2018, 33, 676–685. [Google Scholar]
- Mu, S.; Yang, H.; Li, J.; Chen, Y.; Gang, C.; Zhou, W.; Ju, W. Spatio-temporal dynamics of vegetation coverage and its relationship with climate factors in Inner Mongolia, China. J. Geogr. Sci. 2013, 23, 231–246. [Google Scholar] [CrossRef]
- Bhatt, U.S.; Walker, D.A.; Raynolds, M.K.; Bieniek, P.A.; Epstein, H.E.; Comiso, J.C.; Pinzon, J.E.; Tucker, C.J.; Steele, M.; Ermold, W.; et al. Changing seasonality of panarctic tundra vegetation in relationship to climatic variables. Environ. Res. Lett. 2017, 12, 055003. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Pan, Y.; Zhao, A.; Li, Y. Spatiotemporal changes of cold surges in Inner Mongolia between 1960 and 2012. J. Geogr. Sci. 2015, 25, 259–273. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Hu, Y.N.; Li, S.; Peng, J.; Wang, Y. Analyzing nonlinear variations in terrestrial vegetation in China during 1982–2012. Environ. Monit. Assess. 2015, 187, 722. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Zhao, C.; Shu, J.; Jiaerheng, A.; Yuan, X.; Yin, J.; Fang, S.; He, P. Spatiotemporal changes of vegetation on the Tibetan Plateau and relationship to climatic variables during multiyear periods from 1982–2012. Environ. Earth Sci. 2016, 75, 1–18. [Google Scholar] [CrossRef]
- Davis, M.B. Lags in vegetation response to greenhouse warming. Clim. Chang. 1989, 15, 75–82. [Google Scholar] [CrossRef]
- Gessner, U.; Naeimi, V.; Klein, I.; Kuenzer, C.; Klein, D.; Dech, S. The relationship between precipitation anomalies and satellite-derived vegetation activity in Central Asia. Glob. Planet. Chang. 2013, 110, 74–87. [Google Scholar] [CrossRef]
- Saatchi, S.; Asefi-Najafabady, S.; Malhi, Y.; Aragão, L.E.; Anderson, L.O.; Myneni, R.B.; Nemani, R. Persistent effects of a severe drought on Amazonian forest canopy. Proc. Natl. Acad. Sci. USA 2013, 110, 565–570. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Huang, H.; Hu, M.; Dahlgren, R.A. Influence of lag effect, soil release, and climate change on watershed anthropogenic nitrogen inputs and riverine export dynamics. Environ. Sci. Technol. 2014, 48, 5683–5690. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag effects of global vegetation responses to climate change. Glob. Chang. Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef]
- Xie, B.; Jia, X.; Qin, Z.; Shen, J.; Chang, Q. Vegetation dynamics and climate change on the Loess Plateau, China: 1982–2011. Reg. Environ. Chang. 2016, 16, 1583–1594. [Google Scholar] [CrossRef]
- Hawinkel, P.; Swinnen, E.; Lhermitte, S.; Verbist, B.; Van Orshoven, J.; Muys, B. A time series processing tool to extract climate-driven interannual vegetation dynamics using ensemble empirical mode decomposition (EEMD). Remote Sens. Environ. 2015, 169, 375–389. [Google Scholar] [CrossRef]
- Bunting, E.L.; Munson, S.M.; Villarreal, M.L. Climate legacy and lag effects on dryland plant communities in the southwestern US. Ecol. Indic. 2017, 74, 216–229. [Google Scholar] [CrossRef]

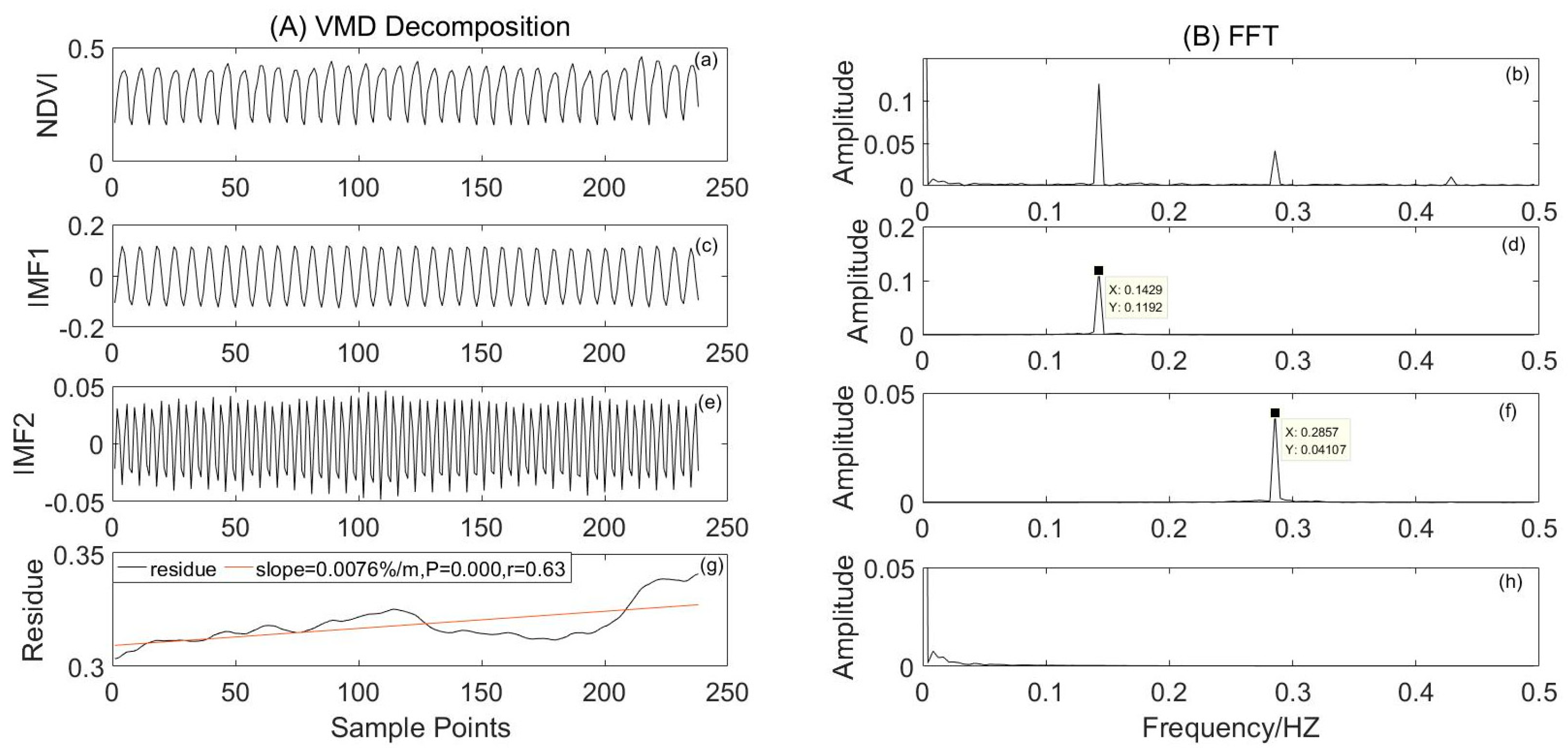





| Month | Factor | Component | Average Amplitude | Center Frequency/HZ | Average Period (Months) |
|---|---|---|---|---|---|
| 4–10 | NDVI | IMF1 | 0.12 | 0.143 | 6.99 |
| IMF2 | 0.04 | 0.286 | 3.49 | ||
| temperature | IMF1 | 8.56 | 0.143 | 6.99 | |
| IMF2 | 1.46 | 0.286 | 3.49 | ||
| precipitation | IMF1 | 33.45 | 0.143 | 6.99 | |
| 3–9 | temperature | IMF1 | 10.51 | 0.143 | 6.99 |
| IMF2 | 3.56 | 0.286 | 3.49 | ||
| IMF3 | 2.56 | 0.429 | 2.33 | ||
| precipitation | IMF1 | 33.91 | 0.143 | 6.99 | |
| 2–8 | temperature | IMF1 | 14.16 | 0.143 | 6.99 |
| IMF2 | 6.18 | 0.286 | 3.49 | ||
| IMF3 | 4.42 | 0.429 | 2.33 | ||
| precipitation | IMF1 | 35.07 | 0.143 | 6.99 | |
| IMF2 | 13.14 | 0.286 | 3.49 | ||
| 1–7 | temperature | IMF1 | 16.45 | 0.143 | 6.99 |
| IMF2 | 6.94 | 0.286 | 3.49 | ||
| IMF3 | 5.44 | 0.429 | 2.33 | ||
| precipitation | IMF1 | 29.9 | 0.143 | 6.99 | |
| IMF2 | 17.03 | 0.286 | 3.49 | ||
| IMF3 | 12.33 | 0.429 | 2.33 |
| Time | Parameter | Modal Components | Fluctuation | Center Frequency/HZ | Period/a |
|---|---|---|---|---|---|
| 1982–2015 | NDVI | IMF1 | 0.044 | 0.059 | 16.95 |
| IMF2 | 0.019 | 0.147 | 6.8 | ||
| IMF3 | 0.023 | 0.206 | 4.85 | ||
| IMF4 | 0.012 | 0.294 | 3.4 | ||
| IMF5 | 0.011 | 0.353 | 2.83 | ||
| IMF6 | 0.009 | 0.382 | 2.61 | ||
| temperature | IMF1 | 0.418 | 0.118 | 8.47 | |
| IMF2 | 0.255 | 0.147 | 6.8 | ||
| IMF3 | 0.248 | 0.235 | 4.26 | ||
| IMF4 | 0.085 | 0.324 | 3.09 | ||
| IMF5 | 0.145 | 0.412 | 2.43 | ||
| IMF6 | 0.115 | 0.441 | 2.27 | ||
| precipitation | IMF1 | 17.19 | 0.059 | 16.95 | |
| IMF2 | 9.709 | 0.147 | 6.8 | ||
| IMF3 | 20.15 | 0.206 | 4.85 | ||
| IMF4 | 5.8 | 0.265 | 3.77 | ||
| IMF5 | 7.694 | 0.324 | 3.09 | ||
| IMF6 | 11.13 | 0.412 | 2.43 | ||
| 1981–2014 | temperature | IMF1 | 0.268 | 0.118 | 8.47 |
| IMF2 | 0.195 | 0.147 | 6.8 | ||
| IMF3 | 0.182 | 0.265 | 3.77 | ||
| IMF4 | 0.136 | 0.324 | 3.09 | ||
| IMF5 | 0.141 | 0.412 | 2.43 | ||
| IMF6 | 0.168 | 0.441 | 2.27 | ||
| precipitation | IMF1 | 18.45 | 0.059 | 16.95 | |
| IMF2 | 11.71 | 0.147 | 6.8 | ||
| IMF3 | 11.5 | 0.206 | 4.85 | ||
| IMF4 | 10.92 | 0.235 | 4.26 | ||
| IMF5 | 6.607 | 0.265 | 3.77 | ||
| IMF6 | 9.558 | 0.412 | 2.43 | ||
| IMF7 | 8.825 | 0.441 | 2.27 | ||
| 1980–2013 | temperature | IMF1 | 0.194 | 0.118 | 8.47 |
| IMF2 | 0.197 | 0.206 | 4.85 | ||
| IMF3 | 0.288 | 0.235 | 4.26 | ||
| IMF4 | 0.114 | 0.324 | 3.09 | ||
| IMF5 | 0.129 | 0.412 | 2.43 | ||
| IMF6 | 0.191 | 0.441 | 2.27 | ||
| precipitation | IMF1 | 17.54 | 0.059 | 16.95 | |
| IMF2 | 11.29 | 0.088 | 11.36 | ||
| IMF3 | 15.49 | 0.177 | 5.65 | ||
| IMF4 | 13.58 | 0.206 | 4.85 | ||
| IMF5 | 9.749 | 0.324 | 3.09 | ||
| IMF6 | 13.94 | 0.412 | 2.43 | ||
| IMF7 | 8.661 | 0.441 | 2.27 | ||
| 1979–2012 | temperature | IMF1 | 0.339 | 0.118 | 8.47 |
| IMF2 | 0.201 | 0.147 | 6.8 | ||
| IMF3 | 0.23 | 0.265 | 3.77 | ||
| IMF4 | 0.131 | 0.324 | 3.09 | ||
| IMF5 | 0.164 | 0.412 | 2.43 | ||
| IMF6 | 0.167 | 0.441 | 2.27 | ||
| precipitation | IMF1 | 13.6 | 0.059 | 16.95 | |
| IMF2 | 8.611 | 0.118 | 6.8 | ||
| IMF3 | 19.88 | 0.206 | 4.85 | ||
| IMF4 | 7.008 | 0.234 | 4.27 | ||
| IMF5 | 8.422 | 0.324 | 3.09 | ||
| IMF6 | 16.57 | 0.412 | 2.43 | ||
| IMF7 | 7.885 | 0.441 | 2.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, D.; Zhang, A.; Tian, Z.; Liu, X.; Hou, Y. Study on NDVI Periodic Change Characteristics of Inner Mongolia Grassland Based on Variational Mode Decomposition Algorithm. Atmosphere 2023, 14, 1039. https://doi.org/10.3390/atmos14061039
Su D, Zhang A, Tian Z, Liu X, Hou Y. Study on NDVI Periodic Change Characteristics of Inner Mongolia Grassland Based on Variational Mode Decomposition Algorithm. Atmosphere. 2023; 14(6):1039. https://doi.org/10.3390/atmos14061039
Chicago/Turabian StyleSu, Deguo, Anbing Zhang, Zhixiu Tian, Xinxia Liu, and Yikai Hou. 2023. "Study on NDVI Periodic Change Characteristics of Inner Mongolia Grassland Based on Variational Mode Decomposition Algorithm" Atmosphere 14, no. 6: 1039. https://doi.org/10.3390/atmos14061039
APA StyleSu, D., Zhang, A., Tian, Z., Liu, X., & Hou, Y. (2023). Study on NDVI Periodic Change Characteristics of Inner Mongolia Grassland Based on Variational Mode Decomposition Algorithm. Atmosphere, 14(6), 1039. https://doi.org/10.3390/atmos14061039





