A Review on Aerodynamic Characteristics and Wind-Induced Response of Flexible Support Photovoltaic System
Abstract
1. Introduction
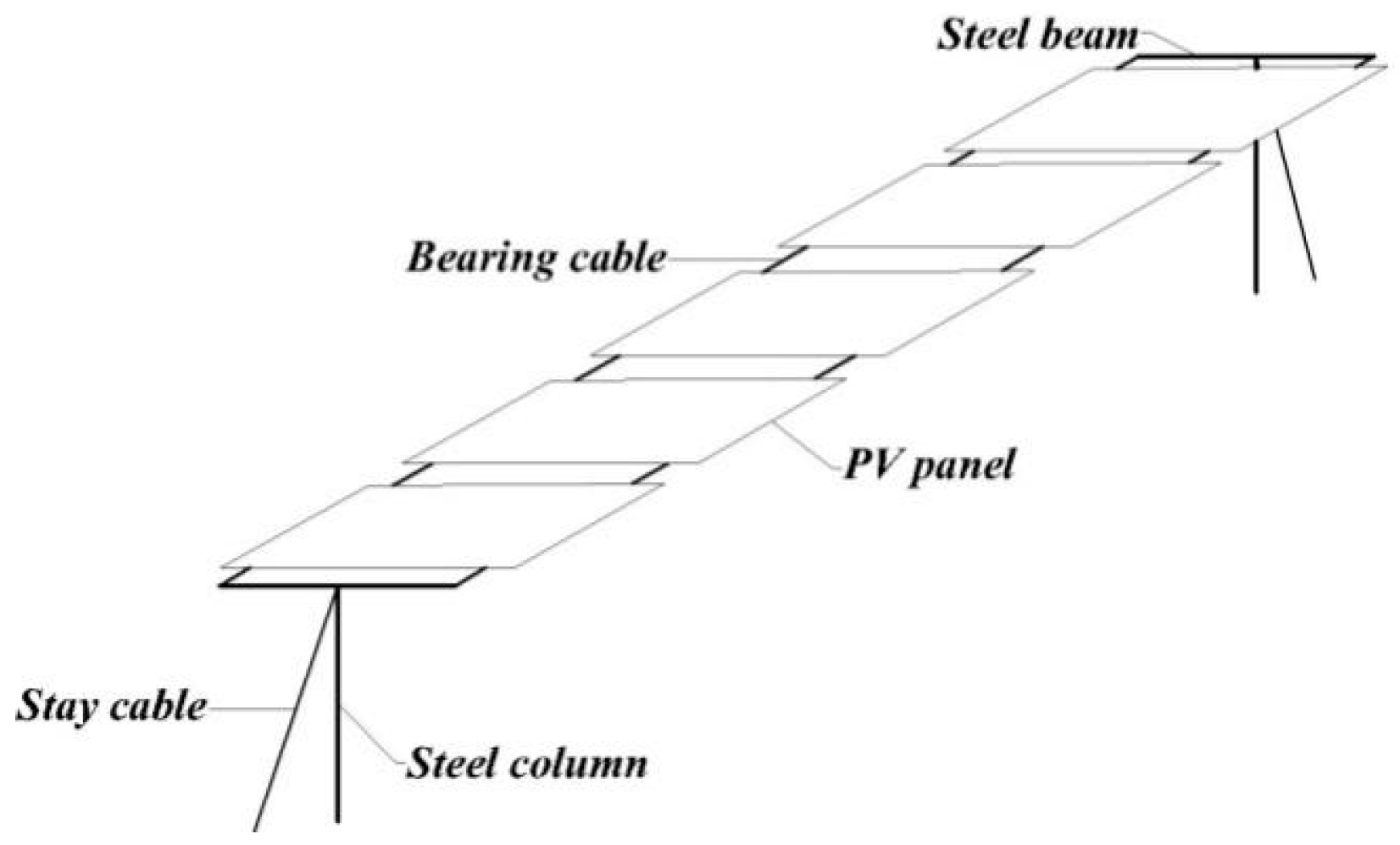
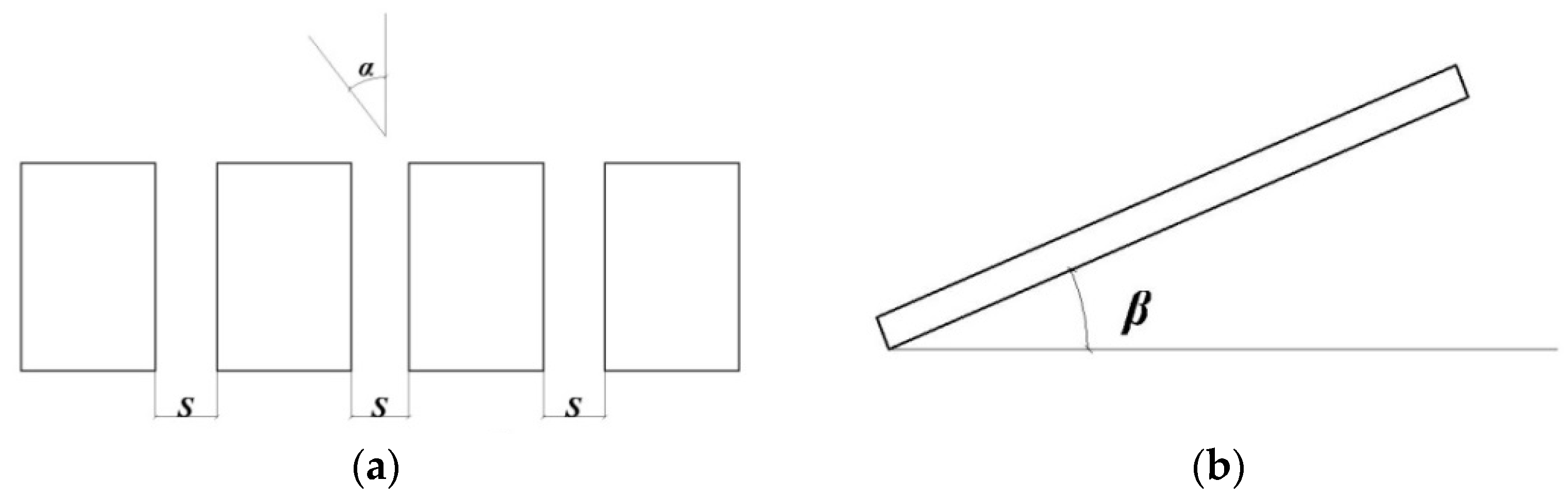
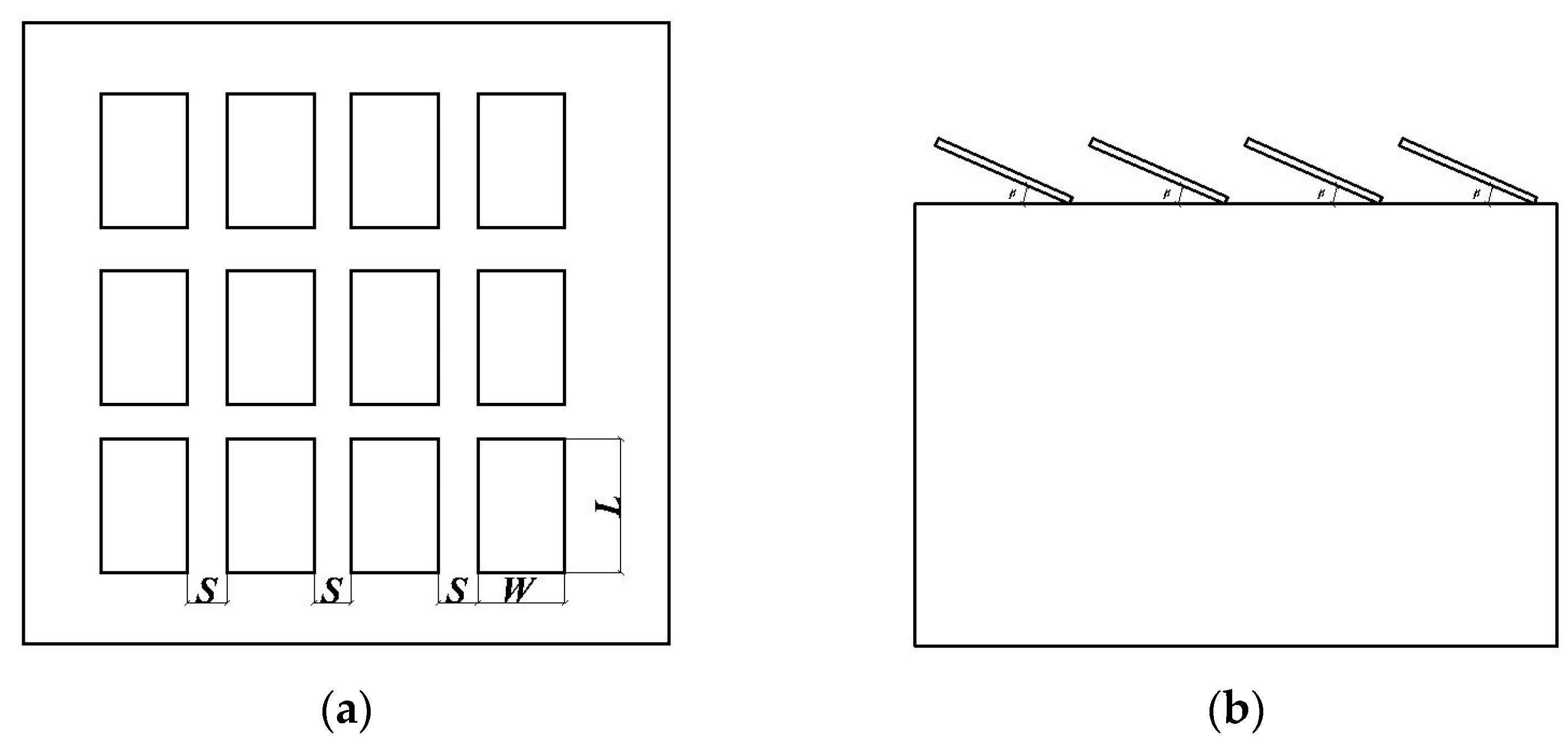
2. Wind Load Characteristics on Flexible PV System
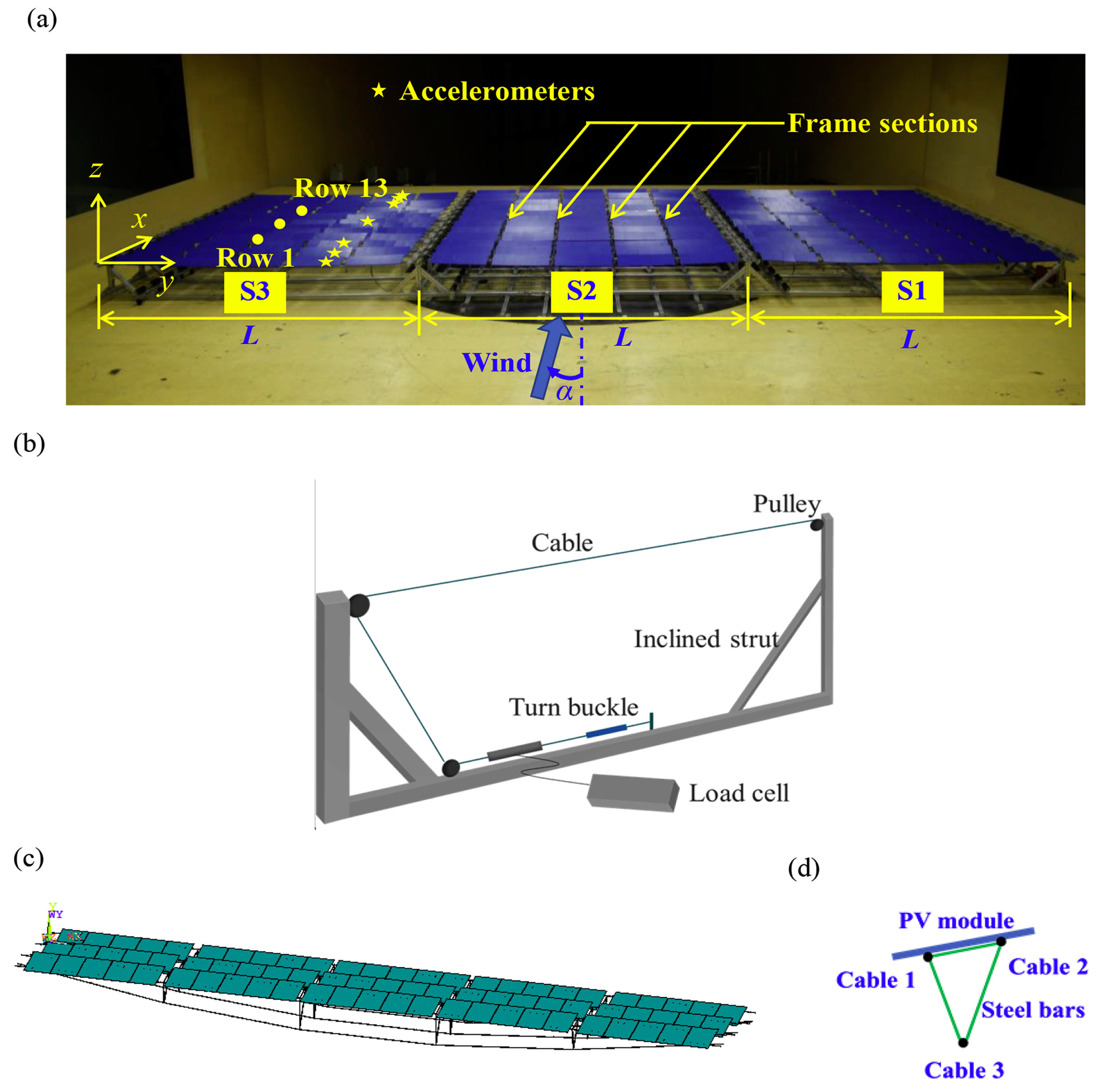
2.1. Wind Tunnel Test
2.2. Numerical Simulation
3. Dynamic Response of Flexible PV Support Structures
3.1. Buffeting
3.2. Flutter
3.3. Vortex-Induced Vibration
4. Conclusions
- The aerodynamic characteristics and wind-induced response of the flexible PV system can be affected by a series of governing factors, such as inclination, inter-plate spacing, wind direction angle, installation position and surrounding environment.
- Regarding the investigation of flexible PV system, both wind tunnel and numerical simulation techniques are considered to be useful. Wind tunnel test is industry standard tool, but it might subject to scale issue. Numerical simulation, on the other hand, is less costly and more efficient.
- As a cable-plate structure system with high flexible and nonlinear vibration, the flexible PV system exhibits pronounced aerodynamic characteristics, such as chattering, vortex, flutter and wake surge responses. However, relevant studies remain limited, which needs to be further considered.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, A.G. China’s goal of achieving carbon peak by 2030 and its main approaches. J. Beijing Univ. Technol. (Soc. Sci. Ed.) 2021, 21, 1–15. [Google Scholar]
- Ma, L.; Guo, X.; Wei, L. Research on islanding detection of solar power system based on new nanomaterials. Nanotechnol. Environ. Eng. 2022, 7, 89–97. [Google Scholar] [CrossRef]
- Rahul, V.; Deepika, C. Solar and thermal power generation. J. Trend Sci. Res. Dev. 2018, 2, 1071–1074. [Google Scholar]
- Jubayer, C.M.; Hangan, H. Numerical simulation of wind effects on a stand-alone ground mounted photovoltaic (PV) system. J. Wind. Eng. Ind. Aerodyn. 2014, 134, 56–64. [Google Scholar] [CrossRef]
- Jiang, M.; Li, J.; Wei, W.; Miao, J.; Zhang, P.; Qian, H.; Liu, J.; Yan, J. Using existing infrastructure to realize low-cost and flexible photovoltaic power generation in areas with high-power demand in China. iScience 2020, 23, 101867. [Google Scholar] [CrossRef] [PubMed]
- Lahlou, Y.; Hajji, A.; Aggour, M. Development of a Management Algorithm for a Compact Photovoltaic—Wind Turbine System; Springer: Singapore, 2022; pp. 711–721. [Google Scholar]
- Baumgartner, F.P.; Büchel, A.; Bartholet, R. Cable-based solar wings tracking system: Two-axis system and progress of one-axis system. In Proceedings of the 25th European Photovoltaic Solar Energy Conference, Valencia, Spain, 8 September 2010. [Google Scholar]
- Baumgartner, F.P.; Büchel, A.; Bartholet, R. Experiences with cable-based solar wings tracking system and progress towards two-axis large scale solar systems. In Proceedings of the 24th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21 September 2009. [Google Scholar]
- Baumgartner, F.P.; Büchel, A.; Bartholet, R. Solar wings: A new lightweight PV tracking system. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference, Valencia, Spain, 1–5 September 2008. [Google Scholar]
- Qian, Y.; Wang, Y.; Yang, X. Application status of photovoltaic technology and “photovoltaic + water” in wastewater treatment plant. Ind. Water Treat. 2022, 42, 40–50. [Google Scholar]
- Aroca-Delgado, R.; Pérez-Alonso, J.; Callejón-Ferre, Á.-J.; Díaz-Pérez, M. Morphology, yield and quality of greenhouse tomato cultivation with flexible photovoltaic rooftop panels (Almería-Spain). Sci. Hortic. 2019, 257, 108768. [Google Scholar] [CrossRef]
- Geurts, C.P.W.; Steenbergen, R.D.J.M. Full scale measurements of wind loads on stand-off photovoltaic systems. In Proceedings of the 5th European & African Conference on Wind Engineering (EACWE), Florence, Italy, 19–23 July 2009. [Google Scholar]
- Kopp, G.A. Wind loads on low-profile, tilted, solar arrays placed on large, flat, low-rise building roofs. J. Struct. Eng. 2014, 140, 04013057. [Google Scholar] [CrossRef]
- Reina, G.P.; De Stefano, G. Computational evaluation of wind loads on sun-tracking ground-mounted photovoltaic panel arrays. J. Wind Eng. Ind. Aerodyn. 2017, 170, 283–293. [Google Scholar] [CrossRef]
- Wang, J.X. Wind Effects and Wind-Resistant Design of Roof-Mounted Solar Arrays. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Zhou, W.; He, B.; Cai, J.; Deng, X.; Liu, D. Wind load characteristics and reduction analysis of a structural system of photovoltaic power station. Struct. Eng. 2018, 34, 86–94. [Google Scholar]
- Counihan, J. Simulation of an adiabatic urban boundary layer in a wind tunnel. Atmos. Environ. (1967) 1973, 7, 673–689. [Google Scholar] [CrossRef]
- Tieleman, H.W.; Reinhold, T.A. Wind Tunnel Model Investigation for Basic Dwelling Geometries; Department of Engineering Science & Mechanics, Virginia Polytechnic Institute & State University: Blacksburg, VA, USA, 1976. [Google Scholar]
- Tieleman, H.W.; Reinhold, T.A.; Marshall, R.D. On the wind-tunnel simulation of the atmospheric surface layer for the study of wind loads on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 1978, 3, 21–38. [Google Scholar] [CrossRef]
- Kutler, P. A perspective of theoretical and applied computational fluid dynamics. AIAA J. 1985, 23, 328–341. [Google Scholar] [CrossRef]
- Boris, J.P. New directions in computational fluid dynamics. Annu. Rev. Fluid Mech. 1989, 21, 345–385. [Google Scholar] [CrossRef]
- Cermak, J.E. Wind-tunnel testing of structures. J. Eng. Mech. Div. 1977, 103, 1125–1140. [Google Scholar] [CrossRef]
- Cermak, J.E. Wind-tunnel development and trends in applications to civil engineering. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 355–370. [Google Scholar] [CrossRef]
- He, R.; Sun, H.; Gao, X.; Yang, H. Wind tunnel tests for wind turbines: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 166, 112675. [Google Scholar] [CrossRef]
- He, X.H.; Ding, H.; Jing, H.Q.; Zhang, F.; Wu, X.P.; Weng, X.J. Wind-induced vibration and its suppression of photovoltaic modules supported by suspension cables. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104275. [Google Scholar] [CrossRef]
- Du, H.; Xu, H.W.; Zhang, Y.L.; Lou, W.J. Wind pressure characteristics and wind vibration response of long-span flexible photovoltaic support structure. J. Harbin Inst. Technol. 2022, 54, 67–74. [Google Scholar]
- Li, S.Y.; Ma, J.; Liu, J.Q.; Chen, Z.Q. Experimental study for flutter performance of flexible photovoltaic system by segmental model test. China Civ. Eng. J. 2023; accepted. [Google Scholar]
- Ma, W.Y.; Chai, X.B.; Ma, C.C. Experimental study on wind load influencing factors of flexible support photovoltaic modules. Acta Energ. Sol. Sin. 2021, 42, 10–18. [Google Scholar]
- Ma, W.Y.; Chai, X.B.; Zhao, H.Y.; Ma, C.C. A study on distribution coefficient of a flexible photovoltaic support cable based on an eccentric moment wind load distribution model. J. Vib. Shock. 2021, 40, 305–310. [Google Scholar]
- Ma, W.Y.; Sun, G.J.; Liu, X.B.; Xing, K.Y.; Liu, Q.K. Tests for wind load distribution model of solar panel. J. Vib. Shock. 2017, 36, 8–13. [Google Scholar]
- Banks, D. The role of corner vortices in dictating peak wind loads on tilted flat solar panels mounted on large, flat roofs. J. Wind Eng. Ind. Aerodyn. 2013, 123, 192–201. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Liu, Z.Z.; Qi, X.H.; Jia, L.Z. Solar photovoltaic panels wind load testing and analysis. Energy Technol. 2010, 31, 93–95. [Google Scholar]
- Ma, W.Y.; Ma, C.C.; Wang, C.Y.; Han, X.L.; Gao, F. Wind tunnel experimental study on the wind load interference effect of solar panel arrays. J. Exp. Fluid Mech. 2021, 35, 19–25. [Google Scholar]
- Alam, M.D.M.; Moriya, M.; Takai, K.; Sakamoto, H. Suppression of fluid forces acting on two square prisms in a tandem arrangement by passive control of flow. J. Fluids Struct. 2002, 16, 1073–1092. [Google Scholar] [CrossRef]
- Shang, J.M.; Zhou, Q.; Alam, M.M.; Liao, H.L.; Cao, S.Y. Numerical studies of the flow structure and aerodynamic forces on two tandem square cylinders with different chamfered-corner ratios. Phys. Fluids 2019, 31, 075102. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Chang, F.Y. Analysis of wind loads on ground-mounted PV arrays with wall shielding. J. Shenyang Aerosp. Univ. 2019, 36, 41–49. [Google Scholar]
- Wang, C.Y.; Ma, W.Y.; Han, X.L.; Gao, F. Effect of parapet on wind load of flat roof array solar panel. Eng. Mech. 2021, 38, 216–222. [Google Scholar]
- Uematsu, Y.; Yambe, T.; Watanabe, T.; Ikeda, H. The benefit of horizontal photovoltaic panels in reducing wind loads on a membrane roofing system on a flat roof. Wind 2021, 1, 44–62. [Google Scholar] [CrossRef]
- Uematsu, Y.; Yambe, T.; Yamamoto, A. Application of a numerical simulation to the estimation of wind loads on photovoltaic panels installed parallel to sloped roofs of residential houses. Wind 2022, 2, 129–149. [Google Scholar] [CrossRef]
- Wood, G.; Denoon, R.; Kwok, K. Wind loads on industrial solar panel arrays and supporting roof structure. Wind Struct. Int. J. 2001, 4, 481–494. [Google Scholar] [CrossRef]
- Erwin, J.; Bitsuamlak, G.; Chowdhury, A.G.; Barkaszi, S.; Gamble, S. Full scale and wind tunnel testing of a photovoltaic panel mounted on residential roofs. Atc Sei Conf. Adv. Hurric. Eng. 2012, 12, 471–482. [Google Scholar]
- Schellenberg, A.; Maffei, J.; Telleen, K.; Ward, R. Structural analysis and application of wind loads to solar arrays. J. Wind Eng. Ind. Aerodyn. 2013, 123, 261–272. [Google Scholar] [CrossRef]
- Kopp, G.A.; Farquhar, S.; Morrison, M.J. Aerodynamic mechanisms for wind loads on tilted, roof-mounted, solar arrays. J. Wind Eng. Ind. Aerodyn. 2012, 111, 40–52. [Google Scholar] [CrossRef]
- Cao, J.; Yoshida, A.; Saha, P.K.; Tamura, Y. Wind loading characteristics of solar arrays mounted on flat roofs. J. Wind Eng. Ind. Aerodyn. 2013, 123, 214–225. [Google Scholar] [CrossRef]
- Wang, J.X.; Yang, Q.S.; Tamura, Y. Effects of building parameters on wind loads on flat-roof-mounted solar arrays. J. Wind Eng. Ind. Aerodyn. 2018, 174, 210–224. [Google Scholar] [CrossRef]
- Alrawashdeh, H.; Stathopoulos, T. Wind loads on solar panels mounted on flat roofs: Effect of geometric scale. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104339. [Google Scholar] [CrossRef]
- Shen, Q.; Uselton, S.; Pang, A. Comparisons of wind tunnel experiments and computational fluid dynamics simulations. J. Vis. 2003, 6, 31–39. [Google Scholar] [CrossRef]
- Dodge, L.G.; Schwalb, J.A. Fuel spray evolution: Comparison of experiment and CFD simulation of nonevaporating spray. J. Eng. Gas Turbines Power 1989, 111, 15–23. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Thordal, M.S.; Bennetsen, J.C.; Koss, H.H.H. Review for practical application of CFD for the determination of wind load on high-rise buildings. J. Wind Eng. Ind. Aerodyn. 2019, 186, 155–168. [Google Scholar] [CrossRef]
- Paterson, D.A.; Papenfuss, A.T. Computation of wind flow around two tall buildings. J. Wind Eng. Ind. Aerodyn. 1993, 50, 69–74. [Google Scholar] [CrossRef]
- Su, K.C.; Chung, K.M.; Hsu, S.T. Numerical simulation of wind loads on solar panels. Mod. Phys. Lett. B 2018, 32, 1840009. [Google Scholar] [CrossRef]
- Meroney, R.N.; Neff, D.E. Wind effects on roof-mounted solar photovoltaic arrays: CFD and wind-tunnel evaluation. In Proceedings of the Fifth International Symposium on Computational Wind Engineering, Chapel Hill, NC, USA, 23–27 May 2010. [Google Scholar]
- Shademan, M.; Barron, R.M.; Balachandar, R.; Hangan, H. Numerical simulation of wind loading on ground-mounted solar panels at different flow configurations. Can. J. Civ. Eng. 2014, 41, 728–738. [Google Scholar] [CrossRef]
- Jubayer, C.M.; Hangan, H. A numerical approach to the investigation of wind loading on an array of ground mounted solar photovoltaic (PV) panels. J. Wind Eng. Ind. Aerodyn. 2016, 153, 60–70. [Google Scholar] [CrossRef]
- Choi, S.M.; Lee, G.R.; Park, C.D.; Cho, S.H.; Lim, B.J. Wind load on the solar panel array of a floating photovoltaic system under extreme hurricane conditions. Sustain. Energy Technol. Assess. 2021, 48, 101616. [Google Scholar] [CrossRef]
- Bitsuamlak, G.T.; Dagnew, A.K.; Erwin, J. Evaluation of wind loads on solar panel modules using CFD. In Proceedings of the Fifth International Symposium on Computational Wind Engineering, Chapel Hill, NC, USA, 23–27 May 2010. [Google Scholar]
- Wang, J.X.; Yang, Q.S.; Van Phuc, P.; Tamura, Y. Characteristics of conical vortices and their effects on wind pressures on flat-roof-mounted solar arrays by LES. J. Wind Eng. Ind. Aerodyn. 2020, 200, 104146. [Google Scholar] [CrossRef]
- Wang, J.X.; Van, P.h.u.c.P.; Yang, Q.S.; Tamura, Y. LES study of wind pressure and flow characteristics of flat-roof-mounted solar arrays. J. Wind Eng. Ind. Aerodyn. 2020, 198, 104096. [Google Scholar] [CrossRef]
- Xie, Z.T.; Castro, I.P. Large-eddy simulation for flow and dispersion in urban streets. Atmos. Environ. 2009, 43, 2174–2185. [Google Scholar] [CrossRef]
- Zheng, D.Q.; Zhang, A.S.; Gu, M. Improvement of inflow boundary condition in large eddy simulation of flow around tall building. Eng. Appl. Comput. Fluid Mech. 2012, 6, 633–647. [Google Scholar] [CrossRef]
- Jubayer, C.M.; Hangan, H. Numerical simulation of wind loading on photovoltaic panels. In Proceedings of the Structures Congress 2012, Chicago, IL, USA, 29–31 March 2012. [Google Scholar]
- Li, J.; Tong, L.; Wu, J.; Pan, Y. Numerical investigation of wind influences on photovoltaic arrays mounted on roof. Eng. Appl. Comput. Fluid Mech. 2019, 13, 905–922. [Google Scholar] [CrossRef]
- Fogaing, M.B.T.; Hemmati, A.; Lange, C.F.; Fleck, B.A. Performance of turbulence models in simulating wind loads on photovoltaic modules. Energies 2019, 12, 3290. [Google Scholar] [CrossRef]
- Irtaza, H.; Ashish, A. CFD simulation of turbulent wind effect on an array of ground-mounted solar PV panels. J. Inst. Eng. (India) Ser. 2018, 99, 205–218. [Google Scholar] [CrossRef]
- Aly, A.M. On the evaluation of wind loads on solar panels: The scale issue. Sol. Energy 2016, 135, 423–434. [Google Scholar] [CrossRef]
- Vita, G.; Salvadori, S.; Misul, D.A.; Hemida, H. Effects of inflow condition on RANS and LES predictions of the flow around a high-rise building. Fluids 2020, 5, 233. [Google Scholar] [CrossRef]
- Inamuro, T.; Adachi, T.; Sakata, H. Simulation of aerodynamic instability of bluff body. J. Wind Eng. Ind. Aerodyn. 1993, 46/47, 611–618. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W.; Li, B. Numerical investigation on VIV energy harvesting of bluff bodies with different cross sections in tandem arrangement. Energy 2017, 133, 723–736. [Google Scholar] [CrossRef]
- Shao, J.Y.; Shu, C.; Liu, N.Y.; Zhao, X. Numerical investigation of vortex induced rotation of two square cylinders in tandem arrangement. Ocean Eng. 2019, 171, 485–495. [Google Scholar] [CrossRef]
- Jing, H.Q.; Xia, Y.; Li, H.; Xu, Y.L.; Li, Y.L. Excitation mechanism of rain–wind induced cable vibration in a wind tunnel. J. Fluids Struct. 2017, 68, 32–47. [Google Scholar] [CrossRef]
- Kim, Y.C.; Tamura, Y.; Yoshida, A.; Ito, T.; Shan, W.; Yang, Q. Experimental investigation of aerodynamic vibrations of solar wing system. Adv. Struct. Eng. 2018, 21, 2217–2226. [Google Scholar] [CrossRef]
- Jain, A.; Jones, N.P.; Scanlan, R.H. Coupled flutter and buffeting analysis of long-span bridges. J. Struct. Eng. 1996, 122, 716–725. [Google Scholar] [CrossRef]
- Katsuchi, H.; Jones, N.P.; Scanlan, R.H. Multimode coupled flutter and buffeting analysis of the Akashi-Kaikyo Bridge. J. Struct. Eng. 1999, 125, 60–70. [Google Scholar] [CrossRef]
- Hu, L.; Xu, Y.L. Extreme value of typhoon-induced non-stationary buffeting response of long-span bridges. Probab. Eng. Mech. 2014, 36, 19–27. [Google Scholar] [CrossRef]
- Davenport, A.G. Buffetting of a suspension bridge by storm winds. J. Struct. Div. 1962, 88, 233–270. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Z.D.; Tao, T.Y.; Cheng, H.Y. Field measurement study on the epsd of non-stationary buffeting response of Sutong bridge based on wt. Eng. Mech. 2016, 33, 164–170. [Google Scholar]
- He, X.H.; Tan, L.F.; Gu, J.H.; Jing, H.Q.; Li, S.C. Study on dynamic response of train—Long span cable—Stayed bridge coupling system considering non-stationary crosswind. J. Hunan Univ. (Nat. Sci.) 2022, 49, 92–100. [Google Scholar]
- Hu, J.; Ou, J. Dynamic reliability of the buffeting responses of suspension bridges considering non-gaussian factors. J. Highw. Transp. Res. Dev. (Engl. Ed.) 2013, 7, 39–43. [Google Scholar] [CrossRef]
- Lei, S.; Cui, W.; Patruno, L.; de Miranda, S.; Zhao, L.; Ge, Y. Improved state augmentation method for buffeting analysis of structures subjected to non-stationary wind. Probab. Eng. Mech. 2022, 69, 103309. [Google Scholar] [CrossRef]
- Cui, W.; Zhao, L.; Ge, Y. Non-Gaussian turbulence induced buffeting responses of long-span bridges based on state augmentation method. Eng. Struct. 2022, 254, 113774. [Google Scholar] [CrossRef]
- Xu, Z.; Dai, G.; Zhang, L.; Chen, Y.F.; Flay, R.G.J.; Rao, H. Effect of non-Gaussian turbulence on extreme buffeting response of a high-speed railway sea-crossing bridge. J. Wind Eng. Ind. Aerodyn. 2022, 224, 104981. [Google Scholar] [CrossRef]
- Da Costa, B.M.; Wang, J.; Jakobsen, J.B.; Øiseth, O.A.; Snæbjörnsson, J.þ. Bridge buffeting by skew winds: A revised theory. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104806. [Google Scholar] [CrossRef]
- Li, M.; Li, M.; Sun, Y. Effects of turbulence integral scale on the buffeting response of a long-span suspension bridge. J. Sound Vib. 2021, 490, 115721. [Google Scholar] [CrossRef]
- Xu, Z.D.; Wang, H.; Liu, Z.Q. Buffeting numerical simulation of streamlined steel box girder of longspan cable-supported bridge using fluid-structural interaction. J. Vib. Eng. 2023, 36, 179–187. [Google Scholar]
- Scanlan, R.H.; Tomko, J.J. Airfoil and bridge deck flutter derivatives. J. Eng. Mech. Div. 1971, 97, 1717–1737. [Google Scholar] [CrossRef]
- Chen, A.; He, X.; Xiang, H. Identification of 18 flutter derivatives of bridge decks. J. Wind Eng. Ind. Aerodyn. 2002, 90, 2007–2022. [Google Scholar] [CrossRef]
- Chen, X.; Kareem, A. Revisiting multimode coupled bridge flutter: Some new insights. J. Eng. Mech. 2006, 132, 1115–1123. [Google Scholar] [CrossRef]
- Ge, Y.J.; Tanaka, H. Aerodynamic flutter analysis of cable-supported bridges by multi-mode and full-mode approaches. J. Wind Eng. Ind. Aerodyn. 2000, 86, 123–153. [Google Scholar] [CrossRef]
- Wei, Z.G.; Ge, Y.J.; Yang, Y.X. Effectiveness of storm ropes for long suspension bridge’s flutter control. J. Tongji Univ. (Nat. Sci.) 2008, 36, 1628–1632. [Google Scholar]
- Wang, Q.; Li, Y.L.; Li, Z.G.; Liao, H.L. Flutter derivatives of a thin plate model under different attack angles. Eng. Mech. 2018, 35, 10–16. [Google Scholar]
- Wu, B.; Wang, Q.; Liao, H.L.; Li, Z.G. Flutter mechanism of thin flat plates under different attack angle. J. Vib. Eng. 2020, 33, 667–678. [Google Scholar]
- Huang, D.M.; Lv, Z.H.; Luo, R.D.; Chen, L.J.; Wang, G.H. Study on aerodynamic forces and flutter stability of I-shaped and T-shaped box girders. J. Railw. Sci. Eng. 2022, accepted. [Google Scholar]
- Tang, L.F.; Liu, Z.; Zheng, C.R.; Wu, Y. Investigation on wind-induced responses and aeroelastic effect of a square-sectional super high-rise building under twisted wind flow. J. Build. Struct. 2022, 43, 20–30. [Google Scholar]
- Nomura, T. Finite element analysis of vortex-induced vibrations of bluff cylinders. J. Wind Eng. Ind. Aerodyn. 1993, 46, 587–594. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.S.; Kim, J.D. Prediction of vortex-induced wind loading on long-span bridges. J. Wind Eng. Ind. Aerodyn. 1997, 67, 267–278. [Google Scholar] [CrossRef]
- Matsumoto, M.; Daito, Y.; Kanamura, T.; Shigemura, Y.; Sakuma, S.; Ishizaki, H. Wind-induced vibration of cables of cable-stayed bridges. J. Wind Eng. Ind. Aerodyn. 1998, 74, 1015–1027. [Google Scholar] [CrossRef]
- Huang, M.F.; Tang, G.; Tao, M.X.; Liao, S.; Gao, M.; Nie, X. Wind-induced high-order vibration of a twin-mast with large cross-section at top of Saige Plaza Building. J. Build. Struct. 2022, 43, 1–10. [Google Scholar]
- Xie, D.; Fan, J. Wind vibration analysis of prestressed flexible photovoltaic support system. Build. Struct. 2021, 51, 15–18. [Google Scholar]
- Liu, J.Q.; Li, S.Y.; Luo, J.; Chen, Z.Q. Experimental study on critical wind velocity of a 33-meter-span flexible photovoltaic support structure and its mitigation. J. Wind Eng. Ind. Aerodyn. 2023, 236, 105355. [Google Scholar] [CrossRef]
- Chen, G.B.; Chen, W.L.; Yang, W.H.; Gao, D.L. Suppression of vortex-induced vibration of a box girder using active suction-jet slit. J. Wind Eng. Ind. Aerodyn. 2021, 216, 104713. [Google Scholar] [CrossRef]
- Li, C.G.; Huang, J.W.; Zhang, J.; Han, Y. Aerodynamic optimization measures for VIV performances of a side girder composite beam based on wind tunnel tests. J. Vib. Shock. 2018, 37, 86–92. [Google Scholar]
- Tamimi, V.; Naeeni, S.; Zeinoddini, M. Flow induced vibrations of a sharp edge square cylinder in the wake of a circular cylinder. Appl. Ocean Res. 2017, 66, 117–130. [Google Scholar] [CrossRef]
- Wang, Z.G.; Zhao, F.F.; Ji, C.M.; Peng, X.F.; Lu, H.Q. Analysis of vibration control of multi-row large-span flexible photovoltaic supports. Eng. J. Wuhan Univ. 2020, 53, 29–34. [Google Scholar]
- Wang, Z.G.; Zhao, F.F.; Ji, C.M.; Peng, X.F.; Lu, H.Q. Wind-induced vibration analysis of multi-row and multi-span flexible photovoltaic supports. Eng. J. Wuhan Univ. 2021, 54, 75–79. [Google Scholar]
- Ryan, K.; Thompson, M.C.; Hourigan, K. Variation in the critical mass ratio of a freely oscillating cylinder as a function of Reynolds number. Phys. Fluids 2005, 17, 241. [Google Scholar] [CrossRef]
- Chen, W.; Ji, C.; Williams, J.; Xu, D.; Yang, L.; Cui, Y. Vortex-induced vibrations of three tandem cylinders in laminar cross-flow: Vibration response and galloping mechanism. J. Fluids Struct. 2018, 78, 215–238. [Google Scholar] [CrossRef]
- Li, S.Y.; Wu, T.; Li, S.K.; Gu, M. Numerical study on the mitigation of rain-wind induced vibrations of stay cables with dampers. Wind Struct. 2016, 23, 615–639. [Google Scholar] [CrossRef]
- Hua, X.G.; Chen, Z.Q.; Lei, X.; Wen, Q.; Niu, H.W. Monitoring and control of wind-induced vibrations of hanger ropes of a suspension bridge. Smart Struct. Syst. 2019, 23, 683–693. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Zhu, Y.; Wang, W.; Shu, Z.; Li, Y. A Review on Aerodynamic Characteristics and Wind-Induced Response of Flexible Support Photovoltaic System. Atmosphere 2023, 14, 731. https://doi.org/10.3390/atmos14040731
Chen F, Zhu Y, Wang W, Shu Z, Li Y. A Review on Aerodynamic Characteristics and Wind-Induced Response of Flexible Support Photovoltaic System. Atmosphere. 2023; 14(4):731. https://doi.org/10.3390/atmos14040731
Chicago/Turabian StyleChen, Fubin, Yuzhe Zhu, Weijia Wang, Zhenru Shu, and Yi Li. 2023. "A Review on Aerodynamic Characteristics and Wind-Induced Response of Flexible Support Photovoltaic System" Atmosphere 14, no. 4: 731. https://doi.org/10.3390/atmos14040731
APA StyleChen, F., Zhu, Y., Wang, W., Shu, Z., & Li, Y. (2023). A Review on Aerodynamic Characteristics and Wind-Induced Response of Flexible Support Photovoltaic System. Atmosphere, 14(4), 731. https://doi.org/10.3390/atmos14040731






