Abstract
We explored spectral diversity in infrared (IR, 4–25 μm) imaginary (k) and real (n) indices of refraction (optical constants) for 26 surface soils that originated from global dust entrainment regions. The k spectra were derived from optical transmission spectra of KBr pellets containing dispersed dust and the n spectra were estimated with the subtractive Kramers–Kronig (SKK) method. We compared k and n obtained by this study with previously published values. Our optical constants from the KBr technique are comparable in magnitude and spectral shape to those from previous studies that used dust aerosols re-suspended in a chamber. This suggests that the SKK method can offer a reliable mechanism for measuring IR spectra of both optical constants for soils. The soils used here exhibit additional spectral variability compared with past studies. We note that the appearance and the shift in positions of the strongest absorption peaks are due to combinations of silicates with overlapping absorption, rather than being related to a single mineral. We note that all dust optical constants have substantially lower magnitudes compared to those of pure minerals. Our results can improve estimates of mineral dust radiative effects and support quantification of surface mineral estimates using satellite and ground-based remote sensing.
1. Introduction
Large amounts of dust (i.e., ~1–2 Pg yr−1 globally [1]) are released into the atmosphere from arid and semi-arid environment surface soils [2,3], and concentrations of these wind-borne dust particles have an impact on how electromagnetic radiation is transmitted through the atmosphere [4,5,6]. Minerals have unique absorption and scattering properties [7,8,9,10] and therefore atmospheric dust spectral radiation perturbations depend on dust mineralogical composition [9]. These dust-radiation interactions cause positive or negative direct radiative forcing [4,11,12], which consequently leads to warming or cooling of the Earth, respectively. Radiative properties of dust particles can be estimated using their material optical properties, the imaginary (k) and real (n) indices of refraction [10] and their size and morphology distributions [13]. Calculating the effect of entrained dust on the climate requires knowledge of such radiative properties. In the infrared (IR) spectrum, quartz, carbonates (e.g., calcite and dolomite), feldspars (e.g., K-feldspar and plagioclase), phyllosilicates (e.g., kaolinite and illite), and sulphates (e.g., gypsum) are absorbing minerals in dust aerosols [14]. However, the IR refractive indices (e.g., OPAC [15]) used for climate modeling and remote sensing applications do not fully represent this mineralogical diversity. Missing minerals in dust aerosols can lead to uncertainties in estimating their radiative effect and quantifying their abundance with remote sensing retrievals. Despite past and recent efforts to estimate spectral signatures and magnitude of global dust IR refractive indices e.g., [16,17,18,19,20], there is still significant uncertainty due to the large variabilities in mineralogical content of global soils. For instance, past studies showed that decimal changes in magnitude of k at the wavelength of 10 µm can significantly alter the estimation of radiative effects of dust in atmosphere [19,21].
We recently conducted spectral measurements on 26 surface soil samples from globally important dust entrainment regions (Figure 1a–c) for the purpose of understanding their spectral properties in relation to specific minerals [14]. We considered both geographic and mineralogical diversity when selecting samples for analysis. These soils, from globally significant dust sources regions, likely have mineral compositions similar to those of atmospheric dust particles entrained from them. Depending on the specific mineral content, absorption properties of these samples vary strongly with wavelength and are expected to have a large impact on direct aerosol radiative forcing [14,19,21]. For this study, we measured the IR transmission (~2.5–25 μm) of these samples mixed in KBr pellets and used this transmission to calculate imaginary refractive index (k) spectra. Real index of refraction (n) spectra were consequently derived from these k spectra with a subtractive Kramers–Kronig (SKK) technique [22]. Past studies of dust optical constants, such as Di Biagio et al. [19] (DB 2014) and Di Biagio et al. [20] (DB 2017), measured IR transmission of dust in KBr pellets and re-suspended in a chamber, respectively. In contrast to our study, they applied Lorentz dispersion theory to derive n from k. We compare n and k obtained in our study with values derived from the KBr method (DB 2014) and with those of samples from similar geographic regions (DB 2017).
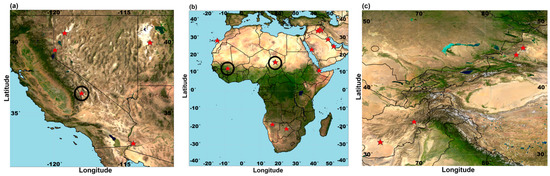
Figure 1.
Stars display soil collection localities in (a) western USA, (b) Africa and Arabian Peninsula, and (c) central and east Asia with two representative samples used from sites marked with black circles. These samples originate from major dust source regions of the world as determined by remote sensing and surface observations [23,24,25]. Appendix A, Table A1 provides more information regarding sample code, location, and collection coordinates of these samples.
Our transmission spectral measurements as well as derived IR refractive indices (both n and k) data are published in a Zenodo archive (https://doi.org/10.5281/zenodo.7672177, accessed on 2 March 2023) for use by the wider climate modeling, remote sensing, and mineral dust communities.
2. Materials and Methods
2.1. Soil Samples and Their Transmission Measurements
The 26 soil samples used in this study originate from numerous dust aerosol source locations throughout the world including the USA (Arizona, California, Nevada, and Utah; Figure 1a), Africa (Chad, Botswana, Djibouti, Mali, Namibia; Figure 1b), Spain (Las Canarias; Figure 1b), Arabian Peninsula (Iraq, Kuwait, Qatar, Saudi Arabia; Figure 1b), and Central and eastern Asia (Afghanistan and China; Figure 1c) [26]. These samples are from the Desert Research Institute (DRI) soils collection [26] and past studies [14,26] measured them to identify their mineralogical compositions using various techniques including reflectance and transmission spectroscopy, optical microscopy, and X-ray diffraction. Here we employed the transmission spectral measurements for these samples to derive their real and imaginary indices of refraction for the first time. For this study we used a subset of these soil samples that were sieved to <38 μm in size [26] and selected for mineralogic and geographic diversity. This size range (<38 μm) is mostly consistent with the particle size and volume distribution measured and estimated for entrained atmospheric dust [27,28], and references in both.
Similar to previous research e.g., [16], we derive the absorption coefficient from transmission spectra of a pellet. As described in Sadrian et al. [14], we blended soil and KBr using a clean mortar and pestle for 2–3 min to ensure uniform dispersion of mineral particles in the KBr matrix. We used a mixture of ~0.5 mg of soil sample with ~200 mg of KBr that was pressed under vacuum for ~5 min at a pressure of ~981 MPa. This procedure produced a hard, transparent pellet 13 mm in diameter. Due to the hygroscopic nature of KBr we immediately placed the pellets in a desiccator box, and measured transmission within 1 to 2 h of preparing the pellet. A benchtop Nicolet 380 Fourier Transform Infrared (FTIR) spectrometer (with a wavelength range from 2.5 to 25 μm and resolution of 4 cm−1) was used to collect the transmission spectrum for each sample. Additionally, we measured a KBr pellet without any sample as a blank. Final transmission measurements were ratioed to this blank and continuum-removed [29] for a consistent baseline of 1.0. Figure 2a,b displays measurements of six representative samples in the wavelength range from 4 to 25 μm with the transmission spectra of pure minerals from Salisbury et al. [30] for comparison. As shown in Figure 2a, carbonates (calcite and dolomite) have unique absorption features near 7, 11.4, and 14 µm [31,32], which are identified in samples S1014 and S1022. In our samples, features at 7 and 11.4 µm arise from the overlapping absorption features in calcite and dolomite. Figure 2b shows representative samples with absorption bands around 9.1, 12–13, and 21.5 μm for quartz (solid lines) [31,32,33] and around 9.5 and 17 μm for feldspar (orthoclase) (dashed lines) [30]. However, most of the samples display strong spectral signatures in the ~7.7–10.4 μm and >15 μm regions that cannot be assigned to any specific mineral but are rather attributed to multiple silicate minerals (quartz, feldspar, phyllosilicates) with overlapping absorptions.
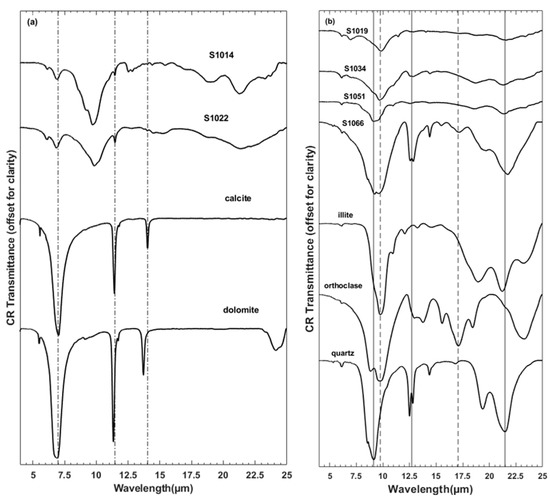
Figure 2.
(a,b) show continuum-removed transmission spectra of six representative soil samples, and pure minerals from Salisbury et al. (1991) [30]. (a) Carbonate in samples is compared with calcite and dolomite absorption features. (b) the strongest silicate absorptions are compared with Si-O bonds in representative silicates (i.e., illite, orthoclase, and quartz). Spectra in both plots are offset for clarity.
2.2. Calculation of IR Refractive Indices
Transmission measurements of KBr-dust pellets have previously been used to estimate the imaginary index of refraction [16,17,18,19]. Transmission data of a sample are related to its absorption coefficient through the Beer–Bouguer–Lambert law [34]:
where t is transmission, βa is absorption coefficient, and x is the path length of radiation, which is (~0.57 mm thickness of the pellet) × (the mass concentration of the dust in KBr) [35]. The imaginary index of refraction (k) is calculated using Equation (2):
where λ is the wavelength. Real (n) and imaginary (k) indices of refraction are tightly coupled through Kramers–Kronig (K–K) relations rather than being allowed to vary independently of one another [36]. For K–K analysis the data should be known across all wavelengths, which is typically not present in most studies. The subtractive Kramers–Kronig (SKK) method [22,37], however, solves this issue by utilizing the widest wavelength domain possible. Because k is only known over a limited wavelength range (2.5–25 µm), the SKK method [22,37] was used in this study to derive n from k. Past studies have successfully used SKK to derive optical constants for a range of minerals [38,39,40,41]. The SKK equation can be written as follows [22]:
where n(λ1) is a known value of the real index of refraction at wavelength λ1, Prin. indicates the Cauchy principal value of the integral, and k(λ) is the imaginary index of refraction at wavelength λ. We implemented the SKK method in MATLAB where we used piecewise-cubic Hermite polynomials to interpolate the complex index of refraction as a function of wavelength. To determine the real refractive index for each wavelength, if λ0 was less than λ1, we divided the integral into three pieces, from λ = 0 to λ0 − ε, λ0 + ε to λ1 − ε, and λ1 + ε to the end of the data. If λ0 was greater than λ1, we did the same procedure but with the appropriate intervals for that case. We computed the SKK integral over each of the regions, summed them, and computed the real refractive index from Equation (3). The MATLAB code we used for SKK is also available through the Zenodo archive (https://doi.org/10.5281/zenodo.7672177, accessed on 2 March 2023).
t(x) = e−βax
k = βaλ/4π
3. Results
3.1. Code Validation
We tested our MATLAB code for SKK by determining values of n from previously published values of k from DB 2017. Figure 3 shows two samples, from Namibia and Taklimakan, and compares values of n using the Lorentz dispersion theory (red dash dot line, DB 2017) and our SKK technique (black line). The shapes and absolute values are within a few %, usually less than 1%. Subtle differences may be due to the method, the assumed value of n(λ1), or that we are only able to integrate SKK from 2.5 to 25 µm, not 0 to ∞. We explored various values of n(λ1) and adopted a single value, n(590 nm) = 1.41, which produced the most accurate fit for n to that determined by DB 2017 (Figure 3). This value is consistent with typical values found in previous studies e.g., [19,20,42,43,44].
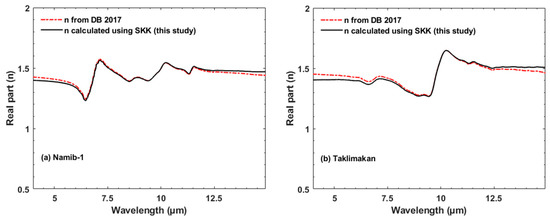
Figure 3.
The real part (n) for Namib-1 (a) and Taklimakan (b) samples [20] that were derived from k using the Lorentz dispersion theory (red line) [20] and our SKK technique (black line).
3.2. Variability of IR Refractive Indices of Global Surface Soils
Figure 4a,b shows calculated imaginary and real indices of refraction for representative samples. We previously described the minerals that present absorption features in the reflectance spectra of these samples [14]. Similar to the transmission spectra (Figure 2), the imaginary indices (k, Figure 4a) show large variation due to differences in mineralogy among the samples.
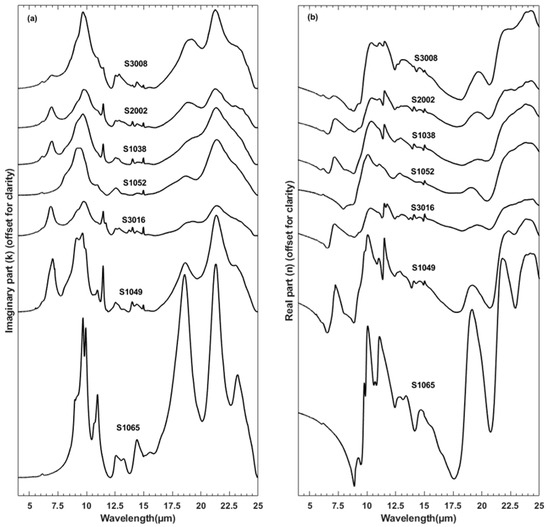
Figure 4.
(a) k and (b) n values derived in this study. Spectra in both plots are offset for clarity. Samples were selected to show diversity. The Zenodo archive (https://doi.org/10.5281/zenodo.7672177, accessed on 2 March 2023) includes values for all 26 samples.
Clay minerals are common in these samples but only some samples show diagnostic phyllosilicate features. For example, sample S1065 contains the most diagnostic kaolinite absorption features near 9, 9.2–10.4, 10.9, 12–13.7, 14.35, and >16 µm. Sample S1049 has kaolinite features near 9.65 and 10.9 µm. However, kaolinite features are weakened or altered at other wavelengths, e.g., at the shoulder near 9 µm and the absorption bands near 12.55 and 21.25 μm. The 10.9 μm band is weaker and modified in samples S1052, S2002, and S3008, which could be due to either other clay minerals (e.g., illite or montmorillonite) or combinations of clays (e.g., illite, montmorillonite, and kaolinite) rather than being representative of only kaolinite.
Quartz is another common component of these samples, yet the majority of samples do not show absorption that can be uniquely attributed to quartz. Rather, the broad and strong absorption feature from ~7.7 to 10.45 μm reflects that of multiple, overlapping silicate features from quartz, feldspars, and phyllosilicates. However, the subtle shoulder near 9.1 μm in samples S3008, S2002, S1038, and S3016 can be attributed to quartz alone. Depending on which combinations of silicates exist in the sample, the peak for this strong absorption will center on different wavelengths. For example, S3008 has the absorption band peak near 9.65 μm while S1052 has its peak about 0.3 μm below near 9.35 μm, in part because sample S3008 additionally contains orthoclase (K-feldspar). As Sadrian et al. [14] discussed, the doublet or triplet absorption peaks that appear ≳16 µm in S3008, S2002, S1038, S1052, and S3016 are also due to combinations of various silicate minerals. Some features are due to quartz and clays, such as the doublet absorption peaks between 12 and 13 μm in samples S3008, S2002, and S3016, which is ascribed to combinations of quartz and muscovite [14].
Carbonates are more diagnostically identified. Sample S1049 displays features for calcite near 7, 11.44, and 14 µm. However, it is often difficult to discriminate between calcite and dolomite as both the 7 and 11 μm features overlap. This is observed in samples S2002 and S3008.
The derived IR real indices of refraction (n, Figure 4b) similarly show a large diversity in their spectra due to the variability in mineralogical composition. A quick comparison reveals a higher diversity in most n spectra estimated in this study (Figure 4b) than in those previously presented by DB 2017. We will compare and contrast our data and DB 2017 in more detail in Section 4.2. For absolute values of k and n, see the plots in later figures as well as the archived data (https://doi.org/10.5281/zenodo.7672177, accessed on 2 March 2023).
4. Comparison with Past Studies
4.1. k Using Dust-KBr Pellets
Both this study and DB 2014 used transmission spectra of dust-KBr pellets to derive k. As shown in Figure 5, we compared our values (solid lines) to those from DB 2014 (dash-dot lines). Although we examined all data, Figure 5 compares only selected samples as examples. Sample S1065, (Section 3.2. Figure 4), has distinct absorption features attributed to kaolinite. Similar to S1065, almost all DB 2014 samples clearly display the kaolinite doublet ~9.2–10.4 µm and a peak near 10.9 µm. However, in sample N93 (DB 2014) the peak near 9.70 µm has become a shoulder, likely due to the overlapping features from other silicates. The shoulder near 9 µm, seen in all spectra in Figure 5, is also caused by contributions from quartz in addition to kaolinite in these samples. With the exception of SOP1–8 (DB 2014), all DB 2014 samples have triplet peaks at >18 μm whose center wavelengths are less than 0.1 µm offset. Similar to features at shorter wavelengths, we interpret these modifications of shape and strength to be due to overlapping absorption from various silicate minerals. Comparison of S1065, DB 2014 samples, and S3008 suggest that the absorption peak center between 9.2–10.4 µm in the latter is ~12 nanometer shifted to shorter wavelength. This could mainly be due to the contributions from K-feldspars (orthoclase) [14]. Sample S3008 also shows stronger carbonate absorptions near 7 and 11.4 µm, as well as a stronger quartz absorption between 12 and 13 µm. The only DB 2014 sample that has weak discernible carbonate peaks is N93. In general, our samples have higher spectral diversity than those presented in DB 2014.
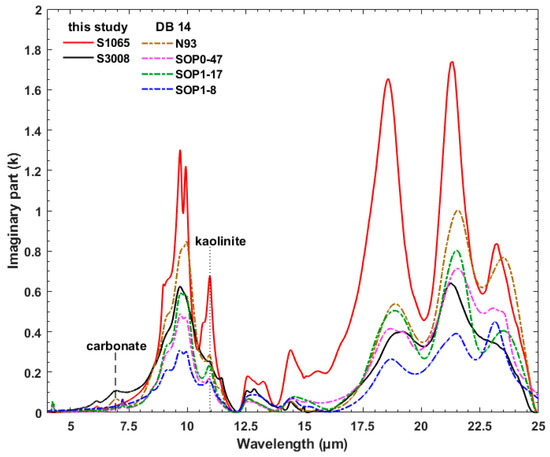
Figure 5.
k spectra obtained in this study (solid lines) are compared with those derived by Di Biagio et al. [19] (dash-dot lines). Vertical dashed and dotted lines represent carbonate and kaolinite absorption features near 7 and 10.9 µm, respectively.
4.2. k and n from Suspended Dust Aerosols
Here we compare IR k and n spectra that we determined using KBr pellets and SSK techniques with the results from DB 2017 that were obtained from transmission measurements of soil suspended in a chamber and Lorentz dispersion theory. We selected samples from both studies that are from the same general geographic locations, though not the same exact sites. As shown in Figure 6a–f (left panel), k for samples from the same regions are often in a good agreement in terms of magnitude, intensity, position, and shape of the strongest absorption peak between ~7.7 and 10.45 μm. For example, Taklimakan samples from this study (S1014, black line) and DB17 (blue line) (Figure 6a) display good agreement in their magnitude and absorption peaks positions. Features near 7 and 11.4 μm are attributed to carbonates, between ~7.7 and 10.45 μm to clays such as montmorillonite, muscovite, and kaolinite, near 9.1 and between 12 and 13 μm to quartz. Considering all geographic regions (Figure 6a–f), the DB 17 samples have stronger carbonate absorptions in the Gobi and Namibian samples. Our Arizona sample has a very strong quartz doublet between 12 and 13 μm and a broader spectral envelope from 7 to 11 μm. The North Africa sample (Figure 6d) shows large differences in the absolute value of both n and k (~6x increase in magnitude of k, ~8x increase in the amplitude of the excursion in n), though good agreement in shape. Figure 6f compares samples from Saudi Arabia with samples from Afghanistan. All three samples show similar features though our sample from Saudi Arabia is lacking carbonate, which is seen in our sample from Afghanistan. As can be expected, this confirms that soils from distinct geographical locations contain comparable spectral features if they have similar mineral contents.
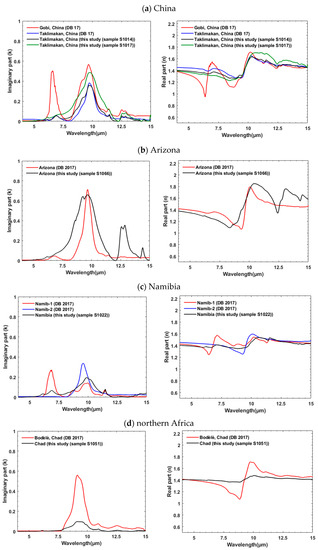
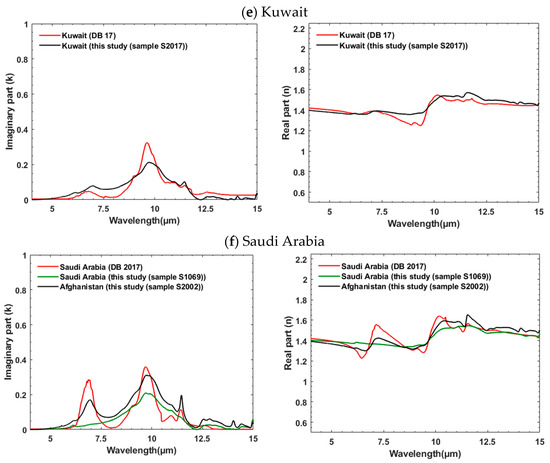
Figure 6.
(a–f) comparison of k (left panel) and n (right panel) obtained from this study with the ones determined by Di Biagio et al. (2017) [20] for samples from similar geographic locations. Figure 6f compares samples from both Saudi Arabia and Afghanistan to illustrate comparable spectral diversity linked to their similar mineralogical content.
Real indices of refraction (n) obtained from this study and DB 17 illustrate good agreement in their magnitudes (typically ~<10%) (right panel, Figure 6a–f) but some spectral shape variations exist. These differences follow those observed in the imaginary component k. For example, the stronger, distinct peaks between 5 and 7.5 μm and between 7.5 and 10 μm for Gobi (red line, right panel, Figure 6a), between 6.5 and 8.5 μm for Namib-1 (red line, right panel, Figure 6c), or between 7.5 and 10 μm and between 9 and 11 μm for Bodélé (red line, right panel, Figure 6d) are from variations in mineralogical composition. In general, the derived values of n from this study show a higher spectral diversity (see Figure 3) compared to those from DB 2017.
5. Discussion
One distinction between our work and that of DB2014 is that we collected surface soil samples, while DB2014 collected airborne dust samples from limited geographic locations (Niger and Algeria). This may have reduced the number of coarser particles (e.g., quartz and feldspars), and therefore their influence on spectral signatures appearing in derived k spectra. The DB 2014 study also performed a nine-point running average to smooth the dust-KBr spectra, which may have led to modifications, distortion, or weakening of some features. In general, the spectra presented in our work have more distinct mineral features compared to those presented by DB 2014.
The DB 2017 study interpreted shifts in absorption band centers, observed by DB 2014 at ~7.7–10.45 μm, to longer wavelengths, relative to those observed by Volz [17], to the use of the KBr pellet technique. However, as shown in Figure 5, and observed in the k spectra of all soil samples we measured, the ~7.7–10.45 μm absorption band can change their peak position towards shorter (~7.7 μm) or longer wavelengths (~10.45 μm) based on the mineralogical content of the samples. For example, the dust samples from both DB 2014 and Volz [17] mainly contain clays and therefore their absorption is shifted to longer wavelengths. Sample S3008 (Figure 5), which is dominated by feldspar and quartz [14,26], has an absorption peak at shorter wavelengths.
Due to dominance of clay minerals in both the DB 2014 and DB 2017 samples [19,20], they concluded that earlier work likely overestimated the strength of absorption between 12 and 13 μm due to quartz. They determined a maximum value for the imaginary index of ~0.12 in this wavelength region. However, our results show a k value for quartz of ~0.36, which is much closer to the magnitude of ~0.48 found by OPAC [15]. This suggests that prior work by Volz [17] and Fouquart et al. [18] did not overestimate the strength of quartz absorption in this wavelength range, but rather values are strongly dependent on sample mineral composition.
In addition, for our measured samples, the strongest excursion of the refractive indices in the wavelength range ~8–12 μm was between ~0.77 and ~2.1 for the real values and ~0.002 and ~1.3 for imaginary values (https://doi.org/10.5281/zenodo.7672177, accessed on 2 March 2023). Our imaginary values are similar to those reported by Volz [16,17], Fouquart et al. [18], DB 2014; DB 2017; and OPAC. Our minimum for the real values is similar to prior studies but our highest values are lower than those determined by Volz [17] and OPAC.
While our values for the imaginary indices are similar to those of previous studies on dust aerosols, peak values are as much as 50% lower than imaginary indices reported for pure minerals (e.g., quartz by Wenrich and Christensen [45], Spitzer and Kleinman [33], and Herbin, et al. [46], illite by Querry [47] and Glotch et al. [48]; kaolinite by Glotch et al. [48]). In addition to the mineral assemblages that will weaken, distort, or even obscure individual mineral features [14], minerals in soils will also undergo physical processes as well as chemical reactions and thus may possess a different physico-chemical characteristics which may weaken the overall absorption when compared to pure mineral samples.
6. Conclusions
In this study, we investigated the variability in complex refractive indices in global soil samples. We derived imaginary index (k) from KBr pellet transmission data. Then, the real index (n) was retrieved from k using a Subtractive Kramers–Kronig (SKK) technique [22]. The result of our calculations showed that using the same input value of k the SKK method provides real indices that are comparable to the computationally more complicated Lorentz approach. We compared our results with k and n obtained in past studies, which revealed additional spectral diversity. These spectral variations are linked to higher mineral diversity and will help improve regional models of mineral dust radiative forcing. We note that many silicate minerals contribute to spectra where absorption is strongest, and few samples exhibit absorption peaks due to a single mineral (Figure 4a).
When compared with prior studies for samples from the same geographic regions (Figure 6) we generally see good spectral agreement. With some exceptions, the magnitude and spectral shape of both k and n are similar between this study and DB 2017. Although these two studies used different measurement and computational techniques, we have similar results. Thus, our sieved soil samples have comparable spectral characteristics to those of mineral dust aerosols. Our results for both k and n encompass the range of refractive indices documented by prior studies [16,17,18,19,20]. These results are in contrast with DB 2017′s conclusion that some peaks and intensities presented in other studies were over- or under-estimated.
The work presented here introduces additional spectral diversity to the collection of complex refractive indices from mineral dust aerosols. This underscores the importance of further dust analysis from diverse mineralogical regions. Such studies would further improve the dust parameters of climate models [49,50]. The data from this research can further validate and constrain the optical constants estimated using data returned by EMIT and SBG [51,52]. The calculated optical constants can also be incorporated into radiative transfer models e.g., [53], to estimate mineral abundances from reflectance spectra measured by satellite remote sensing and in the laboratory e.g., [54,55,56,57,58,59,60].
Author Contributions
Methodology, data curation, formal analysis, investigation, writing—original draft preparation, M.R.S.; conceptualization, M.R.S. and W.M.C.; funding acquisition, project administration, supervision, W.M.C.; software, A.E.P. and M.R.S.; writing—review and editing, M.R.S., W.M.C., J.P.E., H.M. and A.E.P.; resources, W.M.C., J.P.E. and H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the UNR Graduate Student Association Graduate Research Grant and Travel Grant programs, the College of Science Dean’s Office, Nevada NASA EPSCoR Research Infrastructure Seed Grant 18–83 from Federal Award Number NNX15AK48a, and co-author Wendy M. Calvin’s discretionary funds. The work of H.M. was supported in part by NASA grant 80NSSC20M0205 (PACE SAT Project: PACE UV ROAD).
Data Availability Statement
Real and imaginary indices and transmission spectral data produced for this study as well as the MATLAB code for Subtractive Kramers–Kronig are available through Zenodo Digital Repository [61] at https://doi.org/10.5281/zenodo.7672177 (accessed on 2 March 2023).
Acknowledgments
The authors wish to thank the UNR Chemistry Department Shared Instrumentation Laboratory and Vera Samburova for making FTIR and analytical balance facilities available.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Table displays the global soil samples codes, locations, collection coordinates [26], and the Figure numbers, in which they were plotted in this paper.
Table A1.
Table displays the global soil samples codes, locations, collection coordinates [26], and the Figure numbers, in which they were plotted in this paper.
| Sample Code | Country | Collection Coordinates | Transmission and Refractive Indices in Figures |
|---|---|---|---|
| S1009 | Mali | 12°41′17″ N, 8°01′39″ W | - |
| S1010 | Mali | 12°41′17″ N, 8°01′39″ W | - |
| S1014 | China | 45°03′47.4″ N, 84°42′11″ E | Figure 2 and Figure 6 |
| S1017 | China | 46°07′30.8″ N, 85°44′11.6″ E | Figure 6 |
| S1019 | USA | 36°28′2.86″ N, 118°1′41.49″ W | Figure 2 |
| S1022 | Namibia | 18°43′35.92″ S, 17°0′43.89″ E | Figure 2 and Figure 6 |
| S1034 | Spain-Las Canarias | 28°19′40.47″ N, 13°54′43.63″ W | Figure 2 |
| S1038 | Botswana | 21°12′32.42″ S, 24°51′30.47″ E | Figure 4 |
| S1045 | USA | 40°45′10.57″ N, 119°13′59.38″ W | - |
| S1049 | Chad | 16°08′08.34″ N, 18°35′55.80″ E | Figure 4 |
| S1051 | Chad | 16°13′16.38″ N, 18°36′23.82″ E | Figure 2 and Figure 6 |
| S1052 | USA | 39°32′50.58″ N, 119°54′46.53″ W | Figure 4 |
| S1053 | USA | 39°32′45.30″ N, 119°54′56.62″ W | - |
| S1065 | USA | NA | Figure 4 and Figure 5 |
| S1066 | USA | NA | Figure 2 and Figure 6 |
| S1069 | Saudi Arabia | 23°19′55.99″ N, 38°56′53.30″ E | Figure 6 |
| S2001 | Djibouti | 11°32′34.32″ N, 43°09′35.72″ E | - |
| S2002 | Afghanistan | 34°56′25.59″ N, 69°17′6.87″ E | Figure 4 and Figure 6 |
| S2004 | Qatar | 25° 7′4.50″ N, 51°18′59.63″ E | - |
| S2006 | Iraq | 33°56′38.64″ N, 44°21′23.37″ E | - |
| S2009 | Iraq | 34°40′31.27″ N, 43°33′16.94″ E | - |
| S2011 | Iraq | 33°47′28.25″ N, 42°27′24.38″ E | - |
| S2016 | Afghanistan | 31°51′50.13″ N, 64°11′42.75″ E | - |
| S2017 | Kuwait | 29°02′30.66″ N, 48°07′04.79″ E | Figure 6 |
| S3008 | USA | 32°54′25.43″ N, 114°21′20.72″ W | Figure 4 and Figure 5 |
| S3016 | USA | 40°04′36.84″ N, 113°10′14.88″ W | Figure 4 |
NA = Not applicable.
References
- Tanaka, T.Y.; Chiba, M. A numerical study of the contributions of dust source regions to the global dust budget. Glob. Planet. Chang. 2006, 52, 88–104. [Google Scholar] [CrossRef]
- Gillies, J.A. Fundamentals of Aeolian Sediment Transport: Dust Emissions and Transport—Near Surface. In Treatise on Geomorphology; John, F.S., Lancaster, N., Eds.; Academic Press: San Diego, CA, USA, 2013; Volume 11, pp. 43–63. [Google Scholar]
- Goudie, A.; Middleton, N. Desert Dust in the Global System; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–287. [Google Scholar] [CrossRef]
- Miller, R.L.; Tegen, I. Climate Response to Soil Dust Aerosols. J. Clim. 1998, 11, 3247–3267. [Google Scholar] [CrossRef]
- Liao, H.; Seinfeld, J.H. Radiative forcing by mineral dust aerosols: Sensitivity to key variables. J. Geophys. Res. Atmos. 1998, 103, 31637–31645. [Google Scholar] [CrossRef]
- Tegen, I.; Lacis, A.A. Modeling of particle size distribution and its influence on the radiative properties of mineral dust aerosol. J. Geophys. Res. Atmos. 1996, 101, 19237–19244. [Google Scholar] [CrossRef]
- Lafon, S.; Sokolik, I.N.; Rajot, J.L.; Caquineau, S.; Gaudichet, A. Characterization of iron oxides in mineral dust aerosols: Implications for light absorption. J. Geophys. Res. Atmos. 2006, 111, 19. [Google Scholar] [CrossRef]
- Linke, C.; Möhler, O.; Veres, A.; Mohácsi, Á.; Bozóki, Z.; Szabó, G.; Schnaiter, M. Optical properties and mineralogical composition of different Saharan mineral dust samples: A laboratory study. Atmos. Chem. Phys. 2006, 6, 3315–3323. [Google Scholar] [CrossRef]
- Sokolik, I.N.; Toon, O.B.; Bergstrom, R.W. Modeling the radiative characteristics of airborne mineral aerosols at infrared wavelengths. J. Geophys. Res. Atmos. 1998, 103, 8813–8826. [Google Scholar] [CrossRef]
- Sokolik, I.N.; Toon, O.B. Incorporation of mineralogical composition into models of the radiative properties of mineral aerosol from UV to IR wavelengths. J. Geophys. Res. Atmos. 1999, 104, 9423–9444. [Google Scholar] [CrossRef]
- Tegen, I.; Lacis, A.A.; Fung, I. The influence on climate forcing of mineral aerosols from disturbed soils. Nature 1996, 380, 419–422. [Google Scholar] [CrossRef]
- Hansen, J.E.; Sato, M.; Lacis, A.; Ruedy, R.; Tegen, I.; Matthews, E. Climate forcings in the Industrial era. Proc. Natl. Acad. Sci. USA 1998, 95, 12753–12758. [Google Scholar] [CrossRef]
- Durant, A.J.; Harrison, S.P.; Watson, I.M.; Balkanski, Y. Sensitivity of direct radiative forcing by mineral dust to particle characteristics. Prog. Phys. Geogr. Earth Environ. 2009, 33, 80–102. [Google Scholar] [CrossRef]
- Sadrian, M.R.; Calvin, W.M.; Engelbrecht, J.P.; Moosmüller, H. Spectral Characterization of Parent Soils from Globally Important Dust Aerosol Entrainment Regions. J. Geophys. Res. Atmos. 2023, 128, e2022JD037666. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical Properties of Aerosols and Clouds: The Software Package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Volz, F.E. Infrared Refractive Index of Atmospheric Aerosol Substances. Appl. Opt. 1972, 11, 755–759. [Google Scholar] [CrossRef]
- Volz, F.E. Infrared Optical Constants of Ammonium Sulfate, Sahara Dust, Volcanic Pumice, and Flyash. Appl. Opt. 1973, 12, 564–568. [Google Scholar] [CrossRef]
- Fouquart, Y.; Bonnel, B.; Brogniez, G.; Buriez, J.C.; Smith, L.; Morcrette, J.J.; Cerf, A. Observations of Saharan Aerosols—Results of ECLATS Field Experiment. 2. Broad-Band Radiative Characteristics of the Aerosols and Vertical Radiative Flux Divergence. J. Clim. Appl. Meteorol. 1987, 26, 38–52. [Google Scholar] [CrossRef]
- Di Biagio, C.; Boucher, H.; Caquineau, S.; Chevaillier, S.; Cuesta, J.; Formenti, P. Variability of the infrared complex refractive index of African mineral dust: Experimental estimation and implications for radiative transfer and satellite remote sensing. Atmos. Chem. Phys. 2014, 14, 11093–11116. [Google Scholar] [CrossRef]
- Di Biagio, C.; Formenti, P.; Balkanski, Y.; Caponi, L.; Cazaunau, M.; Pangui, E.; Journet, E.; Nowak, S.; Caquineau, S.; Andreae, M.O.; et al. Global scale variability of the mineral dust long-wave refractive index: A new dataset of in situ measurements for climate modeling and remote sensing. Atmos. Chem. Phys. 2017, 17, 1901–1929. [Google Scholar] [CrossRef]
- Highwood, E.J.; Haywood, J.M.; Silverstone, M.D.; Newman, S.; Taylor, J.P. Radiative properties and direct effect of Saharan dust measured by the C-130 aircraft during Saharan Dust Experiment (SHADE): 2. Terrestrial spectrum. J. Geophys. Res. Atmos. 2003, 108, 13. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical Constants of Water in the 200-nm to 200-μm Wavelength Region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef]
- Ginoux, P.; Prospero, J.M.; Gill, T.E.; Hsu, N.C.; Zhao, M. Global-scale attribution of anthropogenic and natural dust sources and their emission rates based on MODIS Deep Blue aerosol products. Rev. Geophys. 2012, 50, 36. [Google Scholar] [CrossRef]
- Prospero, J.M.; Ginoux, P.; Torres, O.; Nicholson, S.E.; Gill, T.E. Environmental characterization of global sources of atmospheric soil dust identified with the Nimbus 7 Total Ozone Mapping Spectrometer (TOMS) absorbing aerosol product. Rev. Geophys. 2002, 40, 31. [Google Scholar] [CrossRef]
- Washington, R.; Todd, M.; Middleton, N.J.; Goudie, A.S. Dust-Storm Source Areas Determined by the Total Ozone Monitoring Spectrometer and Surface Observations. Ann. Assoc. Am. Geogr. 2003, 93, 297–313. [Google Scholar] [CrossRef]
- Engelbrecht, J.P.; Moosmüller, H.; Pincock, S.; Jayanty, R.K.M.; Lersch, T.; Casuccio, G. Technical note: Mineralogical, chemical, morphological, and optical interrelationships of mineral dust re-suspensions. Atmos. Chem. Phys. 2016, 16, 10809–10830. [Google Scholar] [CrossRef]
- Mahowald, N.; Albani, S.; Kok, J.F.; Engelstaeder, S.; Scanza, R.; Ward, D.S.; Flanner, M.G. The size distribution of desert dust aerosols and its impact on the Earth system. Aeolian Res. 2014, 15, 53–71. [Google Scholar] [CrossRef]
- Adebiyi, A.A.; Kok, J.F. Climate models miss most of the coarse dust in the atmosphere. Sci. Adv. 2020, 6, eaaz9507. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Salisbury, J.W.; Walter, L.S.; Vergo, N.; DAria, D.M. Infrared (2.1–25 μm) Spectra of Minerals; Johns Hopkins University Press: Baltimore, Maryland, 1991; ISBN 978-0801844232. [Google Scholar]
- Salisbury, J.W.; Hapke, B.; Eastes, J.W. Usefulness of weak bands in midinfrared remote sensing of particulate planetary surfaces. J. Geophys. Res. Atmos. 1987, 92, 702–710. [Google Scholar] [CrossRef]
- Salisbury, J.W.; Wald, A. The role of volume scattering in reducing spectral contrast of reststrahlen bands in spectra of powdered minerals. Icarus 1992, 96, 121–128. [Google Scholar] [CrossRef]
- Spitzer, W.G.; Kleinman, D.A. Infrared Lattice Bands of Quartz. Phys. Rev. 1961, 121, 1324–1335. [Google Scholar] [CrossRef]
- Petty, G.W. Reflection and Refraction. In A First Course in Atmospheric Radiation, 2nd ed.; Sundog Publishing: Madison, WI, USA, 2006; pp. 55–69. ISBN 978-0-9729033-1-8. [Google Scholar]
- Estep-Barnes, P.A. Infrared spectroscopy. In Physical Methods in Determinative Mineralogy; Zussman, J., Ed.; Academic Press: London, UK, 1977; pp. 529–603. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-Interscience: New York, NY, USA, 1983; ISBN 0-471-05772-X. [Google Scholar]
- Warren, S.G. Optical constants of ice from the ultraviolet to the microwave. Appl. Opt. 1984, 23, 1206–1225. [Google Scholar] [CrossRef]
- Dalton, J.B.; Pitman, K.M. Low temperature optical constants of some hydrated sulfates relevant to planetary surfaces. J. Geophys. Res. Atmos. 2012, 117, 15. [Google Scholar] [CrossRef]
- Pitman, K.M.; Dobrea, E.Z.N.; Jamieson, C.S.; Dalton, I.J.B.; Abbey, W.J.; Joseph, E. Reflectance spectroscopy and optical functions for hydrated Fe-sulfates. Am. Miner. 2014, 99, 1593–1603. [Google Scholar] [CrossRef]
- Roush, T.L.; Esposito, F.; Rossman, G.R.; Colangeli, L. Estimated optical constants of gypsum in the regions of weak absorptions: Application of scattering theories and comparisons to independent measurements. J. Geophys. Res. Atmos. 2007, 112, 17. [Google Scholar] [CrossRef]
- Roush, T.L. Estimation of visible, near-, and mid-infrared complex refractive indices of calcite, dolomite, and magnesite. Icarus 2020, 354, 114056. [Google Scholar] [CrossRef]
- Di Biagio, C.; Formenti, P.; Balkanski, Y.; Caponi, L.; Cazaunau, M.; Pangui, E.; Journet, E.; Nowak, S.; Andreae, M.O.; Kandler, K.; et al. Complex refractive indices and single-scattering albedo of global dust aerosols in the shortwave spectrum and relationship to size and iron content. Atmos. Chem. Phys. 2019, 19, 15503–15531. [Google Scholar] [CrossRef]
- Osborne, S.R.; Johnson, B.T.; Haywood, J.M.; Baran, A.J.; Harrison, M.A.J.; McConnell, C.L. Physical and optical properties of mineral dust aerosol during the Dust and Biomass-burning Experiment. J. Geophys. Res. Atmos. 2008, 113, 14. [Google Scholar] [CrossRef]
- McConnell, C.L.; Formenti, P.; Highwood, E.J.; Harrison, M.A.J. Using aircraft measurements to determine the refractive index of Saharan dust during the DODO Experiments. Atmos. Chem. Phys. 2010, 10, 3081–3098. [Google Scholar] [CrossRef]
- Wenrich, M.L.; Christensen, P.R. Optical constants of minerals derived from emission spectroscopy: Application to quartz. J. Geophys. Res. Solid Earth 1996, 101, 15921–15931. [Google Scholar] [CrossRef]
- Herbin, H.; Deschutter, L.; Deguine, A.; Petitprez, D. Complex refractive index of crystalline quartz particles from UV to thermal infrared. Aerosol Sci. Technol. 2023, 57, 255–265. [Google Scholar] [CrossRef]
- Querry, M.R. Optical Constants of Minerals and Other Materials from the Millimeter to the Ultraviolet, Report CRDEC-CR-88009; US Army Armament Munitions Chemical Command: Kansas City, MO, USA, 1987. [Google Scholar]
- Glotch, T.D.; Rossman, G.R.; Aharonson, O. Mid-infrared (5–100 μm) reflectance spectra and optical constants of ten phyllosilicate minerals. Icarus 2007, 192, 605–622. [Google Scholar] [CrossRef]
- Li, L.; Mahowald, N.M.; Miller, R.L.; García-Pando, C.P.; Klose, M.; Hamilton, D.S.; Ageitos, M.G.; Ginoux, P.; Balkanski, Y.; Green, R.O.; et al. Quantifying the range of the dust direct radiative effect due to source mineralogy uncertainty. Atmos. Chem. Phys. 2021, 21, 3973–4005. [Google Scholar] [CrossRef]
- Scanza, R.A.; Mahowald, N.; Ghan, S.; Zender, C.S.; Kok, J.F.; Liu, X.; Zhang, Y.; Albani, S. Modeling dust as component minerals in the Community Atmosphere Model: Development of framework and impact on radiative forcing. Atmos. Chem. Phys. 2015, 15, 537–561. [Google Scholar] [CrossRef]
- Cawse-Nicholson, K.; Townsend, P.A.; Schimel, D.; Assiri, A.M.; Blake, P.L.; Buongiorno, M.F.; Campbell, P.; Carmon, N.; Casey, K.A.; Correa-Pabón, R.E.; et al. NASA's surface biology and geology designated observable: A perspective on surface imaging algorithms. Remote Sens. Environ. 2021, 257, 112349. [Google Scholar] [CrossRef]
- Green, R.O.; Thompson, D.R.; the EMIT Team. An Earth science imaging spectroscopy mission: The Earth surface mineral dust source investigation (EMIT). In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6262–6265. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Mustard, J.F.; Pieters, C.M. Quantitative abundance estimates from bidirectional reflectance measurements. J. Geophys. Res. Solid Earth 1987, 92, E617–E626. [Google Scholar] [CrossRef]
- Mustard, J.F.; Pieters, C.M. Photometric phase functions of common geologic minerals and applications to quantitative analysis of mineral mixture reflectance spectra. J. Geophys. Res. Solid Earth 1989, 94, 13619–13634. [Google Scholar] [CrossRef]
- Hiroi, T.; Pieters, C.M. Estimation of grain sizes and mixing ratios of fine powder mixtures of common geologic minerals. J. Geophys. Res. Planets 1994, 99, 10867–10879. [Google Scholar] [CrossRef]
- Lucey, P.G. Model near-infrared optical constants of olivine and pyroxene as a function of iron content. J. Geophys. Res. Planets 1998, 103, 1703–1713. [Google Scholar] [CrossRef]
- Cheek, L.C.; Pieters, C.M. Reflectance spectroscopy of plagioclase-dominated mineral mixtures: Implications for characterizing lunar anorthosites remotely. Am. Miner. 2014, 99, 1871–1892. [Google Scholar] [CrossRef]
- Robertson, K.; Milliken, R.; Li, S. Estimating mineral abundances of clay and gypsum mixtures using radiative transfer models applied to visible-near infrared reflectance spectra. Icarus 2016, 277, 171–186. [Google Scholar] [CrossRef]
- Lapotre, M.G.A.; Ehlmann, B.L.; Minson, S.E. A probabilistic approach to remote compositional analysis of planetary surfaces. J. Geophys. Res. Planets 2017, 122, 983–1009. [Google Scholar] [CrossRef]
- Sadrian, M.R.; Calvin, W.M. Infrared Transmission Spectra and Complex Refractive Indices of Surface Soils from Global Dust Entrainment Regions [Dataset]. Zenodo 2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).