A Case Study of the Wavenumber Transition between Westward Quasi-2 Day Wave s = 3 and s = 4 Modes in the Mesosphere

Abstract

We report observations of the wave number transition between two types of westward-propagating quasi-2 day wave (QTDW) with zonal wave number s = 3 and s = 4 in the mesosphere. The Aura/MLS temperature datasets from January and February 2011 are utilized in the analysis. A strong W4 was observed in the Southern Hemisphere in early February, following the fading away of a strong W3 in late January. The W3 and W4 were maximized on days 23 and 36 with maximum amplitudes of ~15 K and ~8 K, respectively. Both the amplitudes and periods were nearly equal on day 30, which coincided with the peak of the Sudden Stratospheric Warming (SSW) on day 31 in the polar region of the Northern Hemisphere. Our analysis shows that the equatorial barotropic/baroclinic and inertial instabilities, which are related with the winter planetary wave activities that lead to the SSW, may have triggered this wavenumber transition event and contributed significantly to the growth of the QTDW. Meanwhile, the relatively strong summer easterly jet at middle and high latitude regions in early February also provided favorable conditions for the amplification of W4 during 2011, and thus facilitated the wavenumber transition.

1. Introduction

The quasi-2 day wave (QTDW) is a predominant phenomenon in the mesosphere and lower thermosphere (MLT) region of the summer hemisphere, occurring shortly after the solstice, which could be amplified at different wave numbers. The westward QTDWs with zonal wave numbers s = 3 (W3) and s = 4 (W4) are the most prominent types of QTDW. The seasonal variations of both the W3 and W4 have been reported extensively in the previous literature, showing that the W3 maximizes mainly during January/February in the Southern Hemisphere, while the W4 is amplified mostly during July/August in the Northern Hemisphere [1,2,3]. Moreover, the W3 is always observed to be much stronger (nearly twice) than W4. Pancheva et al. used MLS/Aura data to study the climatology and interannual variability of QTDW from 2005 to 2014 [4]. They found that the westward-propagating waves with wave numbers 2, 3 and 4 at middle and high latitudes occurred mainly in the summer hemisphere, and that only waves with wave numbers 2 and 3 were observed for the eastward propagation. Pancheva et al. further studied the QTDW from January 2009 to February 2010 based on the Navy Operational Global Atmospheric Prediction System–Advanced-Level Physics High Altitude reanalysis data [5]. Eastward-propagating waves with wave numbers 2 and 3 were observed, and westward-propagating waves with wave numbers 2, 3 and 4 occurred mainly in the summer.

W3 was described in the 1980s as the Rossby-gravity (3, 0) mode [6], which could also be influenced by the summer easterly instabilities [2,7,8,9]. W4 is believed to always result from the baroclinic instabilities related to the summer easterly jet [2,7,10], since it was first observed by Rodgers and Prata [11]. Salby and Callaghan [8] declared that the observed W4 was consistent with the Rossby-gravity (4, 0) normal mode. The simulation results also showed that the strong (weak) summer easterly jet in January (July) were more favorable for the amplification of W3 (W4), which agrees well with previous observations [4]. Aura temperature observations during 2005–2014 clearly show that the W3 QTDW in January is 2–3 times as strong as that in July, while the W4 QTDW in July is evidently stronger than that in January [4]. Tunbridge et al. used EOS Aura Microwave Limb Sounder temperature data from 2004 to 2009 to study QTDW and found that waves in both the Northern and Southern Hemispheres were dominated by W3 and W4 after considering the effect of mixing between different wave numbers [3]. In the Southern Hemisphere, W3 is dominant, while in the Northern Hemisphere W4 is dominant and W3 is smaller or equal. In addition, W3 and W4 vary seasonally in both hemispheres, where W4 is a (4, 0) Rossby-gravity wave as judged by the height–latitude structure. Gu et al. demonstrated that W3 and W4 dominated the QTDW activity at different times in 2007 using the Whole Atmosphere Community Climate Model+ Data Assimilation Research Testbed [12]. Diagnostic analysis showed that the barotropic ally/baroclinically unstable regions amplified W3, and the stronger the instability, the greater the forcing [12].

Wave number transitions between W3 and W4 were reported by Norton and Thuburn [13] with Global Circulation Model (GCM) simulations, which happened during February and August when the W3 decreased and W4 increased. W3 signals were also observed in late July before the maxima of W4 in early August in the boreal summer of 1994 [14], which were suggested to be representative QTDW behaviors [3]. It was suggested that the wave number transitions may have been related to the selective amplification of different unstable wave modes according to the details of the summer easterly jet [3,7,13]. However, the reasons for the wave number transition have not been investigated and discussed in detail yet. Cheng et al. presented W3 and W4 QTDW activities using reanalysis data and four meteor radars located in both hemispheres [15]. W3 and W4 dominated two separate bursts of activity, with a mode transition occurring in between. The results of their analysis demonstrate that both W3 and W4 were caused by jet instabilities.

SSW is a special type of meteorological event taking place in the middle atmosphere that often occurs in the polar stratosphere of the winter hemisphere. When the SSW event occurs, the atmospheric temperature in the stratosphere will suddenly increase by tens of degrees in a very short period of time, which is associated with the complete reversal of the eastward wind to a westward wind in the polar region. SSW events can also have a widespread impact on winds, neutral particles, and atmospheric chemistry. The breaking of the upward-propagating planetary waves is responsible for Sudden Stratospheric Warming [16]. This can be divided into major and minor events, as a major SSW requires a reversal from westerlies to easterlies and an increase in the zonal mean temperature at 10 hPa. In terms of dynamics, vertical waves from the troposphere after a major event do not propagate beyond the middle of the stratosphere. Another classification approach is to divide them into split and displacement according to the SSW morphology. A potential interaction of the SSWs in zonal wavenumber 2 of the troposphere and stratosphere has been identified [17]. Roy and Kuttippurath analyzed the dynamical evolution of all major SSW and minor SSW events during the Arctic winter from 2011 to 2021 [18]. They found that the most severe major SSW during this period occurred in the winter of 2012/13, which was forced by the combined activities of waves 1 and 2.

In this paper, we present a case study of the abnormal QTDW behaviors in January and February of 2011 in the Southern Hemisphere. A strong W4 signal was observed in early February, following the fading away of a strong W3 in late January, which suggested the occurrence of a wavenumber transition between W3 and W4. The coincidence of the SSW peak with the transition makes our study more interesting and significant.

2. Data and Analysis

The Sun-synchronous orbits of the Aura satellite cover latitudinal ranges approximately between 82° S and 82° N from cycle to cycle. The Microwave Limb Sounder (MLS) instrument on board the Aura satellite measures the global temperature from the lower stratosphere to the upper mesosphere continuously during day and night. The temperature precision decreases from ~1 K at 316 hPa to ~3 K at 0.001 hPa, while the vertical resolution is ~3 km at 31.6 hPa and decreases to ~6 km and ~13 km at 316 hPa and 0.001 hPa, respectively [3,19]. The level 2 version 3.3 temperature datasets between 10 hPa and 0.001 hPa during January and February 2011 are utilized here.

A retrospective analysis of modern research based on, and applications of, NASA’s Global Monitoring and Assimilation Office (GMAO), Version 2 (MERRA-2), uses the GEOS-5 Atmospheric Data assimilation system [17,18]. MERRA-2 has been used to study atmospheric planetary wave propagation and amplification processes [19,20,21]. In this study, the wind and temperature dataset from the MERRA-2 reanalysis performed at a spatial resolution of (~0.5 × 0.625) will be used. Anomalous atmospheric dynamics, shifted/split polar vortices, and hemispherical asymmetric conditions during SSWs may lead to uncertainties in planetary wave propagation and amplification. Therefore, it is very important for MERRA-2 data to diagnose and analyze the characteristics of planetary waves during SSWs. In this study, Aura/MLS and MERRA-2 were used to analyze QTDWs in the Southern Hemispheric mid-latitudes during SSWs.

A least square fitting method is here applied to the dataset to extract the QTDW signals with a temporal window of 5 days, stepped by 1 day. The fitting is performed within a latitudinal band of 4 degrees stepped by 2 degrees from 80° S to 80° N. To determine the amplitudes and frequencies of the W3 and W4, we increase the frequency from 0.35 cpd (cycle per day, ~2.8 days in period) to 0.65 cpd (~1.5 days) by 0.01 cpd in every fit. The maximum amplitude and the corresponding frequency are taken as the amplitude and frequency of the QTDW in each 5-day window:

$$y=Acos\left[2\pi \left(\sigma ·t+s·\lambda \right)\right]+Bsin\left[2\pi \left(\sigma ·t+s·\lambda \right)\right]+C,$$

(1)

where $\sigma$, $t$, $s$ and $\lambda$ are the frequency, UT time, zonal wavenumber and longitudes. The amplitude of wave $R$ can be expressed as $R=\sqrt{A^2+B^2}$.

To explain clearly the influence of background wind on the propagation and amplification of QTDW, diagnostic analyses, including of the barotropic/baroclinic instabilities where the latitudinal gradient of the potential vorticity is negative, as well as the inertial instability (II) and the critical layers of QTDW where the background wind equals its phase speed, are calculated as follows:

$${\overline{q}}_{\varphi }=2\mathsf{\Omega }\cos \varphi -{\left(\frac{{\left(\overline{u}\cos \varphi \right)}_{\varphi }}{a\cos \varphi }\right)}_{\varphi }-\frac{a}{\rho }{\left(\frac{f^2}{N^2}\rho {\overline{u}}_z\right)}_z$$

(2)

$$\zeta =f^2\left(1-R{i}^{-1}\right)-\frac{f{\overline{u}}_{\varphi }}{a}$$

(3)

$$\overline{u}-c=0$$

(4)

where $a$, $\mathsf{\Omega }$, $\varphi$, $u$ and $\rho$ are the Earth’s radius (6.371 × 10⁶ m), the angular speed of the Earth’s rotation (7.292 × 10⁻⁵ rad/s), latitude, zonal mean zonal wind, and air density, respectively. Moreover, $f=2\mathsf{\Omega }\sin \varphi$ is the Coriolis parameter, $c$ is the phase speed, $N$ is the Bunt–Väisällä frequency, and $Ri$ is the Richardson number. The subscript $\varphi$ indicates the latitudinal gradient.

3. Results

Figure 1a,b show the dominant QTDW wave modes during days 21–25 (late January) and days 34–38 (early February) in 2011. Temperature observations at 0.01 hPa and 38° S are utilized in the analysis. Figure 1a,b are evidently dominated by the W3 and W4, respectively, both at ~0.5 cpd (2 days in period). The wave perturbations at other frequencies and wave numbers are much weaker compared to W3 and W4. The vertical and global structures of the W3 and W4 during the same period are shown in Figure 1c,d, respectively. The W3 peaks at ~35° S and 0.01 hPa with a maximum amplitude of ~16 K, while the W4 maximizes at ~40° S and 0.02 hPa, with a maximum amplitude of ~9 K. The perturbations of W3 are nearly twice as strong as those of W4. Both the W3 and W4 are limited to the Southern Hemisphere with maxima at the middle-latitude regions. The W3 maximizes at a higher altitude than W4, most likely due to the greater dissipating rate of W4 because of its lower phase velocity than W3 [8].

Figure 2 shows the temporal variations of the W3 and W4 at 0.01 hPa during January and early February in 2011. Only the contours between 20° S and 60° S are exhibited, since the perturbations maximized in middle-latitude regions and decreased quickly when moving poleward and equatorward, with only weak amplitudes at low or high latitudes. W3 began to amplify at the beginning of January and peaked at around day 23, with an amplitude of ~15 K. It faded away quickly after the maximum with an amplitude of only ~5 K one week later on day 30. The W3 on day 30 was almost as strong as that on day 5. In other words, the damping rate of W3 was nearly twice as large as the growing rate.

It is also clear in Figure 2 that the amplitudes of W4 were first observed in low-latitude regions. The wave amplitude was ~3 K on day 23 when W3 reached its maximum. Then, the amplitude of W4 gradually increased with the wave perturbations propagating to middle- and high-latitude regions. At around day 30, the amplitude of W4 reached ~6 K, which is nearly equally as strong as the amplitude of W3. W4 dominated the QTDW oscillations after day 30, and reached a maximum of ~9 K at around day 36 and at ~40° S. The amplitude of W4 dropped to less than 3 K at around day 45.

Figure 3a shows the temporal variations of the wave spectrum at 0.01 hPa and 38° S for both s = 3 and s = 4. Shown in Figure 3b are the temporal variations of the maximum amplitudes of W3 and W4. The maximum amplitudes of W3 were nearly constant (~8 K) during days 4–8, while the frequency corresponding to the maximum amplitude increased from 0.51 cpd to 0.56 cpd. The frequency of W3 decreased gradually from ~0.56 cpd on day 8 to 0.50 cpd on day 20, and the amplitude of W3 increased from ~8 K to ~15 K during the same period. During day 20–23, W3 reached its maximum amplitude of ~15 K with a frequency approximately equal to 0.5 cpd. The amplitude of W3 decreased from ~15 K on day 23 to ~3 K on day 35. The frequency decreased from 0.50 cpd to 0.46 cpd during days 24–26, but with an increasing trend during days 26–30 from 0.46 cpd to 0.52 cpd. The frequency then dropped to 0.44 cpd on day 33 with an amplitude of only ~4 K.

The amplitude of W4 increased gradually from ~2 K on day 23 to a maximum amplitude of ~9 K on day 36, during which time the W3 decreased from the peak value of ~15 K to the extremely low wave strength of ~2 K. After day 36, the amplitude of W4 decreased continuously, with an amplitude of only ~3 K on day 43. The frequency of W4 increased from 0.47 cpd on day 26 to 0.53 cpd on day 29, and then dropped to 0.50 cpd on day 29. In fact, during day 26–29, the frequency of W4 also exhibited an increasing trend. The frequency of W4 decreased to ~0.5 cpd on day 32, with a jump on day 33 to 0.52 cpd. It is interesting to see that both the frequencies and amplitudes of W3 and W4 were almost equal on day 30. The frequency of W4 decreased continuously after day 33, with a frequency of 0.44 cpd on day 40. The frequency of W4 was also approximately equal to 0.5 cpd when its amplitude reached its maximum on day 36, which was the same as that of W3 at around day 23.

Figure 3b also shows the zonal mean temperatures at 70° N and 10 hPa, which are utilized to indicate the Sudden Stratospheric Warming (SSW) at high latitudes of the winter hemisphere. The SSW occurred twice in January and early February of 2011, during days 1–22 and day 25–40, respectively. It is interesting to see that the warming peak on day 31 nearly coincided with the episode in which the amplitudes of W3 and W4 were equally strong, and the corresponding frequencies were also approximately equivalent. After day 30, W4 dominated the QTDW oscillations and W3 came to be indiscernible one week later.

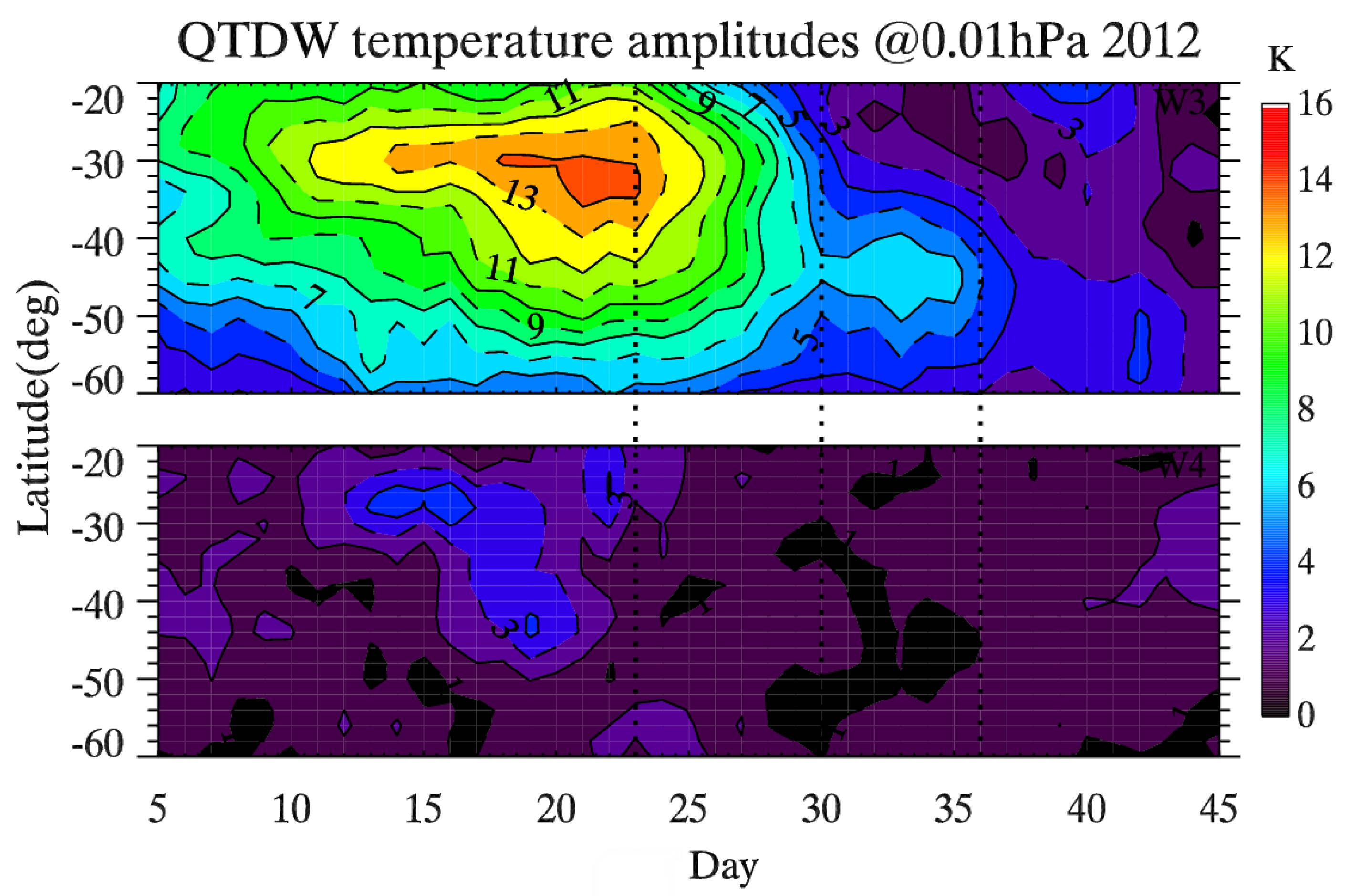
During January and February 2012, only a strong W3 was observed, as shown by Figure 4. The baroclinically unstable regions occurred mainly at middle and high latitudes of the summer hemisphere, as shown by Liu et al. [20] and Yue et al. [9]. It was proposed that wave excitation occurs through wave–mean flow interaction if the critical layer (where the background wind equals the wave phase speed) cuts into an unstable area [2,8,21]. In this case, a relatively strong summer easterly jet provides favorable conditions for the propagation and amplification of W4, and thus promotes the accomplishment of wave number transitions, which can be further expounded by examining the different atmospheric conditions during these two years.

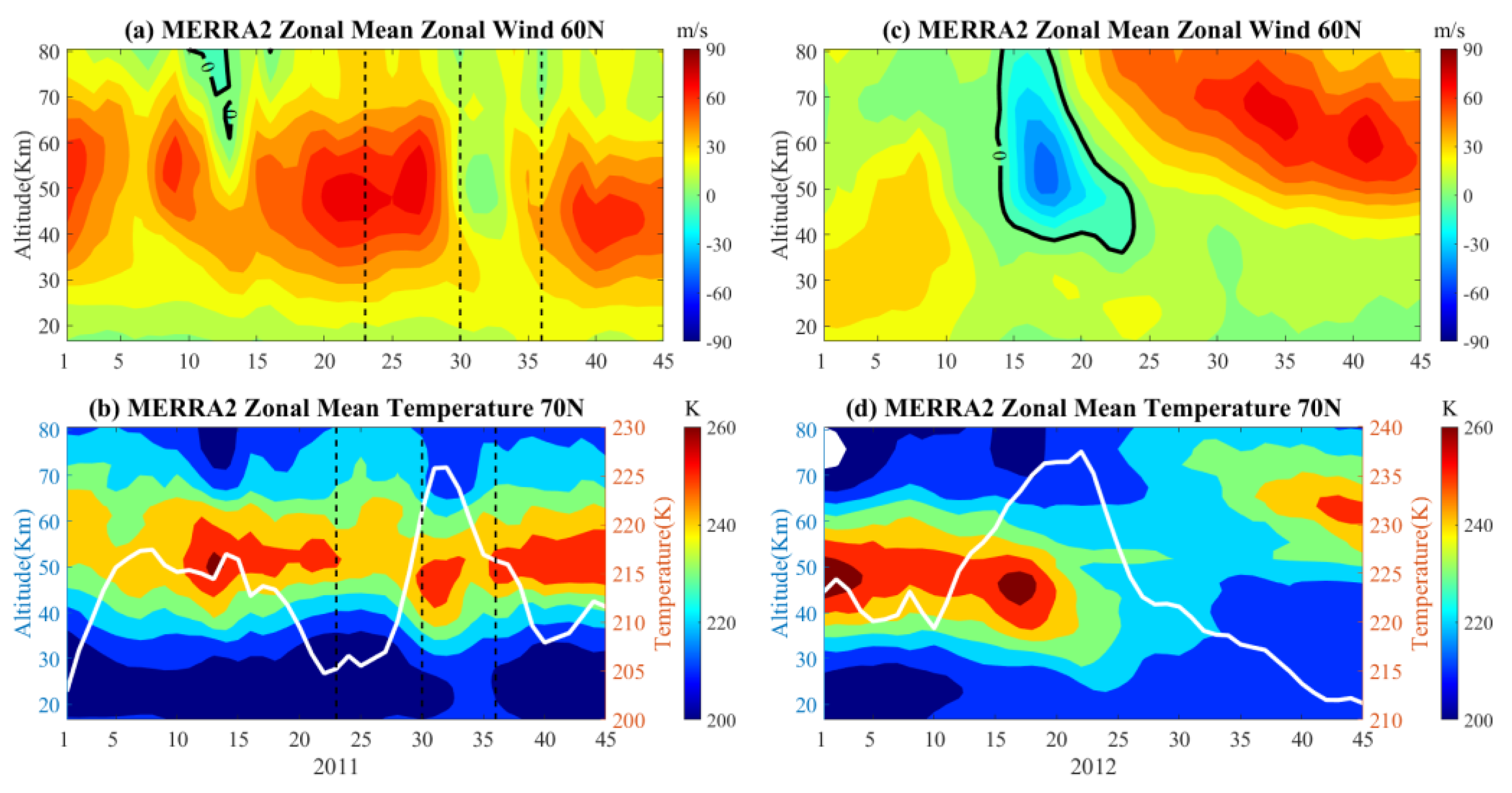
Figure 5a,c show the zonal mean winds at 60° N during the 2011 and 2012 SSWs, respectively. Figure 5b,d show the zonal mean temperatures of 70° N and 10 hPa during 2011 and 2012 SSW, respectively. The results show that the zonal winds reversed significantly in both years, indicating the occurrence of major SSWs. The sudden weakening of the wind speed in Figure 5a,c indicates the onset of sudden stratospheric warming. In 2011, the mean zonal temperatures of 70° N and 10 hPa increased from ~205 K on day 23 to ~220 K on day 30. In 2012, the zonal mean temperature increased from ~220 K on day 10 to ~240 K on day 22, as shown in Figure 5d. The strong W4 event in 2011 with maximum amplitude on day 36 is thus likely to be related to the preceding SSW event, which occurred much later than that in 2012.

The influence of SSW on the amplification of W3 in January 2006 was studied by McCormack et al. [22]. It was found that the winter planetary waves were strong before the occurrence of the SSW, which were also proposed to be important in triggering and amplifying the QTDW [1,2,8]. Inertial instability was formed in the equatorial region where winter planetary waves were absorbed when propagating into the summer hemisphere [8]. The inertially unstable circulation could have reinforced the meridional curvature of the mean zonal wind, which facilitates the formation of barotropic instabilities and thus provides additional forcings for the amplification of QTDW [2,22,23].

It is interesting to see that W4 was first amplified at low-latitude regions, and then propagated to the middle-latitude regions, as shown in Figure 2. The 3 K contour line is limited to within 20° S–30° S on day 23, while it could already be observed between 50° S and 60° S on day 32, with a poleward speed of ~3 degrees/day. The temporal and latitudinal variations of W4 seem to support the proposition that the equatorial barotropic instability related to the inertially unstable circulation may serve as a trigger for the amplification of W4. In this case, the intensive winter planetary wave activities during the SSW event in January 2011 may explain the wave number transitions.

To further investigate the effect of cross-hemispheric coupling on QTDW amplification during the SSW period, the mean zonal wind at low latitude is exhibited. Figure 6 shows the mean zonal winds at 15° S in January and February of 2011 and 2012. The MERRA-2 reanalysis datasets are here utilized. Obviously, the background easterly jet is stronger in 2011 than that in 2012, with the critical line of W4 intruding into February.

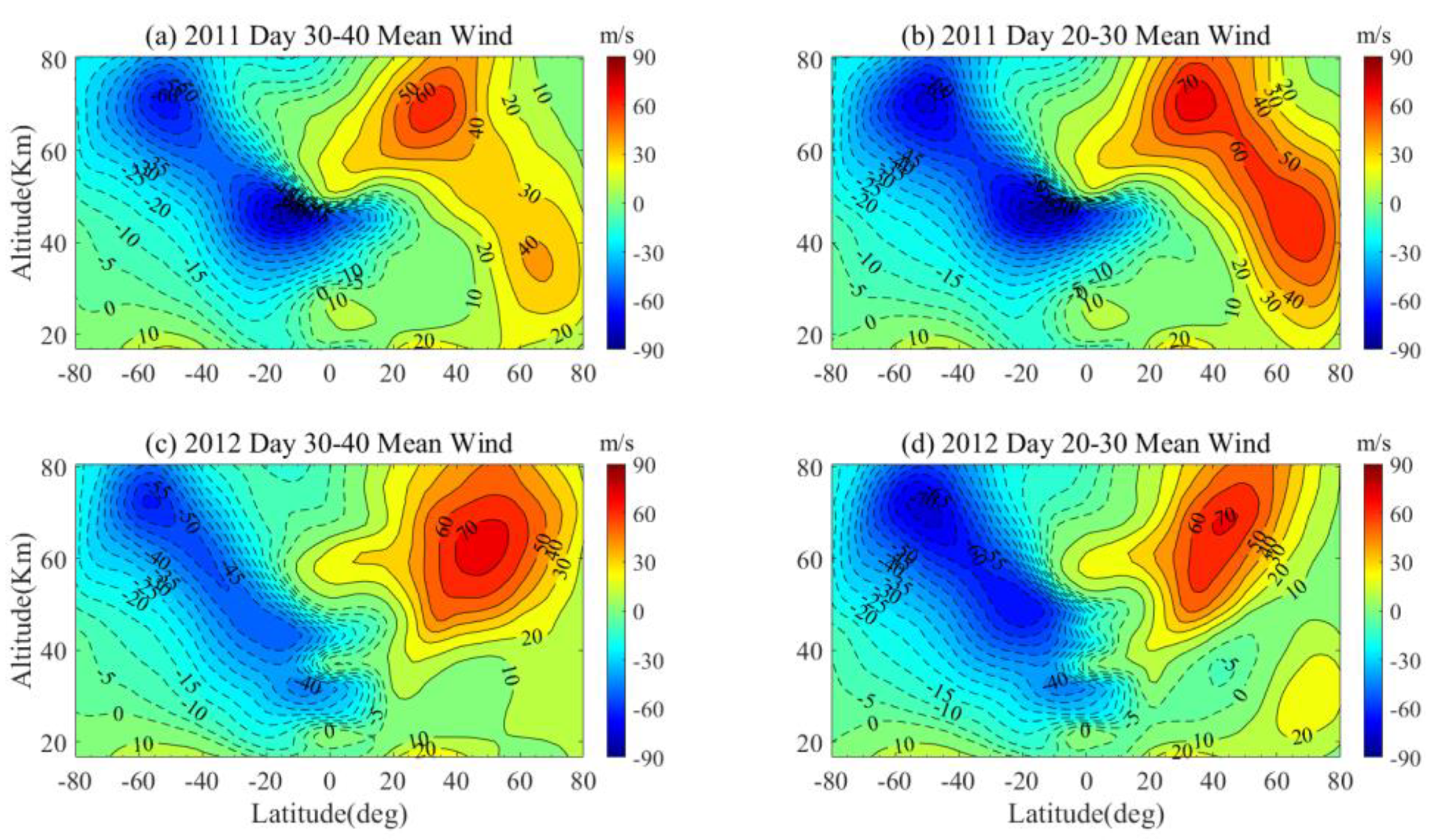
Figure 7a,b respectively, show the vertical and latitudinal distributions of the mean zonal wind during days 30–40 and 20–30 in 2011. It is worth noting that the background wind in the Southern Hemisphere did not change much in early February compared to that in January during 2011. Meanwhile, the background wind in the Northern Hemisphere during late January was significantly stronger than that during early February, which was possibly related to the occurrence of the SSW in early February. Figure 7c,d show the background wind during days 30–40 and 20–30 of 2012, respectively. Differently from Figure 7a,b, the background winds on days 20–30 of 2012 were stronger than those on days 30–40 by about 30 m/s. Besides this, the summer easterly in early February during 2012 was much weaker than that in 2011, especially in the equatorial region. This may have resulted in additional barotropic/baroclinic instability or inertial instability, contributing to the amplification of W4 during 2011.

Figure 8 shows the results of the diagnostic analysis of the atmospheric condition during days 20–30 and 30–40 in 2011 and 2012, including the barotropic/baroclinic instabilities, inertial instabilities, and the QTDW critical layers. Considering that the critical layer has an important effect on the amplification and propagation of planetary waves [15], the instability in the middle latitude, which is above the core of the westerly jet and possibly related to baroclinic instability, worked during the QTDW events in both 2011 and 2012. Besides this, the instability at low latitudes in the Southern Hemisphere, which may indicate barotropic instability, may also have contributed to the strength of both W3 and W4 during 2011. For example, the amplitude of W3 in 2011 was slightly stronger than that in 2012 by 1–2 K in middle January, and the W4 amplitude in 2011 was much stronger than that in 2012. Recently, it was found that inertial instabilities are crucial to trans-equatorial couplings, which may serve as a source for the amplification of QTDW [23,24]. In our analysis, the region with inertial instability extended to as low as 20 km in 2011, while the inertial instability in 2012 had already faded away below 30 km. This indicates that the inertial instability during 2011 was stronger than that in 2012. Thus, both the barotropic/baroclinic instability at low latitudes in the Southern Hemisphere and the equatorial inertial instability in the Northern Hemisphere were responsible for the stronger QTDW events in 2011 than in 2012, and were also responsible for the wavenumber transitions from W3 to W4 in 2011.

4. Summary

In conclusion, we used the MERRA-2 reanalysis and the Aura/MLS dataset to study the reasons for the wavenumber transitions between the westward quasi-2-day wave s = 3 and s = 4 modes during the SSW periods of 2011.

Generally speaking, a strong W3 was observed in austral summer, while W4 reached it maximum mainly in the boreal summer. Nevertheless, strong W3 and W4 were both observed at middle latitudes in the Southern Hemisphere during January 2011, with the growing of W4 following the dampening of W3, which suggests the occurrence of a wave number transition. W3 maximized in the second half of January, while W4 peaked in early February, with the maximum amplitudes of ~15 K and ~8 K, respectively. The frequencies of W4 and W3 were both ~0.5 cpd (2 days in a period) when the maximum amplitudes were reached. The amplitude of W3 was stronger (weaker) than that of W4 before (after) day 30, when both the frequencies and amplitudes of W3 and W4 were approximately equivalent. It is interesting to note that an SSW event occurred in late January and early February, with the warming peak on day 31. The wave number transition between W3 and W4 was most possibly triggered by the intensive winter planetary wave activities that led to the SSW. Meanwhile, we found that the summer easterly jet at middle and high latitudes of the Southern Hemisphere was relatively strong in early February of 2011, and this provided favorable conditions for the amplification of W4. We also found that the barotropic/baroclinic instabilities, as well as the inertial instabilities in the equatorial region, contributed significantly to the amplification of QTDW, which may have enabled the realization of wave number transitions. This speculation is partially supported by the temporal and latitudinal variations of W4, which were first amplified in low-latitude regions and then extended to middle-latitude regions.