Automatic Recognition of Constant-Frequency Electromagnetic Disturbances Observed by the Electric Field Detector on Board the CSES

Abstract

Since the CSES (China Seismo-Electromagnetic Satellite) has been in orbit, it has detected a large number of constant-frequency electromagnetic disturbances (CFEDs), which are horizontal lines on the spectrum. In this paper, we present an algorithm for automatic recognition of CFEDs based on computer vision technology. The relevant results are of great significance for analysis of perturbation events and mining of the transformation laws of global space events. First, a grayscale spectrogram is obtained; then, a horizontal convolution kernel is used to enhance the horizontal edge features of the grayscale graph, and finally, black-and-white binarization is performed to complete data preprocessing. The preprocessed data are then fed into an unsupervised cluster model for training and recognition to realize automatic recognition of CFEDs. Experimental results show that the CFED recognition algorithm proposed in this paper is effective, with a recognition accuracy of more than 98%.

1. Introduction

Since the 1980s, electromagnetic satellites have captured a large number of electromagnetic disturbance phenomena [1,2,3,4,5,6,7] caused by solar magnetic storms, substorms, lightning, atmospheric conditions, tides, artificial VLF transmitter stations, power systems, satellite platforms, etc. Different types of phenomena appear in different shapes in their spectrogram [8]. For example, electromagnetic disturbances produced by the artificial VLF transmitting station, PHRL generated by power systems, and disturbances of the satellite platform itself could cause changes in the spatial physics environment, all of which present as a horizontal shape on the spectrogram. The artificial VLF transmitting station transmits continuous electromagnetic waves at a constant frequency in the range of 10 kHz to 50 kHz, causing a horizontal shape on the spectrogram [9]. Furthermore, the PHRL recorded by the satellite can display a series of parallel lines in the electromagnetic spectrogram. These lines have constant frequency intervals of 50/100 Hz or 60/120 Hz. PHRL is typically distributed in the extremely low frequency (ELF) or VLF range [8,10,11].

In February 2018, the CSES was successfully launched an has since been in orbit for more than 4 years and generated a vast body of data. Faced with the challenge of a massive amount of data, it is urgent to automatically recognize abnormal constant-frequency electromagnetic disturbances (CFEDs). Recently, some progress has been made in automatic recognition of CFEDs. This work can be divided into two categories. The first group is based on the recognition of CFEDs by Hough transformation [12]. This method detects line segments in many directions, although it is time-consuming and leads to unstable performance. The second group is based on density statistics [13], employing a horizontal convolution kernel to enhance the features of the horizontal edge, giving rise to improved recognition performance. However, the robustness of these methods is relatively poor. To overcome this limitation, we performed cluster analysis to propose a novel CFED recognition method.

Cluster analysis is a kind of unsupervised machine learning algorithm that groups objects such that those in the same cluster are similar to each other [14]. Compared with deep learning methods, clustering algorithms not only do not require labels and datasets for training but are also more explanatory [15]. Recently, cluster analysis algorithms have been widely used in geophysics and other related fields. For example, the authors of [16] used cluster analysis to classify types of electrical sounding curves. Among many types of clustering algorithms, the most popular is K-means, which is easy to implement, with a moderate running time [17,18,19,20]. Based on K-means, we propose a novel CFED recognition algorithm to be applied to spectrograms from EFD data. The proposed algorithm provides innovations: (1) an error rate of 0 and (2) robust performance.

2. Data Collection

The CSES is China’s first geophysical exploration satellite. It is mainly used to acquire global electromagnetic field, plasma, high-energy particle observation and other data, are used to provide services such as short-term seismic prediction and geophysical research [21,22,23,24]. The CSES has an orbital inclination of 97.4°, which is a solar-synchronous orbit. The regression period is 5 days. It takes approximately 94 min to complete an orbit around the Earth. Observation data are stored as ascending track (night) and descending track (day), and an observation of each half track (ascending track/descending track) is approximately 34 min. The spatial resolution of adjacent ascending (or descending) tracks within the same day is approximately 2000 km. The CSES carries eight scientific payloads [25,26,27,28,29]: an induction magnetometer, a high-precision magnetometer [30], an electric field detector (EFD), a GNSS occultation receiver [31], a plasma analyzer [32,33], a high-energy particle detector [34], a Langmuir probe [35] and a tri-frequency beacon transmitter [22]. The electric field detector (EFD) detects electric fields in space. Its detection frequency band is divided into ULF (0~16 Hz), ELF (6 Hz~2.2 kHz) and VLF (1.8 kHz~35 MHz). It can not only provide basic data for the study of Sun–Earth space physics; space weather; and interactions between the ionosphere and the upper atmosphere, magnetosphere and other related spheres and their effects but also provides data application services for seismic observation and research [36].

The EFD waveform data of the VLF band-Z component in this referenced in this paper were obtained by the CSES. A spectrogram is obtained by short-time Fourier transformation (STFT) of waveform data. In Figure 1, the y-axis represents the frequency range; the x-axis represents time, longitude and latitude of the satellite orbit; and the color bar on the right represents the intensity of electromagnetic waves.

3. CFED Automatic Recognition Algorithm

The goal of the algorithm is to recognize horizontal lines on the spectrogram; as shown in Figure 1, several horizontal lines are observed easily. The framework of the proposed algorithm is provided in Figure 2. The solid line represents the training flow, and the dotted line is the test flow. By following the training flow, a recognition model for CFEDs is obtained, and by following the test flow, the recognition results are obtained.

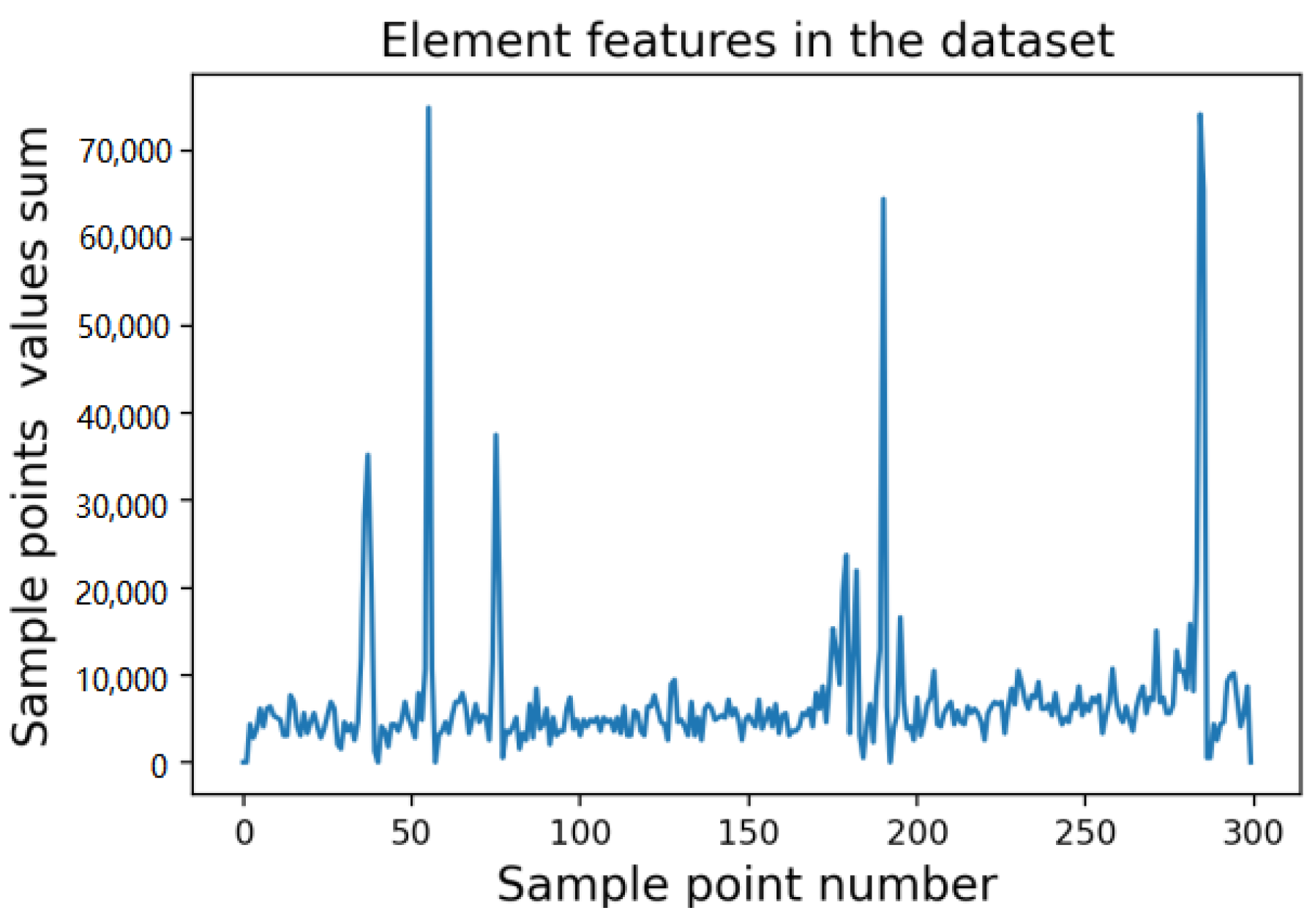
3.1. Grayscale Processing

Information about horizontal shapes in CFEDs is more important than color information. Therefore, we first process the time-frequency diagram from RGB (red, green and blue) to gray. The gray image is obtained using the red, blue or green channel in RGB color space, i.e., ImgG = RGB.R [13]. Note that when the color bar of the spectrogram is changed, the grayscale method is changed accordingly. Experiments show that when the color bar ranges from −10 to 12, the best result of the graying experiment is achieved using the red channel. When the color bar range is −2 to 1, the best result is achieved using the blue channel.

3.2. Horizontal Feature Enhancement

To enhance CFED features for easy recognition, a convolution kernel [13] is used to process the ImgG image. The kernel is provided by Equation (1).

$$\mathrm{kernel}=[1,0,-1]$$

(1)

The method is expressed as Equation (2).

$$\mathrm{dst}(x,y)={\displaystyle \sum _{\begin{array}{l}0\le x^{\prime }<\mathrm{kernel}.\mathrm{cols},\\ 0\le y^{\prime }<\mathrm{kernel}.\mathrm{rows}\end{array}}\mathrm{kernel}(x^{\prime },y^{\prime })\times \mathrm{src}(x+x^{\prime }-\mathrm{anchor}.x,y+y^{\prime }-\mathrm{archor}.y)}$$

(2)

where src is the original image; dst is the target image; kernel is the convolution kernel; anchor is the anchor point of the kernel, indicating the relative position of the kernel filter point; x and y are the coordinates of pixels on the original graph; and x′ and y′ are the coordinates of points in the convolution kernel.

Figure 3a shows the effect of a 5 × 5 pixel spectrogram enlarged 500 times without distortion. A horizontal line is clearly visible above the background. The operational process is shown in Figure 3b, where src is the red channel value of Figure 3a, and dst is the result of the convolution operation. The results show that the convolution operation greatly enhances the edge features of the horizontal line.

3.3. Binarization

In order to separate the object from the background more quickly and accurately, black-and-white binarization is carried out on the convolution result so that the whole image presents an obvious black-and-white effect. Binarization is expressed by Equation (3).

$$\mathrm{dstmap}(px,py)=\{\begin{array}{ll}maxVal& if\mathrm{srcmap}(px,py)>tresh\\ 0& \mathrm{otherwise}\end{array}$$

(3)

where srcmap is the target image after convolution; px and py are the coordinates of a pixel on the target image; maxVal represents the maximum number of pixels, which is set to 255 in this paper; and thresh is the threshold value, which is set to 10 in this paper. if the pixel value of (px,py) is less than thresh, it is 0; otherwise, it is 255. dstmap is the output image after binarization. The results after binarization of Figure 3b (dst) are shown in Figure 4. After binarization, only the pixel value on the line is 255, and the rest is 0.

3.4. K-Means Clustering

The preprocessed data described above are fed into the K-means model. The steps are as follows.

Step 1: Randomly select k sample data points from the sample data to be clustered as the initial clustering center {µ1,µ2,…,µn} (k = 2).

Step 2: In the K-means model, if the sum of the distance between sample points in the cluster and the center of the cluster is small, the samples in the cluster are similar, and the clustering effect is better. The calculation formula is expressed as Equation (4):

$$d={\displaystyle \sum _{i=1}^k{\displaystyle \sum _{p\in C_i}{\Vert p-{\mu }_i\Vert }^2}}$$

(4)

where ${\mu }_{\mathrm{i}}$ is the central sample of cluster $C_{\mathrm{i}}$, and $p$ is the sample point.

Step 3: Recalculate the clustering centers for the newly obtained k clusters. The formula for calculating the center of the cluster is expressed as Equation (5):

$${\mu }_{\mathrm{i}}=\frac{1}{C_{\mathrm{i}}}{\displaystyle \sum _{p\in C_i}p}$$

(5)

Repeat steps 2 and 3 until the termination condition ($\left|{\mu }_{\mathrm{n}+1}-{\mu }_{\mathrm{n}}\right|\le \epsilon$) is satisfied or the preset number of iterations is reached; then, the algorithm terminates.

In this paper, the number of iterations is set to 10, and the iteration with the lowest d value is considered the clustering result.

4. Experiment and Analysis

4.1. Experimental Methods

Python 3.7 is used to implement the detection process described above using the CV2 image library and the SKLearn clustering algorithm library. The following experimental scheme was formulated.

(1)

Data collection

In this experiment, we collected more than 500 spectrograms from EFD data recorded in April 2020, each of which contains several horizontal lines.

(2)

Data preprocessing

First, the spectrogram was processed by taking data from the red channel of the RGB image to generate the gray image; then, the horizontal edge features were extracted, and finally, they were fed into the model after binarization. Some of the results obtained by the above methods are shown in Figure 5.

(3)

Model training

There are three commonly used unsupervised clustering models: BIRCH, K-means, and DBSCAN.

We selected spectrograms with clean CFEDs and processed them to generate binarized data. The binarized data were then fed into three training models.

(4)

Horizontal line recognition

The preprocessed datasets were fed into the three models for line identification, and the experimental results were counted and analyzed to determine which type of model to choose.

4.2. Optimal Clustering Coefficient Selection

Taking the spectrograms in Figure 5 as an example, binarization data can be visualized according to the line graph to check the distribution characteristics of the data. As shown in Figure 6, the x-axis represents the number of rows, and the y-axis represents the sum of pixel values for each row. In the original spectrogram shown in Figure 5a, there are five clearly visible horizontal lines and five sum values greater than 30,000, corresponding to the data distribution characteristics shown in Figure 6.

The DBSCAN (density-based spatial clustering) algorithm uses spatial index technology to search the neighborhood of an object. It treats a cluster as a dense object area separated by a low-density area in the data space. The binarized dataset does not fit the DBSCAN model usage scenario. We also experimentally verified that the DBSCAN classification effect is very poor, and it can hardly recognize horizontal lines. Two other BIRCH and K-means models are discussed below.

BIRCH (balanced iterative reduction and clustering using hierarchies) is a comprehensive hierarchical clustering algorithm. It uses the concepts of clustering feature (CF) and clustering feature tree (CF Tree) to summarize the description of clustering.

The clustering coefficient (k) is an important parameter of the clustering algorithm. With the exception of k, all other parameters in the algorithm adopt default values. There are two common ways to select k values.

(1)

Practical application

The goal is to recognize horizontal lines. According to this practical application requirement, the clustering coefficient (k) should be set to 2; that is, the target is divided into two categories: pixel points on the line and pixel points outside the line.

(2)

Silhouette method

The silhouette method considers the density and dispersion of clusters comprehensively. If the data are divided into ideal k clusters, the samples within the corresponding cluster are very dense, whereas the samples between clusters are very scattered. The silhouette value (s(i)) is expressed by Equation (6). For the ith sample, the larger the s(i) value, the more reasonable the sample distribution is.

$$s(i)=\frac{b(i)-a(i)}{\max \{b(i),a(i)\}}$$

(6)

where a(i) represents the average distance between sample i and other sample points in the same cluster. A low a(i) value indicates that sample i should be clustered in this cluster. The mean distance (bij) between sample i and all samples of other clusters (Cj) is called the dissimilarity between sample i and cluster Cj, indicating the dissimilarity between clusters of sample i: b(i) = min{bi1,bi2… bik}. The silhouette coefficient is the mean of the silhouette coefficient of all sample points. Figure 7 shows the change in silhouette coefficient when the k value changes. When k = 2, the silhouette coefficient value is the maximum, indicating that k = 2 is the best optional reference value.

4.3. Experimental Results

After the clustering operation, the data sample is divided into two clusters, labeled 0 or 1, namely linear cluster and nonlinear clusters, respectively. Then, each row on the original spectrogram is traversed line by a line. If it belongs to the row cluster, the pixel points obtained after binarization are marked in red. Experimental results from both models are shown in Figure 8. According to the recognition results, K-means is superior to BIRCH.

(a)

(b)

In the statistical analysis of detection results, if some horizontal lines are intermittent or indistinct, they are not included in the statistical scope of the experiment. However, if the experiment is recognized by the algorithm, it is not a detection error; if it is not recognized, it is not a missed detection. Statistics of experimental results are shown in

Table 1. Experimental results.

	Accuracy Rate	Missed Rate	Error Rate
K-means	0.989 ± 0.02	0.011 ± 0.03	0
BIRCH	0.8712 ± 0.13	0.1388 ± 0.06	0

.

Therefore, the K-means algorithm with k = 2 is selected for actual line recognition.

4.4. Comparison with Existing Algorithms

At home and abroad, the recognition technology of CFED in the spectrogram is mainly based on Hough line transform [12]. This recognition technology is aimed at straight lines in various directions, and the recognition efficiency and accuracy are relatively low. The authors of [13] proposed an improved row density statistics algorithm, which greatly improved the efficiency and accuracy of recognition. However, the robustness of this method is poor, and the threshold must be set manually. If the threshold is too high, the default rate increases, and if the threshold is too low, many lines are incorrectly recognized as straight lines. The K-means algorithm based on horizontal a convolution kernel proposed in this paper not only has a high accuracy rate and almost zero error rate achieves robust performance. The experimental statistical results of the three methods are shown in

Table 2. Experimental results.

	Accuracy Rate	Miss Rate	Error Rate
Hough	91.12 ± 0.12	8.88 ± 0.18	15.38 ± 0.01
Row density statistics	99.12 ± 0.01	0.0088 ± 0.01	8.1 ± 0.03
K-means	0.989 ± 0.02	0.011 ± 0.03	0

.

5. Discussion

In this section, the influence of horizontal line recognition results is analyzed and discussed in depth, and we explore future research prospects for horizontal line recognition.

5.1. Cause Analysis of Missing and Incorrect Detection

The reasons for missing or misidentified horizontal straight lines are discussed below.

First, the CFED signal itself is relatively weak in the faint visible spectrum, as shown in Figure 9a; second, the horizontal line is disturbed by other spatial electromagnetic waves, and its shape on the spectrogram changes as a result of contrast reduction or clarity reduction, as shown in Figure 9b. Third, the CFED signal itself is interrupted, as shown in Figure 9c.

5.2. Extended Discussion

According to electromagnetic wave propagation theory, most of the energy in VLF/LF wave propagation is confined to the waveguide layer. When the low ionosphere over the propagation path is disturbed by various factors, such as solar flare, magnetic storms, lightning flash discharge, earthquakes, etc., VLF/LF artificial source signal anomalies occur [37]. According to the linear detection algorithm proposed in this paper, when some CFEDs are disturbed by other spatial electromagnetic waves, the CFED signal is abnormal, resulting in the weakening, interruption, or even disappearance of the horizontal straight line on the spectrum diagram, and the corresponding detection results can also be reflected by the marks. The interruption of the line or the weakening of the signal is helpful for the detection of spatial electromagnetic anomaly disturbances. The next step is to analyze the influence of electromagnetic disturbances caused by the 2020 Cuban earthquake on CFEDs.

At 19:10 on 28 January 2020, an earthquake occurred 125 km northwest of the port city of Lusi, Jamaica, at a depth of 10 km (Figure 10). The ionospheric disturbances over the seismogenic zone in the southern seas of Cuba before the earthquake were analyzed based on the observational data of the VLF frequency band of the space electric field.

The geomagnetic activity index is closely related to ionospheric changes in space. In order to obtain and identify anomalous information of ionospheric disturbances related to earthquakes, it is necessary to exclude disturbances caused by known geomagnetic activities. The ∑Kp and Dst indices in the two months prior to the earthquake were collected and plotted; the changes in activity are shown in Figure 11, with the study period of this earthquake covering the geomagnetic quiet period [26,38].

By using the automatic CFED detection and labeling algorithm proposed in this paper, abnormal electromagnetic disturbance in the earthquake area can be judged by statistical point density and sparse morphological changes, as shown in Figure 12.

6. Conclusions

In this paper, we propose a method for automatic recognition of CFEDs on the spectrogram. Three types of clustering models were trained and fed into the data prediction model. Through experimental statistical analysis and various evaluation methods, we found that K-means with k = 2 had the best recognition effect on horizontal lines, with an accuracy rate of more than 98%. It was helpful to further excavate abnormal disturbance events and study temporal and spatial variation of the space ionization field.

However, because some horizontal electromagnetic signals are affected by other spatial electromagnetic interference factors, horizontal lines become weak or disappear, resulting in missed detection. On the other hand, analysis shows that if the mark shape of the detected horizontal line points changes, such as a certain section in the middle becoming sparse, this area can be marked as abnormal, these abnormal areas can be mined, and the causes of the abnormalities can be discussed and analyzed.

Accordingly, future work will focus mainly on the following two areas: (1) excavation and analysis of the phenomena of weakening or disappearance of CFED caused by other electromagnetic interference and (2) automatic recognition of other types of spatial electromagnetic interference events using computer vision processing based on the scheme proposed herein.