Abstract
Non-climatic reasons, such as station replacement and changing the measurement device and calculation method, may make climate data unrepresentative of the actual variation of the regional climate. Data quality control and homogenization tests for climate data are critical. Thus, this study aims to evaluate the quality and homogeneity level of precipitation time series in arid and semi-arid climatic zones and specify the breakpoint in the datasets. The proposed methodology has been used to conduct arid and semi-arid representative case studies comprising 40 annual precipitation series for Iraq between 1979 and 2014. A Box-Cox transformation has been used to adjust the non-normally distributed datasets. Outliers have been censored by truncating extreme values. The results of the outliers indicate that they may be caused more by climate variability than by human-induced reasons. Homogeneity adjustments have been developed by applying these four homogeneity tests: Pettitt’s test, the Standard Normal Homogeneity method, Buishand’s test, and von Neumann’s check. Approximately 40% of the series (i.e., 16 stations out of 40) were homogeneous. Each homogeneity test was evaluated separately, and non-homogeneous stations were identified. Then, the series was classified into three groups that were assigned the labels “useful”, “doubtful”, and “suspect”. The results indicated that twenty-one stations were associated with the class ‘suspect’, three of the stations belonged to the class ‘doubtful’, and sixteen locations were within the class ‘useful’. Furthermore, the data analysis indicated no influence of the outliers on the results of the homogeneity tests. Accordingly, the study recommends further research on homogeneity tests that can be applied without considering outlier tests for similar case studies.
1. Introduction
Rainfall is the primary element of the water cycle and has an important impact on the socioeconomic growth of a geographical location [1,2]. To evaluate the hydro-climatic conditions of an area, long-term homogeneous rainfall records are crucial [3,4]. In fact, different non-climatic reasons affect inhomogeneity in recorded datasets and cause impractical tendencies in time series [5,6,7]. There are many sources that cause inhomogeneity in precipitation datasets such as changes in estimation processes, alterations in equipment, relocation of recording stations, variations in the environments, and broken instruments [8,9,10]. It is necessary to investigate the precipitation data homogeneity before being employed in hydro-climatic research [4,6].
To analyze the homogeneity of datasets, a number of methods have been created and put to use [7,8,9]. These methods can be broadly categorized into two groups: Relative and absolute techniques. Since the test is accomplished by comparing the test time series with the homogenous time series of a nearby station, relative approaches are more trustworthy and therefore advised. However, absolute approaches are preferred when homogenous data series are not available or if there is a weak link between the test and reference series based on their connection [10,11,12]. The availability of uniform data series and knowledge of a region’s geographic or climatic features thus influence the choice of absolute tests.
Precipitation in arid and semi-arid areas is exceedingly unpredictable and scarce; as a result, it varies greatly across a short distance. Furthermore, due to the lack of human habitation, rainfall stations are typically dispersed throughout the majority of the world’s arid regions [13]. Consequently, it is frequently difficult to locate uniform rainfall time series in the surrounding areas [14]. Finding the optimal approach for a given research field is never easy because there are so many different absolute tests available. The characteristics of the target climate variable and the temporal organization of the observational record strongly influence the application of statistical approaches [15]. Consequently, it is generally advised to utilize a variety of techniques to confirm the homogeneity in a time series. The most popular and frequently recommended absolute methods for determining homogeneity are Pettitt’s test (PT) [16], the standard normal homogeneity test (SNHT), the cumulative deviations test, the von Neumann’s ratio test (VNRT), and the Buishand range test (BRT) [17]. Recently, many iterations of these tests have been employed to evaluate the homogeneity of precipitation time series across various climatic zones.
There could be a number of causes for the inhomogeneity of data. Nevertheless, selecting a technique for inhomogeneity detection can be a key factor [13,18]. It has also been stated that various tests frequently produce inconsistent results since their theoretical underpinnings are founded on various assumptions. Moreover, using many approaches increases confidence in the data selection, but does not ensure the robustness of the analysis. As a result, a number of authors [10,19] combined various techniques for the detection of in-homogeneities and reported that the combination of several statistical tests can better identify inhomogeneities and offer a better decision on the selection or rejection of time series.
There are no appropriate guidelines for making suitable decisions based on the results of various examinations. Inappropriate decision-making could result in the analysis of an inhomogeneous data series or the exclusion of a homogeneous data series, which could lead to inaccurate hydro-meteorological measurements. The method suggested by Wijngaard et al. [10] has been applied recently to make decisions about data homogeneity based on the outcomes of multiple homogeneity assessments. According to the number of tests that reject the null hypothesis of data homogeneity, Wijngaard et al. [10] divided the findings of four tests into three categories: Useful, questionable, and suspect. This method’s primary flaw is that it only takes four approaches into account when determining the homogeneity of the dataset. Recently, it was shown that numerous additional techniques were more trustworthy for determining homogeneity. This highlights the importance of employing more than four approaches and basing judgments on the corresponding outcomes.
Precipitation data from many developing countries such as Iraq have not yet undergone thorough comprehensive homogeneity and data quality checks. The homogeneity of some precipitation data from Iraq was examined by Agha et al. [3], Al-Lami et al. [7], and Jaafar and Al-Lami [8]. However, they only conducted homogeneity tests for many weather stations without performing comprehensive data quality controls including outlier assessments, testing of normality, and checking data accuracy. For example, Agha et al. [3] assessed the homogeneity of the seasonal and annual precipitation data for only nine weather stations in northern Iraq.
Based on the results of the most popular absolute homogeneity tests, the current study’s goal is to classify the homogeneity of long-term precipitation datasets in Iraq, which has been selected as a representative study area for arid and semi-arid climatic conditions. The homogeneity of precipitation time series from forty weather stations for the years 1997 to 2013 was evaluated using the aforementioned tests. The study’s objectives are to (a) test the dataset for normality and use the Box–Cox transformation to change the distributional shape of a set of data (i.e., the Iraqi example dataset) so that it is more normally distributed; (b) identify, confirm, and potentially correct or even remove outliers; and (c) use a variety of homogeneity tests to identify inhomogeneities with respect to the test results and meteorological data.
Finally, time series breaks were examined to spot alterations in non-homogeneous time series. It is anticipated that the methods described during the current research will offer guidance to make a reliable assessment of homogeneity.
2. Data and Methodology
2.1. Representative Study Area
Iraq was chosen as an example case study (Figure 1). The country is situated between latitudes 29.5° and 37.5° N and longitudes 38.45° and 48.45° E in the northern Arab world, southwest of central Asia. Iraq is made up of the Great Mesopotamian alluvial plain basin of the Tigris and Euphrates rivers, which is bordered by mountains in the north and east that reach elevations of 3550 m above sea level and by desert regions in the south and west that make up more than 40% of the country’s total land area [3].
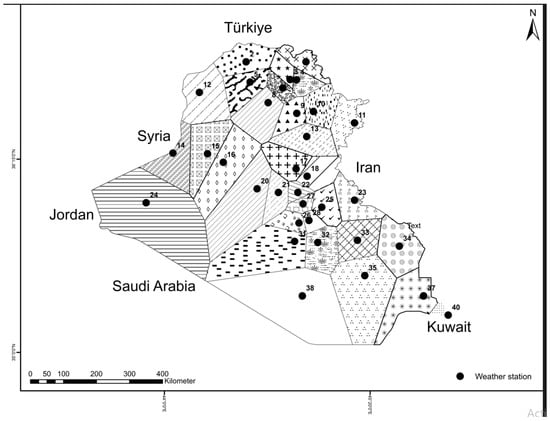
Figure 1.
Map of Iraq revealing the locations and associated regions of the meteorological stations.
Based on the annual rainfall factor, the northern, middle, and southern regions of Iraq are frequently divided into three main rainfall sectors. The rainy season lasts from December to February, with the exception of the north and northeast of the nation, where rain falls from November to April. According to Agha et al. [3], the country receives 650 mm of rain on average each year, with variations in the north and south of 1200 mm and less than 100 mm, respectively. Typically, less than 100 mm of rain falls annually in the nation’s western desert. As a result, the climate is semi-arid in the north with relatively cold winters, while it is arid in the south and center with a mild winter and an exceptionally hot summer [20].
2.2. Data Collection, Projection, and Analyses
Examining climate variability necessitates long-term, reliable historical weather data. From 1979/1980 to 2013/2014, annual precipitation time series data from 40 weather stations dispersed throughout the study area were gathered (Figure 1 and Table 1). The Iraqi meteorological and seismological organization provided the data. Global Administrative Areas’ 2012 version of GADM (http://www.gadm.org, accessed on 3 November 2023) was used to download the shapefile corresponding to the Iraqi border.

Table 1.
Overview of the Iraqi weather stations with the corresponding area (km2) that was computed based on the ArcGis 10.4 programming tool.
The Thiessen network delineation, the projection of the locations of meteorological stations, and the analysis of the spatial distribution of annual precipitation were all undertaken using ArcGIS 10.4 software. To obtain a precise assessment of the spatial distribution of rainfall over the study country, the Thiessen network method was used. Each weather station was given weights according to how much of the surrounding area is located next to it. As shown in Table 1, the area of each polygon (ai, km2) was multiplied by each weather station’s precipitation value. Because this is a simple and computationally undemanding method, the Inverse distance weighting technique was also considered in this study. Inverse distance weighting is a deterministic methodology for multivariate interpolation applying a known set of scattered points. Many academic fields, including the geographical and environmental sciences, use this method [21].
The Grubbs test (GT) is frequently used to identify outliers (one outlier at a time). The assumption that the data are normally distributed underlies the test. As a result, the distribution of the data should be examined prior to applying the test [22]. The following definition of the GT test is of relevance here: In the dataset, H0 indicates that there are no outliers and Ha indicates that there is only one outlier. Four methods, including the Pettitt test (PT), the Standard Normal Homogeneity Procedure (SNHT) for a single break [13], the Buishand range test (BRT), and the von Neumann ratio check (VNRT), were used to test the homogeneity of precipitation datasets [23,24,25]. The annual values of variable X are independent, uniformly distributed, and homogeneous according to the null hypothesis. SNHT, Pettitt Test, and B RT, on the other hand, make the assumption that the time series is non-homogeneous and has a break associated with the average under the alternative hypothesis. Figure 2 reveals the proposed research methodology as a flowchart.
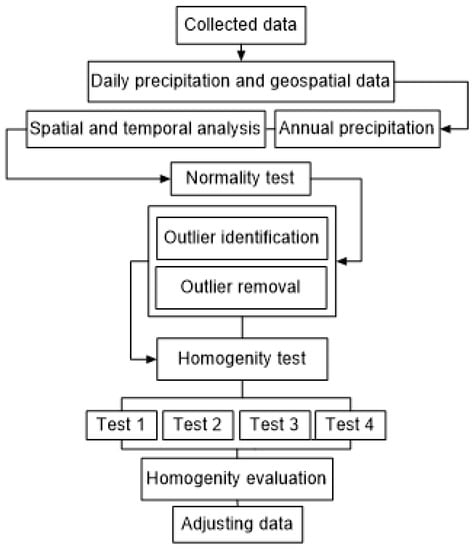
Figure 2.
Flowchart representing the links between the main steps in the proposed research methodology.
Based on methods that reject the null hypothesis of time series homogeneity, Wijngaard et al. [10] classified the outcomes of four tests into the following groups: Useful, doubtful, and suspect. Accordingly, the following three classes of relevance for this investigation were identified [1]:
- If one or no test rejects the null hypothesis, there is no apparent indication of non-homogeneity in the time series, and the series can be considered sufficiently homogeneous for both trend and variability analysis. Then the data series is classified as ‘useful’ under class 1.
- If two tests reject the null hypothesis, the data are classified as ’doubtful’ under class 2. In case there is a sign of non-homogeneity in the time series that exceeds the level expressed by the inter-annual standard deviation of the testing variable series, the outcomes of variability and trend analyses should be assessed carefully for the existence of potential non-homogeneities within the series.
- If three or four tests reject the null hypothesis, then the data are classified as ‘suspect’ (class 3), and the series should not be considered for further analysis. However, the series can be considered for additional investigation, in the case where it can be reasonably assumed that an actual climatic indication rather than a non-climatic one caused unexpected results.
3. Results and Discussion
3.1. Long-term Analysis of the Precipitation Dataset
For climate change and climate variability studies, the long-term analysis of precipitation datasets, such as the normality test, outlier identification, quality control, and homogeneity analysis, is vital. Firstly, a long-term spatio-temporal analysis of the precipitation variation over the studied region from 1979 to 2013 was carried out (Figure 3). The entire area showed a declining precipitation trend over the past 35 analysis years, with a maximum decline of 341 mm/decade. The Iraqi annual precipitation is approximately 211 mm. Extreme precipitation (291 mm) was recorded for 1979/1980, whereas the corresponding smallest (93 mm) was allocated to 2007/2008 (Figure 3). Figure 1 displays how the entire area of Iraq is divided into forty sub-areas, each of which is associated with a particular weather station. The Thiessen Network method was applied to estimate the spatial variation of the average annual precipitation over Iraq during the period between 1979 and 2014 (Figure 1).
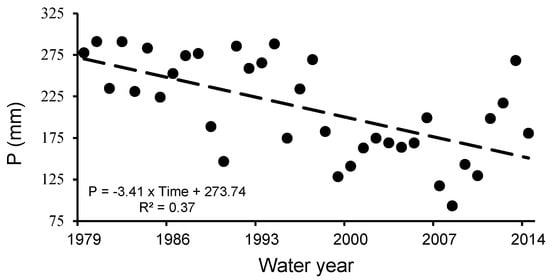
Figure 3.
Temporal variations and the trend of annual average precipitation (P) that was estimated by applying the Thiessen Network method over Iraq during the time period between 1979 and 2014.
However, Figure 4 displays the long-term spatial distribution precipitation variation over the studied region. The long-term analysis of precipitation indicates that the average annual values vary spatially from 84.38 to 233.46 mm and from 233.46 mm to 978.85 in the southern, western, central, and northern parts of the country, respectively (Figure 4). It is important to note that the upper part of Iraq had greater precipitation amounts than the lesser one (Figure 4). Furthermore, the average annual values vary spatially from 172 to 845 mm, 101 to 149 mm, 82 to 196 mm, and 90 to 201 mm in the northern, western, middle, and southern parts of the country, respectively. The corresponding values of standard deviation varied between 58 and 291 mm, 44 and 68 mm, 33 and 68 mm, and 33 and 67 mm in this order. The average annual precipitation varies spatially from 89 mm at Samawa station, which is situated in the southern portion of the country, to 845 mm at Soran station, which is situated in the northern part. The northern part receives precipitation of more than 500 mm. However, in the western and southern areas, the annual precipitation varied from 68 to 154 mm (Figure 4). The coefficient of variation CV, which is the degree of spreading around the average, was also estimated to investigate the spatial inconsistency of annual precipitation for every weather station. This coefficient varied between 29.2 and 46.8%.
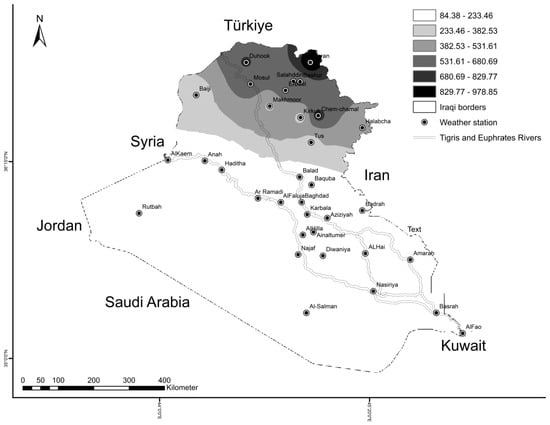
Figure 4.
The long-term spatial distribution of the annual precipitation over Iraq.
3.2. Normality Test and Outliers Detection
The second step in the research methodology is testing that the dataset is normally distributed. The Shapiro–Wilk method has been applied to investigate the distribution of the dataset (Table 2). The results were evaluated at a 95% significance level. The data series was considered non-normally distributed and the p-values were lower than the 5% significance level. Table 2 reveals the obtained results for 40 weather stations. The non-normal precipitation data have been converted to normally distributed data through the application of the Box–Cox transformation method. The bold numbers in Table 2 represent precipitation datasets that are not normally distributed. Based on the obtained results, the datasets at Salahddin, Bashur, Mosul, Erbeel, Makhmoor, Al-Faluja, Baghdad, Rutbah, Al-Hilla, and Najaf weather stations were found to be non-normally distributed, with p-values less than the significant level of 0.05. A normalizing transformation of the data (Box–Cox) has subsequently been used to convert the non-normal precipitation data to normally distributed data before using the dataset for any further analysis.

Table 2.
Results of the Shapiro–Wilk normality test for the Iraqi weather stations.
Outliers are normally defined as data points that depart noticeably from the underlying trend of the dataset. They can be caused by observation and recording errors or severe weather events. Outliers can negatively impact the results of data analysis [25,26,27,28,29]. The detection of outliers should be considered an important step in data quality control. As a possible action, for example, unexpected maximum data can be rejected (if justified) and the problem is changed to one of missing data. However, in the case that such outliers have, for example, a physical background explanation, the question arises whether they should be modified or not, since maximum data may carry important climatological meaning that should or even must not be ignored [29,30,31,32,33].
The GT technique was adopted as a quality control method in this study. Data variability reaches its maximum in the northern part of the country. Data dispersion is low in the central plateau and the southern part of the country, where the frequency of precipitation events is rare.
3.3. Homogeneity Analysis
When variations within a climate time series are brought on by changes in the climate, the time series is said to be homogeneous. However, non-climatic factors such as changes in the environment and the location of the meteorological station, as well as the tools and calculation techniques used, can also contribute to data heterogeneity. Inconsistencies in the climatic dataset could cause the studied environment to be interpreted incorrectly. After determining the annual mean precipitation values from the monthly totals, homogeneity tests were successfully used to evaluate the validity of the data. The records for each weather station were estimated individually during the application of these procedures at a significance level of 5%, and the non-homogeneous years were identified.
The annual values Yi of the testing variable Y are independent and have the same distribution under the null hypothesis (H0), and the series is regarded as homogeneous, while the alternative hypothesis (Ha) is that the series is homogeneous.
The SNHT, BRT, and PT assume that the series consists of breaks in the mean. Between SNHT, BRT, and PT, there are certain differences. In contrast to the BRT and PT, which are sensitive to changes in the middle of a series, the SNHT test is known to find change points toward the beginning and end of the series [3]. These three tests can identify the year that a break takes place. While the null hypothesis for VNRT is the same as for the three other tests, the alternate hypothesis is that the series is not distributed randomly. While evaluating the series’ randomness, VNRT omits information regarding the break’s year. The null hypothesis will be rejected for each of these four tests at a given level of confidence if the test statistic exceeds the critical value.
Due to the precipitation’s fundamental high variability, interruptions in precipitation series can only be seen if they are quite big. However, it becomes more difficult to identify trends in precipitation series. Accordingly, the results of the homogeneity tests continue to be in line with the ability to detect trends in precipitation series [26]. Testing for consistency of the precipitation datasets is challenging due to spatio-temporal variations. As a result, applying multiple tests to the consistency of precipitation can increase the likelihood that a true null hypothesis will be rejected.
Table 2 lists the homogeneity of the annual precipitation in the study area and comparative test statistics estimated by the four methods. Each weather station’s recorded values were examined separately. The inhomogeneities were identified, and each test’s significance level of 0.05 was examined. The results for the annual series indicate that the inhomogeneous structure is generally observed in 1994, 1997, 1998, 2009, 2010, and 2012. Based on PT, the change occurred in 1994 at eight stations, in 1997 at three stations, in 1998 at ten stations, and in 2009 at one station. According to the SNHT test, the changing years for the annual rainfall series at four stations (Soran, Duhook, Chem-chamal, and Tus) were noted for 1994 and at stations in Kirkuk, Halabcha, Aziziyah, and Karbala for 1997. Moreover, for another seven stations (Balad, Baquba, Badrah, Ainaltumer, Kut, AlHai, and Amarah), the breakpoint was recorded in 1998. According to the BRT test, the break occurred in 1994, 1997, and 1998 at six stations, in 2009 and 1988 at one station, and in 2010 at two stations. Overall, data at 16 out of 40 stations were discovered to be linked to homogeneous data (Table 3).

Table 3.
Station addresses with corresponding homogeneity test results for meteorological data series.
Inhomogeneity was noted in precipitation data for the northern and eastern parts of the country. A sudden change in a station location or a sharp increase or decrease in rainfall values may be responsible for a non-climatological spike in the sum of these rainfall series. The Pettit test revealed a single breakpoint in a time series, although the observed breaks were close to the start and end of the data series. The Pettitt test found breaks in the midst of the 1979–2013 period. The findings indicated that conducting a homogeneity analysis before researching climate changes and differences is beneficial.
The annual precipitation series for all stations under consideration was found to be homogeneous based on the results of the VNRT test, which did not provide information about the break year. The PT, however, produced the greatest number of non-homogeneous precipitation series. According to all homogeneity tests, the breakpoints at the Soran, Duhook, and Tus stations, Kirkuk and Halabcha stations, and Badrah, Ainaltumer, Kut, and AlHai stations were connected to 1994, 1997, and 1988, respectively (Table 3).
Additionally, according to the four analyses, the distribution of precipitation data at Mosul, Sinjar, Makhmoor, Ar Ramadi, Baghdad, Rutbah, AlHilla, Nukheb, Najaf, Diwaniya, Nasiriya, Samawa, Basrah, Al-Salman, Busayah, and AlFao stations was homogenous. The obtained overall result is consistent with previous research during which similar trends were found [3,6,7,8]. For example, according to Jaffar and Al-Lami [8], the results of the homogeneity test showed that 5% of the selected stations were assigned to the “doubtful” class with change years recorded in 1998 for PT and BRT. Approximately 45% were assigned to the “suspect” class with change years noticed for PT, SNHT, and BRT, with the majority of break years discovered in 1998 and 1999, representing 28% of break years. Furthermore, 21% of break years were discovered in 1997, and other break years were found between 1991 and 2004, representing 50%. Elzeiny et al. [6] assessed the homogeneity of the yearly rainfall datasets from 30 meteorological stations throughout the Upper Blue Nile River Basin between 1901 and 2013. They noted that the annual series of the stations under consideration are homogeneous, according to the results of the SNHT and BRT, and are categorized as “useful” (p < 0.05). However, six sites are characterized by inhomogeneity as shown by VNRT.
The following stations were identified as having “useful” annual total precipitation data: Mosul, Sinjar, Makhmoor, Ar Ramadi, Baghdad, Rutbah, AlHilla, Nukheb, Najaf, Diwaniya, Nasiriya, Samawa, Basrah, Al-Salman, Busayah, and AlFao. For the purposes of trend and variability analysis, they can be regarded as sufficiently homogeneous. Due to potential non-homogenous annual total precipitation data at the stations of Erbeel, AlFaluja, and Kut, they were labeled “doubtful” and should only be used with caution for trend and variability analysis. It was discovered that the annual total precipitation data from the other stations were labeled “suspect,” which means that these series should not be used for trend and variability analysis unless they are homogenized.
There is no clear effect of the outliers on the identification of the change point in the dataset, according to the homogeneity analysis results, which were identical before and after applying outlier treatments. Therefore, it is advised that, at least for the studied area and other regions with comparable climatic conditions, the homogeneity analysis can be applied without carrying out the outlier detection procedure in future research.
4. Conclusions and Recommendations
The outcomes show that approximately 40% of the example precipitation datasets are homogeneous. Thus, they can be utilized for hydro-climatic studies. The annual rainfall time series data at 21 out of 40 stations were found to be suspect, 3 of the time series were classified as doubtful, and 16 locations were classified as useful. The acquired results were assessed with various tests, and the breakpoints in the non-homogeneous time series were identified. The highest numbers of non-homogeneous time series were obtained by applying the Pettitt test, which can be considered the most sensitive one. Nevertheless, all techniques can be used effectively for the homogeneity investigation of precipitation time series. Metadata of weather stations, if existing, can be used supplementarily to verify the results.
The non-homogeneity detected for many datasets may be attributed to non-climatic factors. However, no metadata confirming that the identified non-homogeneities were related to non-climatic reasons were available. It is anticipated that the proposed tested research methodology will help researchers to use quality data with high confidence in hydro-meteorological research studies. The research can be considered a reference for future climate change and climate variability evaluations and hydro-climatic studies in Iraq and other countries with similar climatic conditions.
The authors recommend future work on the assessment of the history of weather stations. Findings should always be checked in the context of the broader change in atmospheric circulation experienced at the studied location. Regular increasing or decreasing trends and/or sudden changes in climatic parameters may be identified. Based on the homogeneity analysis results, the change points detected simultaneously at many stations in the studied geographical region might imply a common signal of the existence of a general large-scale physical mechanism affecting the inconsistency of the local precipitation.
There was no evidence to support the idea that the identification and treatment of outliers in the precipitation time series might affect the results of the homogeneity analysis. Therefore, for this case study and similar studies in the future, a homogeneity analysis may be used instead of the outlier test.
Author Contributions
Conceptualization, R.M.; methodology, R.M.; software, R.M.; validation, R.M.; formal analysis, R.M.; investigation, R.M.; resources, R.M.; data curation, R.M.; writing—original draft preparation, R.M.; writing—review and editing, M.S.; visualization, R.M.; supervision, M.S.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in [USGS] at [https://earthexplorer.usgs.gov, accessed on 17 January 2023].
Acknowledgments
The authors acknowledge the support of their particular organizations. This research was not externally sponsored. We appreciate the Iraqi Ministry of Agricultural and Water Resources for providing the necessary information for the analysis.
Conflicts of Interest
The authors declare no conflict of interest. The statements and opinions expressed in this article do not necessarily reflect those of any institutions mentioned in the list of affiliations.
References
- Kang, H.M.; Yusof, F. Homogeneity tests on daily rainfall series in Peninsular Malaysia. Int. J. Contemp. Mathem. Sci. 2012, 7, 9–22. [Google Scholar]
- Sahin, S.; Cigizoglu, H.K. Homogeneity analysis of Turkish meteorological data set. Hydrol. Proc. 2010, 24, 981–992. [Google Scholar] [CrossRef]
- Agha, O.M.A.M.; Bağçacı, S.Ç.; Şarlak, N. Homogeneity analysis of precipitation series in North Iraq. IOSR J. Appl. Geol. Geophys. 2017, 5, 57–63. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ogunjobi, K.O. Recent homogeneity analysis and long-term spatio-temporal rainfall trends in Nigeria. Theor. Appl. Climatol. 2017, 128, 275–289. [Google Scholar] [CrossRef]
- Karabork, M.C.; Kahya, E.; Komuscu, A.U. Analysis of Turkish Precipitation Data: Homogeneity and the Southern Oscillation Forcings on Frequency Distributions. Hydrol. Process. 2007, 21, 3203–3210. [Google Scholar] [CrossRef]
- Elzeiny, R.; Khadr, M.; Zahran, S.; Rashwan, E. Homogeneity analysis of rainfall series in the upper blue nile river basin, Ethiopia. J. Eng. Res. 2019, 3, 46–53. [Google Scholar] [CrossRef]
- AL-Lami, A.M.; AL-Timimi, Y.K.; AL-Salihi, A.M. The homogeneity analysis of rainfall time series for selected meteorological stations in Iraq. Diyala J. Pure Sci. 2014, 10, 60–77. [Google Scholar]
- Jaafar, A.J.; Al-Lami, A.M. Quality control of annual precipitation measurement for selected stations in Iraq. Al-Mustansiriyah J. Sci. 2019, 30, 9–17. [Google Scholar]
- González-Rouco, J.F.; Jiménez, J.L.; Quesada, V.; Valero, F. Quality control and homogeneity of precipitation data in the southwest of Europe. J. Clim. 2001, 14, 964–978. [Google Scholar] [CrossRef]
- Wijngaard, J.B.; Tank, A.K.; Können, G.P. Homogeneity of 20th century European daily temperature and precipitation series. Int. J. Climat. 2003, 23, 679–692. [Google Scholar] [CrossRef]
- Göktürk, O.M.; Bozkurt, D.; Şen, Ö.L.; Karaca, M. Quality control and homogeneity of Turkish precipitation data. Hydrol. Proc. Int. J. 2008, 22, 3210–3218. [Google Scholar] [CrossRef]
- Yeşilırmak, E.; Akçay, S.; Dağdelen, N.; Gürbüz, T.; Sezgin, F. Quality control and homogeneity of annual precipitation data in Büyük Menderes Basin, Western Turkey. Fres. Environ. Bull. 2009, 18, 1748–1757. [Google Scholar]
- Talaee, P.H.; Kouchakzadeh, M.; Some’e, B.S. Homogeneity analysis of precipitation series in Iran. Theor. Appl. Climatol. 2014, 118, 297–305. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J. On the critical values of the standard normal homogeneity test (SNHT). Int. J. Clim. J. R. Meteorol. Soc. 2007, 27, 681–687. [Google Scholar] [CrossRef]
- Dikbas, F.; Firat, M.; Koc, A.C.; Güngör, M. Homogeneity test for Turkish temperature series. In Proceedings of the 4th BALWOIS 2010 International Conference, Ohrid, North Macedonia, 25–29 May 2010; pp. 25–29. [Google Scholar]
- Pettitt, A.N. A Non-Parametric Approach to the Change Point Problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Dhorde, A.G.; Zarenistanak, M. Three-way approach to test data homogeneity: An analysis of temperature and precipitation series over south-western Islamic Republic of Iran. J. Indian Geophys. Union 2013, 17, 233–242. [Google Scholar]
- Yozgatligil, C.; Yazici, C. Comparison of homogeneity tests for temperature using a simulation study. Int. J. Climat. 2016, 36, 62–81. [Google Scholar] [CrossRef]
- Mohammed, R.; Scholz, M. The reconnaissance drought index: A method for detecting regional arid climatic variability and potential drought risk. J. Arid Environ. 2017, 144, 181–191. [Google Scholar] [CrossRef]
- Grubbs, F. Procedures for detecting outlying observations in samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; Muthiah, K.; Sridhar, V. Long-term homogeneity, trend, and change-point analysis of rainfall in the arid district of Ananthapuramu, Andhra Pradesh State, India. Water 2020, 12, 211. [Google Scholar] [CrossRef]
- Tadeyo, E.; Chen, D.; Ayugi, B.; Yao, C. Characterization of Spatio-Temporal Trends and Periodicity of Precipitation over Malawi during 1979–2015. Atmosphere 2020, 11, 891. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Y.; Chen, X.; Yang, W. Trend analysis of rainfall time series in Shanxi Province, Northern China (1957–2019). Water 2020, 12, 2335. [Google Scholar] [CrossRef]
- Zamrane, Z.; Mahé, G.; Laftouhi, N.-E. Wavelet analysis of rainfall and runoff multidecadal time series on large river basins in Western North Africa. Water 2021, 13, 3243. [Google Scholar] [CrossRef]
- Bougara, H.; Hamed, K.B.; Borgemeister, C.; Tischbein, B.; Kumar, N. Analyzing trend and variability of rainfall in the Tafna Basin (Northwestern Algeria). Atmosphere 2020, 11, 347. [Google Scholar] [CrossRef]
- Chang, K.-T. Introduction to Geographic Information Systems, 3rd ed.; McGraw Hill: New York, NY, USA, 2008. [Google Scholar]
- Mahmood, R.; Jia, S. Quality control and homogenization of daily meteorological data in the trans-boundary region of the Jhelum River basin. J. Geograph. Sci. 2006, 26, 1661–1674. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Ismail, T.; Nawaz, N.; Wang, X.J. Absolute homogeneity assessment of precipitation time series in an arid region of Pakistan. Atmósfera 2018, 31, 301–316. [Google Scholar] [CrossRef]
- Štěpánek, P.; Zahradníček, P.; Skalák, P. Data quality control and homogenization of air temperature and precipitation series in the area of the Czech Republic in the period 1961–2007. Adv. Sci. Res. 2009, 3, 23–26. [Google Scholar] [CrossRef]
- Mair, A.; Fares, A. Comparison of rainfall interpolation methods in a mountainous region of a tropical island. J. Hydrol. Eng. 2010, 16, 371–383. [Google Scholar] [CrossRef]
- Noori, M.J.; Hassan, H.H.; Mustafa, Y.T. Spatial estimation of rainfall distribution and its classification in Duhok governorate using GIS. J. Water Resour. Prot. 2014, 6, 75–82. [Google Scholar] [CrossRef]
- Zaifoğlu, H.; Akıntuğ, B.; Yanmaz, A.M. Quality control, homogeneity analysis, and trends of extreme precipitation indices in Northern Cyprus. J. Hydrol. Eng. 2017, 22, 05017024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).