An Improved Ensemble-Strategy-Assisted Wind Speed Prediction Method for Railway Strong Wind Warnings
Abstract
:1. Introduction
2. Methodology
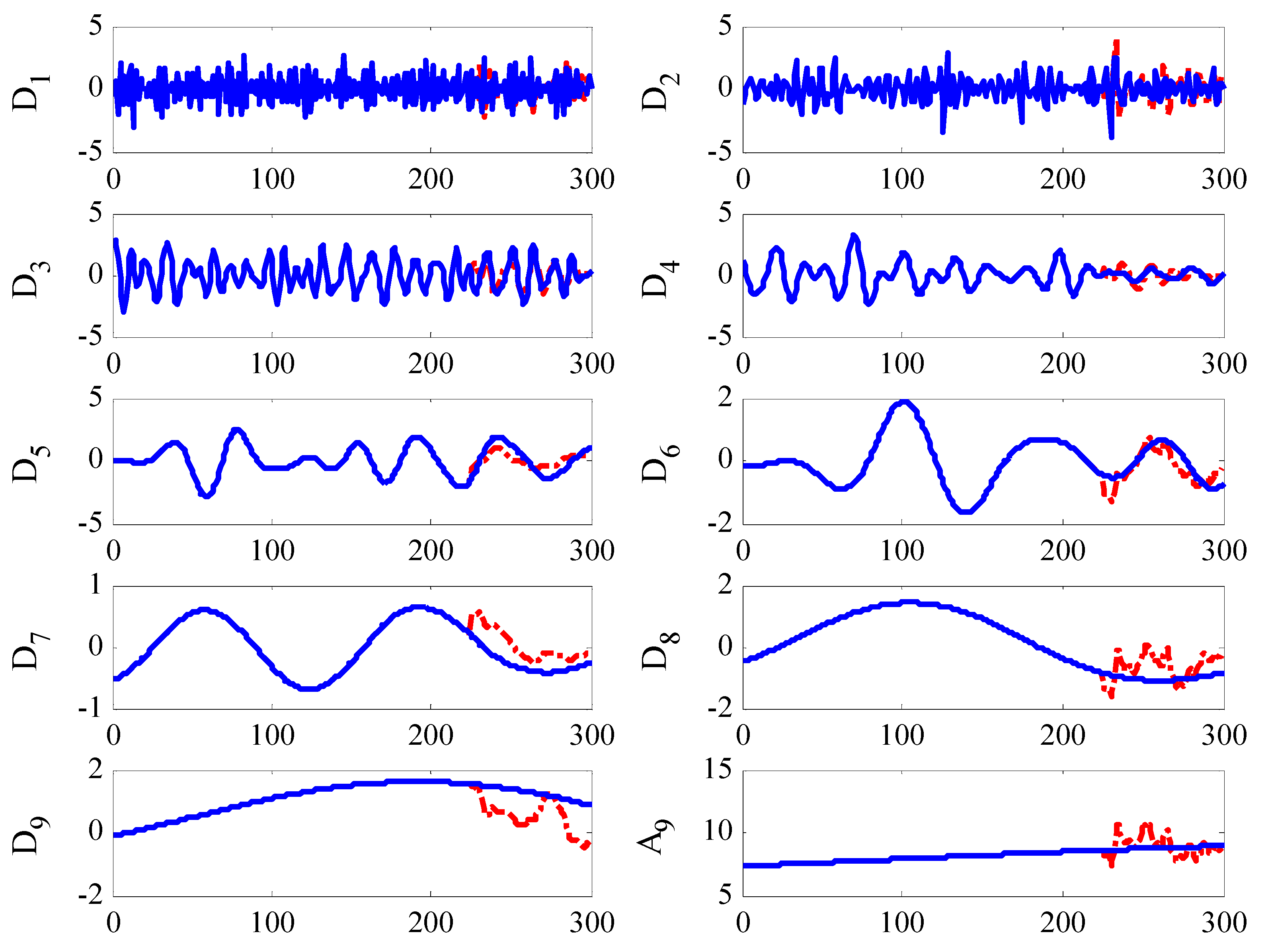
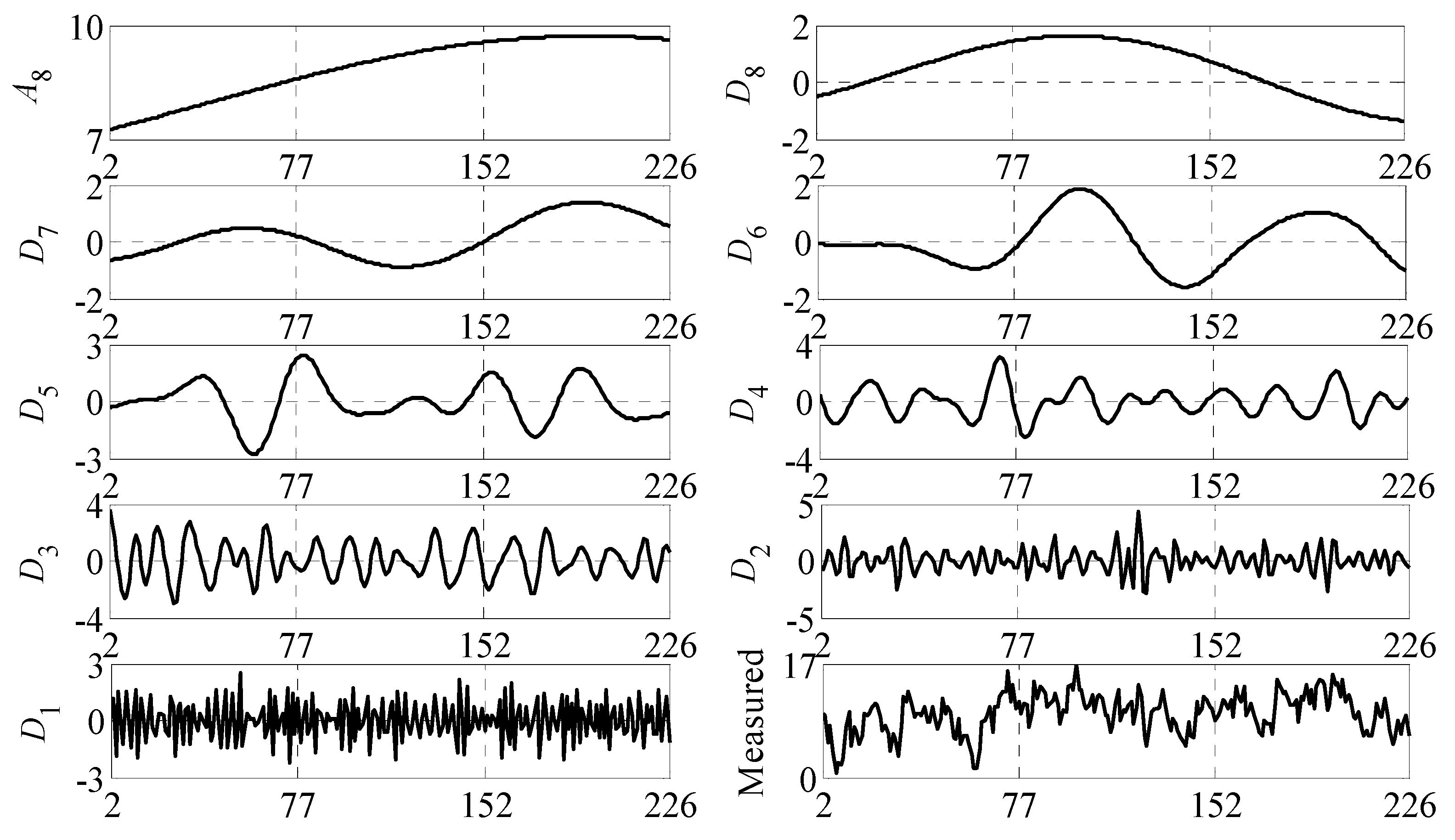
2.1. Discrete Wavelet Transform
2.2. Conditional Kernel Density Estimation
2.3. Evaluation Metrics
3. Review of Traditional Decomposition-Based Prediction Models
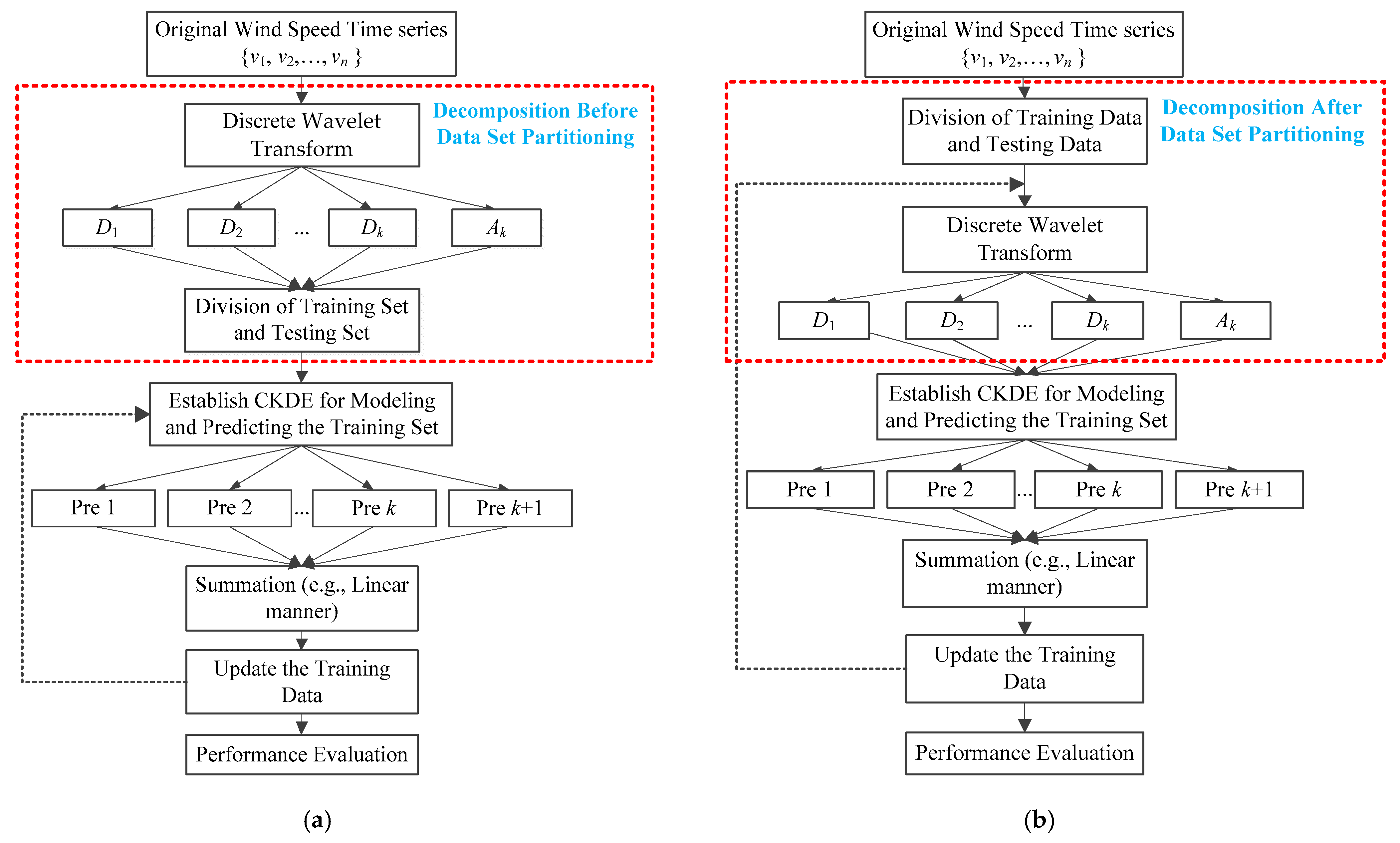
3.1. Steps of Traditional Prediction Methods
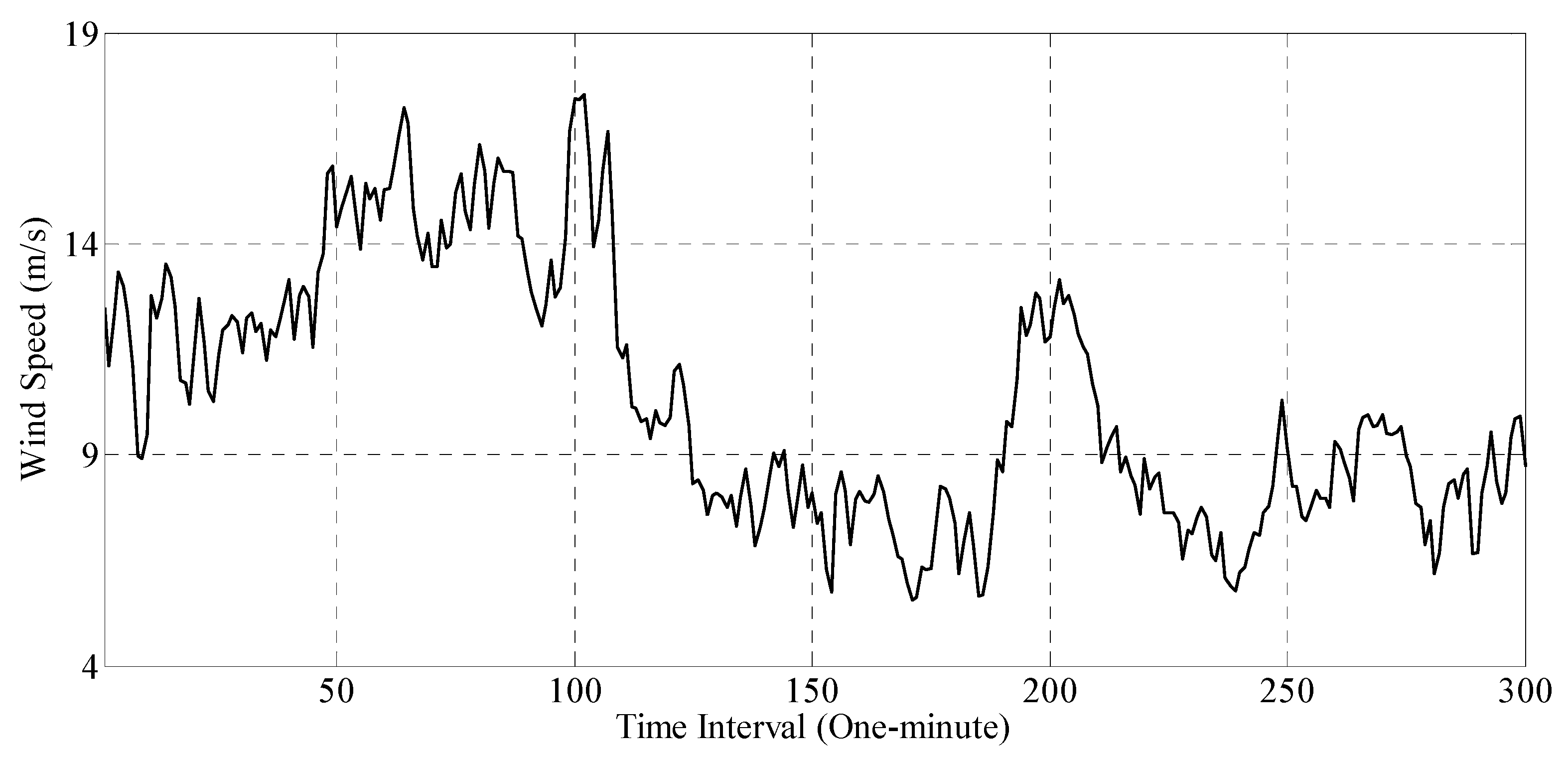
3.2. Experimental Data Illustration
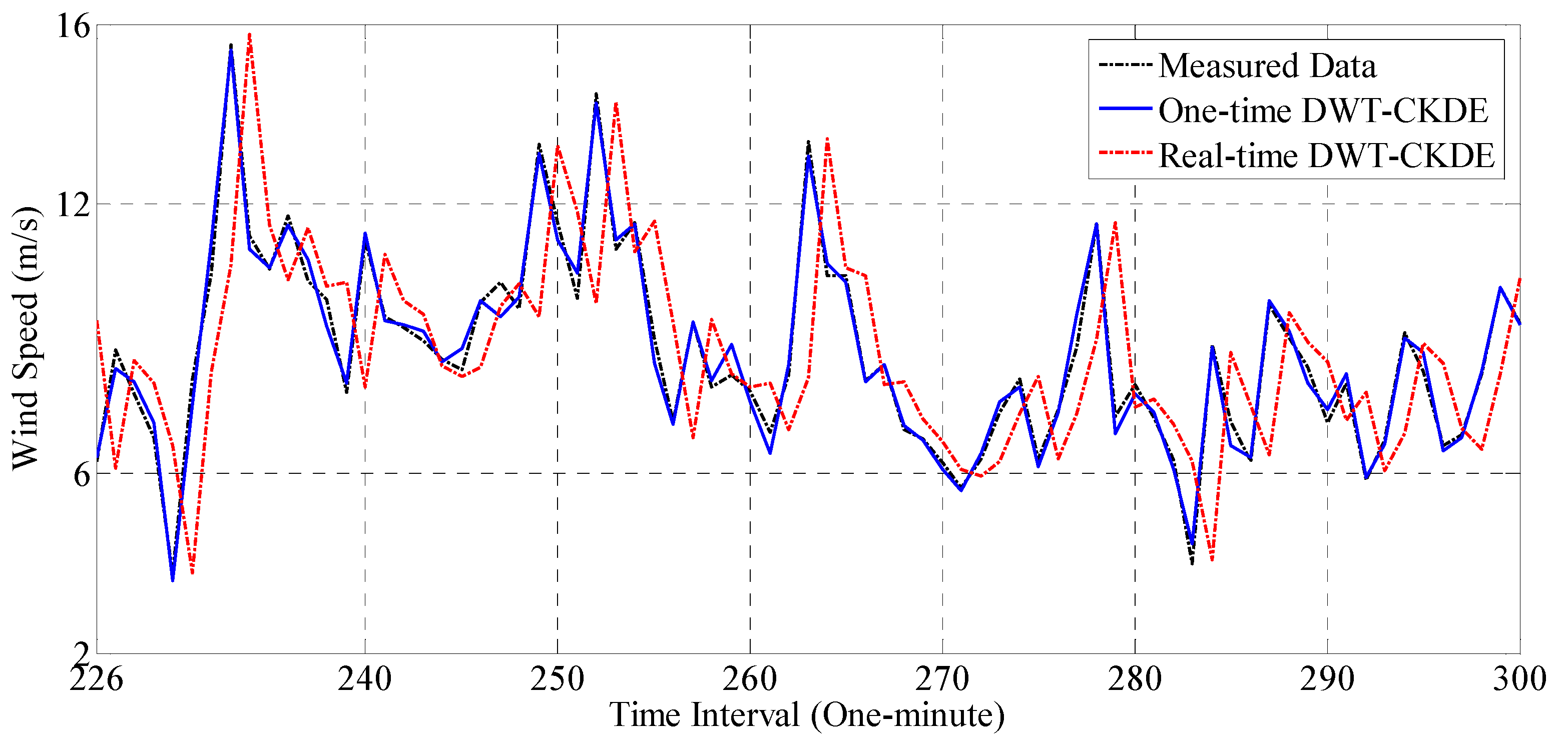
3.3. Performance Comparison of Traditional Decomposition-Based Forecasting Methods
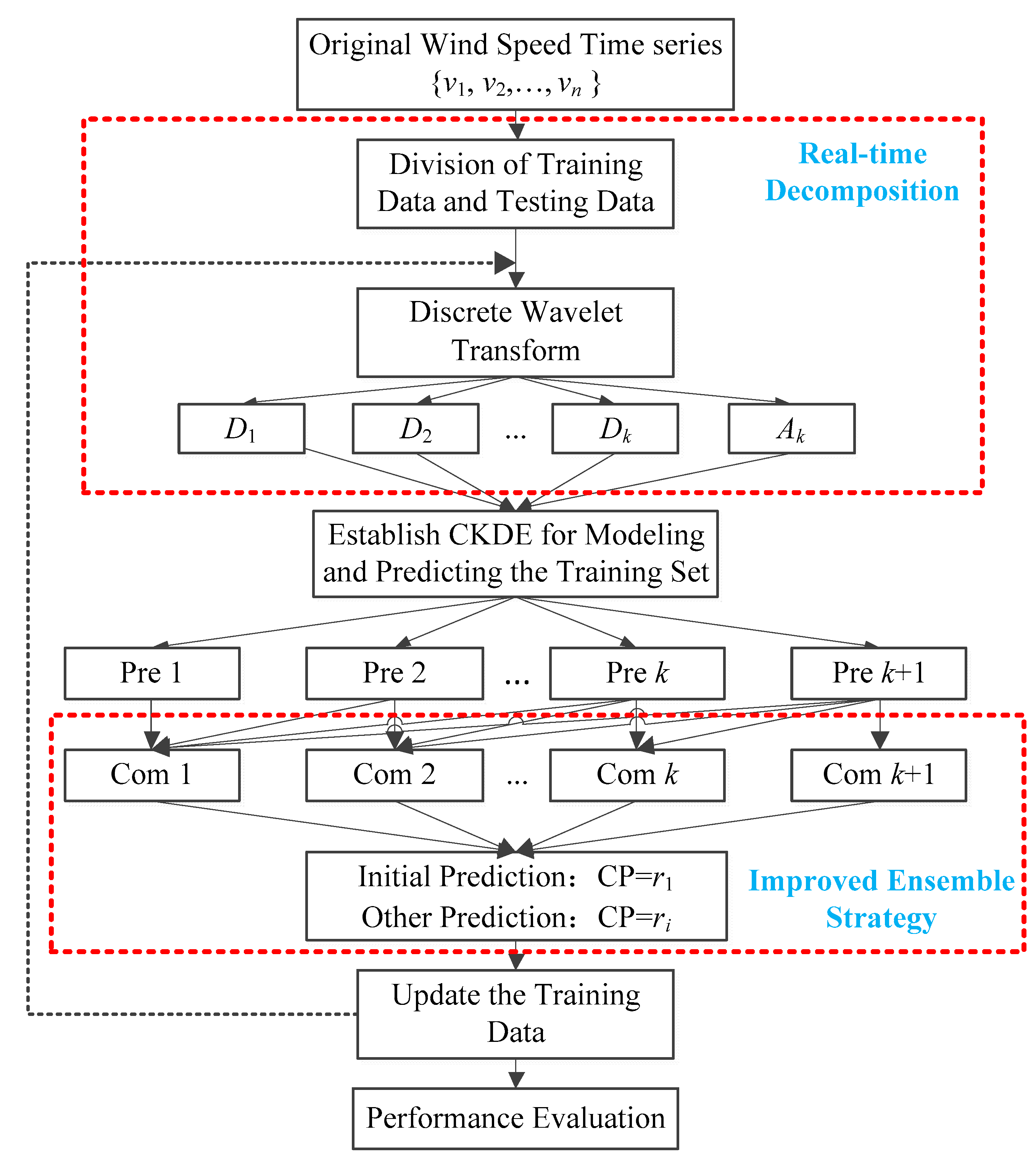
4. The Proposed Forecasting Method
4.1. Processes of the Proposed Method
- (1)
- Divide the original wind speed time series into an initial training set and a testing set ;
- (2)
- Perform the DWT decomposition on the initial training samples (the specified number of decomposition levels is set as 9, i.e., k = 8) to obtain the approximation component and k detailed components . Then, the CKDE model is established for training each decomposed subsequence and implementing individual one-step ahead prediction. The predicted values of all subsequences are combined based on the following combination pattern (CP), i.e., , , …, , . On this basis, it is obvious that there k + 1 different CPs (i.e., ensemble strategies) are reserved for ensemble prediction in the next moment (i.e., the result of ). In above CPs, denotes the one-step ahead forecasting value of the detailed component and stands for the one-step ahead forecasting value of the approximation component ;
- (3)
- When the actual value of is known, the ideal ensemble strategy (marked as the CP r2) in Step (2) can be identified from k + 1 different CPs based on the minimum absolute deviation criterion, i.e., the prediction based on the ideal ensemble strategy has the smallest deviation with its corresponding actual value;
- (4)
- Update the training set to (i.e., the known value of ) and perform the corresponding DWT decomposition where one approximation component and eight detailed components can be obtained. Then, the CKDE model is established to yield nine individual one-step ahead predictions and nine different CPs. With these predictions and the previous CP r2, the one-step ahead prediction of the wind speed data point (i.e., the result of ) can be generated;
- (5)
- When the actual value of is known, the ideal ensemble strategy (marked as the CP r3) in Step (3) can also be identified, and it has a similar deterministic process with that of CP r2. This CP r3 provides an ensemble strategy for the forecasting result ;
- (6)
- Similarly, update the training set to and repeat Step (4) and combine the ensemble strategy CP ri to yield the forecasting result . When the actual value of is known, the ensemble CP ri+1 can be obtained via a similar process with Step (5), which provides an ensemble strategy for the forecasting result , otherwise the prediction should be terminated. Note that the ideal combination pattern at the previous moment is regarded as the ensemble strategy at the current moment;
- (7)
- As for the predicted value of and CP r1, they can be obtained by the following procedures: ① perform the DWT decomposition for the wind speed time series and establish the CKDE model for training and predicting each decomposed subsequence, thereby yielding nine different CPs; ② with the available of the value of , the ideal ensemble strategy CP r1 can be identified; ③ update the training set to and repeat Step (4), then the predicted value of can be generated;
- (8)
- Perform the error analysis based on the performance evaluation indictors given in Section 3.1.
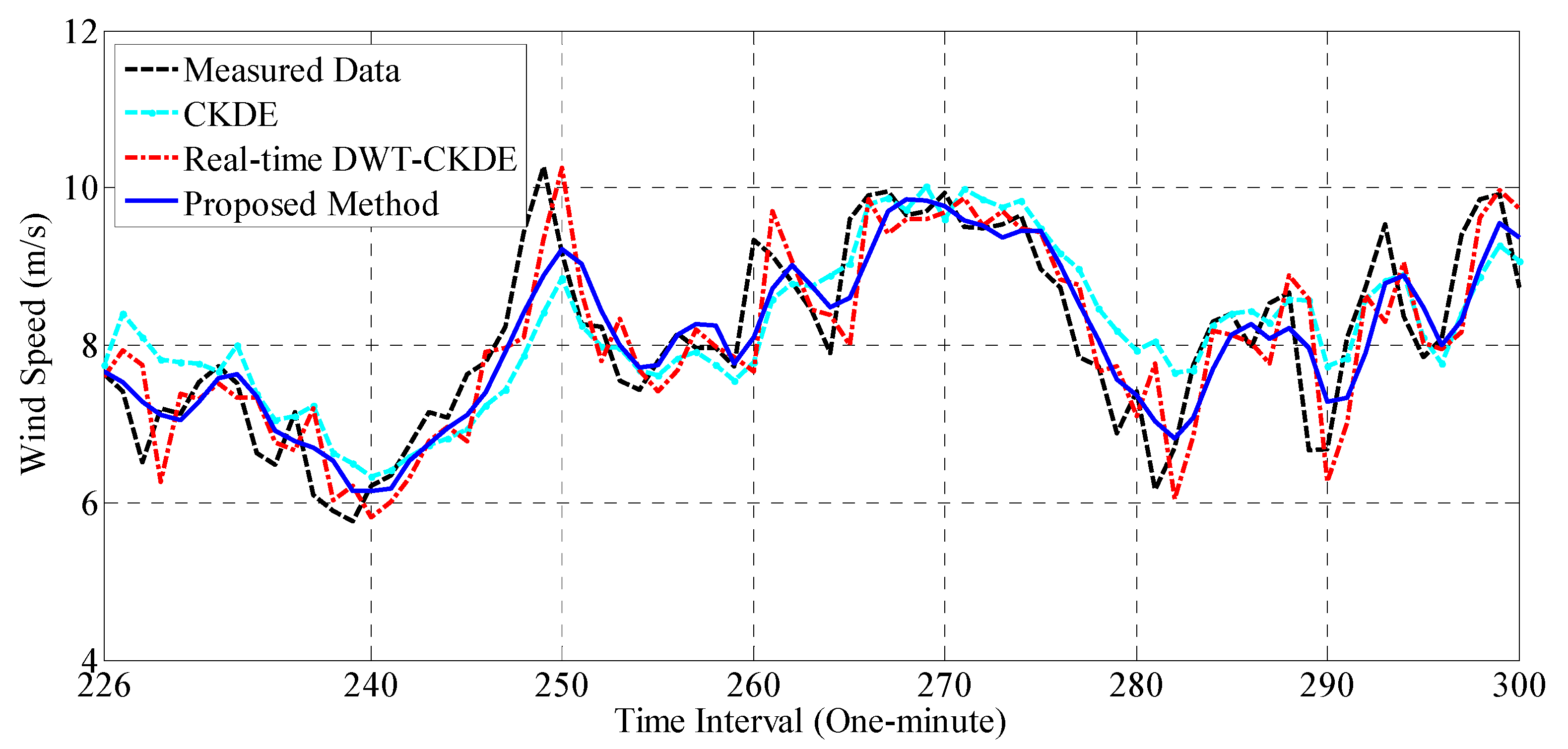
4.2. Numerical Example
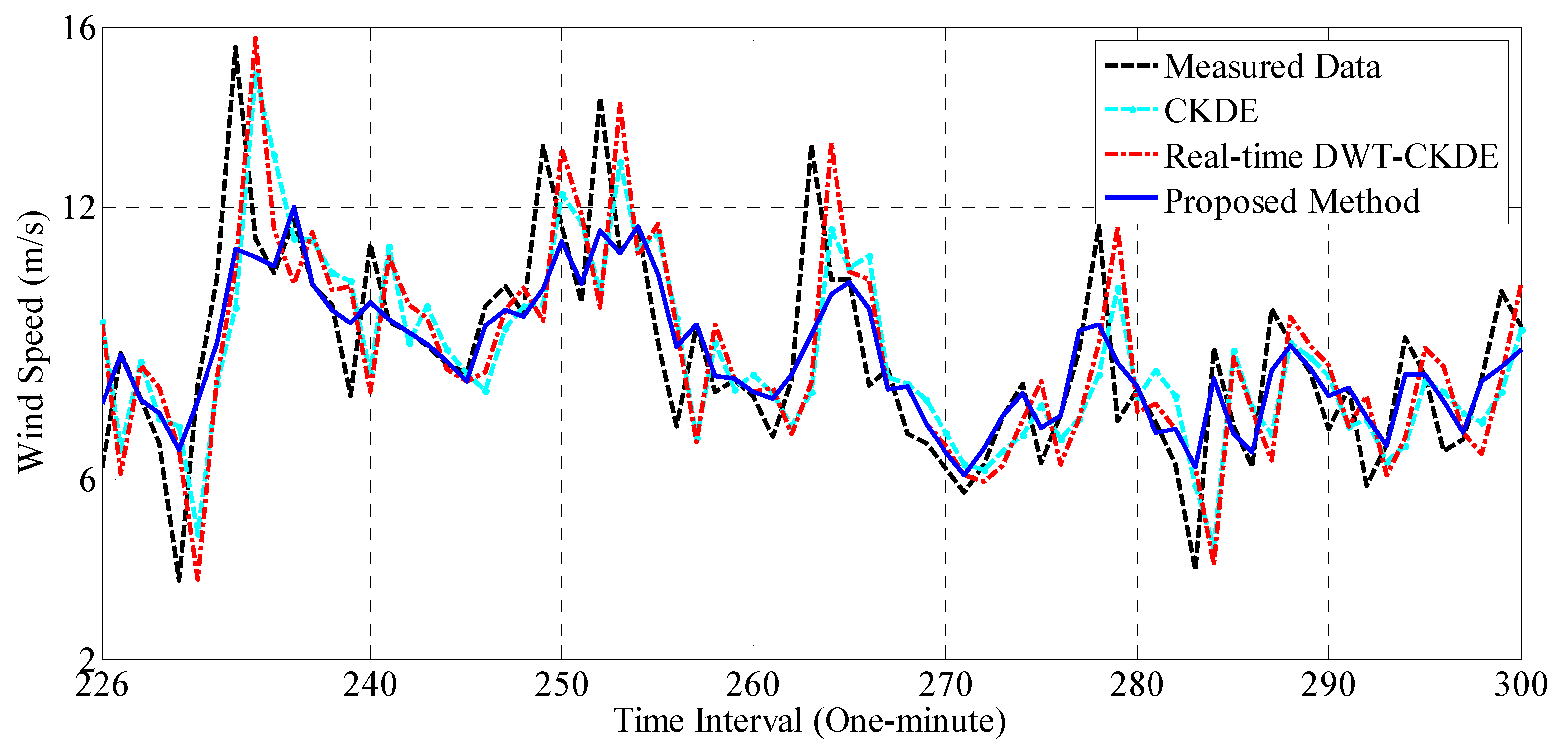
4.3. Practicality Analysis
5. Conclusions
- (1)
- The one-time decomposition-based forecasting method has an extremely good forecasting performance. However, this method cannot provide online prediction because the one-time decomposition operation takes future data into consideration.
- (2)
- The real-time decomposition-based forecasting method can provide online prediction, and thus may have the potential to be implemented in practice. However, the forecasting accuracy of this method is not stable and is sometimes unsatisfactory. Although decomposition methods reduce the nonstationary and nonlinear characteristics of data, they may also greatly increase the volatility of decomposed subsequences (especially for the end part of subsequences), thereby increasing the difficulty of prediction and ultimately leading to poor forecasting results.
- (3)
- CKDE is still effective in the prediction of short-term wind speeds. This method can be regarded as the nonparametric model to some extent, and thus has a powerful applicability in addressing the time series problem. The numerical case in this paper shows that it even performs better than the decomposition-based forecasting method in some scenarios.
- (4)
- The combination of several individual predictions (i.e., the prediction of each decomposed subsequence) may have a higher accuracy than the summation of all predictions in the short-term wind speed prediction. Along with this design concept, an improved ensemble strategy is developed which can perform selective combination prediction by analyzing information in the historical data. The experimental results indicate this strategy can clearly improve the forecasting accuracy of real-time decomposition-based methods and the single method. For example, compared with CKDE, the average degrees of improvement realized by the proposed method in terms of MAE, RMSE, and MRPE are 16.25%, 17.66%, and 16.93, respectively, while those in comparison with the traditional real-time DWT-CKDE method are 17.11%, 18.54%, and 16.84, respectively. Therefore, the proposed method may have great potential for railway strong wind warning systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, M.; Wang, X.; Li, X.; Wang, P. Influence of spatial track alignment of long-span arch bridge on train operational stability. Veh. Syst. Dyn. 2023, 61, 3161–3180. [Google Scholar] [CrossRef]
- Li, X.; He, H.; Wang, M.; Wang, P. Influence of long-span bridge deformation on driving quality of high-speed trains. Int. J. Rail Transp. 2023, 1–19. [Google Scholar] [CrossRef]
- Liu, D.; Wang, T.; Liang, X.; Meng, S.; Zhong, M.; Lu, Z. High-speed train overturning safety under varying wind speed conditions. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104111. [Google Scholar] [CrossRef]
- Yan, N.; Chen, X.; Li, Y. Assessment of overturning risk of high-speed trains in strong crosswinds using spectral analysis approach. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 103–118. [Google Scholar] [CrossRef]
- Wang, M.; Chen, X.; Li, X.; Yan, N.; Wang, Y. A frequency domain analysis framework for assessing overturning risk of high-speed trains under crosswind. J. Wind. Eng. Ind. Aerodyn. 2020, 202, 104196. [Google Scholar] [CrossRef]
- Chen, R.; Zeng, Q.; Huang, Y.; Xiang, J.; Wen, Y.; Guo, X.; Yin, C.; Dong, H.; Zhao, G. Analysis theory of random energy of train derailment inwind. China Phys. Mech. Astron. 2010, 53, 751–757. [Google Scholar] [CrossRef]
- Cheli, F.; Ripamonti, F.; Rocchi, D.; Tomasini, G.I.S.E.L.L.A. Aerodynamic behaviour investigation of the new EMUV250 train to cross wind. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 189–201. [Google Scholar] [CrossRef]
- Duan, F.; Song, Y.; Gao, S.; Liu, Y.; Chu, W.; Lu, X.; Liu, Z. Study on Aerodynamic Instability and Galloping Response of Rail Overhead Contact Line Based on Wind Tunnel Tests. IEEE Trans. Veh. Technol. 2023, 72, 7211–7220. [Google Scholar] [CrossRef]
- Fang, C.; Li, Y.; Wei, K.; Zhang, J.; Liang, C. Vehicle–bridge coupling dynamic response of sea-crossing railway bridge under correlated wind and wave conditions. Adv. Struct. Eng. 2019, 22, 893–906. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Barbosa, D.; Carvalho, H.; Calçada, R. Dynamic effects on a train-bridge system caused by stochastically generated turbulent wind fields. Eng. Struct. 2020, 211, 110430. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Wang, H. A response spectrum analysis of wind deflection in railway overhead contact lines using pseudo-excitation method. IEEE Trans. Veh. Technol. 2021, 70, 1169–1178. [Google Scholar] [CrossRef]
- Reis, E.D.; Carvalho, H.; de Oliveira, C.C.; de Vasconcelos, J.A.; Adriano, R.L.D.S.; Lopes, D.C. Geometric Nonlinear Analysis of Self-Supporting Structures for Overhead Transmission Lines. Pract. Period. Struct. Des. Constr. 2023, 28, 04023003. [Google Scholar] [CrossRef]
- Aly, A.M.; Chapain, S. Large-scale open-jet testing for cladding design in high-rise buildings: Higher peak pressures compared to wind tunnels. Pract. Period. Struct. Des. Constr. 2022, 27, 04022016. [Google Scholar] [CrossRef]
- Arvan, P.A.; Raju, R.D.; Arockiasamy, M. Offshore Wind Turbine Monopile Foundation Systems in Multilayered Soil Strata under Aerodynamic and Hydrodynamic Loads: State-of-the-Art Review. Pract. Period. Struct. Des. Constr. 2023, 28, 03123001. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. An EMD-recursive ARIMA method to predict wind speed for railway strong wind warning system. J. Wind. Eng. Ind. Aerodyn. 2015, 141, 27–38. [Google Scholar] [CrossRef]
- Gou, H.; Chen, X.; Bao, Y. A wind hazard warning system for safe and efficient operation of high-speed trains. Autom. Constr. 2021, 132, 103952. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; He, S.; Chen, J. Short-term strong wind risk prediction for high-speed railway. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4243–4255. [Google Scholar] [CrossRef]
- Hoppmann, U.; Koenig, S.; Tielkes, T.; Matschke, G. A short-term strong wind prediction model for railway application: Design and verification. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1127–1134. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G. Short-term wind speed prediction: Hybrid of ensemble empirical mode decomposition, feature selection and error correction. Energy Convers. Manag. 2017, 144, 340–350. [Google Scholar] [CrossRef]
- Tao, T.; Shi, P.; Wang, H.; Ai, W. Short-term prediction of downburst winds: A double-step modification enhanced approach. J. Wind. Eng. Ind. Aerodyn. 2021, 211, 104561. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, S.; Peng, L.; Zhao, N. A novel wind speed prediction method based on robust local mean decomposition, group method of data handling and conditional kernel density estimation. Energy Convers. Manag. 2019, 200, 112099. [Google Scholar] [CrossRef]
- Landberg, L. Short-term prediction of the power production from wind farms. J. Wind. Eng. Ind. Aerodyn. 1999, 80, 207–220. [Google Scholar] [CrossRef]
- Yu, C.; Li, Y.; Chen, Q.; Lai, X.; Zhao, L. Matrix-based wavelet transformation embedded in recurrent neural networks for wind speed prediction. Appl. Energy 2022, 324, 119692. [Google Scholar] [CrossRef]
- Xin, J.; Jiang, Y.; Zhou, J.; Peng, L.; Liu, S.; Tang, Q. Bridge deformation prediction based on SHM data using improved VMD and conditional KDE. Eng. Struct. 2022, 261, 114285. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. ARMA based approaches for forecasting the tuple of wind speed and direction. Appl. Energy 2011, 88, 1405–1414. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, S.; Zhao, N.; Xin, J.; Wu, B. Short-term wind speed prediction using time varying filter-based empirical mode decomposition and group method of data handling-based hybrid model. Energy Convers. Manag. 2020, 220, 113076. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Short-term wind prediction using Kalman filters. Wind. Eng. 1985, 9, 1–8. [Google Scholar]
- Wang, D.; Yang, S.X. Intelligent feature extraction, data fusion and detection of concrete bridge cracks: Current development and challenges. Intell. Robot. 2022, 2, 391–406. [Google Scholar] [CrossRef]
- Khasanzoda, N.; Zicmane, I.; Beryozkina, S.; Safaraliev, M.; Sultonov, S.; Kirgizov, A. Regression model for predicting the speed of wind flows for energy needs based on fuzzy logic. Renew. Energy 2022, 191, 723–731. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, J.; Li, G. Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 2011, 52, 1990–1998. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Lu, H.; Zhao, W. A novel combined model for wind speed prediction–Combination of linear model, shallow neural networks, and deep learning approaches. Energy 2021, 234, 121275. [Google Scholar] [CrossRef]
- Lai, L.; Hajirasouliha, I.; Pilakoutas, K.; He, X.; Smyl, D. Applying the Continuous Hidden Markov Model to Structural State Estimation. Pract. Period. Struct. Des. Constr. 2023, 28, 04022073. [Google Scholar] [CrossRef]
- Nayak, D.K.; Verma, G.; Dimri, A.; Kumar, R.; Kumar, V. Predicting the Twenty-eight day compressive strength of OPC-and PPC-prepared concrete through hybrid GA-XGB model. Pract. Period. Struct. Des. Constr. 2023, 28, 04023020. [Google Scholar] [CrossRef]
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A survey of optimization methods from a machine learning perspective. IEEE Trans. Cybern. 2019, 50, 3668–3681. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.J.; Bashtannyk, D.M.; Grunwald, G.K. Estimating and visualizing conditional densities. J. Comput. Graph. Stat. 1996, 5, 315–336. [Google Scholar]
- Han, Q.; Meng, F.; Hu, T.; Chu, F. Non-parametric hybrid models for wind speed forecasting. Energy Convers. Manag. 2017, 148, 554–568. [Google Scholar] [CrossRef]
- Méndez-Gordillo, A.R.; Cadenas, E. Wind speed forecasting by the extraction of the multifractal patterns of time series through the multiplicative cascade technique. Chaos Solitons Fractals 2021, 143, 110592. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, N.; Peng, L.; Zhao, L.; Liu, M. Simulation of stationary wind field based on adaptive interpolation-enhanced scheme. J. Wind. Eng. Ind. Aerodyn. 2019, 195, 104001. [Google Scholar] [CrossRef]
- Liu, M.; Peng, L.; Huang, G.; Yang, Q.; Jiang, Y. Simulation of stationary non-Gaussian multivariate wind pressures using moment-based piecewise Hermite polynomial model. J. Wind. Eng. Ind. Aerodyn. 2020, 196, 104041. [Google Scholar] [CrossRef]
- Zhao, N.; Jiang, Y.; Peng, L.; Chen, X. Fast simulation of nonstationary wind velocity fields by proper orthogonal decomposition interpolation. J. Wind. Eng. Ind. Aerodyn. 2021, 219, 104798. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, Y.; Zhao, N.; Jia, S.; Wang, X.; Tan, S. Simulation of stationary and nonstationary wind velocity field along a long-span bridge using a numerical truncation method. J. Wind. Eng. Ind. Aerodyn. 2022, 231, 105206. [Google Scholar] [CrossRef]
- Li, B.; Peng, L.; Jiang, Y.; Wu, F.; Hui, Y.; Luo, Y. Simulation of stationary non-Gaussian stochastic vector processes using an eigenvalue-based iterative translation approximation method. Mech. Syst. Signal Process. 2022, 175, 109128. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.; Yang, Q.; Yan, Z.; Zhang, C. A novel probabilistic wind speed prediction approach using real time refined variational model decomposition and conditional kernel density estimation. Energy Convers. Manag. 2019, 185, 758–773. [Google Scholar] [CrossRef]
- Sun, W.; Liu, M. Wind speed forecasting using FEEMD echo state networks with RELM in Hebei, China. Energy Convers. Manag. 2016, 114, 197–208. [Google Scholar] [CrossRef]
- Li, Y.; Peng, T.; Zhang, C.; Sun, W.; Hua, L.; Ji, C.; Shahzad, N.M. Multi-step ahead wind speed forecasting approach coupling maximal overlap discrete wavelet transform, improved grey wolf optimization algorithm and long short-term memory. Renew. Energy 2022, 196, 1115–1126. [Google Scholar] [CrossRef]
- Meng, A.; Ge, J.; Yin, H.; Chen, S. Wind speed forecasting based on wavelet packet decomposition and artificial neural networks trained by crisscross optimization algorithm. Energy Convers. Manag. 2016, 114, 75–88. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Tang, Q.; Jiang, Y.; Xin, J.; Liao, G.; Zhou, J.; Yang, X. A novel method for the recovery of continuous missing data using multivariate variational mode decomposition and fully convolutional networks. Measurement 2023, 220, 113366. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.; Peng, X.; Li, Y.; Yang, Q. A novel wind speed prediction method: Hybrid of correlation-aided DWT, LSSVM and GARCH. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 28–38. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Four wind speed multi-step forecasting models using extreme learning machines and signal decomposing algorithms. Energy Convers. Manag. 2015, 100, 16–22. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L. On practical challenges of decomposition-based hybrid forecasting algorithms for wind speed and solar irradiation. Energy 2016, 112, 208–220. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Su, Y.; Huang, G.; Xu, Y.L. Derivation of time-varying mean for non-stationary downburst winds. J. Wind. Eng. Ind. Aerodyn. 2015, 141, 39–48. [Google Scholar] [CrossRef]
- Sundararajan, D. Discrete Wavelet Transform: A Signal Processing Approach; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Huang, G.; Su, Y.; Kareem, A.; Liao, H. Time-frequency analysis of nonstationary process based on multivariate empirical mode decomposition. J. Eng. Mech. 2016, 142, 04015065. [Google Scholar] [CrossRef]
- Liu, S.; Luo, Y.; Peng, L.; Jiang, Y.; Meng, E.; Li, B. Wind pressure field reconstruction based on unbiased conditional kernel density estimation. J. Wind. Eng. Ind. Aerodyn. 2022, 223, 104947. [Google Scholar] [CrossRef]
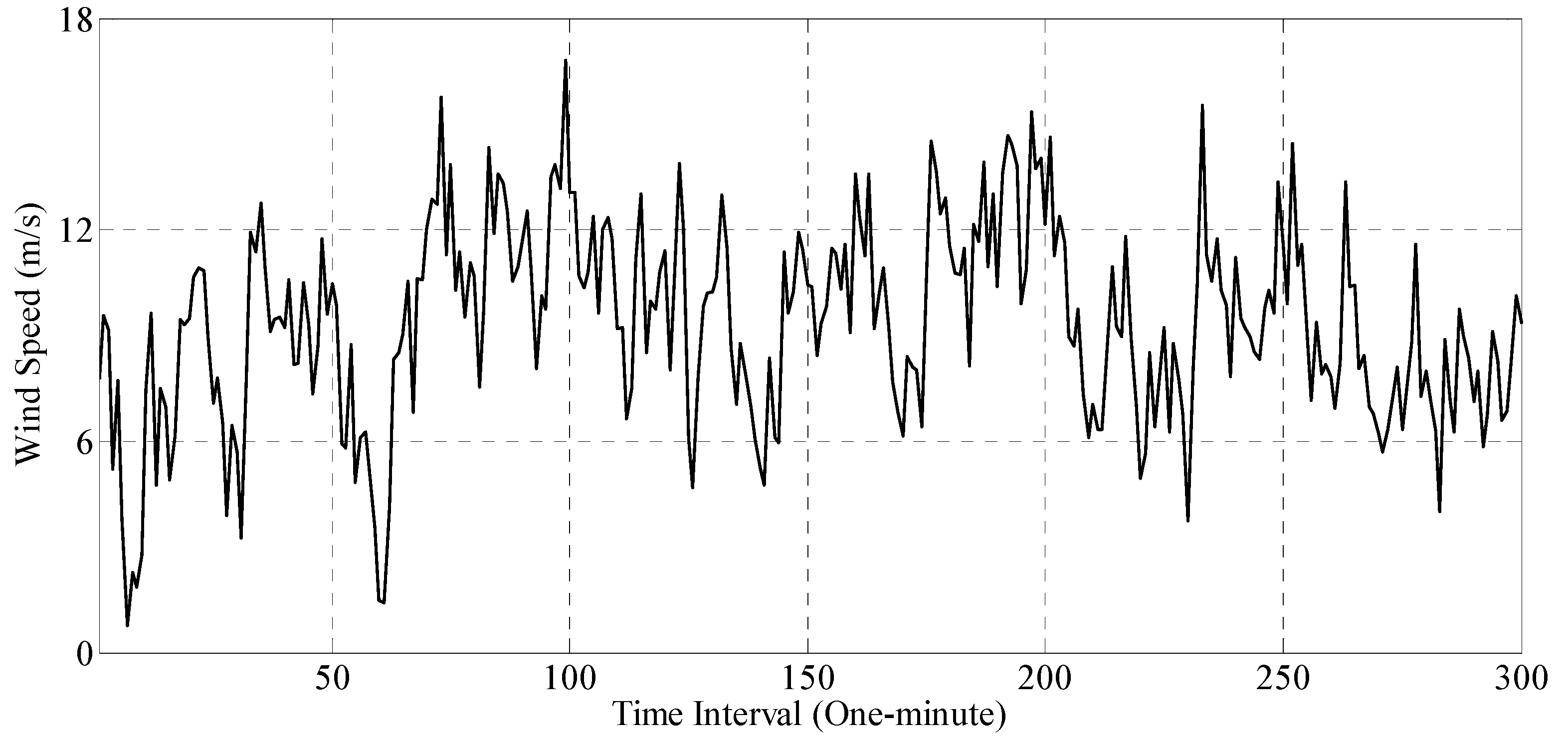
| Statistics | Mean (m/s) | Standard Deviation (m/s) | Maximum (m/s) | Minimum (m/s) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| All Original Data | 9.33 | 2.79 | 16.82 | 0.76 | −0.22 | 3.10 |
| Training Data | 9.54 | 2.94 | 16.82 | 0.76 | −0.48 | 3.09 |
| Testing Data | 8.69 | 2.17 | 15.54 | 3.74 | 0.63 | 3.89 |
| Error Indicators | One-Time DWT-CKDE | Real-Time DWT-CKDE | Absolute Error |
|---|---|---|---|
| MAE | 0.23 | 1.69 | 1.46 |
| RMSE | 0.30 | 2.15 | 1.85 |
| MRPE/% | 2.78 | 19.69 | 16.91 |
| Error Indicator | CKDE | Real-Time DWT-CKDE | Absolute Error | PMAE, PRMSE, PMRPE |
|---|---|---|---|---|
| MAE | 1.56 | 1.69 | −0.13 | −7.69% |
| RMSE | 2.01 | 2.15 | −0.14 | −6.51% |
| MRPE/% | 18.28 | 19.69 | −1.41 | −7.16% |
| Error Indicator | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|
| MAE | 1.05 | 1.00 | 0.95 | 0.87 | 0.84 | 0.77 | 0.73 | 0.78 | 0.86 |
| RMSE | 1.52 | 1.47 | 1.41 | 1.35 | 1.32 | 1.23 | 1.21 | 1.24 | 1.37 |
| MRPE/% | 12.52 | 11.90 | 11.30 | 10.41 | 10.10 | 9.37 | 8.99 | 9.21 | 10.19 |
| Error Indicator | Ideal Ensemble | CKDE | Real-Time DWT-CKDE | ||||
|---|---|---|---|---|---|---|---|
| Result | Absolute Error | Improved Degree | Result | Absolute Error | Improved Degree | ||
| MAE | 0.73 | 1.56 | 0.83 | 53.21% | 1.69 | 0.95 | 56.21% |
| RMSE | 1.21 | 2.01 | 0.80 | 39.80% | 2.15 | 0.94 | 43.72% |
| MRPE/% | 8.99 | 18.28 | 9.29 | 50.82% | 19.69 | 10.70 | 54.34% |
| Subsequences | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Prediction | −0.69 | 0.55 | −0.19 | −1.85 | −0.81 | 0.53 | 1.18 | −1.06 | 9.70 | 8.76 m/s |
| Ideal CP | 8.64 m/s | |||||||||
| Error Indicator | Proposed Method | CKDE | Real-Time DWT-CKDE | ||||
|---|---|---|---|---|---|---|---|
| Result | Absolute Error | Improved Degree | Result | Absolute Error | Improved Degree | ||
| MAE | 1.36 | 1.56 | 0.20 | 12.82% | 1.68 | 0.32 | 19.05% |
| RMSE | 1.79 | 2.01 | 0.22 | 10.95% | 2.15 | 0.36 | 16.74% |
| MRPE/% | 16.41 | 18.28 | 1.87 | 11.40% | 19.69 | 3.28 | 16.66% |
| Statistics | Mean (m/s) | Standard Deviation (m/s) | Maximum (m/s) | Minimum (m/s) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| All Original Data | 10.34 | 3.02 | 17.54 | 5.55 | 0.50 | 2.17 |
| Training Data | 11.10 | 3.08 | 17.54 | 5.55 | 0.12 | 1.94 |
| Testing Data | 8.09 | 1.16 | 10.28 | 5.77 | 0 | 2.10 |
| Error Indicator | Proposed Method | CKDE | Real-Time DWT-CKDE | ||||
|---|---|---|---|---|---|---|---|
| Result | Absolute Error | Improved Degree | Result | Absolute Error | Improved Degree | ||
| MAE | 0.43 | 0.54 | 0.11 | 19.67% | 0.51 | 0.08 | 15.17% |
| RMSE | 0.54 | 0.71 | 0.17 | 24.36% | 0.68 | 0.14 | 20.33% |
| MRPE/% | 5.38 | 6.94 | 1.56 | 22.46% | 6.48 | 1.10 | 17.01% |
| Methods | One-Time DWT-CKDE | Real-Time DWT-CKDE | CKDE | Proposed |
|---|---|---|---|---|
| Time (s) | 4.72 | 4.80 | 0.52 | 4.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Cui, X.; Cheng, C.; Jiang, Y. An Improved Ensemble-Strategy-Assisted Wind Speed Prediction Method for Railway Strong Wind Warnings. Atmosphere 2023, 14, 1787. https://doi.org/10.3390/atmos14121787
Liu J, Cui X, Cheng C, Jiang Y. An Improved Ensemble-Strategy-Assisted Wind Speed Prediction Method for Railway Strong Wind Warnings. Atmosphere. 2023; 14(12):1787. https://doi.org/10.3390/atmos14121787
Chicago/Turabian StyleLiu, Jian, Xiaolei Cui, Cheng Cheng, and Yan Jiang. 2023. "An Improved Ensemble-Strategy-Assisted Wind Speed Prediction Method for Railway Strong Wind Warnings" Atmosphere 14, no. 12: 1787. https://doi.org/10.3390/atmos14121787
APA StyleLiu, J., Cui, X., Cheng, C., & Jiang, Y. (2023). An Improved Ensemble-Strategy-Assisted Wind Speed Prediction Method for Railway Strong Wind Warnings. Atmosphere, 14(12), 1787. https://doi.org/10.3390/atmos14121787






