Prediction of Storm Surge Water Level Based on Machine Learning Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Research Methods
2.3. Data Processing and Model Construction
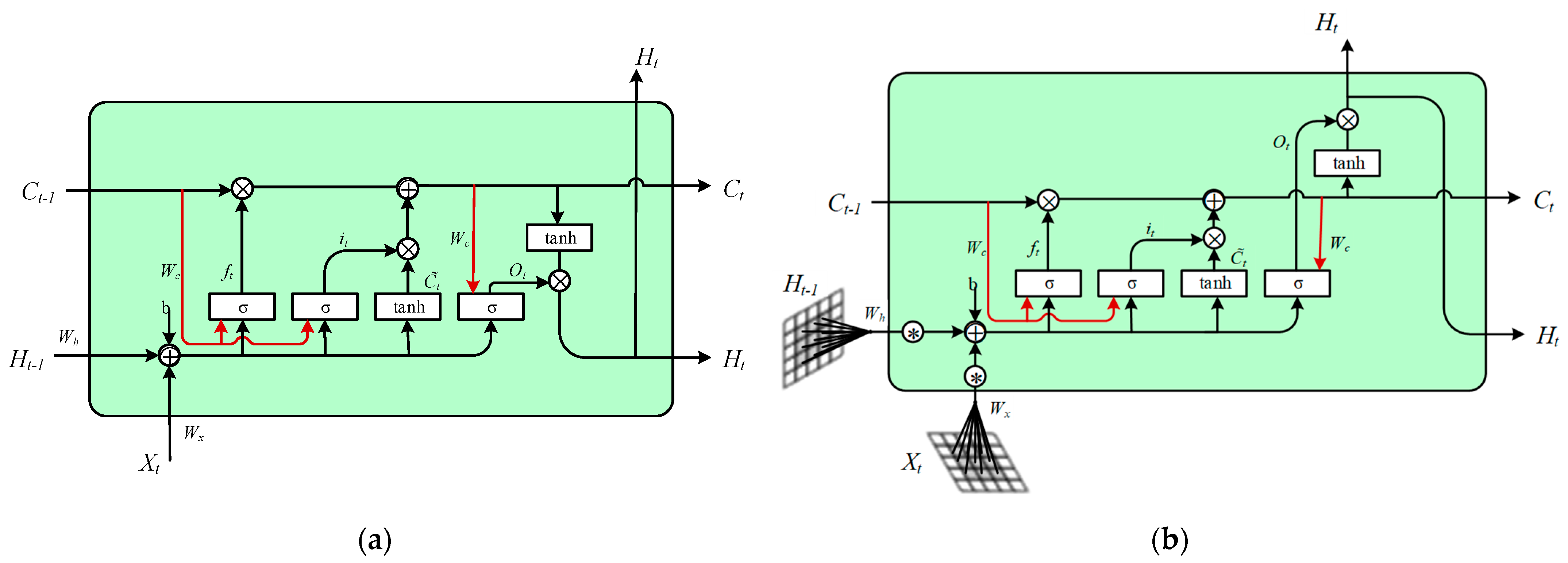
2.3.1. Construction of the ConvLSTM Model
2.3.2. Construction of the Random Forest Model
- The maximum number of decision trees (n_estimators). Selecting an appropriate maximum number of decision trees is crucial, as too few or too many trees can lead to underfitting or overfitting, respectively.
- The maximum number of features considered when dividing the nodes of the decision tree (max_features). Typically, this parameter is set to ‘auto’ or ‘log2.’ However, in scenarios with a substantial number of features, it becomes important to choose an appropriate value to balance the trade-off between the speed and quality of decision tree generation.
- The maximum depth allowed for the decision tree (max_depth). In cases with extensive data and numerous features, decision trees can become excessively large. To prevent overfitting, it is essential to limit the maximum depth of the decision tree.
- The minimum samples required for node splitting (min_samples_split). This parameter governs when internal nodes of the decision tree can continue to split. If the sample size at a node falls below this threshold, further division is halted.
- The minimum number of samples contained at the leaf node (min_samples_leaf). When the number of samples at a leaf node drops below this value, both the node and its brother nodes are pruned.
3. Results and Discussion
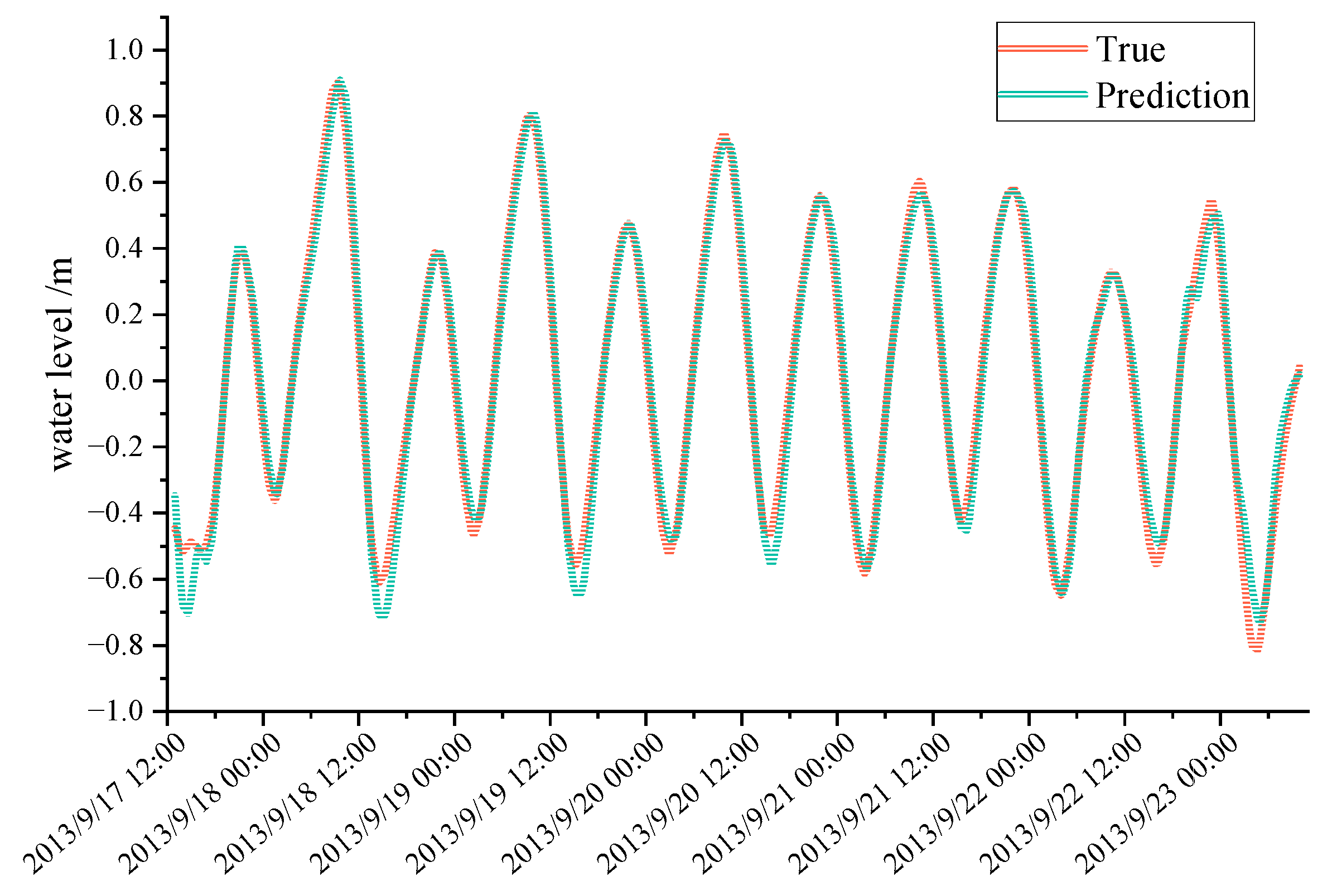
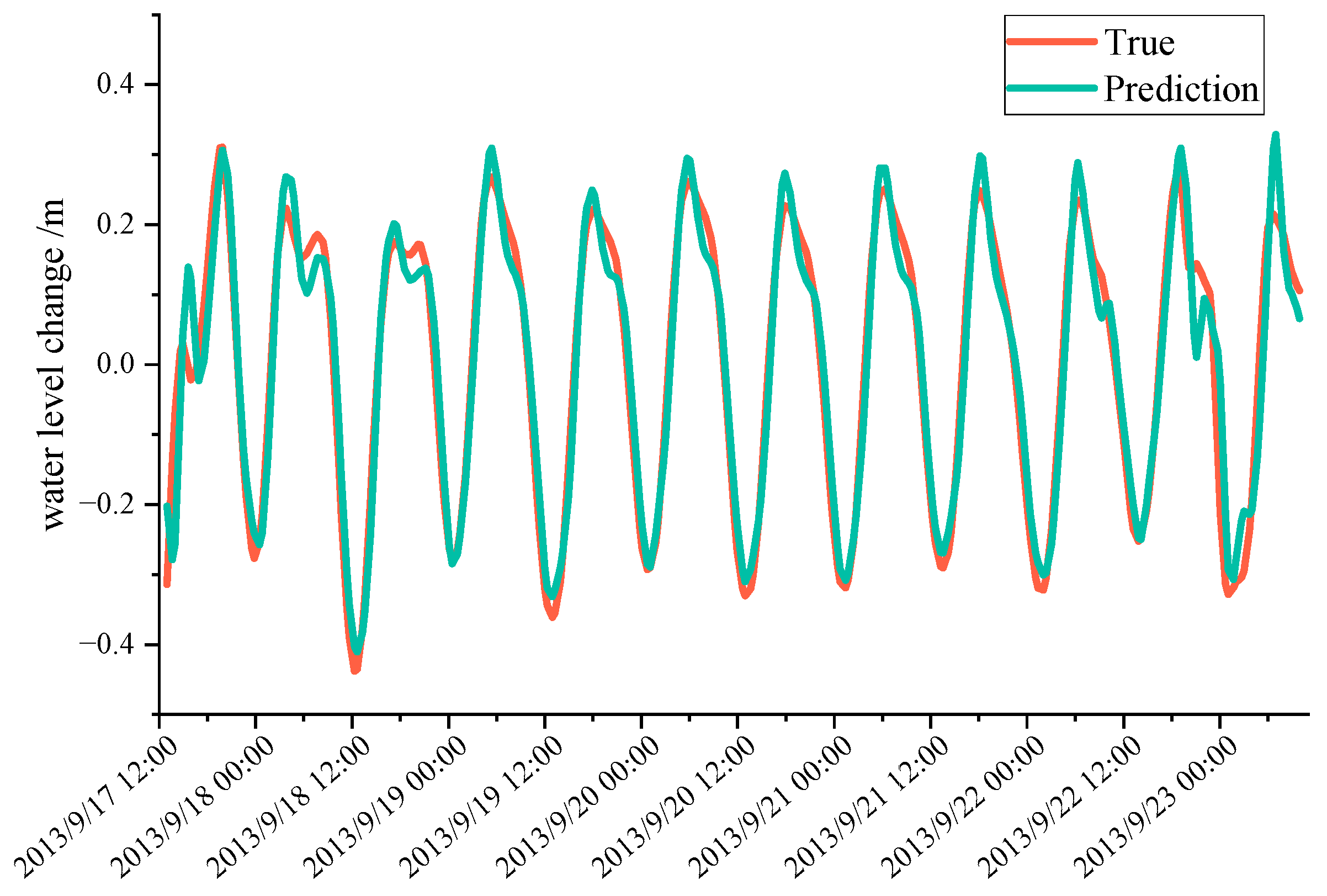
3.1. Spatiotemporal Water Level Prediction Based on the ConvLSTM Model
3.1.1. Results of One-Step Prediction
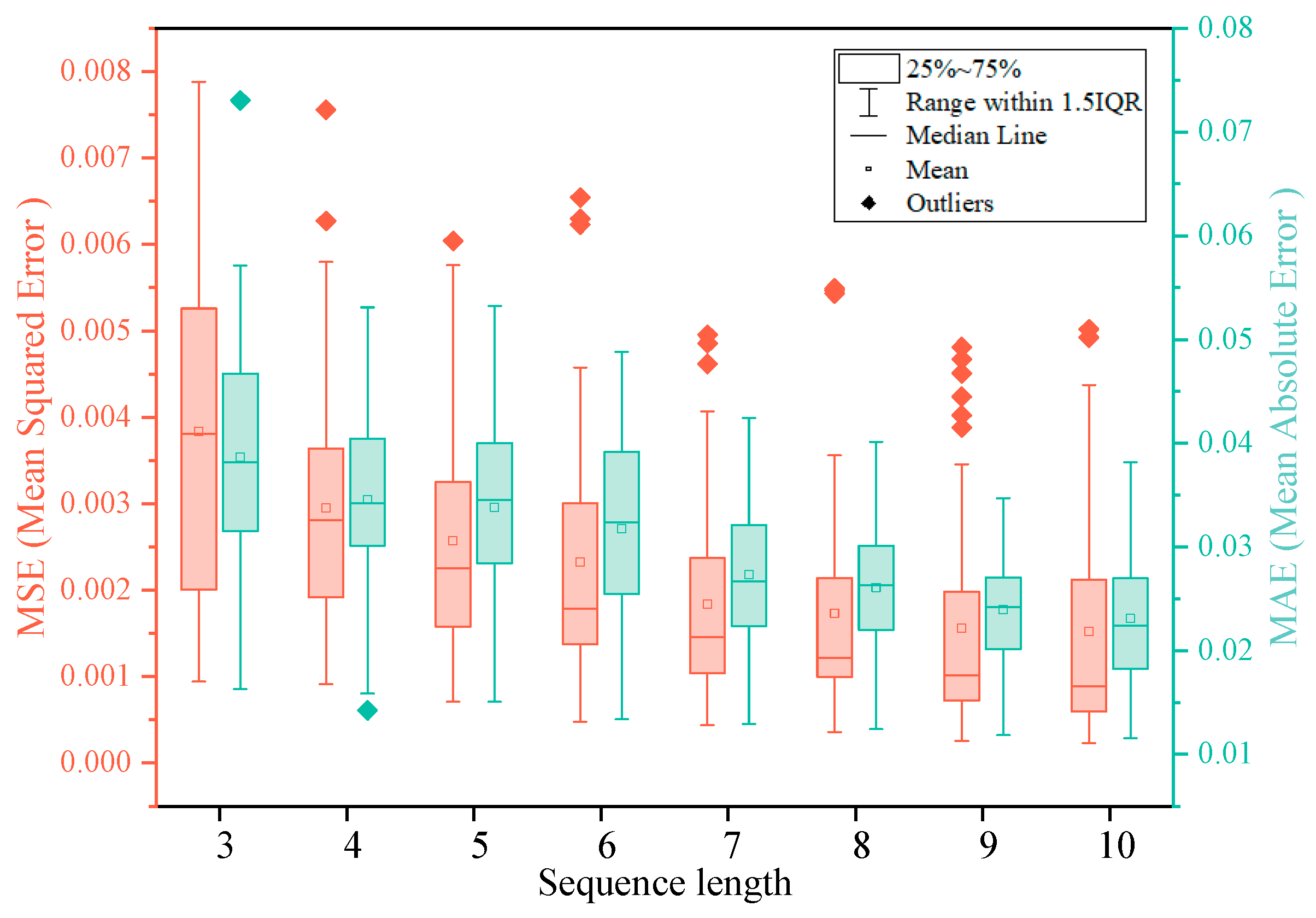
3.1.2. Results of Multi-Step Prediction
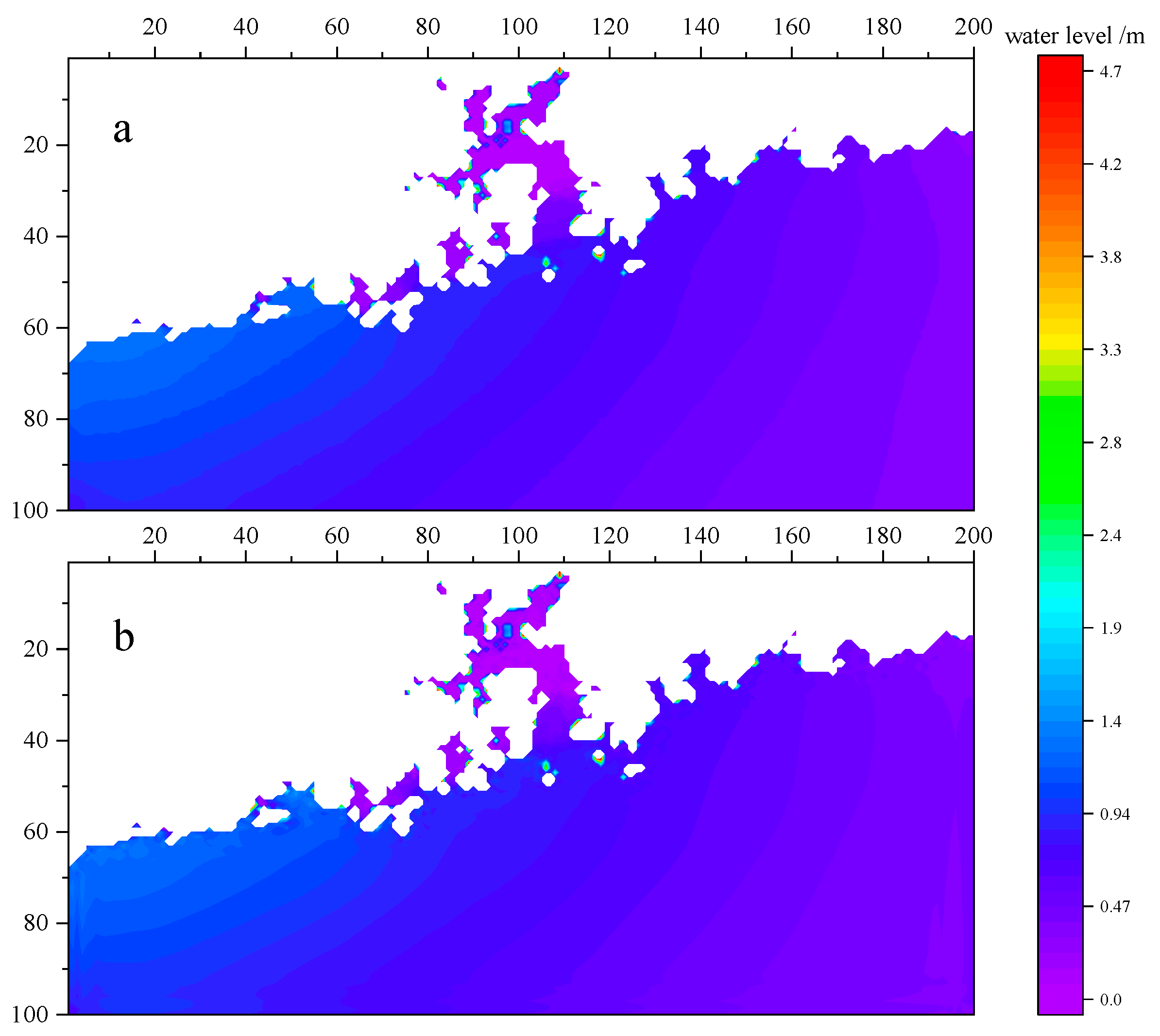
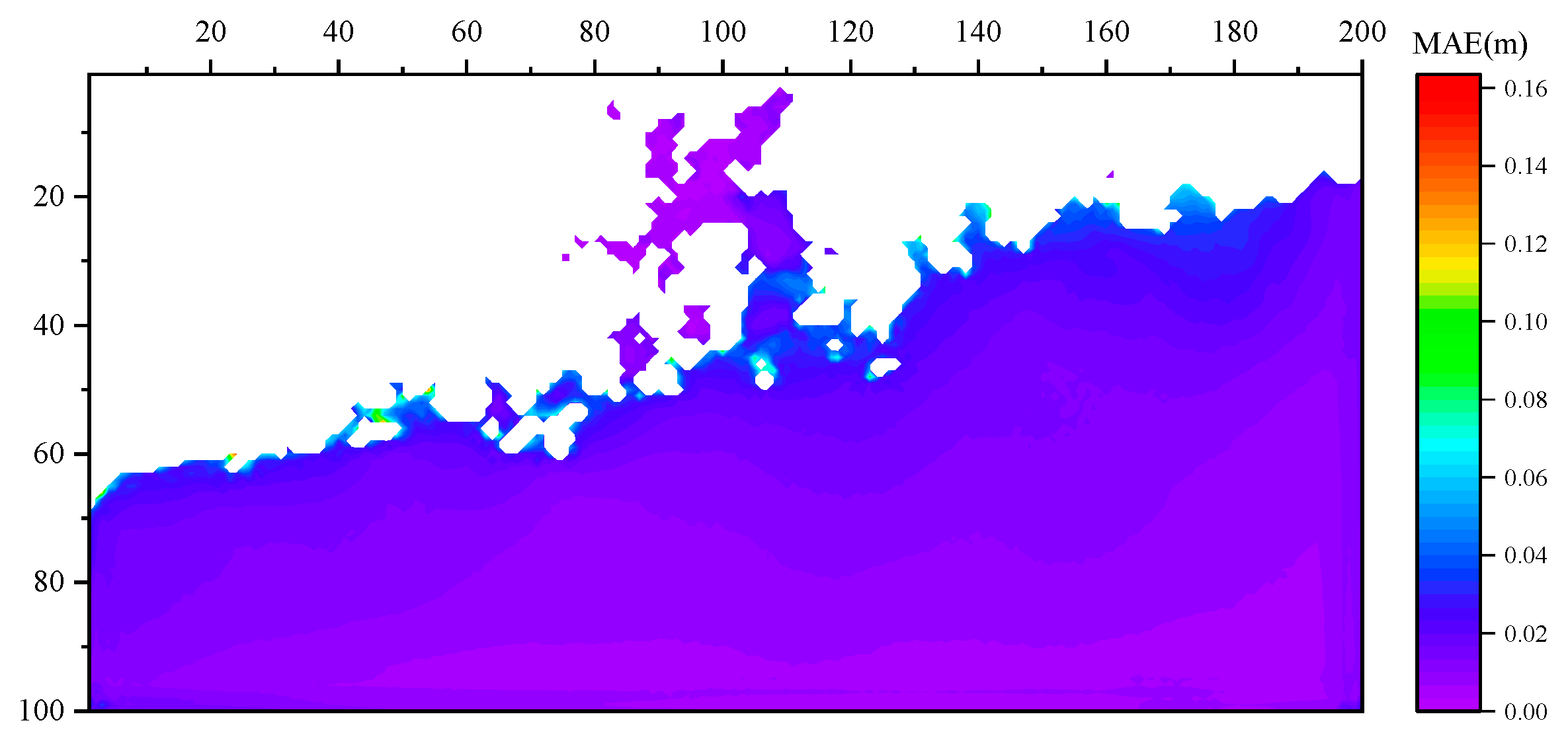
3.1.3. Verification Using Measured Data
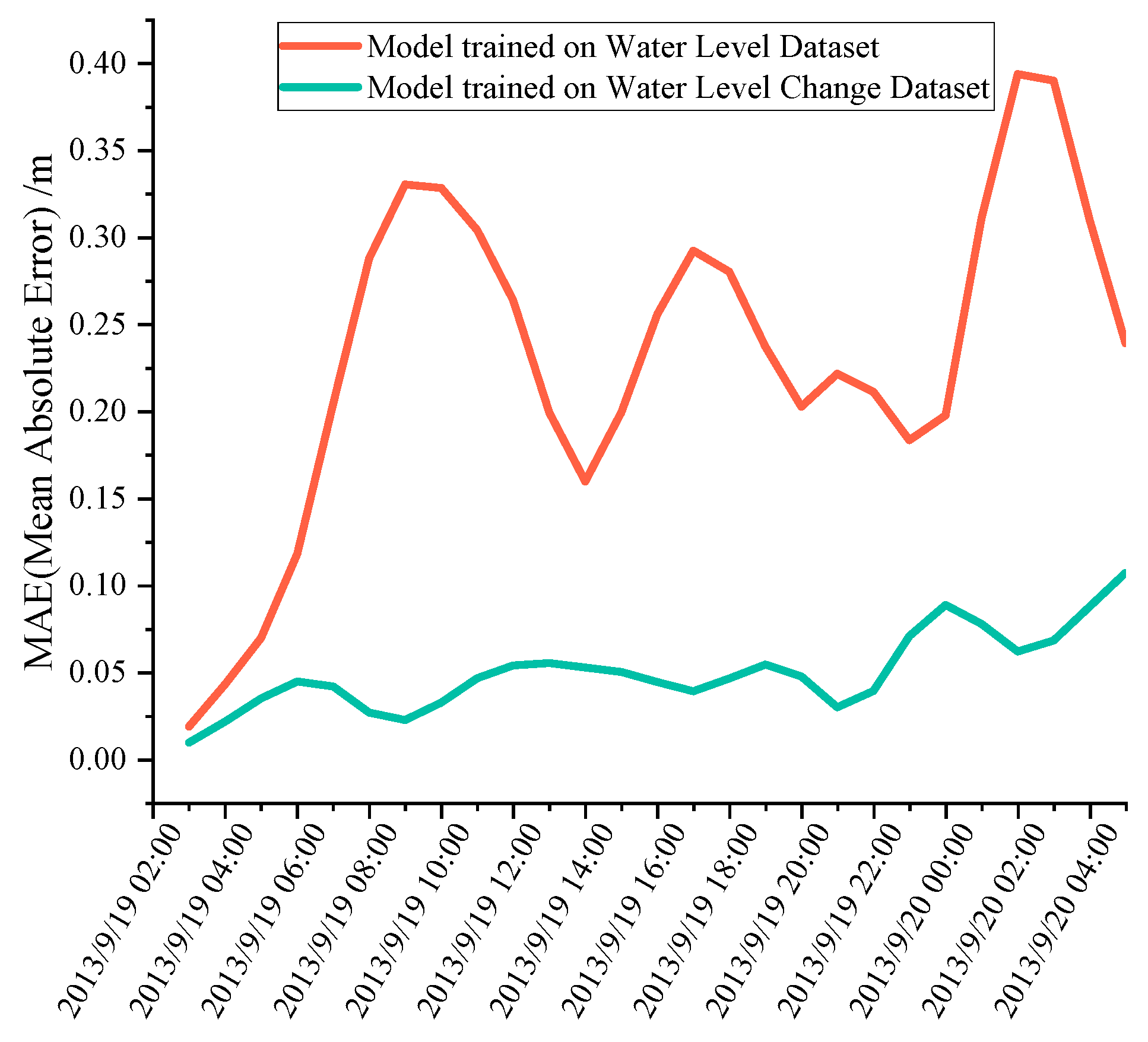
3.1.4. Prediction Results after Adding Feature Channels
3.2. Maximum Water Level Prediction Based on Random Forest Algorithm
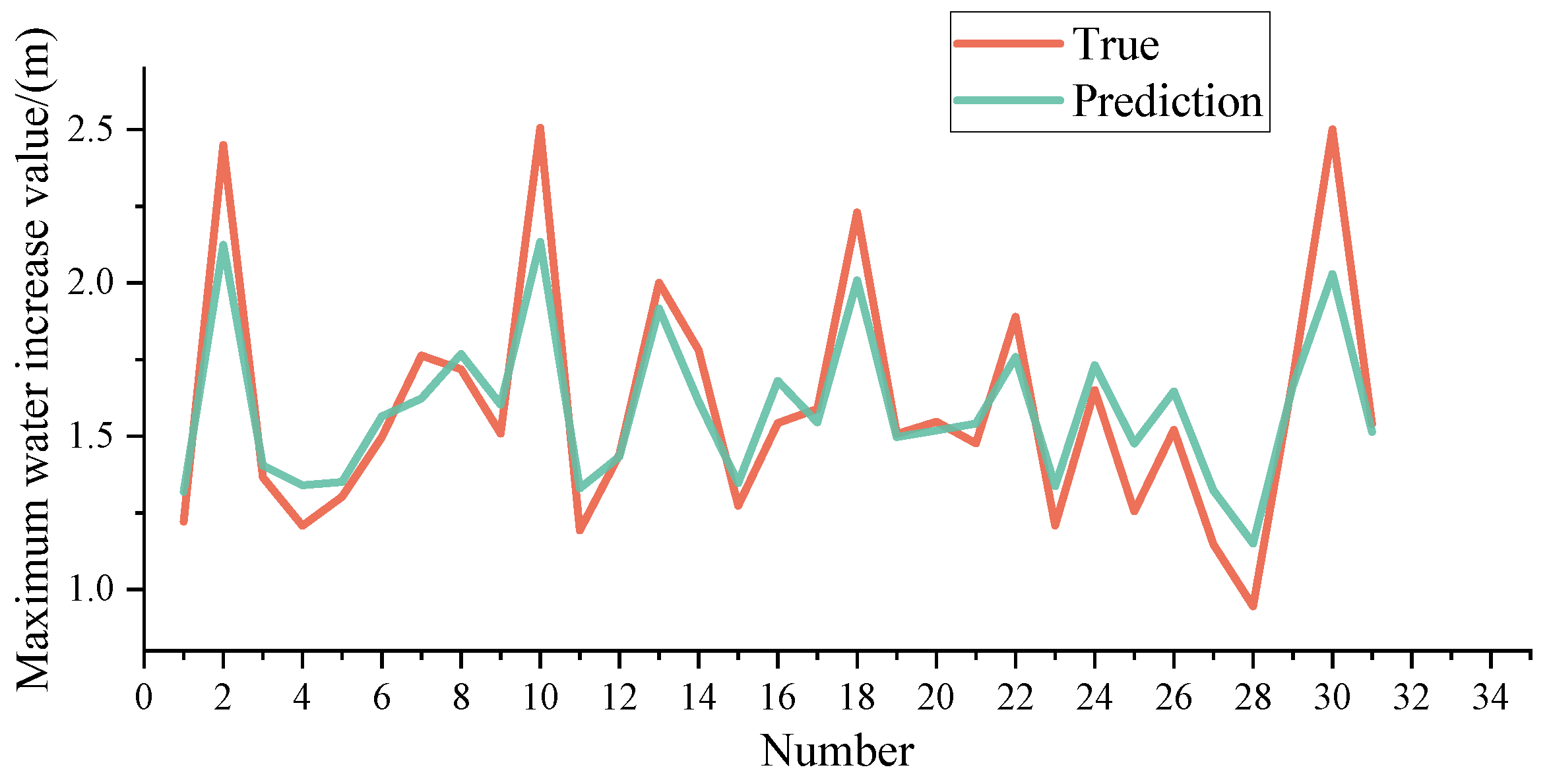
3.2.1. Model Validation
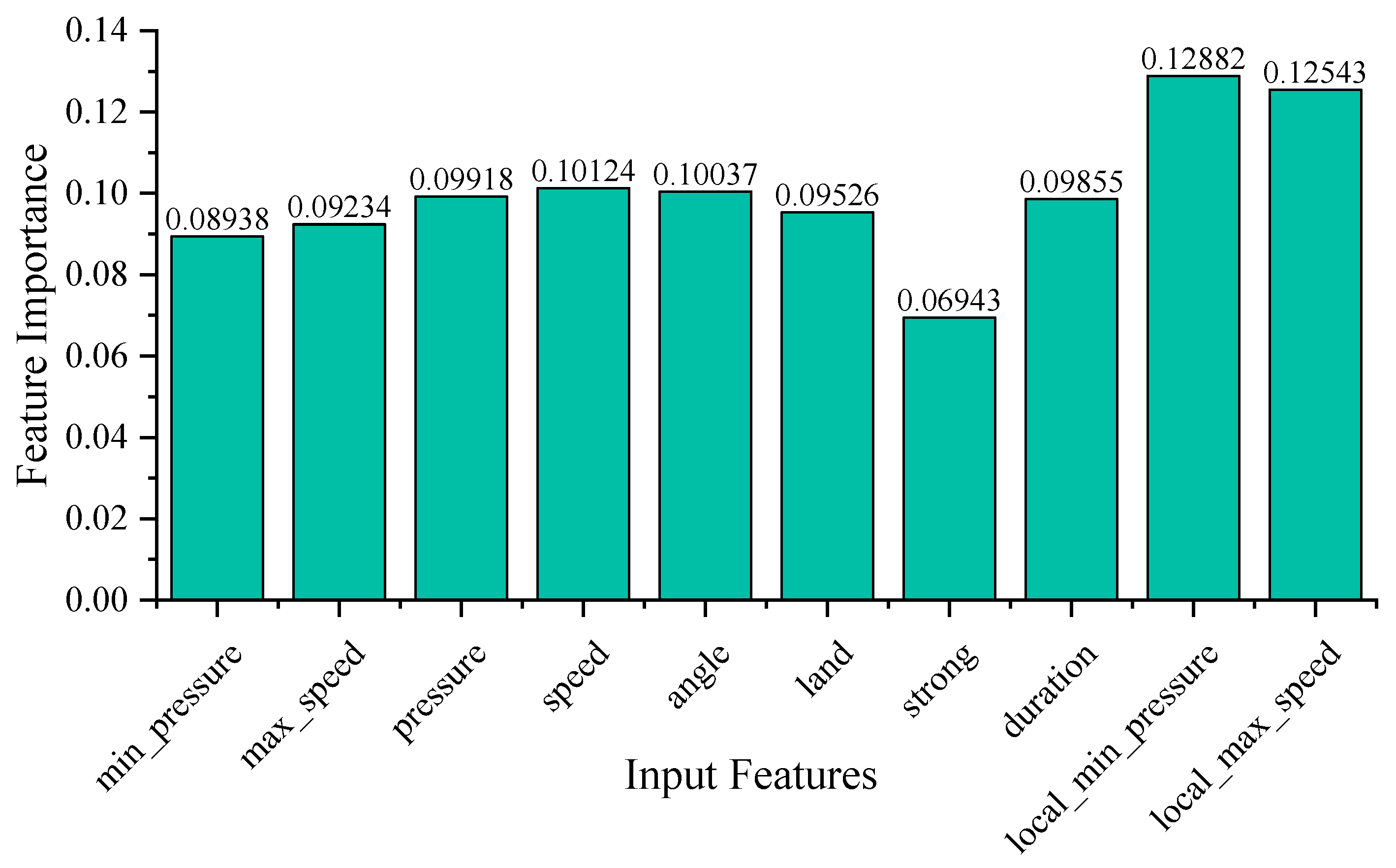
3.2.2. Feature Importance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, S.; Luo, Y.; Wang, H.; Gao, J.; Li, C. Climate change impacts and adaptation in China: Current situation and future prospect. Kexue Tongbao/Chin. Sci. Bull. 2016, 61, 1042–1054. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.-R. Changes in tropical cyclone number, duration, and intensity in a warming environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [PubMed]
- Hoyos, C.D.; Agudelo, P.A.; Webster, P.J.; Curry, J.A. Deconvolution of the factors contributing to the increase in global hurricane intensity. Science 2006, 312, 94–97. [Google Scholar] [CrossRef] [PubMed]
- Michaels, P.J.; Knappenberger, P.C.; Davis, R.E. Sea-surface temperatures and tropical cyclones in the Atlantic basin. Geophys. Res. Lett. 2006, 33, L09708. [Google Scholar] [CrossRef]
- Hsiao, S.-C.; Chiang, W.-S.; Chen, W.-B. Storm tide and wave simulations and assessment. J. Mar. Sci. Eng. 2021, 9, 84. [Google Scholar] [CrossRef]
- Lin, N.; Emanuel, K.; Oppenheimer, M.; Vanmarcke, E. Physically based assessment of hurricane surge threat under climate change. Nat. Clim. Change 2012, 2, 462–467. [Google Scholar] [CrossRef]
- Du, H.; Yu, P.; Zhu, L.; Fei, K.; Gao, L. Assessing the performances of parametric wind models in predicting storm surges in the Pearl River Estuary. J. Wind Eng. Ind. Aerodyn. 2023, 232, 105265. [Google Scholar] [CrossRef]
- Tan, C.; Fang, W. Mapping the wind hazard of global tropical cyclones with parametric wind field models by considering the effects of local factors. Int. J. Disaster Risk Sci. 2018, 9, 86–99. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. SLOSH: Sea, Lake, and Overland Surges from Hurricanes; US Department of Commerce, National Oceanic and Atmospheric Administration: Washington, DC, USA, 1992; Volume 48.
- Heaps, N.S. A two-dimensional numerical sea model. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1969, 265, 93–137. [Google Scholar]
- Warren, I.; Bach, H.K. MIKE 21: A modelling system for estuaries, coastal waters and seas. Environ. Softw. 1992, 7, 229–240. [Google Scholar] [CrossRef]
- Roelvink, J.; Van Banning, G. Design and development of DELFT3D and application to coastal morphodynamics. Oceanogr. Lit. Rev. 1995, 11, 925. [Google Scholar]
- Luettich, R.A.; Westerink, J.J. Formulation and Numerical Implementation of the 2D/3D ADCIRC Finite Element Model Version 44. XX; Luettich, R., Ed.; University of North Carolina: Chapel Hill, NC, USA, 2004; Volume 20. [Google Scholar]
- Chen, C.; Beardsley, R.C.; Cowles, G.; Qi, J.; Lai, Z.; Gao, G. An Unstructured Grid, Finite-Volume Coastal Ocean Model: FVCOM User Manual; SMAST/UMASSD: New Bedford, MA, USA, 2006; pp. 6–8. [Google Scholar]
- Palani, S.; Liong, S.-Y.; Tkalich, P. An ANN application for water quality forecasting. Mar. Pollut. Bull. 2008, 56, 1586–1597. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.S.; Coulibaly, P. Application of support vector machine in lake water level prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Ewees, A.A.; Parmar, K.S.; Yaseen, Z.M.; Shahid, S.; Kisi, O. The viability of extended marine predators algorithm-based artificial neural networks for streamflow prediction. Appl. Soft Comput. 2022, 131, 109739. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Dai, H.-L.; Heddam, S.; Kuriqi, A.; Kisi, O. Pan evaporation estimation by relevance vector machine tuned with new metaheuristic algorithms using limited climatic data. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2192258. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Kisi, O.; Adnan, R.M.; Sadeghifar, T.; Kuriqi, A. Modeling potential evapotranspiration by improved machine learning methods using limited climatic data. Water 2023, 15, 486. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Heddam, S. Estimating reference evapotranspiration using hybrid adaptive fuzzy inferencing coupled with heuristic algorithms. Comput. Electron. Agric. 2021, 191, 106541. [Google Scholar] [CrossRef]
- Adnan, R.M.; Dai, H.-L.; Mostafa, R.R.; Islam, A.R.M.T.; Kisi, O.; Heddam, S.; Zounemat-Kermani, M. Modelling groundwater level fluctuations by ELM merged advanced metaheuristic algorithms using hydroclimatic data. Geocarto Int. 2023, 38, 2158951. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Zounemat-Kermani, M. Advanced hybrid metaheuristic machine learning models application for reference crop evapotranspiration prediction. Agronomy 2022, 13, 98. [Google Scholar] [CrossRef]
- Kim, S.Y.; Matsumi, Y.; Shiozaki, S.; Ota, T. A study of a real-time storm surge forecast system using a neural network at the Sanin Coast, Japan. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–7. [Google Scholar]
- Liu, Y.; Zhang, L.; Li, L.; Liu, Y.; Chen, B.; Zhang, W. Storm surge nowcasting based on multivariable LSTM neural network model. Mar. Sci. Bull. 2020, 39, 689–694. [Google Scholar]
- Hong, S.; Kim, S.; Joh, M.; Song, S.-k. Globenet: Convolutional neural networks for typhoon eye tracking from remote sensing imagery. arXiv 2017, arXiv:1708.03417. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; MIT Press: Montreal, QC, Canada, 2015; Volume 1, pp. 802–810. [Google Scholar]
- Lu, W.; Li, J.; Li, Y.; Sun, A.; Wang, J. A CNN-LSTM-based model to forecast stock prices. Complexity 2020, 2020, 6622927. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Zhou, J.; Fang, W. Multi-source rainfall fusion method based on ConvLSTM. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2022, 50, 33–39. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, W.; Lu, Y.; Wang, Y.; Zhou, Y.; Hui, N.; Dong, C. ConvLSTM-Based Wave Forecasts in the South and East China Seas. Front. Mar. Sci. 2021, 8, 740. [Google Scholar] [CrossRef]
- Kim, S.; Kang, J.-S.; Lee, M.; Song, S.-k. DeepTC: ConvLSTM network for trajectory prediction of tropical cyclone using spatiotemporal atmospheric simulation data. In Proceedings of the Workshop on Modeling and Decision-Making in the Spatiotemporal Domain, 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 30 September 2018. [Google Scholar]
- Xie, W.; Xu, G.; Dong, C. Research on storm surge floodplain prediction based on ConvLSTM machine learning. Trans. Atmos. Sci. 2022, 45, 674–687. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Guo, T.; Li, G.; He, L. Risk assessment of typhoon storm surge based on a simulated annealing algorithm and the least squares method: A case study in Guangdong Province, China. Nat. Hazards Res. 2022, 2, 249–258. [Google Scholar] [CrossRef]
- Jongman, B.; Ward, P.J.; Aerts, J.C. Global exposure to river and coastal flooding: Long term trends and changes. Glob. Environ. Change 2012, 22, 823–835. [Google Scholar] [CrossRef]
- Ying, X.; Zheng, Z.; Ni, J.; Zhao, K. Numerical simulation study on the dynamic impact of typhoon “Mangkhut” storm surge on the sea area near the Hong Kong-Zhuhai-Macao bridge. Phys. Chem. Earth Parts A/B/C 2022, 128, 103269. [Google Scholar] [CrossRef]
- Xu, X. 2015 China’s Township Administrative Division Boundary Data; Resource and Environmental Science Data Registration and Publishing System: Beijing, China, 2023. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; National Centers for Environmental Information: Asheville, NC, USA, 2009. [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Moishin, M.; Deo, R.C.; Prasad, R.; Raj, N.; Abdulla, S. Designing deep-based learning flood forecast model with ConvLSTM hybrid algorithm. IEEE Access 2021, 9, 50982–50993. [Google Scholar] [CrossRef]
- Han, L.; Ji, Q.; Jia, X.; Liu, Y.; Han, G.; Lin, X. Significant Wave Height Prediction in the South China Sea Based on the ConvLSTM Algorithm. J. Mar. Sci. Eng. 2022, 10, 1683. [Google Scholar] [CrossRef]
- Liu, S.; Tao, D.; Zhao, K.; Minamide, M.; Zhang, F. Dynamics and predictability of the rapid intensification of Super Typhoon Usagi (2013). J. Geophys. Res. Atmos. 2018, 123, 7462–7481. [Google Scholar] [CrossRef]







| n_Estimators | Max_Features | Max_Depth | Min_Samples_Split | Min_Samples_Leaf |
|---|---|---|---|---|
| 400 | 1 | 15 | 2 | 1 |
| MAE (m) | MSE (m2) | |
|---|---|---|
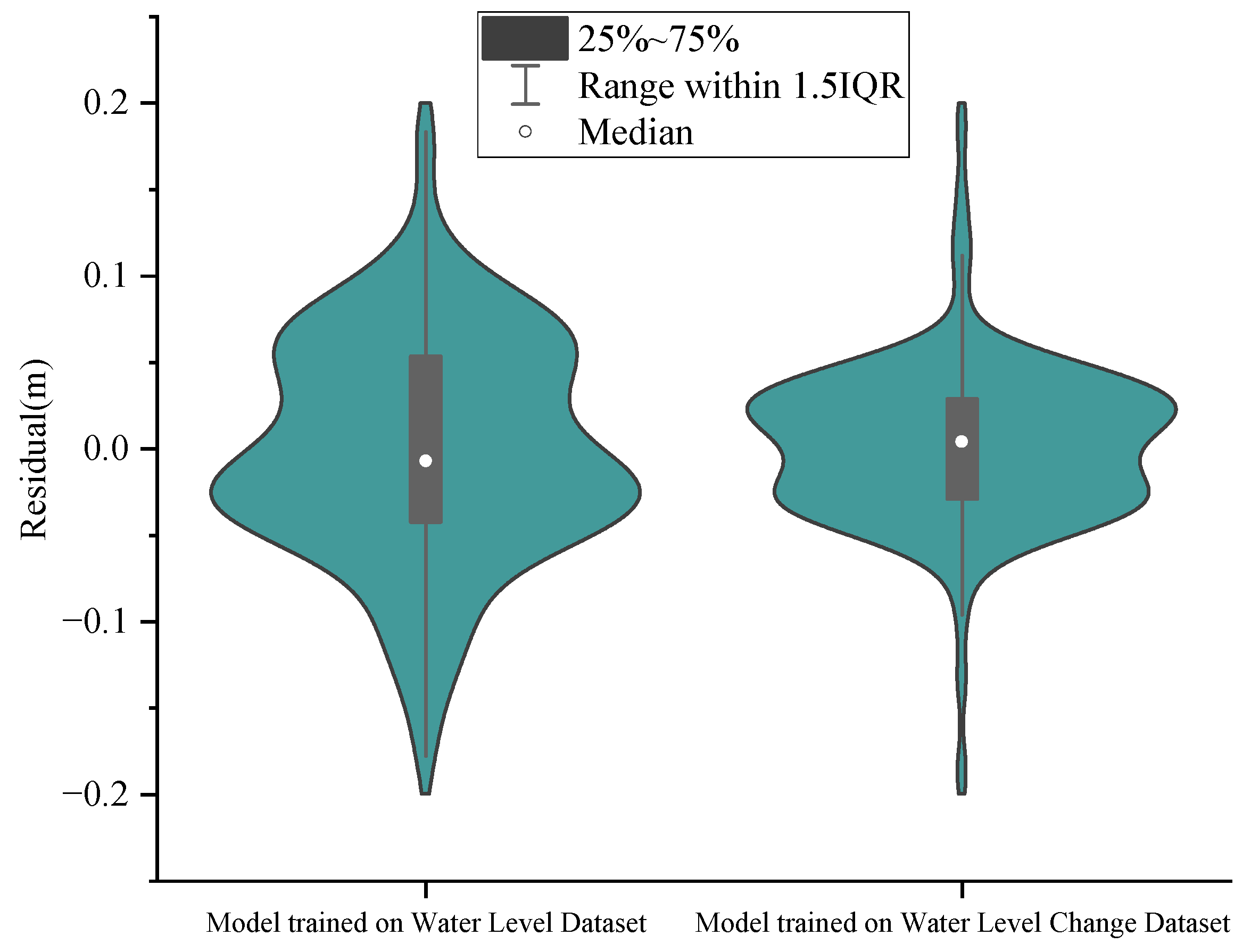
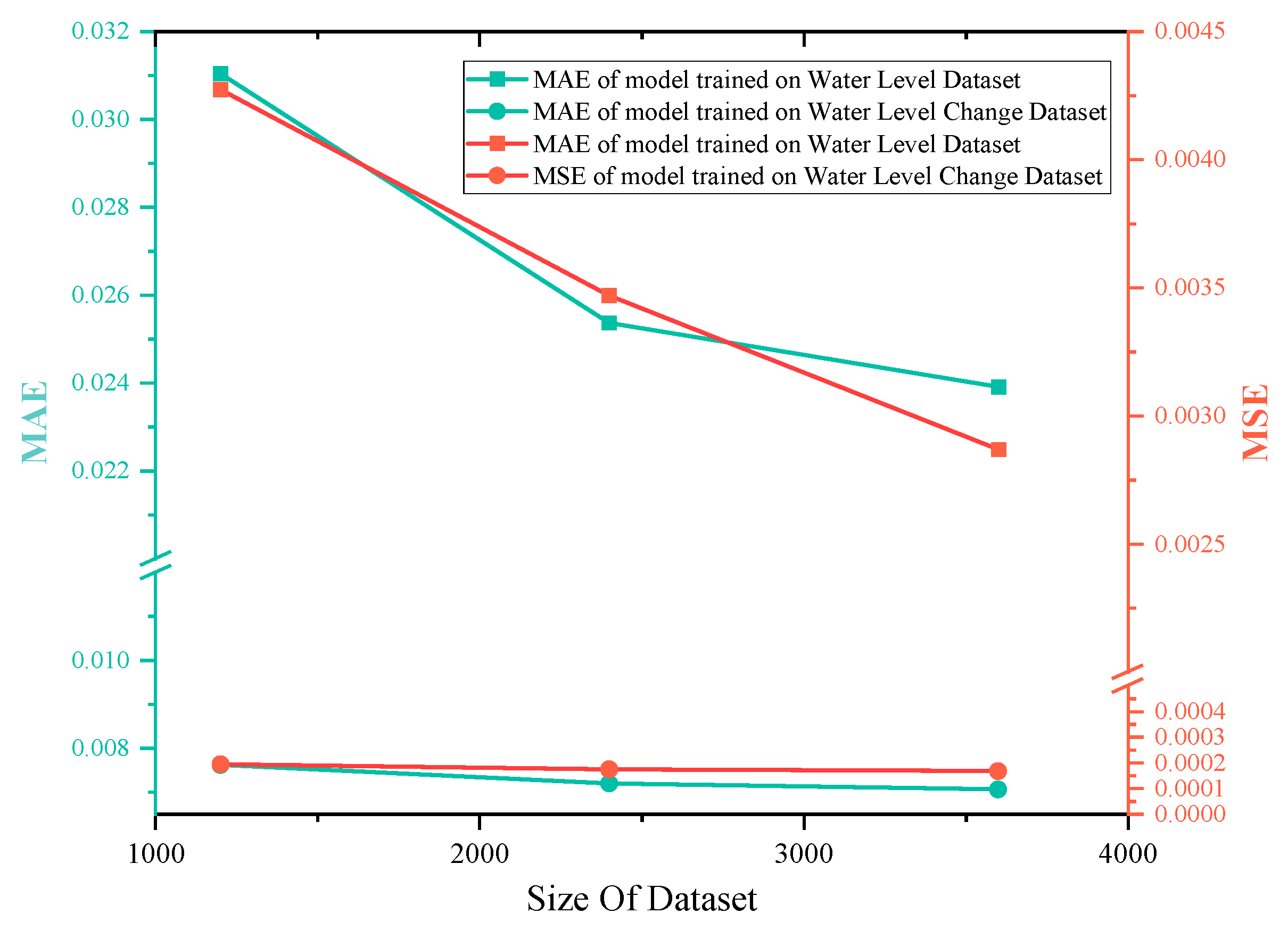
| Model trained on Water Level Dataset | 0.026 | 0.0038 |
| Model trained on Water Level Change Dataset | 0.014 | 0.0007 |
| Typhoon Code | True (m) | Prediction (m) |
|---|---|---|
| 199318 | 1.415 | 1.756 |
| 201622 | 1.783 | 1.764 |
| 201003 | 1.403 | 1.574 |
| 200809 | 1.415 | 1.421 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhao, Q.; Hu, C.; Luo, N. Prediction of Storm Surge Water Level Based on Machine Learning Methods. Atmosphere 2023, 14, 1568. https://doi.org/10.3390/atmos14101568
Liu Y, Zhao Q, Hu C, Luo N. Prediction of Storm Surge Water Level Based on Machine Learning Methods. Atmosphere. 2023; 14(10):1568. https://doi.org/10.3390/atmos14101568
Chicago/Turabian StyleLiu, Yun, Qiansheng Zhao, Chunchun Hu, and Nianxue Luo. 2023. "Prediction of Storm Surge Water Level Based on Machine Learning Methods" Atmosphere 14, no. 10: 1568. https://doi.org/10.3390/atmos14101568
APA StyleLiu, Y., Zhao, Q., Hu, C., & Luo, N. (2023). Prediction of Storm Surge Water Level Based on Machine Learning Methods. Atmosphere, 14(10), 1568. https://doi.org/10.3390/atmos14101568






