How Should a Numerical Weather Prediction Be Used: Full Field or Anomaly? A Conceptual Demonstration with a Lorenz Model
Abstract
1. Introduction
2. Lorenz Model (Lorenz-84) and Experiment Design
2.1. Basic Model
2.2. Observed Climate with a Perfect Model
2.3. Model Climate with an Imperfect Model
2.4. Evaluation Forecasts
3. Results
3.1. Model Assessment
3.2. Forecast Improvement
3.3. Mechanism
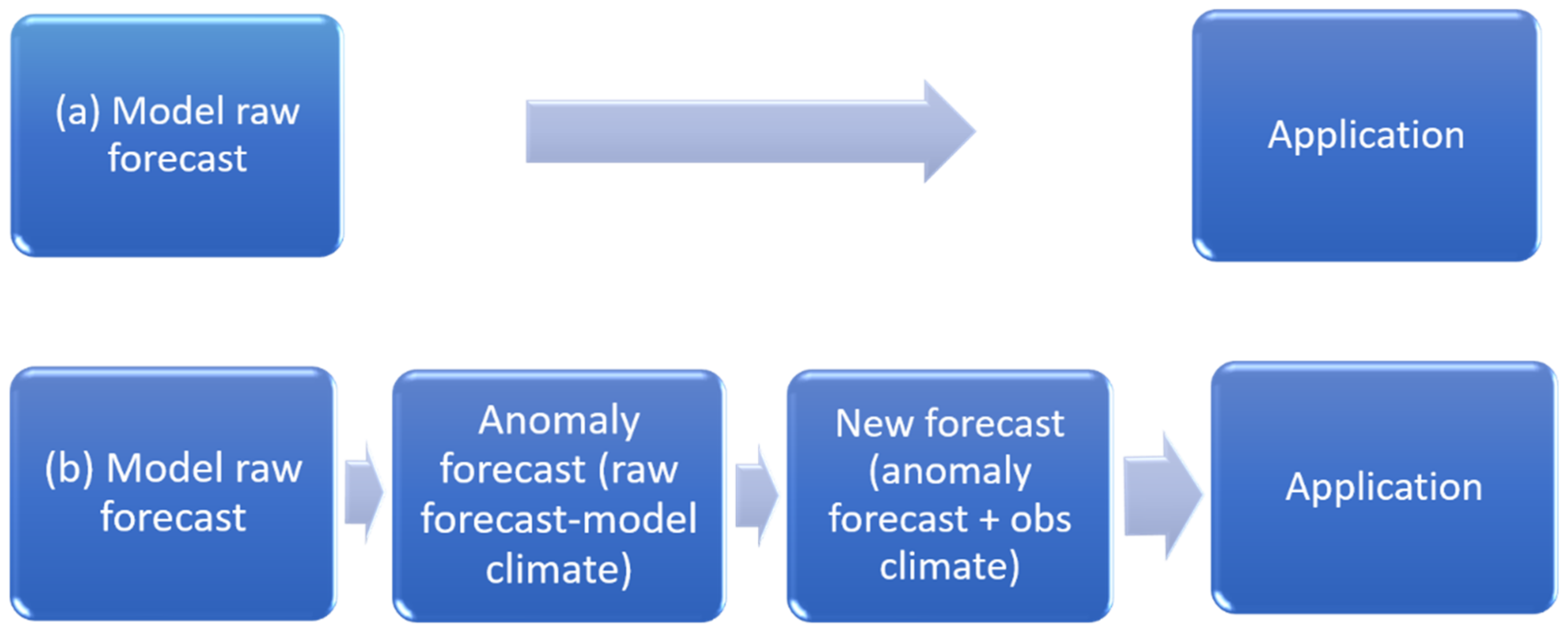
3.4. Construction of an Anomaly Forecast
4. Summary and Discussion
- (1)
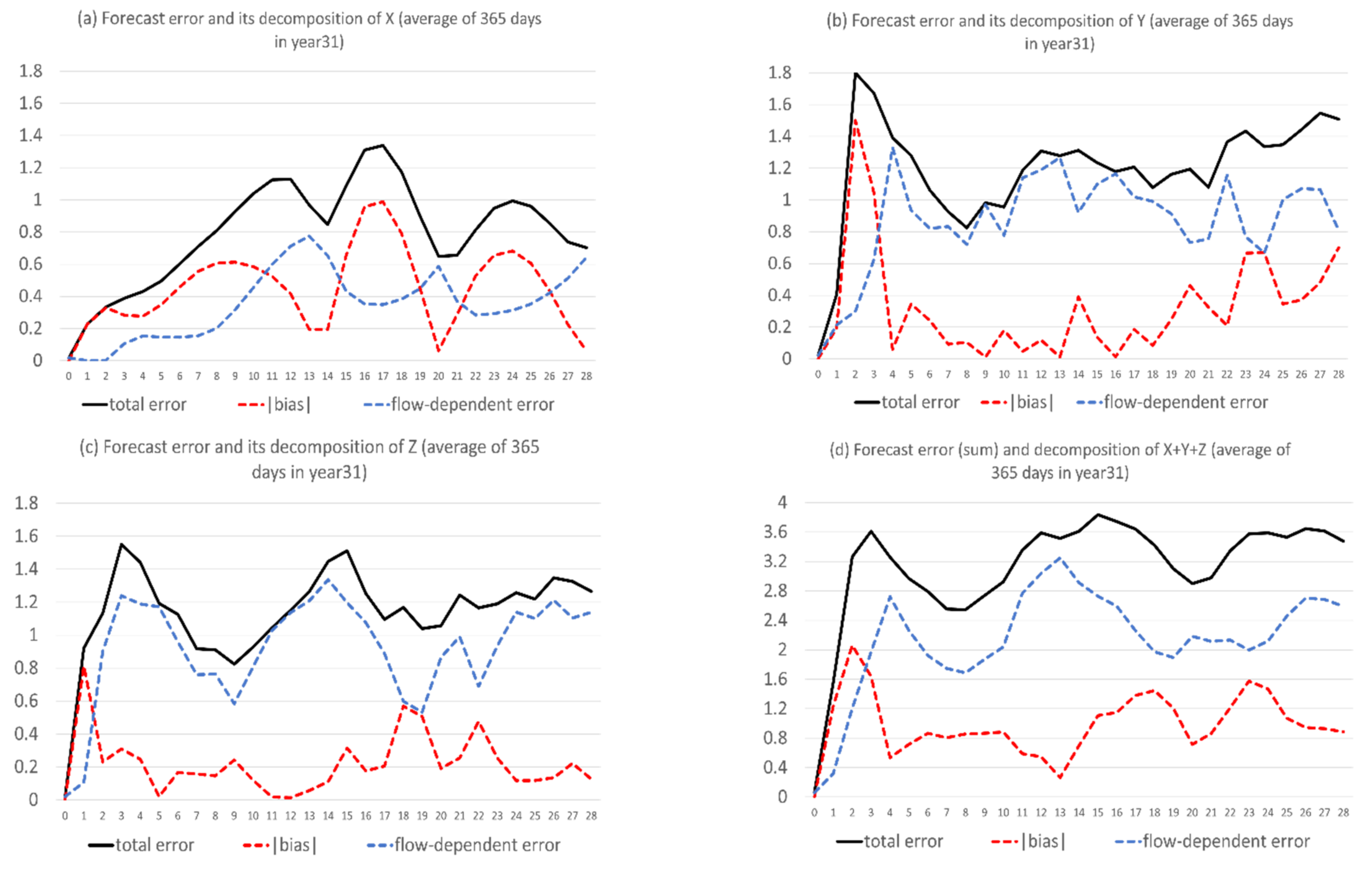
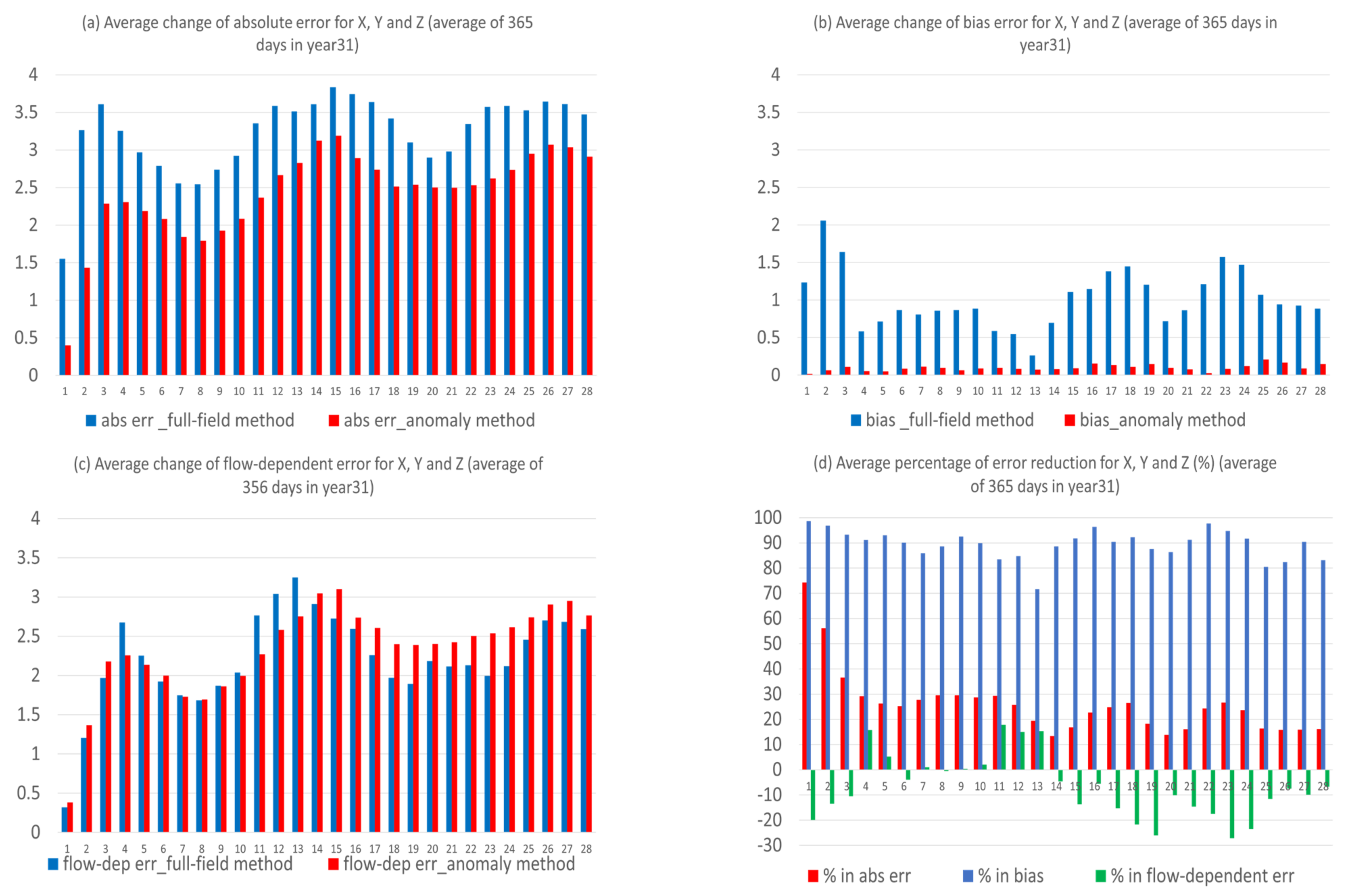
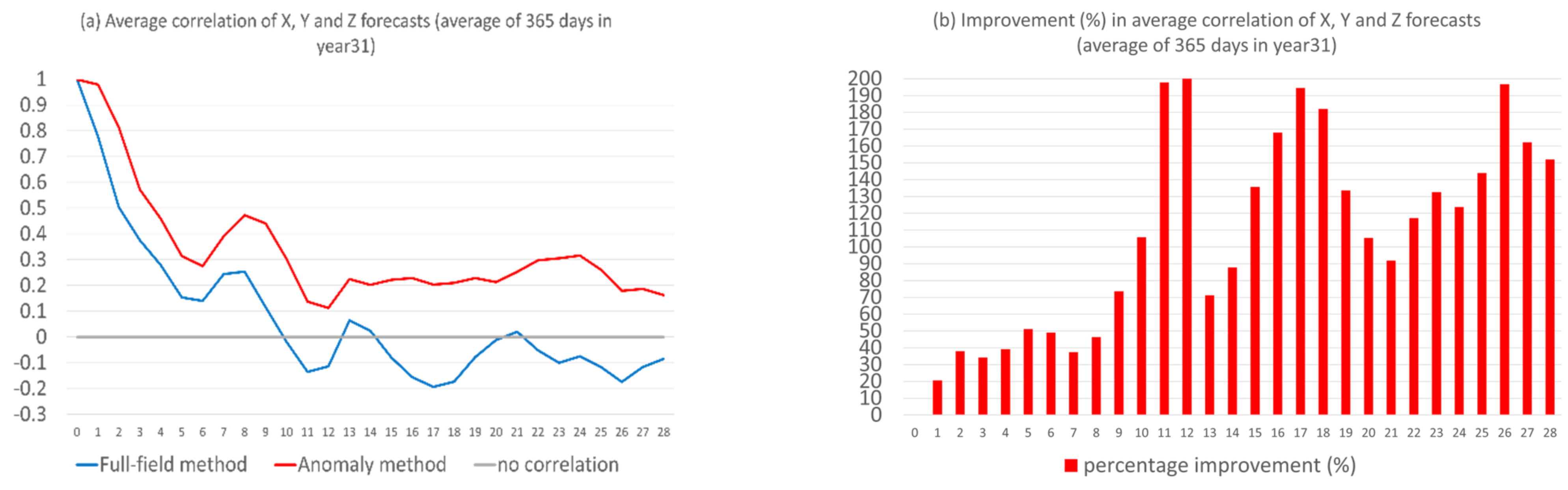
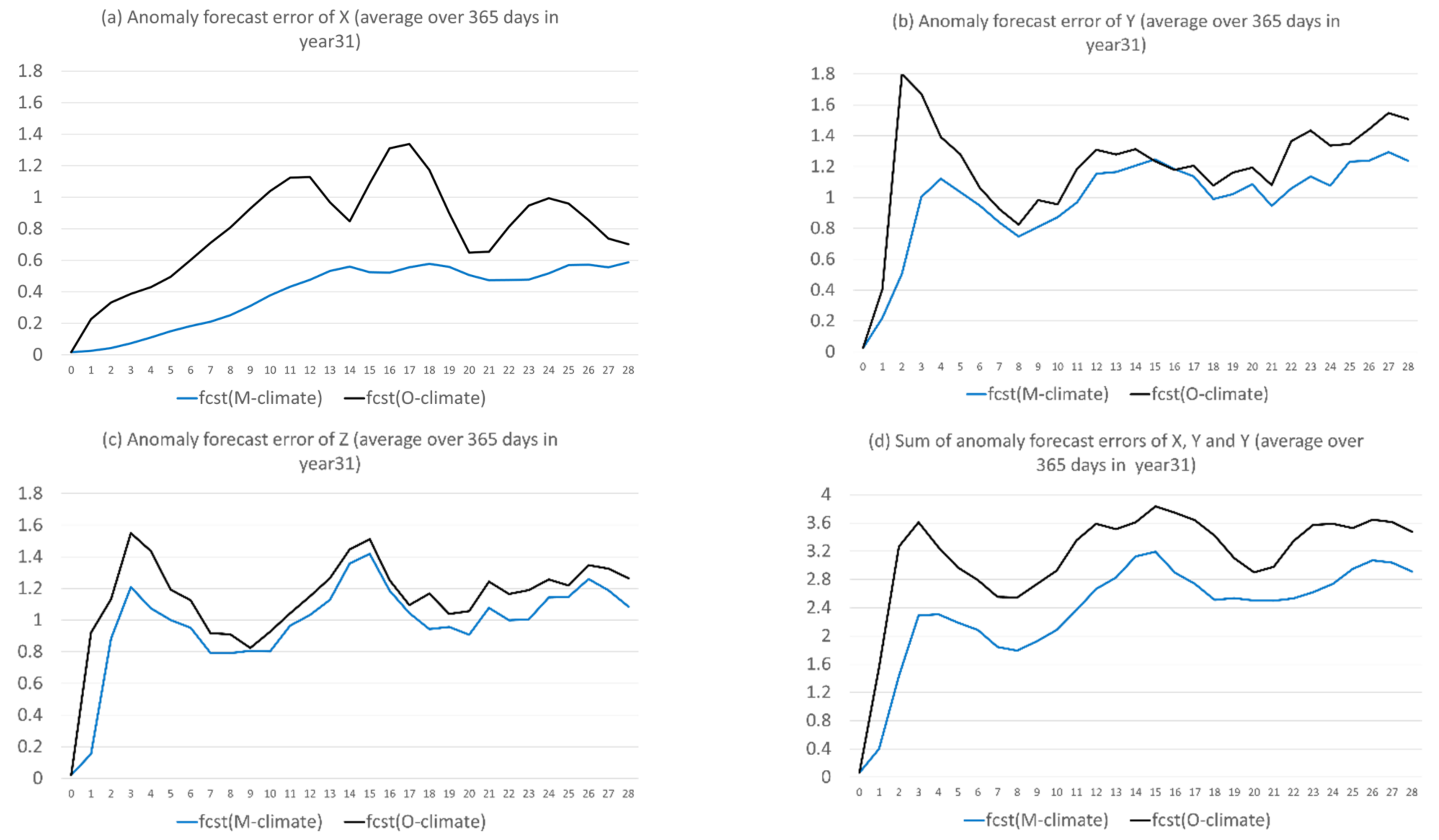
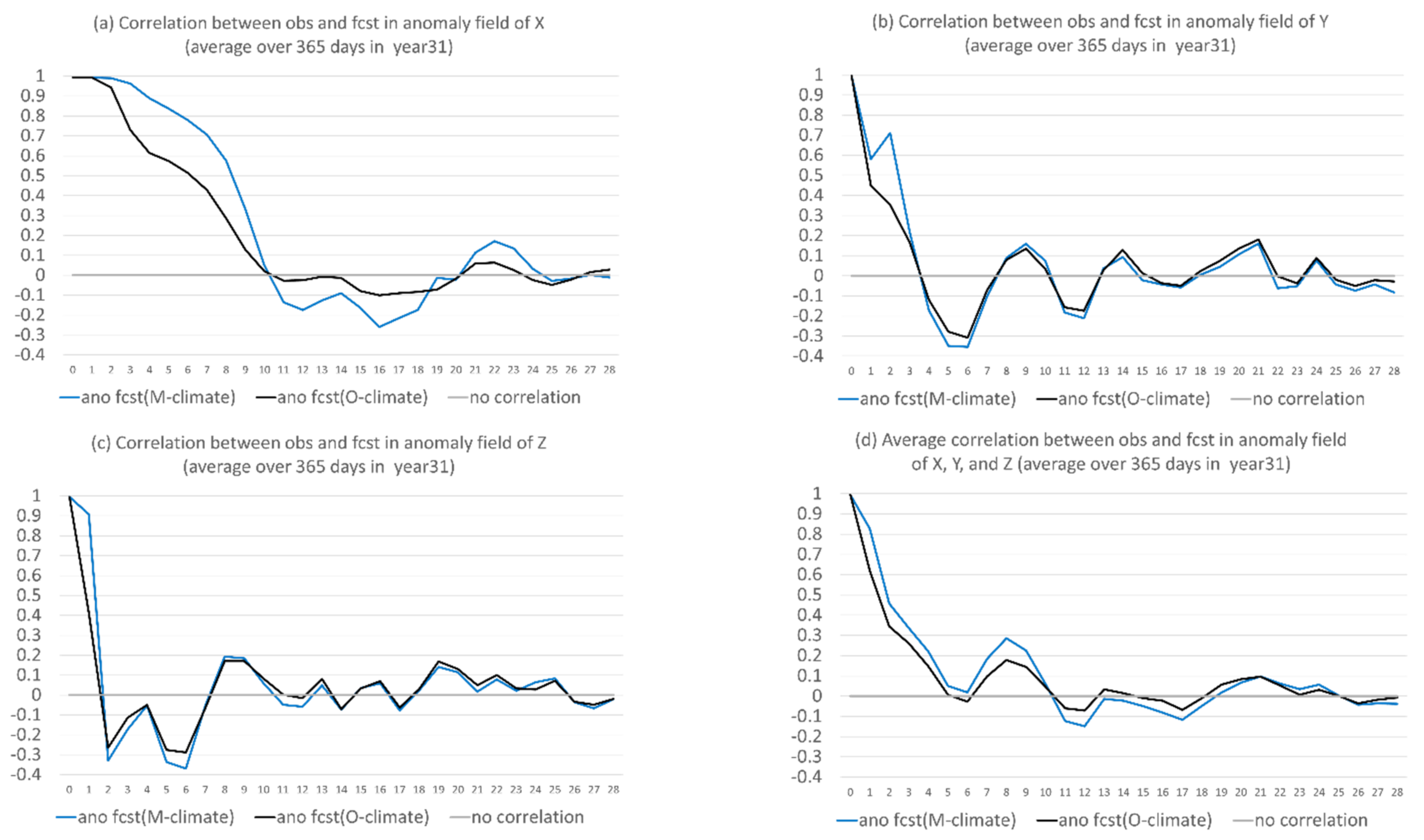
- The proposed anomaly-based approach can significantly and steadily increase model forecast accuracy in both magnitude and structure (time-evolution pattern) throughout the entire forecast period (28 model days in lead time). On average of the three variables, the total forecast error was reduced by about 25%, and the correlation was boosted by about 100–200% (from negative to positive). The correlation improvement increases with the increasing of forecast length: from about 20% at day 1 to 150% at day 28.
- (2)
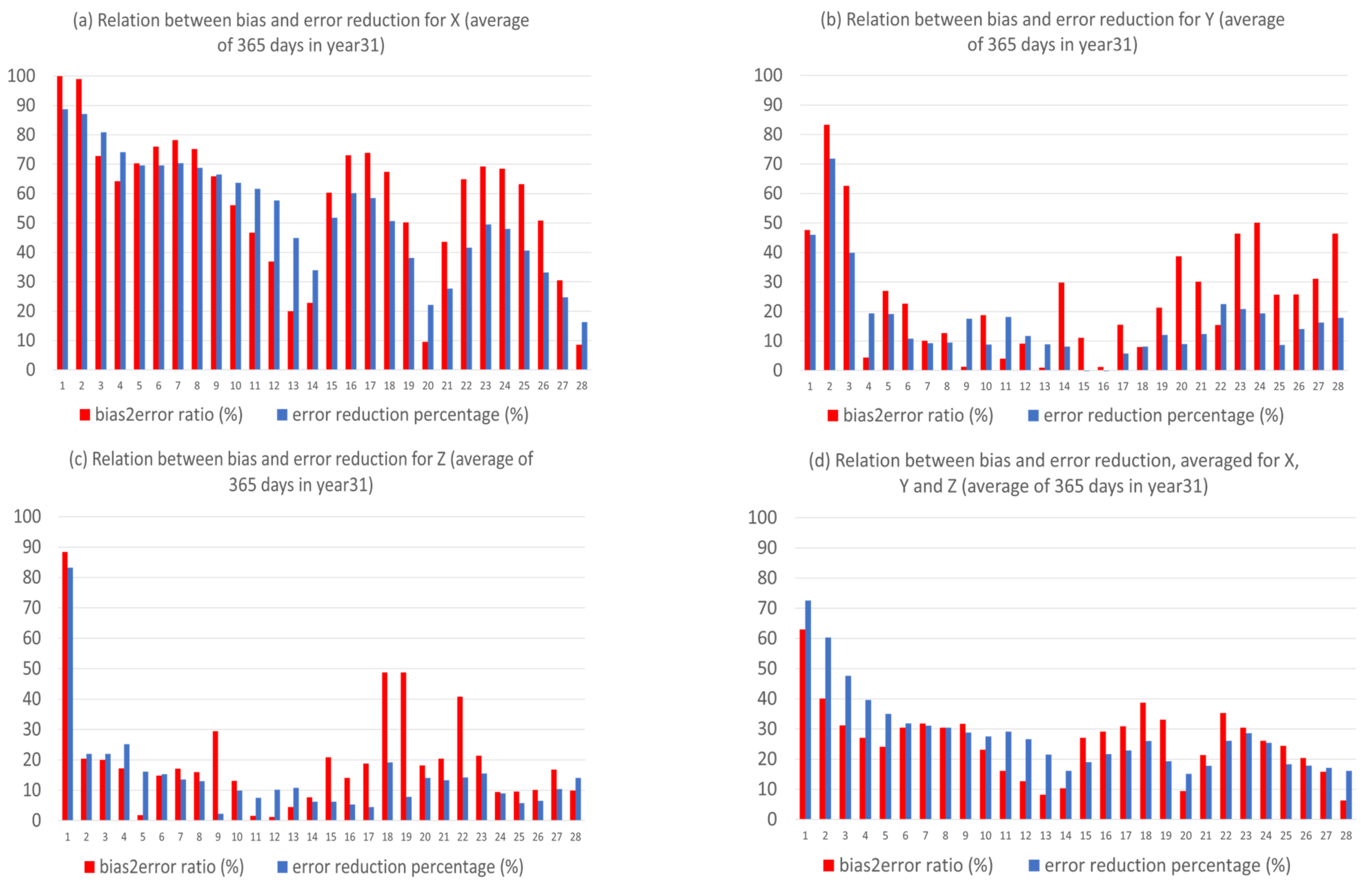
- The anomaly-based method has different impacts on different types of forecast error. By decomposing the forecast error into systematic (bias) and flow-dependent (random error) errors, we found that the bias error was almost eliminated (over 90% in reduction) over the entire forecast period. However, the flow-dependent error was only slightly reduced in the first two weeks, and then became worse. On average, the reduction was about 5% over the first two weeks, and the worsening was about 15% over the last two weeks.
- (3)
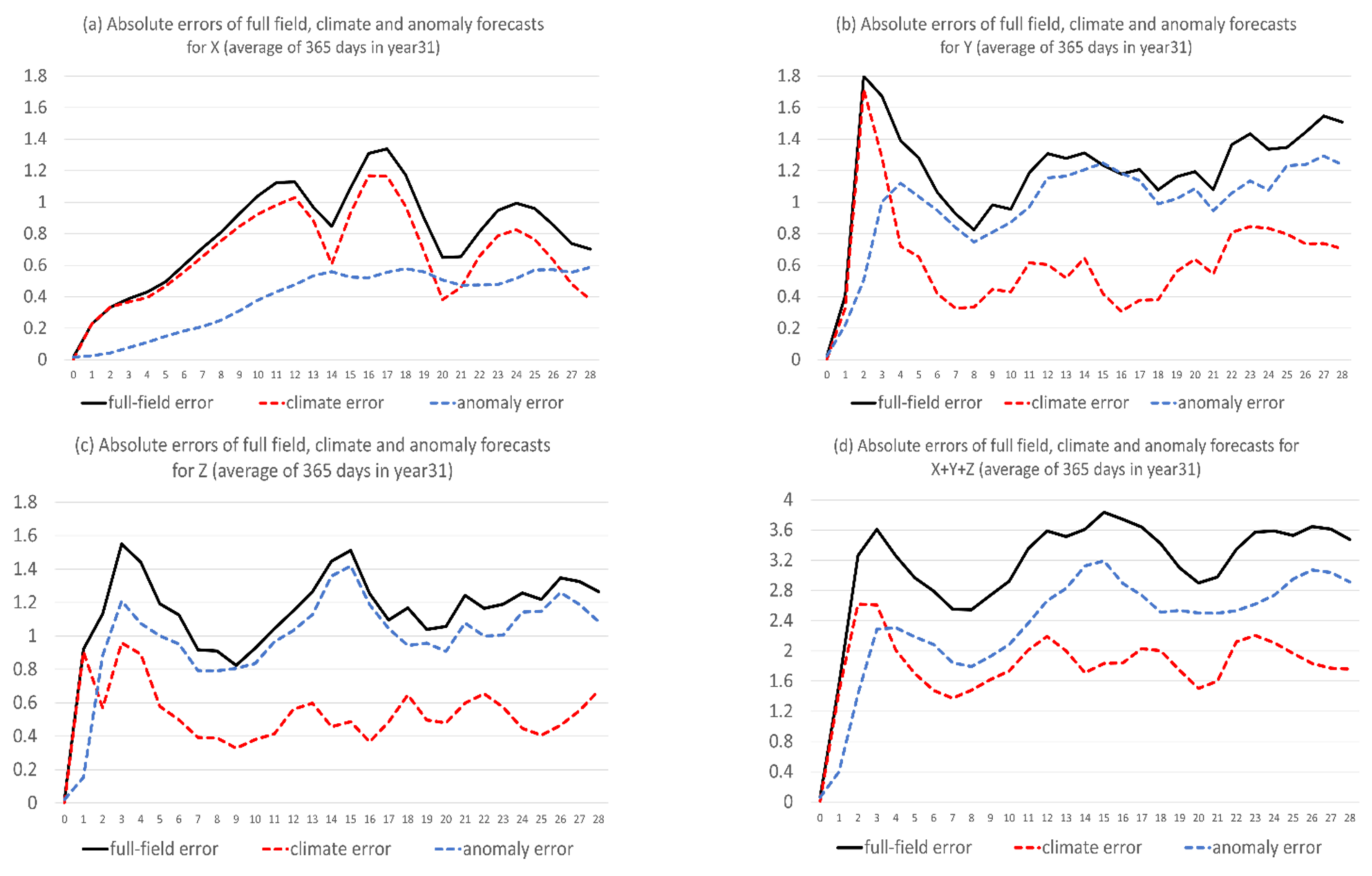
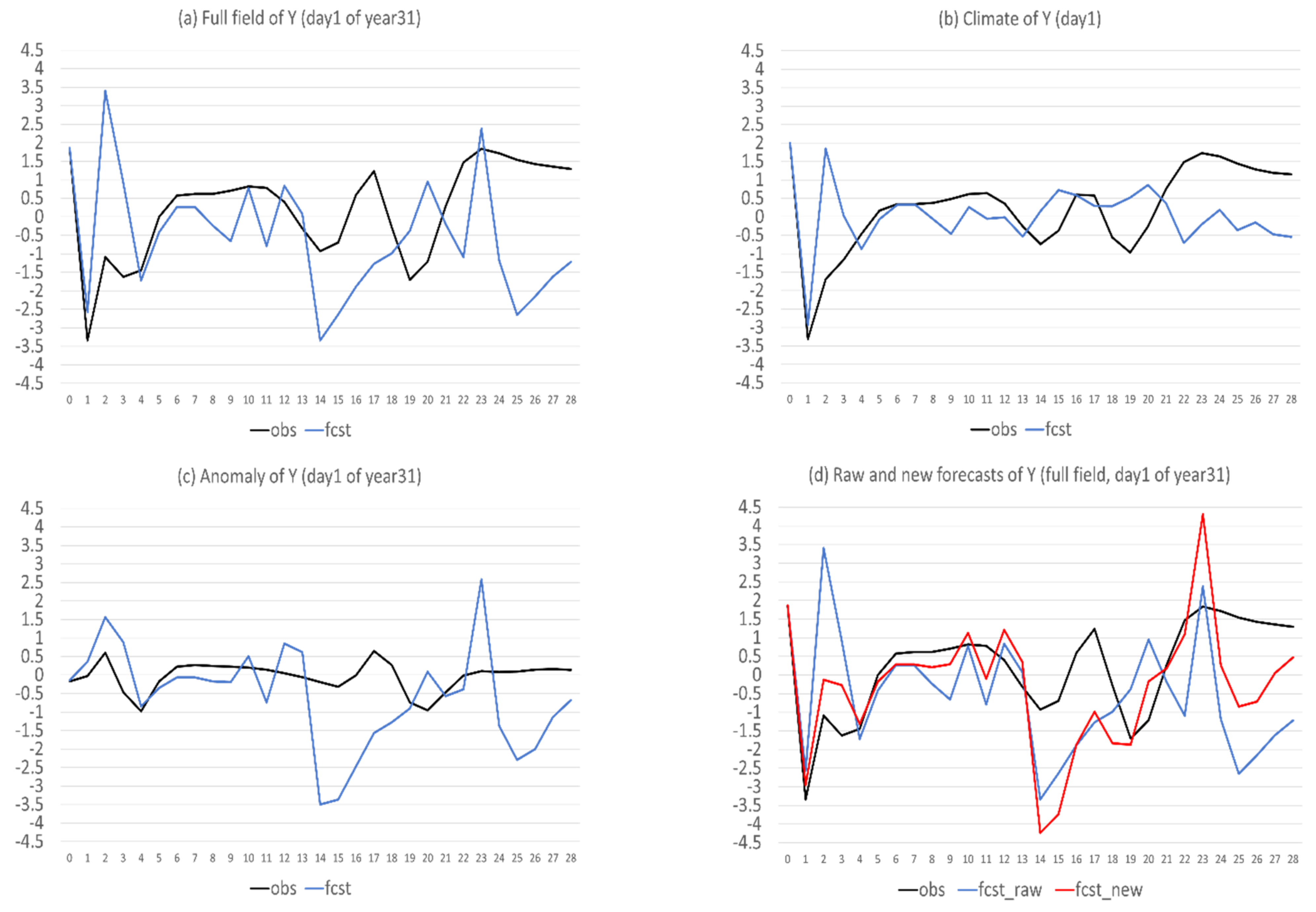
- The reason why there is such a dramatic reduction in bias is because bias error mainly stems from model climate prediction. Since this method improves a forecast through eliminating climate forecast error, forecast improvement will be larger when model climate error or bias is larger, such as in X (about 40% in total error reduction); otherwise, it will be smaller, such as in Y and Z (about 20% and 15%). Therefore, this method is more useful for more challenging days, such as drop-off events and longer-range forecasts, when the model’s basic state (model climate) has drifted away from the true basic state (observed climate).
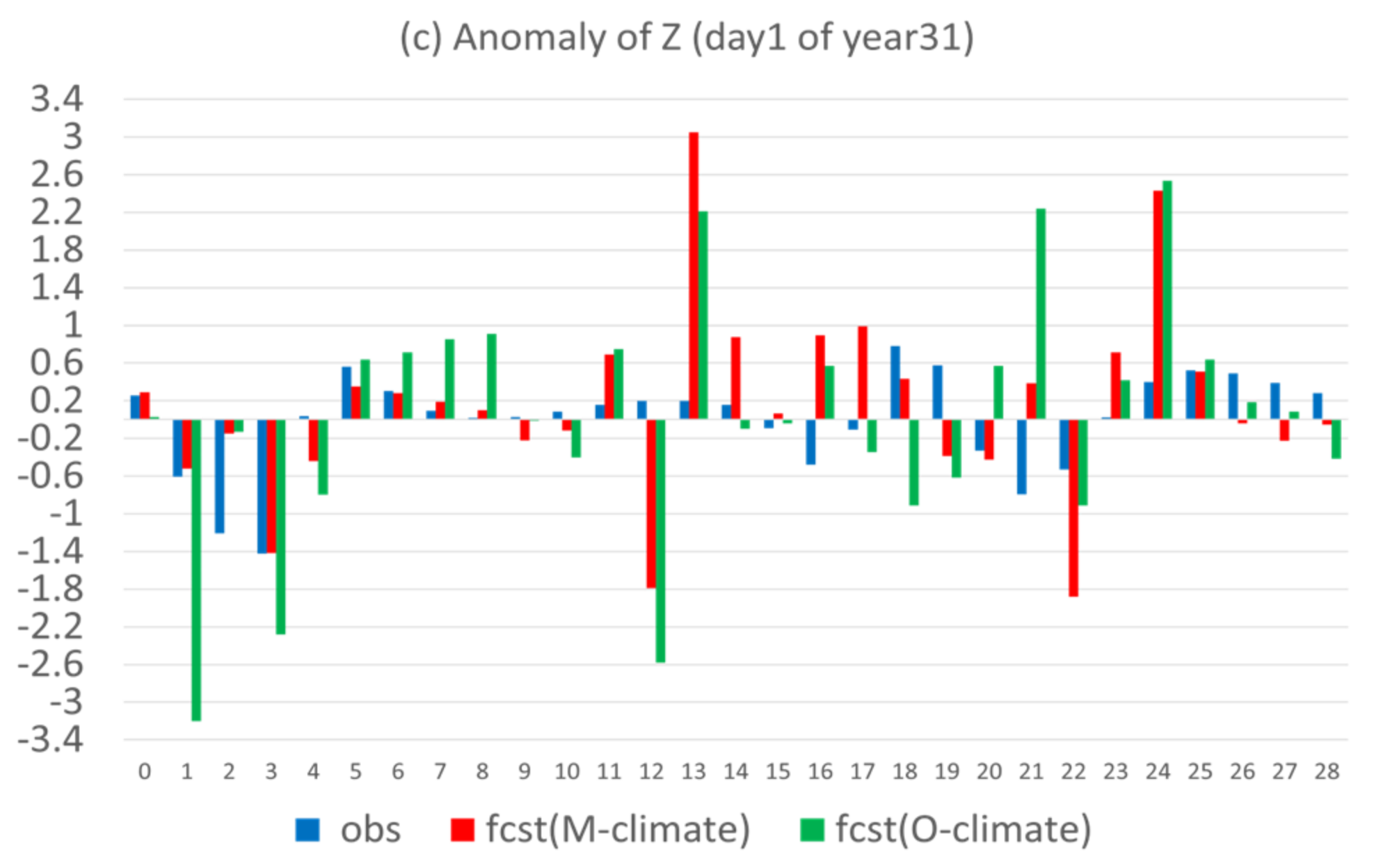
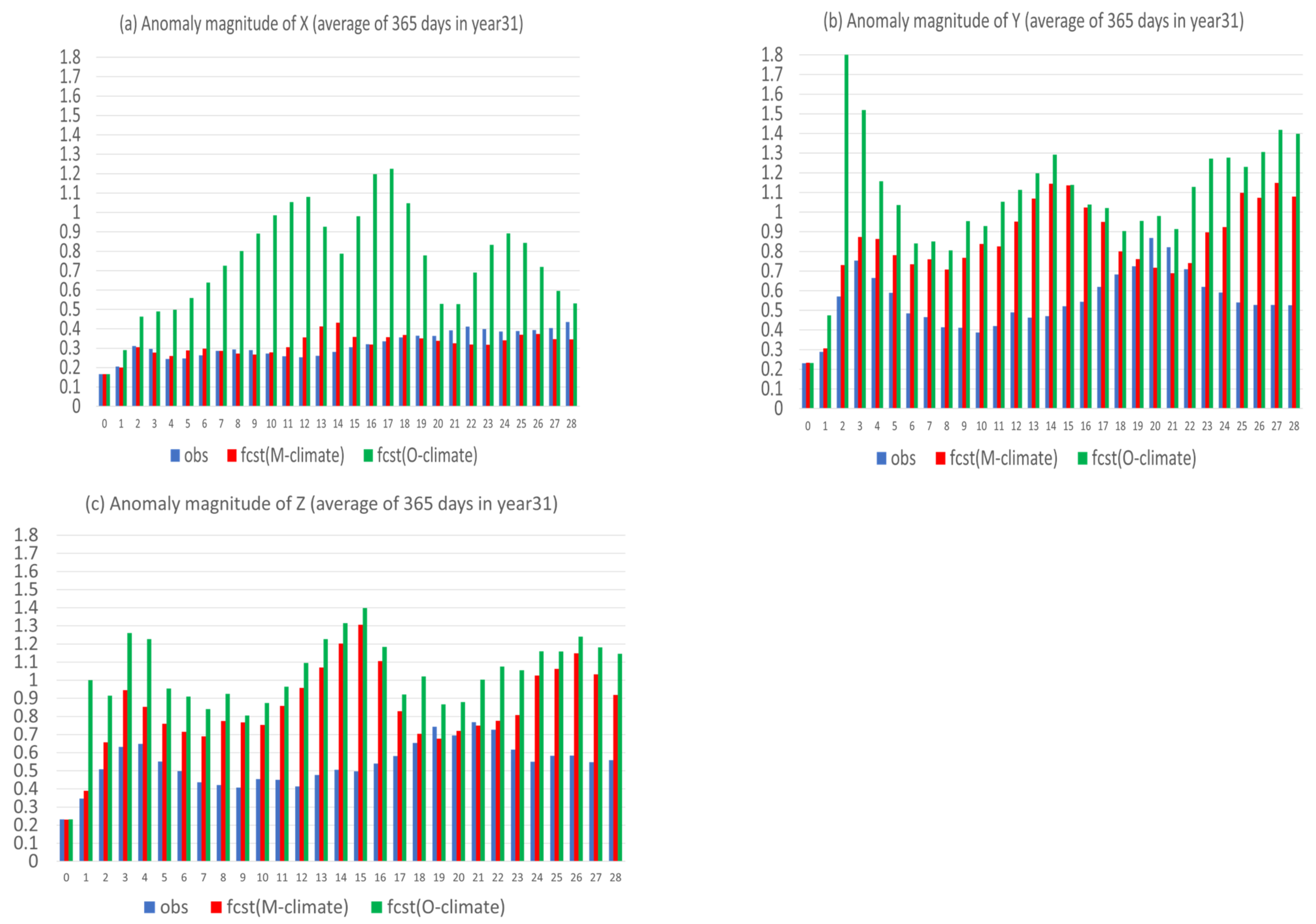
- (4)
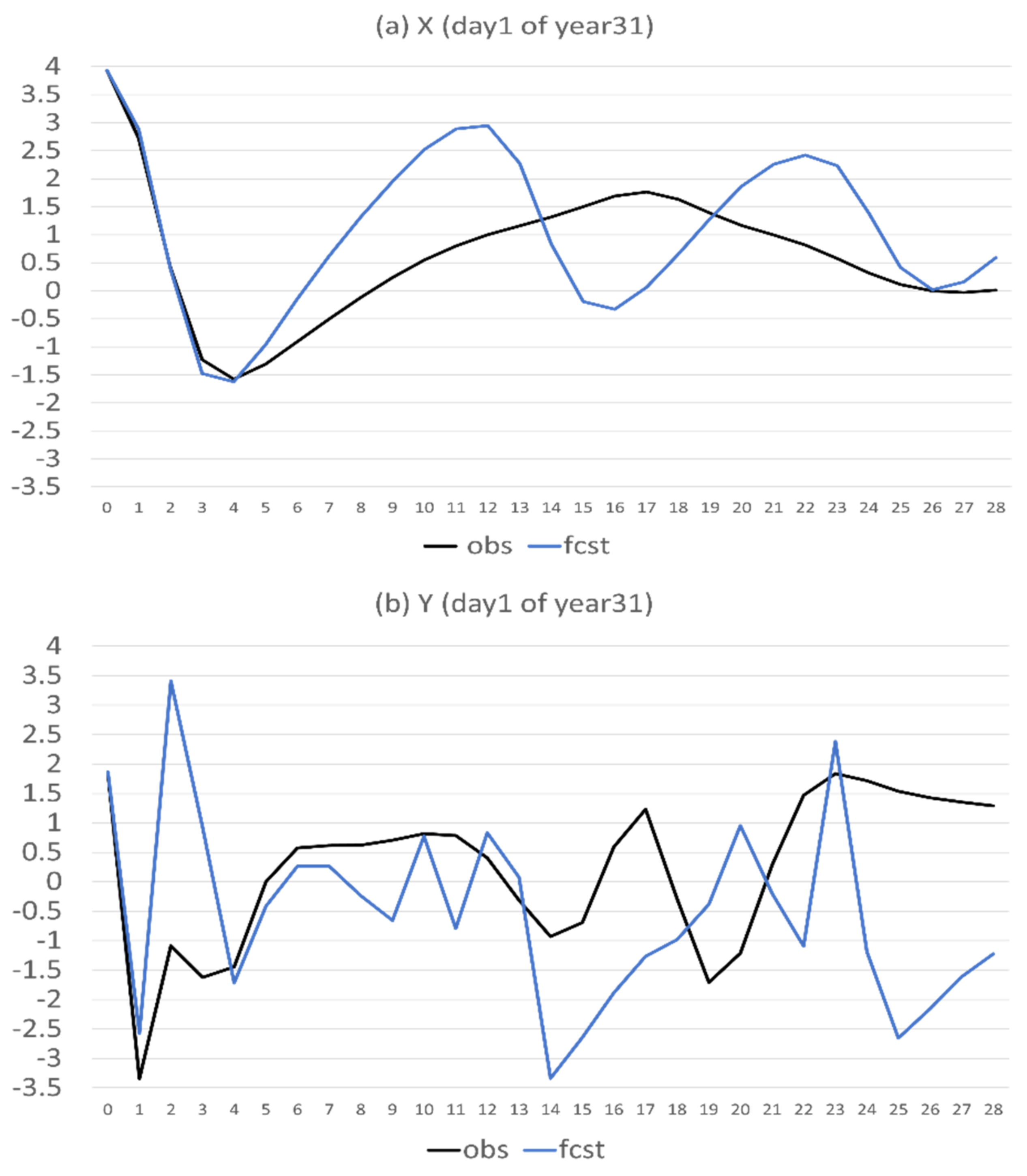
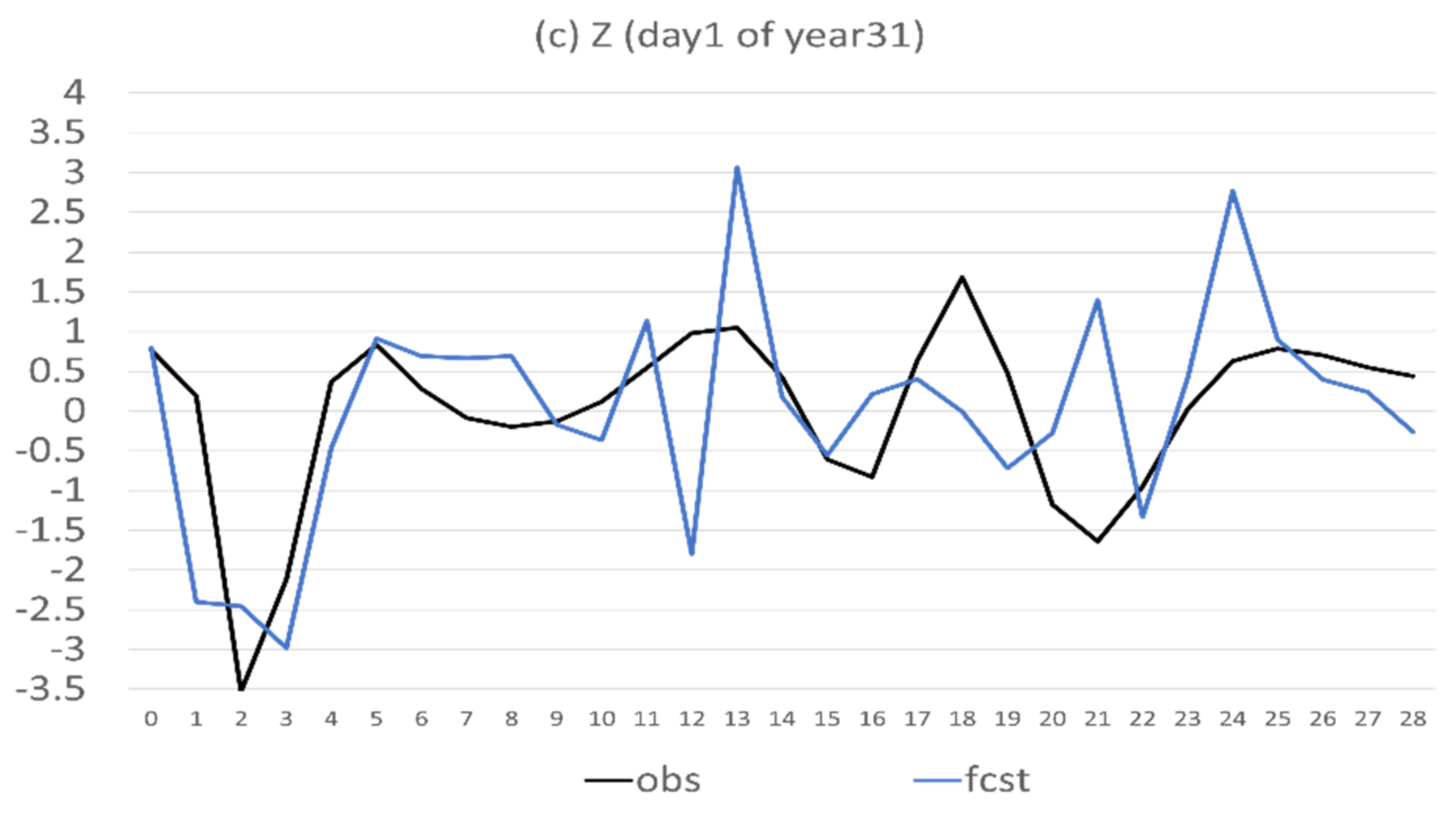
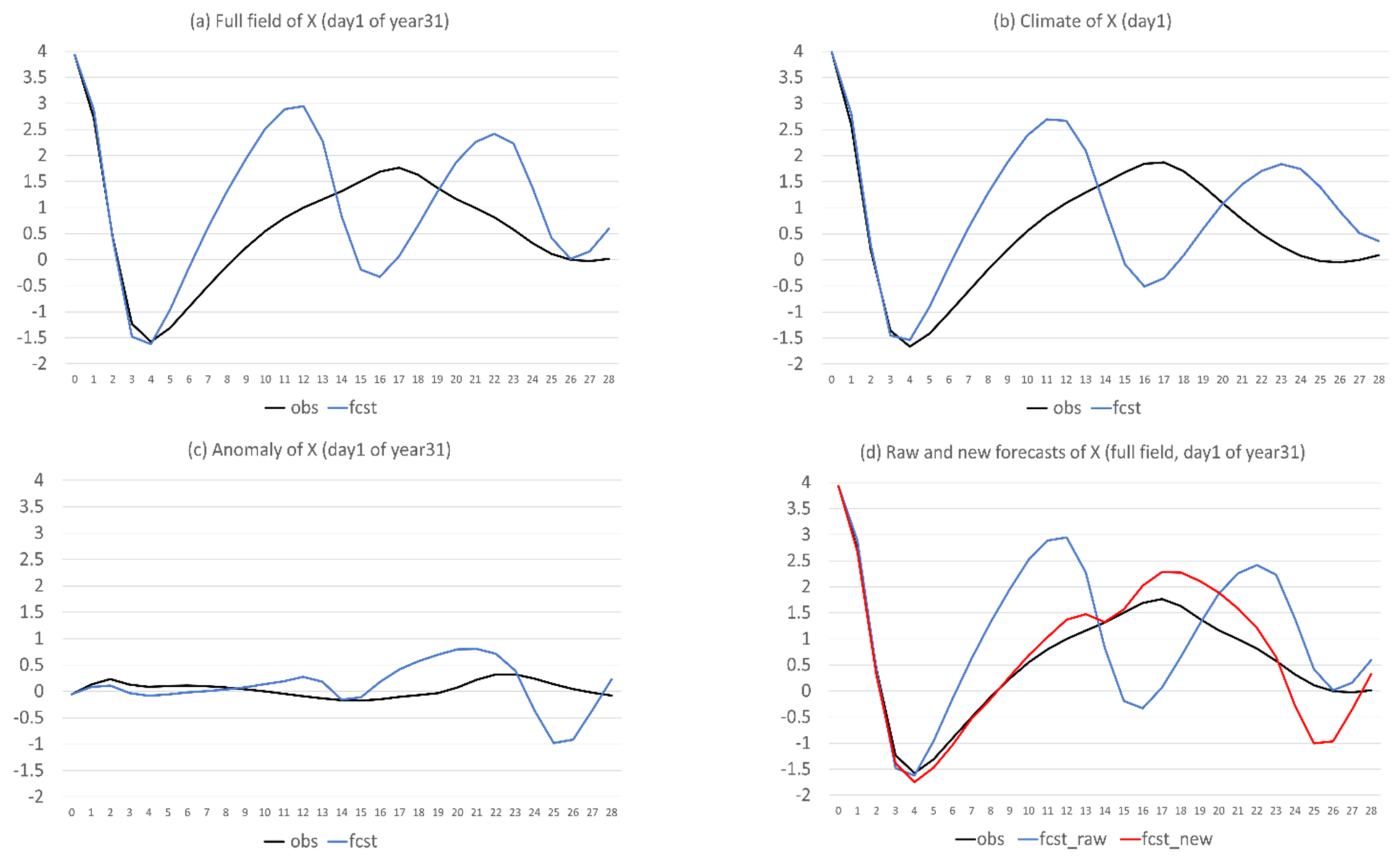
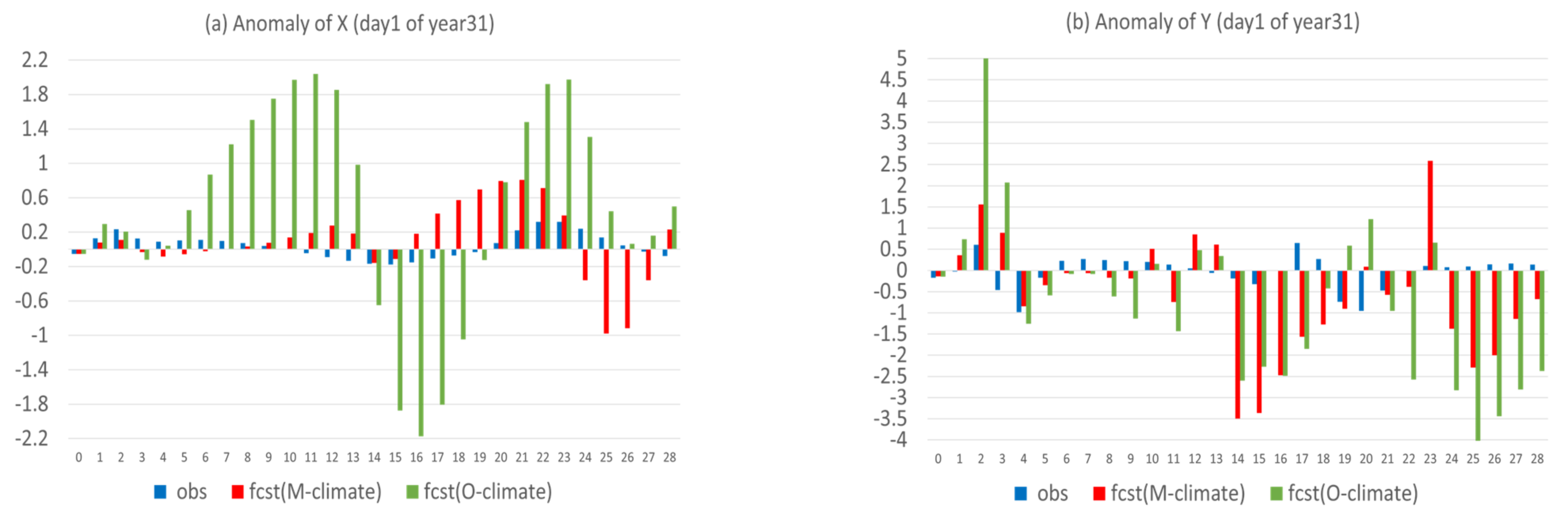
- Flow-dependent error is largely associated with anomaly forecasts. As a result, flow-dependent error will be smaller when the forecast anomaly is similar to the observed anomaly, such as X (cf. Figure 3a and Figure 13a); otherwise, it will be larger when forecast anomaly is very different from observed anomaly, such as Y and Z (cf. Figure 3b–c and Figure 13b–c). In this study the predicted anomaly was much larger than the observed anomaly for Y and Z (Figure 13b–c). Therefore, their anomaly forecast errors were large, which led to large flow-dependent error in the new forecasts (Figure 6c). A consequence of this is that the flow-dependent error became even worse in many forecast hours for the new forecasts. Physically, the worsening of flow-dependent error can be explained by the “correct forecast for wrong reasons” situation that raw forecasts were accidently corrected by model bias. If the predicted anomaly magnitudes were smaller and closer to the observed (i.e., model variation is similar to the nature variation), the worsening of flow-dependent error would be to a lesser degree, and the new method would work even more effectively by reducing a larger portion of the total error.
- (5)
- Lastly, a more accurate anomaly-forecast needs to be constructed, relative to model climate, rather than observed climate, by taking advantage of cancelling model systematic error under the perfect-model assumption.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, A.S.; Jourdain, N.C.; Brown, J.N.; Monselesan, D. Climate drift in the CMIP5 models. J. Clim. 2013, 26, 8597–8615. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Du, J.; Zhang, Y.; Xia, Y.; Deng, G. Sensitivity of Ensemble Forecast Verification to Model Bias. Mon. Weather Rev. 2018, 146, 781–796. [Google Scholar] [CrossRef]
- Yin, L.; Fu, R.; Shevliakova, E.; Dickinson, R.E. How well can CMIP5 simulate precipitation and its controlling processes over tropical South America? Clim. Dyn. 2013, 41, 3127–3143. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteor. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Qian, W.; Du, J.; Ai, Y. A Review: Anomaly-Based versus Full-Field-Based Weather Analysis and Forecasting. Bull. Am. Meteorol. Soc. 2021, 102, E849–E870. [Google Scholar] [CrossRef]
- Huang, J.; Du, J.; Qian, W. A Comparison between a Generalized Beta–Advection Model and a Classical Beta–Advection Model in Predicting and Understanding Unusual Typhoon Tracks in Eastern China Seas. Weather Forecast. 2015, 30, 771–792. [Google Scholar] [CrossRef]
- Qian, W.; Du, J. Anomaly Format of Atmospheric Governing Equations with Climate as a Reference Atmosphere. Meteorology 2022, 1, 127–141. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Mullen, S.L. Reforecasts: An Important Dataset for Improving Weather Predictions. Bull. Am. Meteorol. Soc. 2006, 87, 33–46. [Google Scholar] [CrossRef]
- Lorenz, E.N. Irregularity: A fundamental property of the atmosphere. Tellus A 1984, 36A, 98–110. [Google Scholar] [CrossRef]
- Lorenz, E.N. Can chaos and intransitivity lead to interannual variability? Tellus A 1990, 42, 378–389. [Google Scholar] [CrossRef]
- Pielke, R.A.; Zeng, X. Long-Term Variability of Climate. J. Atmos. Sci. 1994, 51, 155–159. [Google Scholar] [CrossRef]
- Gonzàlez-Miranda, J.M. Predictability in the Lorenz low-order general atmospheric circulation model. Phys. Lett. A 1997, 233, 347–354. [Google Scholar] [CrossRef]
- Roebber, P.J. Climate variability in a low-order coupled atmosphere-ocean model. Tellus A 1995, 47, 473–494. [Google Scholar] [CrossRef][Green Version]
- Van Veen, L.; Opsteegh, T.; Verhulst, F. Active and passive ocean regimes in a low-order climate model. Tellus A 2001, 53, 616–627. [Google Scholar] [CrossRef]
- Van Veen, L. Baroclinic Flow and the Lorenz-84 Model. Int. J. Bifurc. Chaos 2003, 13, 2117–2139. [Google Scholar] [CrossRef]
- Lorenz, E.N. Chaos, Spontaneous Climatic Variations and Detection of the Greenhouse Effect. In Greenhouse-Gas-Induced Climatic Change: A Critical Appraisal of Simulations and Observations; Schlesinger, M.E., Ed.; Elsevier Science Publishers B. V.: Amsterdam, The Netherlands, 1991; pp. 445–453. [Google Scholar]
- Shen, B.-W. Aggregated Negative Feedback in a Generalized Lorenz Model. Int. J. Bifurc. Chaos 2019, 29, 1950037. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Wen, G. Dynamical Analysis of the Lorenz-84 Atmospheric Circulation Model. J. Appl. Math. 2014, 2014, 296279. [Google Scholar] [CrossRef]
- Shen, B.-W. Lecture #12 of Math537: Linearization Theorem; Last updated: 24 September 2020; San Diego State University: San Diego, CA, USA, 2017. [Google Scholar] [CrossRef]
- Koh, T.-Y.; Wang, S.; Bhatt, B.C. A diagnostic suite to assess NWP performance. J. Geophys. Res. 2012, 117, D13109. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, J.; Du, J.; Zhi, X.; Wang, J.; Li, X. A Unified Scheme of Stochastic Physics and Bias Correction in an Ensemble Model to Reduce Both Random and Systematic Errors. Weather Forecast. 2019, 34, 1675–1691. [Google Scholar] [CrossRef]
- Du, J.; Berner, J.; Buizza, R.; Charron, M.; Houtekamer, P.; Hou, D.; Jankov, I.; Mu, M.; Wang, X.; Wei, M.; et al. Ensemble Methods for Meteorological Predictions. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H., Schaake, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–52. [Google Scholar] [CrossRef]
- Du, J.; DiMego, G. A regime-dependent bias correction approach. In Proceedings of the 19th Conference on Probability and Statistics, New Orleans, LA, USA, 20–24 January 2008; Available online: https://ams.confex.com/ams/88Annual/webprogram/Paper133196.html (accessed on 11 September 2022).
- Glahn, H.R.; Lowry, D.A. The Use of Model Output Statistics (MOS) in Objective Weather Forecasting. J. Appl. Meteo. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E.; Westveld, A.H.; Goldman, T. Calibrated Probabilistic Forecasting Using Ensemble Model Output Statistics and Minimum CRPS Estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Kumar, V.; Simon, A.; Bhardwaj, A.; Ghosh, T.; Ross, R. A review of multimodel superensemble forecasting for weather, seasonal climate, and hurricanes. Rev. Geophys. 2016, 54, 336–377. [Google Scholar] [CrossRef]
- Cui, B.; Tóth, Z.; Zhu, Y.; Hou, D. Bias Correction for Global Ensemble Forecast. Weather Forecast. 2012, 27, 396–410. [Google Scholar] [CrossRef]
- Ebert, E.E. Ability of a poor man’s ensemble to predict the probability and distribution of precipitation. Mon. Weather Rev. 2001, 129, 2461–2480. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Chen, C. Applications of frequency-matching method to ensemble precipitation forecasts. Meteorol. Mon. 2015, 41, 674–684. [Google Scholar]
- Zhu, Y.; Luo, Y. Precipitation Calibration Based on the Frequency-Matching Method. Weather Forecast. 2015, 30, 1109–1124. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather Rev. 2017, 133, 1155–1174. [Google Scholar] [CrossRef]
- Herr, H.D.; Krzysztofowicz, R. Ensemble Bayesian forecasting system Part I: Theory and algorithms. J. Hydrol. 2015, 524, 789–802. [Google Scholar] [CrossRef]
- Herr, H.D.; Krzysztofowicz, R. Ensemble Bayesian forecasting system Part II: Experiments and properties. J. Hydrol. 2019, 575, 1328–1344. [Google Scholar] [CrossRef]
- Yuan, H.; Gao, X.; Mullen, S.L.; Sorooshian, S.; Du, J.; Juang, H.H. Calibration of Probabilistic Quantitative Precipitation Forecasts with an Articial Neural Network. Weather Forecast. 2007, 22, 1287–1303. [Google Scholar] [CrossRef]
- Hamill, T.M.; Scheuerer, M.; Bates, G.T. Analog Probabilistic Precipitation Forecasts Using GEFS Reforecasts and Climatology-Calibrated Precipitation Analyses. Mon. Weather Rev. 2015, 143, 3300–3309. [Google Scholar] [CrossRef]
- Eckel, F.A.; Monache, L.D. A Hybrid NWP–Analog Ensemble. Mon. Weather Rev. 2016, 144, 897–911. [Google Scholar] [CrossRef]
- Chan, M.H.K.; Wong, W.K.; Au-Yeung, K.C. Machine learning in calibrating tropical cyclone intensity forecast of ECMWF EPS. Meteorol. Appl. 2021, 26, e2041. [Google Scholar] [CrossRef]
- Han, L.; Chen, M.; Chen, K.; Chen, H.; Zhang, Y.; Lu, B.; Song, L.; Qin, R. A Deep Learning Method for Bias Correction of ECMWF 24–240 h Forecasts. Adv. Atmos. Sci. 2021, 38, 1444–1459. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Du, J.; Xia, Y.; Hongqi, L. Forecast bias correction through model integration: A dynamical wholesale approach. Q. J. R. Meteorol. Soc. 2020, 146, 1149–1168. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Deng, G. How Should a Numerical Weather Prediction Be Used: Full Field or Anomaly? A Conceptual Demonstration with a Lorenz Model. Atmosphere 2022, 13, 1487. https://doi.org/10.3390/atmos13091487
Du J, Deng G. How Should a Numerical Weather Prediction Be Used: Full Field or Anomaly? A Conceptual Demonstration with a Lorenz Model. Atmosphere. 2022; 13(9):1487. https://doi.org/10.3390/atmos13091487
Chicago/Turabian StyleDu, Jun, and Guo Deng. 2022. "How Should a Numerical Weather Prediction Be Used: Full Field or Anomaly? A Conceptual Demonstration with a Lorenz Model" Atmosphere 13, no. 9: 1487. https://doi.org/10.3390/atmos13091487
APA StyleDu, J., & Deng, G. (2022). How Should a Numerical Weather Prediction Be Used: Full Field or Anomaly? A Conceptual Demonstration with a Lorenz Model. Atmosphere, 13(9), 1487. https://doi.org/10.3390/atmos13091487





