Prediction of PM2.5 Concentration in Ningxia Hui Autonomous Region Based on PCA-Attention-LSTM
Abstract
:1. Introduction
2. Data Presentation
2.1. Study Area Profiles
2.2. Sources and Data Presentation
2.2.1. Statistical Analysis of Data
2.2.2. Time Dimension Analysis of PM2.5 Concentration
2.2.3. Variable Correlation Analysis
2.3. Data Preprocessing
2.3.1. Data Quality Control
2.3.2. Data Normalization and Data Segmentation
3. Research Methodology
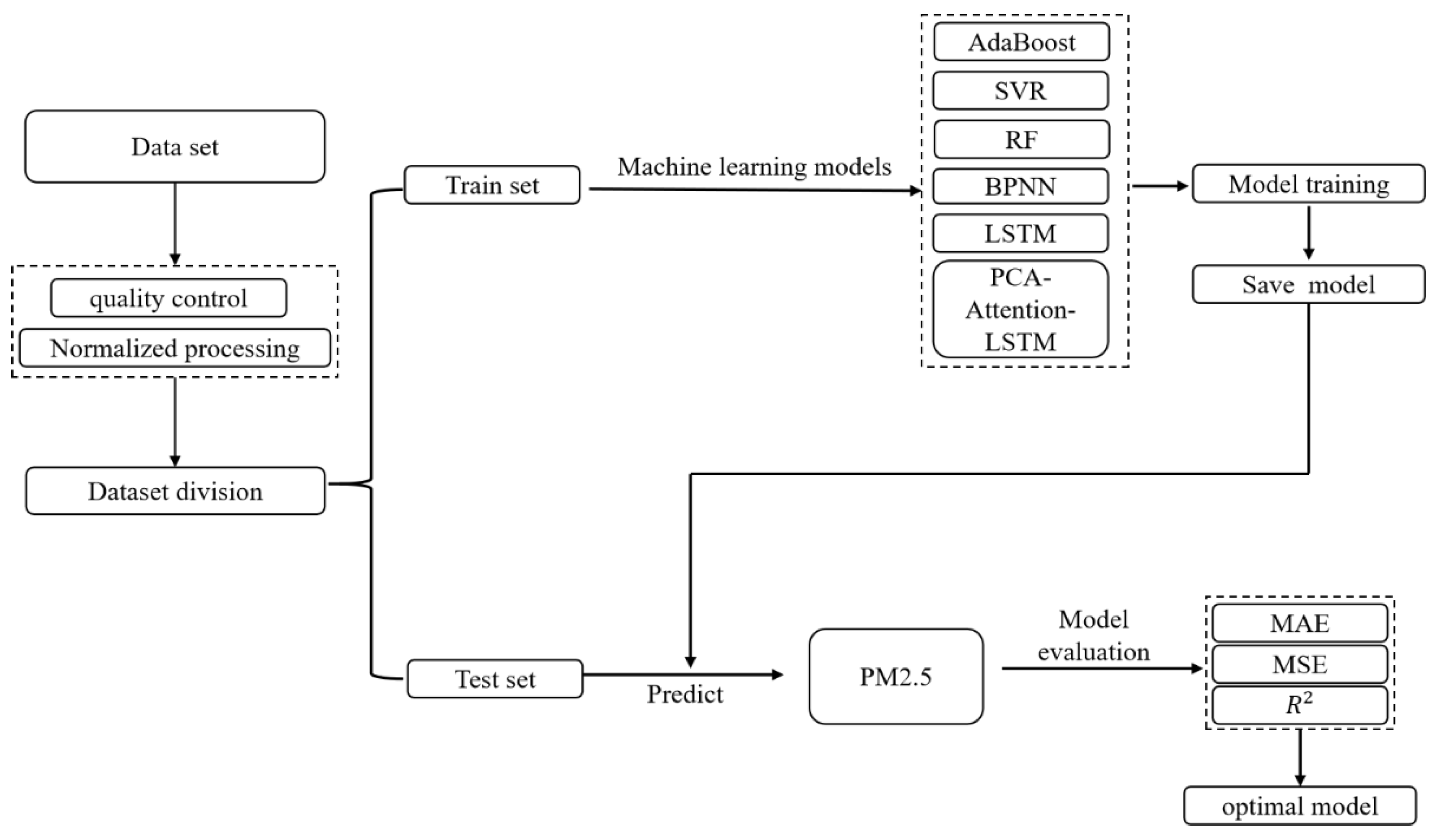
3.1. Experimental Process and Evaluation Method
3.2. Machine Learning Methods
3.3. PCA-Attention-LSTM
3.3.1. Principal Component Analysis (PCA)
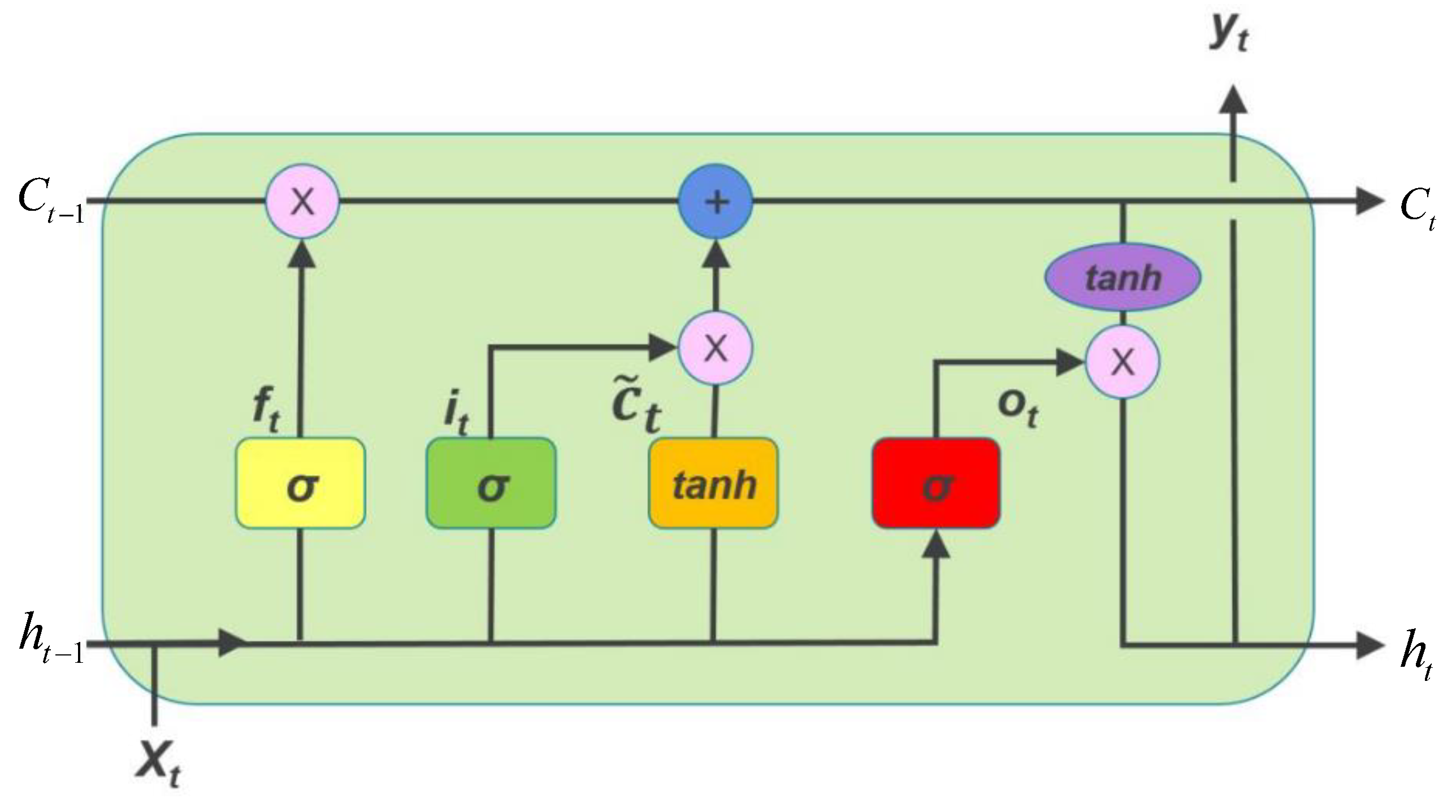
3.3.2. Long Short-Term Memory Neural Network (LSTM)
3.3.3. Attention Mechanism
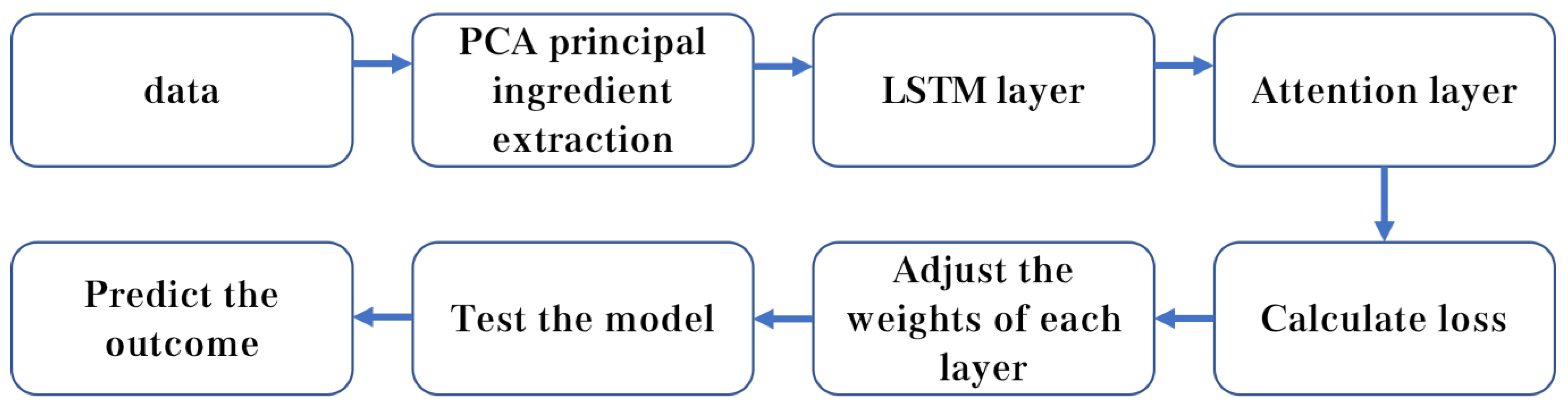
3.3.4. PCA-Attention-LSTM Forecasting Model
4. Experimental Results and Analysis
4.1. PCA-Attention-LSTM Model Building Results
4.2. Model Parameter Selection
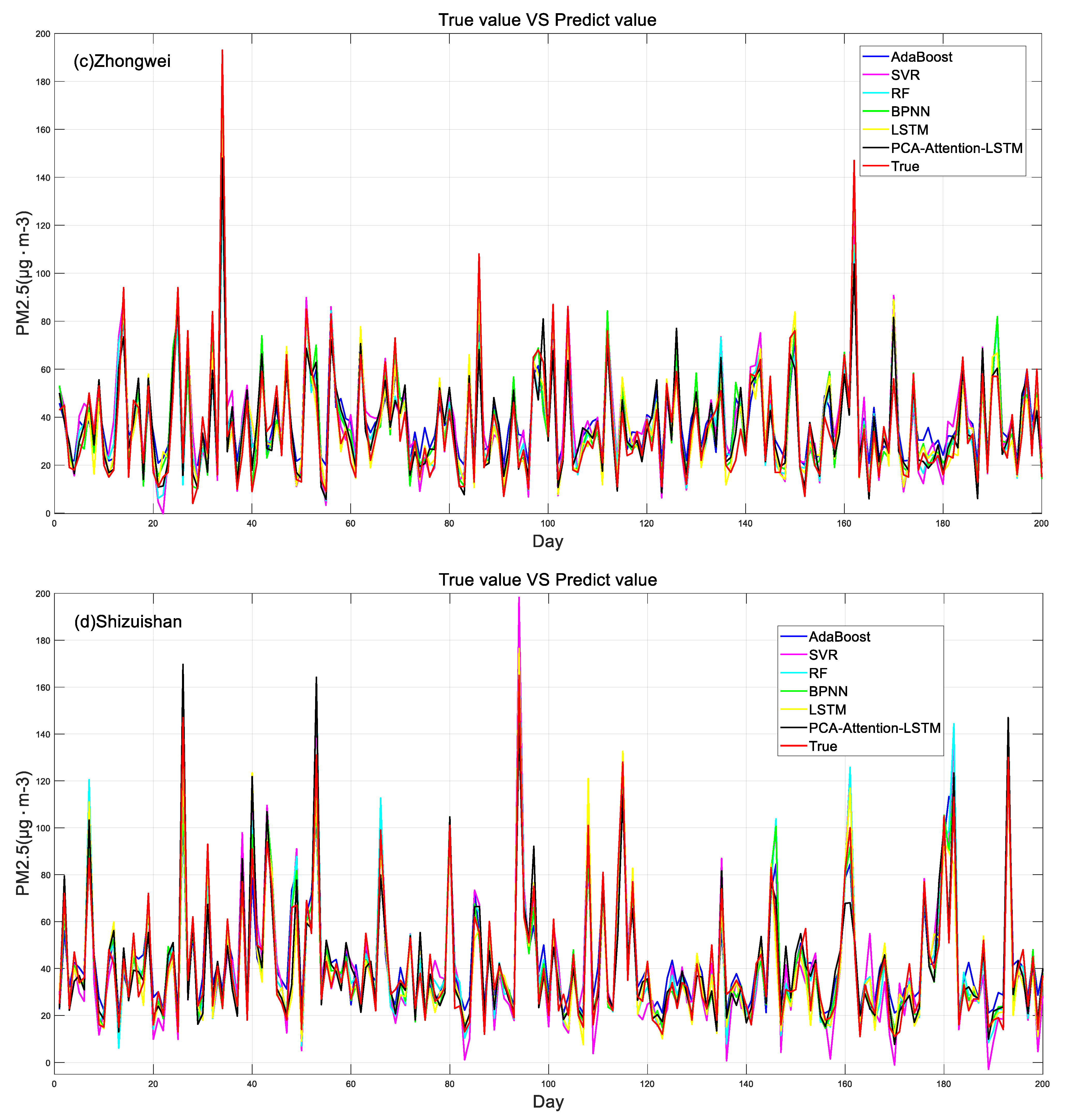
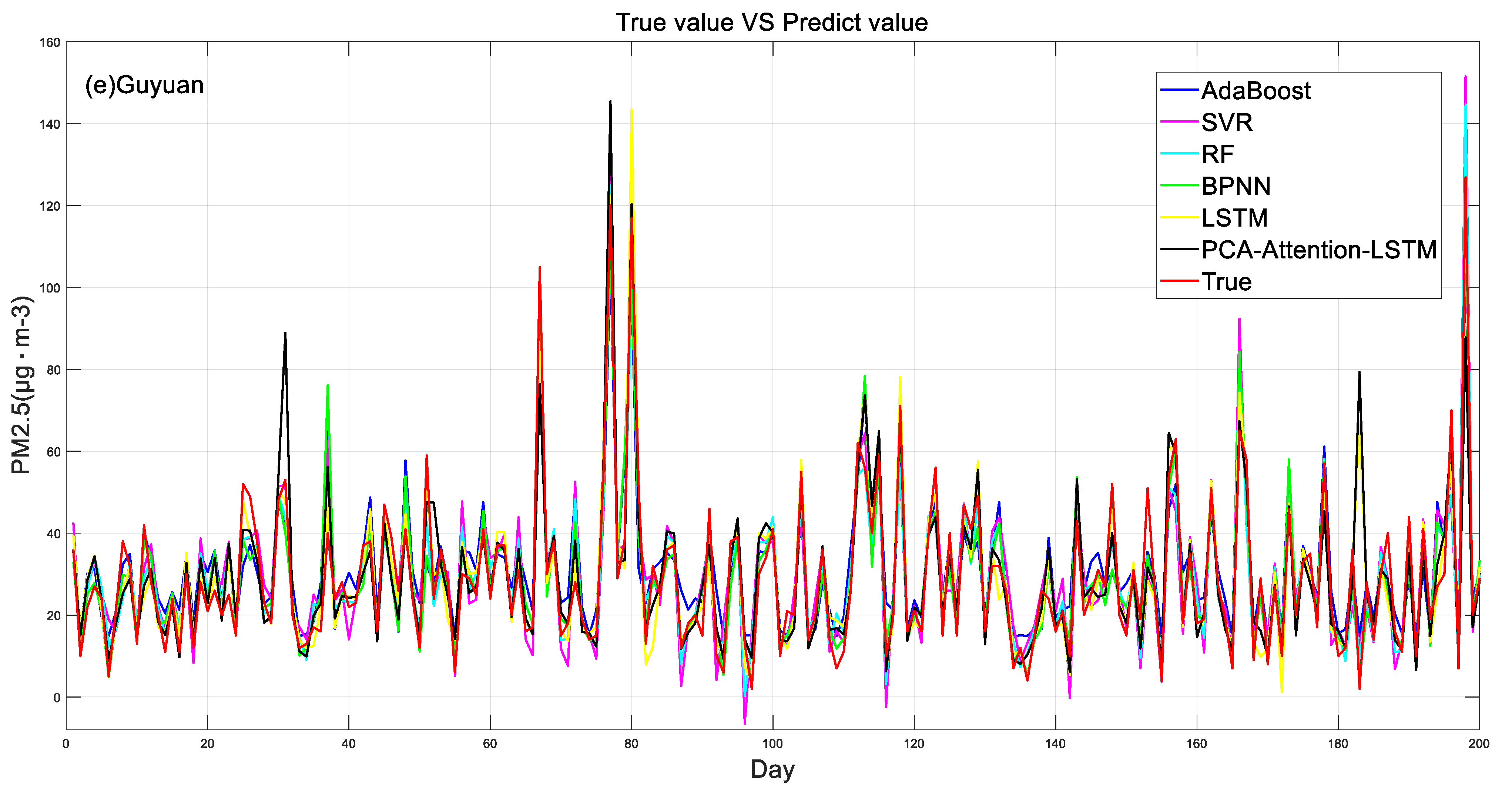
4.3. Model Prediction Results and Comparisons
5. Conclusions and Discussions
- (1)
- Statistical analysis of the data shows that the overall indicators of Guyuan are better than those of the other four cities, and the worst is Shizuishan City, which has a clear correlation with the geographical location of the municipal areas, and the overall air quality in the southern mountainous areas is better than that of the Yellow River irrigation area in the north.
- (2)
- The three-year data of five cities in Ningxia were integrated and divided into four seasons and month by month. The results showed that the PM2.5 concentration showed an obvious seasonal change trend, which was the lowest in summer and the highest in winter. This was mainly related to the dust emission from coal combustion and gas or fuel during winter heating in Ningxia.
- (3)
- Through the analysis of variable importance, the results show that PM10 is the most important, followed by air quality index, air quality grade, and CO having equal importance, and precipitation in meteorological elements is also a relatively important variable. For future studies of PM2.5 concentration prediction, the week can also be used as an input variable, indicating that PM2.5 concentration generation is also affected by weekdays and non-working days.
- (4)
- The concentration of PM2.5 was predicted by using six models, and the results showed that the PCA-attention-LSTM model had the best prediction accuracy, and its correlation coefficient was 0.91~0.93. The prediction accuracy of the SVR model was poor, and its correlation coefficient was 0.75~0.83. The LSTM model and the BPNN model also predicted better results.
- (5)
- Experimental results show that the training evaluation results of the PCA-attention-LSTM model are better than those of the LSTM model, which shows that the cumulative variance contribution rate of the selected principal components reaches 85–90%, which reduces the data dimension and reduces the time complexity and spatial complexity of the model. At the same time, the attention mechanism can better capture important information.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Zhou, Y.; Lu, J. Exploring the relationship between air pollution and meteorological conditions in China under environ-mental governance. Nat. Res. Sci. Rep. 2020, 10, 14518. [Google Scholar] [CrossRef] [PubMed]
- Ding, W.; Zhang, J.; Leung, Y. A hierarchical Bayesian model for the analysis of space-time air pollutant concentrations and an application to air pollution analysis in Northern China. Stoch. Environ. Res. Risk Assess. 2021, 35, 2237–2271. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, J. Prediction of Air Pollutants Concentration Based on an Extreme Learning Machine: The Case of Hong Kong. Int. J. Environ. Res. Public Health 2017, 14, 114. [Google Scholar]
- Ding, W.; Zhang, J.; Leung, Y. Prediction of air pollutant concentration based on sparse response back-propagation training feedforward neural networks. Environ. Sci. Pollut. Res. 2016, 23, 19481–19494. [Google Scholar] [CrossRef]
- Bell, M.; Ebisu, K.; Dominici, F. Spatial and temporal variation in PM2.5 chemical composition in the United States. Palaeontology 2006, 58, 133–140. [Google Scholar] [CrossRef]
- Qin, W.; Zhang, Y.; Chen, J.; Yu, Q.; Cheng, S.; Li, W.; Liu, X.; Tian, H. Variation, sources and historical trend of black carbon in Beijing, China based on ground observation and MERRA-2reanalysis data. Environ. Pollut. 2019, 245, 853–863. [Google Scholar] [CrossRef]
- Liag, M.; Wang, L.; Liu, J.; Gao, W.; Song, T.; Sun, Y.; Li, L.; Li, X.; Wang, Y.; Liu, L.; et al. Exploring the regional pollution characteristics and meteorological formation mechanism of PM2.5 in North China during 2013–2017. Environ. Int. 2020, 134, 105283. [Google Scholar]
- Jin, J.; Du, Y.; Xu, L.; Chen, Z.; Chen, J.; Wu, Y.; Ou, C. Using Bayesian spatio-temporal model to determine the socio-economic and meteorological factors influencing ambient PM2.5 levels in 109 Chinese cities. Environ. Pollut. 2019, 254, 113023. [Google Scholar] [CrossRef]
- Chen, B.; Lin, Y.; Deng, J.; Li, Z.; Dong, L.; Huang, Y.; Wang, K. Spatiotemporal dynamics and exposure analysis of daily PM2.5 using a remote sensing-based machine learning model and multi-time meteorological parameters. Atmos. Pollut. Res. 2021, 12, 23–31. [Google Scholar] [CrossRef]
- Rybarczyk, Y.; Zalakeviciute, R. Machine learning approach to forecasting urban pollution: A case study of Quito. In Proceedings of the IEEE Ecuador Technical Chapters Meeting, (ETCM’16), Guayaquil, Ecuador, 12–14 October 2016. [Google Scholar]
- Wang, J.; Ogawa, S. Effects of meteorological conditions on PM2.5 concentrations in Nagasaki, Japan. Int. J. Environ. Res. Public Health 2015, 12, 9089–9101. [Google Scholar] [CrossRef]
- Jimenez, P.A.; Dudhia, J. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef]
- Ni, X.; Huang, H.; Du, W. Relevance analysis and short-term prediction of PM2.5 concentrations in Beijing based on multi-source data. Atmos. Environ. 2017, 150, 146–161. [Google Scholar] [CrossRef]
- Brokamp, C.; Jandarov, R.; Hossain, M.; Ryan, P. Predicting daily urban fine particulate matter Concentrations using a random forest model. Environ. Sci. Technol. 2018, 52, 4173–4179. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, X.X.; Xue, B.; Zhang, J.Q.; Ren, W.X. Short period PM2.5 prediction based on multivariate linear regression model. PLoS ONE 2018, 13, e0201011. [Google Scholar] [CrossRef]
- Akbal, Y.; Ünlü, K.D. A deep learning approach to model daily particular matter of Ankara: Key features and forecasting. Int. J. Environ. Sci. Technol. 2021, 19, 5911–5927. [Google Scholar] [CrossRef]
- Brokamp, C.; Jandarov, R.; Rao, M.B.; LeMasters, G.; Ryan, P. Exposure assessment models for elemental components of particulate matter in an urban environment: A comparison of regression and random forest approaches. Atmos. Environ. 2017, 151, 1–11. [Google Scholar] [CrossRef]
- Russo, A.; Raischel, F.; Lind, P.G. Air quality prediction using optimal neural networks with stochastic variables. Atmos. Environ. 2013, 79, 822–830. [Google Scholar] [CrossRef]
- Singh, K.P.; Gupta, S.; Rai, P. Identifying pollution sources and predicting urban air quality using ensemble learning methods. Atmos. Environ. 2013, 80, 426–437. [Google Scholar] [CrossRef]
- Karimian, H.; Li, Q.; Wu, C.; Qi, Y.; Mo, Y.; Chen, G.; Zhang, X.; Sachdeva, S. Evaluation of different machine learning approaches to forecasting PM2.5 mass concentrations. Aerosol Air Qual. Res. 2019, 19, 1400–1410. [Google Scholar] [CrossRef]
- Osowski, S.; Garanty, K. Engineering Applications of Artificial Intelligence. Eng. Appl. Artif. Intell. 2007, 20, 745–755. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.-C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Song, L.; Pang, S.; Longley, I.; Olivares, G.; Sarrafzadeh, A. Spatio-temporal PM 2.5 prediction by spatial data aided incremental support vector regression. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 623–630. [Google Scholar]
- Arhami, M.; Kamali, N.; Rajabi, M.M. Predicting hourly air pollutant levels using artificial neural networks coupled with uncertainty analysis by Monte Carlo simulations. Environ. Sci. Pollut. Res. 2013, 20, 4777–4789. [Google Scholar] [CrossRef]
- Zheng, H.; Shang, X. Study on prediction of atmospheric PM2.5 based on RBF neural network. In Proceedings of the IEEE Fourth International Conference on Digital Manufacturing and Automation (ICDMA), Qindao, China, 29–30 June 2013; pp. 1287–1289. [Google Scholar]
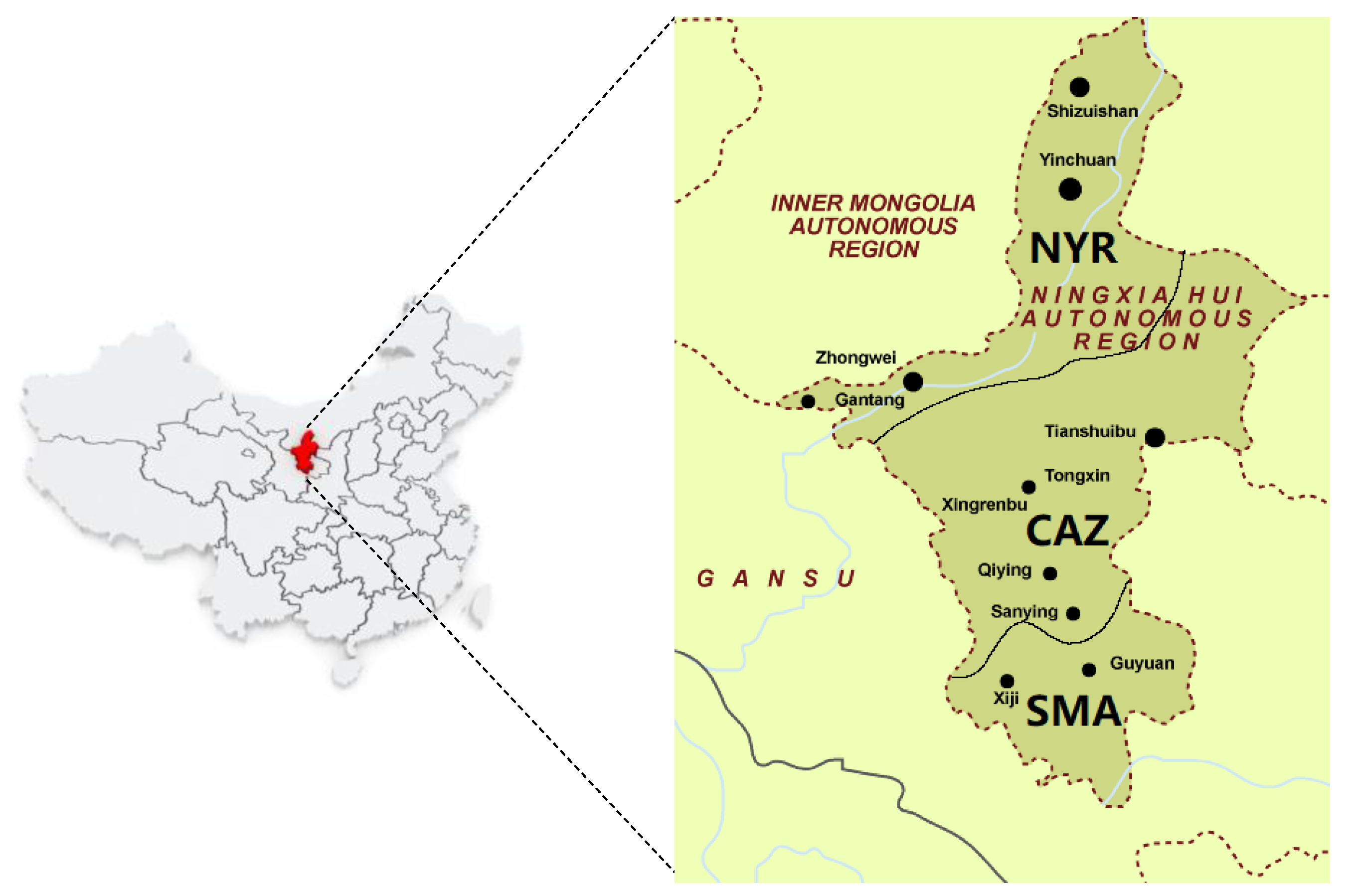
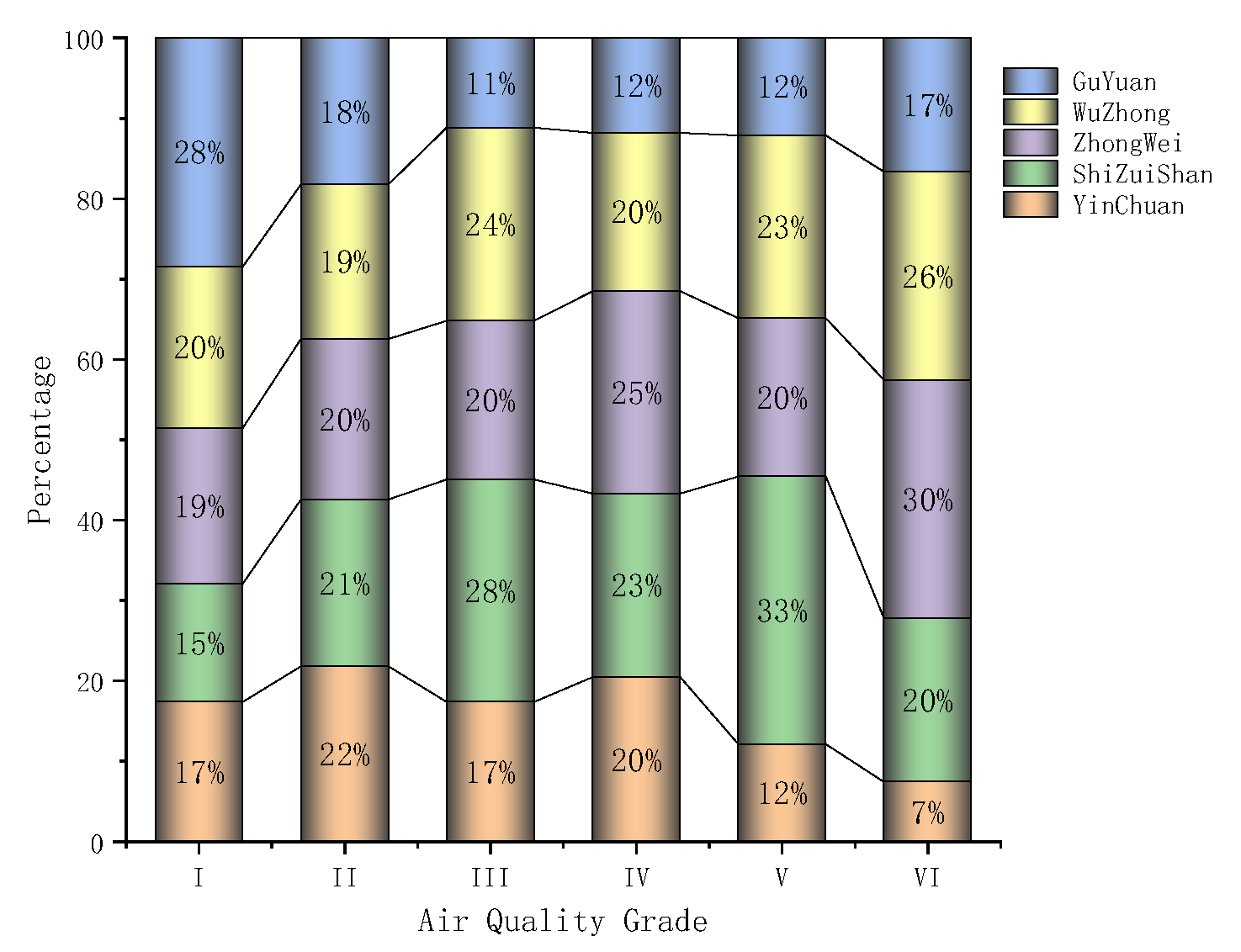
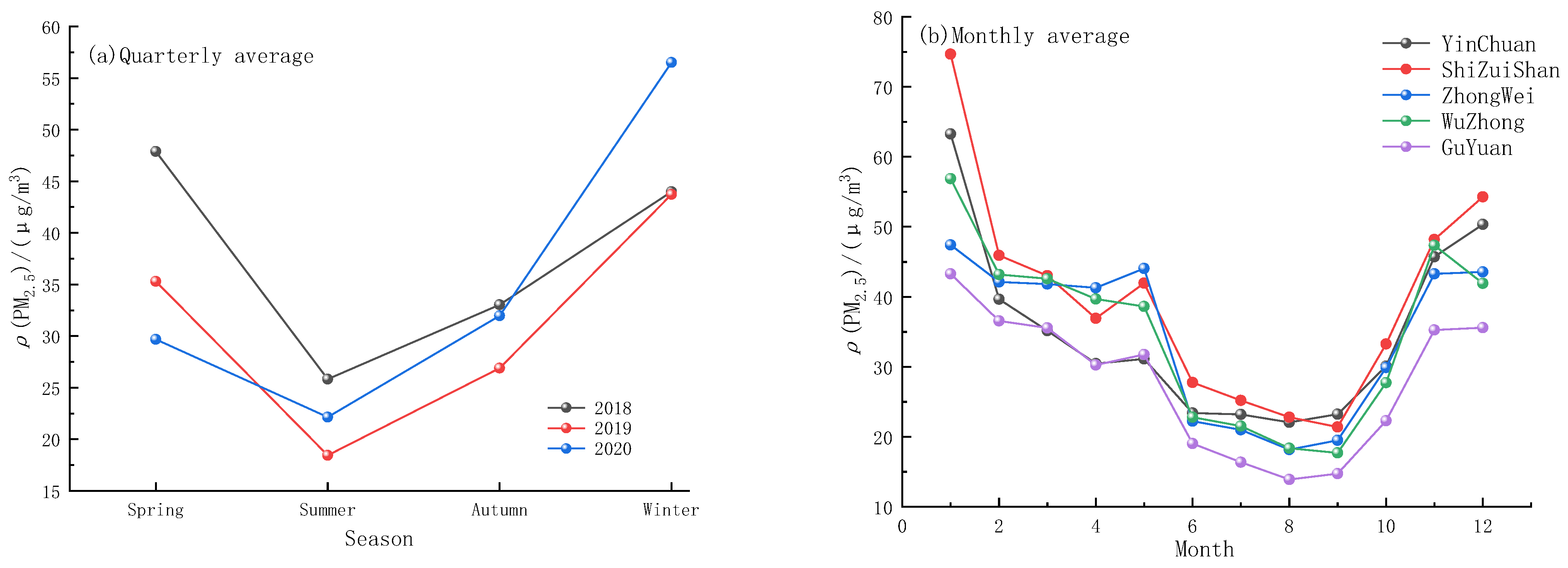
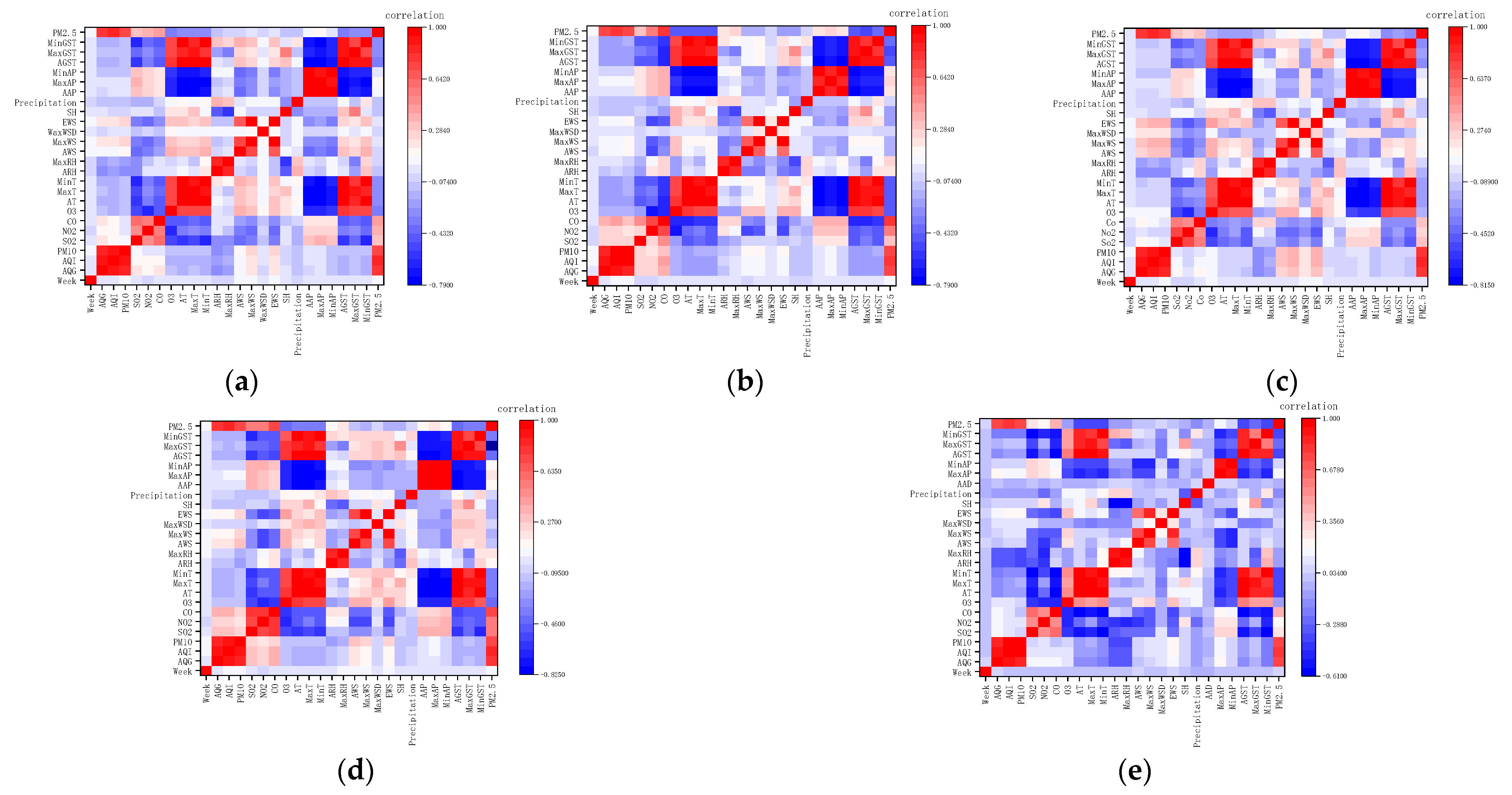


| Site Number | Monitor the Site Name | Municipal Level | Longitude | Latitude | Elevation (m) |
|---|---|---|---|---|---|
| 53614 | Yinchuan | Yinchuan City | 106°12′ | 38°28′ | 1110.9 |
| 53615 | Taole | Shizuishan City | 106°42′ | 38°48′ | 1101.6 |
| 53704 | Zhongwei | Zhongwei City | 105°11′ | 37°32′ | 1226.7 |
| 53810 | Tongxin | Wuzhong City | 105°54′ | 36°58′ | 1336.4 |
| 53817 | Guyuan | Guyuan City | 106°16′ | 36°00′ | 1752.8 |
| Statistical Indicators | Yinchuan | Shizuishan | Zhongwei | Wuzhong | Guyuan |
|---|---|---|---|---|---|
| Minimum (µg m−3) | 9 | 8 | 4 | 4 | 2 |
| Maximum (µg m−3) | 240 | 207 | 217 | 239 | 169 |
| average value (µg m−3) | 33.90 | 40.26 | 35.02 | 35.39 | 28.29 |
| standard deviation | 20.90 | 28.03 | 24.61 | 26.16 | 18.79 |
| City | Principal Component | Eigenvalue | Contribution Rate % | Cumulative Contribution Rate % |
|---|---|---|---|---|
| Wuzhong | 1 | 3.0824 | 0.3800 | 0.3800 |
| 2 | 1.8978 | 0.1441 | 0.5241 | |
| 3 | 1.6590 | 0.1101 | 0.6342 | |
| 4 | 1.4086 | 0.0794 | 0.7136 | |
| 5 | 1.1236 | 0.0505 | 0.7640 | |
| 6 | 1.0012 | 0.0401 | 0.8041 | |
| 7 | 0.9901 | 0.0392 | 0.8434 | |
| 8 | 0.9293 | 0.0345 | 0.8779 | |
| Yinchuan | 1 | 3.1003 | 0.3845 | 0.3845 |
| 2 | 1.8770 | 0.1409 | 0.5254 | |
| 3 | 1.6928 | 0.1146 | 0.6400 | |
| 4 | 1.4783 | 0.0874 | 0.7274 | |
| 5 | 1.0550 | 0.0445 | 0.7720 | |
| 6 | 1.0200 | 0.0416 | 0.8136 | |
| 7 | 0.9766 | 0.0381 | 0.8518 | |
| Zhongwei | 1 | 3.0270 | 0.3665 | 0.3665 |
| 2 | 2.0319 | 0.1651 | 0.5317 | |
| 3 | 1.6637 | 0.1107 | 0.6424 | |
| 4 | 1.4807 | 0.0877 | 0.7301 | |
| 5 | 1.1071 | 0.0490 | 0.7791 | |
| 6 | 0.9926 | 0.0394 | 0.8185 | |
| 7 | 0.9313 | 0.0347 | 0.8532 | |
| Shizuishan | 1 | 3.1661 | 0.4010 | 0.4010 |
| 2 | 1.9037 | 0.1450 | 0.5460 | |
| 3 | 1.6964 | 0.1151 | 0.6611 | |
| 4 | 1.5811 | 0.1000 | 0.7610 | |
| 5 | 1.0097 | 0.0408 | 0.8018 | |
| 6 | 0.9549 | 0.0365 | 0.8383 | |
| 7 | 0.9472 | 0.0359 | 0.8742 | |
| Guyuan | 1 | 2.7533 | 0.3032 | 0.3032 |
| 2 | 1.9831 | 0.1573 | 0.4605 | |
| 3 | 1.8137 | 0.1316 | 0.5921 | |
| 4 | 1.4256 | 0.0813 | 0.6734 | |
| 5 | 1.1952 | 0.0571 | 0.7305 | |
| 6 | 1.0271 | 0.0422 | 0.7727 | |
| 7 | 1.0165 | 0.0413 | 0.8141 | |
| 8 | 0.9750 | 0.0380 | 0.8521 |
| City | Evaluation Methods | BPNN | SVR | RF | AdaBoost | LSTM | PCA-Attention-LSTM |
|---|---|---|---|---|---|---|---|
| Wuzhong | R2 | 0.81 | 0.75 | 0.78 | 0.77 | 0.87 | 0.91 |
| MAE | 6.47 | 9.61 | 6.67 | 8.32 | 5.79 | 5.57 | |
| MSE | 140.61 | 181.92 | 157.82 | 167.86 | 97.17 | 78.49 | |
| Yinchuan | R2 | 0.90 | 0.79 | 0.89 | 0.87 | 0.91 | 0.93 |
| MAE | 4.85 | 8.12 | 5.10 | 6.50 | 4.35 | 4.07 | |
| MSE | 54.15 | 107,34 | 56.01 | 64.15 | 43.57 | 39.59 | |
| Zhongwei | R2 | 0.88 | 0.81 | 0.84 | 0.84 | 0.89 | 0.91 |
| MAE | 6.52 | 7.77 | 6.67 | 7.86 | 5.64 | 5.40 | |
| MSE | 96.12 | 111.58 | 97.41 | 93.45 | 68.02 | 54.64 | |
| Shizuishan | R2 | 0.89 | 0.83 | 0.89 | 0.87 | 0.90 | 0.91 |
| MAE | 5.98 | 8.11 | 6.08 | 6.95 | 5.28 | 4.92 | |
| MSE | 86.96 | 101.03 | 89.42 | 96.84 | 64.30 | 67.81 | |
| Guyuan | R2 | 0.87 | 0.79 | 0.85 | 0.81 | 0.87 | 0. 90 |
| MAE | 5.23 | 6.35 | 5.29 | 7.05 | 4.89 | 4.72 | |
| MSE | 59.31 | 69.91 | 62.01 | 78.32 | 57.81 | 50.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; Zhu, Y. Prediction of PM2.5 Concentration in Ningxia Hui Autonomous Region Based on PCA-Attention-LSTM. Atmosphere 2022, 13, 1444. https://doi.org/10.3390/atmos13091444
Ding W, Zhu Y. Prediction of PM2.5 Concentration in Ningxia Hui Autonomous Region Based on PCA-Attention-LSTM. Atmosphere. 2022; 13(9):1444. https://doi.org/10.3390/atmos13091444
Chicago/Turabian StyleDing, Weifu, and Yaqian Zhu. 2022. "Prediction of PM2.5 Concentration in Ningxia Hui Autonomous Region Based on PCA-Attention-LSTM" Atmosphere 13, no. 9: 1444. https://doi.org/10.3390/atmos13091444
APA StyleDing, W., & Zhu, Y. (2022). Prediction of PM2.5 Concentration in Ningxia Hui Autonomous Region Based on PCA-Attention-LSTM. Atmosphere, 13(9), 1444. https://doi.org/10.3390/atmos13091444







