Abstract
Changes in rainfall onset and cessation dates are critical for improving decision making and adaptation strategies in numerous socio-economic sectors. An objective method of determining onset and cessation date is employed over Southern West Africa (SWA) in this study. The method is applied over 34 years of the quasi-global rainfall dataset from the Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS) and five High Resolution Model Intercomparison Project (HighResMIP) model datasets under the Coupled Model Intercomparison Project Phase 6 (CMIP6) experiment. Generally, a strong agreement exists between CHIRPS and the HighResMIP models in capturing the behaviour of seasonal rainfall over SWA, with models able to capture the bimodal rainfall season. The ability of models in capturing onset and cessation dates as observed in CHIRPS shows the strength of these models in representing the short break between the two wet seasons that is otherwise known as the ‘Little Dry Season’. Patterns observed in the onset and cessation dates over the SWA region are consistent with the northward and southward displacement of the Intertropical Convergence Zone (ITCZ). The seasonal timing of the models shows good agreement with observations such that most mean onset/cessation dates agree within 26 days. While IPSL-CM6A-ATM-HR, a model among the five HighResMIPs used in the study, best agrees with CHIRPS in representing onset and cessation dates during the unimodal rainfall season, no one model best agrees with CHIRPS during the bimodal season, with models outperforming each other in representing onset/cessation dates with little variation.
1. Introduction
The economy of many sectors (e.g., hydroelectric power generation, industries, health, and agriculture) in Southern West African countries (including Benin, Ghana, and the Ivory Coast) rely on climate information to function efficiently. For instance, hydroelectric power generation and agriculture are typically rain fed and thus are heavily reliant on rainfall information such as onset, cessation, intensity, and frequency of rainfall.
The climate of Southern West Africa (SWA) is mainly driven by the West African monsoon (WAM; []). The timing of the seasonal cycle determines the length of the growing season and agricultural yields [] and this is critical for agriculture and food security in the region. The region has been identified to have low adaptive capacity to the impacts of climate change, making it one of the most vulnerable regions according to the Intergovernmental Panel on Climate Change []. Recent studies [,,,,,] have also pointed out the likelihood of more extreme rainfall events over the region, which may possibly lead to increased incidences of flooding. Thus, understanding the possible changes in rainfall onset and cessation dates is critical for improving decision making and adaptation strategies in numerous socio-economic sectors of countries in SWA.
Generally, low- to medium-resolution global climate models (GCMs) have shown notable deficiencies in simulating seasonal rainfall in West Africa [,,]. This has frequently been attributed to the absence of the regional drivers of rainfall, such as the role of vegetation and orography in these GCMs [] and also the correct representation of Sea Surface Temperature (SST) patterns along the Guinea Coast []. Consequently, the GCMs have difficulty in reproducing rainfall associated with synoptic, sub-synoptic, and mesoscale convective systems [,,]. This difficulty has led climate scientists to often use statistical or dynamical downscaling techniques to improve the resolution of such models to produce useful regional climate information. However, this information from downscaled GCMs can often have high uncertainties as a result of uncertainties from driving GCMs and/or the poor resolution of large-scale processes by the regional climate model under certain conditions [,,,].
Studies on onset and cessation determination over West Africa have mainly used empirical models [,,]. Ref. [] also pointed out that the forecasting of onset relied on the interannual variability of certain atmospheric and climate factors that are known to influence onset and cessation determination, such as the African Easterly Jet (AEJ), the Tropical Easterly Jet (TEJ), and the Sahara Heat Low. Due to the low forecast skills of empirical models and their inability to account for these important factors driving the WAM dynamics, recent studies have resorted to using dynamic climate models to understand and improve onset and cessation information over West Africa [,]. Ref. [] proposed a methodology to objectively analyse onset and cessation dates. This methodology is an extension of a method proposed earlier by []. Ref. [] presents a robust methodology that is able to identify regimes over regions with timing biases where the use of the standard meteorological seasons may underestimate the seasonal cycle. The reader is referred to the methods section and additionally to [] for more information on the technique.
Recently, some modelling groups participating in the Coupled Model Intercomparison Project, Phase 6 (CMIP6; []) have focused on addressing this challenge of uncertainties and biases from downscaling by introducing the High-Resolution Model Intercomparison Project (HighResMIP) which is geared towards improving regional climate information from the models [,]. It is asserted that these HighResMIP simulations have the ability to simulate mesoscale convective systems and represent multi-scale interactions that may not be well represented by the low- to medium-resolution GCMs [,]. Ref. [] has explored the impact of the higher resolution of HighResMIP models on the West African climate and found that high-resolution GCMs without regional components such as topography, vegetation, or waterbodies may be biased in providing accurate and regionally resolved climate information.
This study examines how a set of HighResMIP models that participated in the CMIP6 experiment captured onset and cessation information over SWA using the methodology proposed by []. The paper is organised as follows: Section 2 summarises the data and methods used in the study, while in Section 3 the results are discussed and concluded in Section 4.
2. Data and Methods
2.1. Observation Data and Model Output
Long records of gauge-based observed daily precipitation data are a scarce resource (particularly in parts of the tropics) and are only available over limited land regions. Due to the scarcity of gauge-based observational precipitation datasets over SWA, data from the Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS) were used in this study as the observation data for the validation of the GCMs to reproduce precipitation. CHIRPS is a quasi-global rainfall dataset. The main aim of CHIRPS is to monitor meteorological hazards, especially drought events []. CHIRPS is made up of many inputs, namely, the monthly precipitation climatology CHPclim, thermal infrared measurements from geostationary satellites issued from National Oceanic and Atmospheric Administration-Climate Prediction Centre, the National Climatic Data Centre, and Tropical Rainfall Measurement Mission 3B42. These inputs are merged with in situ rain gauge observation data to estimate precipitation. CHIRPS extends over the band of 50° N and 50° S latitude, with a spatial resolution of 0.05° for daily observation and 0.25° for monthly coverage. It provides daily, pentad, and monthly precipitation from 1981 to present. To overcome uncertainties that may result from the scarcity of rain gauge observation, blended station data have been added to CHIRPS to enhance its performance []. CHIRPS was used to assess how the high-resolution GCMs simulate onset and cessation dates over the study area. Based on previous studies by [,,], the mean precipitation of West Africa from the CHIRPS dataset shows a similar performance when compared with the commonly used satellite products such as CMORPH, PERSIANN, and TRMM at the monthly and seasonal time scales. There has been the recognition of a satisfactory replication of the seasonal trends (1981–2015) of the mean precipitation and the number of wet days from the CHIRPS dataset against 18 daily rain gauge stations across the Guinea Coast and the Sahel [,]. An exception was mentioned, however, along the Guinea Coast that the CHIRPS dataset shows a tendency towards more (less) frequent and less (more) intense precipitation during both rainy seasons (during the first rainy season) when compared with the rain gauge stations [,].
The study also incorporates historical simulations from five (5) high-resolution models covering the period 1950–2014 (Table 1). These datasets are archived on the Earth System Grid Federation (ESGF) portal under CMIP6 HighResMIP, which can be found at https://esgf-node.llnl.gov/search/cmip6/, accessed on 18 February 2021. The HighResMIP model dataset is an approved CMIP6 model inter-comparison effort designed mainly to assess the role of model resolution in the representation of relevant climate processes. The HighResMIP experimental design comprises both atmospheric-only and coupled simulations performed at standard (~100 km or coarser) and enhanced (~25 km) horizontal resolution in the atmosphere and the ocean. Here, 65-year simulations of the forced atmosphere experiment that cover the present climate are considered, in which observed sea surface temperature, sea–ice concentration, and incoming radiation are used as forcings. This type of experiment under HighResMIP is known as ‘HighRes-SST-present’. Within these model experiments, only models having a ‘365 day’ calendar year and also possessing a resolution with grid spacings of 50 km or finer were used due to the nature of the indices calculated. Based on the selection criterion employed for robust analysis, only 5 of the CMIP6 HighResMIP models were suitable (Table 1).

Table 1.
Details of the 5 CMIP6 HighResMIP models used in this study.
The datasets were re-gridded using bilinear interpolation to a common 0.5° × 0.5° grid to enable comparison in multi-models. Onset and cessation dates of rainfall seasons were calculated after re-gridding. For these simulations, onset and cessation dates were calculated over the 34-year period 1981 to 2014 due to CHIRPS being available only from 1981 and also the historical simulations of the HighResMIP models ending in 2014.
2.2. Methodology for Identifying Onset and Cessation of Rainfall Seasons
To calculate the onset and cessation dates for the unimodal and bimodal regimes, the methodology of [], which is an extension to the methodology of [] to produce a precipitation climatology over the African continent, was used.
The processes for calculating onset dates are in three phases, with full subtleties laid out in []. To begin with, harmonic analysis was used to categorise the number of rainfall seasons experienced in a year. The rainfall regime at each grid point is categorised as being dominantly unimodal (one rainfall season per year) or bimodal regime (two rainfall seasons per year). This is accomplished by computing the ratio of the amplitude of the second harmonic to the first harmonic. If the ratio is greater than 0.75, the amplitude of the second harmonic is larger, and the grid point is classified as having a bimodal rainfall regime. If the ratio is less than 0.75, the grid point is classified as having a unimodal rainfall regime. This is marked in Figure 1 as a contour line. The second harmonic is relatively large generally near the equator and portrays the two wet seasons that occur following the two crossings of the solar zenith []. The harmonic analysis approach used in this study is similar to that used in [,] to analyse the number of wet seasons per year over Africa, although [] used a threshold ratio of 0.75 over monthly rather than daily precipitation data and [] used a threshold ratio of 1.0. The threshold ratio value of 0.75 is chosen due to its sensitivity to the unimodal and bimodal rainfall regimes. Choosing a lower threshold ratio (less than 0.75) means some regions observing a unimodal rainfall regime become part of R1, making it challenging to refer to all grid points under R1 as bimodal. On the other hand, a larger threshold ratio (greater than 0.75) means region R1 becomes smaller, with part of R1 merging with R2. The choice of the selected threshold ratio (here 0.75) is seen, in this instance, to better represent the two regimes with little or no overlapping over Southern West Africa.
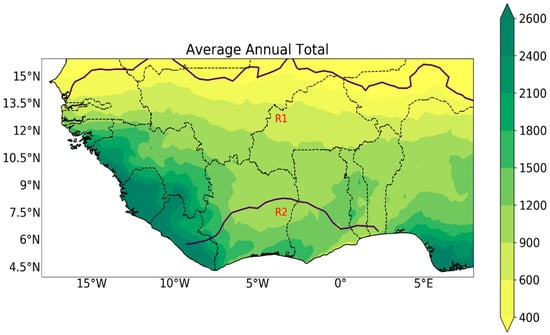
Figure 1.
Annual average precipitation (mm) from 1981 to 2014 from CHIRPS data. Region R1 indicates unimodal regions, while region R2 represents areas defined as bimodal regions for each grid point in CHIRPS based on the ratio of the amplitudes of the first two harmonics. A ratio greater than 0.75 indicated a bimodal point and a ratio less than 0.75 indicated a point with a unimodal regime.
Furthermore, a process to identify minima and maxima in the climatological cumulative daily mean rainfall anomaly is carried out to determine when the rainfall season occurs in a calendar year. The climatological cumulative daily mean rainfall anomaly is determined by initially computing the climatological mean rainfall for each day of the calendar year and the long-term climatological daily mean rainfall. The climatological period of the two rainy seasons for areas with a bimodal regime is identified using the extension in the method of [] presented in []. Onset and cessation dates are finally determined for each season and year by computing the daily cumulative rainfall anomaly in each season and the minima and maxima in the daily cumulative rainfall anomaly.
Analysis of mean onset and mean cessation dates were carried out for both unimodal and bimodal rainfall regimes to compare the CMIP6 HighResMIP models with the CHIRPS observations using Taylor diagrams. Taylor diagrams are most useful in gauging the relative skill of many different models []. This was done to assess the statistical performance of how closely models match observation patterns in terms of the correlation, the amplitude of variations (represented by the standard deviation), and the centred root-mean-square (RMS) difference. Correlations, RMS difference, and standard deviations are calculated based on the observed (here CHIRPS) over a specified region under R1 and R2 for a fair comparison. The correlation coefficient and the RMS difference provide corresponding statistical information quantifying the relationship between two patterns. The variances (or standard deviations) of fields are also given for a more complete characterisation of the fields. Considering two variables, mn and rn, which are defined at N discrete points (in time and/or space), the correlation coefficient R between m and r is defined as
and the centred pattern RMS difference is defined by
where and are the mean values and and are the standard deviations of m and r, respectively. The standard deviations of the model field () and the observation field () are given by
and
3. Study Area
The SWA region was divided into two regions such that each represents a consistent unimodal or bimodal regime across all data sets (Figure 1). Region R1 experiences a unimodal regime while region R2 experiences a bimodal regime (Figure 1). Precipitation over the SWA is mostly rainfall and so the two words (rainfall and precipitation) will be used interchangeably.
4. Results and Discussion
The map of annual mean precipitation based on CHIRPS data (1981–2014) to show the spatial distribution of precipitation over the years is analysed (Figure 1). Regions occupying the north of 15° N receive less than 500 mm yr−1 of precipitation, while the wettest areas located south of 10° N realise an average of 1500 mm yr−1 of precipitation. Areas with maximum rainfall in West Africa are observed mostly in regions with high altitudes such as the Guinea Highlands and Mount Cameroon.
4.1. Characteristics of the Rainfall Regime
The representation of the unimodal and bimodal rainfall regimes in the observation and model simulations is explored. In West Africa, a bimodal rainfall regime is observed over a small region that lies on the coast [].
4.2. Unimodal Rainfall Regime
From Figure 2 and Figure 3, good agreement is observed between the observation dataset (CHIRPS) and the CMIP6 HighResMIP datasets with respect to the onset and cessation dates. Onset dates generally are observed between late March and late June over regions with unimodal rainfall patterns, marking the start of the monsoon. Onset dates agree closely with that observed by [,] using different definitions for onset. The rainfall season starts close to the southernmost coast of West Africa in early March. Figure 2 shows that onset dates for MRI-AGCM3-2-S, EC-Earth3P-HR, CAMS-CSM1-0, and IPSL-CM6A-ATM-HR agree closely with CHIRPS, while in Figure 3 all models show good agreement in representing cessation dates as observed in CHIRPS. The general meridional progression of onset and cessation dates across the region is seen as ‘late onset’ as rainfall progresses northward and ‘late cessation’ as rainfall progress south. The observed late start in onset dates as the rainfall progresses north has been associated with the delay transport of moisture into the continent due to the processes of the West African Monsoon [,,].
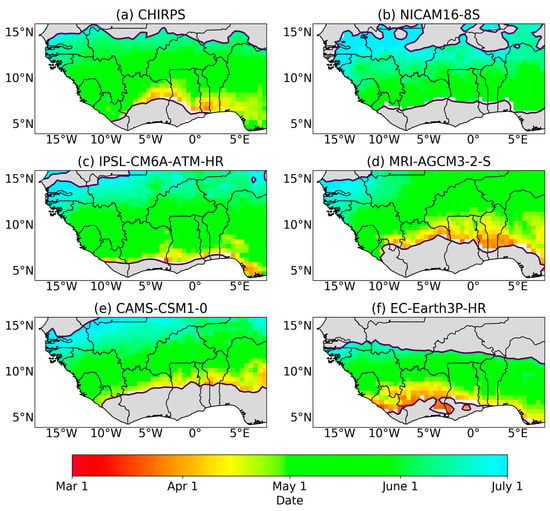
Figure 2.
Mean onset date for unimodal regime regions for all data sets. Dark grey at the south indicates regions with bimodal regimes and grey at the north indicates dry regions.
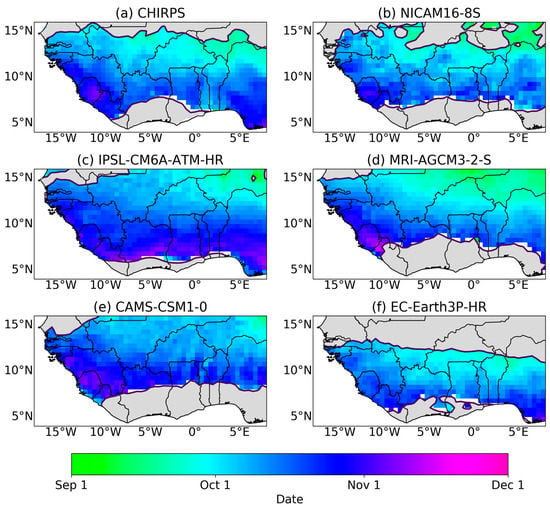
Figure 3.
Mean cessation date for unimodal regime regions for all data sets. Dark grey at the south indicates regions with bimodal regimes and grey at the north indicates dry regions.
4.3. Statistical Evaluation of Models for the Unimodal Rainfall Regime
To investigate the performance of the CMIP6 HighResMIP models, Taylor diagrams were constructed to provide a graphical summary of how close models behave with respect to observations. The similarities between CHIRPS and selected CMIP6 HighResMIP are quantified in terms of their spatial correlation, their centred root mean square (RMS) difference, and the amplitude of their spatial variations (represented by their spatial standard deviations).
Figure 4 depicts how close models simulate onset and cessation dates of rainfall as compared with observations. It is evident from the statistical evaluations that all CMIP6 HighResMIP models have a low pattern correlation of r < 0.5, with MRI-AGCM3-2-S recording the highest r of about 0.26 (Figure 4a). IPSL-CM6A-ATM-HR agrees well with CHIRPS in capturing onset dates in the unimodal rainfall regime having the smallest root mean square error of about 9.1 days and a slightly higher spatial variability (with a standard deviation of about 7.5 days compared with the observed value of 6.2 days), with EC-Earth3P-HR and MRI-AGCM3-2-S giving a close performance as IPSL-CM6A-ATM-HR in capturing onset dates. On the poor performing models, CAMS-CSM1-0 depicts much larger variations when compared with CHIRPS, resulting also in a relatively large (about 12.2 days) centred root mean square error in capturing onset dates.
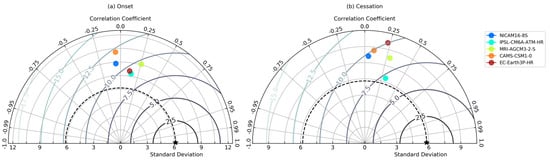
Figure 4.
Statistical evaluation of models using Taylor diagram analysis to show the coefficient of correlation, standard deviation, and centred root mean square error for (a) onset and (b) cessation over region R1. Different coloured dots represent different datasets as described in the legend. Five-pointed star represents the observational dataset.
For the cessation of rainfall, although all models show very low pattern correlations, IPSL-CM6A-ATM-HR presents a similar standard deviation to CHIRPS (Figure 4b). IPSL-CM6A-ATM-HR agrees best with the observation data in capturing cessation dates, followed closely by MRI-AGCM3-2-S shown by their small root mean square errors. CAMS-CSM1-0, EC-Earth3P-HR, and NICAM16-8S weakly capture cessation dates with all observing equal root mean square errors a little above the good performing models when compared with CHIRPS and a very high amplitude in variations, specifically in EC-Earth3P-HR. There is not much of a difference in RMS values across models.
4.4. Bimodal Rainfall Regime
The SWA region experiences a bimodal rainfall season with two wet seasons per year. Figure 5 and Figure 6 show the mean onset and cessation for the first (major) rainfall season, respectively. It is evident from the figures that all models show onset and cessation periods for bimodal regions along SWA, indicating that the models are capturing the biannual regime, which is not always captured in model simulations []. The biannual region in these CMIP6 models, however, is found to cover a larger region (Sierra Leone through to Nigeria for NICAM16-8S, MRI-AGCM3-2-S, and CAMS-CSM1-0, and central Sierra Leone to eastern Benin for IPSL-CM6A-ATM-HR and EC-Earth3P-HR) than the smaller biannual region that is depicted by observations (from eastern Sierra Leone to Togo for CHIRPS). We find that the mean onset and cessation dates for the first (major) rainfall season are well captured by the models (late March and late July, respectively) with a late start (early May) for NICAM16-8S and a late cessation (late July) in MRI-AGCM3-2-S. Patterns observed from the CHIRPS observation dataset are similar to findings from [,].
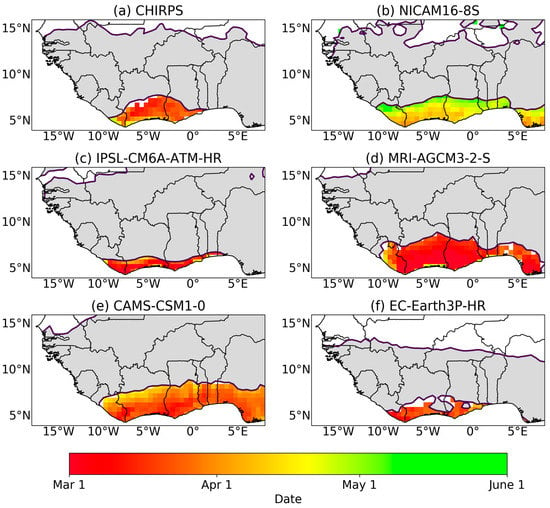
Figure 5.
Mean onset date for first (major) rains for all data sets. Dark grey indicates regions with a unimodal regime and white indicates dry regions.
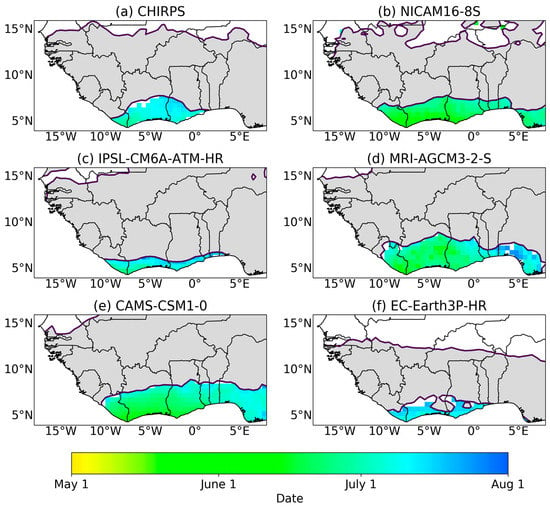
Figure 6.
Mean cessation date for first (major) rains for all data sets. Dark grey indicates regions with a unimodal regime and white indicates dry regions.
For the second (minor) rainfall season, some differences are observed in onset dates as compared with cessation dates which have subtle differences (Figure 7 and Figure 8). Onset dates are observed to be between late August and late September for observations, which is also found in EC-Earth3P-HR over the majority of the region, but NICAM16-8S, IPSL-CM6A-ATM-HR, and CAMS-CSM1-0 observe onsets of the minor rainfall season from late September to late October for the majority of the region, with small portions of the region recording onsets of late August. The ability of models in capturing onset dates as observed in CHIRPS depicts the strength of these models in representing the short break between the two wet seasons which is otherwise known as the ‘Little Dry Season’. This indicates that the majority of the models are reliable in representing seasonal rainfall over SWA. Cessation dates are observed to have a subtle variation between early November and late November.
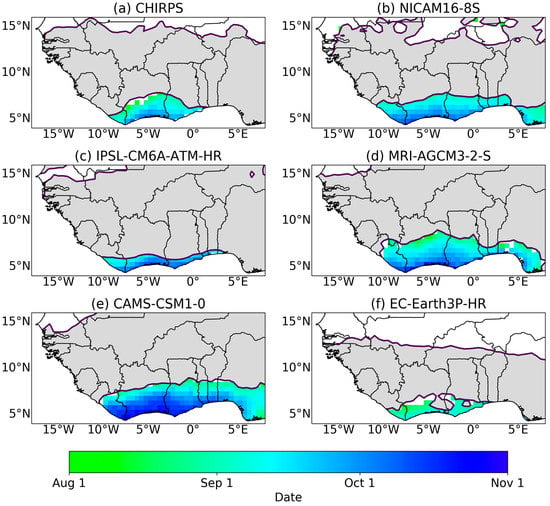
Figure 7.
Mean onset date for second (minor) rains for all data sets. Dark grey indicates annual regimes and white indicates dry regions.
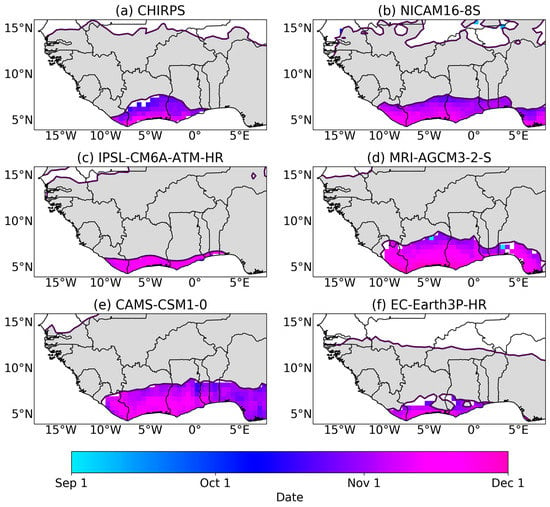
Figure 8.
Mean cessation date for second (minor) rains for all data sets. Dark grey indicates annual regimes and white indicates dry regions.
It is evident from the statistical evaluations that most CMIP6 HighResMIPs have a low pattern correlation of r < 0.5 compared with CHIRPS during the first onset and second cessation of rains (Figure 9a,d), suggesting the difficulty of the models in simulating onset of the major rainfall season and cessation of the minor rainfall season. All models reproduce similar but little spatial variability compared with CHIRPS in representing the onset dates (Figure 9a). However, MRI-AGCM3-2-S agrees well with CHIRPS, having the smallest root mean square error in capturing onset dates during the first (major) bimodal rainfall regime. EC-Earth3P-HR and IPSL-CM6A-ATM-HR poorly pick up the onset date signals, with the former having a very high RMS error and the latter exhibiting a much lower amplitude of the variation (i.e., the standard deviation) when compared with CHIRPS. In Figure 9b, although models EC-Earth3P-HR, MRI-AGCM3-2-S, and IPSL-CM6A-ATM-HR perform very well in capturing the cessation dates in the first (major) rainfall regime, with the models observing remarkably close spatial variations to that of the observation, EC-Earth3P-HR is highly correlated with the observation, and this results in a relatively low root mean square error in EC-Earth3P-HR. On the poor performance of models, although all models show relatively good correlation with CHIRPS, NICAM16-8S and CAMS-CSM1-0 both show variations much smaller (~8 days) than the observation (~12 days), while MRI-AGCM3-2-S and IPSL-CM6A-ATM-HR show high centred root mean square error capturing cessation dates in the first (major) rainfall regime.
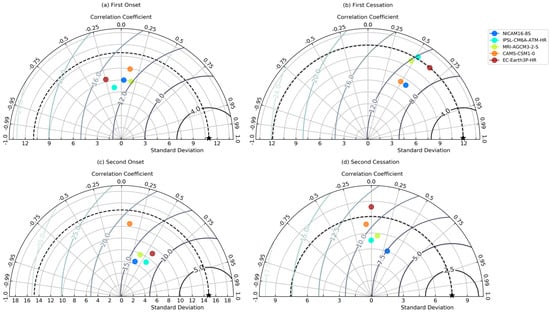
Figure 9.
Statistical evaluation of models using Taylor diagram analysis to show the coefficient of correlation, standard deviation, and centred root mean square error of (a) first onset, (b) first cessation, (c) second onset, and (d) second cessation over region R2. Different colour dots represent different datasets as described in the legend. Five-pointed star represents the observational dataset.
During the onset of the second (minor) rainfall regime, it can be seen that IPSL-CM6A-ATM-HR and EC-Earth3P-HR generally agree best with CHIRPS, with both recording similar RMS error of about 12 days and both models also have a relatively high correlation (Figure 9c). CAMS-CSM1-0, however, simulates the amplitude of the variations much better than the other models while observing the highest RMS error. For the cessation dates in the second (minor) rainfall regime, it can be seen that models EC-Earth3P-HR and CAMS-CSM1-0 simulate better the amplitude of the variations than other models (Figure 9d). NICAM16-8S, although having much lower variations, agrees well with the observation due to its small RMS error and its relatively high pattern correlation.
4.5. Interannual Variability in Observations and CMIP6 HighResMIP over West Africa
Notable differences in onset and cessation dates can be observed in the time series analysis of rainfall events over the region (Figure 10). The interannual variability over region R1 (regions with unimodal rainfall regime) indicates an earlier onset in MRI-AGCM3-2-S, with a mean onset date of 6 May and a late mean onset date of 4 June in NICAM16-8S, with all other datasets recording mean onset dates between 14 May and 20 May (Figure 10a). Less variability is observed in cessation dates, with EC-Earth3P-HR exhibiting an early cessation at the beginning of October and the latest cessation in IPSL-CM6A-ATM-HR around mid-October.
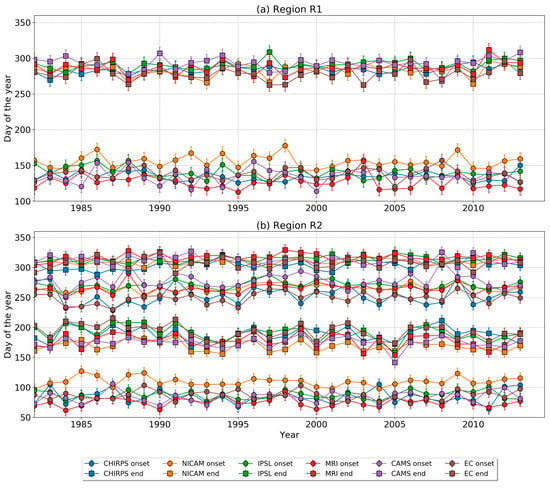
Figure 10.
Time series of mean onset and cessation over regions (a) R1 and (b) R2. Different coloured lines indicate different data sets. The error bars show the standard deviation in onset/cessation across the region at each time.
Regions that observe the bimodal rainfall regime show an early onset in MRI-AGCM3-2-S, with the mean onset date of 16 March, and the NICAM16-8S showing a late mean onset date of 19 April for the major rainfall period (Figure 10b). The rainfall cessation for the major rain season observes the CHIRPS mean cessation date around 8 July, with EC-Earth3P-HR recording a late mean cessation date of 13 July. NICAM16-8S, MRI-AGCM3-2-S, and CAMS-CSM1-0 observe an earlier cessation, with NICAM16-8S recording a cessation date as early as 18 June.
In the minor rainfall season, EC-Earth3P-HR observes an early mean onset date of 6 September, CAMS-CSM1-0 observes a late mean onset date of 4 October, while all other models recorded mean onset dates between 22 September and 27 September. The cessation dates observed in the minor rainfall regime are observed to be between 31 October and 12 November for both observation and models, with MRI-AGCM3-2-S recording a late cessation date.
The length of the wet season is shown in Figure 11. The time series from Figure 11a, shows that CHIRPS records a longer mean wet season annually of about 150 days, with IPSL-CM6A-ATM-HR observing the same length in the wet season in region R1. NICAM16-8S observes the shortest length in rainy days over areas with a unimodal rainfall season, with a mean length of about 127 days. This is possible due to the late start and early cessation of rainfall in NICAM16-8S. MRI-AGCM3-2-S, on the other hand, witnessed the longest period of rainy days. In Figure 11b, it can be observed that for the major rainy season during the bimodal regime, the mean length of days from observation was about 105 days, with EC-Earth3P-HR overestimating the mean length in rainy days by 3 days. NICAM16-8S continues to perform poorly in capturing the early onset in the observation, therefore realising a time lag of over a month to CHIRPS.
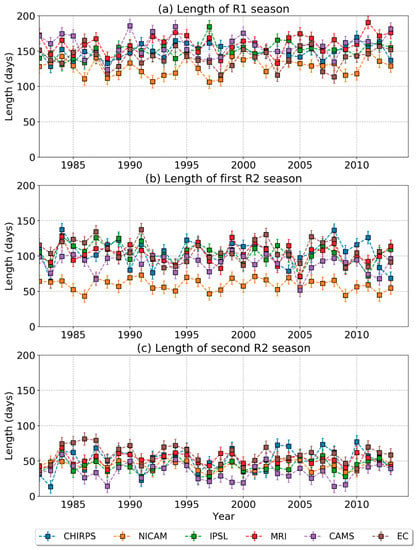
Figure 11.
Time series of the length of the rainy season for (a) regions with annual rainfall, (b) first rainy season, and (c) second rainy season. Different coloured lines indicate different data sets. The error bars show the standard deviation in length of the rainy season across the region at each time.
For the minor rainfall season, it is observed that the length of the wet season varies largely over time, with most models lasting a few days shorter than the observation (Figure 11c). This reflects the earlier onset of rainfall in EC-Earth3P-HR (as observed in CHIRPS) during the second rainy season of the bimodal regime. The variations observed between CHIRPS and CMIP6 HighResMIP models can be attributed to the differing onset dates, since there are similarities in their cessation dates (Figure 11b).
5. Summary and Conclusions
The performance of CMIP6 HighResMIP models, which have been forced by observed SSTs, in capturing onset and cessation of seasonal rainfall across Southern West Africa were evaluated against CHIRPS. This was achieved by applying a robust method of calculating onset and cessation dates using cumulative daily mean precipitation anomalies for quantifying seasonal rainfall [,].
We find that, generally, regions (R1 and R2) with early onset dates coincide with areas that experience maximum rainfall along the coast of West Africa (Figure 1). It is noteworthy that all the datasets show good agreement in capturing onset and cessation dates during both unimodal and bimodal rainfall regimes, especially in the southern part of West Africa. This depicts the ability of high-resolution models in representing the seasonal cycle of rainfall due to their ability in capturing similar patterns of seasonal rainfall over SWA, although there exist differences in their spatial extent. The timing of the rainfall season over SWA depicts a northward progression of onset dates and a southward progression of cessation dates. The coast of SWA that exhibits the bimodal regime receives a relatively high amount of rainfall, with a region characterised by reduced rainfall amounts separating the two seasons. Onset/cessation patterns observed over the SWA region are consistent with the northward and southward displacement of the ITCZ. The forced atmosphere experiments represent the bimodal rainfall regime well over the coast SWA. Seasonal timing in the SST forced atmosphere simulations shows good agreement with observations, such that most mean onset/cessation dates agree within 26 days, with MRI-AGCM3-2-S exhibiting an early onset of the major season (~9 days early) and NICAM16-8S displaying a late onset of about 25 days. NICAM16-8S exhibits an early cessation as compared with observation (~25 days early), and EC-Earth3P-HR shows about 5 days delay in cessation in the major rainfall season. Similar agreements existed during the minor season, with EC-Earth3P-HP presenting an early onset of about 3 days and CAMS-CSM1-0 presenting a late onset (~25 days late).
Using Taylor diagrams, we were able to quantitatively determine how well HighResMIP datasets compare with observation in representing the onset and cessation of rainfall. Most of the GCM models had a relatively low correlation with the observation dataset. While IPSL-CM6A-ATM-HR best agrees with CHIRPS in representing onset and cessation dates in the unimodal rainfall region, the models outperform each other in representing onset/cessation dates in the bimodal rainfall season with little variation. This means that no immediate conclusion can be arrived at as to which model simulation best represents onset/cessation dates in Southern West Africa during the bimodal rainfall regime. It is encouraging to note, however, that the seasonal cycle of rainfall based on onset and cessation is typically consistent among models. This demonstrates that high-resolution models can be employed in the understanding of seasonal rainfall in SWA to enhance future climate predictions based on climate change projections.
Author Contributions
Conceptualization, F.N; methodology and software, C.W. and F.N; validation, G.M.L.D.Q., F.N., K.A.Q.; formal analysis, F.N., K.T.Q. and G.M.L.D.Q.; investigation, F.N. and C.W.; resources, F.N. and C.W.; data curation, F.N.; writing—original draft preparation, F.N; writing—review and editing, N.A.B.K., K.A.Q. and A.A.; visualization, F.N., K.T.Q.; supervision, N.A.B.K.; project administration, N.A.B.K.; funding acquisition, F.N. and N.A.B.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by a grant from the Government of Canada, provided through Global Affairs Canada, www.international.gc.ca (accessed on 1 January 2021), and the International Development Research Centre, www.idrc.ca, (accessed on 1 June 2022) to the African Institute for Mathematical Sciences—Next Einstein Initiative (AIMS-NEI) [Number: 108246-001]. Caroline Wainwright acknowledges funding of the Grantham Research Fellowship from the Grantham Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
CHIRPS: https://data.chc.ucsb.edu/products/CHIRPS-2.0/africa_daily/ (accessed on 2 May 2021). CMIP6 HighResMIP: https://esgf-node.llnl.gov/search/cmip6/ (accessed on 18 February 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fink, A.H.; Engel, T.; Ermert, V.; van der Linden, R.; Schneidewind, M.; Redl, R.; Afiesimama, E.; Thiaw, W.M.; Yorke, C.; Evans, M.; et al. Mean Climate and Seasonal Cycle. In Meteorology of Tropical West Africa: The Forecasters’ Handbook; John Wiley & Sons: Chichester, UK, 2017; pp. 1–39. [Google Scholar]
- Vizy, E.K.; Cook, K.H.; Chimphamba, J.; McCusker, B. Projected changes in Malawi’s growing season. Clim. Dyn. 2015, 45, 1673–1698. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar] [CrossRef] [Green Version]
- Engel, T.; Fink, A.H.; Knippertz, P.; Pante, G.; Bliefernicht, J. Extreme Precipitation in the West African Cities of Dakar and Ouagadougou: Atmospheric Dynamics and Implications for Flood Risk Assessments. J. Hydrometeorol. 2017, 18, 2937–2957. [Google Scholar] [CrossRef]
- Lafore, J.-P.; Beucher, F.; Peyrillé, P.; Diongue-Niang, A.; Chapelon, N.; Bouniol, D.; Caniaux, G.; Favot, F.; Ferry, F.; Guichard, F.; et al. A multi-scale analysis of the extreme rain event of Ouagadougou in 2009. Q. J. R. Meteorol. Soc. 2017, 143, 3094–3109. [Google Scholar] [CrossRef]
- Maranan, M.; Fink, A.H.; Knippertz, P.; Francis, S.D.; Akpo, A.B.; Jegede, G.; Yorke, C. Interactions between Convection and a Moist Vortex Associated with an Extreme Rainfall Event over Southern West Africa. Mon. Weather Rev. 2019, 147, 2309–2328. [Google Scholar] [CrossRef]
- Nkrumah, F.; Vischel, T.; Panthou, G.; Klutse, N.A.B.; Adukpo, D.C.; Diedhiou, A. Recent Trends in the Daily Rainfall Regime in Southern West Africa. Atmosphere 2019, 10, 741. [Google Scholar] [CrossRef] [Green Version]
- Klutse, N.A.B.; Ajayi, V.O.; Gbobaniyi, E.O.; Egbebiyi, T.S.; Kouadio, K.; Nkrumah, F.; Dosio, A. Potential impact of 1.5 C and 2 C global warming on consecutive dry and wet days over West Africa. Environ. Res. Lett. 2018, 13, 055013. [Google Scholar] [CrossRef]
- Klutse, N.A.B.; Quagraine, K.A.; Nkrumah, F.; Berkoh-Oforiwaa, R.; Dzrobi, J.F.; Sylla, M.B. The Climatic Analysis of Summer Monsoon Extreme Precipitation Events over West Africa in CMIP6 Simulations. Earth Syst. Environ. 2021, 5, 25–41. [Google Scholar] [CrossRef]
- Dunning, C.M.; Allan, R.P.; Black, E. Identification of deficiencies in seasonal rainfall simulated by CMIP5 climate models. Environ. Res. Lett. 2017, 12, 114001. [Google Scholar] [CrossRef]
- Hourdin, F.; Musat, I.; Guichard, F.; Ruti, P.M.; Favot, F.; Filiberti, M.; Marquet, P. AMMA-Model Intercomparison Project. Bull. Am. Meteorol. Soc. 2010, 91, 95–104. [Google Scholar] [CrossRef]
- Xue, Y.; De Sales, F.; Lau, W.K.-M.; Boone, A.; Feng, J.; Dirmeyer, P.; Guo, Z.; Kim, K.-M.; Kitoh, A.; Kumar, V.; et al. Intercomparison and analyses of the climatology of the West African Monsoon in the West African Monsoon Modeling and Evaluation project (WAMME) first model intercomparison experiment. Clim. Dyn. 2010, 35, 3–27. [Google Scholar] [CrossRef] [Green Version]
- Raj, J.; Bangalath, H.K.; Stenchikov, G. West African Monsoon: Current state and future projections in a high-resolution AGCM. Clim. Dyn. 2019, 52, 6441–6461. [Google Scholar] [CrossRef] [Green Version]
- Wainwright, C.M.; Hirons, L.C.; Klingaman, N.P.; Allan, R.P.; Black, E.; Turner, A.G. The impact of air–sea coupling and ocean biases on the seasonal cycle of southern West African precipitation. Clim. Dyn. 2019, 53, 7027–7044. [Google Scholar] [CrossRef] [Green Version]
- Samanta, D.; Karnauskas, K.B.; Goodkin, N.F. Tropical Pacific SST and ITCZ Biases in Climate Models: Double Trouble for Future Rainfall Projections? Geophys. Res. Lett. 2019, 46, 2242–2252. [Google Scholar] [CrossRef] [Green Version]
- Klutse, N.A.B.; Abiodun, B.J.; Hewitson, B.; Gutowski, W.J.; Tadross, M. Evaluation of two GCMs in simulating rainfall inter-annual variability over Southern Africa. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2016, 123, 415–436. [Google Scholar] [CrossRef]
- Gusain, A.; Ghosh, S.; Karmakar, S. Added value of CMIP6 over CMIP5 models in simulating Indian summer monsoon rainfall. Atmos. Res. 2020, 232, 104680. [Google Scholar] [CrossRef]
- Lazenby, M.; Todd, M.; Wang, Y. Climate model simulation of the South Indian Ocean Convergence Zone: Mean state and variability. Clim. Res. 2016, 68, 59–71. [Google Scholar] [CrossRef] [Green Version]
- Pinto, I.; Jack, C.; Hewitson, B. Process-based model evaluation and projections over southern Africa from Coordinated Regional Climate Downscaling Experiment and Coupled Model Intercomparison Project Phase 5 models. Int. J. Clim. 2018, 38, 4251–4261. [Google Scholar] [CrossRef]
- Leduc-Leballeur, M.; de Coëtlogon, G.; Eymard, L. Air-sea interaction in the Gulf of Guinea at intraseasonal time-scales: Wind bursts and coastal precipitation in boreal spring. Q. J. R. Meteorol. Soc. 2013, 139, 387–400. [Google Scholar] [CrossRef]
- Dodd, D.E.; Jolliffe, I.T. Early detection of the start of the wet season in semiarid tropical climates of western Africa. Int. J. Clim. 2001, 21, 1251–1262. [Google Scholar] [CrossRef]
- Omotosho, J.B.; Balogun, A.; Ogunjobi, K. Predicting monthly and seasonal rainfall, onset and cessation of the rainy season in West Africa using only surface data. Int. J. Clim. 2000, 20, 865–880. [Google Scholar] [CrossRef]
- Kumi, N.; Abiodun, B.J.; Adefisan, E.A. Performance Evaluation of a Subseasonal to Seasonal Model in Predicting Rainfall Onset Over West Africa. Earth Space Sci. 2020, 7, 8. [Google Scholar] [CrossRef]
- Diaconescu, E.P.; Gachon, P.; Scinocca, J.; Laprise, R. Evaluation of daily precipitation statistics and monsoon onset/retreat over western Sahel in multiple data sets. Clim. Dyn. 2015, 45, 1325–1354. [Google Scholar] [CrossRef] [Green Version]
- Mounkaila, M.S.; Abiodun, B.J.; Omotosho, J.B. Assessing the capability of CORDEX models in simulating onset of rainfall in West Africa. Theor. Appl. Climatol. 2015, 119, 255–272. [Google Scholar] [CrossRef]
- Dunning, C.M.; Black, E.C.L.; Allan, R.P. The onset and cessation of seasonal rainfall over Africa. J. Geophys. Res. 2016, 121, 405–11424. [Google Scholar] [CrossRef] [Green Version]
- Liebmann, B.; Bladé, I.; Kiladis, G.N.; Carvalho, L.M.V.; Senay, G.B.; Allured, D.; Leroux, S.; Funk, C. Seasonality of African Precipitation from 1996 to 2009. J. Clim. 2012, 25, 4304–4322. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef] [Green Version]
- Haarsma, R.J.; Roberts, M.J.; Vidale, P.L.; Senior, C.A.; Bellucci, A.; Bao, Q.; Chang, P.; Corti, S.; Fučkar, N.S.; Guemas, V.; et al. High Resolution Model Intercomparison Project (HighResMIP v1.0) for CMIP6. Geosci. Model Dev. 2016, 9, 4185–4208. [Google Scholar] [CrossRef] [Green Version]
- Roberts, M.J.; Camp, J.; Seddon, J.; Vidale, P.L.; Hodges, K.; Vannière, B.; Mecking, J.; Haarsma, R.; Bellucci, A.; Scoccimarro, E.; et al. Projected Future Changes in Tropical Cyclones Using the CMIP6 HighResMIP Multimodel Ensemble. Geophys. Res. Lett. 2020, 47, e2020GL088662. [Google Scholar] [CrossRef]
- Gibba, P.; Sylla, M.B.; Okogbue, E.C.; Gaye, A.T.; Nikiema, M.; Kebe, I. State-of-the-art climate modeling of extreme precipitation over Africa: Analysis of CORDEX added-value over CMIP5. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2019, 137, 1041–1057. [Google Scholar] [CrossRef]
- Ajibola, F.; Zhou, B.; Gnitou, G.T.; Onyejuruwa, A. Evaluation of the Performance of CMIP6 HighResMIP on West African Precipitation. Atmosphere 2020, 11, 1053. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—a new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poméon, B.; Jakisch, T.; Diekkrüger, D. Evaluating the performance of remotely sensed and reanalysed precipitation data over West Africa using HBV light. J. Hydrol. 2017, 547, 222–235. [Google Scholar] [CrossRef]
- Nile, B.; Bayissa, Y. Evaluation of Satellite-Based Rainfall Estimates and Application to Monitor Meteorological Drought for. Remote Sens. Artic. 2017, 9, 1–17. [Google Scholar]
- Kouadio, K.; Bastin, S.; Konare, A.; Ajayi, V.O. Does convection-permitting simulate better rainfall distribution and extreme over Guinean coast and surroundings? Clim. Dyn. 2020, 55, 153–174. [Google Scholar] [CrossRef]
- Bichet, A.; Diedhiou, A. Less frequent and more intense rainfall along the coast of the Gulf of Guinea in West and Central Africa (1981–2014). Clim. Res. 2018, 76, 191–201. [Google Scholar] [CrossRef] [Green Version]
- Bichet, A.; Diedhiou, A. West African Sahel has become wetter during the last 30 years, but dry spells are shorter and more frequent. Clim. Res. 2018, 75, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Kodama, C.; Ohno, T.; Seiki, T.; Yashiro, H.; Noda, A.T.; Nakano, M.; Sugi, M. The non-hydrostatic global atmospheric model for CMIP6 HighResMIP simulations (NICAM16-S): Experimental design, model description, and sensitivity experiments. Geosci. Model Dev. 2021, 14, 795–820. [Google Scholar] [CrossRef]
- Boucher, O.; Denvil, S.; Levavasseur, G.; Cozic, A.; Caubel, A.; Foujols, M.A.; Meurdesoif, Y.; Ghattas, J. IPSL IPSL-CM6A-ATM-HR model output prepared for CMIP6 HighResMIP. Earth System Grid Federation, 2019. Available online: https://doi.org/10.22033/ESGF/CMIP6.2361 (accessed on 1 April 2022).
- Mizuta, R.; Yoshimura, H.; Ose, T.; Hosaka, M.; Yukimoto, S. MRI MRI-AGCM3-2-S model output prepared for CMIP6 HighResMIP highresSST-future. Earth Syst. Grid Fed. 2019. [Google Scholar] [CrossRef]
- Rong, X.; Li, J.; Chen, H.; Xin, Y.; Su, J.; Hua, L.; Zhou, T.; Qi, Y.; Zhang, Z.; Zhang, G.; et al. The CAMS Climate System Model and a Basic Evaluation of Its Climatology and Climate Variability Simulation. J. Meteorol. Res. 2018, 32, 839–861. [Google Scholar] [CrossRef]
- Haarsma, R.; Acosta, M.; Bakhshi, R.; Bretonnière, P.A.; Caron, L.P.; Castrillo, M.; Wyser, K. HighResMIP versions of EC-Earth: EC-Earth3P and EC-Earth3P-HR–description, model computational performance and basic validation. Geosci. Model Dev. 2020, 13, 3507–3527. [Google Scholar] [CrossRef]
- IPCC. Climate change 2001: The scientific basis. In Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., Van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- Herrmann, S.M.; Mohr, K.I. A Continental-Scale Classification of Rainfall Seasonality Regimes in Africa Based on Gridded Precipitation and Land Surface Temperature Products. J. Appl. Meteorol. Clim. 2011, 50, 2504–2513. [Google Scholar] [CrossRef]
- Le Barbé, L.; Lebel, T.; Tapsoba, D. Rainfall Variability in West Africa during the Years 1950–90. J. Clim. 2002, 15, 187–202. [Google Scholar] [CrossRef]
- Vellinga, M.; Arribas, A.; Graham, R. Seasonal forecasts for regional onset of the West African monsoon. Clim. Dyn. 2013, 40, 3047–3070. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).