The Influence of Teleconnections on the Precipitation in Baluchistan
Abstract
1. Introduction
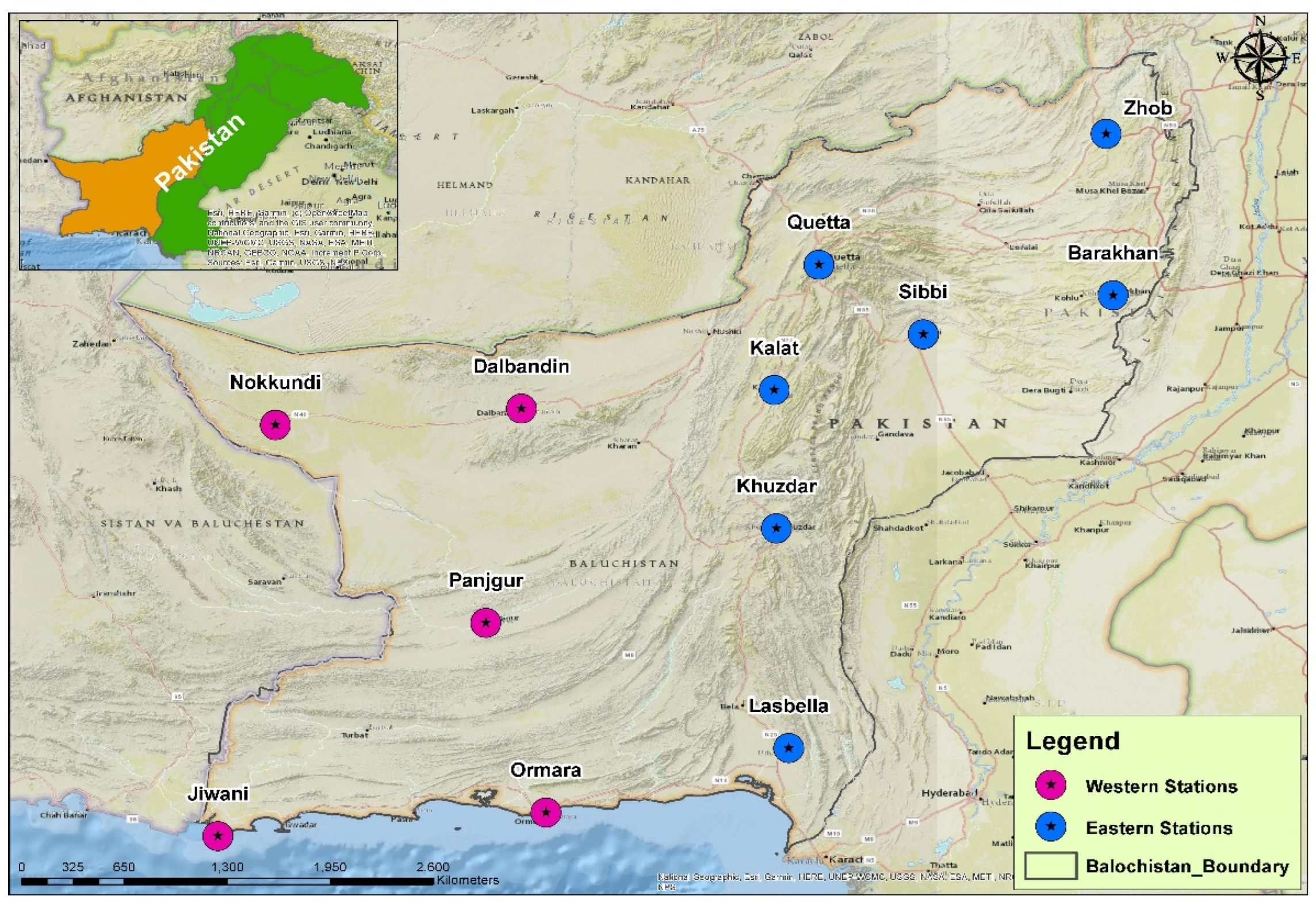
2. Study Area
3. Data Collection and Preparation
3.1. Precipitation Data
3.2. Climatic Indices
4. Methodology
4.1. Mann–Kendall for Trend Detection
4.2. Pearson’s Correlation for Finding Linear Associations
4.3. Theil–Sen (TS) Slope
4.4. Partial Mann–Kendall for Examining the Influence of Climatic Indices on Precipitation Trends
5. Results and Discussion
5.1. Trends in Precipitations
5.2. Linear Association of Climatic Indices with Precipitation
5.3. Influence of Climatic and Atmospheric Indices on Precipitation Trends
5.4. Analysis of PMK and Correlation Depicting the Influences of Climatic Indices—A Combined Approach
5.4.1. Weak Effect of -NAO/-AO
5.4.2. Weak Effect of ENSO-MEI/IOD/AMO/PDO
5.4.3. Significant Effects of EQWIN and EMI
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Sr. No. | Stations | Mean | Standard Deviation | Kurtosis | Skewness |
|---|---|---|---|---|---|
| 1 | Barakhan | 421.376 | 140.047 | 0.769 | 0.455 |
| 2 | Dalbandin | 82.085 | 48.085 | −0.214 | 0.585 |
| 3 | Jiwani | 99.795 | 88.784 | 2.266 | 1.519 |
| 4 | Kalat | 200.413 | 170.917 | 10.050 | 2.612 |
| 5 | Khuzdar | 265.875 | 118.215 | 1.147 | 0.994 |
| 6 | Lasbella | 180.154 | 115.972 | 1.134 | 1.137 |
| 7 | Nokkundi | 34.354 | 37.975 | 5.998 | 2.202 |
| 8 | Ormara | 70.928 | 92.889 | 11.605 | 3.031 |
| 9 | Panjgur | 94.884 | 56.881 | 3.950 | 1.641 |
| 10 | Pasni | 100.098 | 81.228 | 0.902 | 1.034 |
| 11 | Quetta | 270.502 | 152.860 | 9.365 | 2.542 |
| 12 | Sibbi | 182.203 | 89.558 | −0.724 | 0.310 |
| 13 | Zhob | 281.859 | 92.734 | −0.101 | 0.193 |
Appendix B
| S. No | Stations | Shapiro–Wilk | Anderson–Darling | Lilliefors | Jarque–Bera |
|---|---|---|---|---|---|
| 1 | Dalbandin | passed | passed | passed | passed |
| 2 | Jiwani | failed | failed | failed | failed |
| 3 | Kalat | failed | failed | failed | failed |
| 4 | Lasbella | failed | failed | failed | failed |
| 5 | Nokkundi | failed | failed | failed | failed |
| 6 | Ormara | failed | failed | failed | failed |
| 7 | Panjgur | failed | failed | failed | failed |
| 8 | Pasni | failed | failed | failed | failed |
| 9 | Quetta | failed | failed | failed | failed |
| 10 | Sibbi | passed | passed | passed | passed |
| 11 | Zhob | passed | passed | passed | passed |
| 12 | Khuzdar | failed | failed | failed | failed |
| 13 | Barakhan | passed | passed | passed | passed |
Appendix C
| Cum. Prob | t 0.50 | t 0.75 | t 0.80 | t 0.85 | t 0.90 | t 0.95 | t 0.975 | t 0.99 | t 0.995 | t 0.999 | t 0.9995 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| One-Tail | 0.50 | 0.25 | 0.20 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 |
| Two-Tails | 1.00 | 0.50 | 0.40 | 0.30 | 0.20 | 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 |
| df | |||||||||||
| 1 | 0.000 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 | 318.31 | 636.62 |
| 2 | 0.000 | 0.816 | 1.061 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 22.327 | 31.599 |
| 3 | 0.000 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 10.215 | 12.924 |
| 4 | 0.000 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 7.173 | 8.610 |
| 5 | 0.000 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 5.893 | 6.869 |
| 6 | 0.000 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 5.208 | 5.959 |
| 7 | 0.000 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.785 | 5.408 |
| 8 | 0.000 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 4.501 | 5.041 |
| 9 | 0.000 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 4.297 | 4.781 |
| 10 | 0.000 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 4.144 | 4.587 |
| 11 | 0.000 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 4.025 | 4.437 |
| 12 | 0.000 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.930 | 4.318 |
| 13 | 0.000 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.852 | 4.221 |
| 14 | 0.000 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.787 | 4.140 |
| 15 | 0.000 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.733 | 4.073 |
| 16 | 0.000 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.686 | 4.015 |
| 17 | 0.000 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.646 | 3.965 |
| 18 | 0.000 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.610 | 3.922 |
| 19 | 0.000 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.579 | 3.883 |
| 20 | 0.000 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.552 | 3.850 |
| 21 | 0.000 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.527 | 3.819 |
| 22 | 0.000 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.505 | 3.792 |
| 23 | 0.000 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.485 | 3.768 |
| 24 | 0.000 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.467 | 3.745 |
| 25 | 0.000 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.450 | 3.725 |
| 26 | 0.000 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.435 | 3.707 |
| 27 | 0.000 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.421 | 3.690 |
| 28 | 0.000 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.408 | 3.674 |
| 29 | 0.000 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.396 | 3.659 |
| 30 | 0.000 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.385 | 3.646 |
| 40 | 0.000 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 3.307 | 3.551 |
| 60 | 0.000 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 3.232 | 3.460 |
| 80 | 0.000 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 3.195 | 3.416 |
| 100 | 0.000 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 3.174 | 3.390 |
| 1000 | 0.000 | 0.675 | 0.842 | 1.037 | 1.282 | 1.646 | 1.962 | 2.330 | 2.581 | 3.098 | 3.300 |
| z | 0.000 | 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 3.090 | 3.291 |
| 0% | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99.8% | 99.9% | |
| Confidence Level | |||||||||||
Appendix D
| Critical Values for Pearson’s r: (For a Two-Tailed Test:) | ||||
|---|---|---|---|---|
| df: | 0.1 | 0.05 | 0.02 | 0.01 |
| 1 | 0.988 | 0.997 | 0.9995 | 0.9999 |
| 2 | 0.9 | 0.95 | 0.98 | 0.99 |
| 3 | 0.805 | 0.878 | 0.934 | 0.959 |
| 4 | 0.729 | 0.811 | 0.882 | 0.917 |
| 5 | 0.669 | 0.754 | 0.833 | 0.874 |
| 6 | 0.622 | 0.707 | 0.789 | 0.834 |
| 7 | 0.582 | 0.666 | 0.75 | 0.798 |
| 8 | 0.549 | 0.632 | 0.716 | 0.765 |
| 9 | 0.521 | 0.602 | 0.685 | 0.735 |
| 10 | 0.497 | 0.576 | 0.658 | 0.708 |
| 11 | 0.476 | 0.553 | 0.634 | 0.684 |
| 12 | 0.458 | 0.532 | 0.612 | 0.661 |
| 13 | 0.441 | 0.514 | 0.592 | 0.641 |
| 14 | 0.426 | 0.497 | 0.574 | 0.623 |
| 15 | 0.412 | 0.482 | 0.558 | 0.606 |
| 16 | 0.4 | 0.468 | 0.542 | 0.59 |
| 17 | 0.389 | 0.456 | 0.528 | 0.575 |
| 18 | 0.378 | 0.444 | 0.516 | 0.561 |
| 19 | 0.369 | 0.433 | 0.503 | 0.549 |
| 20 | 0.36 | 0.423 | 0.492 | 0.537 |
| 21 | 0.352 | 0.413 | 0.482 | 0.526 |
| 22 | 0.344 | 0.404 | 0.472 | 0.515 |
| 23 | 0.337 | 0.396 | 0.462 | 0.505 |
| 24 | 0.33 | 0.388 | 0.453 | 0.496 |
| 25 | 0.323 | 0.381 | 0.445 | 0.487 |
| 26 | 0.317 | 0.374 | 0.437 | 0.479 |
| 27 | 0.311 | 0.367 | 0.43 | 0.471 |
| 28 | 0.306 | 0.361 | 0.423 | 0.463 |
| 29 | 0.301 | 0.355 | 0.416 | 0.456 |
| 30 | 0.296 | 0.349 | 0.409 | 0.449 |
| 35 | 0.275 | 0.325 | 0.381 | 0.418 |
| 40 | 0.257 | 0.304 | 0.358 | 0.393 |
| 45 | 0.243 | 0.288 | 0.338 | 0.372 |
| 30 | 0.296 | 0.349 | 0.409 | 0.449 |
| 40 | 0.257 | 0.304 | 0.358 | 0.393 |
| 45 | 0.243 | 0.288 | 0.338 | 0.372 |
| 50 | 0.231 | 0.273 | 0.322 | 0.354 |
| 60 | 0.211 | 0.25 | 0.295 | 0.325 |
| 70 | 0.195 | 0.232 | 0.274 | 0.303 |
| 80 | 0.183 | 0.217 | 0.256 | 0.283 |
| 90 | 0.173 | 0.205 | 0.242 | 0.267 |
| 100 | 0.164 | 0.195 | 0.23 | 0.254 |
Appendix E
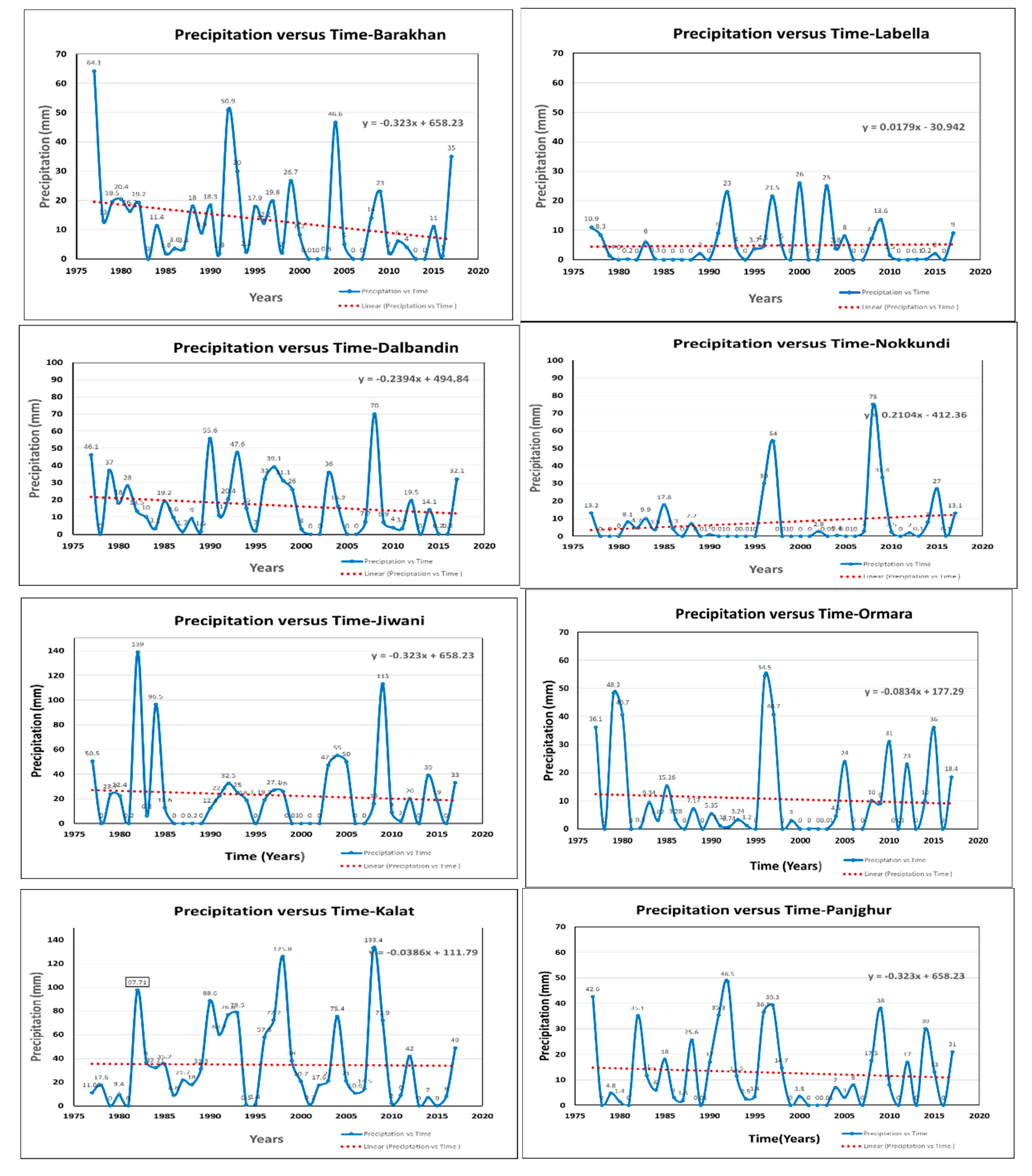
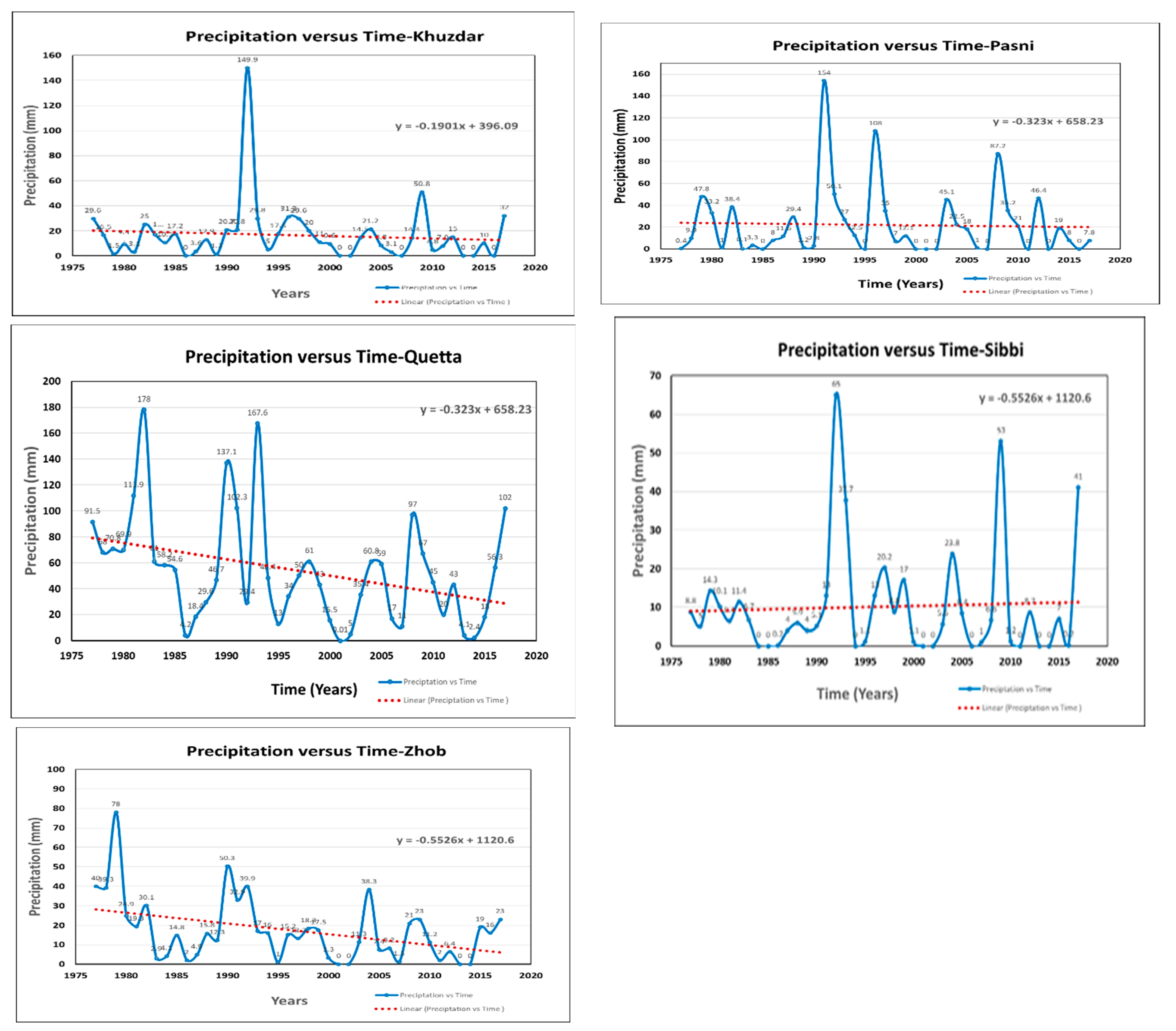



References
- Aamir, E.; Hassan, I. The impact of climate indices on precipitation variability in Baluchistan, Pakistan. Tellus A Dyn. Meteorol. Oceanogr. 2020, 72, 1–46. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Weather. Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527–21532. [Google Scholar] [CrossRef] [PubMed]
- Krichak, S.O.; Breitgand, J.S.; Gualdi, S.; Feldstein, S.B. Teleconnection–extreme precipitation relationships over the Mediterranean region. Theor. Appl. Climatol. 2014, 117, 679–692. [Google Scholar] [CrossRef]
- COC. Intergovernmental Panel on Climate Change; World Meteorological Organization: New York, NY, USA, 2014. [Google Scholar]
- Hussain, M.S.; Lee, S. The regional and the seasonal variability of extreme precipitation trends in Pakistan. Asia Pac. J. Atmos. Sci. 2013, 49, 421–441. [Google Scholar] [CrossRef]
- Hussain, M.S.; Lee, S. Long-term variability and changes of the precipitation regime in Pakistan. Asia Pac. J. Atmos. Sci. 2014, 50, 271–282. [Google Scholar] [CrossRef]
- Wang, S.Y.; Davies, R.E.; Huang, W.R.; Gillies, R.R. Pakistan’s two-stage monsoon and links with the recent climate change. J. Geophys. Res. Atmos. 2011, 116, D16. [Google Scholar] [CrossRef]
- Webster, P.J.; Toma, V.E.; Kim, H.M. Were the 2010 Pakistan floods predictable? Geophys. Res. Lett. 2011, 38, L04806. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Ali, S. Ecosystems, and environment, A new crop yield forecasting model based on satellite measurements applied across the Indus Basin, Pakistan. Agric. Ecosyst. Environ. 2003, 94, 321–340. [Google Scholar] [CrossRef]
- Eckstein, D.; Künzel, V.; Schäfer, L.; Winges, M. Global Climate Risk Index 2020; Germanwatch: Bonn, Germany, 2019. [Google Scholar]
- Kreft, S.; Eckstein, D. Global Climate Risk Index 2014—Who Suffers Most from Extreme Weather Events? Weather-Related Loss Events in 2012 and 1993 to 2012, UK Collaborative on Development Research. 2013. Available online: https://policycommons.net/artifacts/2101506/global-climate-risk-index-2014/2856804/ (accessed on 9 June 2022).
- Aamir, E.; Hassan, I. Trend Analysis in Precipitation at Individual and Regional Levels in Baluchistan, Pakistan. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 414, p. 012042. [Google Scholar]
- Liu, D.; Guo, S.; Chen, X.; Shao, Q. Analysis of trends of annual and seasonal precipitation from 1956 to 2000 in Guangdong Province, China. Hydrol. Sci. J. 2012, 57, 358–369. [Google Scholar] [CrossRef]
- Athar, H. Teleconnections and variability in observed rainfall over Saudi Arabia during 1978–2010. Atmos. Sci. Lett. 2015, 16, 373–379. [Google Scholar] [CrossRef]
- Krishnamurthy, L.; Krishnamurthy, V. Indian monsoon’s relation with the decadal part of PDO in observations and NCAR CCSM4. Int. J. Climatol. 2017, 37, 1824–1833. [Google Scholar] [CrossRef]
- Liess, S.; Geller, M.A. On the relationship between QBO and distribution of tropical deep convection. J. Geophys. Res. Atmos. 2012, 117, D3. [Google Scholar] [CrossRef]
- Afzal, M.; Haroon, M.A.; Rana, A.S.; Imran, A. Influence of North Atlantic oscillations and Southern oscillations on winter precipitation of Northern Pakistan. Pak. J. Meteorol. 2013, 9, 18. [Google Scholar]
- Iqbal, M.F.; Athar, H. Climatology, Variability, trends, and teleconnections of observed precipitation over Pakistan. Theor. Appl. Climatol. 2018, 134, 613–632. [Google Scholar] [CrossRef]
- Naz, F.; Dars, G.H.; Ansari, K.; Jamro, S.; Krakauer, N.Y. Drought trends in Balochistan. Water 2020, 12, 470. [Google Scholar] [CrossRef]
- Ashraf, M.; Routray, J.K. Spatio-temporal characteristics of precipitation and drought in Balochistan Province, Pakistan. Nat. Hazard 2015, 77, 229–254. [Google Scholar] [CrossRef]
- Ahmad, S.; Hussain, Z.; Qureshi, A.S.; Majeed, R.; Saleem, M. Drought Mitigation in Pakistan: Current Status and Options for Future Strategies; IWM: London, UK, 2004. [Google Scholar]
- Ali, S.; Khalid, B.; Kiani, R.S.; Babar, R.; Nasir, S.; Rehman, N.; Adanan, M.; Goheer, M.A. Spatio-temporal variability of summer monsoon onset over Pakistan. Asia Pac. J. Atmos. Sci. 2020, 56, 147–172. [Google Scholar] [CrossRef]
- Butt, M.J.; Iqbal, M.F. Impact of climate variability on snow cover: A case study of northern Pakistan. Pak. J. Meteorol. 2009, 5, 53–63. [Google Scholar]
- Zahid, M.; Rasul, G.J.S.I. Frequency of extreme temperature and precipitation events in Pakistan 1965–2009. Sci. Int. 2011, 23, 313–319. [Google Scholar]
- Hanif, M.; Khan, A.H.; Adnan, S. Latitudinal precipitation characteristics and trends in Pakistan. J. Hydrol. 2013, 492, 266–272. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation trends over time using Mann-Kendall and spearman’s rho tests in swat river basin, Pakistan. Adv. Meteorol. 2015, 2015, 431860. [Google Scholar] [CrossRef]
- Gadiwala, M.S.; Burke, F. Climate change and precipitation in Pakistan-a meteorological prospect. Int. J. Econ. Environ. Geol. 2019, 4, 10–15. [Google Scholar]
- Burn, D.H.; Elnur, M.A.H. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K. Time series analysis of hydrologic data for water resources planning and management: A review. J. Hydrol. Hydromech. 2006, 54, 237–257. [Google Scholar]
- Scarpati, O.E.; Spescha, L.B.; Lay, J.A.F.; Capriolo, A.D. Soil water surplus in salado river basin and its variability during the last forty years (Buenos Aires province, Argentina). Water 2011, 3, 132–145. [Google Scholar] [CrossRef]
- Yang, X.L.; Xu, L.R.; Liu, K.K.; Li, C.H.; Hu, J.; Xia, X.H. Trends in temperature and precipitation in the Zhangweinan River Basin during the last 53 years. Procedia Environ. Sci. 2012, 13, 1966–1974. [Google Scholar] [CrossRef][Green Version]
- Chaouche, K.; Neppel, L.; Dieulin, C.; Pujol, N.; Ladouche, B.; Martin, E.; Salas, D.; Caballero, Y. Analyses of precipitation, temperature and evapotranspiration in a French Mediterranean region in the context of climate change. C. R. Geosci. 2010, 342, 234–243. [Google Scholar] [CrossRef]
- Verworn, H.R.; Krämer, S.; Becker, M.; Pfister, A. The Impact of Climate Change on Rainfall Runoff Statistics in the Emscher-Lippe Region. In Proceedings of the 11th International Conference on Urban Drainage, Edingburg, UK, 31 August–5 September 2008; Volume 31, pp. 1–10. [Google Scholar]
- Towner, J.; Ficchí, A.; Cloke, H.L.; Bazo, J.; Coughlan de Perez, E.; Stephens, E.M. Influence of ENSO and tropical Atlantic climate variability on flood characteristics in the Amazon basin. Hydrol. Earth Syst. Sci. 2021, 25, 3875–3895. [Google Scholar] [CrossRef]
- Chervenkov, H.; Slavov, K. Theil-Sen estimator vs. ordinary least squares–trend analysis for selected ETCCDI climate indices. C. R. Acad. Bulg. Sci. 2019, 72, 47–54. [Google Scholar]
- Libiseller, C.; Grimvall, A. Performance of partial Mann–Kendall tests for trend detection in the presence of covariates. Environ. Off. J. Int. Environ. Soc. 2022, 13, 71–84. [Google Scholar] [CrossRef]
- Van Oldenborgh, G.J.; Philip, S.Y.; Collins, M. El Niño in a changing climate: A multi-model study. Ocean Sci. 2005, 1, 81–95. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean. 2007, 112, C11. [Google Scholar] [CrossRef]
- Hajani, E.; Rahman, A.; Ishak, E. Trends in extreme rainfall in the state of New South Wales, Australia. Hydrol. Sci. J. 2017, 62, 2160–2174. [Google Scholar] [CrossRef]
- Yadav, R.K.; Rupa Kumar, K.; Rajeevan, M. Increasing influence of ENSO and decreasing influence of AO/NAO in the recent decades over northwest India winter precipitation. J. Geophys. Res. Atmos. 2009, 114, D12. [Google Scholar] [CrossRef]
- Rashid, A. Impact of El-Nino on summer monsoon rainfall of Pakistan. Pak. J. Meteorol. 2004, 1, 2. [Google Scholar]
- Abraham, A.; Philip, N.S.; Joseph, K.B. Will We Have a Wet Summer? Soft Computing Models for Long-term Rainfall Forecasting. In Proceedings of the 15th European Simulation Conference ESM, Prague, Czech Republic, 6–9 June 2001. [Google Scholar]
- Khan, A. The influence of La-Nina phenomena on Pakistan’s precipitation. Pak. J. Metrol. 2004, 1, 23–31. [Google Scholar]
- Adnan, M.; Rehman, N.; Sheikh, M.M.; Khan, A.A.; Mir, K.A.; Khan, M. A Influence of natural forcing phenomena on precipitation of Pakistan. Pak. J. Meteorol. 2016, 12, 24. [Google Scholar]
- Vázquez-Patiño, A.; Campozano, L.; Ballari, D.; Córdova, M.; Samaniego, E. Virtual control volume approach to the study of climate causal flows: Identification of humidity and wind pathways of influence on rainfall in Ecuador. Atmosphere 2020, 11, 848. [Google Scholar] [CrossRef]
- Sanabria, J.; Carrillo, C.M.; Labat, D. Unprecedented rainfall and moisture patterns during El Niño 2016 in the Eastern Pacific and Tropical Andes: Northern Peru and Ecuador. Atmosphere 2019, 10, 768. [Google Scholar] [CrossRef]
- Chakraborty, A.; Behera, S.K.; Mujumdar, M.; Ohba, R.; Yamagata, T. Diagnosis of tropospheric moisture over Saudi Arabia and influences of IOD and ENSO. Mon. Weather. Rev. 2006, 134, 598–617. [Google Scholar] [CrossRef]
| Stations | Winter | Spring/Pre-Monsoon | Monsoon | Post-Monsoon | Annual Precipitation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dec. | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | |||
| Barakhan | Eastern | 6.5 | 13.1 | 21.1 | 31.3 | 34.6 | 24.7 | 48.2 | 108.4 | 84.6 | 35 | 9.1 | 4.9 | 421.5 |
| Kalat | 30.3 | 34.7 | 37.8 | 31 | 11 | 3.9 | 6.7 | 16.3 | 13.4 | 4.6 | 5 | 5.8 | 200.5 | |
| Khuzdar | 14.7 | 16.5 | 30.9 | 29.3 | 16.3 | 14.1 | 16.5 | 51.2 | 56.6 | 9.1 | 6.5 | 4.3 | 266.0 | |
| Lasbella | 7.3 | 4.8 | 11.4 | 10.4 | 7.4 | 19.7 | 11.2 | 53.2 | 39.3 | 8.6 | 5 | 1.9 | 180.2 | |
| Quetta | 30.8 | 53.8 | 51.7 | 55.5 | 26 | 7.5 | 4 | 12.5 | 11.1 | 3.1 | 5.7 | 8.8 | 270.5 | |
| Sibbi | 5.6 | 10.1 | 17.9 | 22.3 | 9.8 | 6 | 15.7 | 38.6 | 39.1 | 12.4 | 3.1 | 1.6 | 182.2 | |
| Zhob | 9.2 | 17.1 | 26.9 | 43.5 | 29.1 | 14.8 | 17.7 | 56.2 | 44.8 | 11.1 | 5.8 | 5.6 | 281.8 | |
| Dalbandin | Western | 9.4 | 16.8 | 16 | 20.5 | 4.8 | 1.3 | 3 | 3.7 | 0.7 | 0.1 | 2.2 | 3.1 | 81.6 |
| Jiwani | 20.2 | 22.9 | 22.5 | 14.3 | 3.7 | 0.1 | 7.6 | 3 | 2.3 | 0 | 1.1 | 3.6 | 101.3 | |
| Nokkundi | 2 | 7.8 | 9.6 | 8.7 | 2.2 | 0.2 | 2 | 0.7 | 0.3 | 0 | 0.5 | 0.6 | 34.6 | |
| Ormara | 11.8 | 10.7 | 10 | 9.9 | 1.6 | 0.2 | 9.7 | 11.3 | 3.8 | 0.3 | 2 | 0.5 | 71.8 | |
| Punjgur | 10 | 12.8 | 15 | 15.1 | 8.3 | 3.5 | 5 | 12.1 | 7.7 | 1.7 | 2.1 | 1.6 | 94.9 | |
| Region4 | 12.8 | 15.2 | 14.4 | 12.9 | 3.6 | 0.9 | 6.2 | 6.5 | 4.4 | 0.5 | 1.6 | 1.6 | 67.8 | |
| Monthly Avg. | 13.7 | 18.7 | 22.0 | 23.7 | 12.1 | 7.4 | 11.8 | 28.6 | 24.0 | 6.7 | 3.9 | 3.4 | ||
| Seasonal Sum | 54.3 | 43.2 | 71.1 | 7.3 | ||||||||||
| Stations | Parameters | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barakhan | S | −177 | −70 | −144 | −57 | −1 | 175 | −76 | 44 | −79 | 7 | −211 | −74 |
| P | 4.62% | 43.14% | 10.57% | 52.20% | 99.10% | 4.93% | 39.33% | 62.12% | 37.49% | 93.32% | 1.07% | 38.76% | |
| TS | −0.205 * | −0.206 | −0.478 | −0.187 | 0.000 | 0.832 * | −0.767 | 0.354 | −0.291 | 0.000 | 0.000 | 0.000 | |
| Dalbandin | S | −132 | −43 | −79 | −53 | −98 | −21 | −42 | −67 | 13 | −24 | −91 | −208 |
| P | 13.74% | 62.70% | 37.29% | 54.73% | 22.36% | 76.83% | 49.35% | 27.46% | 74.52% | 71.94% | 23.49% | 1.64% | |
| TS | −0.240 | −0.027 | −0.113 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.051 | |
| Jiwani | S | −13 | −158 | −72 | −93 | −30 | −59 | −34 | −58 | 0 | −32 | −72 | −245 |
| P | 88.23% | 6.31% | 39.71% | 19.20% | 20.49% | 30.99% | 57.93% | 41.59% | 0.00% | 48.30% | 24.04% | 0.37% | |
| TS | 0.000 | −0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.074 | |
| Kalat | S | −43 | 47 | 28 | −35 | 23 | 68 | −167 | −68 | 9 | −68 | 66 | −114 |
| P | 62.89% | 59.72% | 75.22% | 69.12% | 78.48% | 39.87% | 5.41% | 43.02% | 89.95% | 28.97% | 42.94% | 18.86% | |
| TS | −0.079 | 0.130 | 0.004 | 0.000 | 0.000 | 0.000 | −0.117 | 0.000 | 0.000 | 0.000 | 0.000 | −0.049 | |
| Khuzdar | S | −97 | −67 | 28 | −47 | 28 | 31 | −20 | −59 | 30 | −93 | −151 | −178 |
| P | 27.45% | 45.12% | 75.27% | 59.65% | 75.21% | 72.56% | 82.22% | 50.75% | 73.06% | 21.50% | 6.45% | 4.01% | |
| TS | −0.117 | −0.242 | 0.092 | −0.011 | 0.000 | 0.000 | −0.067 | −0.380 | 0.000 | 0.000 | 0.000 | −0.094 | |
| Lasbella | S | 9 | −120 | 58 | 41 | 133 | 78 | −92 | −60 | 105 | −84 | −90 | −57 |
| P | 91.68% | 16.84% | 50.54% | 63.79% | 13.09% | 37.58% | 29.86% | 49.69% | 16.15% | 23.88% | 19.32% | 39.36% | |
| TS | 0.000 | −0.046 | 0.000 | 0.000 | 0.292 | 0.004 | −0.225 | −0.150 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Nokkundi | S | 62 | 8 | −2 | 12 | 20 | 59 | −48 | −63 | 0 | 39 | −26 | −72 |
| P | 47.94% | 92.72% | 98.19% | 87.98% | 77.89% | 24.13% | 34.06% | 11.52% | 0.00% | 52.48% | 68.56% | 37.15% | |
| TS | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Ormara | S | −19 | −28 | −73 | −67 | −205 | 108 | 82 | 66 | 5 | −407 | −20 | −19 |
| P | 82.81% | 74.38% | 37.14% | 31.60% | 0.63% | 7.82% | 30.15% | 35.46% | 92.09% | 0.01% | 69.13% | 82.32% | |
| TS | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.005 | 0.000 | 0.000 | |
| Panjgur | S | −28 | −93 | −56 | −32 | 135 | 18 | −195 | −78 | −5 | −76 | −90 | −176 |
| P | 75.17% | 29.40% | 52.60% | 70.43% | 8.89% | 80.07% | 2.28% | 31.75% | 93.79% | 13.13% | 17.80% | 3.51% | |
| TS | 0.000 | −0.131 | −0.019 | 0.000 | 0.000 | 0.000 | −0.083 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Pasni | S | −52 | −64 | −60 | 0 | −35 | 15 | 10 | −116 | 6 | −50 | 49 | −91 |
| P | 55.68% | 46.03% | 48.35% | 100.00% | 38.15% | 81.53% | 89.61% | 12.19% | 89.54% | 27.30% | 42.43% | 28.44% | |
| TS | −0.006 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Quetta | S | −224 | −44 | −157 | 130 | 165 | 206 | −33 | −12 | 153 | 8 | 76 | −169 |
| P | 1.19% | 62.11% | 7.78% | 14.38% | 6.07% | 1.26% | 70.15% | 88.99% | 3.14% | 91.50% | 37.77% | 5.74% | |
| TS | −1.223 * | −0.265 | −0.966 | 0.200 | 0.019 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | −0.543 | |
| Sibbi | S | −69 | 23 | −91 | −42 | 154 | 186 | 22 | 21 | 153 | −57 | −61 | −63 |
| P | 43.55% | 79.55% | 30.66% | 62.80% | 6.78% | 2.59% | 80.46% | 81.35% | 6.70% | 32.66% | 43.44% | 45.50% | |
| TS | −0.031 | 0.000 | −0.185 | 0.000 | 0.000 | 0.000 | 0.042 | 0.069 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Zhob | S | −201 | −19 | −132 | −39 | 38 | 161 | 56 | −122 | 77 | −38 | −39 | −160 |
| P | 2.39% | 83.08% | 13.81% | 66.12% | 66.85% | 7.04% | 52.93% | 17.06% | 38.20% | 61.98% | 64.03% | 6.63% | |
| TS | −0.417 * | −0.029 | −0.655 | −0.078 | 0.044 | 0.250 | 0.264 | −0.559 | 0.029 | 0.000 | 0.000 | −0.056 |
| PMD Stations | Month | NAO | AO | IOD | PDO | ENSO-MEI | EQWIN | EMI-MODOKI | OLR |
|---|---|---|---|---|---|---|---|---|---|
| Barakhan | January | −15.83% | −0.02% | −1.22% | −1.57% | 1.77% | −14.05% | 21.46% | −44.79% |
| June | −6.05% | −6.59% | 4.74% | 31.85% | 6.40% | 3.94% | −0.34% | −2.81% | |
| November | 11.61% | 25.03% | 40.10% | 1.08% | 37.93% | 59.39% | −42.18% | −3.97% | |
| Dalbandin | December | −7.74% | 5.24% | 8.22% | −5.84% | 14.75% | 39.38% | −12.64% | 26.08% |
| Jiwani | December | −27.97% | −2.45% | 8.93% | 0.86% | 26.66% | 55.29% | −34.32% | 25.29% |
| Khuzdar | December | −0.17% | 12.84% | 9.50% | −18.98% | 22.22% | 30.97% | −20.08% | 14.76% |
| Ormara | May | 14.77% | 1.18% | −15.80% | 41.16% | 24.07% | −4.80% | −26.83% | 14.05% |
| October | −13.33% | −2.67% | −7.96% | 14.66% | 9.79% | 5.90% | −6.90% | −34.94% | |
| Panjgur | July | 6.10% | −15.01% | 2.24% | 1.52% | −24.26% | 21.98% | 11.83% | 6.50% |
| December | 14.52% | 19.09% | 8.45% | −5.95% | 24.03% | 37.27% | −21.87% | 12.53% | |
| Quetta | January | −0.93% | 14.93% | 3.70% | −12.46% | 3.66% | 13.20% | −23.98% | −19.27% |
| June | −17.37% | −11.43% | 16.90% | 7.14% | −3.48% | 27.02% | 17.05% | −21.23% | |
| September | −11.23% | 9.12% | 33.63% | −33.02% | 0.48% | 25.04% | 1.42% | 15.25% | |
| Sibbi | June | −24.40% | −12.08% | 20.67% | 2.41% | −1.29% | 31.57% | 12.99% | −17.16% |
| Zhob | January | −28.68% | −18.96% | 11.76% | −11.04% | 14.91% | 23.30% | −20.99% | −9.06% |
| PMD Stations | Month | NAO | AO | IOD | PDO | ENSO-MEI | EQWIN | EMI-MODOKI | OLR |
|---|---|---|---|---|---|---|---|---|---|
| Barakhan | January | −15.83% | −0.02% | −1.22% | −1.57% | 1.77% | −14.05% | 21.46% | −44.79% |
| June | −6.05% | −6.59% | 4.74% | 31.85% | 6.40% | 3.94% | −0.34% | −2.81% | |
| Khuzdar | December | −0.17% | 12.84% | 9.50% | −18.98% | 22.22% | 30.97% | −20.08% | 14.76% |
| Quetta | January | −0.93% | 14.93% | 3.70% | −12.46% | 3.66% | 13.20% | −23.98% | −19.27% |
| Zhob | January | −28.68% | −18.96% | 11.76% | −11.04% | 14.91% | 23.30% | −20.99% | −9.06% |
| S. No | Condition | Influence Type |
|---|---|---|
| 1 | MK and PMK show no significant trends. | Insignificant |
| 2 | MK shows no significant trend and PMK shows a significant trend or vice versa; OR both MK and PMK show significant trends; the addition of the influencing variable changes the MK statistics by up to 10%. | Weak |
| 3 | MK shows no significant trend and PMK shows a significant trend or vice versa; OR both MK and PMK show significant trends; the addition of the influencing variable changes the MK statistics from 10% to 20%. | Moderate |
| 4 | MK shows no significant trend and PMK shows a significant trend or vice versa; OR both MK and PMK show significant trends; the addition of the influencing variable changes the MK statistics by greater than 20%. | Strong |
| Climatic Index | Months | Stations | Mann–Kendall | Partial Mann–Kendall with Covariate | % Change in MK Statistics due to NAO as Covariate | Influence Type | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| p-Value | MK Statistics | Trend Type | p-Value | PMK Statistics | Trend Type | |||||
| NAO | January | Barakhan | 0.0462 | −177 | Decreasing | 0.0480 | −174.1 | Decreasing | 1.64% | Weak |
| Quetta | 0.0119 | −224 | Decreasing | 0.0121 | −223.4 | Decreasing | 0.27% | Weak | ||
| Zhob | 0.0239 | −201 | Decreasing | 0.0245 | −196.8 | Decreasing | 2.09% | Weak | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.0576 | 168.8 | Increasing | 3.54% | Weak | |
| December | Khuzdar | 0.0401 | −178 | Decreasing | 0.0574 | −162 | Decreasing | 8.99% | Weak | |
| AO | January | Barakhan | 0.0462 | −177 | Decreasing | 0.0397 | −179 | Decreasing | 1.13% | Weak |
| Quetta | 0.0119 | −224 | Decreasing | 0.0113 | −225.4 | Decreasing | 0.63% | Weak | ||
| Zhob | 0.0239 | −201 | Decreasing | 0.0268 | −196.1 | Decreasing | 2.44% | Weak | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.0457 | 176.5 | Increasing | 0.86% | Weak | |
| December | Khuzdar | 0.0401 | −178 | Decreasing | 0.0215 | −179.3 | Decreasing | 0.73% | Weak | |
| IOD | January | Barakhan | 0.0462 | −177 | Decreasing | 0.0338 | −188 | Decreasing | 6.21% | Weak |
| Quetta | 0.0119 | −224 | Decreasing | 0.0086 | −233.4 | Decreasing | 4.20% | Weak | ||
| Zhob | 0.0239 | −201 | Decreasing | 0.0124 | −221 | Decreasing | 9.95% | Weak | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.0485 | 175.6 | Increasing | 0.34% | Weak | |
| December | Khuzdar | 0.0401 | −178 | Decreasing | 0.0205 | −197.5 | Decreasing | 10.96% | Moderate | |
| PDO | January | Barakhan | 0.0462 | −177 | Decreasing | 0.0325 | −185.9 | Decreasing | 5.03% | Weak |
| Quetta | 0.0119 | −224 | Decreasing | 0.0097 | −228.8 | Decreasing | 2.14% | Weak | ||
| Zhob | 0.0239 | −201 | Decreasing | 0.0219 | −203.5 | Decreasing | 1.24% | Weak | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.0357 | 183.4 | Increasing | 4.80% | Weak | |
| December | Khuzdar | 0.0401 | −178 | Decreasing | 0.0304 | −182.7 | Decreasing | 2.64% | Weak | |
| ENSO-MEI | January | Barakhan | 0.0462 | −177 | Decreasing | 0.0437 | −182.5 | Decreasing | 3.11% | Weak |
| Quetta | 0.0119 | −224 | Decreasing | 0.0161 | −213 | Decreasing | 4.91% | Weak | ||
| Zhob | 0.0239 | −201 | Decreasing | 0.0362 | −183.7 | Decreasing | 8.61% | Weak | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.0410 | 181 | Increasing | 3.43% | Weak | |
| December | Khuzdar | 0.0401 | −178 | Decreasing | 0.0751 | −150.5 | Decreasing | 15.45% | Moderate | |
| EMI | January | Barakhan | 0.0416 | −181 | Decreasing | 0.1119 | −139.4 | Decreasing | −22.95% | Strong |
| Quetta | 0.0118 | −224 | Decreasing | 0.1035 | −136.7 | Decreasing | −38.95% | Strong | ||
| Zhob | 0.0238 | −201 | Decreasing | 0.1797 | −112.4 | Decreasing | −44.07% | Strong | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.1075 | 140.8 | Increasing | −19.49% | Moderate | |
| December | Khuzdar | 0.0400 | −178 | Decreasing | 0.1190 | −133.0 | Decreasing | −25.27% | Strong | |
| EQWIN | January | Barakhan | 0.0416 | −181 | Decreasing | 0.0708 | −158.0 | Decreasing | −12.68% | Moderate |
| Quetta | 0.0118 | −224 | Decreasing | 0.0210 | −202.5 | Decreasing | −9.56% | Weak | ||
| Zhob | 0.0238 | −201 | Decreasing | 0.0521 | −166.9 | Decreasing | −16.95% | Moderate | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.0080 | 210.8 | Increasing | 20.50% | Strong | |
| December | Khuzdar | 0.0400 | −178 | Decreasing | 0.3695 | −68.1 | Decreasing | −61.71% | Strong | |
| OLR | January | Barakhan | 0.0461 | −177 | Decreasing | 0.0425 | −179.8 | Decreasing | 1.61% | Weak |
| Quetta | 0.0118 | −224 | Decreasing | 0.0383 | −177.1 | Decreasing | −20.93% | Strong | ||
| Zhob | 0.0238 | −201 | Decreasing | 0.0769 | −154.6 | Decreasing | −23.04% | Strong | ||
| June | Barakhan | 0.0493 | 175 | Increasing | 0.0526 | 171.2 | Increasing | −2.17% | Weak | |
| December | Khuzdar | 0.0400 | −178 | Decreasing | 0.0497 | −166.5 | Decreasing | −6.42% | Weak | |
| Variables | Months | Stations | Mann–Kendall | Partial Mann–Kendall with Covariate | % Change in MK Statistics Due to Addition of Covariate | Influence Type as per PMK | Pearson Correlation | ||
|---|---|---|---|---|---|---|---|---|---|
| p-Value | MK Statistics | p-Value | PMK Statistics | ||||||
| NAO | January | Quetta | 0.0119 | −224 | 0.0121 | −223.4 | 0.27% | Weak | −0.93% |
| AO | Barakhan | 0.0462 | −177 | 0.0397 | −179 | 1.13% | Weak | −0.02% | |
| IOD | Barakhan | 0.0462 | −177 | 0.0338 | −188 | 6.21% | Weak | −1.22% | |
| Quetta | 0.0119 | −224 | 0.0086 | −233.4 | 4.20% | Weak | 3.70% | ||
| PDO | Barakhan | 0.0462 | −177 | 0.0325 | −185.9 | 5.03% | Weak | −1.57% | |
| ENSO-MEI | Barakhan | 0.0462 | −177 | 0.0437 | −182.5 | 3.11% | Weak | 1.77% | |
| Quetta | 0.0119 | −224 | 0.0161 | −213 | 4.91% | Weak | 3.66% | ||
| IOD | June | Barakhan | 0.0493 | 175 | 0.0485 | 175.6 | 0.34% | Weak | 4.74% |
| EMI | Barakhan | 0.0493 | 175 | 0.1076 | 140.9 | −19.49% | Moderate | −0.34% | |
| EQWIN | Barakhan | 0.0493 | 175 | 0.0080 | 210.9 | 20.50% | Strong | 3.94% | |
| OLR | Barakhan | 0.0493 | 175 | 0.0527 | 171.2 | −2.17% | Weak | −2.81% | |
| NAO | December | Khuzdar | 0.0401 | −178 | 0.0574 | −162 | 8.99% | Weak | −0.17% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aamir, E.; Khan, A.; Abubakar Tariq, M. The Influence of Teleconnections on the Precipitation in Baluchistan. Atmosphere 2022, 13, 1001. https://doi.org/10.3390/atmos13071001
Aamir E, Khan A, Abubakar Tariq M. The Influence of Teleconnections on the Precipitation in Baluchistan. Atmosphere. 2022; 13(7):1001. https://doi.org/10.3390/atmos13071001
Chicago/Turabian StyleAamir, Erum, Aamir Khan, and Muhammad Abubakar Tariq. 2022. "The Influence of Teleconnections on the Precipitation in Baluchistan" Atmosphere 13, no. 7: 1001. https://doi.org/10.3390/atmos13071001
APA StyleAamir, E., Khan, A., & Abubakar Tariq, M. (2022). The Influence of Teleconnections on the Precipitation in Baluchistan. Atmosphere, 13(7), 1001. https://doi.org/10.3390/atmos13071001





