Abstract
Prediction of adsorption isotherms under different temperatures is significant to reserve estimation of shale gas reservoirs. Based on the Polanyi adsorption potential theory and Langmuir adsorption theory, a method was presented to predict adsorption isotherms at different temperatures. In this method, the relationship between Langmuir pressure and temperature was quantified. By utilizing this method, we predicted adsorption isotherms of Longmaxi shale from 45 °C to 120 °C according to experimental data at 30 °C. Meanwhile, by considering the pressure and temperature gradients, we also predicted the adsorption capacity of Longmaxi shale with geologic depth. Results show that the adsorption data predicted by our method are in accord with experimental data and the error coefficient is less than 5%. In addition, the isosteric heat of adsorption for Longmaxi shale can be calculated by predicted adsorption data based on the Clausius–Clapeyron equation of capillary systems. Therefore, our study illustrates theoretical foundations for the efficient evaluation of adsorbed gas content in shale gas reservoirs at geologic conditions.
1. Introduction
Studying the methane adsorption capacity of shale under reservoir conditions is the basis for the development of shale gas reservoirs, and it is also critical for predicting gas reservoir resource and productivity evaluation [1,2,3]. Generally, the evaluation of the adsorbed gas content of shale is mainly based on experiments, and adsorption experiments at low temperature condition are easily conducted (such as below 65 °C [4,5]). However, the actual temperature in the geologic system of a shale reservoir is generally between 80 °C and 150 °C [6], and even as high as 175 °C [7,8]. The adsorption isotherm under low temperature (below 65 °C) will have a large gap with this under geologic temperature conditions. Since the temperature is one of the main factors affecting the adsorption capacity of shale, it is also one of the necessary research factors to evaluate the adsorption capacity of shale under reservoir conditions. At the same time, most experiments are based on a constant temperature. A single test can only obtain the relationship between methane adsorption capacity and pressure at a certain temperature; if we want to understand the relationship between shale adsorption capacity and pressure at different temperatures, we need to carry out several tests of adsorption at different temperatures [9]. Therefore, the prediction of adsorption curves at other temperatures (high temperature) through a small number of adsorption isotherms at known temperatures (low temperature) will be of great significance to the development and evaluation of shale gas reservoirs.
At present, the prediction of the adsorption curve under different temperature conditions can be divided into two methods: one is based on the Polanyi adsorption potential theory [10] to fit the “adsorption characteristic curve”. This method uses the principle that the adsorption characteristic curve of methane in shale is independent of temperature. The adsorption characteristic curve is obtained by “fitting” the adsorption data at a known temperature, so as to predict the adsorption curve at an unknown temperature. This method has achieved certain success in the prediction of the adsorption curve of activated carbon, coal and shale for methane, nitrogen and other non-polar gases [11,12], but the model for the adsorption characteristic curve is obtained by “fitting”. Such fitting lines do not have strict theoretical derivation and physical meaning. In order to ensure the accuracy of the fitting, it is generally necessary to know the adsorption curves at multiple temperatures.
Another method to predict adsorption isotherms under different temperatures is based on the isosteric heat of adsorption calculated by the Clausius–Clapeyron equation (shortened to adsorption heat) [13] to obtain the relationship between equilibrium pressure and temperature [14]. This method uses the principal that the adsorption heat of methane in shale does not change with temperature. The “linear relationship” between the logarithm and the reciprocal temperature allows the prediction of the adsorption curve at an unknown temperature. This method also achieves a certain effect in the prediction of the adsorption curve of activated carbon, coal rock, shale and other non-polar gases, but the calculation of the adsorption heat also requires at least two adsorption isotherms at different temperatures.
In addition to classical adsorption theories, such as Polanyi’s adsorption potential theory and the Clausius–Clapeyron equation mentioned before, some computational approaches are also employed to calculate methane adsorption isotherms. These computational approaches include the SLD (Simplified Local Density) model [15], the DFT (Density Functional Theory) model [16], and molecular simulation methods such as MD (Molecular Dynamics) simulations and GCMC (grand canonical Monte Carlo) simulations [17,18]. In earlier studies, the computational modellings and simulations were generally performed on gas adsorption inside a single pore (such as a single graphite slit pore); in recent years, simulations for gas adsorptions inside pore networks (such as realized kerogen pore network and MOFs) are widely reported benefits from the fast development of computing power [19,20,21]. Indeed, computational methods have advantages in investigating density profile distributions, analyzing gas phase behaviors, determining adsorption amounts and analyzing adsorption thermodynamics, and can give deeper insights into the methane adsorption process. However, the complexities in both theories and calculations obviously increase the threshold for industrial applications of these computational approaches; for example, the accuracy of the outputs by simulation tools largely depends on the knowledge of the engineers. Therefore, we focus on proposing a “simple” method based on classical adsorption theories for its convenience in applications.
In this work, based on the Polanyi adsorption potential theory and Langmuir adsorption model, we propose a method of “using only one adsorption isotherm to predict other isotherms at different temperatures”. The reason for choosing the Langmuir model is that methane adsorption in shale occurs at geologic conditions with high pressures and high temperatures, where methane behaves as a supercritical gas; and thus, the supercritical methane cannot condense as a liquid phase during adsorption and the adsorbed methane molecules almost concentrate on/near pore surfaces behaving as “monolayer adsorption” layers [22,23]. As a typical monolayer adsorption model [24,25], the Langmuir model has been widely used to describe adsorption behaviors for coal-bed methane [26] and shale gas [27,28] for its specific theoretical assumptions and brief equation frames.
Besides, based on our model, the effect of temperature on the adsorption curve is revealed. At the same time, combined with the adsorption data of the actual shale samples and the reservoir pressure gradient/geothermal gradient, the shale adsorption capacity under geologic depth can be predicted. Therefore, our method will lay a theoretical foundation for evaluating the adsorbed gas content of shale under geologic conditions, and thus it has certain practical significances.
2. Basic Theory
2.1. Polanyi Adsorption Potential
The Polanyi (1963) theory [10] believes that there is an adsorption potential field in a certain space near the surface of the adsorbent, and the gas molecules are adsorbed once they fall into this range. The density of the adsorbed gas in the adsorption space decreases with the increase of the distance from the surface, and the density of the adsorbed gas at the outermost edge of the adsorption space has no difference with the external gas. The theory defines the work required per mole of gas to pull from infinity (outer space) to a point as the adsorption potential:
where, ε is the adsorption potential, J/mol; P is the equilibrium pressure of the gas phase, MPa; R is the gas constant, taken as 8.314 J/(mol·K); T is the thermodynamic temperature, K; P0 is the saturated vapor pressure of the gas, MPa.
2.2. Virtual Saturated Vapor Pressure
The adsorption potential theory is mainly for gases below the critical temperature (when a gas is condensed). The physical adsorption heat of a gas is equivalent to the heat of condensation, and the adsorption phase pressure can be expressed by the saturated vapor pressure P0. However, the actual shale reservoir temperature is usually much higher than the critical temperature of methane (−80.4 °C/190.7 K), and it is impossible for methane to liquefy. At this time, the saturated vapor pressure P0 loses the corresponding physical meaning. In this study, the equation proposed by Amankwah et al. (1995) [29] is used to calculate the virtual saturated vapor pressure P* for methane in a supercritical condition:
where, Pc is the critical pressure and it is 4.59 MPa for methane; Tc is the critical temperature, and it is 190.7 K for methane; k is the adsorption characteristic value, and Dubinnin et al. (1960) [30] took k = 2 to describe the adsorption of methane on activated carbon.
Combining Equations (1) and (2), the adsorption potential ε of methane in shale can be determined as:
2.3. Adsorption Volume
Based on the adsorption potential theory, the adsorption volume is defined as the space where the attractive potential field acts on the adsorbent surface, which can be expressed as:
where, ω is the adsorption volume, cm3/g; Vad is the absolute adsorption capacity of the gas (standard condition), cm3/g; M is the molecular weight of the gas, g/mol; ρad is the adsorbed phase density, g/cm3.
The calculation of the adsorption volume involves the adsorption phase density ρad. Dubinnin (1960) et al. [30] gave an empirical equation for the adsorption phase density of supercritical gases:
In this work, we use M = 16 g/mol, Pc = 4.59 MPa and Tc = 190.7 K for calculate the density for the adsorbed methane, and ρad is about 0.375 g/cm3. In fact, Haydel (1967) [31] and Ambrose (2012) [23] also evaluate the ρad through experimental methods and numerical simulations, it is determined with a range of 0.34–0.37 g/cm3, which is similar to our calculation. It can be found that the density for the adsorbed methane is less than that of the liquid methane 0.42 g/cm3 (Mavor et al., 2012 [32]). In this study, we use ρad = 0.375 g/cm3 for calculation.
At the same time, the calculation of the adsorption space is related to the adsorption amount Vad. Generally, the adsorption amount of methane in the shale can be expressed by the Langmuir adsorption equation as [24,25]:
Among them: Vad is the absolute adsorption capacity of methane under equilibrium pressure, cm3/g; Vm is the maximum (limit) adsorption capacity of methane, cm3/g; P is the equilibrium pressure, MPa; PL is Langmuir pressure, MPa.
Substituting Equations (5) and (6) into Equation (4), the adsorption volume can be expressed as:
For methane, α = 0.0019 and it is a constant.
2.4. Characteristic Curve
The adsorption potential theory indicates that the adsorption layer (adsorption space) can be divided into several equipotential surfaces, and the adsorption potential ε at each equipotential surface is a function of the distance between the gas molecules and the surface (adsorption space ω), which can be expressed as [10]:
where, f is adsorption characteristic curve function; the relationship between the adsorption space ω and the adsorption potential ε is called the characteristic curve. For a physical adsorption process, the adsorption force is dominated by dispersion force and the related adsorption potential is independent of temperature, and thus the adsorption characteristic curve will not change with temperature. The adsorption of methane in shale nanopores is always regarded as physical adsorption [33,34,35], therefore the characteristic curve for methane adsorption in shale is independent of temperature.
Combined with Equations (3), (7) and (8), the following equation can be obtained:
The adsorption characteristic curve in Equation (8) can be calculated by Equation (9). The left term represents the adsorption potential ε. The right end bracket represents the adsorption space ω. In this work, we will further use investigate the relationship between ε and ω, so as to quantify the methane adsorption curve under different temperature conditions.
3. Method and Validation
3.1. Relationship between Langmuir Pressure at Different Temperatures
For methane adsorption on the same shale rocks at two different temperatures (T1 and T2), the Langmuir pressure PL is different, and we use PL1 and PL2 to describe them. However, the maximum adsorption capacity Vm is almost the same because the maximum adsorption space for the same shale sample does change with temperature. Therefore, for methane adsorption at temperature T1, we use PL1 to replace the P in the Equation (9), so we can conclude that:
In addition, we can obtain a similar equation on temperature T2:
Because the adsorption characteristic curve function f does not change with temperature, Equation (10a,b) have the same value, so we can conclude that:
According to Equation (11), the relationship between PL1 and PL2 can be obtained:
where, T1 and T2 are methane adsorption equilibrium temperatures, K; PL1 and PL2 are the Langmuir pressures at T1 and T2 at PL1 and PL2, MPa; Tc is the critical temperature of methane, K; Pc is the critical pressure of methane, MPa; k is the characteristic value of adsorption.
If we obtain methane adsorption isotherms at temperature T1, the value of PL1 and Vm can be obtained by fitting the adsorption data by using the Langmuir model, i.e., Equation (6). Therefore, the Langmuir pressure at other temperatures (such as PL2 at T2) can be predicated by Equation (12). Then, we can calculate the adsorption isotherm at T2 by PL2 and Vm through the Langmuir model. However, we can find that the value of k in Equation (12) is still unknown, and thus we need to further analyze the range of k.
3.2. Estimating k Value for Methane Adsorption on Shale
According to Equation (9), when we displace the pressure P to the Langmuir pressure PL, we can determine that:
where C is a constant to replace the term f(α·Vm/2); and Equation (13) can be further transformed into:
If we take “X = T·ln(T/Tc)” as the X-axis and “Y = T·ln(Pc/PL)” as the Y-axis, we can obtain:
Therefore, the slope of the straight line between “X = T·ln(T/Tc)” and “Y = T·ln(Pc/PL)” is the characteristic value k.
In this work, 13 sets of data for methane adsorption on shales at different temperatures (38 °C, 65 °C, 100 °C, 150 °C) were selected to calculate the characteristic value k of methane adsorption on shale [7]. The PL values at different temperatures, as well as the calculated “X = T·ln(T/Tc)” and “Y = T·ln(Pc/PL)” are shown in Table A1 in Appendix A. The linear relationship determined by the “X” and “Y” values is shown in Figure 1, and the slope is the k value.
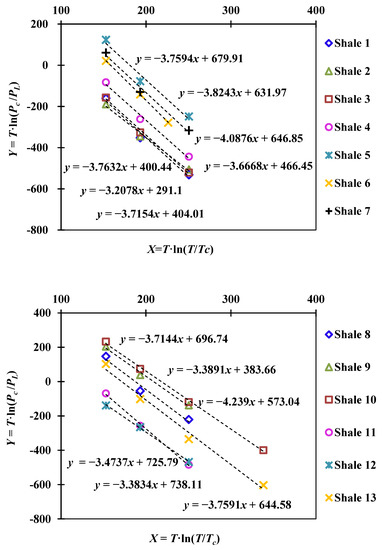
Figure 1.
Linear relationship between “X” and “Y” for different shale samples.
In fact, the range of k value has been discussed elsewhere, and it largely depends on the structures of adsorbents and the species of adsorbates. Amankwah (1995) [29] determines the k value for methane adsorption on activated carbon with temperatures ranging from −10 °C to 25 °C, and the obtained k value is about 2.10–2.73. In this work, for methane adsorption on 13 different shale samples with temperatures ranging from 38 °C to 150 °C, the determined k value is about 3.2–4.2, as shown in Figure 2. Considering that the obtained k value around 3.7, we use k = 3.7 for calculation in this study.

Figure 2.
Characteristic value ‘k’ with different shale samples.
3.3. Model Validation
Further, we use the adsorption data in Gasparik’s (2014) work [7] to validate our model. We select methane adsorption isotherms at low temperature, i.e., T = 311 K (38 °C) to predict methane adsorption at high temperatures, i.e., T = 338 K (65 °C), 373 K (100 °C) and 423 K (150 °C).
The adsorption isotherms of Posidonia shales A and B with pressure ranging from 0.1 MPa to 15 MPa are shown in Figure 3 and Figure 4, respectively. The Langmuir equation can be used to fit the experimental data (black solid line) well, with a fitting degree of about 99%, and the fitting results of related parameters are shown in Table 1.
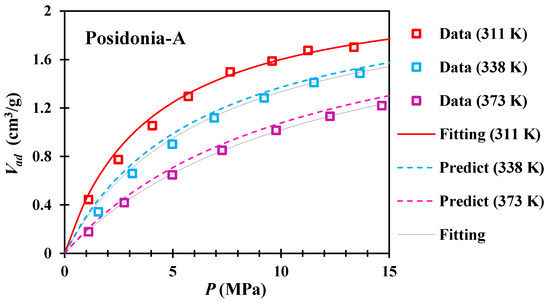
Figure 3.
The adsorption data and predicted isotherms of shale A (311–373 K).

Figure 4.
The adsorption data and predicted isotherms of shale B (311–423 K).

Table 1.
Comparation of model calculation with fitting results.
Based on our method, the Langmuir parameters of shale A and shale B at a low temperature with T = 311 K are used to predict the adsorption isotherms at relatively high temperatures (T = 338 K, 373 K and 423 K). For shale A, substituting T1 = 311 K, PL = 4.12 MPa, k = 3.7, Pc = 4.59 MPa, Tc = 190.7 K into Equation (12), the relationship between PL(A) and temperature T can be expressed as:
Similarly, for shale B, substituting T1 = 311 K, PL = 3.01 MPa, k = 3.7, Pc = 4.59 MPa, Tc = 190.7 K into Equation (12), then PL(B) and temperature T The relationship can be expressed as:
According to Equations (16) and (17), the PL of shale A and shale B at different temperatures can be calculated, and thus the adsorption curves at different temperatures can be obtained.
Therefore, based on our proposed method, we can use low-temperature adsorption isotherms to predict other isotherms at high temperatures. For shale A and shale B, the predicted isotherm (dashed line) is in good agreement with the experimental data (Figure 3 and Figure 4), and the error is basically within 5% (Table 1).
4. Results and Discussions
4.1. Basic Data for Shale Formation
In this section, we will use the proposed method to predict the gas adsorption capacity in our studied shale gas field. The studied sample S1 was collected from the Longmaxi formation in the Lower Silurian period. The organic matter in the studied sample belongs to Type-I kerogen with a vitrinite reflectance Ro% of 2.42%, indicating that it mainly generates dry gas. The mineral composition of shale S1 was analyzed by X-ray diffraction, the content of brittle minerals is about 56.5% and the content of the clay minerals is about 38.2%. The clay minerals are mainly dominated by illite (It) and illite/smectite mixed layer (IS). Among them, It content is about 35.8%, and IS content is about 42.4%. The total organic matter content (TOC) is about 5.3% in weight percentage.
In this study, the methane adsorption data at 303 K (30 °C), 333 K (60 °C), and 363 K (90 °C) were tested and shown in Figure 5. The adsorption data were fitted by the Langmuir model. During the fitting process, the maximum adsorption capacity Vm is kept as a constant, and only the Langmuir pressure PL changes with temperature, and the values of related parameters are shown in Table 2.
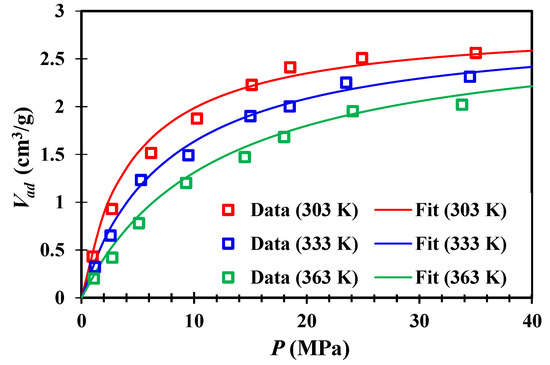
Figure 5.
Adsorption isotherms for shale S1 at 303 K, 333 K and 363 K.

Table 2.
Langmuir parameters of shale S1.
4.2. Prediction of Adsorption Isotherms
First, we will use the low-temperature adsorption isotherm at 303 K to predict the adsorption isotherm under different temperatures. Substituting the following adsorption parameters of shale S1: T = 303 K, PL = 4.496 MPa, k = 3.7, Pc = 4.59 MPa, Tc = 190.7 K into Equation (12), the relationship between PL(S) and temperature T can be expressed as:
where: PL(S) is the Langmuir pressure of shale S1 at different temperatures, MPa. According to equation (18), we can calculate the PL value under the conditions of temperature T = 318 K, 333 K, 348 K, 363 K, 378 K, 393 K, and the calculation results are shown in Table 3. The results show that the PL values calculated at 333 K (60 °C) and 363 K (90 °C) are in good agreement with those determined by experiments in Table 2. Based on the data in Table 3, the adsorption isotherms at different temperatures are plotted in Figure 6.

Table 3.
Langmuir parameter of shale with different temperatures.
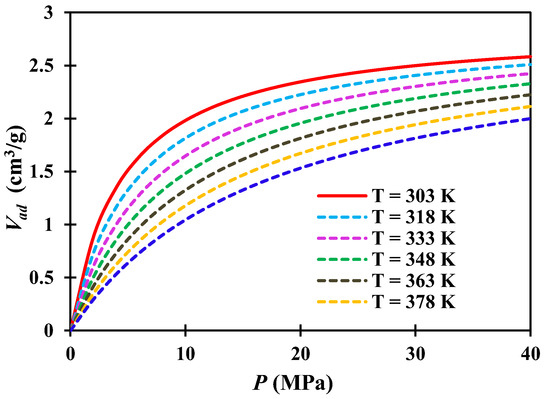
Figure 6.
Methane adsorption isotherms at different temperatures.
4.3. Adsorption Characteristic Curve
Then, we plotted the adsorption characteristic curve for our studied sample, where the adsorption volume ω is the X-axis and the adsorption potential ε is the Y-axis, as shown in Equation (8). The calculation details of ω and ε can be found in Equations (3) and (7) respectively, and the related parameters can be found in Table 2 and Table 3.
The adsorption characteristic curves at different temperatures are calculated and plotted in Figure 7. It can be found that the adsorption characteristic curves at different temperature conditions basically coincide with each other, indicating that the adsorption characteristic curve for methane adsorption on shale does not change with temperature. Therefore, the fundamental theory in our method almost stands and thus we proposed a new consideration on predicting methane adsorption on shales at different temperatures.

Figure 7.
Characteristic adsorption curves at different temperatures.
4.4. Isosteric Heat of Adsorption
Further, we can determine the adsorption heat for methane adsorption on our studied shale, which is an important thermodynamic parameter for adsorption. Xia and Tang (2012) [36] deduced the relationship between the Langmuir constant (1/PL) and temperature (T) based on adsorption thermodynamics, which is given by:
where, qst is the isosteric heat of adsorption, kJ/mol; R is the gas constant, 8.314 J/mol·K; c is a constant.
This equation shows that a linear relationship exists between ln(1/PL) and 1/T, and the slope is qst/R, which is related to the adsorption heat. Therefore, the adsorption heat of our sample can be determined based on the adsorption parameters at different temperatures in Table 3. The fitting results between ln(1/PL) and 1/T are shown in Figure 8, and the slope of the straight line is about 1797.9. Then, the adsorption heat of our studied shale is calculated by qst = 1797.9 × 8.314 = 14947.7 J/mol ≈ 14.95 kJ/mol, indicating a typical physical adsorption process.
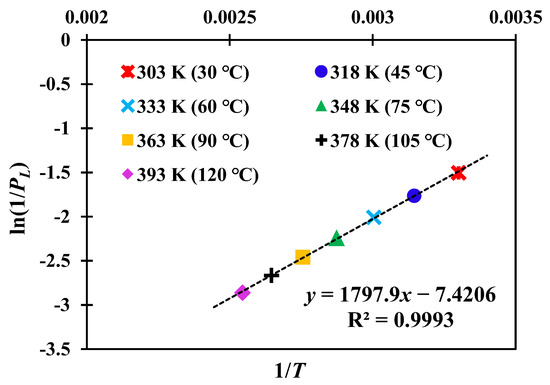
Figure 8.
Relationship between ln(1/PL) and 1/T at different temperatures.
5. Applications
The primary application of our method is to predict the methane adsorption capacity at geologic conditions. According to well-drilling data, the target layer of the studied shale is about 2413–2513 m in depth. The pressure gradient is about 1.41–1.55 MPa/100 m, and the geothermal gradient is about 2.80–2.85 K/100 m. In this study, using surface pressure P0 = 0.1 MPa, surface temperature T0 = 293.15 °C, pressure gradient KP = 1.45 MPa/100 m, and geothermal gradient KT = 2.83 °C/100 m, the geologic temperature and pressure can be calculated as:
As we know, the methane adsorption capacity is a function of both temperature and pressure. If we relate the temperature and pressure to the burial depth through Equations (20) and (21), the methane adsorption capacity can be written as:
where, Vm is the maximum adsorption capacity, which is 2.875 cm3/g for our studied sample, and is independent of both temperature and pressure. P(h) is the formation pressure related to the burial depth, MPa; PL(h) is the Langmuir pressure, MPa. Considering that the value of PL changes with temperature, it can be further related to the burial depth. According to Equation (12), the relationship between Langmuir pressure PL(h) and burial depth h can be expressed as:
where PL* is the Langmuir pressure at T* (indicating low temperature conditions in our work), which is 4.496 MPa for methane adsorption when T* = 303 K (see in Table 2); Pc is the critical pressure of methane, 4.59 MPa; Tc is the critical temperature of methane, which is 190.7 K, and k is the characteristic value of adsorption.
Substituting Equations (20), (21) and (23) into Equation (22), the relationship between adsorption capacity and burial depth can be obtained. Here, we calculated the adsorption capacity at different depths, with characteristic values k = 3.2, 3.5, 3.7, 4.0, as shown in Figure 9. It can be found that, when the reservoir is in shallow depth with h < 1500 m, the effect of k value on the adsorption capacity is weak; with the increase in burial depth, the effect of k value become obvious, and a larger k value leads to a smaller adsorption capacity. For our studied shale with a burial depth of h ≈ 2500 m, the calculated adsorption capacities with different characteristic k values are: 2.235 cm3/g, 2.195 cm3/g, 2.168 cm3/g, and 2.125 cm3/g. Overall, however, the effect of k value on the adsorption capacity for our studied sample is negligible; for example, the relative error between the adsorption capacity at k = 3.2 and k = 4.0 is only 4.89%. Therefore, using k = 3.7 can predict the adsorption capacity for our studied shale gas fields.
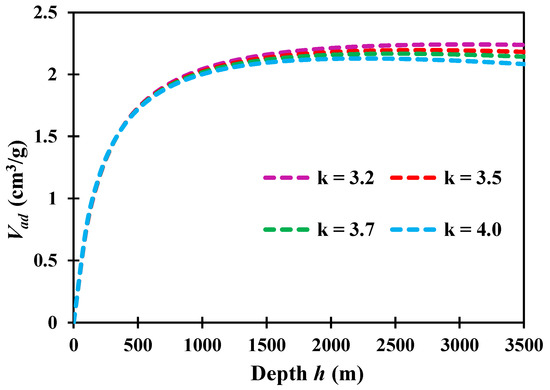
Figure 9.
Relationship between and methane adsorption capacity and depth.
Bedsides, it is found that the adsorption capacity Vad does not monotonically increase with the growth of burial depth h. This phenomenon is caused by the coupling effect of pressure and temperature on gas adsorption. Deeper burial depth leads to larger reservoir pressure, which has a positive influence on gas adsorption. At the same time, however, a deeper burial depth also leads to a higher reservoir temperature, which has a negative effect on gas adsorption. Based on this work, we found that a larger k value leads to a more obvious decrease in gas adsorption at greater depth, indicating that the k value mainly dominates the sensitivity of the gas adsorption to temperature. As the value of k grows, the effect of temperature on gas adsorption becomes significant.
6. Conclusions
In this work, a new method was established for predicting adsorption isotherms at different temperatures, in which we combined two famous adsorption theories: the Polanyi adsorption theory and Langmuir adsorption theory. Based on our method, we can predict adsorption isotherms at any temperatures by using only one isotherm at a given temperature. Therefore, we can use the gas adsorption isotherm at low-temperature conditions to predict the shale gas adsorption capacity in geologic high-temperature conditions. Such application has been illustrated by our studied case for shale gas storage in Longmaxi formation in the Lower Silurian period.
In addition, the effect of the burial depth of the reservoir on the adsorption capacity of shale is analyzed. With the combined effect of temperature and pressure, the adsorption capacity of shale does not monotonously increase with burial depth, but shows a parabola-like curve. At the same time, this phenomenon is related to the k value (adsorption characteristic value). The larger the k value, the more obvious the parabola-liked phenomenon behaves.
Author Contributions
Conceptualization, D.Z.; methodology, D.Z.; writing, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The adsorption data for 13 different shales at different temperatures.
Table A1.
The adsorption data for 13 different shales at different temperatures.
| Sample | T (K) | 1/T | PL (MPa) | lnPL | X | Y | k |
|---|---|---|---|---|---|---|---|
| WIC-149 (Shale 1) | 311.53 | 0.00321 | 7.58 | 2.03 | 152.89 | −160.04 | 3.7632 |
| 337.84 | 0.00296 | 12.86 | 2.55 | 193.20 | −351.94 | ||
| 373.13 | 0.00268 | 18.86 | 2.94 | 250.46 | −531.62 | ||
| HAR-038 (Shale 2) | 311.53 | 0.00321 | 8.34 | 2.12 | 152.89 | −189.64 | 3.2078 |
| 337.84 | 0.00296 | 12.60 | 2.53 | 193.20 | −345.18 | ||
| 373.13 | 0.00268 | 17.58 | 2.87 | 250.46 | −505.50 | ||
| HAR-060 (Shale 3) | 311.53 | 0.00321 | 7.51 | 2.02 | 152.89 | −156.93 | 3.7154 |
| 337.84 | 0.00296 | 11.91 | 2.48 | 193.20 | −325.92 | ||
| 373.13 | 0.00268 | 18.36 | 2.91 | 250.46 | −521.54 | ||
| HAD-119 (Shale 4) | 311.53 | 0.00321 | 5.92 | 1.78 | 152.89 | −82.78 | 3.6668 |
| 337.84 | 0.00296 | 9.84 | 2.29 | 193.20 | −261.40 | ||
| 373.13 | 0.00268 | 14.91 | 2.70 | 250.46 | −443.93 | ||
| Haynesville (Shale 5) | 311.53 | 0.00321 | 3.05 | 1.12 | 152.89 | 123.45 | 3.7594 |
| 337.84 | 0.00296 | 5.71 | 1.74 | 193.20 | −77.61 | ||
| 373.13 | 0.00268 | 8.84 | 2.18 | 250.46 | −248.78 | ||
| Alum_D (Shale 6) | 311.53 | 0.00321 | 4.24 | 1.44 | 152.89 | 21.27 | 4.0876 |
| 337.84 | 0.00296 | 6.90 | 1.93 | 193.20 | −141.46 | ||
| 358.42 | 0.00279 | 9.87 | 2.29 | 226.17 | −278.40 | ||
| Alum_O (Shale 7) | 311.53 | 0.00321 | 3.73 | 1.32 | 152.89 | 60.83 | 3.8243 |
| 337.84 | 0.00296 | 6.67 | 1.90 | 193.20 | −129.98 | ||
| 373.13 | 0.00268 | 10.59 | 2.36 | 250.46 | −316.32 | ||
| Alum_G (Shale 8) | 311.53 | 0.00321 | 2.82 | 1.04 | 152.89 | 148.06 | 3.7144 |
| 337.84 | 0.00296 | 5.32 | 1.67 | 193.20 | −53.63 | ||
| 373.13 | 0.00268 | 8.18 | 2.10 | 250.46 | −220.05 | ||
| Alum_S2-16 (Shale 9) | 311.53 | 0.00321 | 2.36 | 0.86 | 152.89 | 204.13 | 3.4737 |
| 337.84 | 0.00296 | 4.05 | 1.40 | 193.20 | 38.60 | ||
| 373.13 | 0.00268 | 6.56 | 1.88 | 250.46 | −137.59 | ||
| Alum_S2-18 (Shale 10) | 311.53 | 0.00321 | 2.14 | 0.76 | 152.89 | 233.42 | 3.7144 |
| 337.84 | 0.00296 | 3.64 | 1.29 | 193.20 | 74.41 | ||
| 373.13 | 0.00268 | 6.25 | 1.83 | 250.46 | −119.30 | ||
| 423.73 | 0.00236 | 11.63 | 2.45 | 338.30 | −399.04 | ||
| Barnett_M1-576 (Shale 11) | 311.53 | 0.00321 | 5.66 | 1.73 | 152.89 | −68.76 | 4.239 |
| 337.84 | 0.00296 | 9.70 | 2.27 | 193.20 | −256.67 | ||
| 373.13 | 0.00268 | 16.61 | 2.81 | 250.46 | −484.23 | ||
| Barnett_M1-586a (Shale 12) | 311.53 | 0.00321 | 7.07 | 1.96 | 152.89 | −138.23 | 3.3383 |
| 337.84 | 0.00296 | 9.93 | 2.30 | 193.20 | −264.77 | ||
| 373.13 | 0.00268 | 15.89 | 2.77 | 250.46 | −467.81 | ||
| Barnett_B1 (Shale 13) | 311.53 | 0.00321 | 3.26 | 1.18 | 152.89 | 103.20 | 3.7591 |
| 337.84 | 0.00296 | 6.12 | 1.81 | 193.20 | −101.26 | ||
| 373.13 | 0.00268 | 11.13 | 2.41 | 250.46 | −334.98 | ||
| 423.73 | 0.00236 | 18.82 | 2.94 | 338.30 | −602.85 |
References
- Li, X.; Wang, X.; Li, Y.; Wu, K.; Shi, J.; Yang, L.; Feng, D.; Zhang, T.; Yu, P. Water distribution characteristic and effect on methane adsorption capacity in shale clay. Int. J. Coal Geol. 2016, 159, 135–154. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Wu, K.; Wang, X.; Shi, J.; Yang, L.; Zhang, H.; Sun, Z.; Wang, R.; Feng, D. Water sorption and distribution characteristics in clay and shale: Effect of surface force. Energy Fuels 2016, 30, 8863–8874. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Wu, K.; Feng, D.; Zhang, T.; Zhang, Y. Thickness and stability of water film confined inside nanoslits and nanocapillaries of shale and clay. Int. J. Coal Geol. 2017, 179, 253–268. [Google Scholar] [CrossRef]
- Guo, W.; Gao, S.; Hu, Z.; Liu, H.; Yu, R. Impact of temperature on the isothermal adsorption/desorption of shale gas. Pet. Explor. Dev. 2013, 40, 514–519. [Google Scholar] [CrossRef]
- Tang, X.; Ripepi, N.; Stadie, N.P.; Yu, L. Thermodynamic analysis of methane adsorption on gas shale. J. Cent. South Univ. 2014, 45, 2871–2877. [Google Scholar]
- Ross, D.J.K.; Bustin, M.R. Characterizing the shale gas resource potential of Devonian–Mississippian strata in the Western Canada sedimentary basin: Application of an integrated formation evaluation. AAPG Bull. 2008, 92, 87–125. [Google Scholar] [CrossRef]
- Gasparik, M.; Bertier, P.; Gensterblum, Y.; Ghanizadeh, A.; Krooss, B.M.; Littke, R. Geological controls on the methane storage capacity in organic-rich shales. Int. J. Coal Geol. 2014, 123, 34–51. [Google Scholar] [CrossRef]
- Rexer, T.F.T.; Benham, M.J.; Aplin, A.C.; Thomas, K.M. Methane Adsorption on Shale under Simulated Geological Temperature and Pressure Conditions. Energy Fuels 2013, 27, 3099–3109. [Google Scholar] [CrossRef] [Green Version]
- Gasparik, M.; Ghanizadeh, A.; Gensterblum, Y.; Kroossa, B.M. “Multi-temperature” method for high-pressure sorption measurements on moist shales. Rev. Sci. Instrum. 2013, 84, 1–9. [Google Scholar] [CrossRef]
- Polanyi, M. The Potential Theory of Adsorption. Science 1963, 141, 1010–1013. [Google Scholar] [CrossRef]
- Su, X.B.; Chen, R.; Lin, X.Y.; Song, Y. Application of adsorption potential theory in the fractionation of coalbed gas during the process of adsorption/desorption. Acta Geol. Sin. 2008, 82, 1382–1389. [Google Scholar]
- Du, X.; Wu, E. Application of the adsorption potential theory to hydrogen adsorption on zeolites above critical temperature. Acta Phys. Chim. Sin. 2007, 23, 813–819. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Pastor, A.J.; Bulnes, F. Differential heat of adsorption in the presence of an order-disorder phase transition. Phys. A 2000, 283, 198–203. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, S.; Yao, X.; Hu, X.; Chen, S. Evaluation of Gas Adsorption in Nanoporous Shale by Simplified Local Density Model Integrated with Pore Structure and Pore Size Distribution. Langmuir 2022, 38, 3641–3655. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Tian, Y.; Wu, J. Classical density functional theory for methane adsorption in metal-organic framework materials. AIChE J. 2015, 61, 3012–3021. [Google Scholar] [CrossRef]
- Yu, X.; Li, J.; Chen, Z.; Wu, K.; Zhang, L.; Yang, S. Effects of helium adsorption in carbon nanopores on apparent void volumes and excess methane adsorption isotherms. Fuel 2020, 270, 117499. [Google Scholar] [CrossRef]
- Yu, X.; Li, J.; Chen, Z.; Wu, K.; Zhang, L. Effects of an adsorbent accessible volume on methane adsorption on shale. Comput. Methods Appl. Mech. Eng. 2020, 370, 113222. [Google Scholar] [CrossRef]
- Huang, L.; Ning, Z.; Wang, Q.; Qi, R.; Zeng, Y.; Qin, H.; Ye, H.; Zhang, W. Molecular simulation of adsorption behaviors of methane, carbon dioxide and their mixtures on kerogen: Effect of kerogen maturity and moisture content. Fuel 2018, 211, 159–172. [Google Scholar] [CrossRef]
- Yu, X.; Li, J.; Chen, Z.; Wu, K.; Zhang, L.; Yang, S.; Hui, G.; Yang, M. Determination of CH4, C2H6 and CO2 adsorption in shale kerogens coupling sorption-induced swelling. Chem. Eng. J. 2021, 410, 127690. [Google Scholar] [CrossRef]
- Getman, R.B.; Bae, Y.S.; Wilmer, C.E.; Snurr, R.Q. Review and analysis of molecular simulations of methane, hydrogen, and acetylene storage in metal–organic frameworks. Chem. Rev. 2012, 112, 703–723. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, K.; Chen, Z.; Wang, K.; Luo, J.; Xu, J.; Li, R.; Yu, R.; Li, X. On the negative excess isotherms for methane adsorption at high pressure: Modeling and experiment. SPE J. 2019, 24, 2504–2525. [Google Scholar] [CrossRef]
- Ambrose, R.J.; Hartman, R.C.; Diaz-Campos, M.; Akkutlu, I.Y.; Sondergeld, C.H. Shale gas-in-place calculations part I: New pore-scale considerations. Spe J. 2012, 17, 219–229. [Google Scholar] [CrossRef]
- Langmuir, I. The evaporation, condensation and reflection of molecules and the mechanism of adsorption. Phys. Rev. 1916, 8, 149. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, X.; Shi, J.; Zhang, H.; Wu, K.; Chen, Z. Mechanism of liquid-phase adsorption and desorption in coalbed methane systems: A new insight into an old problem. SPE Reserv. Eval. Eng. 2017, 20, 639–653. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Wu, K.; Wang, K.; Luo, J.; Feng, D.; Qu, S.; Li, X. A multi-site model to determine supercritical methane adsorption in energetically heterogeneous shales. Chem. Eng. J. 2018, 349, 438–455. [Google Scholar] [CrossRef]
- Li, J.; Wu, K.; Chen, Z.; Wang, W.; Yang, B.; Wang, K.; Luo, J.; Yu, R. Effects of energetic heterogeneity on gas adsorption and gas storage in geologic shale systems. Appl. Energy 2019, 251, 113368. [Google Scholar] [CrossRef]
- Amankwah, K.A.G.; Schwarz, J.A. A modified approach for estimating pseudo-vapor pressures in the application of the Dubinin-Astakhov equation. Carbon 1995, 33, 1313–1319. [Google Scholar] [CrossRef]
- Dubinin, M.M. The Potential Theory of Adsorption of Gases and Vapors for Adsorbents with Energetically Nonuniform Surfaces. Chem. Rev. 1960, 60, 235–241. [Google Scholar] [CrossRef]
- Haydel, J.J.; Kobayashi, R. Adsorption Equilibria in Methane-Propane-Silica Gel System at High Pressures. Ind. Eng. Chem. Fundam. 1967, 6, 546–554. [Google Scholar] [CrossRef]
- Mavor, M.J.; Hartman, C.; Pratt, T.J. Uncertainty in sorption isotherm measurements. In Proceedings of the International Coalbed Methane Symposium, Tuscaloosa, AL, USA, 11 April 2004. [Google Scholar]
- Ji, L.; Zhang, T.; Milliken, K.L.; Qu, J.; Zhang, X. Experimental investigation of main controls to methane adsorption in clay-rich rocks. Appl. Geochem. 2012, 27, 2533–2545. [Google Scholar] [CrossRef]
- Liu, D.; Yuan, P.; Liu, H.; Li, T.; Tan, D.; Yuan, W.; He, H. High-pressure adsorption of methane on montmorillonite, kaolinite and illite. Appl. Clay Sci. 2013, 85, 25–30. [Google Scholar] [CrossRef]
- Zhang, T.; Ellis, G.; Ruppel, S.C.; Milliken, K.; Yang, R. Effect of organic matter type and thermal maturity on methane adsorption in shale-gas systems. Org. Geochem. 2012, 47, 120–131. [Google Scholar] [CrossRef]
- Xia, X.; Tang, Y. Isotope fractionation of methane during natural gas flow with coupled diffusion and adsorption/desorption. Geochim. Cosmochim. Acta 2012, 77, 489–503. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).