Abstract
Thailand is located in the Southeast Asian region, where the summer rainfall exhibits strong interannual variability, and the successful simulation of rainfall variation in Thailand by current climate models remains a challenge. Therefore, this paper evaluates the capability of the state-of-the-art Atmospheric GCM of the Institute of Atmospheric Physics (IAP-AGCM) in simulating summer rainfall over Thailand by comparing the model’s results with ground-truth observation during 1981–2012. Generally, the model shows a certain skill in reproducing the observed spatial distribution of the summer rainfall climatology and its interannual variability over Thailand, although the model underestimated both rainfall amount and its variability. Using Empirical Orthogonal Function (EOF) analysis, it is found that the IAP climate model reproduced creditably the spatial patterns of the first three dominant modes of summer rainfall in Thailand, whereas it underestimated the explained variance of the observed EOF-1 and overestimated the explained variance of the observed EOF-2 significantly. It was further found that the correlation between the observed rainfall anomalies in Thailand and the Niño3.4 index can be reproduced by the IAP model. However, the observed negative correlation is largely underestimated by the IAP climate model, and this could be the reason for the underestimation of explained variance of the EOF-1 by the IAP model. The evaluation results would be of great importance for further model improvement and thus potential application in seasonal prediction in the region.
1. Introduction
With the advances in scientific understanding and improvements in computing capabilities, the current general circulation models (GCMs) have involved many components of the Earth system and can be used for long-term simulations, ranging from seasons to decades, of historical climate and projection of future climate change [1]. These GCMs have been widely applied in climate studies and for seasonal climate forecasts from the global scale to the regional scale, and have been improved not only in spatial and vertical resolution but also in parameterizations, to obtain a better representation of the different processes within climate and earth system [2]. However, before adopting one specific model for the simulation and prediction of climate anomalies or hydro-meteorological disasters in any region, we need to first verify the model’s performance in the region [3]. It is also essential to identify the model’s systematic biases and the possible reasons for these biases, so that we can know the direction for further model improvement [4], as well as bias correction for better model applications.
Given the need for an enhanced understanding of rainfall variation and its impacts on societies and ecology, many studies have attempted to develop GCMs to provide this important information in advance in different time scales [1,2]. However, applying different climate models for a region could yield different results, as demonstrated by Li et al. [5], when evaluating the performance of GCMs in reproducing rainfall patterns over the Asian–Australian monsoon region. Following their results, it was found that climate models can generally reproduce the observed rainfall patterns over Southeast Asia (SEA) region, but still overestimated its intensity. It is also reported that rainfall climatology over the SEA region is still difficult to be simulated by an individual GCM, but can be improved when a multi-model ensemble approach is employed [6]. Furthermore, the skill of climate models in estimating rainfall over an area is also dependent upon the sea surface temperature (SST) specified during the model integration [7]. Besides, many efforts have been made to improve the model performance by increasing the GCM’s resolution [8]. Based on the improved high-resolution GCM outputs (20–50 km) that participated in the Coupled Model Intercomparison Project Phase 6 (CMIP6) [9], it was found that monsoon onset and rainfall climatology over the SEA can be simulated better than that of its original resolution [10]. Moreover, applying a bias correction method to a GCM output can also yield more realistic results than its original output [11]. However, model bias in rainfall simulation exhibits spatial variations, depending on the area and model configuration [7,11,12,13]; therefore, a systematic model evaluation is important before applying the climate model in the study region.
In Thailand, summer rainfall exhibits strong interannual variation; hence, it is exposed to frequent floods and drought conditions, leading to adverse impacts on many sectors (e.g., agriculture and economy) [14,15]. For instance, the 2011 flood was particularly severe as a result of record-breaking rainfall extremes that caused huge economic losses, estimated at 30 billion USD [16]. In turn, Khadka et al. [17] showed that devastating drought events occur every 6 years in the northeastern part of Thailand, with a notable impact on the agricultural sector. Moreover, summer rainfall in Thailand is largely influenced by the interannual variation in SST anomalies (SSTA) over the tropical Pacific Ocean (ENSO events) [15,18], which serves as a predictor of summer rainfall in the country [19,20,21]. Nonetheless, strong ENSO events are linked to summer rainfall extremes, as in the case that triggered the 2011 devastating flood event over Thailand [19]. Therefore, monthly and seasonal climate predictions are important for guidance in managing risks in the water resources of the country. During the past decade, the capability of dynamical regional climate models in reproducing rainfall characteristics has also been examined for Thailand [22,23]. Based on the previous studies, the simulation of rainfall characteristics in Thailand has remained a challenge, which could be largely ascribed to the complexity of the topography of the country [22,23], in addition to the inability of the models to reproduce the driving impact of ENSO events on summer rainfall [24,25,26]. Meanwhile, the model performance in simulating the rainfall characteristics is shown to be spatially and seasonally different [23] and was also dependent on the model’s physics parameterizations [22]. Hence, before applying any climate model for the climate simulation and prediction in a region, the behavior of the model in reproducing its historical climate variation must be evaluated first.
The atmospheric component of the Chinese Academy of Sciences–Earth System Model (CAS-ESM), the IAP-AGCM (Atmospheric GCM of the Institute of Atmospheric Physics, Chinese Academy of Sciences), has been widely applied for climate simulation and prediction studies over different parts of the world [27,28,29,30,31]. For example, it is found that the model can reproduce the observed relationship between the summer rainfall anomalies in East Asia and the East Asian subtropical western jet [30], and has shown promising applications for extreme event simulation and prediction over mid-latitude regions, particularly in China [27,29]. For the tropical region, it also shows good skills in the simulation of temperature and rainfall variations in West Africa [28]. In an attempt to apply the IAP climate model for a climate simulation and future climate change projection study, it is imperative to understand whether the IAP model can reproduce the observed characteristics of summer rainfall over Thailand. Moreover, for the potential application of the IAP climate model in the seasonal prediction for disaster management in Thailand, it is very important to understand whether the IAP model can reproduce the observed relationship between ENSO and summer rainfall anomalies in the region, as ENSO has already been identified as the key driver and predictor for summer rainfall anomalies in Thailand [19,20,21,32]. Furthermore, it is also interesting to understand how the model’s capability in reproducing the ENSO and summer rainfall relationship can be linked to the model’s capability in simulating the observed rainfall variation in the country. The rest of the paper is organized as follows: a brief description of the IAP climate model, study region, data, and analytical method used are explained in Section 2; the results are presented in Section 3; and the discussion and conclusions are summarized in Section 4.
2. Model Description, Study Region, Data, and Methods
2.1. Model Description and Experimental Setup
The model used in this study is IAP-AGCM version 4.1 (IAP-AGCM4.1), with a horizontal resolution of about 1.4° × 1.4° and with 30 vertical levels, and the model top is at 2.2 hPa. Its dynamic core is formulated based on the transformed velocity as the control variable of air motion by the finite-difference method [33]. The model was originally developed based on a two-level atmospheric general climate model [34] and has been continually improved in its dynamic core, parametrizations, and adding a more realistic view of Earth’s complexity in later versions [35,36,37,38].
The model uses a finite-difference scheme with a terrain-following sigma vertical coordinate [39]. The model grid system is built from a two-dimensional horizontal staggered Arakawa C-grid [40]. Formulation of the governing equations and the finite-difference schemes of the current IAP-AGCM version is based on the baroclinic primitive equations with subtraction of the standard stratification and conserves the total available energy, which is a summation of kinetic energy, the available potential energy, and the available surface potential energy rather than total energy. Compared to its previous version, IAP-AGCM4.1 incorporates the more advanced physics parameterizations from the Community Atmosphere Model version 5 (CAM5) physics packages. A general evaluation of IAP-AGCM4.1 was done by Zhang et al. [33] and the model shows a reasonable performance.
An Atmospheric Model Intercomparison Project (AMIP)-type global simulation with IAP-AGCM4.1 was performed for the 1978–2012 period, which is driven by observed SST and sea-ice from the Hadley Centre Sea Ice and Sea Surface Temperature dataset (HadISST) [41]. The greenhouse gas concentrations, anthropogenic aerosol, and precursor gas emissions from the Coupled Model Intercomparison Project Phase 5 (CMIP5) [1] were applied during the simulation, which varies from year to year. The simulation was initialized from a former 10-year AMIP-like simulation forced by the observed climatology of the SST and sea ice concentration. The last 32 years (1981–2012) of the model’s results were used for the analysis, by discarding the first 3 years (1978–1980) as a spin-up period.
2.2. Study Region, Observation Data, and Model Evaluation Methods
Located in the SEA region, Thailand is significantly affected by the Asia monsoon system, with abundant rainfall recorded in the summer season, as well as a strong interannual variability of rainfall in the summer season. Meanwhile, the climate pattern over Thailand can be divided into five distinct sub-regions, namely, Central, Eastern, Northeastern, Northern, and Southern (see Figure 1), by which the first four sub-regions (i.e., the North, Northeast, Central, and East) may be aggregately called Upper Thailand [42].
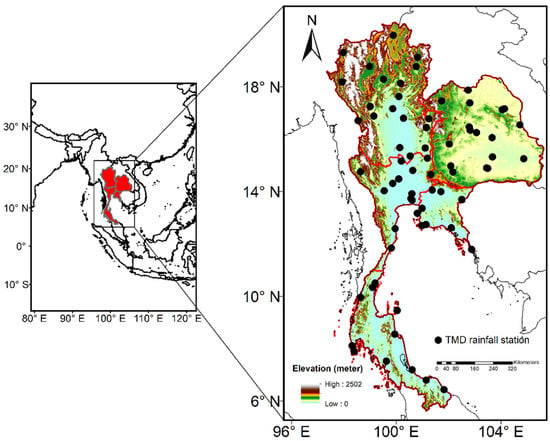
Figure 1.
Spatial distribution of the Thai Meteorological Department’s rainfall stations (black dots) used in this study. The red line represents the border of Thailand and its five sub-regions (i.e., the North, Northeast, Central, East, and South), superimposed on the terrain elevation obtained from the 30-m Shuttle Radar Topography Mission (SRTM) elevation data.
As seen in Figure 1, the geography of Thailand is quite different, in which the Northern part is mostly characterized by hilly and mountainous terrain. Meanwhile, the Northeastern part of Thailand is dominated by a high land plain, generally called the northeast plateau. For the Central part, the sub-region is mostly a low-level large plain area, with a mountainous range extending from the northern sub-region to the western part of the Central sub-region. In the Eastern part, most of the sub-region is plain land and valleys with small hills in its northern, central, and eastern parts, while its southern and southwestern parts are adjacent to the Gulf of Thailand. Whereas the Southern part of Thailand is a peninsula with the Andaman Sea adjacent to its western part, and the South China Sea in its eastern part.
In this study, rain gauge observations from 69 stations of the Thai Meteorological Department (TMD), covering the period of 1981 to 2012, were used for model evaluation. Originally, we obtained daily rainfall datasets for 120 rain gauge stations from the TMD. However, after general quality checks (e.g., negative rainfall, missing values, and length of data record), only 69 stations’ data have a long-historical record from 1981 to 2012. The selected 69 stations contain at least 80% of the observed daily rainfall (i.e., less than 20% missing values). The spatial distribution of the selected TMD stations is depicted in Figure 1. As seen, there is a relatively high density of TMD stations distributed across Thailand, consisting of 19 stations in the North, 18 stations in the Northeast, 12 stations in the Central, 9 stations in the East, and the rest in the South.
As summer is the rainy season in Thailand, the simulated summer (June–July–August; JJA) rainfall by the IAP climate model was examined. Besides the summer mean and the variability, we also investigated the model’s capability in reproducing the spatial–temporal variation in the observed rainfall in Thailand using the Empirical Orthogonal Function (EOF) analysis, which is one of the most popular and widely used methods to characterize the important features of the climate variables [43,44,45,46]. Meanwhile, the temporal correlation coefficient (TCC), as well as pattern correlation coefficients (PCC) between the observation and the model simulation, were also computed for comparison, following Equations (1) and (2), respectively.
where SD is the standard deviation of the observation (TMD) and simulation (IAP) over time (t) space for TCC (N is the number of years) and grid space (i) for PCC (M is the number of grid cells).
To quantify the error statistics between the observation and simulation, the monthly gridded rainfall based on the 69 TMD stations’ data was constructed with a 0.5° × 0.5° latitude/longitude resolution, via an iterative objective analysis [47]. Meanwhile, the simulated monthly rainfall was bi-linearly interpolated into a 0.5°-grid resolution to facilitate its comparison with the observation.
Moreover, regional statistics are herein provided for the aforementioned five sub-regions of Thailand (see Figure 1). Note that to obtain a regional daily or monthly time series, daily or monthly values from all stations or the grid cells in a sub-region were firstly aggregated and averaged.
3. Results
3.1. Climatological Distribution of Summer Rainfall
Figure 2a shows the 32-year mean of the observed summer rainfall over Thailand. Essentially, the seasonal rainfall shows a strong spatial variation in the sub-regions. For instance, in Northern Thailand, the average rainfall intensity ranges between 2.0 and 10.0 mm day−1 in the summer season over the sub-region. However, a lower rainfall intensity (<4.0 mm day−1) is observed in the narrow part of Central and a small part of Southern Thailand. Meanwhile, the highest intensity of the summer rainfall is found in Upper Thailand and some parts of the Southern sub-region (>10.0 mm day−1). Nonetheless, Figure 2a further suggests that rainfall distribution in the center of the upper part of Thailand is largely homogeneous, with a magnitude of about 6.0 mm day−1.
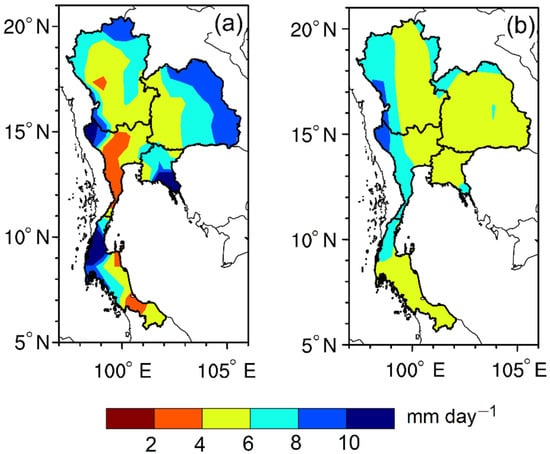
Figure 2.
Spatial distribution of summer rainfall (mm day−1) over Thailand averaged over 1981–2012: (a) observed; (b) simulated by the IAP AGCM4.1.
Furthermore, it is observed that during the summer season, the narrow end of Central Thailand experiences a drier condition relative to other parts of the sub-region, while a wetter condition is observed in the east, northeast, and western part of Central Thailand, and some parts of Southern Thailand. Notably, the foregoing demonstrates that the magnitude of rainfall in the Eastern sub-region and west coast of Southern Thailand are similar, perhaps because of their proximity to the Gulf of Thailand and the Andaman Sea, respectively. Meanwhile, a drier summer is observed on the southeast coast of Southern Thailand, with a rainfall intensity of less than 6.0 mm day−1. Therefore, during the summer season, Southern Thailand is remarkably characterized by dry conditions on its east coast and wet conditions on its west coast area. This is consistent with the findings of Wang et al. [48], which also demonstrated that a high rainfall intensity occurs on the southwest coast during the summer season. The authors further suggest that, in July, heavy rainfall is centered northward around 10° N, which is associated with the seasonal migration of the intertropical convergence zone (ITCZ) [48].
Figure 2b depicts the spatial distribution of the 32-year mean of the simulated summer rainfall as simulated by the IAP model. Interestingly, similar to the observation, the model simulated summer rainfall with an intensity of 10.0 mm day−1. As compared to the observation, the model reproduced largely the spatial patterns of rainfall distribution in the Northern part, Northeast, Central, East, and Southern parts of Thailand with PCC of 0.10, 0.07, 0.34, 0.44, and 0.33, respectively. This indicates that the spatial distribution of the simulated rainfall pattern suggests that the intensity varies depending on the sub-region (Figure 2b). In general, the model shows better performance in reproducing the spatial distribution pattern of observed rainfall intensity in areas where the rainfall intensity is 6.0 mm day−1, especially on the Central and east coast of Southern Thailand. However, in some sub-regions, the model could not reproduce the magnitude of the observed rainfall intensity but the model captured, to a considerable extent, the magnitude and the spatial distribution of rainfall intensity in the drier and moderate sub-regions. In turn, it underestimated the magnitude of the rainfall intensity in the wetter sub-regions (see, Figure 2b).
Furthermore, we show in Figure 3 the overall performance of the model in reproducing the average summer rainfall in each sub-region. It was found that the model seems to underestimate the summer rainfall, with a mean bias of −1.24 mm day−1 (Figure 3a). However, the dry bias is seemingly apparent in the Eastern part of Thailand and other areas characterized by mountainous terrain (Figure 3c–f), with bias = −3.65, −1.45, −0.14, and −1.75 mm day−1 for the East, Northeast, North, and the South, respectively. Although the IAP model seems to overestimate and underestimate the summer rainfall intensity in the Central and Northern parts of Thailand, respectively, the magnitude of the difference between the model and the observation is relatively small, with a magnitude between 0.49 and −0.14 mm day−1. Therefore, it can be inferred that the models performed better in simulating the magnitude of summer rainfall in the Central and Northern parts of Thailand. Meanwhile, we speculate that the model’s gross underestimation of the summer rainfall intensity over the Eastern part of Thailand may be related to its proximity to the Gulf of Thailand, where local impacts induced by the sea breeze process could be an important factor controlling the local and sub-regional rainfall intensity [49,50,51]. Moreover, it has been noted that global climate models find it difficult to resolve rainfall processes in areas smaller than their grid cell, especially in coastal regions affected by a range of physical processes [52,53,54]. Interestingly, Feng et al. [55] noted that the considerable systematic underestimation of summer rainfall over Thailand is one of the limitations of GCMs. Despite a significant improvement in CMIP6, a satisfactory accuracy of the rainfall simulations over a region is still a challenge for the GCM models [12].
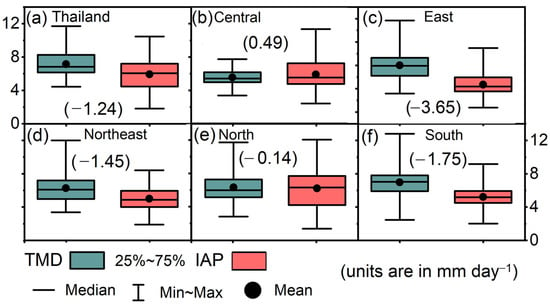
Figure 3.
The box–whisker plots show the maximum, minimum, mean, lower quartile, upper quartile, and median of the observed and simulated rainfall over the 32-year period (1981–2012) for (a) Thailand, (b) Central, (c) East, (d) Northeast, (e) North, and (f) South. Numbers in parenthesis present the bias between the mean of the observed and simulated rainfall.
3.2. Distribution of Interannual Variability of Summer Rainfall
Figure 4a shows the observed standard deviation (SD) that is commonly used to represent the interannual variability in rainfall. Notably, it is observed that the summer season rainfall variability is higher than 2.0 mm day−1 in most parts of Thailand, except in the Central part where the variability of the summer rainfall is relatively small (SD < 2.0 mm day−1). However, it was found that higher rainfall variability, with SD greater than 3.5 mm day−1, occurs in the upper part of the Northern, the fringes of the Northeast, the narrow tip of the East, and the west coast of the Southern sub-regions. In addition, a high summer rainfall variability is also observed in the western part of Central Thailand close to the mountainous areas, adjacent to Myanmar, whereas on the east coast of Southern Thailand, a lower rainfall variability, with SD less than 2.0 mm day−1 is observed.
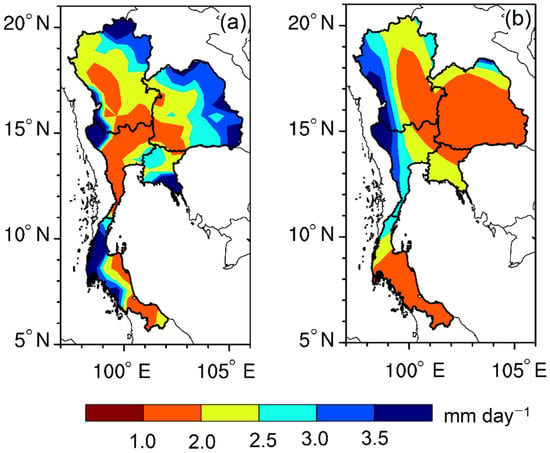
Figure 4.
Spatial pattern of the standard deviation of summer rainfall (mm day−1) over Thailand during 1981–2012: (a) observed; (b) simulated by IAP AGCM4.1.
As compared to the observation, the model’s capability in reproducing the spatial pattern of the observed variability is also largely dependent on the sub-region (Figure 4b). Overall, the model shows better performance in reproducing the spatial pattern of the rainfall variability in Central Thailand and followed by the Eastern and Southern parts, with a PCC equal to 0.70, 0.64, and 0.59, respectively. Additionally, it also was found that the IAP model reproduced to a reasonable extent the spatial pattern of the observed rainfall variability in Northeastern Thailand, with the PCC = 0.47, and fails to capture the spatial pattern of the observed rainfall variability over Northern Thailand, with a PCC less than 0.05. It is imperative to note that the IAP model underestimated the magnitude of the summer rainfall variability in some parts of Thailand where the SD is greater than 3.0 mm day−1, except in the western part of Central Thailand, where the simulated SD matches the observation. In fact, the model shows a good agreement with the observation in reproducing rainfall variability in some portions of Central, Northern, Northeast, and Southern Thailand. Moreover, the spatial pattern suggests that the model captured to a certain extent the distribution of the dry and wet zone on the east and west coasts of Southern Thailand.
3.3. Dominant Modes of Summer Rainfall and Their Variations
Next, we present comparatively the spatial–temporal variation of the simulated and observed dominant modes of summer rainfall over Thailand. Figure 5 shows the first three EOF modes of the observed summer rainfall and their corresponding IAP model simulated EOF modes. Essentially, Figure 5a–c indicates that the first EOF (EOF-1) and the second EOF (EOF-2) modes account for 23.1% and 20.7% of the total variance, respectively while 10.2% is accounted for by the third EOF (EOF-3). Moreover, it was found that the observed EOF-1 exhibits a dipolar structure, with a reverse signal in rainfall pattern in Central Thailand and elsewhere. It was also observed that the explained variances of the first two dominant modes are nearly equal, indicating these two dominant modes are equally important for rainfall variation patterns in Thailand. However, the EOF-2 exhibits a uniform pattern in most parts of Thailand. Whereas, the EOF-3 exhibits a dipolar mode with opposite rainfall signs in the northeast and elsewhere in Thailand.
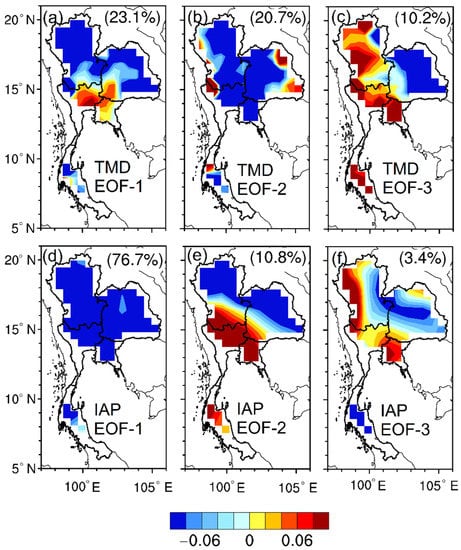
Figure 5.
Spatial distribution of the first three dominant EOF modes of summer rainfall over Thailand during 1981–2012: (a–c) observed; (d–f) IAP-AGCM4.1 simulation. Numbers in parenthesis indicate the explained variance.
Figure 5d indicates that the simulated summer rainfall EOF-1 mode is found to be relatively uniform and accounts for 76.7% of the total variance. Meanwhile, EOF-2 and EOF-3 exhibit a dipole structure that accounts only for 10.8%, and 3.4%, respectively, of the total variance (Figure 5d–f). As compared to the corresponding EOF mode of the observation, it can be found that the IAP model seems not to reproduce the spatial pattern of its corresponding observed EOF modes for the first two dominant patterns, with PCC = 0.05 for the EOF-1 and PCC = 0.15 for EOF-2. Remarkably, the spatial pattern of the simulated EOF-1 and observed EOF-2 show relatively similar patterns (see Figure 5b,d). This suggests that there is a shift in the simulated EOF models, such that the model reproduced the observed EOF-1 in its EOF-2 mode, as shown in Figure 5a,e, with the PCC = 0.25. Besides, the spatial pattern of the observed EOF-3 is similar to the simulated EOF-3 mode, with the PC = 0.22. Hence, we infer that the model can reproduce the spatial structures of the observed dominant EOF modes of summer rainfall over Thailand, albeit with the overestimation and underestimation of the observed explained variance of EOF-1 and EOF-2 respectively.
Furthermore, we examined the temporal variation in the observed dominant modes of the summer rainfall (Figure 6a–c; red lines). The PC-1 and PC-2 suggest that after the 1990s, the summer rainfall of Thailand exhibited strong interannual variation (Figure 6a,b), while PC-3 shows variation at a longer time scale (Figure 6c). Notably, the variation in SST anomalies (SSTA) in the tropical Pacific Ocean (ENSO event) plays an important role in controlling rainfall variability over Asia [56]. Hence, we further demonstrate the relationship between summer rainfall variation in Thailand and the ENSO index, the so-called Oceanic Niño Index (ONI) [57,58]. Meanwhile, the index is computed based on the variations in the 3-month running means of SST in the east-central tropical Pacific region defined as Niño3.4 [57].
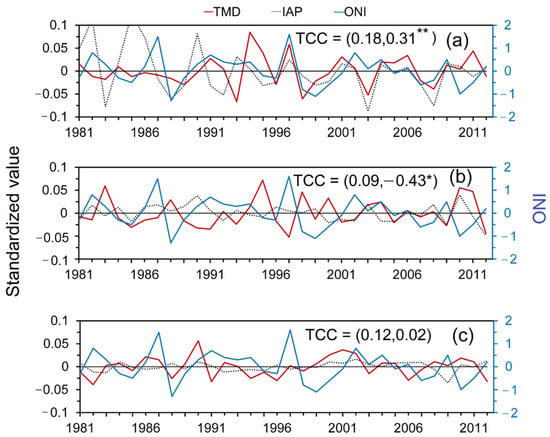
Figure 6.
PC time series for the first three dominant modes of observed (solid red line) and IAP-AGCM simulated (Dotted black line) summer rainfall over Thailand during 1981–2012 for (a) EOF-1, (b) EOF-2, and (c) EOF-3, together with the ONI value (solid blue line). The first TCC value in parenthesis indicates the correlation coefficient between TMD and IAP, while the second value is for the coefficient between TMD and ONI. A single asterisk (*) indicates significance at p < 0.05, while double asterisks (**) is for significance at p < 0.10.
The results show that the first two dominant PC time series of the observed rainfall are significantly correlated with ENSO, such that the temporal variation of EOF-1 shows a positive correlation with SSTA in the Niño3.4 region, with the TCC = 0.31 (statistically significant at 90% confidence level), while the observed PC-2 variation shows a negative correlation with the ENSO index (TCC = −0.43, statistically significant at 95% confidence level). This suggests that SSTA over the Niño3.4 region influences summer rainfall variation in Thailand. Moreover, many studies have revealed the inverse relationship between ENSO and Asian summer monsoon rainfall variation, such that drier conditions are experienced in an ENSO warm phase and wet conditions are recorded as a response to the ENSO cold phase [56]. This interannual variation pattern is found between summer rainfall and the ENSO episodes over Thailand, consistent with the findings of [18]. Furthermore, this relationship seems to be more pronounced during extreme rainfall events in the country [18]. The foregoing shows that the first two dominant EOF modes of the summer rainfall and their PC time series are largely influenced by the interannual variation in SSTA in the Niño3.4 region.
As compared to the observation, the simulated PC time series of the first three EOF modes also show strong interannual variation. However, the PC time series did not match well with their corresponding observed PC modes, with the TCC = 0.18, 0.09, and 0.12 for PC-1, PC-2, and PC-3, respectively. As indicated in Figure 5, the observed EOF-1 and the simulated EOF-2 exhibit relatively similar patterns and vice versa for the observed EOF-2 and the simulated EOF-1. Hence, we compared the TCC between the observed PC-1 and simulated PC-2 and vice versa. The results show that the observed PC-1 and the simulated PC-2 are similar, with the TCC equal to 0.25 (Figure 7a), which is higher than the TCC obtained when compared with their corresponding PC time series directly. A better relationship is obtained for the observed PC-2 and simulated PC-1, with the TCC equal to 0.44 (Figure 7b). This thus demonstrates that the model can reproduce the spatial and temporal pattern of the observed dominant EOF modes of summer rainfall over Thailand.
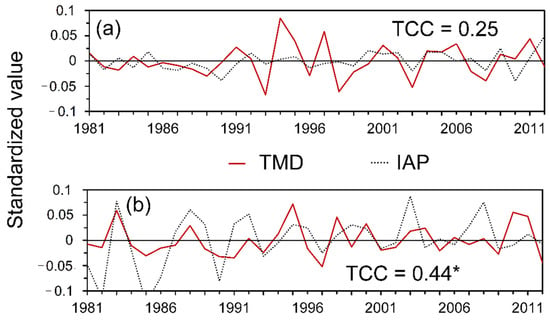
Figure 7.
PC time series for shifting modes of the observed (solid red line) and IAP-AGCM simulated (dotted black line) summer rainfall over Thailand during 1981–2012 for (a) TMD PC-1 versus IAP PC-2 and (b) TMD PC-2 versus IAP PC-2. A single asterisk (*) at the TCC value indicates significance at p < 0.05.
3.4. Relationship between ENSO and Summer Rainfall over Thailand
It is suggested that there is a significant negative relationship between summer rainfall over Thailand and the variation in SSTA in the east-central tropical Pacific Ocean [18]. Given that the study used only a few rain-gauge stations located only in the Central part of Thailand, it is, therefore, fair to state that the spatial–temporal variation in summer rainfall over Thailand in response to the variability of ENSO is not well understood. Hence, we re-examined the relationship between ENSO and the variation in summer rainfall in each sub-region of Thailand, using the 69 TMD rainfall stations (see Figure 1). Furthermore, we also investigated whether the model simulation can be ascribed to the model’s response to SSTA in the east-central tropical Pacific region. Hence, the Niño3.4 index was computed using observed SST data, which were also used to force the model simulation. The SST data were further used to calculate the relationship between the Niño3.4 index and summer rainfall anomalies in Thailand for both observation and model simulation. Note that the linear trend in the SST anomaly was removed before calculating the TCC between the rainfall time series and the Niño3.4 SSTA.
Figure 8a shows the spatial distribution of TCC between the Niño3.4 SSTA and observed summer rainfall anomalies in Thailand. It was found that indeed the rainfall variation in Thailand is negatively correlated with the ENSO in most parts of Thailand. Moreover, the results indicate that rainfall anomalies in upper Thailand are significantly and inversely correlated with the Niño3.4 index, with a TCC of about −0.4, especially in the Central, East, and Northern parts of Thailand. Besides the negative response of the rainfall to the ENSO signal, a positive correlation (TCC < 0.2) can also be found in the extremities of the Northeast and western part of Central Thailand, adjacent to Myanmar’s border.
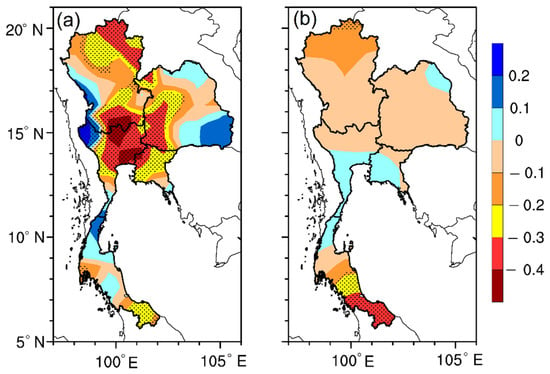
Figure 8.
Temporal correlation coefficient (TCC) between (a) the detrended anomalies of the observed summer rainfall and sea surface temperature anomalies (SSTA) in the Niño3.4 region during the 1981–2012 period, and (b) the same, but for the simulated rainfall and the SSTA in the Niño3.4 region. Dotted regions indicate a significant correlation at the 90% level.
Interestingly, the model can well reproduce the spatial distribution of the observed relationship between the Niño3.4 index and summer rainfall over Thailand (Figure 8b). Although the spatial pattern of the observed relationship between the summer rainfall and Niño3.4 index is significant in most parts of Thailand (at 99% significance levels), the simulated summer rainfall response to the ENSO is relatively weak (at TCC < 0.2) in most parts of Thailand, but the negative response of rainfall anomalies at the tip of the Southern sub-region to the ENSO is well reproduced by the model. The weaker correlation between the summer rainfall anomalies and the ENSO signal in IAP-AGCM4.1 can be ascribed to the fact that atmosphere–ocean coupling process is not considered in the atmospheric general circulation model used in this study [28], and it is further suggested that this underestimation could be the main reason for the underestimation of the explained variance in EOF-1 by the IAP model.
4. Discussion and Conclusions
This study evaluates the performance of the IAP atmospheric general circulation model version 4.1 (IAP-AGCM4.1) in simulating summer rainfall variation over Thailand using the model’s AMIP simulation results for the 1981–2012 period. Specifically, in comparison with the observed TMD station-gauge rainfall data, we focused on the model’s capability in reproducing the observed summer rainfall distribution, interannual variabilities, and the spatial–temporal variation for the 32-year period. To facilitate comparison, the observed and simulated rainfall datasets were interpolated into the same spatial resolution, and regional statistics were considered for five of Thailand’s sub-regions, namely, Central, East, Northeast, North, and Southern Thailand. Moreover, this study evaluated the similarity between the model and the observation using the temporal correlation coefficient (TCC) and pattern correlation coefficient (PCC). The spatial–temporal variation of the simulated rainfall was computed using the EOF analysis and then compared with the observed dominant modes of summer rainfall over Thailand. In addition, this study also examined the capability of IAP-AGCM4.1 in reproducing the observed summer rainfall response to the SSTA in the Niño3.4 region.
Results reveal that the model can reasonably reproduce the observed spatial distribution of summer rainfall over Thailand, with a better performance in the Northern and Central parts of Thailand. However, the model seems to underestimate the observed rainfall in some parts of Thailand, except in Central Thailand where the model overestimated the observed summer rainfall by 0.5 mm day−1. Furthermore, it is also found that the IAP-AGCM4.1 can reproduce the observed spatial distribution of interannual variability in summer rainfall, with better performance in Central, Eastern, and Southern Thailand. However, the low performance of the model in the northern and east coasts of Thailand can also be found, which could be related to the inability of the model in resolving rainfall processes over mountainous terrain because of its horizontal resolution [59,60], especially in the high mountainous areas of the Northern sub-region and upland high plateau in the Northeastern sub-region. A higher resolution IAP model is expected to capture the spatial distribution of summer rainfall in these mountainous areas.
Furthermore, it was found that the observed EOF-1 and EOF-2 account for about 23.1% and 20.7% of the total EOF variance. As such, the EOF-1 and EOF-2 are the most important dominant modes of summer rainfall over Thailand. The spatial pattern of the observed EOF-1 exhibit a dipole mode with an opposite rainfall sign mostly in Central Thailand and elsewhere in Thailand, while the EOF-2 exhibits a uniform pattern, which is found to be the dominant mode that is significantly associated with the ENSO. Interestingly, the simulated EOF-1 exhibits a similar pattern to the observed EOF-2, and vice versa for the simulated EOF-2 and the observed EOF-1. Furthermore, the TCC between the observed PC-1 and simulated PC-2 as well as the observed PC-2 and the simulated PC-1 is higher than the TCC obtained when they are directly compared with their corresponding PC time series. Hence, we infer that the IAP model can reproduce the observed dominant EOF modes of summer rainfall over Thailand, albeit with some level of overestimation of the observed EOF-1 loading.
Based on observation datasets, it was found that the observed summer rainfall over Thailand is negatively associated with SSTA in the Niño3.4 region, with the highest significant correlation of about 0.4 (in absolute terms) found in the Northern, Central, some parts of the Northeastern, and the Eastern sub-regions. The IAP model also captured the spatial pattern of the summer rainfall response to the ENSO signal, but with a certain degree of underestimation when compared with the observation. It is further suggested that the simulated weak response of summer rainfall to the ENSO signal in the model could be the main reason for the underestimation of explained variance of EOF-1 by IAP-AGCM4.1, and later versions of the IAP-coupled climate system model may improve the model’s performance over Thailand through a consideration of a robust atmosphere–ocean coupling processes. Therefore, further efforts are required to assess the performance of the IAP atmosphere–ocean coupled model in simulating summer rainfall variations over Thailand, as well as the associated air–sea interaction processes.
It is noteworthy that we only evaluated the relationship between ENSO and summer rainfall in Thailand as simulated in IAP-AGCM in this study. However, previous studies have shown that the SSTA over the Indian Ocean can also influence the summer rainfall anomalies over Thailand to a certain extent [19,32,61], so the model’s simulated response of summer rainfall to the Indian Ocean SST anomalies is subject to further verification in future studies, which could be helpful for the further model improvement. Furthermore, besides the model evaluation method and metrics used in this study, many other comprehensive statistical metrics have already been proposed [62,63]. Further climate model assessment with a combination of current and newly developed metrics will be needed, and this will be of great importance for better application of the climate model simulations and thus better seasonal disaster predictions over Thailand and the Southeast Asia region.
Author Contributions
Conceptualization and methodology, Z.L. and K.T.; validation, K.T.; formal analysis, K.T.; data curation, Y.Y.; C.W. and H.Z.; writing—original draft preparation, K.T.; writing—review and editing, Z.L. and V.N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was jointly supported by the National Key Research and Development Program of China (2017YFA0604304), and the Thailand Science Research and Innovation (TSRI) under Fundamental Fund No. 48873 and No. 160399. The numerical experiment is conducted at “Earth System Science Numerical Simulator Facility” (EarthLab) which is supported by the National Key Scientific and Technological Infrastructure project.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors sincerely thank the Thai Meteorological Department (TMD) for the daily rainfall data for rainfall data. Kritanai Torsri also thanks to the CAS-TWAS President’s Fellowship Programme.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Vitart, F.; Robertson, A.W. The sub-seasonal to seasonal prediction project (S2S) and the prediction of extreme events. NPJ Clim. Atmos. Sci. 2018, 1, 3. [Google Scholar] [CrossRef]
- Dike, V.N.; Lin, Z.; Kece, F.; Langendijk, G.S.; Nath, D. Evaluation and multi-model projection of seasonal precipitation extremes over Central Asia based on CMIP6 simulations. Int. J. Climatol. 2022. [Google Scholar] [CrossRef]
- Nahar, J.; Johnson, F.; Sharma, A. Assessing the extent of non-stationary biases in GCMs. J. Hydrol. 2017, 549, 148–162. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.-M.; Wang, B. Evaluation of NESMv3 and CMIP5 models’ performance on simulation of Asian-Australian monsoon. Atmosphere 2018, 9, 327. [Google Scholar] [CrossRef]
- Raghavan, S.V.; Liu, J.; Nguyen, N.S.; Vu, M.T.; Liong, S.-Y. Assessment of CMIP5 historical simulations of rainfall over Southeast Asia. Theor. Appl. Climatol. 2017, 132, 989–1002. [Google Scholar] [CrossRef]
- Tang, W.; Lin, Z.-H.; Luo, L.-F. Assessing the seasonal predictability of summer precipitation over the Huaihe river basin with multiple APCC models. Atmos. Ocean. Sci. Lett. 2013, 6, 185–190. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.M.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Haarsma, R.J.; Roberts, M.J.; Vidale, P.L.; Senior, C.A.; Bellucci, A.; Bao, Q.; Chang, P.; Corti, S.; Fučkar, N.S.; Guemas, V.; et al. High Resolution Model Intercomparison Project (HighResMIP v1.0) for CMIP6. Geosci. Model Dev. 2016, 9, 4185–4208. [Google Scholar] [CrossRef]
- Hariadi, M.H.; Schrier, G.v.d.; Steeneveld, G.J.; Sopaheluwakan, A.; Tank, A.K.; Roberts, M.J.; Moine, M.P.; Bellucci, A.; Senan, R.; Tourigny, É.; et al. Evaluation of onset, cessation and seasonal precipitation of the Southeast Asia rainy season in CMIP5 regional climate models and HighResMIP global climate models. Int. J. Climatol. 2021, 42, 3007–3024. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, Z.L. An improved dynamical downscaling method with GCM bias corrections and its validation with 30 years of climate simulations. J. Clim. 2012, 25, 6271–6286. [Google Scholar] [CrossRef]
- Xin, X.; Wu, T.; Zhang, J.; Yao, J.; Fang, Y. Comparison of CMIP6 and CMIP5 simulations of precipitation in China and the East Asian summer monsoon. Int. J. Climatol. 2020, 40, 6423–6440. [Google Scholar] [CrossRef]
- Tan, Y.; Guzman, S.M.; Dong, Z.; Tan, L. Selection of effective GCM bias correction methods and evaluation of hydrological response under future climate scenarios. Climate 2020, 8, 108. [Google Scholar] [CrossRef]
- Komori, D.; Nakamura, S.; Kiguchi, M.; Nishijima, A.; Yamazaki, D.; Suzuki, S.; Kawasaki, A.; Oki, K.; Oki, T. Characteristics of the 2011 Chao Phraya River flood in Central Thailand. Hydrol. Res. Lett. 2012, 6, 41–46. [Google Scholar] [CrossRef]
- Limsakul, A.; Paengkaew, W.; Kummueang, A.; Limjirakan, S.; Suttamanuswong, B. PDSI-based variations of droughts and wet spells in Thailand: 1951–2005. EnvironmentAsia 2010, 4, 12–20. [Google Scholar]
- Gale, E.L.; Saunders, M.A. The 2011 Thailand flood: Climate causes and return periods. Weather 2013, 68, 233–237. [Google Scholar] [CrossRef]
- Khadka, D.; Babel, M.S.; Shrestha, S.; Virdis, S.G.P.; Collins, M. Multivariate and multi-temporal analysis of meteorological drought in the northeast of Thailand. Weather Clim. Extrem. 2021, 34, 100399. [Google Scholar] [CrossRef]
- Singhrattna, N.; Rajagopalan, B.; Kumar, K.K.; Clark, M. Interannual and interdecadal variability of Thailand summer monsoon season. J. Clim. 2005, 18, 1697–1708. [Google Scholar] [CrossRef]
- Imada, Y.; Kanae, S.; Kimoto, M.; Watanabe, M.; Ishii, M. Predictability of Persistent Thailand Rainfall during the Mature Monsoon Season in 2011 Using Statistical Downscaling of CGCM Seasonal Prediction. Mon. Weather Rev. 2015, 143, 1166–1178. [Google Scholar] [CrossRef]
- Singhrattna, N.; Rajagopalan, B.; Clark, M.; Krishna Kumar, K. Seasonal forecasting of Thailand summer monsoon rainfall. Int. J. Climatol. 2005, 25, 649–664. [Google Scholar] [CrossRef]
- Supriyasilp, T.; Pongput, K. El Niño-Southern Oscillation and rainfall characteristics in Northern Thailand: Implications for adaptation in rainfed farms. Reg. Environ. Chang. 2021, 21, 123. [Google Scholar] [CrossRef]
- Chotamonsak, C.; Salathe, E.; Kreasuwan, J.; Chantara, S. Evaluation of precipitation simulations over Thailand using a WRF regional climate model. Chiang Mai J. Sci. 2012, 39, 623–628. [Google Scholar]
- Torsri, K.; Octaviani, M.; Manomaiphiboon, K.; Towprayoon, S. Regional mean and variability characteristics of temperature and precipitation over Thailand in 1961–2000 by a regional climate model and their evaluation. Theor. Appl. Climatol. 2012, 113, 289–304. [Google Scholar] [CrossRef]
- Bellenger, H.; Guilyardi, E.; Leloup, J.; Lengaigne, M.; Vialard, J. ENSO representation in climate models: From CMIP3 to CMIP5. Clim. Dyn. 2014, 42, 1999–2018. [Google Scholar] [CrossRef]
- Dieppois, B.; Rouault, M.; New, M. The impact of ENSO on Southern African rainfall in CMIP5 ocean atmosphere coupled climate models. Clim. Dyn. 2015, 45, 2425–2442. [Google Scholar] [CrossRef]
- Hayashi, M.; Jin, F.-F.; Stuecker, M.F. Dynamics for El Niño-La Niña asymmetry constrain equatorial-Pacific warming pattern. Nat. Commun. 2020, 11, 4230. [Google Scholar] [CrossRef]
- Dong, X.; Xue, F.; Zhang, H.; Zeng, Q.-C. Evaluation of surface air temperature change over China and the globe during the twentieth century in IAP AGCM4.0. Atmos. Ocean. Sci. Lett. 2012, 5, 435–438. [Google Scholar] [CrossRef][Green Version]
- Adeniyi, M.O.; Lin, Z.; Zhang, H. Evaluation of the performance of IAP-AGCM4.1 in simulating the climate of West Africa. Theor. Appl. Climatol. 2018, 136, 1419–1434. [Google Scholar] [CrossRef]
- Lin, Z.-H.; Yu, Z.; Zhang, H.; Wu, C.-L. Quantifying the attribution of model bias in simulating summer hot days in China with IAP AGCM 4.1. Atmos. Ocean. Sci. 2016, 9, 436–442. [Google Scholar] [CrossRef]
- Yan, Z.-B.; Lin, Z.-H.; Zhang, H. The relationship between the East Asian Subtropical Westerly Jet and summer precipitation over East Asia as simulated by the IAP AGCM4.0. Atmos. Ocean. Sci. Lett. 2014, 7, 487–492. [Google Scholar] [CrossRef]
- Su, T.; Xue, F.; Zhang, H. Simulating the intraseasonal variation of the East Asian summer monsoon by IAP AGCM4.0. Adv. Atmos. Sci. 2014, 31, 570–580. [Google Scholar] [CrossRef]
- Bridhikitti, A. Connections of ENSO/IOD and aerosols with Thai rainfall anomalies and associated implications for local rainfall forecasts. Int. J. Climatol. 2013, 33, 2836–2845. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.; Zeng, Q.-C. Sensitivity of simulated climate to two atmospheric models: Interpretation of differences between dry models and moist models. Mon. Weather Rev. 2013, 141, 1558–1576. [Google Scholar] [CrossRef]
- Zeng, Q.-C.; Zhang, X.-H.; Liang, X.-Z.; Yuan, C.-G.; Chen, S.-F. Documentation of IAP (Institute of Atmospheric Physics) Two-Level Atmospheric General Circulation Model; Institute of Atmospheric Physics, Chinese Academy of Sciences: Beijing, China, 1989. [Google Scholar]
- Bi, X. IAP 9L AGCM and Climate Simulation. Ph.D. Dissertation, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China, 1993; 210p. (In Chinese). [Google Scholar]
- Liang, X. Description of a nine-level grid point atmospheric general circulation model. Adv. Atmos. Sci. 1996, 13, 269–298. [Google Scholar] [CrossRef]
- Zuo, R. Development of New Generation Grid Point Atmospheric General Circulation Model with High Resolution. Ph.D. Thesis, China People’s Liberation Army University of Science and Technology, Changsha, China, 2003; 328p. (In Chinese). [Google Scholar]
- Zhang, H. Development of IAP Atmospheric General Circulation Model Version 4.0 and Its Climate Simulations. Ph.D. Thesis, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China, 2009; 194p. (In Chinese). [Google Scholar]
- Phillips, N.A. A coordinate system having some special advantages for numerical forecasting. J. Meteorol. 1957, 14, 184–185. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational design of the basic dynamical processes of the UCLA general circulation model. In Methods in Computational Physics: Advances in Research and Applications; Chang, J., Ed.; Elsevier: Amsterdam, The Netherlands, 1977; Volume 17, pp. 173–265. [Google Scholar]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108, 4407. [Google Scholar] [CrossRef]
- TMD. Climate of Thailand. Available online: http://www.tmd.go.th/en/archive/thailand_climate.pdf (accessed on 20 March 2022).
- Navarra, A.; Simoncini, V. Empirical Orthogonal Functions. In A Guide to Empirical Orthogonal Functions for Climate Data Analysis; Springer: Amsterdam, The Netherlands, 2010; pp. 39–67. [Google Scholar]
- Hu, W.; Newell, R.E.; Wu, Z.-X. Modes of variability of global sea surface temperature, free atmosphere temperature and oceanic surface energy flux. Clim. Dyn. 1994, 10, 377–393. [Google Scholar] [CrossRef]
- Polonskii, A.B.; Basharin, D.V. Large-scale patterns of Eurasian surface meteorological fields influenced by the climate shift of 1976–1977. Russ. Meteorol. Hydrol. 2008, 33, 280–289. [Google Scholar] [CrossRef]
- Rao, A.R.; Hsieh, C.H. Empirical orthogonal function analysis of rainfall and runoff series. Water Resour. Manag. 1991, 4, 235–250. [Google Scholar] [CrossRef]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Wang, Z.; Chang, C.P.; McBride, J.; Liu, C.-H. Annual cycle of Southeast Asia—Maritime continent rainfall and the asymmetric monsoon transition. J. Clim. 2005, 18, 287–301. [Google Scholar] [CrossRef]
- Nounmusig, W. Analysis of rainfall in the eastern Thailand. Int. J. GEOMATE 2018, 14, 150–155. [Google Scholar] [CrossRef]
- Miller, S.T.K.; Keim, B.D.; Talbot, R.W.; Mao, H. Sea breeze: Structure, forecasting, and impacts. Rev. Geophys. 2003, 41, 1011. [Google Scholar] [CrossRef]
- Alomar-Garau, G.; Grimalt-Gelabert, M. Impacts of coastal breezes on the environment and human Life: The case of Mallorca (Western Mediterranean). Coasts 2022, 2, 2. [Google Scholar] [CrossRef]
- Fagundes, M.; Litvin, S.Y.; Micheli, F.; De Leo, G.; Boch, C.A.; Barry, J.P.; Omidvar, S.; Woodson, C.B. Downscaling global ocean climate models improves estimates of exposure regimes in coastal environments. Sci. Rep. 2020, 10, 14227. [Google Scholar] [CrossRef]
- Crosman, E.T.; Horel, J.D. Sea and lake breezes: A review of numerical studies. Bound.-Layer Meteorol. 2010, 137, 1–29. [Google Scholar] [CrossRef]
- Zhong, S.; Takle, E.S. The effects of large-scale winds on the sea land-breeze circulations in an area of complex coastal heating. J. Appl. Meteorol. Climatol. 1993, 32, 1181–1195. [Google Scholar] [CrossRef]
- Feng, J.; Wei, T.; Dong, W.; Wu, Q.; Wang, Y. CMIP5/AMIP GCM simulations of East Asian summer monsoon. Adv. Atmos. Sci. 2014, 31, 836–850. [Google Scholar] [CrossRef]
- Wang, B.; Luo, X.; Liu, J. How robust is the Asian precipitation–ENSO relationship during the industrial warming period (1901–2017). J. Clim. 2020, 33, 2779–2792. [Google Scholar] [CrossRef]
- NOAA. Cold & Warm Episodes by Season. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 20 March 2022).
- Glantz, M.H.; Ramirez, I.J. Reviewing the Oceanic Niño Index (ONI) to enhance societal readiness for El Niño’s impacts. Int. J. Disaster Risk Sci. 2020, 11, 394–403. [Google Scholar] [CrossRef]
- Cannon, F.; Carvalho, L.M.V.; Jones, C.; Norris, J.; Bookhagen, B.; Kiladis, G.N. Effects of topographic smoothing on the simulation of winter precipitation in high mountain Asia. J. Geophys. Res. Atmos. 2017, 122, 1456–1474. [Google Scholar] [CrossRef]
- Posada-Marín, J.A.; Rendón, A.M.; Salazar, J.F.; Mejía, J.F.; Villegas, J.C. WRF downscaling improves ERA-Interim representation of precipitation around a tropical Andean valley during El Niño: Implications for GCM-scale simulation of precipitation over complex terrain. Clim. Dyn. 2019, 52, 3609–3629. [Google Scholar] [CrossRef]
- Chansaengkrachang, K.; Luadsong, A.; Aschariyaphotha, N. A Study of the Time Lags of the Indian Ocean Dipole and Rainfall Over Thailand by Using the Cross Wavelet Analysis. Arab. J. Sci. Eng. 2015, 40, 215–225. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, X.; Zhou, Q.; Chen, D.; Li, J. DISO: A rethink of Taylor diagram. Int. J. Climatol. 2019, 39, 2825–2832. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, D.; Hu, Z.; Chen, X. Decompositions of Taylor diagram and DISO performance criteria. Int. J. Climatol. 2021, 41, 5726–5732. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).