A Novel Reference-Based and Gradient-Guided Deep Learning Model for Daily Precipitation Downscaling
Abstract
1. Introduction
- For the task of downscaling of daily precipitation data, we selected daily average values for multiple meteorological elements. By correcting and filtering the data, a meteorological data set suitable for daily precipitation downscaling tasks was constructed.
- In order to extract the characteristics of different meteorological elements, we constructed a feature-extraction module called the residual dense channel attention block (RDCAB). The RDCAB has a strong convergence ability and great recognition ability for different features, both of which are suitable for the considered task.
- We also explored the effects of using the gradient feature and reference feature on precipitation downscaling. Due to the spatial discontinuity of precipitation itself, the precipitation area often corresponds to the area of a large precipitation gradient, such that its gradient information is also of great significance for precipitation reconstruction. Due to the ill-posed nature of precipitation, we used reference feature of high-resolution monthly precipitation data as a supplement based on deformable convolution.
- We propose a precipitation-downscaling model, named gradient-guided deep learning model (RBGGM), which is divided into a precipitation branch, a gradient branch, and a reference branch. The precipitation branch completes the downscaling of precipitation, while the gradient branch and the reference branch guide the downscaling of precipitation. Experiments show that our approach restores more details in areas with heavy precipitation.
2. Related Work
2.1. Single-Image Super-Resolution
2.2. Reference-Based Super-Resolution
2.3. SISR for Precipitation Downscaling
3. Dataset
3.1. Study Area
3.2. GPM Precipitation Data
3.3. ERA5 Re-Analysis Data
3.4. Topography
3.5. Data Pre-Processing
4. Methods
4.1. Feature Extraction Module
4.1.1. Channel Attention Block
4.1.2. Residual Dense Channel Attention Block
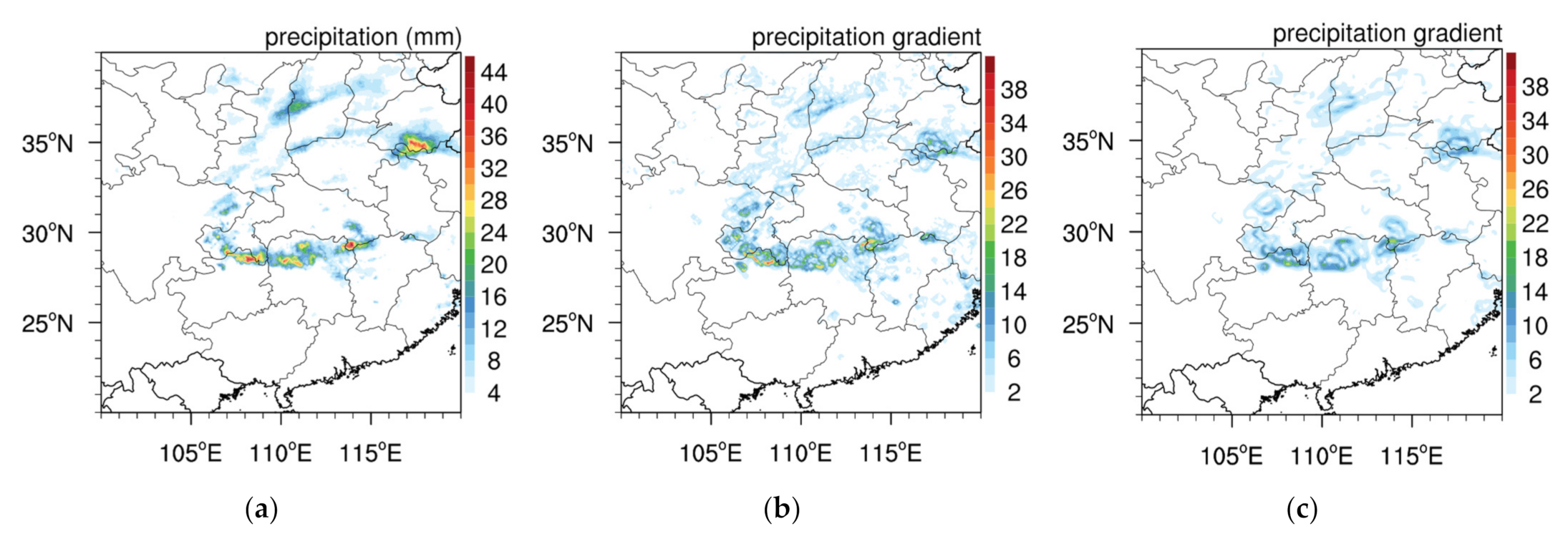
4.2. Gradient Feature for Precipitation Downscaling
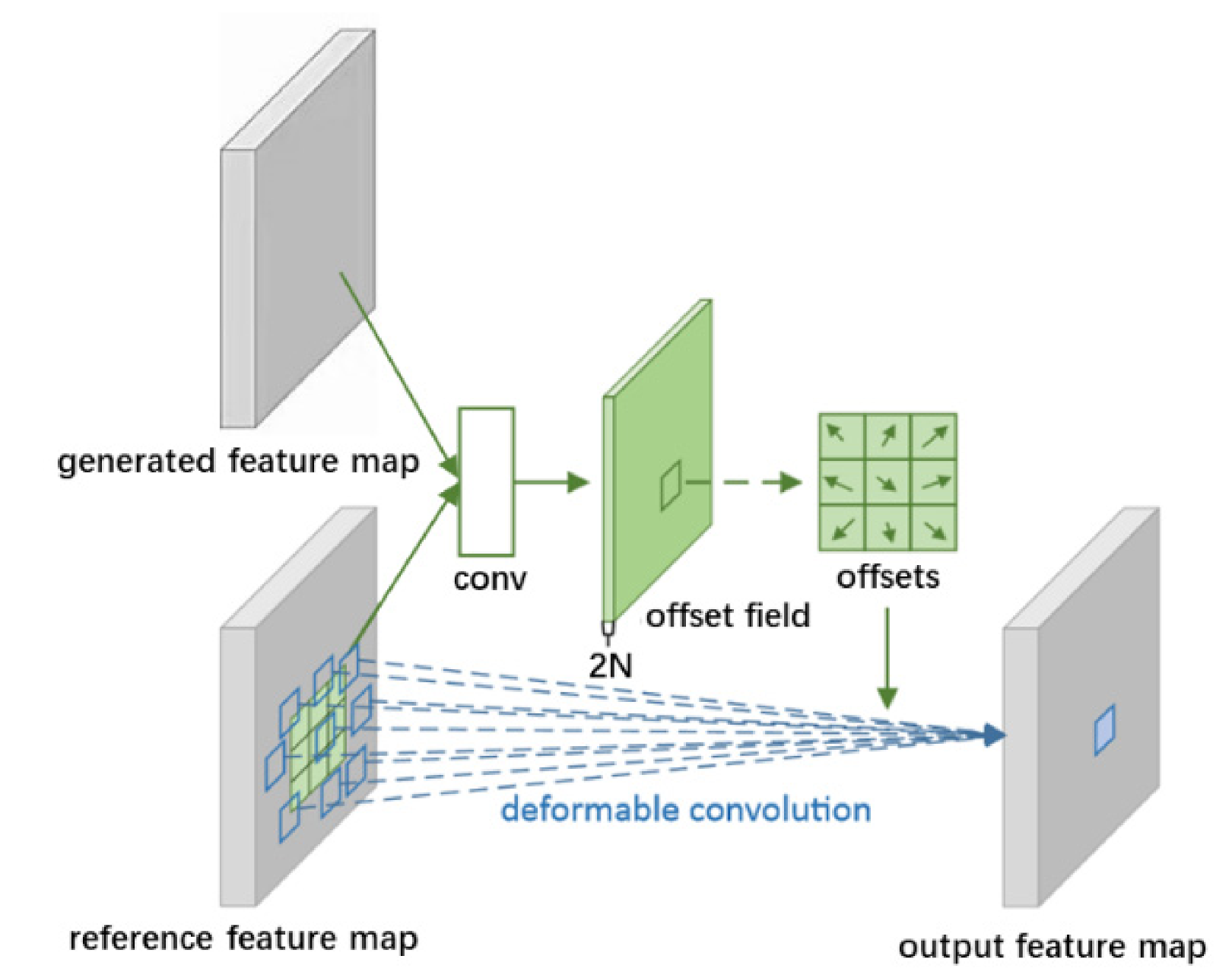
4.3. Reference Feature Extraction of Monthly Precipitation
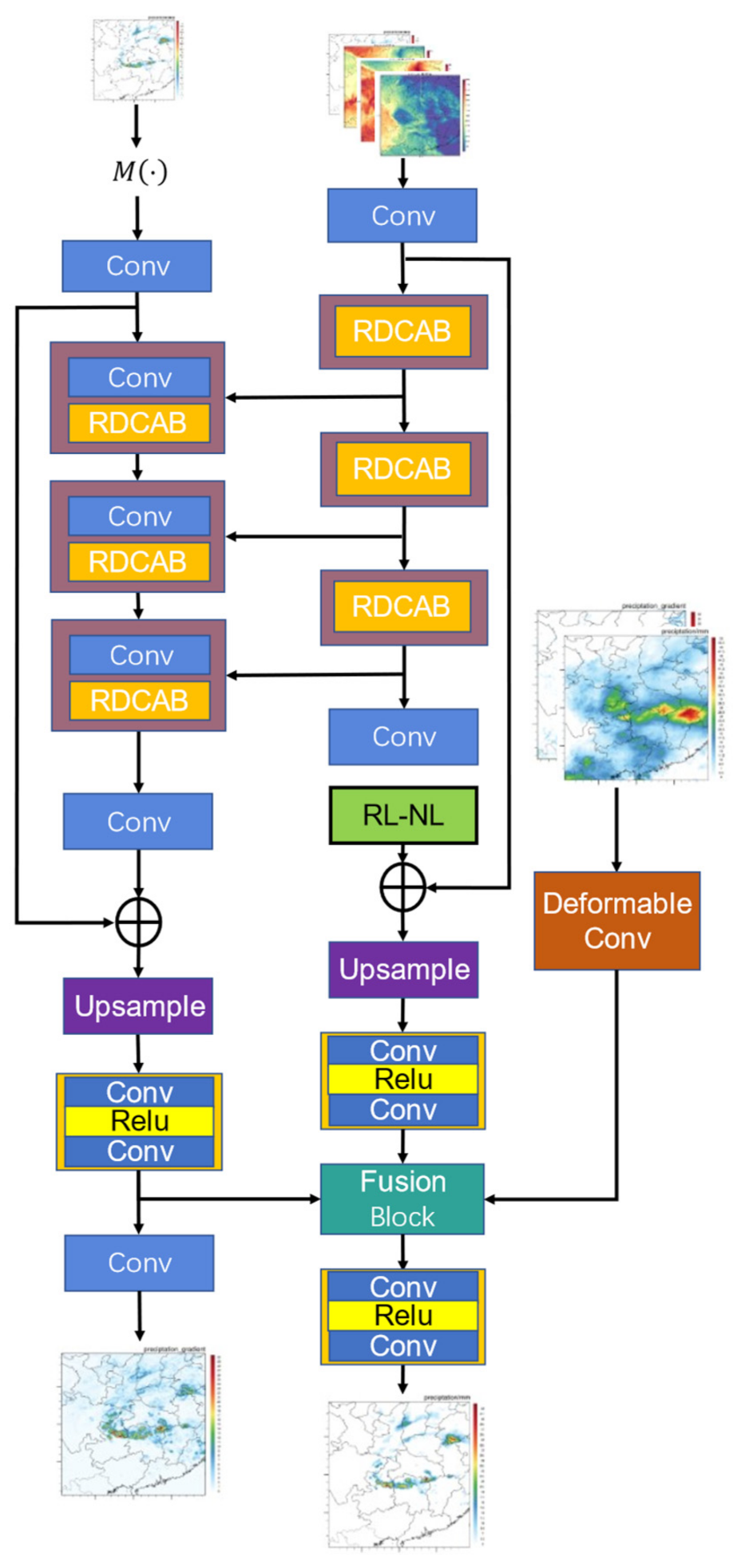
4.4. RBGGM for Precipitation Downscaling
4.5. Loss Functions
4.6. Baseline Methods
4.7. Evaluation Metrics
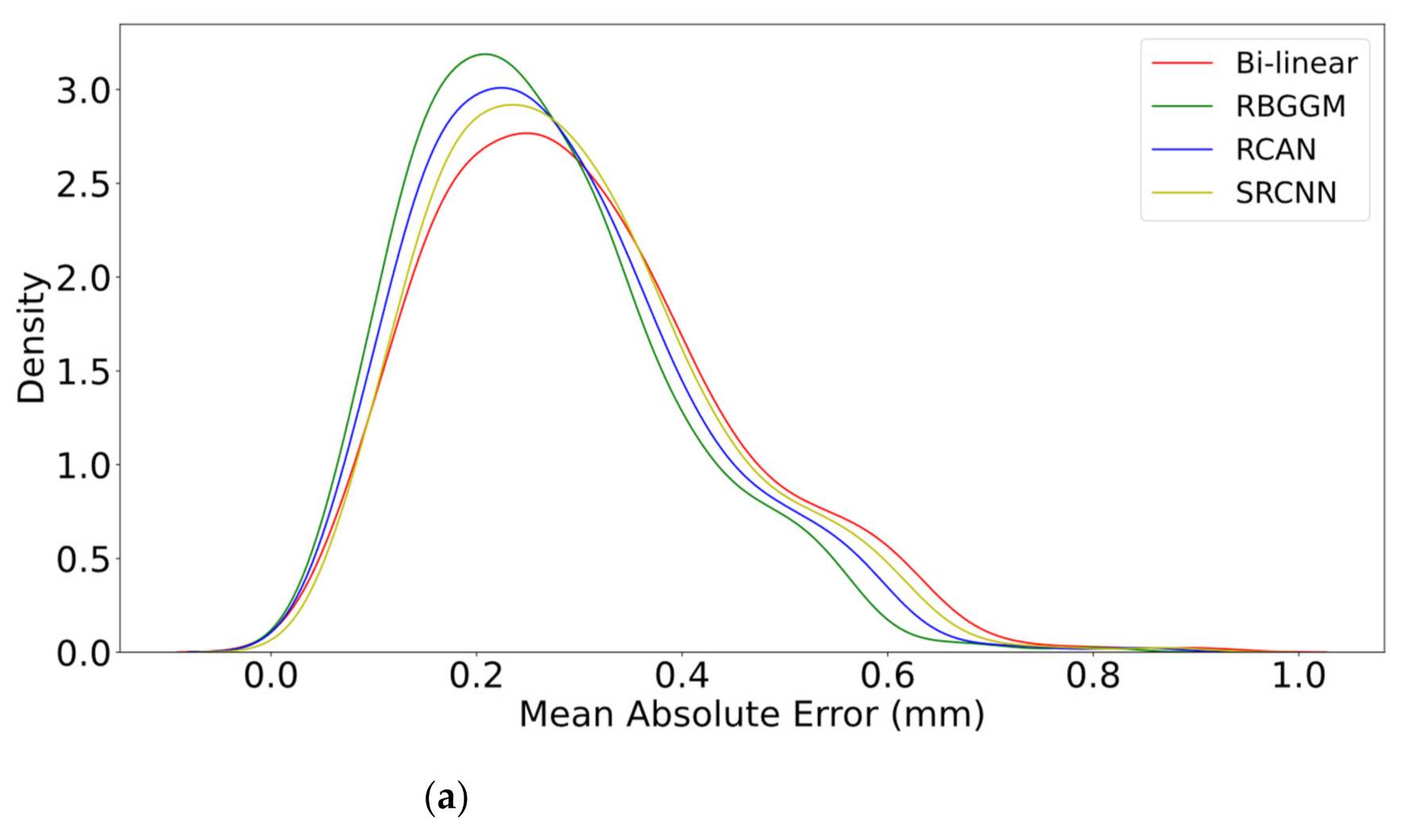
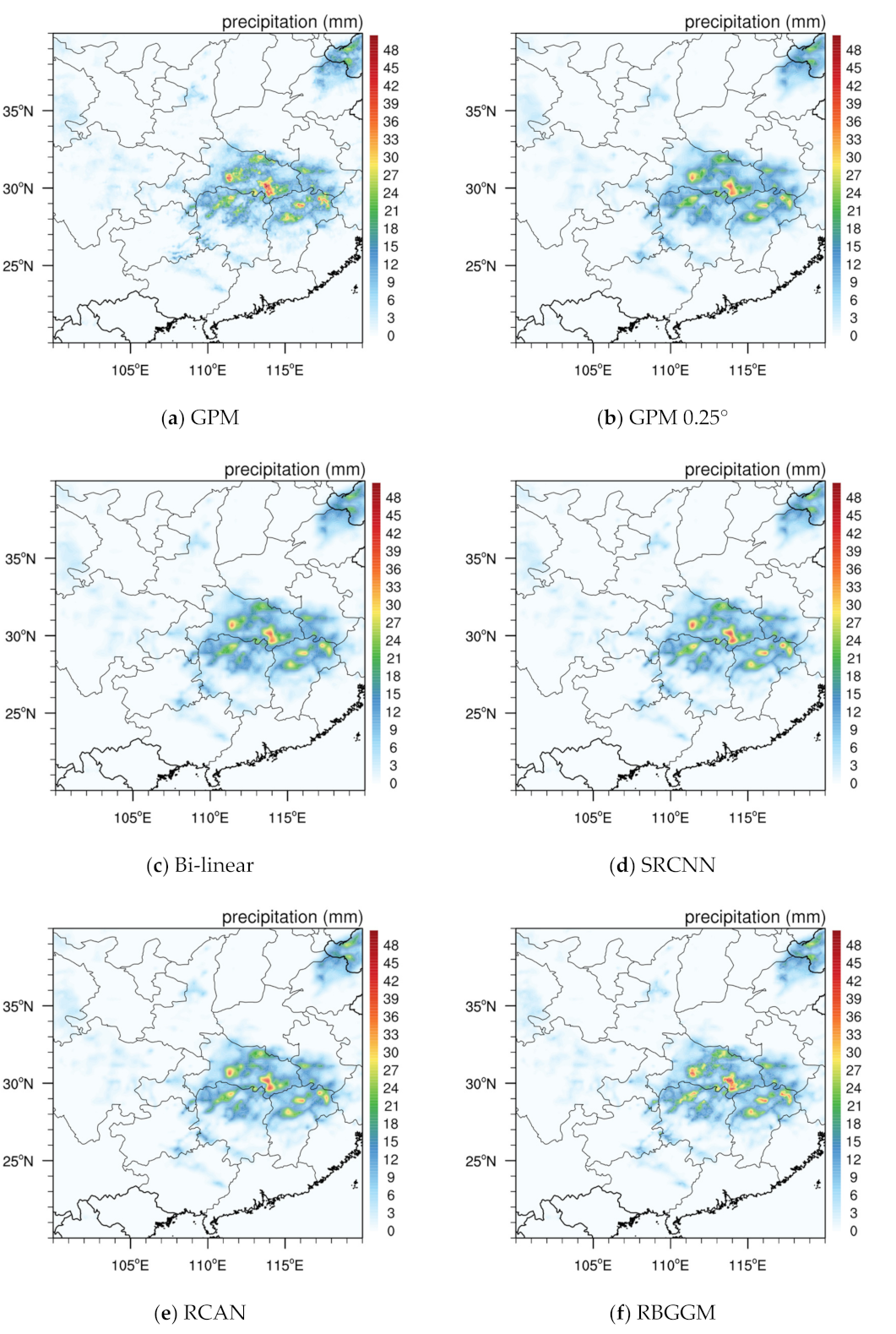
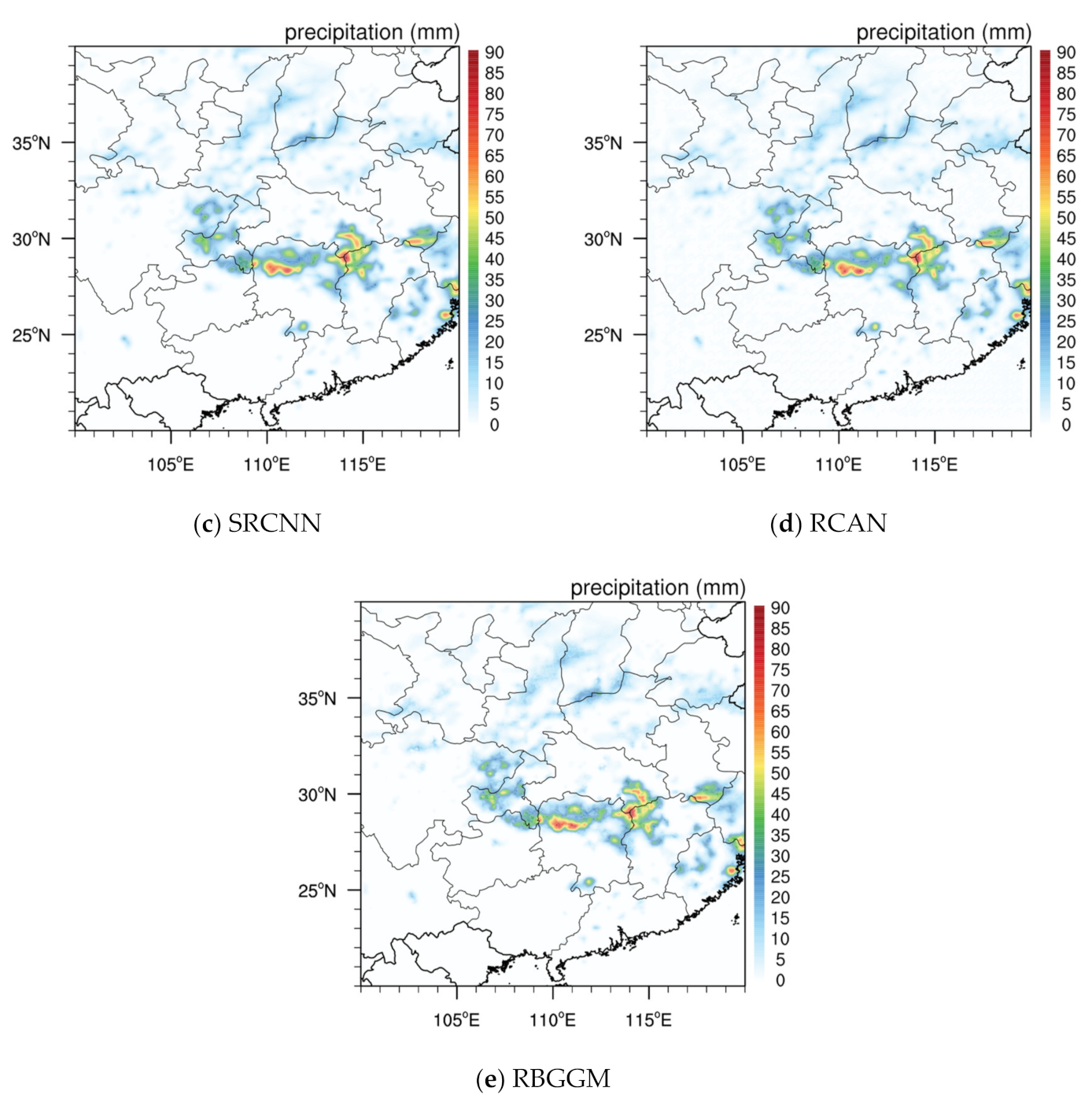
5. Results
5.1. Performance of the Generated Precipitation
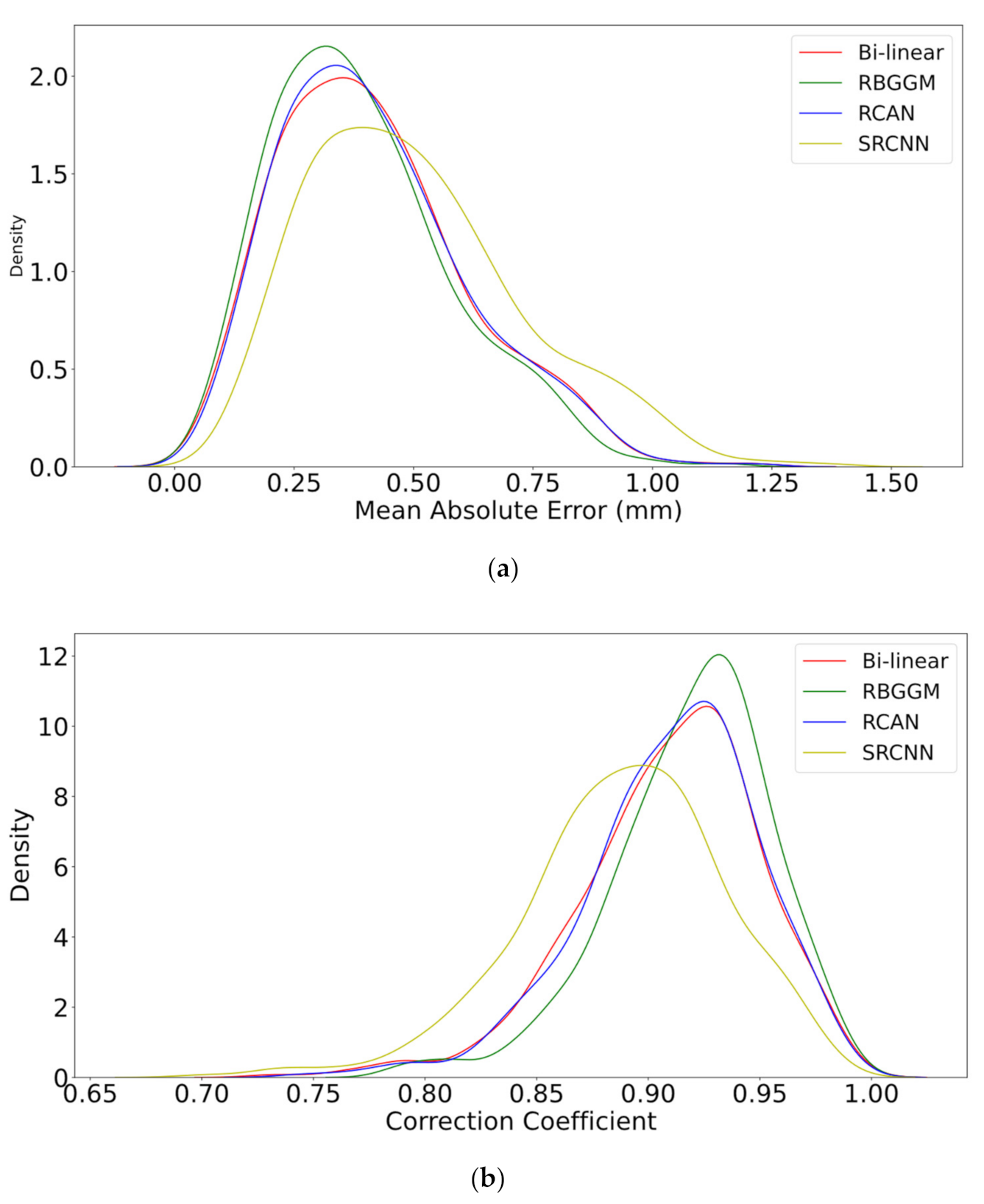
5.1.1. Performance on Evaluation Indicators
5.1.2. Performance on Precipitation Distribution
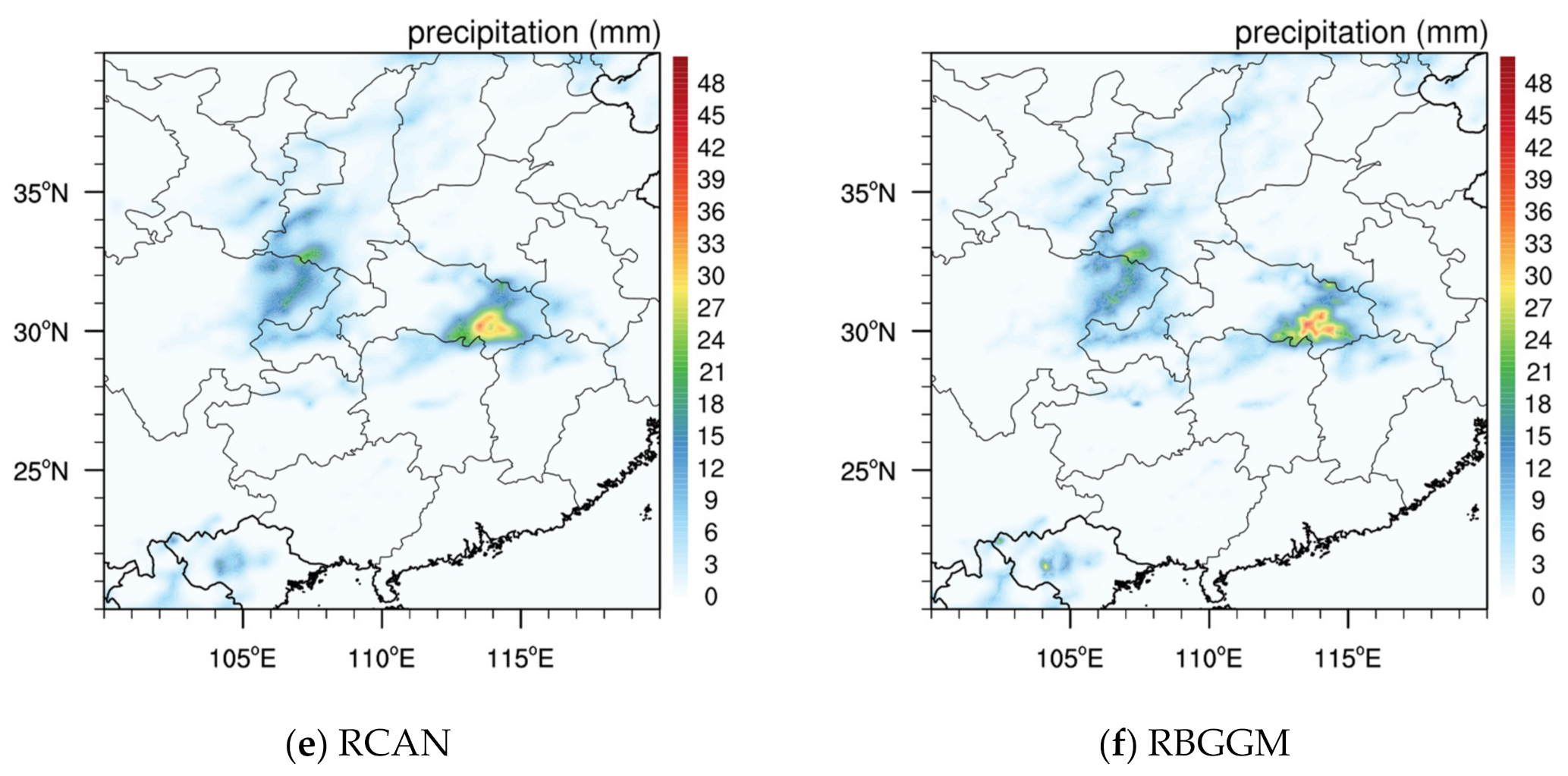
5.2. Scalability on TRMM Data Set and ERA5 Re-Analysis Data Set
5.3. Precipitation Downscaling Methods for Different Downscaling Factors
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Villén-Peréz, S.; Heikkinen, J.; Salemaa, M.; Mäkipää, R. Global warming will affect the maximum potential abundance of boreal plant species. Ecography 2020, 43, 801–811. [Google Scholar] [CrossRef]
- Aryal, Y.; Zhu, J. Evaluating the performance of regional climate models to simulate the US drought and its connection with El Nino Southern Oscillation. Theor. Appl. Climatol. 2021, 145, 1259–1273. [Google Scholar] [CrossRef]
- Schiermeier, Q. The real holes in climate science. Nature 2010, 463, 284–287. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Politi, N.; Vlachogiannis, D.; Sfetsos, A.; Nastos, P.T. High-resolution dynamical downscaling of ERA-Interim temperature and precipitation using WRF model for Greece. Clim. Dyn. 2021, 57, 799–825. [Google Scholar] [CrossRef]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Comput. Sci. Rev. 2021, 40, 100379. [Google Scholar] [CrossRef]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.; Zhang, L. Second-order attention network for single image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition CVPR 2019, Long Beach, CA, USA, 16–20 June 2019; pp. 11065–11074. [Google Scholar] [CrossRef]
- Wang, L.; Chen, R.; Han, C.; Yang, Y.; Liu, J.; Liu, Z.; Wang, X.; Liu, G.; Guo, S. An improved spatial–temporal downscaling method for TRMM precipitation datasets in Alpine regions: A case study in northwestern China’s Qilian Mountains. Remote Sens. 2019, 11, 870. [Google Scholar] [CrossRef]
- Elnashar, A.; Zeng, H.; Wu, B.; Zhang, N.; Tian, F.; Zhang, M.; Zhu, W.; Yan, N.; Chen, Z.; Sun, Z.; et al. Downscaling TRMM monthly precipitation using google earth engine and google cloud computing. Remote Sens. 2020, 12, 3860. [Google Scholar] [CrossRef]
- Yan, X.; Chen, H.; Tian, B.; Sheng, S.; Wang, J.; Kim, J.S. A Downscaling–Merging Scheme for Improving Daily Spatial Precipitation Estimates Based on Random Forest and Cokriging. Remote Sens. 2021, 13, 2040. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, J.; Wang, J.; Chen, Q.; Cao, J.; Deng, Z.; Xu, Y.; Tan, M. Closed-loop matters: Dual regression networks for single image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition CVPR 2020, Seattle, WA, USA, 14–19 June 2020; pp. 5407–5416. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 184–199. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 391–407. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 147–3155. [Google Scholar] [CrossRef]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.-H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 624–632. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision ECCV, Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar] [CrossRef]
- Ma, C.; Rao, Y.; Cheng, Y.; Chen, C.; Lu, J.; Zhou, J. Structure-preserving super resolution with gradient guidance. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition CVPR, Seattle, WA, USA, 13–19 June 2020; pp. 7769–7778. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Lin, Z.; Qi, H. Image super-resolution by neural texture transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (ICCVW), Seoul, South Korea, 27–28 October 2019; pp. 7982–7991. [Google Scholar] [CrossRef]
- Zheng, H.; Ji, M.; Wang, H.; Liu, Y.; Fang, L. Crossnet: An end-to-end reference-based super resolution network using cross-scale warping. In Proceedings of the European Conference on Computer Vision ECCV, Munich, Germany, 8–14 September 2018; pp. 88–104. [Google Scholar] [CrossRef]
- Kumar, B.; Chattopadhyay, R.; Singh, M.; Chaudhari, N.; Kodari, K.; Barve, A. Deep learning–based downscaling of summer monsoon rainfall data over Indian region. Theor. Appl. Climatol. 2021, 143, 1145–1156. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A.R. Deepsd: Generating high resolution climate change projections through single image super-resolution. In Proceedings of the 23rd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar] [CrossRef]
- Sha, Y.; Gagne, D.J., II.; West, G.; Stull, R. Deep-learning-based gridded downscaling of surface meteorological variables in complex terrain. Part II: Daily precipitation. J. Appl. Meteorol. Climatol. 2020, 59, 2075–2092. [Google Scholar] [CrossRef]
- Wang, F.; Tian, D.; Lowe, L.; Kalin, L.; Lehrter, J. Deep learning for daily precipitation and temperature downscaling. Water Resour. Res. 2021, 57, e2020WR029308. [Google Scholar] [CrossRef]
- Baño-Medina, J.; Manzanas, R.; Gutiérrez, J.M. Configuration and intercomparison of deep learning neural models for statistical downscaling. Geosci. Model Dev. 2020, 13, 2109–2124. [Google Scholar] [CrossRef]
- Mu, B.; Qin, B.; Yuan, S.; Qin, X. A Climate Downscaling Deep Learning Model considering the Multiscale Spatial Correlations and Chaos of Meteorological Events. Math. Probl. Eng. 2020, 2020, 7897824. [Google Scholar] [CrossRef]
- Cheng, J.; Kuang, Q.; Shen, C.; Liu, J.; Tan, X.; Liu, W. ResLap: Generating high-resolution climate prediction through image super-resolution. IEEE Access 2020, 8, 39623–39634. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated multi-satellite retrievals for the global precipitation measurement (GPM) mission (IMERG). In Satellite Precipitation Measurement; Springer: Cham, Switzerland, 2020; pp. 343–353. [Google Scholar]
- Chen, Y.; Zhang, A.; Zhang, Y.; Cui, C.; Wan, R.; Wang, B.; Fu, Y. A heavy precipitation event in the Yangtze River Basin led by an eastward moving Tibetan Plateau cloud system in the summer of 2016. J. Geophys. Res. Atmos. 2020, 125, e2020JD032429. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (ICCVW), Seoul, South Korea, 27–28 October 2019; pp. 3146–3154. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Mesinger, F. Bias adjusted precipitation threat scores. Adv. Geosci. 2010, 16, 137–142. [Google Scholar] [CrossRef][Green Version]
- Hwang, S.; Graham, W.D. Development and comparative evaluation of a stochastic analog method to downscale daily GCM precipitation. Hydrol. Earth Syst. Sci. 2013, 17, 4481–4502. [Google Scholar] [CrossRef]
- Marsham, J.H.; Trier, S.B.; Weckwerth, T.M.; Wilson, J.W. Observations of elevated convection initiation leading to a surface-based squall line during 13 June IHOP_2002. Mon. Weather Rev. 2011, 139, 247–271. [Google Scholar] [CrossRef][Green Version]
- Zhu, X.; Wu, T.; Li, R.; Xie, C.; Hu, G.; Qin, Y.; Wang, W.; Hao, J.; Yang, S.; Ni, J.; et al. Impacts of summer extreme precipitation events on the hydrothermal dynamics of the active layer in the Tanggula permafrost region on the Qinghai-Tibetan plateau. J. Geophys. Res. Atmos. 2017, 122, 11549–11567. [Google Scholar] [CrossRef]
- Wu, H.; Yang, Q.; Liu, J.; Wang, G. A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]








| Data Set | Resolution | Frequency | Variable | Period | Producer |
|---|---|---|---|---|---|
| GPM_3IMERGDF | 0.1° | 1 day | Daily precipitation | 2000–present | NASA GSFC PPS |
| GPM_3IMERGM | 0.1° | 1 month | Monthly precipitation | 2000–present | NASA GSFC PPS |
| ERA5 Re-analysis Data | 0.25° | 1 h | Temperature, relative humidity, etc. | 1979–present | ECMWF |
| DEM | 0.25° | / | height | / | ALOS |
| Confusion Matrix | Prediction | ||
|---|---|---|---|
| 1 | 0 | ||
| Reality | 1 | hit | miss |
| 0 | false alarm | correct negative | |
| Algorithm | MAE | CC | CSI | POD | FAR |
|---|---|---|---|---|---|
| Bi-linear | 0.301 | 0.950 | 0.826 | 0.856 | 0.041 |
| SRCNN | 0.294 | 0.952 | 0.802 | 0.845 | 0.060 |
| RCAN | 0.278 | 0.954 | 0.841 | 0.916 | 0.089 |
| RBGGM | 0.263 | 0.962 | 0.848 | 0.923 | 0.086 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, L.; Xiang, J.; Guan, J.; Zhang, F.; Zhao, Y.; Zhang, L. A Novel Reference-Based and Gradient-Guided Deep Learning Model for Daily Precipitation Downscaling. Atmosphere 2022, 13, 511. https://doi.org/10.3390/atmos13040511
Xiang L, Xiang J, Guan J, Zhang F, Zhao Y, Zhang L. A Novel Reference-Based and Gradient-Guided Deep Learning Model for Daily Precipitation Downscaling. Atmosphere. 2022; 13(4):511. https://doi.org/10.3390/atmos13040511
Chicago/Turabian StyleXiang, Li, Jie Xiang, Jiping Guan, Fuhan Zhang, Yanling Zhao, and Lifeng Zhang. 2022. "A Novel Reference-Based and Gradient-Guided Deep Learning Model for Daily Precipitation Downscaling" Atmosphere 13, no. 4: 511. https://doi.org/10.3390/atmos13040511
APA StyleXiang, L., Xiang, J., Guan, J., Zhang, F., Zhao, Y., & Zhang, L. (2022). A Novel Reference-Based and Gradient-Guided Deep Learning Model for Daily Precipitation Downscaling. Atmosphere, 13(4), 511. https://doi.org/10.3390/atmos13040511






