The Effect of Continuous Trapezoidal Straight Spoiler Plates on the Vortex-Induced Vibration of Wind Turbine Towers
Abstract
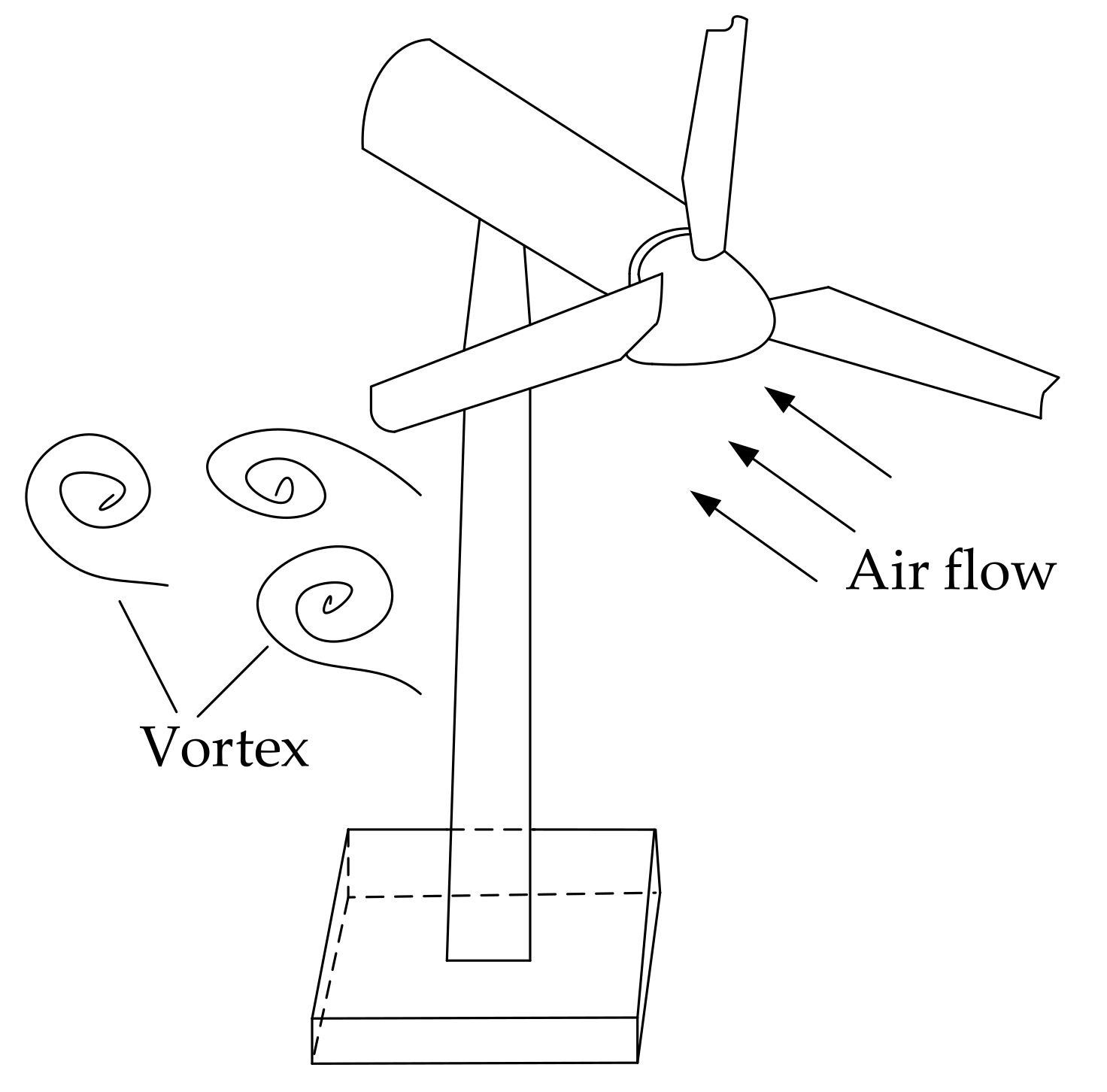
1. Introduction
2. Theoretical Basis
2.1. Flow Control Equation and Fluid Parameters
2.2. Control Equations of Cylindrical Vibration
3. Computational Model and Verification
3.1. Computational Fluid Domain
- Computing algorithm: laminar;
- Transient scheme: second-order backward Euler;
- Convergence criteria: the residual type is RMS, and the residual target is 0.001;
- To simulate the fluid state around the towers, the partial fluid domain which contains the monitor point is meshed as a boundary layer;
- The computational fluid domain is initialized with velocity–pressure conditions.
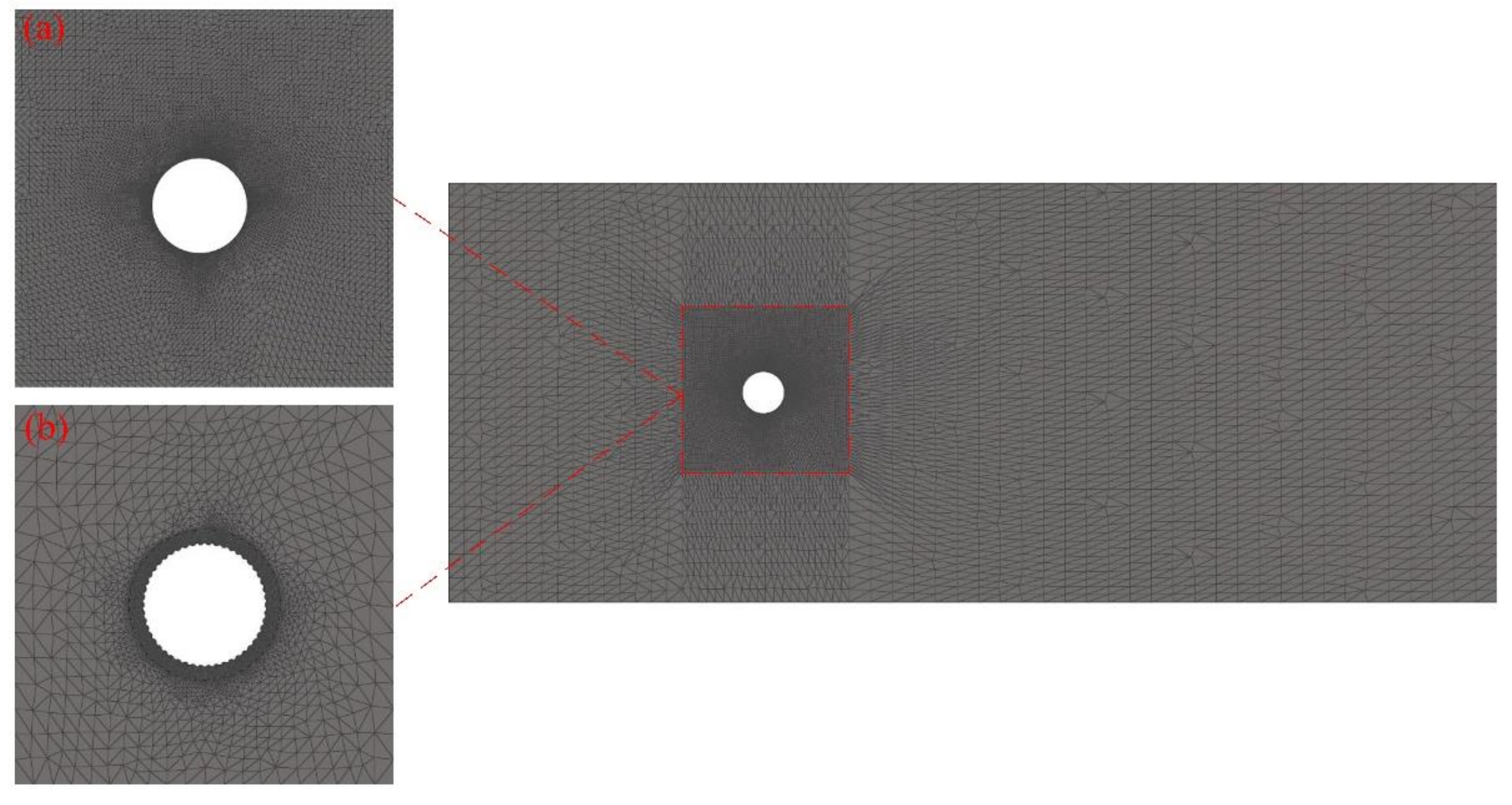
3.2. Meshing
- All elements are first-order tetrahedral, and the type is Solid185;
- Aspect ratio > 5;
- Tetrahedral collapse ratio < 0.5;
- Equiangle skew ratio > 0.7;
- Volume skew ratio > 0.95;
- Jacobian < 0.7.
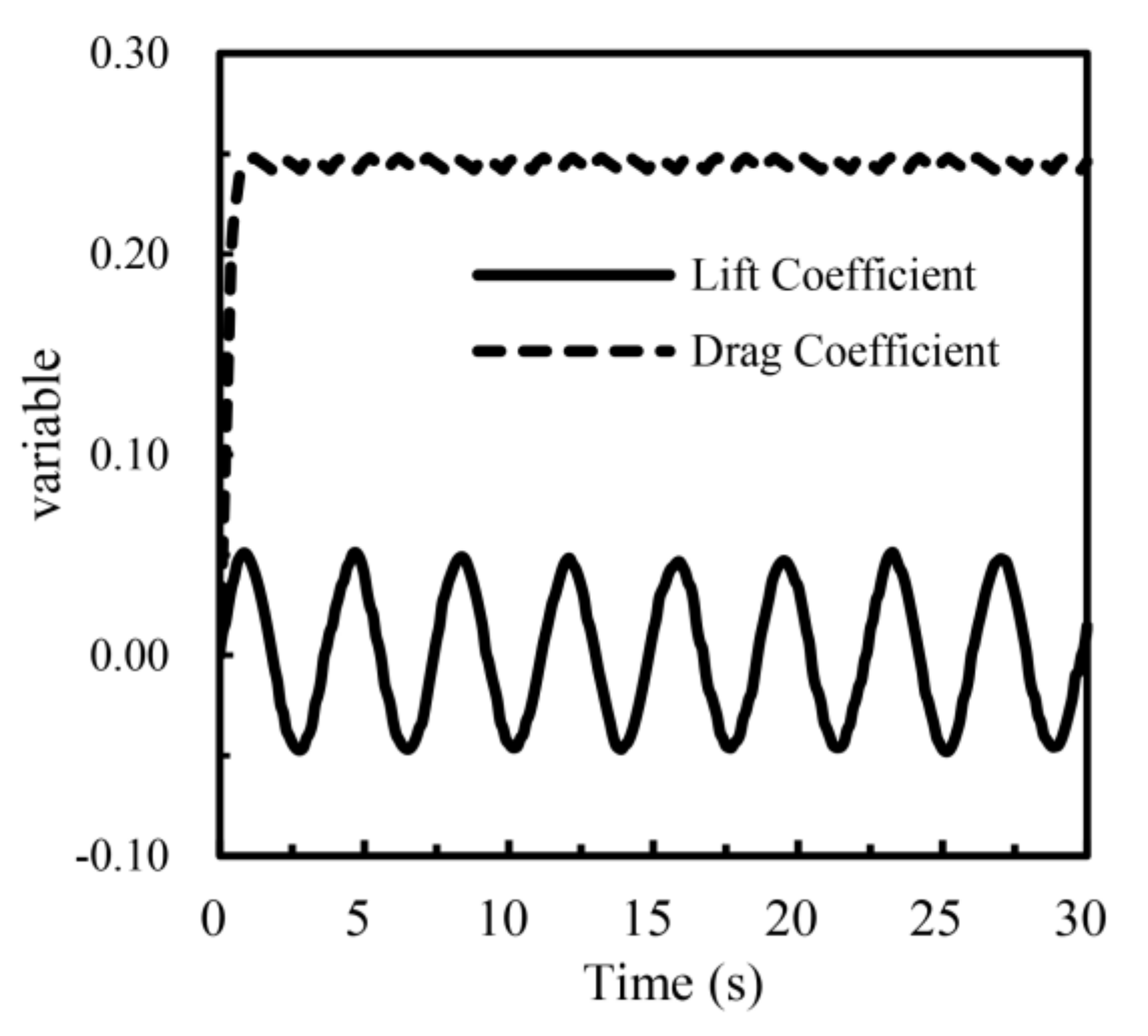
3.3. Plausibility Verification
4. Numerical Simulation of Vortex-Induced Vibration of the TS–tower
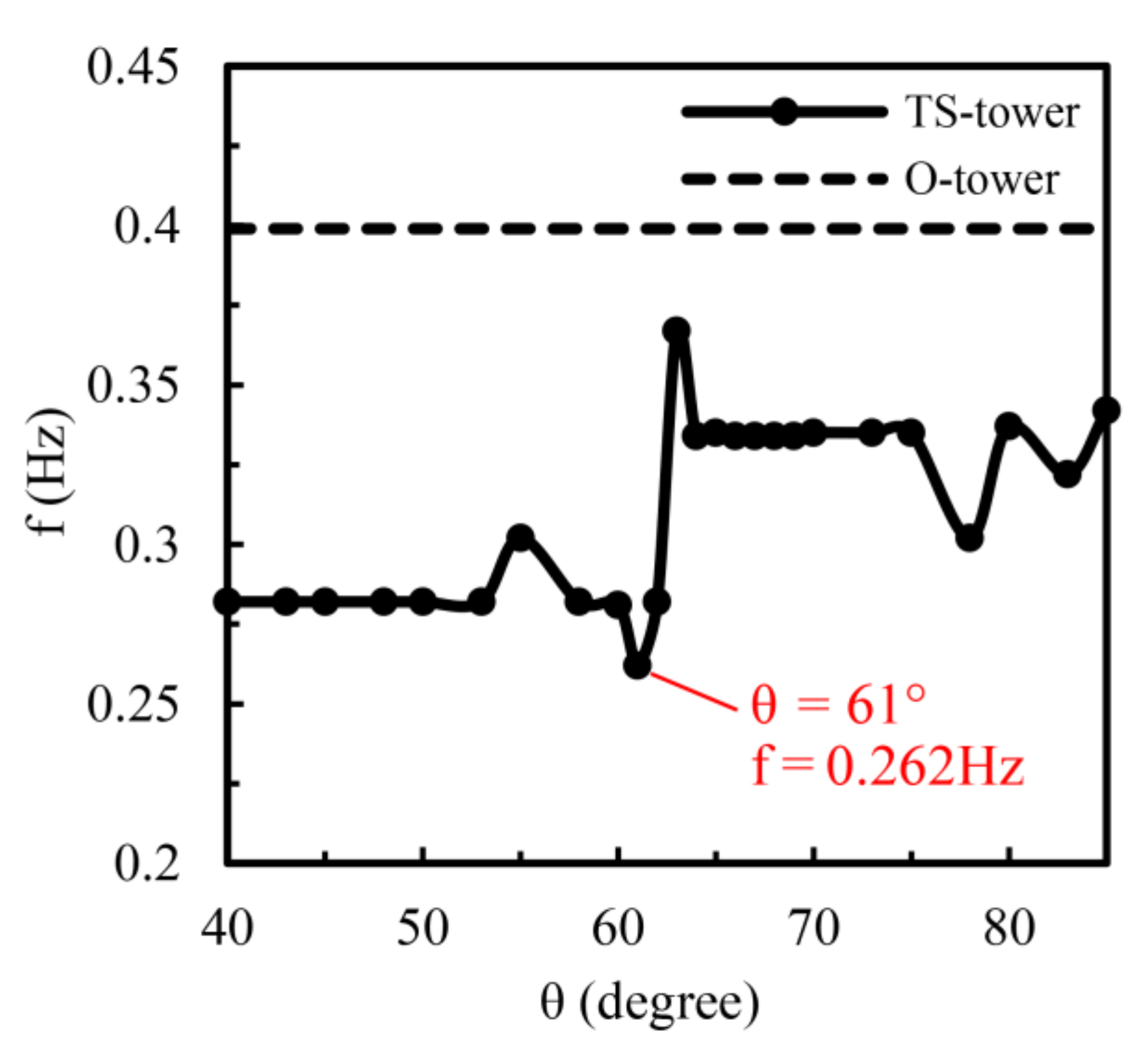
4.1. Influence of the θ Parameter on the VIV Frequency
- 1.
- The VIV frequency of the O–tower fw is 0.399 Hz, and the VIV frequencies of TS–towers with different θ parameters (f) are much lower than that of the O–tower;
- 2.
- When θ varies within the range of 40° to 53°, the value of f is steady;
- 3.
- When θ is larger than 53°, the value of f varies in an obvious manner, and the minimum f is 0.262 Hz when θ is 61°; the VIV frequency is 34.3% lower than that of the O–tower;
- 4.
- When θ changes within the range of 61° to 64°, the value of f increases sharply, and the maximum f is 0.367 Hz when θ is 63°; it is also less than fw;
- 5.
- When θ changes within the range of 64° to 85°, the value of f has limited variation between 0.322 Hz and 0.342 Hz.
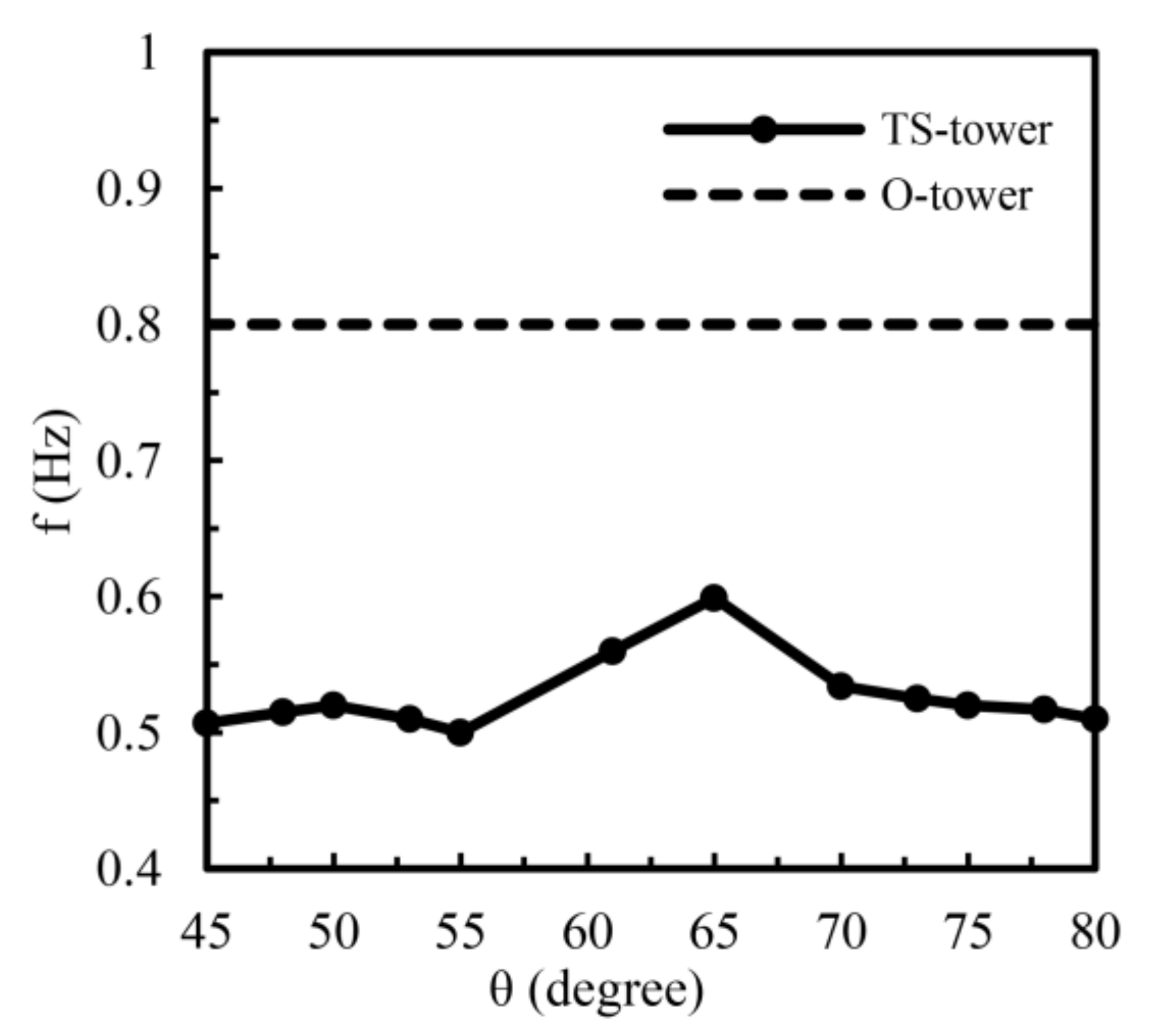
4.2. Influence of the n Parameter on the VIV Frequency
4.3. Further Comparison and Discussion
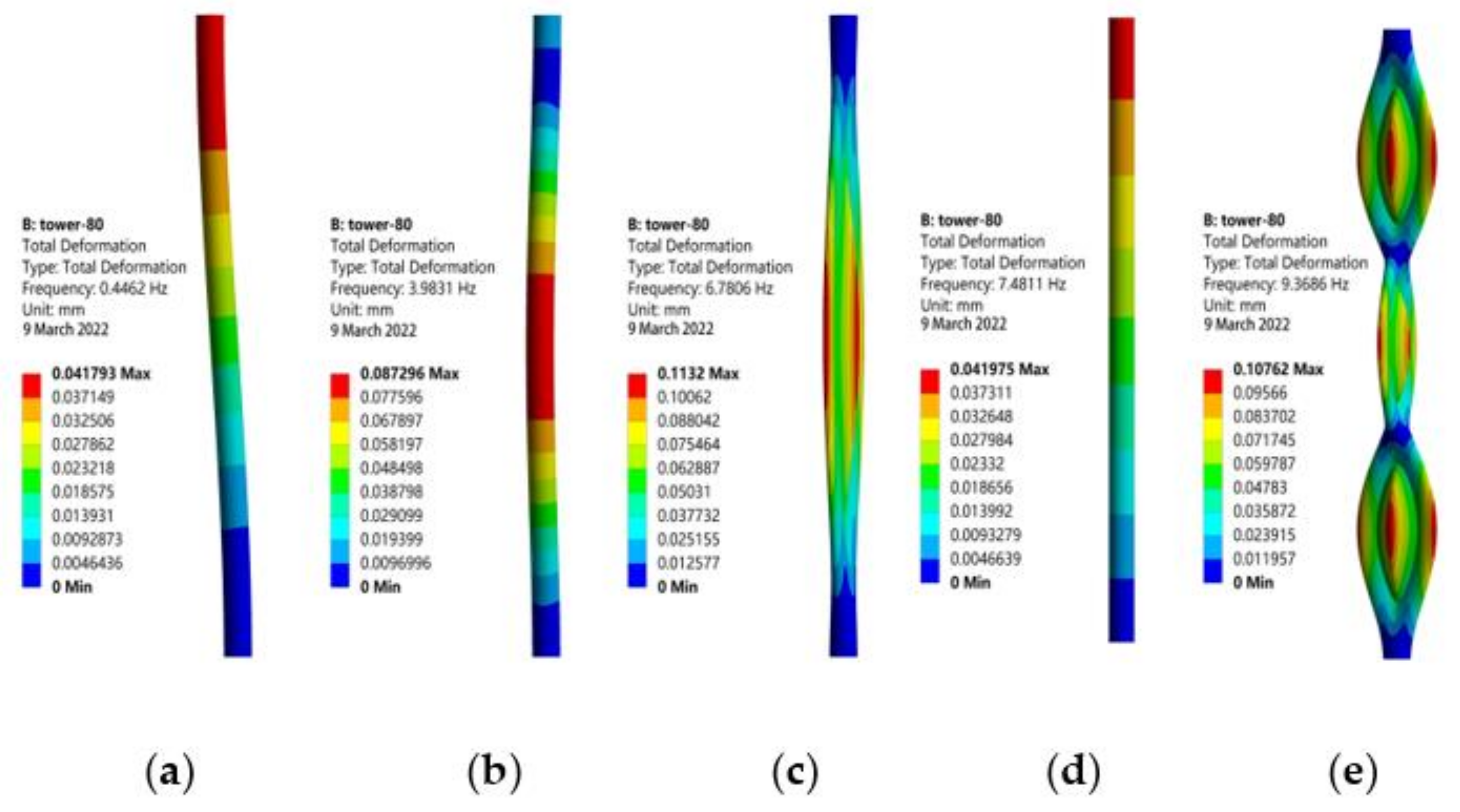
4.4. Modal Analysis of Wind Turbine Towers
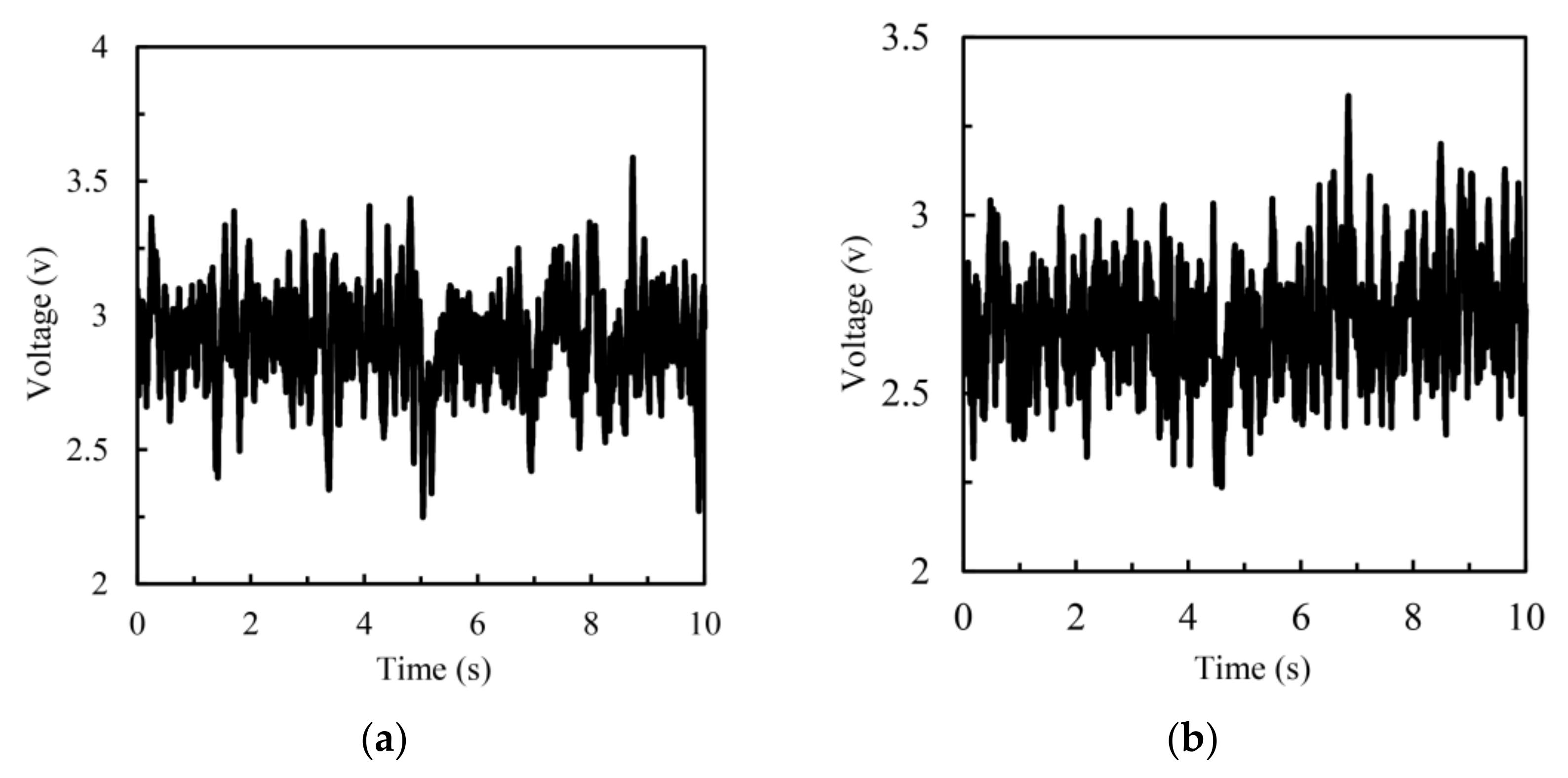
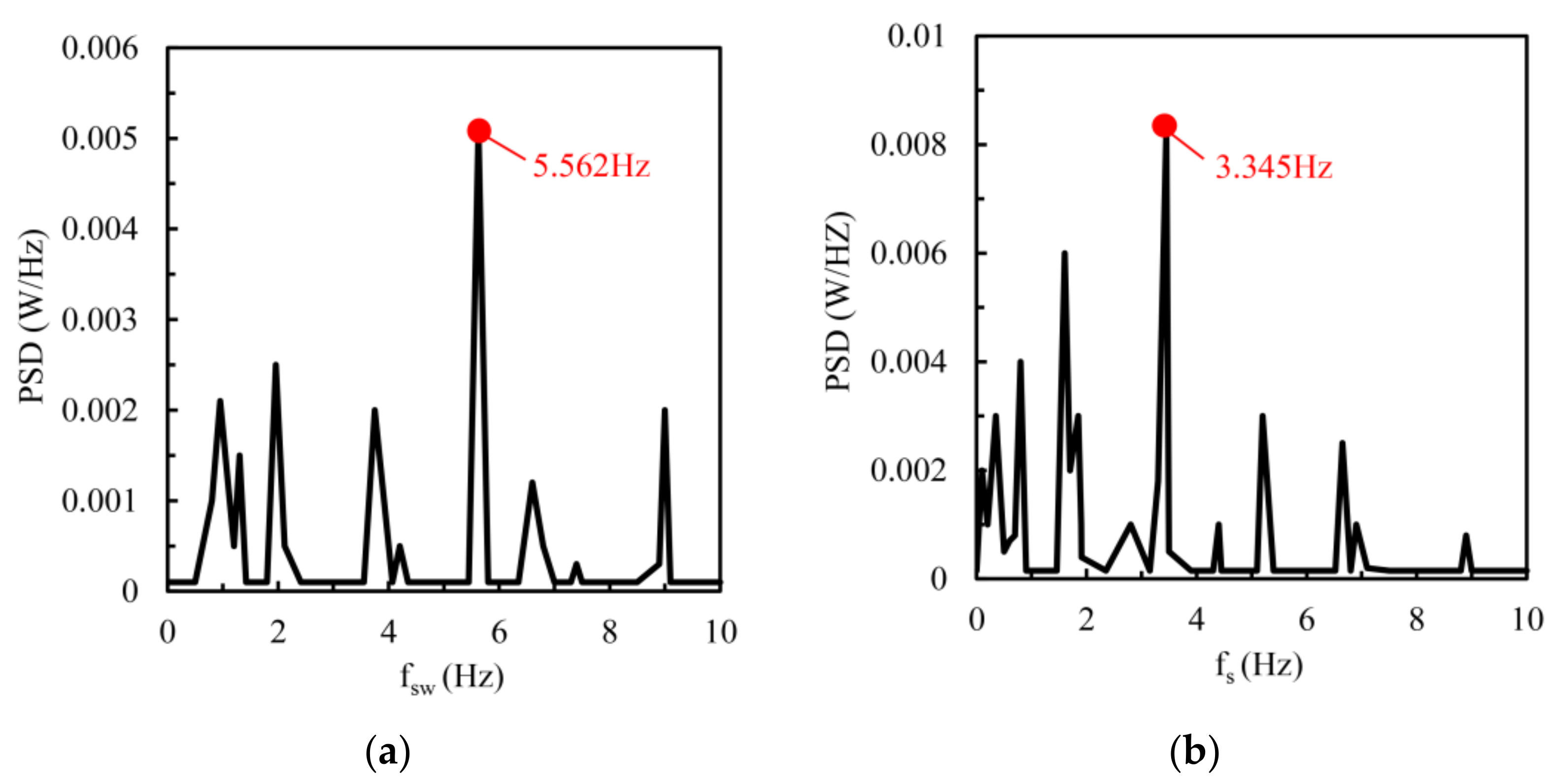
4.5. Wind Tunnel Experimental Study
5. Conclusions
- 1.
- The proposed model can be used to analyze the vortex-induced vibration (VIV) problems of wind turbine towers. The reliability of the algorithm is validated by consulting relevant theoretical results and data from the literature (see Table 2).
- 2.
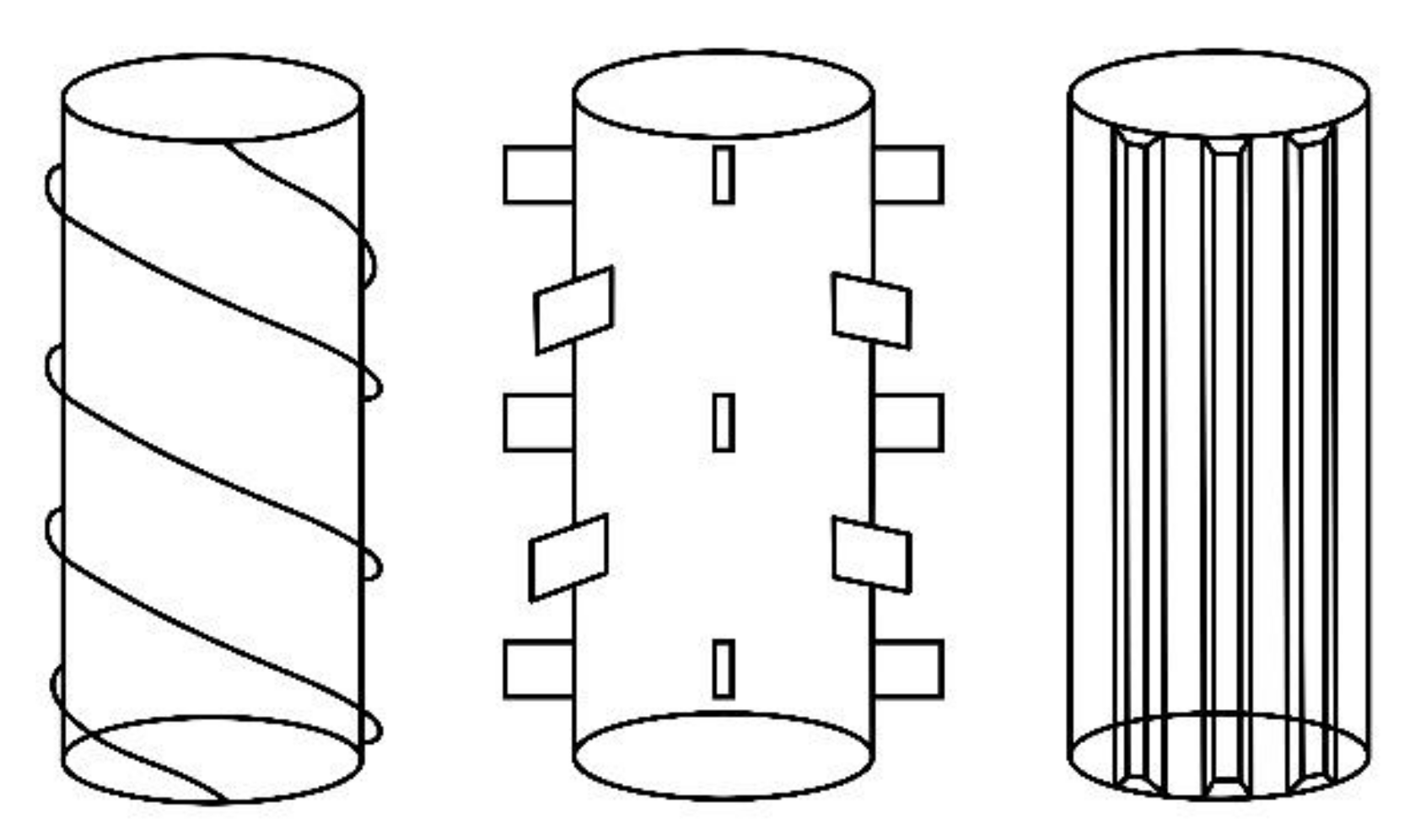
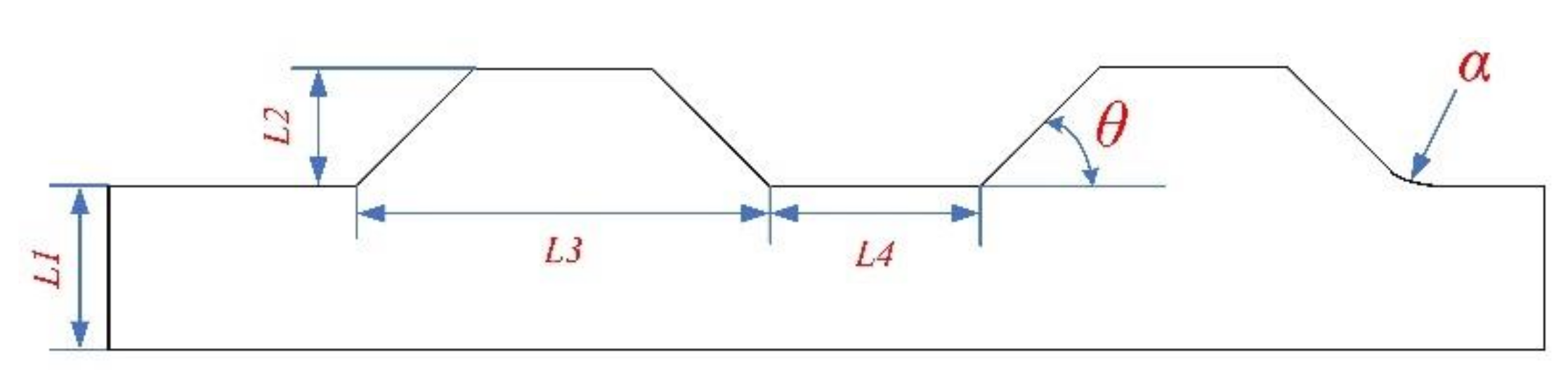
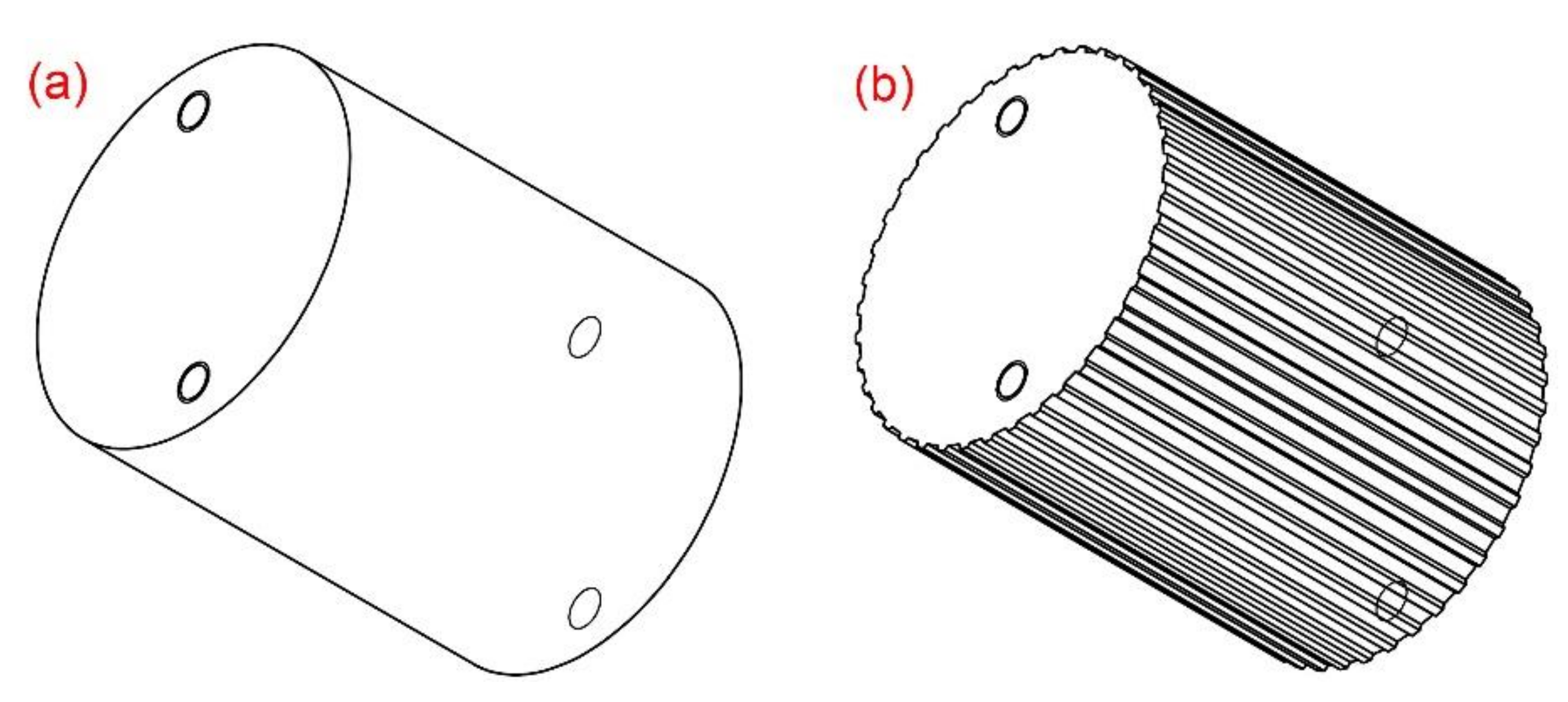
- Manufacturing continuous trapezoidal straight spoiler plates (TS) on the outer surface of wind turbine towers can decrease the VIV frequency significantly. To obtain the most optimized effectiveness, the recommended geometry parameters of the TS are: an angle, θ, of less than 60°; a number of TS, n, greater than 8; L3 and L4 being relative to the tower diameter, D, and n; as well as L1 and L2 being relative to the thickness of the base plate (see Figure 2).
- 3.
- The TS do not influence the eigenfrequencies of wind turbine structures significantly, but can decrease the exciting frequency (VIV frequency) in an obvious manner. It is effective for avoiding the vortex-induced resonance risk of wind turbine towers.
- 4.
- The function of reducing the VIV frequency of TS is validated by an analogical wind tunnel test that uses small-scale specimens (with the consideration of the geometry similarity). The results indicate that the experimental VIV frequency deduction rate reached 40.53%, similar to the rate of this simulation (34.3%).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| VIV | Vortex-induced vibration |
| CFD | Computational fluid mechanics |
| O–tower | Original tower |
| TS–tower | Tower with trapezoid straight spoiler plates |
| Re | Reynolds number |
| St | Strouhal number |
| FFT | Fast Fourier transform |
| Re | Reynolds number |
| St | Strouhal number |
| F | Lift force |
| Fd | Drag force |
| Cl | Lift coefficient |
| Cd | Drag coefficient |
| D | Characteristic diameter |
| H | Characteristic height |
| W | The weight of the tower |
| U | Flow velocity |
| t | Flow time |
| ρ | Fluid density |
| p | Fluid pressure |
| v | Kinematic viscosity of fluid |
| μ | Dynamic viscosity of fluid |
| L1 | The thickness of plate |
| L2 | The height of TS |
| L3 | The width of TS |
| L4 | The spacing of TS |
| n | The number of TS |
| θ | The angle of TS |
| α | The fillet of TS |
| fw | VIV frequency of the O–tower |
| f | VIV frequency of the TS–tower |
| fsw | VIV frequency of a small-scale O–tower |
| fs | VIV frequency of a small-scale TS–tower |
References
- Li, Y.; Li, A.; Deng, Y. Performance Investigation of Circular Tld Devices Used in Wind Turbine Generation Tower Via Both Experiment and Numerical Simulation. J. Vib. Eng. Technol. 2021, 9, 1715–1732. [Google Scholar] [CrossRef]
- Kang, L.; Ge, F.; Wu, X.; Hong, Y. Experiments and Modeling on the Maximum Displacement of a Long Tensioned Mooring Tether Subjected to Vortex-induced Vibration. Procedia Eng. 2016, 166, 83–90. [Google Scholar] [CrossRef]
- Mendis, P.; Ngo, T.; Haritos, N.; Hira, A.; Samali, B.; Cheung, J. Wind Loading on Tall Buildings. Electron. J. Struct. Eng. 2007, 7, 41–54. [Google Scholar] [CrossRef]
- Christensen, R.M.; Nielsen, M.G.; Ulrik, S.-A. Effective Vibration Dampers: Mast, Towers and Chimneys. In Proceedings of the EUROSTEEL, Copenhagen, Denmark, 13–15 September 2017; Ernst & Sohn GmbH: Berlin, Germany, 2017; Volume 1, pp. 4351–4360. [Google Scholar] [CrossRef]
- Chizfahm, A.; Yazdi, E.A.; Eghtesad, M. Dynamic modeling of vortex induced vibration wind turbines. Renew. Energy 2018, 121, 632–643. [Google Scholar] [CrossRef]
- Khodaie, N. Vibration control of super-tall buildings using combination of tapering method and TMD system. J. Wind Eng. Ind. Aerodyn. 2019, 196, 104031. [Google Scholar] [CrossRef]
- Liang, S.; Yang, W.; Song, J.; Wang, L.; Hu, G. Wind-induced responses of a tall chimney by aeroelastic wind tunnel test using a continuous model. Eng. Struct. 2018, 176, 871–880. [Google Scholar] [CrossRef]
- Song, M.T.; Cao, D.Q.; Zhu, W.D. Vortex-Induced Vibration of a Cable-Stayed Bridge. Shock Vib. 2016, 2016, 1928086. [Google Scholar] [CrossRef]
- Zhang, Y.; Habashi, W.G.; Khurram, R.A. Predicting Wind-Induced Vibrations of High-Rise Buildings Using Unsteady Cfd and Modal Analysis. J. Wind. Eng. Ind. Aerodyn. 2015, 136, 165–179. [Google Scholar] [CrossRef]
- Chou, J.-S.; Tu, W.-T. Failure analysis and risk management of a collapsed large wind turbine tower. Eng. Fail. Anal. 2011, 18, 295–313. [Google Scholar] [CrossRef]
- Sarpkaya, T. A Critical Review of the Intrinsic Nature of Vortex-Induced Vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Jafari, M.; Alipour, A. Methodologies to Mitigate Wind-Induced Vibration of Tall Buildings: A State-of-the-Art Review. J. Build. Eng. 2021, 33, 101582. [Google Scholar] [CrossRef]
- Kareem, A.; Kijewski, T.; Tamura, Y. Mitigation of Motions of Tall Buildings with Specific Examples of Recent Applications. Wind Struct. 1999, 2, 201–251. [Google Scholar] [CrossRef]
- Talib, E.; Shin, J.-H.; Kwak, M.K. Designing multi-input multi-output modal-space negative acceleration feedback control for vibration suppression of structures using active mass dampers. J. Sound Vib. 2018, 439, 77–98. [Google Scholar] [CrossRef]
- Yang, D.-H.; Shin, J.-H.; Lee, H.; Kim, S.-K.; Kwak, M.K. Active vibration control of structure by Active Mass Damper and Multi-Modal Negative Acceleration Feedback control algorithm. J. Sound Vib. 2016, 392, 18–30. [Google Scholar] [CrossRef]
- Momtaz, A.A.; Abdollahian, M.A.; Farshidianfar, A. Study of wind-induced vibrations in tall buildings with tuned mass dampers taking into account vortices effects. Int. J. Adv. Struct. Eng. 2017, 9, 385–395. [Google Scholar] [CrossRef]
- Xie, S.; Jin, X.; He, J.; Zhang, C. Structural responses suppression for a barge-type floating wind turbine with a platform-based TMD. IET Renew. Power Gener. 2019, 13, 2473–2479. [Google Scholar] [CrossRef]
- Yang, J.; He, E. Coupled modeling and structural vibration control for floating offshore wind turbine. Renew. Energy 2020, 157, 678–694. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, S.; Ren, T.; Xiong, Y.; Song, L. VIV response of a long flexible riser fitted with strakes in uniform and linearly sheared currents. Appl. Ocean Res. 2015, 52, 102–114. [Google Scholar] [CrossRef]
- Hong, K.-S.; Shah, U.H. Vortex-induced vibrations and control of marine risers: A review. Ocean Eng. 2018, 152, 300–315. [Google Scholar] [CrossRef]
- Wang, J.-S.; Fan, D.; Lin, K. A review on flow-induced vibration of offshore circular cylinders. J. Hydrodyn. 2020, 32, 415–440. [Google Scholar] [CrossRef]
- Holland, V.; Tezdogan, T.; Oguz, E. Full-scale CFD investigations of helical strakes as a means of reducing the vortex induced forces on a semi-submersible. Ocean Eng. 2017, 137, 338–351. [Google Scholar] [CrossRef][Green Version]
- Assi, G.R.; Crespi, T.; Gharib, M. Novel geometries of serrated helical strakes to suppress vortex-induced vibrations and reduce drag. Appl. Ocean Res. 2022, 120, 103034. [Google Scholar] [CrossRef]
- Sukarnoor, N.I.M.; Quen, L.K.; Abu, A.; Kuwano, N.; Hooi-Siang, K.; Desa, S.M. The effectiveness of helical strakes in suppressing vortex-induced vibration of tandem circular cylinders. Ain Shams Eng. J. 2021, 13, 101502. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.; Guo, W.; Gho, W.M.; Tan, S.K. Experimental study on flow past a circular cylinder with rough surface. Ocean Eng. 2015, 109, 7–13. [Google Scholar] [CrossRef]
- Bianchi, V.; Silva, L.S.; Cenci, F.; Hirabayashi, S.; Suzuki, H.; Gonçalves, R.T. Spoiler plate effects on the suppression of vortex-induced motions of a single circular cylinder. Ocean Eng. 2020, 210, 107569. [Google Scholar] [CrossRef]
- Goncalves, R.T.; Fujarra, A.L.; Rosetti, G.F.; Nishimoto, K. Mitigation of Vortex-Induced Motion, (Vim) on a Monocolumn Platform: Forces and Movements. J. Offshore Mech. Arct. Eng. 2010, 132, 041102. [Google Scholar] [CrossRef]
- Lubbad, R.K.; Løset, S.; Moe, G. Experimental Investigations of the Efficiency of Round-Sectioned Helical Strakes in Suppressing Vortex Induced Vibrations. J. Offshore Mech. Arct. Eng. 2011, 133, 041102. [Google Scholar] [CrossRef]
- Quen, L.K.; Abu, A.; Kato, N.; Muhamad, P.; Sahekhaini, A.; Abdullah, H. Investigation on the effectiveness of helical strakes in suppressing VIV of flexible riser. Appl. Ocean Res. 2014, 44, 82–91. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, S.-X.; Cao, J.; Chen, Y.-F. Experimental study on response performance of VIV of a flexible riser with helical strakes. China Ocean Eng. 2015, 29, 673–690. [Google Scholar] [CrossRef]
- Xu, F.; Chen, W.-L.; Xiao, Y.-Q.; Li, H.; Ou, J.-P. Numerical study on the suppression of the vortex-induced vibration of an elastically mounted cylinder by a traveling wave wall. J. Fluids Struct. 2014, 44, 145–165. [Google Scholar] [CrossRef]
- Roshko, A. On the Development of Turbulent Wakes from Vortex Streets; National Advisory Committee for Aeronautics: Washington, DC, USA, 1954. [Google Scholar]
- Braza, M.; Chassaing, P.; Minh, H.H. Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder. J. Fluid Mech. 1986, 165, 79–130. [Google Scholar] [CrossRef]
- Mittal, S.; Tezduyar, T.E. Computation of Unsteady Incompressible Flows Past Oscillating Cylinders. In Proceedings of the Fourth International Conference on Computing in Civil and Building Engineering, Tokyo, Japan, 29–31 July 1991; pp. 95–102. Available online: https://www.researchgate.net/publication/303813048_Computation_of_Unsteady_Incompressible_Flows_Past_Oscillating_Cylinders (accessed on 19 January 2022).
- Jin, Y.; Gu, J.; Ma, L. Static strength and modal analysis of large wind turbine tower. Mech. Eng. Autom. 2017, 1, 63–65. Available online: https://kns.cnki.net/kcms/detail/14.1319.TH.20170112.1349.050.html (accessed on 19 January 2022).
- Ma, P.; Li, H.; Lin, D.; Zhang, L.; Wang, L. Research on Differential Pressure Vibration Measurement Device for Flow Induced Vibration Test. Chin. J. Sci. Instrum. 2020, 41, 170–177. [Google Scholar] [CrossRef]
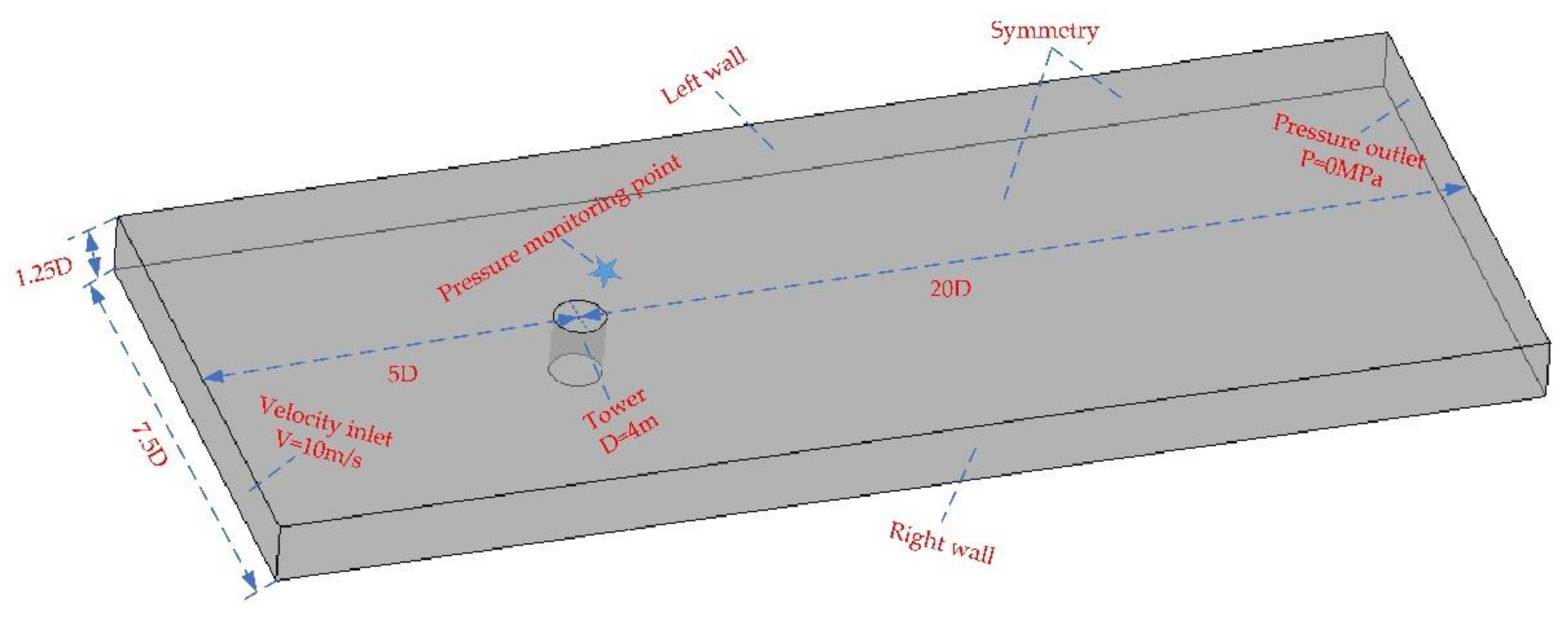








| Diameter of tower (D) | 4 m | Inlet velocity | 10 m/s |
| Height of fluid domain | 1.25 D | Outlet static pressure | 0 MPa |
| Length of fluid domain | 20 D | Solving time | 100 s |
| Wide of inlet/outlet | 7.5 D | Time step | 0.1 s |
| Researcher | C1 | Cd | fw |
|---|---|---|---|
| Braza [33] | ±0.4 | 1.37 | 0.418 |
| Mittal [34] | ±0.319 | 1.37 | 0.418 |
| This paper | ±0.319 | 1.36 | 0.399 |
| D (m) | H (m) | L2 (mm) | L3 (mm) | θ (degree) | n (piece) | α (mm) |
|---|---|---|---|---|---|---|
| 4 | 5 | 50 | 150 | 40–85 | 0–50 | 6 |
| Height (m) | Diameter (m) | L1 (mm) | L2 (mm) | L3 (mm) | θ (Degree) | n (Piece) | Weight (t) | Mass21 (t) | |
|---|---|---|---|---|---|---|---|---|---|
| O–tower | 80 | 4 | 40 | — | — | — | — | 31.5 | 455 |
| TS–tower | 80 | 4 | 16.5 | 50 | 150 | 61 | 50 | 31.5 | 455 |
| Mode | O–tower | TS–tower | ||
|---|---|---|---|---|
| Eigenfrequency (Hz) | Mode Shapes | Eigenfrequency (Hz) | Mode Shapes | |
| 1 | 0.4462 | Radial oscillating | 0.4535 | Radial oscillating |
| 2 | 3.9831 | Radial bending | 2.8794 | Harmonic |
| 3 | 6.7804 | Harmonic | 3.9641 | Radial bending |
| 4 | 7.4811 | Radial oscillating | 4.3289 | Harmonic |
| 5 | 9.3686 | Harmonic | 7.0978 | Harmonic |
| VIV Frequency | 0.399 Hz | 0.262 Hz |
| Model | Height (mm) | Diameter (mm) | L2 (mm) | L3 (mm) | n (Piece) | θ (Degree) |
|---|---|---|---|---|---|---|
| O-spec. | 100 | 80 | — | — | — | — |
| TS-spec. | 100 | 80 | 1 | 3 | 50 | 61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, T.; Chen, Y.; Wang, Z. The Effect of Continuous Trapezoidal Straight Spoiler Plates on the Vortex-Induced Vibration of Wind Turbine Towers. Atmosphere 2022, 13, 447. https://doi.org/10.3390/atmos13030447
Li Z, Zhang T, Chen Y, Wang Z. The Effect of Continuous Trapezoidal Straight Spoiler Plates on the Vortex-Induced Vibration of Wind Turbine Towers. Atmosphere. 2022; 13(3):447. https://doi.org/10.3390/atmos13030447
Chicago/Turabian StyleLi, Zheng, Tianhe Zhang, Yang Chen, and Ziqi Wang. 2022. "The Effect of Continuous Trapezoidal Straight Spoiler Plates on the Vortex-Induced Vibration of Wind Turbine Towers" Atmosphere 13, no. 3: 447. https://doi.org/10.3390/atmos13030447
APA StyleLi, Z., Zhang, T., Chen, Y., & Wang, Z. (2022). The Effect of Continuous Trapezoidal Straight Spoiler Plates on the Vortex-Induced Vibration of Wind Turbine Towers. Atmosphere, 13(3), 447. https://doi.org/10.3390/atmos13030447






