Evaluation of Wave Contributions in Hurricane Irma Storm Surge Hindcast
Abstract
:1. Introduction
2. Methodology
2.1. ADCIRC
2.2. ADCIRC+SWAN
3. Model Setup
3.1. Model Domain
3.2. Surface Wind and Pressure Forcing
3.3. Model Parameters
3.4. Model Validation
4. Results
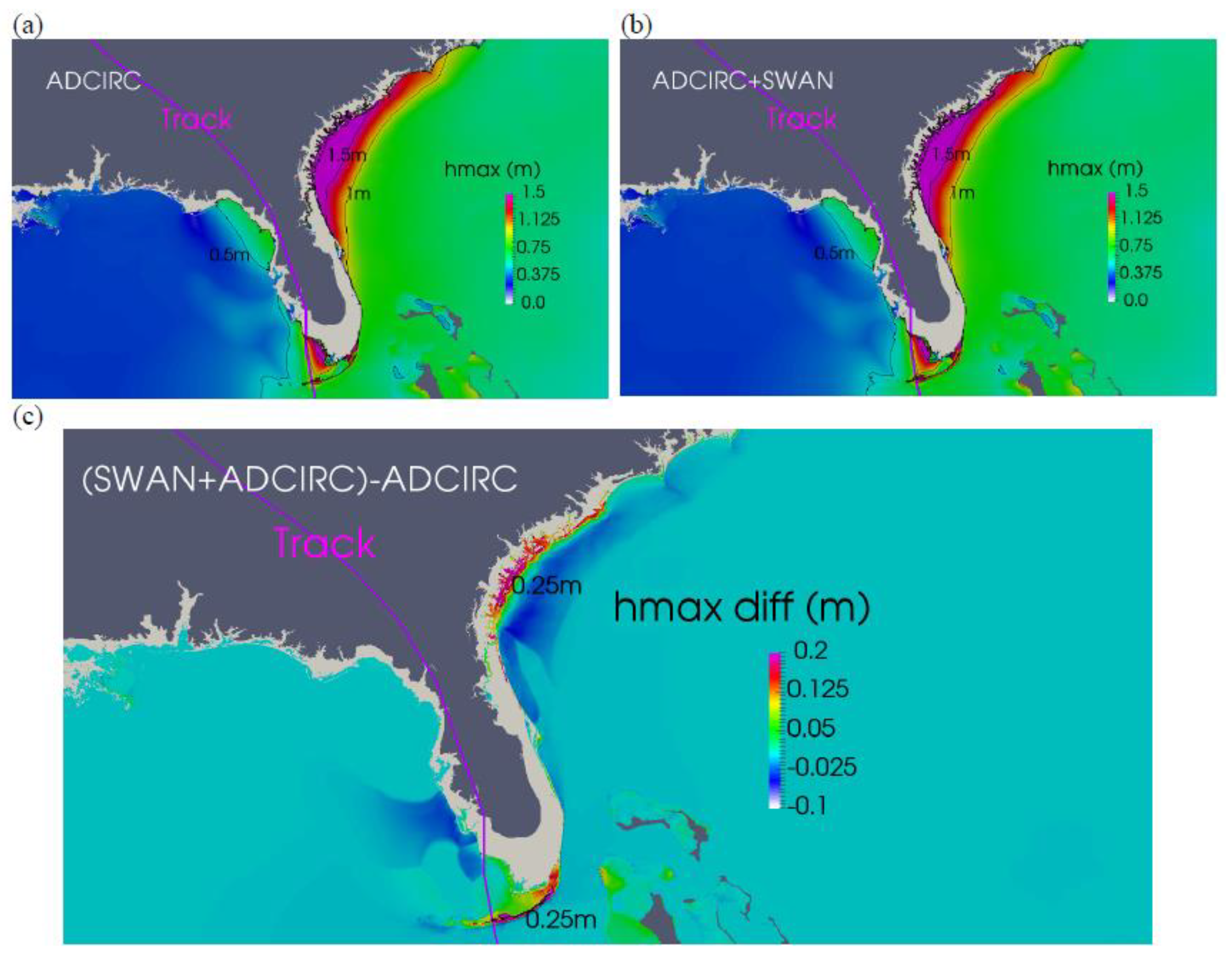
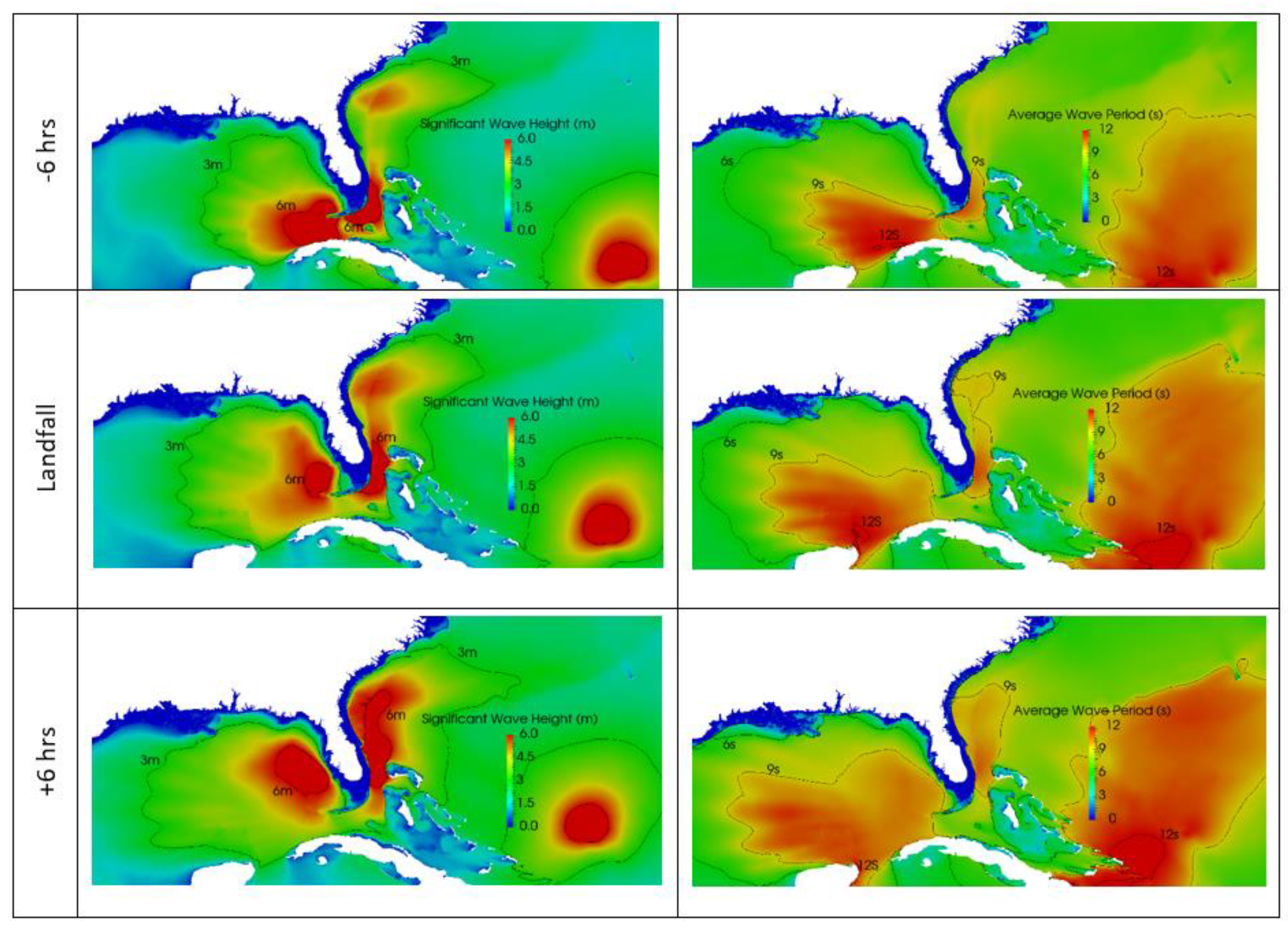
4.1. Evolution of Surges and Waves
4.2. Validation of Water Levels
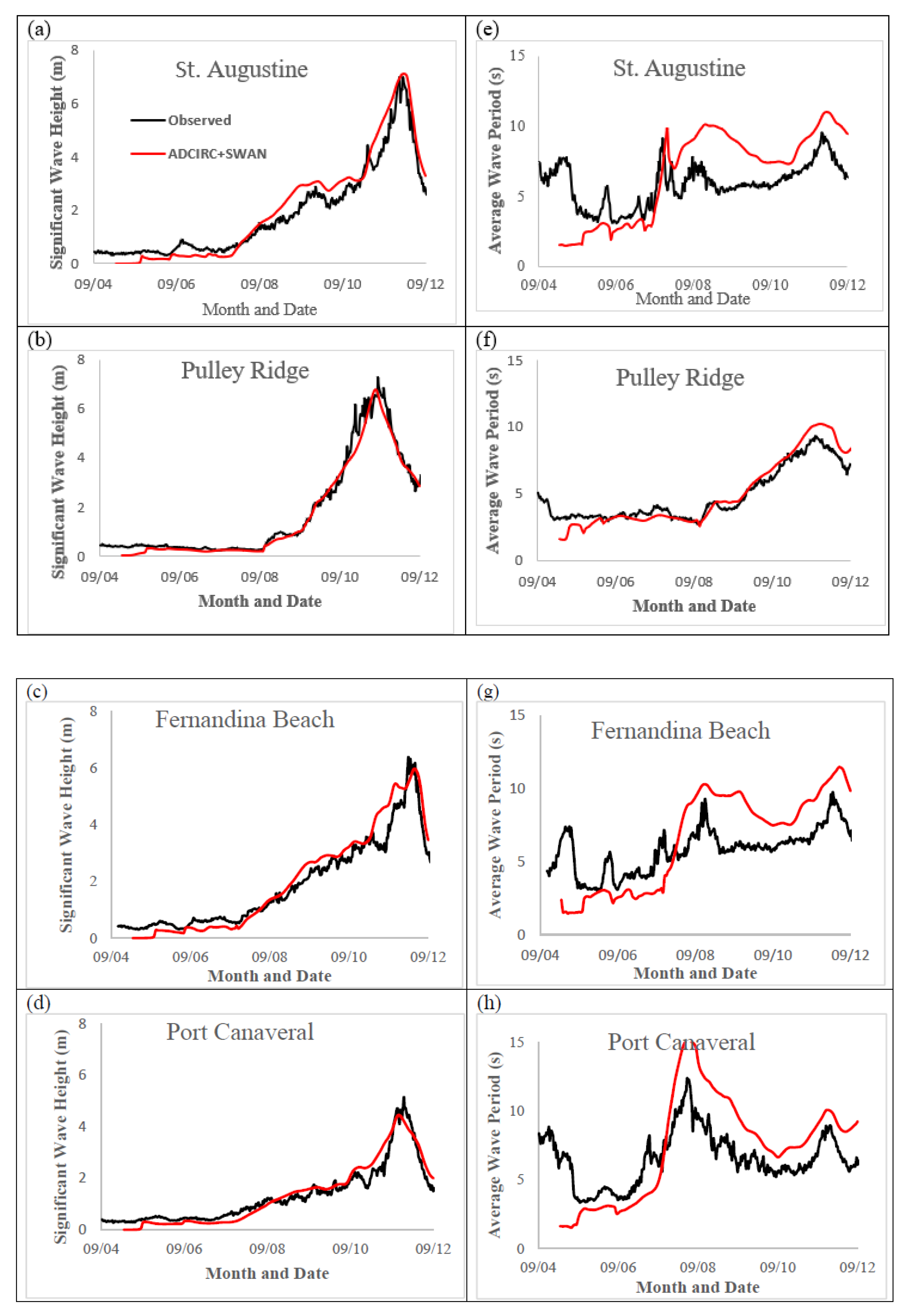
4.3. Validation of Waves
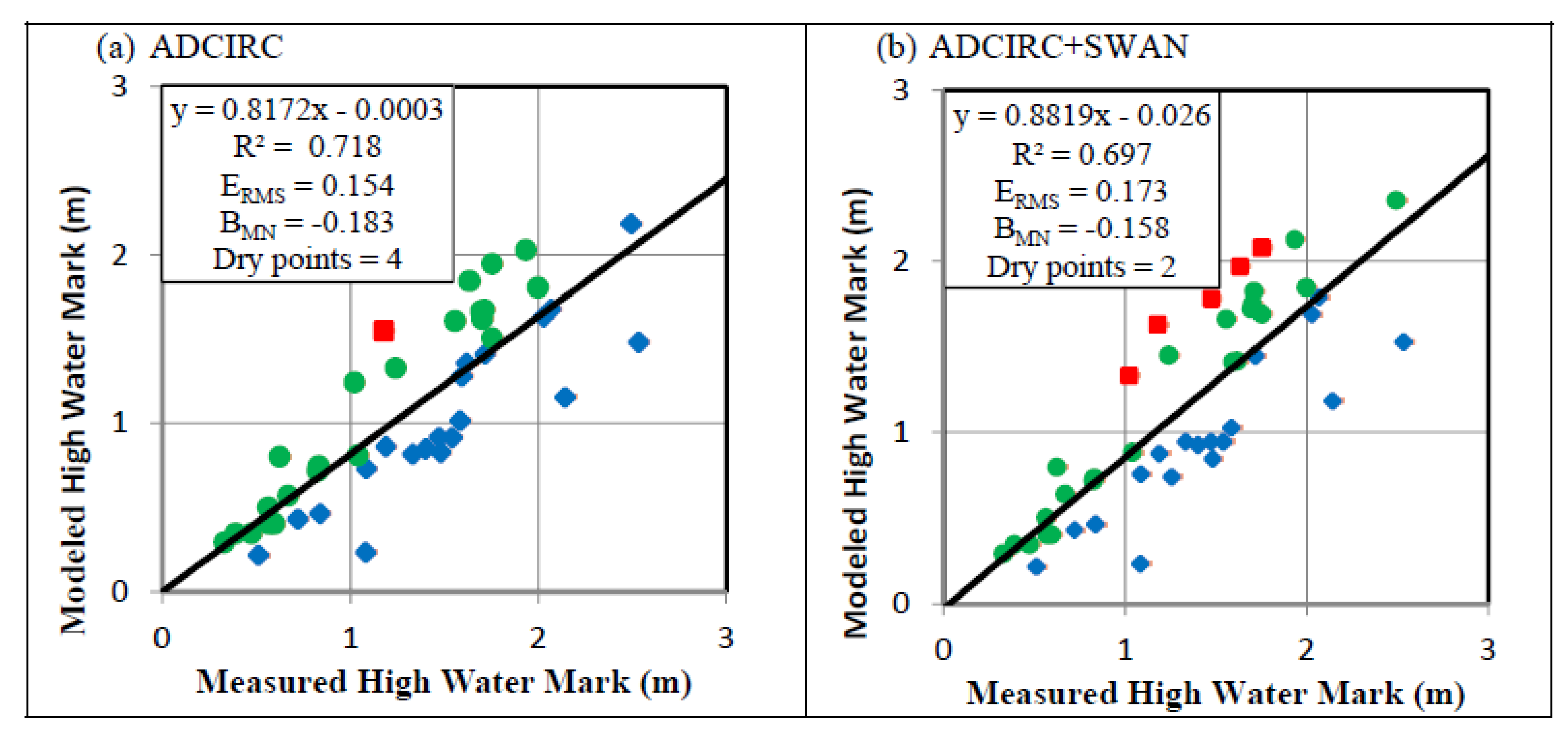
4.4. High-Water Marks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National Hurricane Center. Introduction to Storm Surge. Available online: https://www.nhc.noaa.gov/surge/surge_intro.pdf (accessed on 11 November 2021).
- Jelesnianski, C.P. SLOSH: Sea, Lake, and Overland Surges from Hurricanes; US Department of Commerce: Washington, DC, USA; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA; National Weather Service: Silver Spring, MD, USA, 1992; Volume 48. [Google Scholar]
- Luettich, R.A.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts and Estuaries; Report 1: Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL; Technical Report DRP-92-6; United States Department of the Army, United States Army Corps of Engineers (USACE): Washington, DC, USA, 1991.
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. In Deep Sea Research and Oceanographic Abstracts; Elsevier: Amsterdam, The Netherlands, 1964; Volume 11, pp. 529–562. [Google Scholar]
- New South Wales. Coastline Management Manual; New South Wales Government: Parramatta, NSW, Australia, 1990.
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991; Volume 2. [Google Scholar]
- Kennedy, A.B.; Westerink, J.J.; Smith, J.M.; Hope, M.E.; Hartman, M.; Taflanidis, A.; Tanaka, S.; Westerink, H.; Cheung, K.F.; Smith, T.; et al. Tropical cyclone inundation potential on the Hawaiian Islands of Oahu and Kauai. Ocean Model. 2012, 52, 54–68. [Google Scholar] [CrossRef]
- Joyce, B.R.; Gonzalez-Lopez, J.; Van Der Westhuysen, A.J.; Yang, D.; Pringle, W.J.; Westerink, J.J.; Cox, A.T. U.S. IOOS Coastal and Ocean Modeling Testbed: Hurricane-Induced Winds, Waves, and Surge for Deep Ocean, Reef-Fringed Islands in the Caribbean. J. Geophys. Res. Oceans. 2019, 124, 2876–2907. [Google Scholar] [CrossRef]
- Hope, M.E.; Westerink, J.J.; Kennedy, A.B.; Kerr, P.C.; Dietrich, J.C.; Dawson, C.; Bender, C.J.; Smith, J.M.; Jensen, R.E.; Zijlema, M.; et al. Hindcast and validation of Hurricane Ike (2008) waves, forerunner, and storm surge. J. Geophys. Res. Oceans 2013, 118, 4424–4460. [Google Scholar] [CrossRef] [Green Version]
- Kerr, P.C.; Martyr, R.C.; Donahue, A.; Hope, M.E.; Westerink, J.J.; Luettich, R.A., Jr.; Kennedy, A.; Dietrich, J.; Dawson, C.U.S. IOOS coastal and ocean modeling testbed: Evaluation of tide, wave, and hurricane surge response sensitivities to mesh resolution and friction in the Gulf of Mexico. J. Geophys. Res. Oceans. 2013, 118, 4633–4661. [Google Scholar] [CrossRef]
- Wiegel, R.L. Wind waves and swell. Coast. Eng. Proc. 1961, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- Stevenson, T. The Design and Construction of Harbours: A Treatise on Maritime Engineering; A. and C. Black: London, UK, 1988. [Google Scholar]
- Fagherazzi, S.; Wiberg, P.L. Importance of wind conditions, fetch, and water levels on wave-generated shear stresses in shallow intertidal basins. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Bolaños, R.; Sánchez-Arcilla, A. A note on nearshore wave features: Implications for wave generation. Prog. Oceanogr. 2006, 70, 168–180. [Google Scholar] [CrossRef]
- Nick, T.; Place, T.N. LESSON 4: Coastal Ecosystems—Beach, Estuary, Marsh & Swamp. University of Florida. 2017. Available online: https://edis.ifas.ufl.edu/pdf%5C4H%5C4H35000.pdf (accessed on 30 November 2021).
- Feng, Z.; Reniers, A.; Haus, B.K.; Solo-Gabriele, H.M.; Kelly, E.A. Wave energy level and geographic setting correlate with Florida beach water quality. Mar. Pollut. Bull. 2016, 104, 54–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Westerink, J.J.; Luettich, R.A.; Blain, C.A.; Scheffner, N.W. Adcirc: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts and Estuaries; Report 2: Users’ Manual for ADCIRC-2DDI; Department of the Army, USACE: Washington, DC, USA, 1992.
- Luettich, R.A., Jr.; Westerink, J.J. Implementation of the Wave Radiation Stress Gradient as a Forcing for the ADCIRC Hydrodynamic Model.: Upgrades and Documentation for ADCIRC Version 34.12; Contractors Report, Department of the Army, US Army Corps of Engineers, Waterways Experiment Station: Vicksburg, MS, USA, 1999; p. 9. [Google Scholar]
- Dietrich, J.C.; Zijlema, M.; Westerink, J.J.; Holthuijsen, L.H.; Dawson, C.; Luettich Jr, R.A.; Jensen, R.E.; Smith, J.M.; Stelling, G.S.; Stone, G.W. Modeling hurricane waves and storm surge using integrally-coupled, scalable computations. Coast. Eng. 2011, 58, 45–65. [Google Scholar] [CrossRef]
- Riverside Technology, Inc. AECOM. In Mesh Development, Tidal Validation, and Hindcast Skill Assessment of an ADCIRC Model for the Hurricane Storm Surge Operational Forecast System on the US Gulf-Atlantic Coast; Riverside Technology, Inc.: Fort Collins, CO, USA; AECOM: Dallas, TX, USA, 2015. [Google Scholar] [CrossRef]
- Thompson, E.F.; Cardone, V.J. Practical modeling of hurricane surface wind fields. J. Waterw. Port Coast. 1996, 122, 195–205. [Google Scholar] [CrossRef]
- Cox, A.T.; Greenwood, J.A.; Cardone, V.J.; Swail, V.R. An interactive objective kinematic analysis system. In Proceedings of the Fourth International Workshop on Wave Hindcasting and Forecasting, Banff, Alberta, 16–20 October 1995; pp. 109–118. [Google Scholar]
- Cardone, V.J.; Cox, A.T. Tropical cyclone wind field forcing for surge models: Critical issues and sensitivities. Nat. Hazards 2009, 51, 29–47. [Google Scholar] [CrossRef]
- Musinguzi, A.; Akbar, M.K.; Fleming, J.G.; Hargrove, S.K. Understanding Hurricane Storm Surge Generation and Propagation Using a Forecasting Model, Forecast Advisories and Best Track in a Wind Model, and Observed Data—Case Study Hurricane Rita. J. Mar. Sci. Eng. 2019, 7, 77. [Google Scholar] [CrossRef] [Green Version]
- Akbar, M.K.; Kanjanda, S.; Musinguzi, A. Effect of bottom friction, wind drag coefficient, and meteorological forcing in hindcast of Hurricane Rita storm surge using SWAN+ ADCIRC model. J. Mar. Sci. Eng. 2017, 5, 38. [Google Scholar] [CrossRef] [Green Version]
- Kolar, R.L.; Gray, W.G.; Westerink, J.J.; Luettich, R.A. Shallow water modeling in spherical coordinates: Equation formulation, numerical implementation, and application. J. Hydraul. Res. 1994, 32, 3–24. [Google Scholar] [CrossRef]
- SWAN—Scientific and Technical Documentation Version 40.91AB. Delft University of Technology, Environmental Fluid Mechanics Section. Available online: http://www.swan.tudelft.nl (accessed on 20 November 2021).
- National Oceanic and Atmospheric Administration. Tides and Currents. Available online: https://tidesandcurrents.noaa.gov/ (accessed on 2 December 2021).
- National Oceanic and Atmospheric Administration. National Data Buoy Center. Available online: https://www.ndbc.noaa.gov/ (accessed on 2 December 2021).
- Cangialosi, J.P.; Latto, A.S.; Berg, R. National Hurricane Center Tropical Cyclone Report: Hurricane Irma; Report no. AL112017; National Oceanic and Atmospheric Administration and National Hurricane Center: Miami, FL, USA, 2018.


| Tidal Gauges | Wave Buoys | ||||||
|---|---|---|---|---|---|---|---|
| Name | Lon | Lat | Bathymetry (m) | Name | Lon | Lat | Bathymetry (m) |
| Mayport | −81.430 | 30.397 | −8.313 | St. Augustine | −81.080 | 30.000 | −22.093 |
| Lake Worth Pier | −80.033 | 26.612 | −6.437 | Fernandina Beach | −81.292 | 30.709 | −15.216 |
| Virginia Key | −80.162 | 25.731 | −3.686 | Pulley Ridge | −83.650 | 25.701 | −82.006 |
| Key West | −81.808 | 24.556 | −1.388 | Cape Canaveral | −80.533 | 28.400 | −11.018 |
| Vaca Key | −81.113 | 24.712 | −1.512 | ||||
| Naples | −81.808 | 26.132 | −0.323 | ||||
| Fort Myers | −81.873 | 26.648 | −2.067 | ||||
| Port Manatee | −82.563 | 27.638 | 0.235 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musinguzi, A.; Reddy, L.; Akbar, M.K. Evaluation of Wave Contributions in Hurricane Irma Storm Surge Hindcast. Atmosphere 2022, 13, 404. https://doi.org/10.3390/atmos13030404
Musinguzi A, Reddy L, Akbar MK. Evaluation of Wave Contributions in Hurricane Irma Storm Surge Hindcast. Atmosphere. 2022; 13(3):404. https://doi.org/10.3390/atmos13030404
Chicago/Turabian StyleMusinguzi, Abram, Lokesh Reddy, and Muhammad K. Akbar. 2022. "Evaluation of Wave Contributions in Hurricane Irma Storm Surge Hindcast" Atmosphere 13, no. 3: 404. https://doi.org/10.3390/atmos13030404
APA StyleMusinguzi, A., Reddy, L., & Akbar, M. K. (2022). Evaluation of Wave Contributions in Hurricane Irma Storm Surge Hindcast. Atmosphere, 13(3), 404. https://doi.org/10.3390/atmos13030404





