Impact of Land Use on Atmospheric Particulate Matter Concentrations: A Case Study of the Beijing–Tianjin–Hebei Region, China
Abstract
:1. Introduction
2. Methods
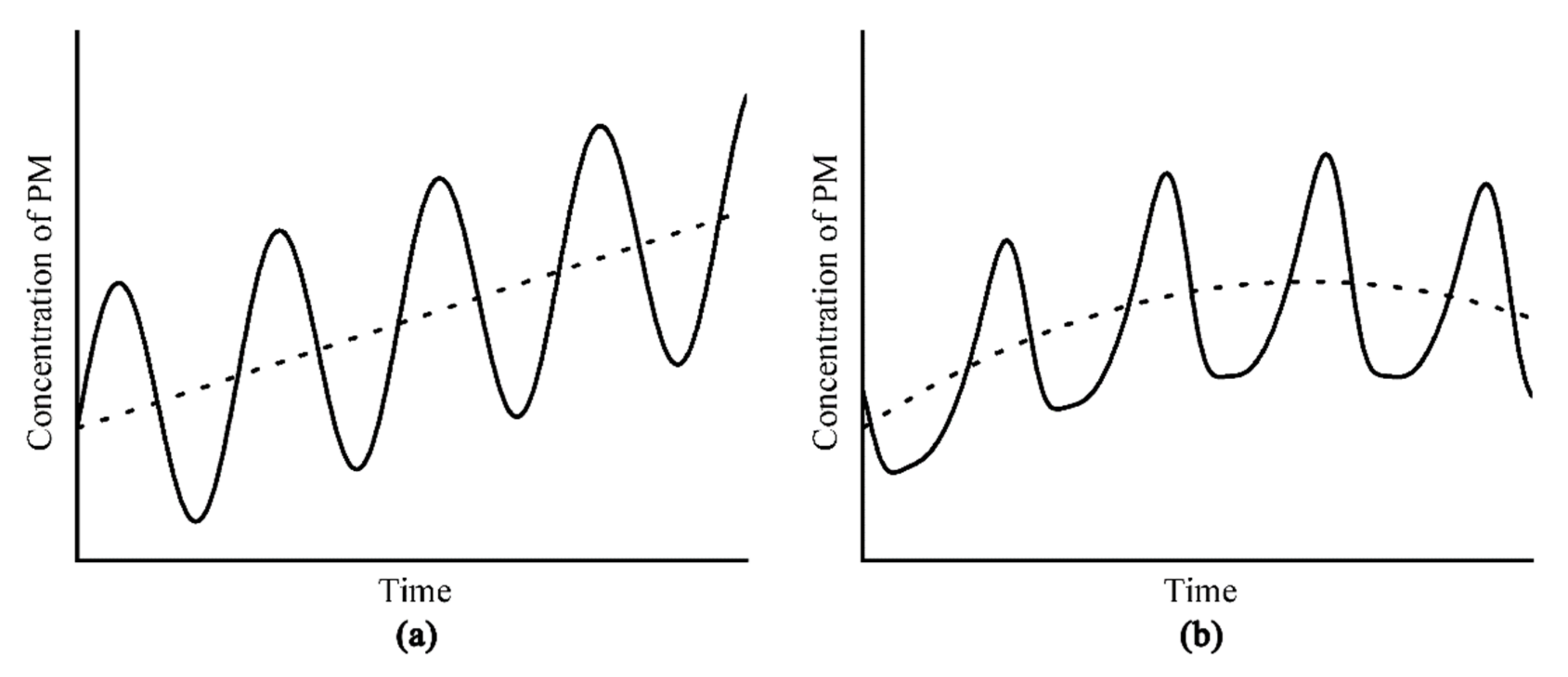
2.1. Optimized Particle Concentration Fitting Model
- (1)
- Regarding general concentration change trends, a quadratic function is employed instead of a linear function, and this function can suitably fit various situations, such as initially rising and then falling, initially falling and then rising, accelerated rising or falling, decelerated rising or falling, and steadily rising or falling concentrations.
- (2)
- In particulate matter concentration fluctuations, when the overall concentration increases, the fluctuation range also increases. When the overall concentration decreases, the fluctuation amplitude also decreases. Therefore, the first half of a quadratic function, i.e., , is added to the coefficient of the original sine function. This improvement ensures that the amplitude no longer remains fixed over time but varies with the overall concentration change trend.
- (3)
- At the monthly scale, changes in the particulate matter concentration are often not symmetrical periodic fluctuations, and often, the durations of periods with low values are long, while the durations of periods with high values are short. Notably, narrower peaks and wider valleys or the opposite, i.e., wider peaks and narrower valleys, may occur. Considering these concentration change characteristics, this paper replaces the original sine function with and adds a deformation factor Ft to control the shape of the sine function based on its magnitude.
- (4)
- The particulate matter concentration variation during a given cycle is often not symmetrical or uniform, and the concentration increase and decrease rates in this case are not equal. In particular, the time from one wave peak to the next wave trough is not the same as the time from one wave trough to the next wave peak. According to this feature, an oscillation term with the same period and a π/2-phase difference is added to x in the sine function; x is replaced with ; and the left/right shifting of the peak or trough is controlled by the magnitude of the offset factor Ht.
2.2. Landscape Pattern Index
2.2.1. Landscape Level
2.2.2. Class Level
3. Results and Discussion
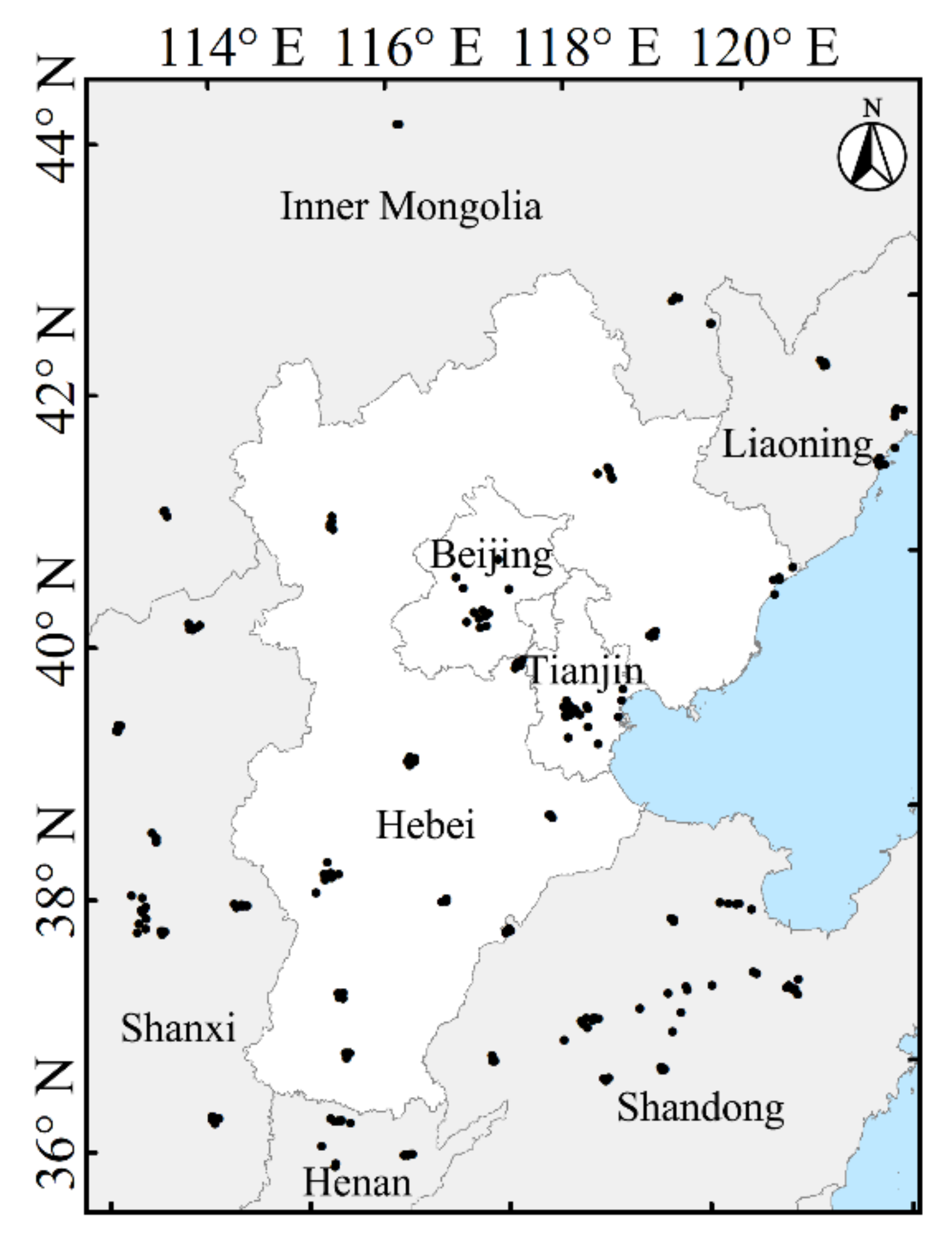
3.1. Overview of the Study Area and Data
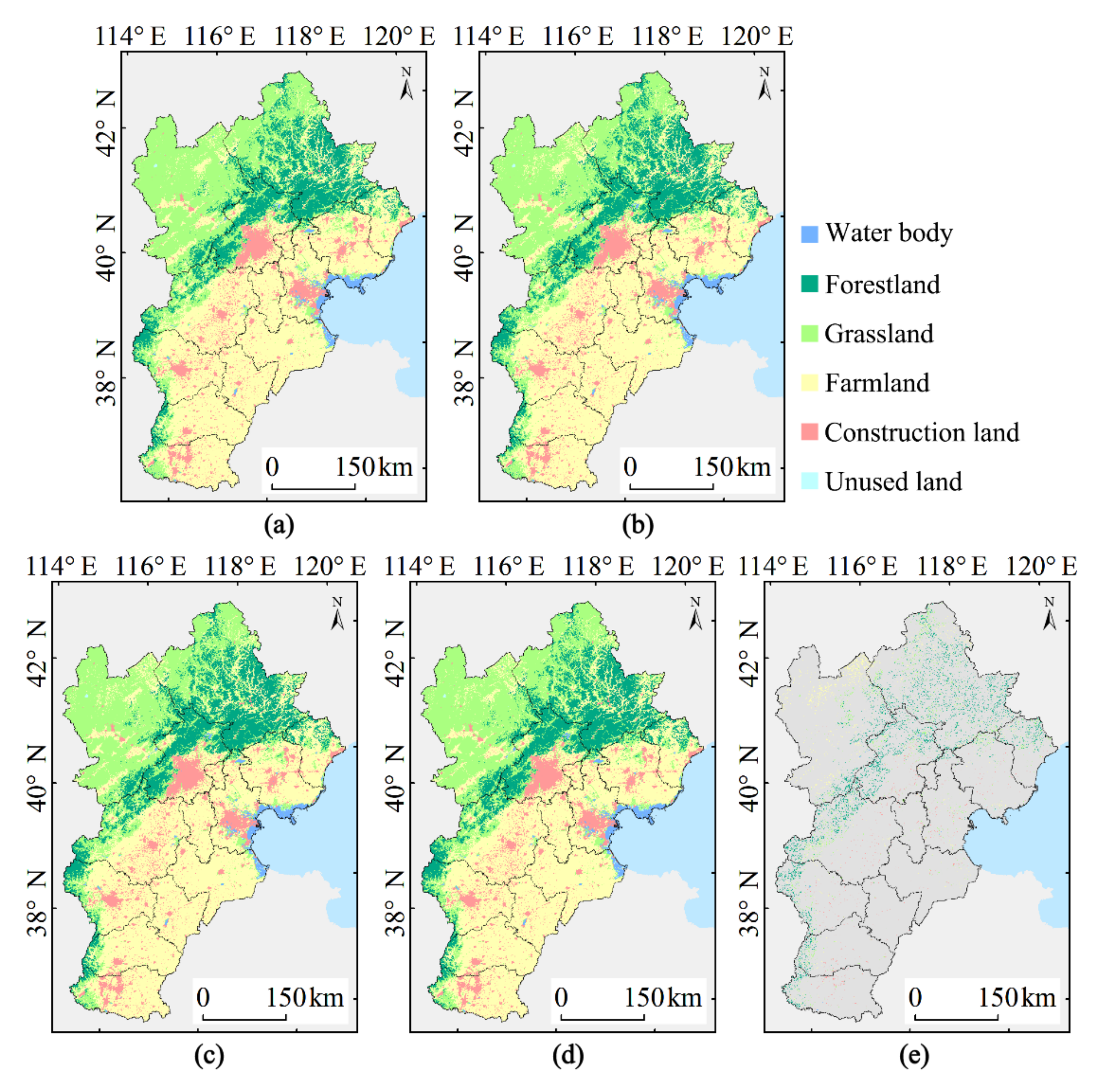
3.1.1. Land Use Data
3.1.2. Air Quality Monitoring Data
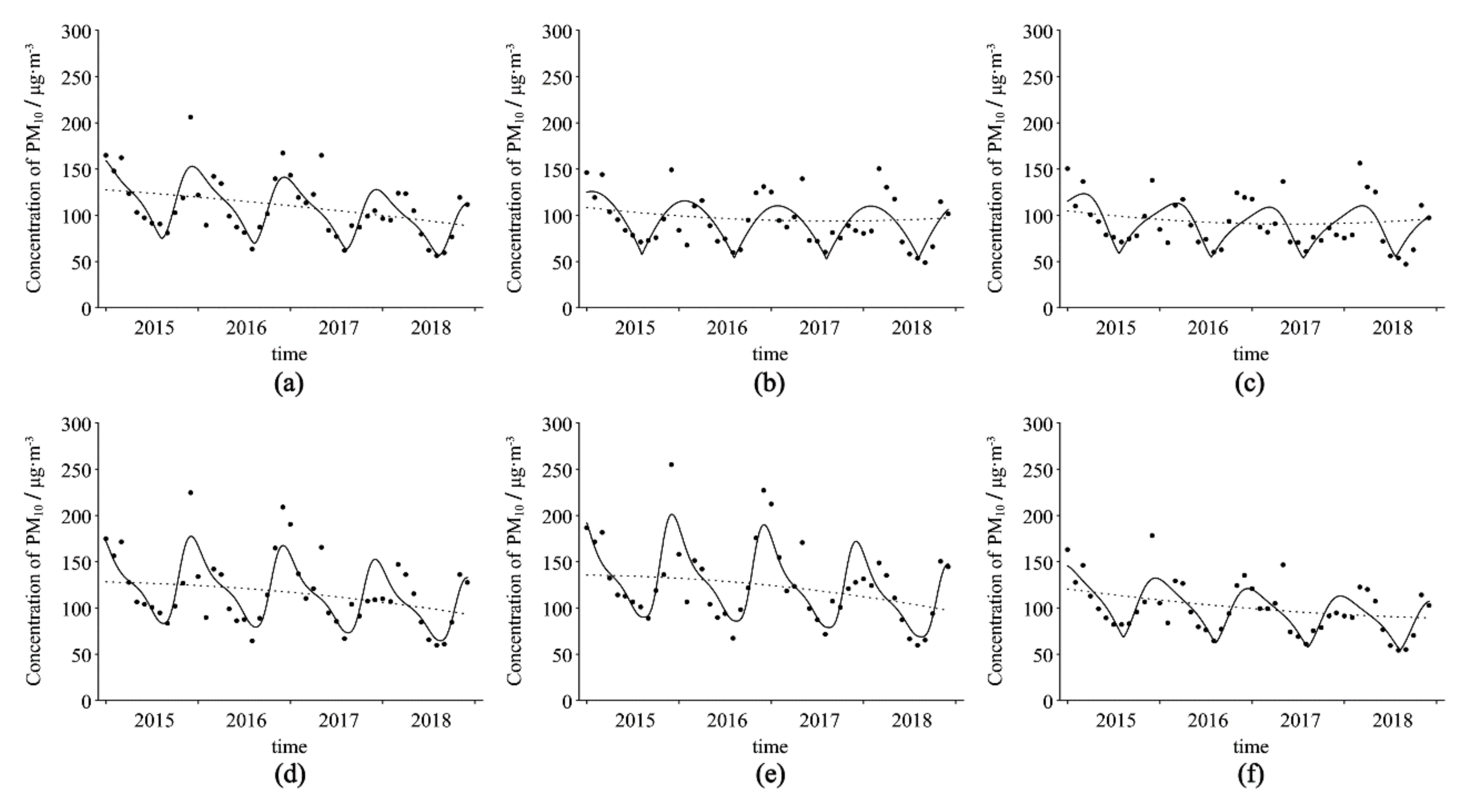
3.1.3. Accuracy Verification of the Optimization Model
3.2. Influence of Land Use on the Atmospheric Particulate Matter Concentration
3.2.1. Spatiotemporal Characteristics of Land Use
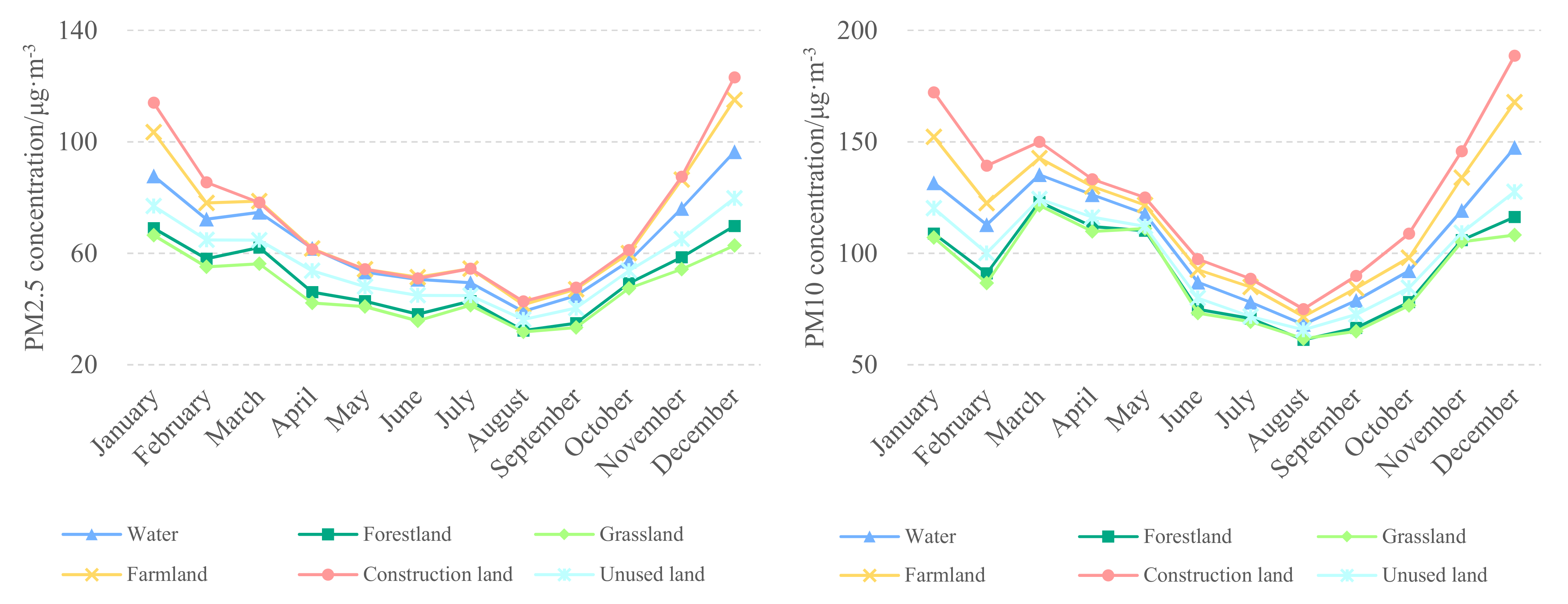
3.2.2. Comparison of Atmospheric Particulate Matter Concentrations between Various Land Use Types
3.2.3. Variation Patterns of the Atmospheric Particulate Matter Concentration for Different Land Use Types
3.3. Influence of Landscape Pattern on the Atmospheric Particulate Matter Concentration
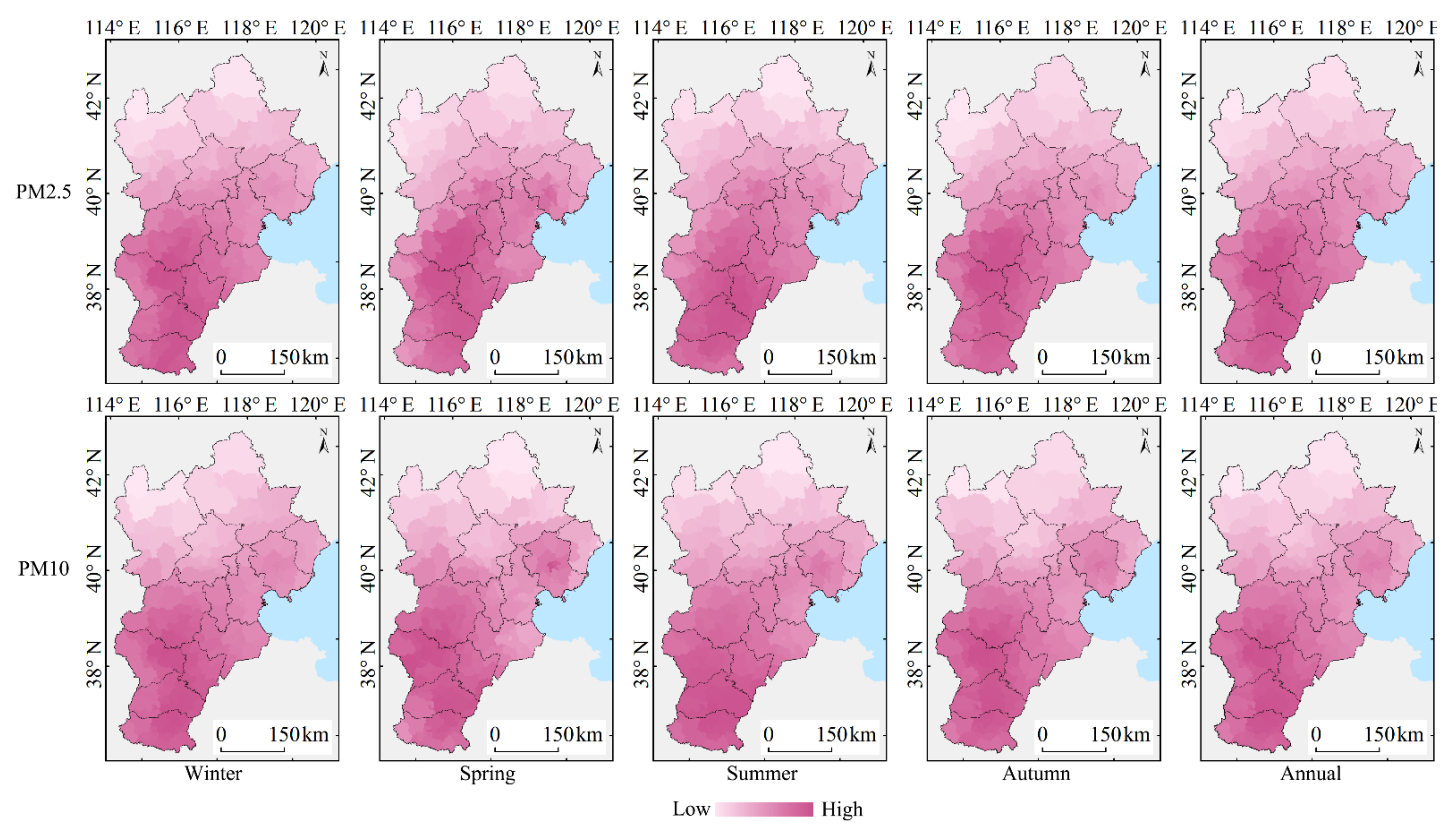
3.3.1. Atmospheric Particulate Matter Concentration Distribution
3.3.2. Effects of Land Use Types on Atmospheric Particulate Matter Concentrations
4. Implications and Limitations
5. Conclusions
- (1)
- The optimized sine function model can better represent periodic changes in atmospheric particulate matter concentrations. The experimental results reveal that the concentrations corresponding to land use types with higher concentrations, such as construction land and farmland, generally exhibited rapid downward trends, while the concentrations corresponding to land use types with lower concentrations, such as forestland and grassland, generally exhibited gradual downward or consistent trends.
- (2)
- The concentration gradually decreased in spring and summer and rapidly increased in autumn and winter. Human activities such as heating in winter in construction land areas and planting and harvesting of crops in farmland areas were the main factors affecting the concentration fluctuations. The concentrations in forestland and grassland areas were the lowest; the differences between high and low values were small; the fluctuation patterns of the particulate matter concentrations remained relatively uniform; and the peak times occurred slightly later than those of the other land use types. Natural sources greatly influenced the concentration fluctuations, among which the frequent dusty weather conditions in spring imposed a greater influence on forestland and grassland than on the other land use types.
- (3)
- The landscape pattern associated with the land use type significantly affects the particulate matter concentration. Overall, the lower the aggregation degree, the higher the fragmentation degree, the more complex the shape, and the higher the landscape abundance, the lower the particle concentration is. Among the land use types, the density and diversity of forestland, grassland, farmland, and construction land patches contribute to a reduction in the particulate matter concentration. The higher the dominance of forestland and grassland patches in the landscape, the more favorable the setting is to a reduction in the particulate matter concentration.
- (4)
- The protection of the atmosphere is essential in the context of high social and economic development. According to the experimentally observed results, the limiting effect of vegetation such as trees and grasses on the concentration of particulate matter is significant. Theoretically, increasing the percentage of vegetation can help control air pollution. However, in a highly developed urban city with high population density such as Beijing, the area of land that can be changed is very limited. Therefore, it is more important to adjust the rationality of land use in densely populated and motorized built-up areas. The area of urban green space can be appropriately increased to create better connectivity of vegetation in order to give full play to the limiting effect of green vegetation on particulate matter concentration. In addition, targeted selection of tree species for urban greening and increasing the rationality of the vertical level of vegetation are also key to improving the efficiency of urban land use and environmental protection functions.
Author Contributions
Funding
Conflicts of Interest
References
- Zhai, H.; Tang, X.; Wang, G.; Li, J.; Liu, K. Characteristic analyses, simulations and predictions of land use in poor mountainous cities: A case study in the central area of Chengde County, China. Environ. Earth Sci. 2018, 77, 585. [Google Scholar] [CrossRef]
- Gong, J.; Xie, Y.; Jia, Z.; Qian, D. Recent progress in land use and cover change in Heihe River Basin. J. Lanzhou Univ. (Nat. Sci.) 2014, 50, 390–397, 407. [Google Scholar] [CrossRef]
- Zhang, X. Simulation of land use change scenarios of Tangshan Coastal Zone Based on CLUE-S Model. Master’s Thesis, Hebei Normal University, Shijiazhuang, China, 20 March 2008. [Google Scholar] [CrossRef]
- Yan, J.; Zhai, H. Dynamic simulation of land use with CLUE-S model and change rate of land-sea gradient. Int. J. Earth Sci. Eng. 2016, 9, 1447–1453. [Google Scholar]
- Yan, J.; Zhai, H.; Cheng, F. Spatio-temporal evolution of land use and its socio-economic effects in the Shandong Peninsula. Int. J. Earth Sci. Eng. 2015, 8, 1994–2003. [Google Scholar]
- Wang, G.; Yang, K.; Yang, Y. The spatio-temporal variation of PM2.5 pollution and the its correlation with the impervious surface expansion. China Environ. Sci. 2017, 37, 2470–2481. [Google Scholar]
- Yang, K.; Wang, G.; Yang, Y.; Luo, Y. Association between impervious surface and PM2.5 concentrations in Kunming, China. Res. Environ. Sci. 2017, 30, 499–509. [Google Scholar] [CrossRef]
- Xu, S.; Zou, B.; Pu, Q.; Guo, Y. Impact analysis of land use/cover on air pollution. J. Geo-Inf. Sci. 2015, 17, 290–299. [Google Scholar] [CrossRef]
- Fu, B. The spatial pattern analysis of agricultural landscape in the loess area. Acta Ecol. Sin. 1995, 15, 113–120. [Google Scholar] [CrossRef]
- Tang, X.; Liu, H.; Li, J.; Xie, Z.; Zhao, W. Response analysis of haze/particulate matter pollution to Land Use/Cover in Beijing. China Environ. Sci. 2015, 35, 2561–2569. [Google Scholar] [CrossRef]
- Shi, J.; Cui, L.; He, Q.; Sun, L. The changes and causes of fog and haze days in Eastern China. Acta Geogr. Sin. 2010, 65, 533–542. [Google Scholar] [CrossRef]
- Shi, J.; Cui, L.; Zhou, W. Change trend of climatic factors in the Yangtze River Delta from 1959 to 2005. Resour. Sci. 2008, 30, 1803–1810. [Google Scholar]
- Peng, W.; Zhou, J.; Luo, H.; Yang, C.; Zhao, J. Relationship between land use change and its urban air environmental impacts. Res. Soil Water Conserv. 2010, 17, 87–91. [Google Scholar]
- Font, A.; Baker, T.; Mudway, I.S.; Purdie, E.; Dunster, C.; Fuller, G.W. Degradation in urban air quality from construction activity and increased traffic arising from a road widening scheme. Sci. Total Environ. 2014, 497-498, 123–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhai, H.; Tang, X.; Wang, G.; Li, J.; Xing, L. Impact of impervious surface expansion on tropospheric NO2 column density in Chinese megacities. Acta Sci. Circumstantiae 2019, 39, 797–808. [Google Scholar] [CrossRef]
- Wei, J.; Sun, L.; Liu, S.; Duan, D.; Guo, Y.; Mi, X.; Tian, X.; Yu, H. Response analysis of particulate air pollution to Land-use and land-cover change. Acta Ecol. Sin. 2015, 35, 5495–5506. [Google Scholar] [CrossRef]
- Mo, L.; Yu, X.; Zhao, Y.; Sun, F.; Mo, N.; Xia, H. Correlation analysis between urbanization and particle pollution in Beijing. Ecol. Environ. Sci. 2014, 23, 806–811. [Google Scholar] [CrossRef]
- Sun, N. Using Satellite Remote Sensing Data for Monitoring PM10 Concentrating in the Pearl River Delta and Study on the Correlation between PM10 and Underlying Surface. Master’s Thesis, China University of Geosciences, Beijing, China, 1 May 2013. [Google Scholar]
- Lou, C.; Liu, H.; Li, Y.; Li, Y. Research on the response of air particles (PM2.5, PM10) to landscape structure: A review. Acta Ecol. Sin. 2016, 36, 6719–6729. [Google Scholar] [CrossRef]
- Lou, C. Tempo-spatial characteristics of PM2.5 at multi-scales and its influencing in the core of the Yangtze River Delta. Ph.D. Thesis, Nanjing Normal University, Nanjing, China, 19 May 2018. [Google Scholar]
- Zhuang, Y.; Chen, D.; Li, R.; Chen, Z.; Cai, J.; He, B.; Gao, B.; Cheng, N.; Huang, Y. Understanding the Influence of Crop Residue Burning on PM2.5 and PM10 Concentrations in China from 2013 to 2017 Using MODIS Data. Int. J. Environ. Res. Public Health 2018, 15, 1504. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Y.; Li, R.; Yang, H.; Chen, D.; Chen, Z.; Gao, B.; He, B. Understanding Temporal and Spatial Distribution of Crop Residue Burning in China from 2003 to 2017 Using MODIS Data. Remote Sens. 2018, 10, 390. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, H.; Wang, G.; Guo, J.; Zhai, H. A new method of high resolution urban water extraction based on index. Remote. Sens. Inf. 2018, 33, 99–105. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, R.; Zhu, K.; Li, Z. Numerical simulation on the air pollution potential in the severe air pollution episodes in Beijing-Tianjin-Hebei Region. Acta Sci. Circumstantiae 2015, 35, 2681–2692. [Google Scholar] [CrossRef]
- Wang, X.; Lang, J.; Cheng, S.; Chen, G.; Liu, X. Study on transportation of PM2.5 in Beijing-Tianjin-Hebei (BTH) and its surrounding area. China Environ. Sci. 2016, 36, 3211–3217. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Qiao, Z.; Lu, Y. Atmospheric transmission rule on air pollution in Beijing-Tianjin-Hebei urban agglomeration: A comparative analysis of two emission inventories. China Environ. Sci. 2019, 39, 4561–4569. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, W.; Xiong, Q.; Wang, L.; Zhao, W. Spatio-temporal distribution of PM2.5 in Beijing-Tianjin-Hebei (BTH) area in 2016 and its relationship with meteorological factors. Ecol. Environ. Sci. 2017, 26, 1747–1754. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, T.; Wan, Q.; Tan, H.; Deng, X.; Li, F.; Deng, T. Spatio-temporal characteristics of NO2 in concentrated PRD Urban Districts and analysis of anthropogenic influences based on OMI remote sensing data. J. Trop. Meteorol. 2015, 31, 193–201. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, H.; Zhang, X.; Zhou, G.; Yu, S.; Xiao, Z. Temporal-spatial distribution of tropospheric NO2 in China using OMI satellite remote sensing data. Res. Environ. Sci. 2009, 22, 932–937. [Google Scholar] [CrossRef]
- Zhang, Y.; Niu, Z.; Wang, L.; Chang, C. Study on tropospheric NO2 change trend in cities using OMI satellite data. Geogr. Geo-Inf. Sci. 2008, 24, 96–99. [Google Scholar]
- Xu, J.; Jiang, H.; Xiao, Z. Estimate PM10 concentration over the Yangtze Delta using remote sensing: Analysis of spatial and temporal variations. Chin. J. Environ. Eng. 2016, 10, 1349–1357. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, H. Estimation of PM2.5 concentration over the Yangtze Delta using remote sensing: Analysis of spatial and temporal variations. Environ. Sci. 2015, 36, 3119–3127. [Google Scholar] [CrossRef]
- Zhai, H.; Yao, J.; Wang, G.; Tang, X. Spatio-Temporal Characteristics and Variation Pattern of the Atmospheric Particulate Matter Concentration: A Case Study of the Beijing–Tianjin–Hebei Region, China. Atmosphere 2022, 13, 120. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Ene, E. Fragstats v4: Spatial Pattern Analysis Program for Categorical and Continuous Maps. Computer Software Program Produced by the Authors at the University of Massachusetts, Amherst. 2012. Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 8 May 2013).
- Fu, B.; Chen, L. Landscape diversity types and their ecological significance. Acta Geogr. Sin. 1996, 51, 454–462. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Friedl, M.A. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product. 2018. Available online: https://lpdaac.usgs.gov/documents/101/MCD12_User_Guide_V6.pdf (accessed on 8 December 2021).
- Sulla-Menashe, D.; Gray, J.; Abercrombie, S.P.; Friedl, M.A. Hierarchical mapping of annual global land cover 2001 to present: The MODIS Collection 6 Land Cover product. Remote Sens. Environ. 2019, 222, 183–194. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Wang, G.; Zhai, H.; Han, M.; Cheng, Q. Plastic-mulched farmland extraction with multi-source satellite data. Bull. Surv. Mapp. 2018, 78–82. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, Y.; Pei, T.; Zhou, Z. The effect of adsorbing fine particulate matter (PM2.5) by garden plants: A review. Chin. J. Ecol. 2014, 33, 2558–2566. [Google Scholar] [CrossRef]
- Matsuda, K.; Fujimura, Y.; Hayashi, K.; Takahashi, A.; Nakaya, K. Deposition velocity of PM2.5 sulfate in the summer above a deciduous forest in central Japan. Atmos. Environ. 2010, 44, 4582–4587. [Google Scholar] [CrossRef]
- Freer-Smith, P.H.; Holloway, S.; Goodman, A. The uptake of particulates by an urban woodland: Site description and particulate composition. Environ. Pollut. 1997, 95, 27–35. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Wang, Y.; Zhang, H. Interactions between fine particulate matter (PM2.5) and vegetation: A review. Chin. J. Ecol. 2013, 32, 2203–2210. [Google Scholar] [CrossRef]
- Chen, A.; Lei, Y.; Sun, R.; Chen, L. How many metrics are required to identify the effects of the landscape pattern on land surface temperature? Ecol. Indic. 2014, 45, 424–433. [Google Scholar] [CrossRef]
- Kang, X.; Cui, L.; Zhao, X.; Li, W.; Zhang, M.; Wei, Y.; Lei, Y.; Ma, M. Effect of wetlands on reducing atmospheric fine particles PM2.5 in Beijing. Chin. J. Ecol. 2015, 34, 2807–2813. [Google Scholar] [CrossRef]
- Zhu, C.; Zeng, Y.; Chen, Y.; Guo, H. Effects of urban lake wetland on air PM10 and PM2.5 concentration: A case study of Wuhan. Chin. Landsc. Archit. 2016, 88–93. [Google Scholar]


| Parameters | Definition | Range | Description |
|---|---|---|---|
| At | Quadratic coefficient | (−∞, ∞) | At determines the opening direction and magnitude of the parabolic curve, namely: (1) for At > 0, the parabolic curve opens upwards; (2) for At < 0, the parabolic curve opens downwards. Additionally, the larger the absolute value of At is, the smaller the opening of the parabolic curve, while the smaller the absolute value of At is, the larger the opening of the parabolic curve. |
| Bt | Primary term coefficient | (−∞, ∞) | Bt and At jointly determine the position of the axis of symmetry. |
| Bt/2At | Axis of symmetry | (1) When the axis of symmetry occurs within the studied time range, for At > 0, the concentration first decreases and then increases. Conversely, for At < 0, the concentration first increases and then decreases. (2) When the axis of symmetry occurs on the left side of the studied time range, for At > 0, the concentration continuously increases, and the rate of increase rises. Conversely, for At < 0, the concentration continuously decreases, but the rate of decrease rapidly declines. (3) When the axis of symmetry is located on the right side of the studied time range, for At > 0, the concentration continuously decreases, but the rate of decrease declines. Conversely, for At < 0, the concentration continuously increases, but the rate of increase declines. In addition, when the axis of symmetry is located far from the studied time range, the concentration can be considered to increase or decrease at an approximately constant rate. | |
| Ct | Constant | (−∞, ∞) | Ct determines the intersection of the parabolic curve and Y-axis and represents the overall particulate matter concentration at the starting time of the analysis. |
| Dt | Amplitude | [0, ∞) | Dt indicates the differences between peak and valley values and determines the oscillation amplitude. The larger its value, the stronger the fluctuations are. |
| Et | Cycle | 12 | Et represents the fluctuation duration. Because particulate matter fluctuation over a year is considered in this paper, a fixed Et value of 12 is adopted. |
| Ft | Deformation factor | (0, ∞) | Ft indicates the duration of periods with high or low values during a given cycle: (1) for Ft = 1, the curve of the sine function uniformly oscillates; (2) for Ft > 1, the function curve exhibits narrow peaks and wide valleys, and the larger the Ft value is, the stronger the deformation; (3) for 0 < Ft < 1, the function curve exhibits wide peaks and narrow valleys, and the closer the Ft value is to 0, the stronger the deformation. |
| Gt | Phase | [0, 12] | Gt determines the occurrence positions of peaks. During a given period, the larger the value, the later peaks and valleys occur. |
| Ht | Offset factor | (−∞, ∞) | Ht indicates the relative positions of peaks and valleys, namely: (1) for Ht = 0, the left and right positions of valleys are located at the centers of two adjacent peaks, i.e., the time when one peak reaches the next valley is equal to the time when one valley rises to reach the next peak; (2) for Ht > 0, the trough moves towards the right, i.e., the time required for one peak to reach the next trough increases, and the time required for one trough to reach the next peak decreases; (3) for Ht < 0, the trough moves towards the left, i.e., the time required for one peak to reach the next trough decreases, and the time required for one trough to reach the next peak increases. The larger the absolute value of Ht is, the larger the offset. |
| Land Use Type | Description |
|---|---|
| Water bodies | Permanent water coverage rates not lower than 60%. |
| Forestland | Tree cover not lower than 10%. |
| Grassland | Dominated by herbaceous annuals (less than 2 m) with no cultivation. |
| Farmland | Dominated by herbaceous annuals (less than 2 m) and no less than 60% cereal crops or broadleaf crops. |
| Construction land | Impervious surface coverage, including building materials, asphalt, and vehicles, not lower than 30%. |
| Unused land | Unvegetated barren (sand, rock, soil) with less than 10% vegetation. |
| PM2.5 | PM10 | |||
|---|---|---|---|---|
| The Traditional Model | The Improved Model | The Improved Model | The Improved Model | |
| The BTH region | 0.60 | 0.74 | 0.53 | 0.58 |
| Beijing | 0.36 | 0.50 | 0.29 | 0.32 |
| Tianjin | 0.50 | 0.67 | 0.51 | 0.56 |
| Shijiazhuang | 0.52 | 0.67 | 0.48 | 0.56 |
| Tangshan | 0.53 | 0.64 | 0.48 | 0.57 |
| Qinhuangdao | 0.55 | 0.56 | 0.60 | 0.64 |
| Handan | 0.50 | 0.77 | 0.53 | 0.68 |
| Xingtai | 0.64 | 0.81 | 0.63 | 0.68 |
| Baoding | 0.66 | 0.81 | 0.65 | 0.72 |
| Zhangjiakou | 0.08 | 0.18 | 0.19 | 0.34 |
| Chengde | 0.54 | 0.59 | 0.36 | 0.42 |
| Cangzhou | 0.58 | 0.76 | 0.60 | 0.71 |
| Langfang | 0.50 | 0.67 | 0.43 | 0.50 |
| Hengshui | 0.63 | 0.84 | 0.64 | 0.74 |
| 2018 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Water Bodies | Forestland | Grassland | Farmland | Construction Land | Unused Land | Total | ||
| 2015 | Water bodies | 2650 | 0 | 4 | 0 | 0 | 5 | 2658 |
| Forestland | 1 | 30,066 | 1404 | 107 | 4 | 0 | 31,582 | |
| Grassland | 53 | 3404 | 57,858 | 2008 | 115 | 23 | 63,461 | |
| Farmland | 7 | 304 | 1861 | 98,473 | 447 | 0 | 101,091 | |
| Construction land | 0 | 0 | 0 | 0 | 16613 | 0 | 16,613 | |
| Unused land | 4 | 0 | 36 | 0 | 2 | 348 | 390 | |
| Total | 2714 | 33,773 | 61,163 | 100,588 | 17181 | 376 | 215,795 | |
| Unit: km2 | ||||||||
| R2 | Average Concentration | At | Bt | Turning Point | Overall Trend | Average Monthly Variation | Ct | Dt | Et | Ft | Gt | Ht | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PM2.5 | Water bodies | 0.71 | 64 | −0.0066 | −0.13 | Before 2015 | Descends rapidly | −0.46 | 53.20 | 1.20 | 12 | 1.95 | 1.86 | 1.43 |
| Forestland | 0.63 | 50 | 0.0008 | −0.45 | After 2018 | Descends slowly | −0.41 | 46.92 | 0.97 | 12 | 1.77 | 2.09 | 1.00 | |
| Grassland | 0.63 | 47 | 0.0040 | −0.62 | After 2018 | Descends slowly | −0.42 | 47.69 | 0.87 | 12 | 1.93 | 2.22 | 0.72 | |
| Farmland | 0.71 | 69 | −0.0148 | 0.19 | 2015.06 | Rises and then descends | −0.54 | 56.19 | 1.48 | 12 | 2.85 | 1.86 | 1.41 | |
| Construction land | 0.79 | 72 | −0.0154 | 0.24 | 2015.07 | Rises and then descends | −0.51 | 56.23 | 1.60 | 12 | 3.12 | 1.84 | 1.25 | |
| Unused land | 0.71 | 56 | 0.0026 | −0.56 | After 2018 | Descends slowly | −0.43 | 52.46 | 0.99 | 12 | 1.81 | 2.00 | 1.19 | |
| PM10 | Water bodies | 0.58 | 108 | −0.0027 | −0.37 | Before 2015 | Descends rapidly | −0.50 | 78.17 | 1.09 | 12 | 0.76 | 1.73 | 1.18 |
| Forestland | 0.41 | 93 | 0.0082 | −0.53 | 2017.08 | Descends and then rises | −0.13 | 61.02 | 1.09 | 12 | 0.46 | 0.97 | 0.14 | |
| Grassland | 0.38 | 91 | 0.0101 | −0.60 | 2017.06 | Descends and then rises | −0.11 | 62.81 | 1.02 | 12 | 0.58 | 0.54 | –0.86 | |
| Farmland | 0.57 | 117 | −0.0080 | −0.10 | Before 2015 | Descends rapidly | −0.49 | 84.77 | 1.15 | 12 | 1.17 | 1.74 | 1.46 | |
| Construction land | 0.66 | 126 | −0.0102 | −0.05 | Before 2015 | Descends rapidly | −0.55 | 91.18 | 1.26 | 12 | 1.37 | 1.76 | 1.42 | |
| Unused land | 0.56 | 99 | 0.0058 | −0.69 | After 2018 | Descends slowly | −0.40 | 73.82 | 1.00 | 12 | 0.63 | 1.60 | 0.94 |
| PM2.5 | PM10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Winter | Spring | Summer | Autumn | All | Winter | Spring | Summer | Autumn | All | |
| PD | −0.185 ** | −0.108 | −0.181 ** | −0.158 * | −0.170 * | −0.155 * | −0.114 | −0.144 * | −0.128 | −0.143 * |
| LPI | 0.401 ** | 0.368 ** | 0.407 ** | 0.372** | 0.399 ** | 0.366 ** | 0.291 ** | 0.346 ** | 0.309 ** | 0.343 ** |
| ED | −0.362 ** | −0.307 ** | −0.395 ** | −0.322 ** | −0.356 ** | −0.331 ** | −0.280 ** | −0.358 ** | −0.284 ** | −0.320 ** |
| CONTAG | 0.249 ** | 0.200 ** | 0.251 ** | 0.195 ** | 0.234 ** | 0.227 ** | 0.154 * | 0.214 ** | 0.168 * | 0.203 ** |
| SPLIT | −0.385 ** | −0.387 ** | −0.419 ** | −0.386 ** | −0.398 ** | −0.343 ** | −0.330 ** | −0.357 ** | −0.317 ** | −0.342 ** |
| SHDI | −0.446 ** | −0.332 ** | −0.403 ** | −0.373 ** | −0.415 ** | −0.425 ** | −0.324 ** | −0.382 ** | −0.362 ** | −0.395 ** |
| SIDI | −0.418 ** | −0.320 ** | −0.386 ** | −0.349 ** | −0.391 ** | −0.395 ** | −0.293 ** | −0.355 ** | −0.329 ** | −0.364 ** |
| AI | 0.291 ** | 0.263** | 0.333 ** | 0.265 ** | 0.293 ** | 0.254 ** | 0.198 ** | 0.281 ** | 0.205 ** | 0.241 ** |
| PM2.5 | PM10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Winter | Spring | Summer | Autumn | All | Winter | Spring | Summer | Autumn | All | ||
| Forestland | PLAND | −0.382 ** | −0.346 ** | −0.372 ** | −0.359 ** | −0.376 ** | −0.389 ** | −0.367 ** | −0.424 ** | −0.378 ** | −0.393 ** |
| PD | −0.280 ** | −0.289 ** | −0.286 ** | −0.269 * | −0.285 ** | −0.255 * | −0.176 | −0.255 * | −0.212 | −0.235 * | |
| LPI | −0.270* | −0.195 | −0.222 * | −0.229 * | −0.246 * | −0.293 ** | −0.252 * | −0.306 ** | −0.278 * | −0.288 ** | |
| LSI | −0.464 ** | −0.551 ** | −0.530 ** | −0.487 ** | −0.502 ** | −0.444 ** | −0.468 ** | −0.477 ** | −0.439 ** | −0.457 ** | |
| SPLIT | 0.099 | 0.113 | 0.088 | 0.070 | 0.095 | 0.106 | 0.053 | 0.094 | 0.070 | 0.088 | |
| Grassland | PLAND | −0.656 ** | −0.791 ** | −0.713 ** | −0.713 ** | −0.712 ** | −0.623 ** | −0.515 ** | −0.592 ** | −0.564 ** | −0.598 ** |
| PD | −0.394 ** | −0.259 ** | −0.351 ** | −0.333 ** | −0.360 ** | −0.369 ** | −0.325 ** | −0.348 ** | −0.336 ** | −0.357 ** | |
| LPI | −0.588 ** | −0.737 ** | −0.648 ** | −0.653 ** | −0.647 ** | −0.560 ** | −0.462 ** | −0.530 ** | −0.508 ** | −0.537 ** | |
| LSI | −0.528 ** | −0.505 ** | −0.553 ** | −0.515 ** | −0.535 ** | −0.509 ** | −0.507 ** | −0.527 ** | −0.487 ** | −0.514 ** | |
| SPLIT | 0.237 ** | 0.174 * | 0.212 ** | 0.199 ** | 0.220 ** | 0.237 ** | 0.162 * | 0.188 * | 0.183 * | 0.210 ** | |
| Farmland | PLAND | 0.631 ** | 0.619 ** | 0.618 ** | 0.602 ** | 0.633 ** | 0.630 ** | 0.512 ** | 0.586 ** | 0.554 ** | 0.597 ** |
| PD | −0.267 ** | −0.291 ** | −0.278 ** | −0.261 ** | −0.276 ** | −0.236 ** | −0.138 | −0.183 * | −0.170 * | −0.202 ** | |
| LPI | 0.626 ** | 0.613 ** | 0.614 ** | 0.597 ** | 0.627 ** | 0.621 ** | 0.508 ** | 0.576 ** | 0.543 ** | 0.588 ** | |
| LSI | −0.507 ** | −0.587 ** | −0.594 ** | −0.541 ** | −0.549 ** | −0.483 ** | −0.510 ** | −0.531 ** | −0.471 ** | −0.498 ** | |
| SPLIT | −0.058 | −0.014 | −0.018 | −0.031 | −0.040 | −0.081 | −0.048 | −0.068 | −0.079 | −0.075 | |
| Construction land | PLAND | 0.084 | 0.242 ** | 0.195 ** | 0.188 ** | 0.150 * | 0.026 | 0.058 | 0.083 | 0.046 | 0.044 |
| PD | 0.555 ** | 0.503 ** | 0.505 ** | 0.538 ** | 0.548 ** | 0.551 ** | 0.536 ** | 0.510 ** | 0.524 ** | 0.545 ** | |
| LPI | 0.034 | 0.189 ** | 0.147 * | 0.135 | 0.098 | −0.021 | 0.015 | 0.043 | 0.002 | −0.002 | |
| LSI | 0.388 ** | 0.365 ** | 0.344 ** | 0.371 ** | 0.383 ** | 0.370 ** | 0.335 ** | 0.294 ** | 0.324 ** | 0.349 ** | |
| SPLIT | −0.378 ** | −0.492 ** | −0.458 ** | −0.435 ** | −0.428 ** | −0.357 ** | −0.390 ** | −0.384 ** | −0.356 ** | −0.371 ** | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, H.; Yao, J.; Wang, G.; Tang, X. Impact of Land Use on Atmospheric Particulate Matter Concentrations: A Case Study of the Beijing–Tianjin–Hebei Region, China. Atmosphere 2022, 13, 391. https://doi.org/10.3390/atmos13030391
Zhai H, Yao J, Wang G, Tang X. Impact of Land Use on Atmospheric Particulate Matter Concentrations: A Case Study of the Beijing–Tianjin–Hebei Region, China. Atmosphere. 2022; 13(3):391. https://doi.org/10.3390/atmos13030391
Chicago/Turabian StyleZhai, Haoran, Jiaqi Yao, Guanghui Wang, and Xinming Tang. 2022. "Impact of Land Use on Atmospheric Particulate Matter Concentrations: A Case Study of the Beijing–Tianjin–Hebei Region, China" Atmosphere 13, no. 3: 391. https://doi.org/10.3390/atmos13030391
APA StyleZhai, H., Yao, J., Wang, G., & Tang, X. (2022). Impact of Land Use on Atmospheric Particulate Matter Concentrations: A Case Study of the Beijing–Tianjin–Hebei Region, China. Atmosphere, 13(3), 391. https://doi.org/10.3390/atmos13030391









