Attribution Analysis of Annual Precipitation Simulation Differences and Its Correction of CMIP5 Climate Models on the Chinese Mainland

Abstract

Using the self-organizing maps (SOM) method, we ranked and compared the simulation results of atmospheric circulation and precipitation for 32 global climate models (GCMs) in the Coupled Model Intercomparison Project Phase 5 (CMIP5) over China, and found that the ranking of the GCM’s ability to simulate the frequency of sea level pressure (SLP) weather patterns (WPs) was not correlated with the ranking of its ability to simulate annual precipitation WPs. Then, we attributed the precipitation simulation differences and identified three main components for the differences in the multi-model simulation results: internal variability, frequency differences, and the combined term of the two, with internal variability being the largest of the three components. These three deviations depend ultimately on two factors: the ability to simulate the frequency of WPs and the ability to simulate the corresponding average daily precipitation generated by these WPs, with the second factor playing a decisive role. Then, to address the drawback that the model ensemble results cannot be effectively improved when each single model that makes up the ensemble model is dry or wet, a solution was proposed to correct for the simulation differences: the nodal precipitation differences of each WP were corrected. After the correction of the simulation differences, the simulation capability of all the individual models was greatly improved, which increases our confidence in using the CMIP5 models for future weather patterns and precipitation simulation and forecasting.

1. Introduction

The study of future precipitation changes in the Chinese region is of great strategic importance to the socio-economic development and rational layout of water resources in China. At the same time, the results of future precipitation prediction can also provide a scientific basis for the prevention and control of extreme precipitation disasters. Global climate models (GCMs) are the most direct and important means to study future precipitation changes, but their prediction results are subject to large uncertainties. This uncertainty becomes an important issue to be addressed when assessing the regional impacts of climate change, especially at low resolution [1,2,3,4,5]. The credibility of model results for future climate change prediction depends on the ability of the model to simulate the contemporary climate. Therefore, before making future climate predictions, it is necessary to check how well the model can simulate the current climate [6,7,8].

In recent years, the assessment of the simulation capability of different atmospheric circulation models at a regional scale has become a popular research topic. Many international meteorologists have conducted related studies [9,10,11,12,13]. The Atmospheric Model Comparison Program (AMIP), Ocean Model Comparison Program, Land Surface Process Comparison Program (PILPS), and Coupled Model Comparison Program (CMIP) are organized and launched by the World Climate Research Program. PILPS and CMIP have been organized and launched by WCRP to provide insight into model performance by comparing model output with observations [14].

In the context of global warming, changes in precipitation characteristics are reflected in changes in both total precipitation and precipitation structure [15,16]. Previous studies have mostly focused on the long-term trends and spatial and temporal variability of precipitation in East Asia. Changes in precipitation structure (i.e., the distribution function of cumulative precipitation and precipitation frequency with precipitation intensity, or PDF) involve precipitation frequency, precipitation intensity, and the variability characteristics of different levels of precipitation [16]. In addition, due to the limitation of data, the changes in the precipitation structure in East Asia have been less studied. In the context of warming, studying the characteristics of precipitation structure and its transformation can better reflect the effect of temperature increase on precipitation, etc. [16]. It helps to understand the past changes of precipitation and predict its possible future changes.

A multi-model ensemble is an effective way to improve the simulation capability of GCMs. However, the improvement in the simulation capability by a model ensemble relies mainly on offsetting the deviations of each single GCM in the set of GCMs, while the simulation capability of each single GCM itself is not improved. The problem arises that, when a large number of GCMs exhibit positive deviations or negative deviations (i.e., deviations of the same sign), the simulation capability of the model ensemble cannot be improved by the offsetting of individual GCMs, and the model ensemble becomes powerless. If we can identify the causes that affect the GCM’s ability to simulate the annual mean precipitation, we can correct the simulation differences, so that the simulation ability of each single GCM can be effectively improved.

Self-organizing maps (SOMs) are a form of unsupervised artificial neural network model. Kohonen proposed the SOM algorithm in 1982 [17] and described the process of its implementation [17]. The SOM method changes the network parameters and structure in a self-organizing and adaptive way by automatically finding the intrinsic laws and essential properties in the samples. The SOM can cluster the high-dimensional meteorological field change data to obtain various types of dominant circulation types and their evolution. Compared with the objective typing methods commonly used in meteorology, the SOM method has many advantages. For example, the SOM can be effectively applied to model identification and feature extraction, and has the characteristics of nonlinearity, validity, and robustness. The SOM clustering results are accurate and continuous. The SOM method also takes into account the continuity of atmospheric processes and reflects the fractal characteristics of the circulation, so the clustering results have some physical significance [18]. A large number of studies have shown that the SOM can effectively handle a large quantity of meteorological data, and the ability to analyze meteorological data is better than that of the traditional classification methods [19,20]. In recent years, this method has been widely used in weather circulation typing [18,19,20,21,22,23].

The fractal shape of the circulation of the surface sea level pressure field enables the effective identification of the characteristics of precipitation events under different weather patterns (WPs). This enables understanding the frequency characteristics of each WP, in addition to the corresponding precipitation event characteristics (daily mean precipitation) for each WP. The SOM is useful for this analysis as an analytical tool that allows us to analyze in detail the causes of these differences [23].

Therefore, the purpose of this study was to assume that the future evolution will be the same as the past, and the past differences in the GCM can be used to correct the future GCM simulation results to achieve a higher prediction accuracy. Self-organizing maps (SOMs) are used as an analysis tool that allows a detailed understanding of the causes of the differences between reanalysis and model data [17].

The model ensemble results cannot be effectively improved when each single GCM of the ensemble model is either dry or wet [23], and we use the SOM method to subdivide the factors influencing the GCM’s annual precipitation simulation results and identify the most important factors. We also propose a method to correct the simulation differences based on the distribution characteristics of the differences, in which the average daily precipitation of each GCM is corrected. As a result of the correction of the differences, the simulation capability of all GCMs is greatly improved. This also provides the advantage of eliminating the blindness of the multi-model ensemble, and removes the uncertainty surrounding the differences, thus increasing our confidence in using the Coupled Model Intercomparison Project 5 (CMIP5) [24] models for the simulation and forecasting of future weather patterns and precipitation.

The remainder of this paper is organized as follows. The following section introduces the study area, data information, and the self-organized mapping method. Section 3 presents the experimental results. Section 4 provides a detailed discussion about the sources of GCM simulation differences. Section 5 proposes the solution, i.e., the method used for the correction of GCM simulation differences and the analysis of the correction results. Finally, the Section 6 presents the conclusion.

2. Data and Methods

2.1. Analysis Domains

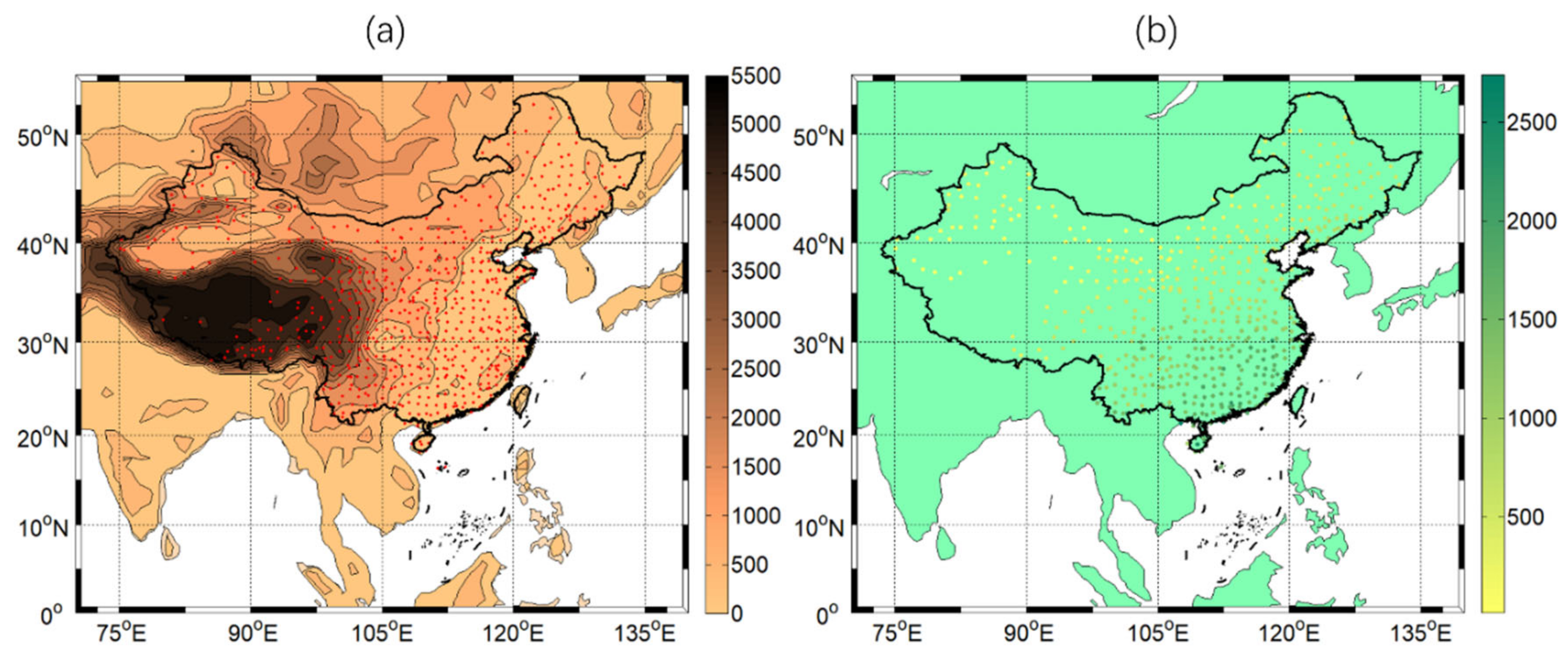
China is in the East Asian monsoon region, a typical monsoon climate zone and one of the regions with the highest precipitation variability worldwide [25]. China is widely affected by alternating winter and summer winds. The complex and diverse climate types and the complex and varied topography make China very rich in crops and plant and animal resources. However, China also frequently experiences catastrophic weather, which often has a negative impact on production, construction, and people’s lives.

The main study area of this paper refers to the region from 0° to 55° N and 70° to 140° E. The main focus is the weather patterns (WPs) affecting the Chinese region and the precipitation within 20° to 53° N and 75° to 135° E of the Chinese continental range. China’s high topography in the west and low topography in the east exacerbates the complex diversity of the climate (Figure 1a). In general, oceanic air currents enter the interior and are blocked by layers of mountain ranges, causing precipitation to decrease from the southeast to the northwest (Figure 1b).

2.2. Model Output

In order to ensure that the SOM method captures daily weather-scale precipitation events, daily sea level pressure (SLP) and precipitation (PR) data from 32 CMIP5 models (archived by the PCMDI at http://pcmdi9.llnl.gov/esgf-web-fe/, accessed on 3 September 2021) [24] were used for the study. The time period of the study was 1960–1999, for a total of 40 years. In order to test the validity of the method in this paper, an additional 5 years from 2000–2004 were selected. Each CMIP5 model has its own resolution, and the details are listed in

Table 1. Model identification, originating center, and atmospheric resolution.

GCMs	Institution	Resolution
ACCESS1-0	Commonwealth Scientific and Industrial Research Organisation and Bureau of Meteorology, Australia	1.875° × 1.25°
ACCESS1-3	Commonwealth Scientific and Industrial Research Organisation and Bureau of Meteorology, Australia	1.875° × 1.25°
bcc-csm1-1	Beijing Climate Center, China Meteorological Administration, China	2.8° × ~2.8°
bcc-csm1-1-m	Beijing Climate Center, China Meteorological Administration, China	1.125° × ~1.12°
BNU-ESM	Beijing Normal University, China	2.8° × ~2.8°
CanESM2	Canadian Centre for Climate Modelling and Analysis, Canada	2.8° × ~2.8°
CCSM4	National Center for Atmospheric Research (NCAR), USA	1.25° × ~0.9°
CESM1-FASTCHEM	National Science Foundation/Department of Energy NCAR, USA	1.25° × ~0.9°
CMCC-CM	Centro Euro-Mediterraneo per i Cambiamenti, Italy	0.75° × ~0.75°
CMCC-CMS	Centro Euro-Mediterraneo per i Cambiamenti, Italy	1.875° × ~1.875°
CNRM-CM5	Centre National de Recherches Meteorologiques, Meteo-France, France	1.4° × ~1.4°
CSIRO-Mk3-6-0	Australian Commonwealth Scientific and Industrial Research Organization, Australia	1.875° × ~1.875°
EC-EARTH	Royal Netherlands Meteorological Institute, The Netherlands	1.125° × 1.125°
FGOALS-g2	Institute of Atmospheric Physics, Chinese Academy of Sciences, China	2.8° × ~1.65°
GFDL-CM3	Geophysical Fluid Dynamics Laboratory, USA	2.5° × 2.0°
GFDL-ESM2G	Geophysical Fluid Dynamics Laboratory, USA	2.5° × ~2.0°
GFDL-ESM2M	Geophysical Fluid Dynamics Laboratory, USA	2.5° × ~2.0°
GISS-E2-R	NASA Goddard Institute for Space Studies, USA	2.5° × 2.0°
HadCM3	Met Oce Hadley Centre, UK	3.75° × 2.5°
HadGEM2-CC	Met Oce Hadley Centre, UK	1.875° × 1.25°
HadGEM2-ES	Met Oce Hadley Centre, UK	1.875° × 1.25°
IPSL-CM5A-LR	Institut Pierre-Simon Laplace, France	3.75° × ~1.895°
IPSL-CM5A-MR	Institut Pierre-Simon Laplace, France	2.5° × ~1.27°
MIROC-ESM	Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology (MIROC)	2.8° × ~2.8°
MIROC-ESM-CHEM	AORI, NIES, JAMSTEC, Japan	2.8° × ~2.8°
MIROC4h	AORI, NIES, JAMSTEC, Japan	~0.56° × ~0.56°
MIROC5	AORI, NIES, JAMSTEC, Japan	~1.4° × 1.4°
MPI-ESM-LR	Max Planck Institute for Meteorology, Germany	1.875° × ~1.875°
MPI-ESM-MR	Max Planck Institute for Meteorology, Germany	1.875° × ~1.875°
MPI-ESM-P	Max Planck Institute for Meteorology, Germany	1.875° × ~1.875°
MRI-CGCM3	Meteorological Research Institute, Japan	1.125° × ~1.125°
NorESM1-M	Norwegian Climate Centre, Norway	2.5° × ~1.89°

. All of the models were interpolated to a common grid with a resolution of 2.5° × 2.5°.

2.3. Validation Data

In this study, the SLP lattice information from the National Center for Atmospheric Research (NCEP) reanalysis data [26] was used as a proxy for the actual atmospheric circulation field (OBS). In addition to the reanalysis data, the gridded precipitation data were also used (referred to as CHEN05) [27]. The data resolution is 0.5° by 0.5°. This dataset was also obtained from 753 operational surface stations of the China Meteorological Administration by ordinary kriging interpolation, with small interpolation differences in the eastern part of China due to the high station density. The CHEN05 daily precipitation dataset has been made available for the scientific community (http://rcg.gvc.gu.se/, accessed on 3 September 2021). The simulation results of each GCM for SLP were compared with the NCEP reanalysis data, and then the simulation results of precipitation for each GCM in various WPs were compared with the corresponding OBS.

2.4. Methods

2.4.1. Clustering of Weather Patterns (WPs)

Self-organizing maps (SOMs) [17] are a form of self-organizing neural network algorithm, similar to fuzzy clustering, that are useful for visualization and clustering of high-dimensional data, and have been widely used in meteorological and oceanographic research [19]. The SOM technique is considered to be a proven method for model assessment, and can be used to provide an exhaustive view of the differences between individual model simulations of the general circulation and observations. The SOM methods have been described in detail [18,19,20,21], and this paper focuses the study on the discussion of the results [21] been presented in detail, and this paper focuses mainly on the shortcomings of the results.

2.4.2. Decomposition of Simulation Differences

An ideal model has the ability to reproduce weather patterns (WPs) in the actual atmosphere (represented here by NCEP). Each WP obtained by the model should occur at the same frequency as that of NCEP. The frequency of occurrence ($f_n$) (%) of each of the WPs is represented as a percentage of the total number of daily samples. In the formula, $n$ represents the number of WPs. The average daily precipitation of WP ($p_n$) (mm) was calculated by averaging, for each WP, the precipitation over all of China each time a WP occurred.

Following [21], the mean WP contribution was calculated by multiplying $p_n$ (mm/day) by $f_n$ (%). Summing over all WPs (n) gives the mean annual precipitation ($P$) (mm) given by Formula (1). In this article, the $n\_WT$ value in the formula is the total number of WPs.

$$P={\displaystyle \sum }_{n=1}^{n\_WT}{f}_n{p}_n$$

(1)

The difference between the results simulated by each model and the observed data is a measure of the model’s simulation capability. Furthermore, the difference can also be decomposed (using the difference of $f_n$ and $p_n$). The attribution of the mean annual precipitation difference can be determined by rewriting Formula (1) as:

$$P={\displaystyle \sum _{n=1}^{n\_WT}(f_n+\Delta f_n)(p_n}+\Delta p_n)$$

(2)

The annual precipitation simulated by the model is equal to the sum of all nodes of the observed data (OBS) plus the difference (delta) term. The frequency simulated by the model is now represented by the OBS frequency ($f_n$) plus the difference in the frequency between the model and OBS ($f_n$ + $\Delta f_n$). The precipitation simulated by the model is then represented by the OBS precipitation ($p_n$) plus the difference in precipitation between the model and OBS ($p_n$ + $\Delta p_n$). Expanding the expression in Formula (2) gives Formula (3):

$$P={\displaystyle \sum _{n=1}^{n\_WT}(f_n{p}_n+f_n\Delta p_n+\Delta f_n{p}_n+\Delta f_n\Delta p_n})$$

(3)

Formula (3) indicates that the total annual precipitation simulated by a model can be represented as the OBS precipitation (first term), plus three terms that represent the net difference in annual precipitation between the model and OBS. The first difference term ($f_n\Delta p_n$) is referred to as the intrapattern variability component (deviation_A); the difference represented by this term is caused by the difference in the simulated precipitation when the frequency is correct. The second difference term ($\Delta f_n{p}_n$) is referred to as the pattern frequency component (deviation_B); this term represents the difference introduced by the different frequency of different WPs. The third difference term ($\Delta f_n\Delta p_n$) is referred to as the combined term (deviation_C). This term is the difference representing the modeled precipitation and the modeled frequency difference, and usually accounts for a very small fraction of the difference.

3. Simulation of CMIP5 Models

Before using a GCM to simulate the future climate, the first task is to optimize the GCM, mainly by comparing the GCM’s past simulation results with the reanalysis data to judge its simulation capability. In this study, we classified the WPs of NCEP reanalysis data using the SOM method. We then evaluated the ability of each GCM to simulate these WPs, and evaluated the simulation of the daily average precipitation corresponding to each WP.

3.1. Simulation of Occurrences of Weather Patterns

The number of SOM output nodes (each node represents a WP) is highly subjective; if the number of output nodes is too small, the classification results (WPs) will appear to be too coarse; conversely, if the number of output nodes is too large, the number of days divided into each node will appear to be too small. In previous studies of WPs, it has usually been considered reasonable to choose 5 × 7 = 35 SOM output nodes [18,22,28]. Here, we determined the number of SOM output nodes as 6 × 6 = 36, which can better reflect the type of actual WPs to a certain extent. 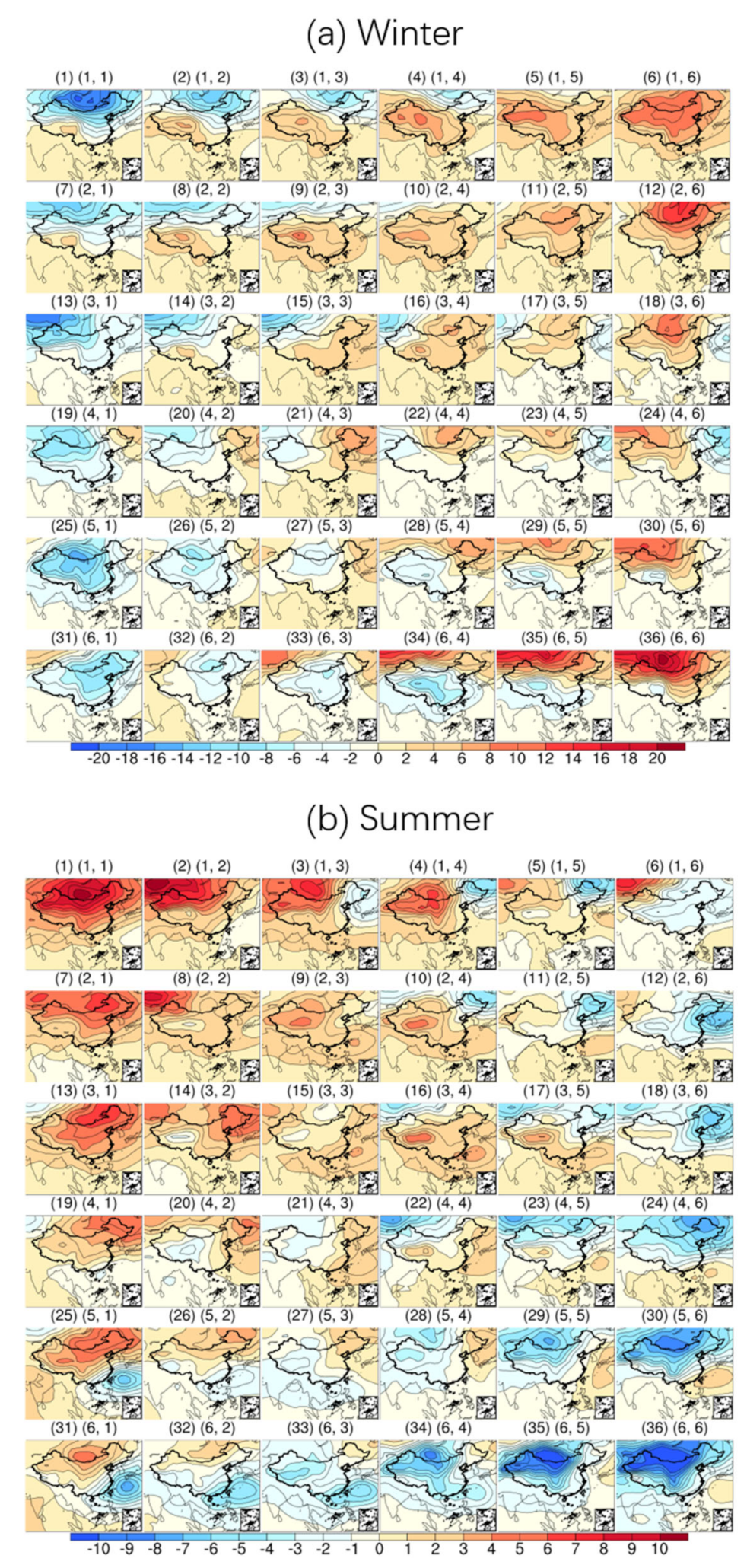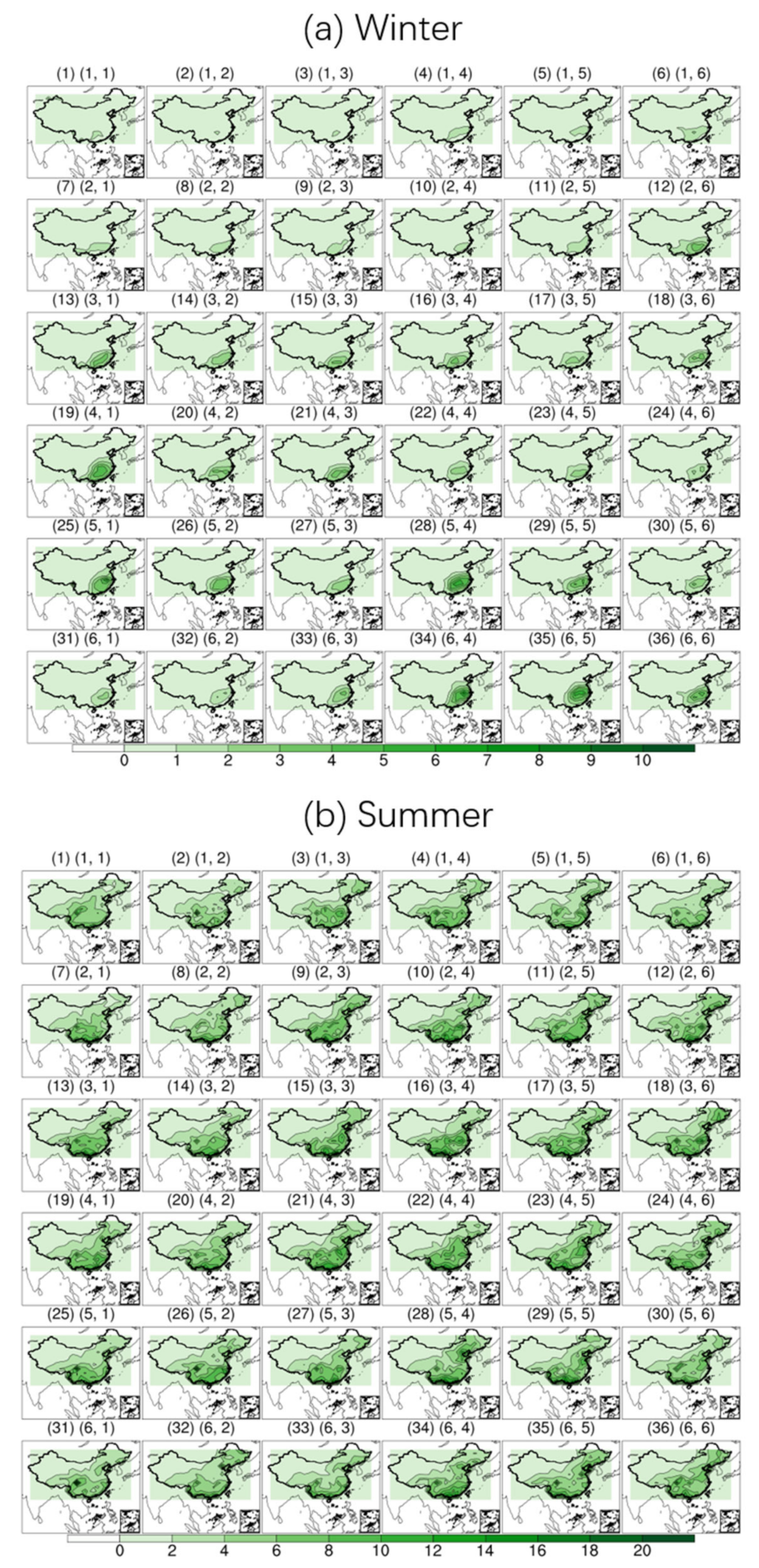Figure 2 shows the classification results of WPs in winter and summer, and Figure 3 shows the distribution of average daily precipitation; the positions of each node in Figure 3 correspond to those in Figure 2.

Atmospheric circulation is influenced by the distribution of land and sea, topographic relief, and other factors, and becomes very complex. In general, the basic feature of the atmospheric circulation in the northern hemisphere is the break of the pressure belt into several closed high- and low-pressure centers. In the Chinese region, the most dominant high-pressure system in winter is the Mongolian high-pressure system (Figure 2a). The main low-pressure system in summer is the Indian low-pressure system, and the high-pressure system is the Pacific subtropical high-pressure system (Figure 2b).

Due to the difference in the thermal properties of land and sea, the closed high- and low-pressure systems will change with the seasons. The pressure situation is more stable in winter and summer, and more active in spring and autumn. The main characteristics of the seasonal changes are that the changes in air pressure show periodicity. In winter, the overall latitudinal distribution is high in the north and low in the south. In summer, the overall distribution is longitudinal, with a high in the east and a low in the west. The latitudinal gradient reaches its maximum value in winter and its minimum value in summer. From January to June, the longitudinal gradient shows a decreasing trend, and from August to December, the longitudinal gradient shows an increasing trend.

There is a topological relationship between the output nodes using the SOM method. The distribution of the output nodes clearly shows that the loop types with similar characteristics are located closer to each other in the output nodes, whereas the more different loop types are further apart in the output node distribution. This is clearly shown in Figure 2. From the sea level pressure field in winter (Figure 2a), the circulation types in the upper-left corner (1, 1) and the lower-right corner (6, 6) show two opposite states of high and low, and the change from the upper-left corner to the lower-right corner represents the evolution of the Mongolian high-pressure system from negative to positive anomalies. In summer (Figure 2b), the situation is more complicated than in winter. Although the Mongolian high-pressure system is still present, its amplitude variation is much smaller than in winter, and its influence is mainly in the high latitudes. The middle and low latitudes are mainly subject to the Indian low-pressure system, and the subtropical high-pressure system in the western Pacific Ocean has some intensity variations. This obvious difference in the characteristics of the more distant nodes is clearly shown in Figure 2. The above results show that the SOM method is effective in typing, and the circulation types with different characteristics are effectively separated from each other.

Figure 4. Weather pattern frequencies (%) for (a) NCEP and (b) BNU-ESM in winter.

Figure 4. Weather pattern frequencies (%) for (a) NCEP and (b) BNU-ESM in winter.

Figure 5. Mean daily precipitation (mm/day) for (a) OBS and (b) BNU-ESM in winter.

Figure 5. Mean daily precipitation (mm/day) for (a) OBS and (b) BNU-ESM in winter.

Table 2. Correlation coefficients between node frequencies of 6 × 6 SOMs in the OBS and each GCM, on a seasonal basis. SOMs are given for the temporal SLP anomalies over the domain.

GCMs	Correlation Coefficient				Rank
	MAM	JJA	SON	DJF	MAM	JJA	SON	DJF
ACCESS1-0	0.63	0.04	0.46	0.26	13	20	28	31
ACCESS1-3	0.34	−0.03	0.42	0.16	30	23	30	32
bcc-csm1-1	0.67	0.46	0.77	0.79	8	1	7	8
bcc-csm1-1-m	0.62	0.35	0.50	0.77	14	3	26	9
BNU-ESM	0.73	0.25	0.77	0.80	4	8	5	7
CanESM2	0.71	0.03	0.68	0.84	7	21	13	1
CCSM4	0.57	−0.03	0.77	0.75	22	24	6	13
CESM1-FASTCHEM	0.33	−0.08	0.82	0.80	31	27	3	6
CMCC-CM	0.76	0.14	0.67	0.59	1	15	14	23
CMCC-CMS	0.71	0.26	0.72	0.75	6	6	10	14
CNRM-CM5	0.75	0.10	0.50	0.77	3	17	27	10
CSIRO-Mk3-6-0	0.37	−0.05	0.56	0.31	29	25	20	30
EC-EARTH	0.65	0.13	0.43	0.81	10	16	29	4
FGOALS-g2	0.58	−0.06	0.82	0.64	20	26	1	22
GFDL-CM3	0.75	0.16	0.51	0.45	2	13	24	27
GFDL-ESM2G	0.62	0.09	0.70	0.72	16	18	11	16
GFDL-ESM2M	0.66	0.05	0.67	0.70	9	19	15	18
GISS-E2-R	−0.01	−0.13	0.07	0.76	32	31	32	11
HadCM3	0.55	0.26	0.69	0.40	24	7	12	29
HadGEM2-CC	0.57	0.18	0.53	0.45	21	11	23	26
HadGEM2-ES	0.65	0.27	0.51	0.43	12	5	25	28
IPSL-CM5A-LR	0.53	−0.19	0.60	0.69	25	32	18	20
IPSL-CM5A-MR	0.50	−0.12	0.66	0.66	27	29	17	21
MIROC-ESM	0.60	0.15	0.56	0.83	19	14	21	2
MIROC-ESM-CHEM	0.65	0.19	0.53	0.81	11	10	22	5
MIROC4h	0.48	0.00	0.57	0.70	28	22	19	19
MIROC5	0.60	−0.10	0.66	0.52	18	28	16	25
MPI-ESM-LR	0.52	0.33	0.73	0.71	26	4	9	17
MPI-ESM-MR	0.61	0.38	0.74	0.82	17	2	8	3
MPI-ESM-P	0.73	0.19	0.81	0.76	5	9	4	12
MRI-CGCM3	0.62	0.18	0.23	0.73	15	12	31	15
NorESM1-M	0.56	−0.13	0.82	0.57	23	30	2	24

gives the correlation coefficient (at the 95% confidence level) between the simulated pattern occurrence frequencies of each mode in the four seasons (winter months of December–January–February (DJF), spring months of March–April–May (MAM), summer months of June–July–August (JJA), and autumn months of September–October–November (SON)) and the pattern occurrence frequencies of NCEP training, and the ranking of the simulated ability (RANK).

3.2. Simulation of Annual Precipitation

The correlation coefficients between the average daily precipitation corresponding to the various WPs simulated by each GCM in the four seasons and the actual conditions are given in

Table 3. Deviation of the simulation between nodes in the OBS and each GCM.

GCMs	Differences (mm)				Rank
	MAM	JJA	SON	DJF	MAM	JJA	SON	DJF
ACCESS1-0	61.39	61.35	27.73	22.44	29	27	17	22
ACCESS1-3	79.77	95.99	49.00	30.50	32	31	26	28
bcc-csm1-1	47.02	13.91	30.87	36.37	23	6	18	31
bcc-csm1-1-m	31.25	−11.44	6.71	23.83	12	5	3	24
BNU-ESM	56.65	42.91	40.59	29.26	27	22	23	27
CanESM2	28.80	4.27	9.71	12.57	11	2	4	4
CCSM4	45.05	78.22	44.14	16.80	22	28	25	10
CESM1-FASTCHEM	42.98	80.47	42.67	17.61	21	29	24	11
CMCC-CM	49.54	14.49	14.34	31.31	25	7	8	29
CMCC-CMS	47.09	8.03	12.44	32.96	24	4	6	30
CNRM-CM5	33.95	28.59	17.54	24.02	13	16	13	25
CSIRO-Mk3-6-0	25.50	18.70	1.28	2.79	10	11	2	1
EC-EARTH	25.10	−3.81	14.36	13.95	9	1	9	7
FGOALS-g2	51.40	−6.20	32.86	19.19	26	3	20	14
GFDL-CM3	37.70	22.05	31.72	27.08	14	12	19	26
GFDL-ESM2G	38.96	44.72	16.72	13.28	15	23	11	6
GFDL-ESM2M	41.00	50.33	23.37	16.32	19	26	16	9
GISS-E2-R	63.55	26.47	40.13	42.07	30	14	22	32
HadCM3	19.60	14.69	58.84	15.28	8	8	28	8
HadGEM2-CC	18.41	45.29	74.64	19.87	7	25	30	16
HadGEM2-ES	18.26	44.86	75.46	19.91	6	24	31	17
IPSL-CM5A-LR	14.49	15.49	20.03	23.57	5	9	14	23
IPSL-CM5A-MR	14.35	16.79	12.41	19.97	4	10	5	18
MIROC-ESM	4.48	38.08	75.54	18.30	2	19	32	12
MIROC-ESM-CHEM	4.13	36.38	73.49	18.80	1	17	29	13
MIROC4h	39.31	26.66	22.44	10.89	16	15	15	3
MIROC5	63.95	92.51	38.63	12.83	31	30	21	5
MPI-ESM-LR	42.09	37.53	17.16	21.12	20	18	12	19
MPI-ESM-MR	40.69	40.64	13.92	21.79	18	21	7	21
MPI-ESM-P	39.45	38.22	15.38	21.42	17	20	10	20
MRI-CGCM3	8.55	−23.74	0.10	6.75	3	13	1	2
NorESM1-M	58.24	97.74	49.45	19.26	28	32	27	15

, along with the ranking of the simulation ability (rank).

The average daily precipitation distribution of all WPs of each GCM has a high correlation coefficient (at the 95% confidence level) with the actual value (OBS). However, the magnitude of the correlation coefficient of the precipitation distribution is not a comprehensive measure of the ability to simulate precipitation, because it only judges whether the distribution pattern of the magnitude of precipitation of the GCM in each WP is consistent with OBS, and cannot measure the deviation between the simulated and actual values of precipitation in each WP.

Therefore, we also calculated the simulated deviation in the daily average precipitation separately at each WP and ranked the GCM simulation ability by the absolute value of the deviation magnitude. Table 3 shows the magnitude of the deviations (differences) between the simulated and actual daily mean precipitation corresponding to the various WPs simulated by each GCM in the four seasons and the ranking of the simulation ability (rank).

We ranked the ability of the SOM to simulate the frequency of WPs and the ability to simulate the daily average precipitation corresponding to each WP separately. We then wished to know the correlation between the two ranking results; that is, can a GCM with better simulation capability for the frequency of WP also possess better simulation capability for the daily average precipitation? Next, we analyze the correlation between the two ranking results.

3.3. Relationship between Simulation of Annual Precipitation and Simulation of Occurrences of Weather Patterns

Next, we analyzed the correlation between the two ranking results for each of the four seasons: spring, summer, autumn, and winter.

Based on the calculated results (spring r = 0.22; summer r = −0.04; autumn r = 0.04; winter r = −0.09; and annual r = −0.22), we can conclude that the ranking of the GCM’s ability to simulate the frequency of SLP WPs does not correlate with its ranking of the annual precipitation WP ability. Similarly, the results (spring r = 0.04; summer r = 0.20; autumn r = −0.05; winter r = −0.01; and annual r = 0.11) lead to a similar conclusion: the ranking of the GCM’s ability to simulate the frequency of the occurrence of the SLP WP does not correlate with the ranking of its ability to simulate annual precipitation.

The above results indicate that even if the GCM is able to simulate the frequency of the SLP WP well, it is not guaranteed to simulate the same amount of precipitation as the actual amount for the same WP; that is, the GCM’s ability to simulate annual precipitation does not correlate with its ability to simulate WP frequencies.

3.4. Simulation of the Multi-Model Ensemble

Firstly, the best three GCMs in each season were selected from the model ranking results of the WPs to form a multi-model ensemble, and the frequency correlation coefficients of the model ensemble and NCEP were relatively improved to different degrees than those of a single model. We aimed to determine if the simulation differences in precipitation could be reduced. Thus, we analyzed the precipitation simulation capability of the multi-model ensemble, and also selected the best three GCMs from the simulation ranking results of each season to form a multi-model ensemble.

The simulated deviations of the three single GCMs of the composed model ensemble in summer have positive and negative deviations, so that the simulated results of the model ensemble are smaller than the deviations of any of the single models. This confirms our previous analysis: only when the simulation deviations of each single model have positive and negative deviations, is it possible for the multiple models of the ensemble to cancel each other out, and thus improve the simulation ability of the multi-model ensemble for precipitation. However, if the deviations of each single model are the same, the simulation capability of the multi-model ensemble cannot be effectively improved. Thus, the above results show that the simulation ability of the multi-model ensemble is not always better than that of all of the single models when the deviations of each single model in the multi-model ensemble are the same.

Therefore, if the model’s ability to simulate annual precipitation is to be improved, it is necessary to look for another solution than the model ensemble alone, i.e., if the simulation differences of a single model can be corrected, it will greatly improve the confidence in future applications. Thus, the focus of the following question is the correction of the model simulation differences, and identifying the factors that depend on the magnitude of the model simulation differences. The next section focuses on the attribution of model simulation differences and the model correction.

4. Attribution Analysis of Annual Precipitation Simulation Differences

We used the Chinese BNU-ESM model as an example for our analysis. The frequencies of each WP of the NCEP and BNU-ESM models in winter are plotted in Figure 4a,b, respectively, and their correlation coefficients are 0.7961 (at the 95% confidence level). The frequency distribution of the WPs is low in the middle and high otherwise. The frequency distribution of the WPs is basically consistent with the WPs of the NCEP reanalysis data. This indicates that the GCM has a relatively good ability to simulate the frequency of the WPs.

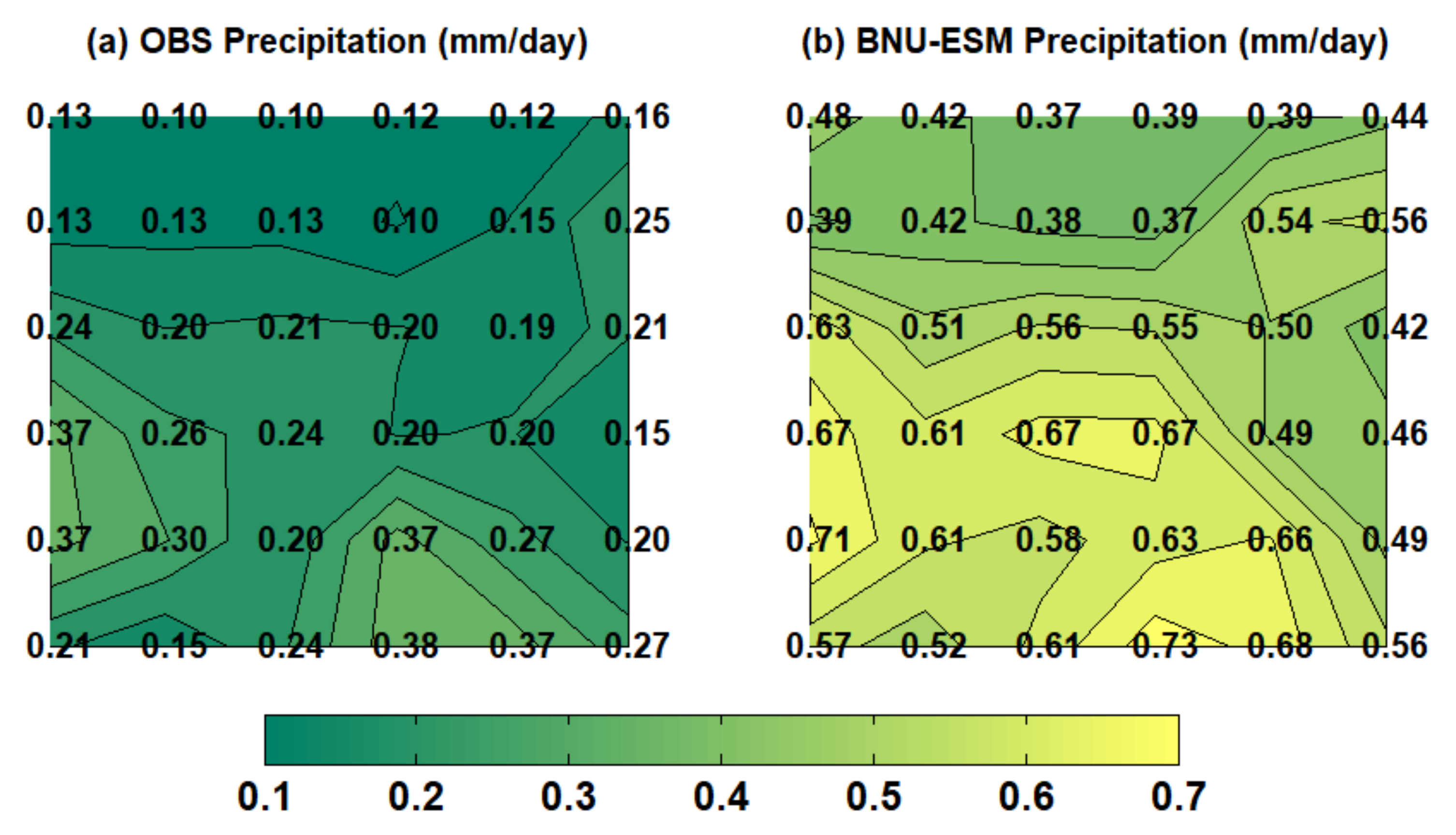
Next, we plot the average precipitation in each WP of the CHEN05 precipitation grid data in Figure 5a, and the precipitation of model BNU-ESM in Figure 5b. The precipitation distributions of the WPs in the two figures are basically the same, having a smaller upper-left side and a larger lower-right side, indicating that the model has a good ability to simulate the size distribution of the WPs’ precipitation with a correlation coefficient of 0.8697 (at the 95% confidence level). However, the ability of the model to simulate precipitation by correlation coefficients alone is not reasonable. The correlation coefficient only measures whether the precipitation distribution of the WP simulated by the model matches the actual situation. Whether the actual precipitation values are also well simulated requires further quantitative analysis. That is, in order to compare the strengths and weaknesses of the precipitation simulation ability, the simulation deviations must be calculated for each WP. From Figure 5, we can observe that the simulation deviation of each WP is relatively large, where the minimum actual value is 0.10 mm/day and the maximum is 0.38 mm/day, whereas the minimum simulation value is 0.37 mm/day and the maximum is 0.73 mm/day.

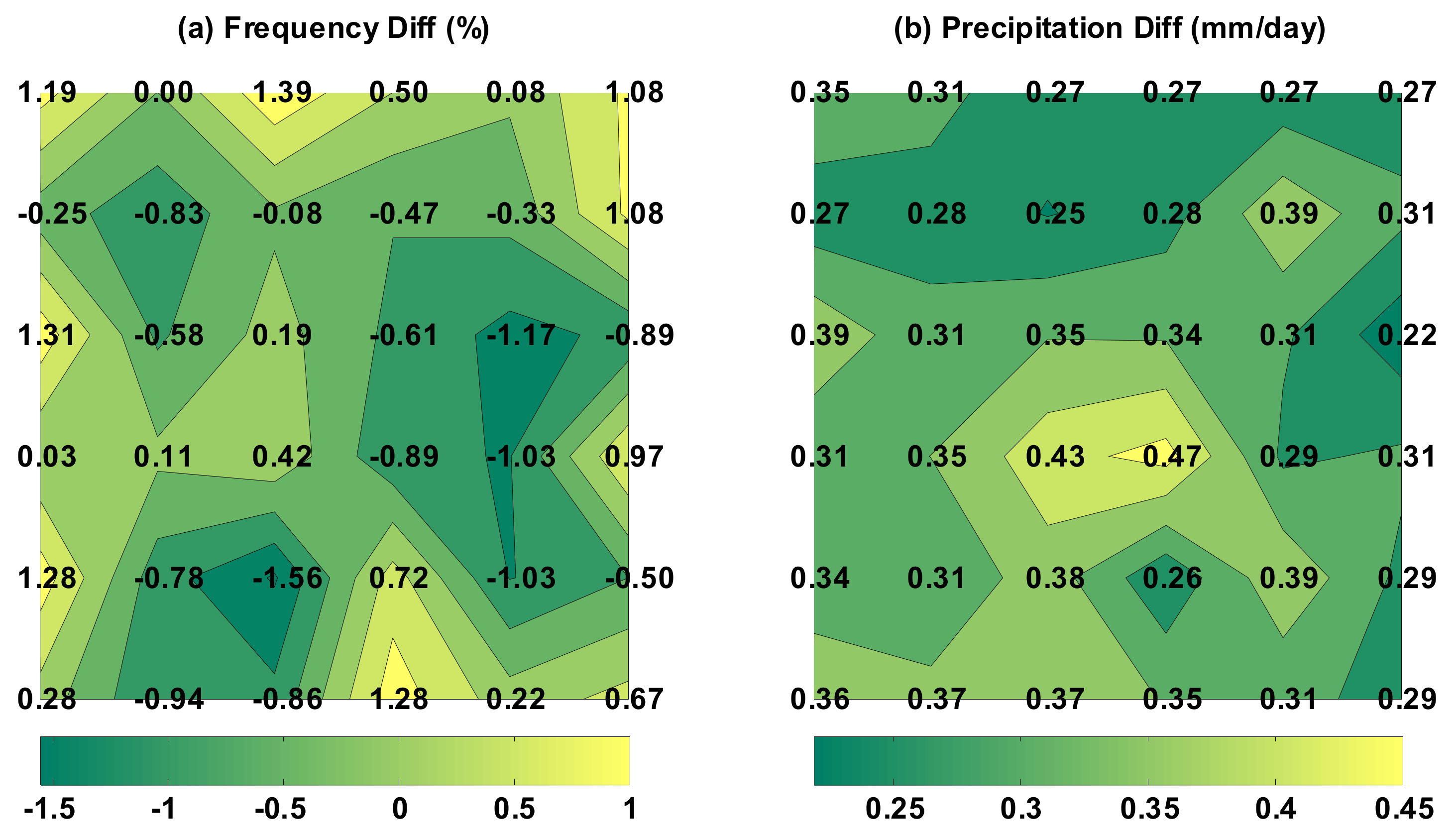
In order to quantitatively analyze the distribution of the simulated deviations of the GCM for frequency and precipitation, we plot the simulated deviations of frequency and the simulated deviations of daily average precipitation in Figure 6a,b, respectively. From Figure 6, we can see that the frequency deviations are mostly high at the edges and low in the middle, whereas the precipitation deviations all show systematic wet deviations (all positive values), indicating that the GCM has systematic wet deviations.

We calculated the magnitude of the three deviations after decomposition separately, and the results are listed in

Table 4. Attribution of China’s precipitation difference between OBS and the individual GCMs in winter.

GCM	Precipitation (mm)	Difference (mm)	Intrapattern Variability Component (mm)	Pattern Frequency Component (mm)	Combined Term (mm)
OBS	19.00	---	(a)	(b)	(c)
ACCESS1-0	42.36	22.94	23.06	−0.08	−0.05
ACCESS1-3	50.60	31.17	31.24	−0.33	0.26
bcc-csm1-1	56.61	37.18	37.06	0.17	−0.05
bcc-csm1-1-m	43.79	24.36	24.13	0.23	0.01
BNU-ESM	49.34	29.91	29.65	0.41	−0.15
CanESM2	32.27	12.85	12.69	0.12	0.04
CCSM4	36.60	17.17	17.13	−0.20	0.24
CESM1-FASTCHEM	37.42	18.00	18.15	−0.10	−0.05
CMCC-CM	51.43	32.01	31.05	0.42	0.54
CMCC-CMS	53.12	33.69	32.59	0.68	0.43
CNRM-CM5	43.98	24.55	24.43	0.05	0.07
CSIRO-Mk3-6-0	22.28	2.86	3.01	−0.07	−0.08
EC-EARTH	33.69	14.26	14.67	−0.32	−0.08
FGOALS-g2	39.04	19.61	19.79	−0.31	0.14
GFDL-CM3	47.11	27.68	27.19	0.27	0.23
GFDL-ESM2G	33.01	13.58	13.84	−0.18	−0.07
GFDL-ESM2M	36.11	16.68	16.60	0.03	0.05
GISS-E2-R	62.43	43.00	43.03	−0.06	0.04
HadCM3	35.05	15.62	15.47	−0.01	0.16
HadGEM2-CC	39.74	20.31	20.23	−0.34	0.42
HadGEM2-ES	39.78	20.35	19.97	−0.04	0.42
IPSL-CM5A-LR	43.52	24.09	23.71	0.52	−0.14
IPSL-CM5A-MR	39.84	20.42	19.84	0.49	0.09
MIROC-ESM	38.13	18.71	18.34	0.22	0.15
MIROC-ESM-CHEM	38.64	19.21	19.11	0.14	−0.03
MIROC4h	30.55	11.13	11.13	−0.03	0.03
MIROC5	32.54	13.11	13.57	−0.29	−0.16
MPI-ESM-LR	41.02	21.59	20.88	0.40	0.32
MPI-ESM-MR	41.70	22.27	21.65	0.35	0.28
MPI-ESM-P	41.33	21.90	21.91	0.18	−0.19
MRI-CGCM3	26.33	6.90	6.43	0.19	0.28
NorESM1-M	39.12	19.69	19.84	−0.01	−0.13

for winter and in

Table 5. Attribution of China’s precipitation difference between OBS and the individual GCMs in summer.

GCM	Precipitation (mm)	Difference (mm)	Intrapattern Variability Component (mm)	Pattern Frequency Component (mm)	Combined Term (mm)
OBS	165.84	---	(a)	(b)	(c)
ACCESS1-0	227.19	61.35	60.97	0.12	0.26
ACCESS1-3	261.83	95.99	94.96	0.45	0.58
bcc-csm1-1	179.75	13.91	14.31	−0.73	0.33
bcc-csm1-1-m	154.40	−11.44	−10.74	−1.27	0.58
BNU-ESM	208.75	42.91	43.15	−0.46	0.23
CanESM2	170.11	4.27	3.12	−0.82	1.97
CCSM4	244.06	78.22	77.71	0.39	0.13
CESM1-FASTCHEM	246.31	80.47	82.73	0.67	−2.94
CMCC-CM	180.33	14.49	12.82	0.14	1.53
CMCC-CMS	173.87	8.03	7.09	−0.85	1.79
CNRM-CM5	194.43	28.59	28.49	−0.21	0.32
CSIRO-Mk3-6-0	184.54	18.70	17.68	0.32	0.70
EC-EARTH	162.03	−3.81	−5.39	−0.49	2.06
FGOALS-g2	159.64	−6.20	−6.64	0.65	−0.20
GFDL-CM3	187.89	22.05	22.06	−0.61	0.60
GFDL-ESM2G	210.56	44.72	42.18	−1.10	3.64
GFDL-ESM2M	216.17	50.33	48.77	−0.55	2.11
GISS-E2-R	192.31	26.47	22.81	1.72	1.93
HadCM3	180.53	14.69	12.04	−1.99	4.63
HadGEM2-CC	211.13	45.29	41.39	−1.76	5.66
HadGEM2-ES	210.70	44.86	43.08	−2.07	3.85
IPSL-CM5A-LR	181.33	15.49	14.50	1.40	−0.41
IPSL-CM5A-MR	182.63	16.79	13.56	1.26	1.97
MIROC-ESM	203.92	38.08	38.34	−0.22	−0.03
MIROC-ESM-CHEM	202.22	36.38	36.81	0.01	−0.44
MIROC4h	192.50	26.66	25.57	0.96	0.13
MIROC5	258.35	92.51	89.87	1.23	1.41
MPI-ESM-LR	203.37	37.53	37.51	−0.65	0.67
MPI-ESM-MR	206.48	40.64	40.99	−1.39	1.03
MPI-ESM-P	204.06	38.22	40.09	−0.36	−1.51
MRI-CGCM3	142.10	−23.74	−23.98	−0.34	0.58
NorESM1-M	263.58	97.74	96.80	0.55	0.40

for summer.

Table 4 and Table 5 show that, among the three deviation components (the last three columns), the one with the largest absolute value is the intrapattern variability component, which is the most important contributor to the simulation deviation (the penultimate column). The absolute values of the last two are small and basically negligible. This is true for both winter and summer, a result that is consistent with the findings of Schuenemann [21]. The simulation results for the vast majority of GCMs in both winter and summer are on the wet side, with the smallest differences in the winter simulation being those ofCSIRO-Mk3-6-0; the smallest differences in the summer simulation are from EC-EARTH.

To summarize this section, we decomposed the simulated variance of annual precipitation using the SOM, a powerful analysis tool, and identified the most influential component to be the intrapattern variability component, followed by the pattern frequency component; the smallest was the combined term. In the GCM evaluation of precipitation simulation, the most important factor causing the differences in the calculation of annual average precipitation in the region, both in winter and summer, is the differences in the GCM’s ability to simulate daily average precipitation. The results of this experiment confirm the previous conclusion that the GCM’s ability to simulate annual precipitation depends mainly on the GCM’s own ability to simulate daily precipitation, and less on the GCM’s ability to simulate the frequency of circulation modes.

5. Correction of Annual Precipitation Simulation Differences

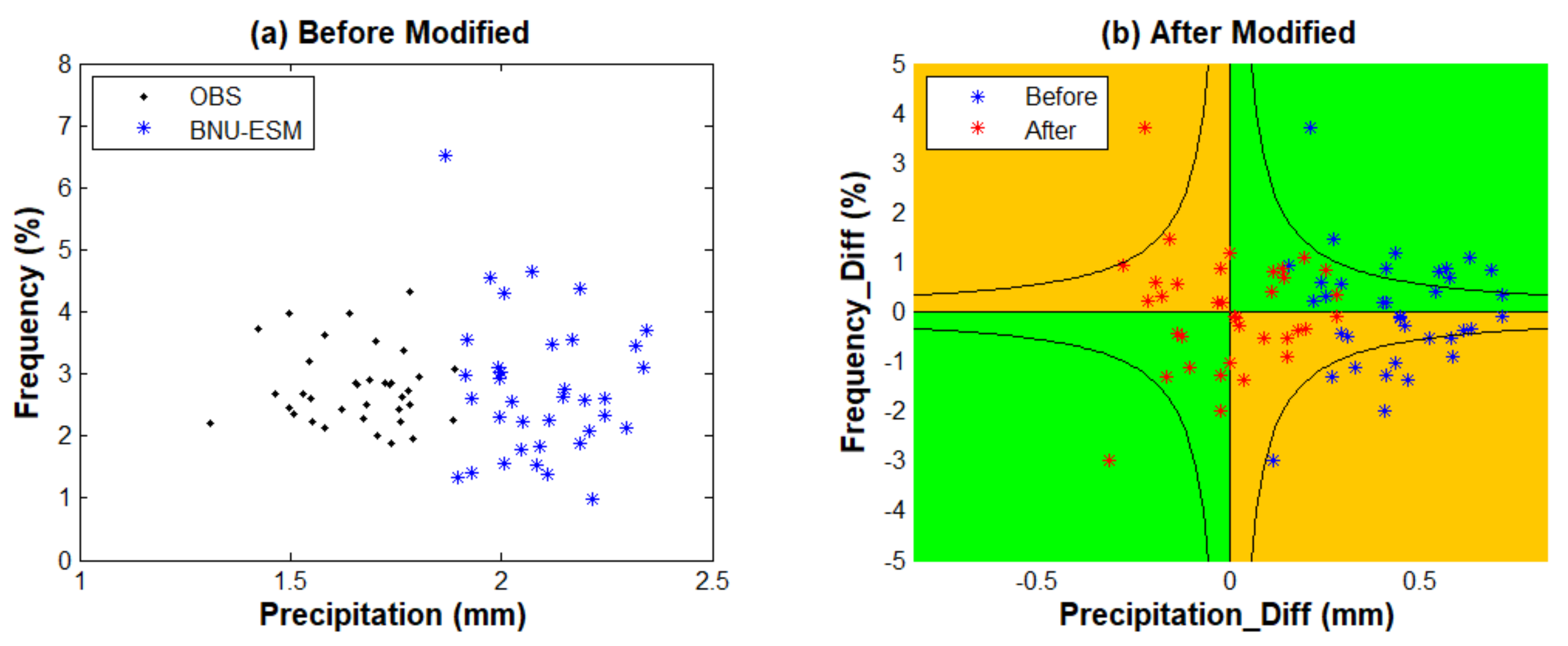
Since the annual average precipitation of the GCM was obtained by accumulating the product of the daily average precipitation value of WP and the frequency of occurrence of its corresponding WP, the value of the annual average precipitation is directly related to the above two factors. Now, we take precipitation difference (mm) as the x-axis and frequency difference (%) as the y-axis to establish a coordinate system, and represent it in two-dimensional form. Then, the simulated deviation in 36 WPs is represented as 36 random two-dimensional plane points. Since the analysis is more obvious due to the larger precipitation in summer, the simulated deviations of the BNU-ESM model for China in summer were selected for the following analysis.

In Figure 7a, all black dots indicate the frequency of the actual OBS and the distribution of precipitation in the 2D coordinate system, and the simulations of the BNU-ESM model are indicated by blue stars. It can be seen that the simulated results of BNU-ESM deviate significantly from the case of OBS, and the blue stars are all to the right of the black dots, i.e., the system is wet.

In Figure 7b, the horizontal axis is the precipitation difference and the vertical axis is the frequency difference. The green quadrant indicates a wet differences and the orange quadrant indicates a dry difference. Each blue star represents the difference between one WP of the GCM and the corresponding true value. The distribution of all blue stars represents the distribution of simulated deviations of all WPs of the GCM (combining simulated deviations of occurrence frequency WPs and simulated deviations of daily precipitation). The curves in the figure represent the contours of the product of the vertical and horizontal axes (the appropriate values can be chosen according to the season). If all the black points fall within the interval surrounded by the curve and the two axes, the deviation is small, and if they fall outside the range, the deviation is large. If the blue stars are evenly distributed around the origin, and the left and right sides can cancel each other out, the simulation result of the GCM will be better. If the blue stars are scattered—not only far from the origin, but also having positive and negative values that cannot cancel each other out—the simulation result of the GCM will be more deviated (right side is wet, left side is dry).

As we found earlier, the largest proportion of the three components affecting the simulation results of the annual average precipitation is the first one, i.e., this item has little to do with the frequency of the GCM simulation, but is closely related to the magnitude of the GCM’s simulation deviation from the daily average precipitation. Therefore, it is important to observe in the figure whether the blue stars of the GCM on both sides of the vertical axis can cancel each other out. We can shift all the blue stars horizontally to the left by one value (we can take the average of the horizontal coordinates of the blue star points), so that all the stars are evenly distributed on both sides of the dot (as in Figure 7b where the red stars are located), thus allowing positive and negative offsetting. In this way, the simulation results of each GCM can be corrected, and the results are calculated as follows.

The results in

Table 6. The values of precipitation and its difference before and after modification in winter.

GCM	Precipitation (mm)		Difference (mm)
	Original	Corrected	Original	Corrected
ACCESS1-0	42.36	18.99	22.94	−0.01
ACCESS1-3	50.60	18.86	31.17	−0.14
bcc-csm1-1	56.61	18.97	37.18	−0.03
bcc-csm1-1-m	43.79	19.25	24.36	0.25
BNU-ESM	49.34	19.26	29.91	0.26
CanESM2	32.27	19.21	12.85	0.21
CCSM4	36.60	19.31	17.17	0.31
CESM1-FASTCHEM	37.42	18.55	18.00	−0.45
CMCC-CM	51.43	19.74	32.01	0.74
CMCC-CMS	53.12	19.68	33.69	0.68
CNRM-CM5	43.98	18.89	24.55	−0.11
CSIRO-Mk3-6-0	22.28	18.98	2.86	−0.02
EC-EARTH	33.69	18.68	14.26	−0.32
FGOALS-g2	39.04	18.93	19.61	−0.07
GFDL-CM3	47.11	19.33	27.68	0.33
GFDL-ESM2G	33.01	18.75	13.58	−0.25
GFDL-ESM2M	36.11	19.20	16.68	0.20
GISS-E2-R	62.43	19.09	43.00	0.09
HadCM3	35.05	19.28	15.62	0.28
HadGEM2-CC	39.74	18.84	20.31	−0.16
HadGEM2-ES	39.78	19.38	20.35	0.38
IPSL-CM5A-LR	43.52	19.43	24.09	0.43
IPSL-CM5A-MR	39.84	19.67	20.42	0.67
MIROC-ESM	38.13	19.36	18.71	0.36
MIROC-ESM-CHEM	38.64	19.10	19.21	0.10
MIROC4h	30.55	18.81	11.13	−0.19
MIROC5	32.54	18.56	13.11	−0.44
MPI-ESM-LR	41.02	19.91	21.59	0.91
MPI-ESM-MR	41.70	19.44	22.27	0.44
MPI-ESM-P	41.33	19.02	21.90	0.02
MRI-CGCM3	26.33	19.68	6.90	0.68
NorESM1-M	39.12	18.92	19.69	−0.08

and

Table 7. The values of precipitation and its difference before and after modification in summer.

GCM	Precipitation (mm)		Difference (mm)
	Original	Corrected	Original	Corrected
ACCESS1-0	227.19	166.15	61.35	0.31
ACCESS1-3	261.83	166.72	95.99	0.88
bcc-csm1-1	179.75	165.15	13.91	−0.69
bcc-csm1-1-m	154.40	164.45	−11.44	−1.39
BNU-ESM	208.75	165.31	42.91	−0.53
CanESM2	170.11	167.17	4.27	1.33
CCSM4	244.06	166.68	78.22	0.84
CESM1-FASTCHEM	246.31	164.28	80.47	−1.56
CMCC-CM	180.33	167.10	14.49	1.26
CMCC-CMS	173.87	166.75	8.03	0.91
CNRM-CM5	194.43	165.89	28.59	0.05
CSIRO-Mk3-6-0	184.54	167.11	18.70	1.27
EC-EARTH	162.03	166.92	−3.81	1.08
FGOALS-g2	159.64	166.58	−6.20	0.74
GFDL-CM3	187.89	165.95	22.05	0.11
GFDL-ESM2G	210.56	167.88	44.72	2.04
GFDL-ESM2M	216.17	166.58	50.33	0.74
GISS-E2-R	192.31	169.21	26.47	3.37
HadCM3	180.53	167.92	14.69	2.08
HadGEM2-CC	211.13	169.57	45.29	3.73
HadGEM2-ES	210.70	167.62	44.86	1.78
IPSL-CM5A-LR	181.33	166.87	15.49	1.03
IPSL-CM5A-MR	182.63	168.82	16.79	2.98
MIROC-ESM	203.92	165.68	38.08	−0.16
MIROC-ESM-CHEM	202.22	165.51	36.38	−0.33
MIROC4h	192.50	166.99	26.66	1.15
MIROC5	258.35	168.23	92.51	2.39
MPI-ESM-LR	203.37	165.42	37.53	−0.42
MPI-ESM-MR	206.48	165.87	40.64	0.03
MPI-ESM-P	204.06	164.73	38.22	−1.11
MRI-CGCM3	142.10	165.87	−23.74	0.03
NorESM1-M	263.58	166.57	97.74	0.73

show that the deviations after the correction were improved significantly compared with those before the correction (winter: the mean value of the absolute annual average precipitation deviation was reduced from 21.15 to 0.30 mm; summer: the mean value of the absolute annual average precipitation deviation was reduced from 36.89 to 1.16 mm).

The solution involves mapping the WP frequencies and the nodal precipitation totals of the GCM to a series of two-dimensional points in a two-dimensional plane rectangular coordinate system for analysis. In this way, the simulation deviation of the GCM can be substantially corrected. The significance of this is that, assuming that the future follows the same WP as in the past, the past differences of the climate GCM can be used to correct the GCM’s simulation results for the future, thus achieving a high prediction accuracy. In addition, the multi-model ensemble relies on the offsetting of wet and dry WPs of each GCM, but the degree of offsetting is highly contingent; the approach proposed in this paper is to use only a single GCM instead of a GCM ensemble, and, after correction, the biased dry or wet WPs of the GCM itself can be offset around the origin of the coordinates.

To test the correctness and robustness of the above method, we corrected the precipitation difference for the last 5 years (2000–2004) with the corrected values of the precipitation difference for the first 40 years (1960–1999). The results are plotted in Figure 8, where Figure 8a,b show the winter and summer cases, respectively.

Firstly, the annual precipitation difference was significantly reduced after correction. The average value of total difference in winter was reduced from 21.51 to 0.53 mm (Figure 8a). The average value of total difference in summer was reduced from 43.80 to 7.53 mm (Figure 8b). This means that the corrected values of the simulation differences of the global model in the present can be used for the correction of the future prediction results.

Secondly, the total difference contains three difference components: A, B and C. Their contributions in the total difference are significantly different. The reduction in the total difference is mainly caused by the significant reduction in the A component, and the two components B and C do not change significantly. This means that the source of precipitation difference fundamentally depends on the model’s ability to simulate precipitation in each WP.

Finally, the revision method of the model differences proposed in this paper is correct and effective. It is of great significance for the improvement of the simulation capability of a single model because the method of future climate prediction no longer depends on the use of a multi-model ensemble, and is thus worthy of being promoted and applied in practice.

It is worth noting that the correction of the future simulation results cannot be made directly with the total difference and the individual differences. Instead, the differences in the frequency and precipitation should be calculated first according to the method proposed in the paper; then each difference component should be calculated, and finally the total precipitation difference can be obtained by adding up each component difference.

6. Summary and Conclusions

In order to find a single GCM or multi-model ensemble that can best reproduce the WPs and annual mean precipitation on a daily time scale, we used the 32 CMIP5 models and the daily SLP anomalies and other information from NCEP reanalysis data, precipitation simulation data from 32 GCMs, and CHEN05 precipitation grid data from 1960 to 1999 in the Chinese region, and 36 SOM SLP WPs were analyzed. The aim was to analyze and predict the future precipitation of individual Chinese regions using the methods presented in this paper.

By comparing the correlation between the frequency of occurrence of NCEP and each single model, it is concluded that the ability of the GCMs to simulate the frequency of the WPs is not correlated with their ability to simulate precipitation, i.e., the ranking of the GCMs’ ability to simulate precipitation differs significantly from the ranking of the SLP simulations.

The ability of these GCMs to reproduce precipitation in the Chinese region was the focus of the analysis in this study: each single model, and the three-model ensemble, was compared with OBS. The following conclusions are drawn from the analysis of the study results:

(a)

For the period from 1960 to 1999, the OBS results for the annual average precipitation in the Chinese region were 70.55 mm/year in spring, 165.84 mm/year in summer, 61.54 mm/year in autumn, and 19.00 mm/year in winter.

(b)

The simulation results for most of the GCMs in winter and summer are on the wet side, with CSIRO-Mk3-6-0 in winter being closest to the actual value, having a deviation of 2.86 mm/year, and EC-EARTH in summer being closest to the actual value, having a deviation of −3.81 mm/year.

(c)

In calculating the annual average precipitation corresponding to the GCM using the product of the frequency of the WP occurrence and the daily average precipitation corresponding to the corresponding WP, the multi-mode ensemble can effectively reduce the frequency deviation, but the weakening of the frequency deviation is not enough to compensate for the large deviation of the GCM in the simulation of daily average precipitation; only when part of the single GCM in the composition of the integrated GCM is dry and the other part of the single GCM is wet, can the dry and wet offset each other and effectively improve the annual average precipitation simulation ability of the integrated GCM. When the precipitation simulated by several single GCMs in the composition of the integrated GCM is all dry or all wet, the integrated GCM is not necessarily better than the single GCM.

(d)

The differences between the GCMs and OBS are attributed to three main reasons: internal variability, frequency differences, and the combined term of the two. The internal variability is attributed to the difference in the mean annual precipitation in the WPs, and the frequency difference is attributed to the difference in the frequency. The precipitation differences are mainly attributed to the internal variability component (depending on the ability of each WP in the GCM to simulate precipitation), and the differences in the WP frequencies account for a small percentage.

(e)

Although correlation coefficients are suitable for assessing the GCM’s ability to simulate the frequency of WPs, it is not scientific to use correlation coefficients to assess the ability to simulate precipitation. Thus, it may be more reasonable to rank precipitation simulations in terms of simulation differences when assessing the ability to simulate precipitation.

(f)

Since the most important factor affecting the precipitation simulation capability of the GCM is the precipitation simulation differences, to improve the results, all two-dimensional points can be shifted toward the origin direction overall, and the simulation differences of the GCM can be substantially corrected by this method. The implication of this is that the method can be used to correct the GCM’s simulation results for the future with a high prediction accuracy, assuming that the future follows the same climate evolution as in the past.

All the GCMs were improved and good results were obtained in reproducing the SLP and Chinese regional precipitation simulated between 1960 and 1999. This increases the confidence in using this approach for future weather modeling and precipitation simulation.