A Novel Komodo Mlipir Algorithm and Its Application in PM2.5 Detection
Abstract
1. Introduction
2. Basic Komodo Mlipir Algorithm
3. Improvements of Basic Komodo Mlipir Algorithm
3.1. Proposed Initialization of Position by Chaotic Sequence
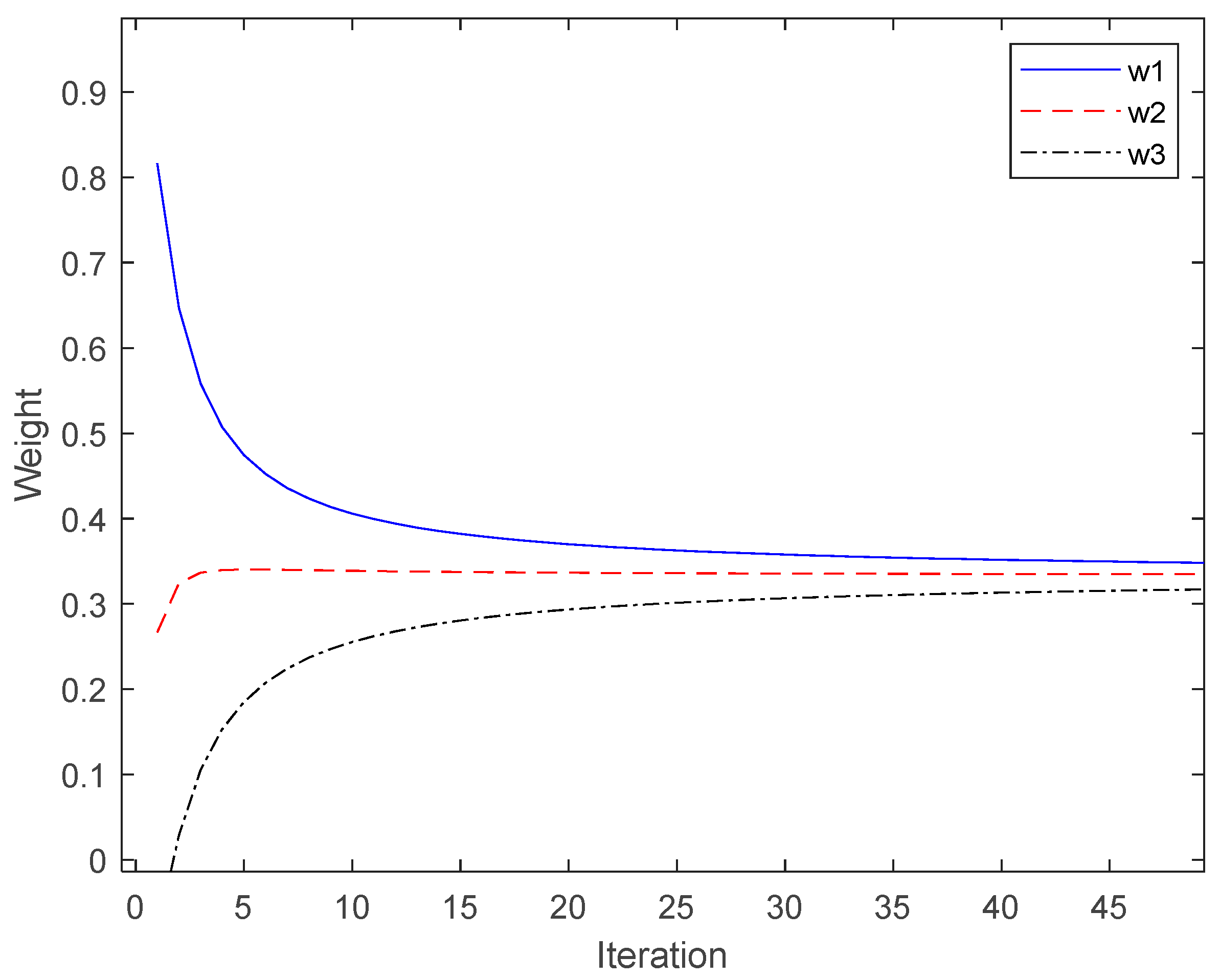
3.2. Proposed Variable Weight Strategy
3.3. Proposed Tent Chaos Disturbance Strategy
3.4. VWCKMA Process
4. Time Complexity Analysis
5. Empirical Studies
5.1. Benchmark Functions
5.2. Experimental Data and Analysis
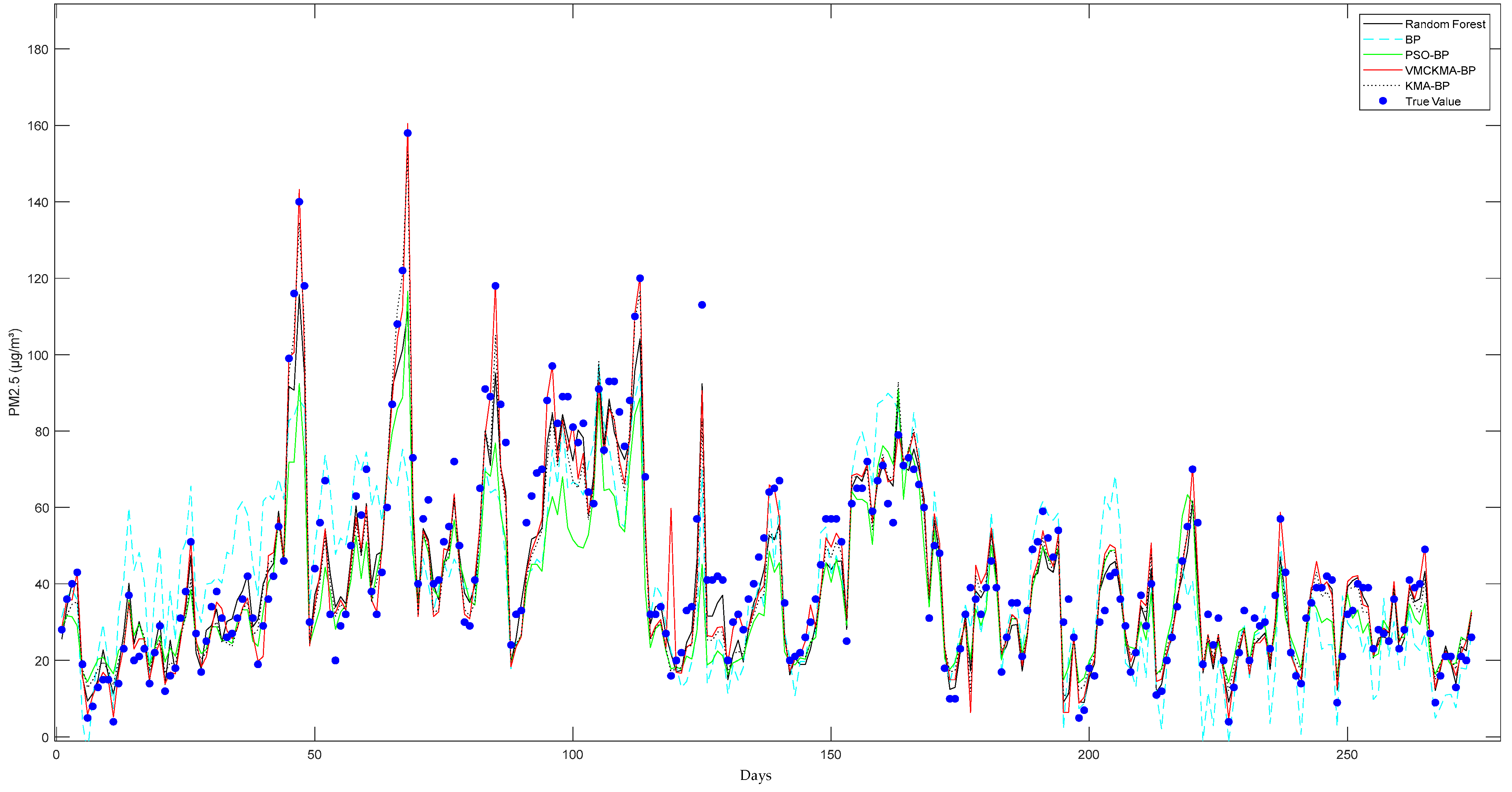
6. Practical Application
Results Analysis
Author Contributions
Funding
Conflicts of Interest
References
- Lin, S.; Kernighan, B.W. An effective heuristic algorithm for the traveling-salesman problem. Oper. Res. 1973, 21, 498–516. [Google Scholar] [CrossRef]
- Grefenstette, J.; Gopal, R.; Rosmaita, B.J.; Gucht, D.V. Genetic algorithms for the traveling salesman problem. In Proceedings of the the First International Conference on Genetic Algorithms and Their Applications, Pittsburgh, PA, USA, 24–26 July 1985; pp. 160–168. [Google Scholar]
- Hu, Y.; Yang, S.X. A knowledge based genetic algorithm for path planning of a mobile robot. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 2004, pp. 4350–4355. [Google Scholar]
- Ismail, A.; Sheta, A.; Al-Weshah, M. A mobile robot path planning using genetic algorithm in static environment. J. Comput. Sci. 2008, 4, 341–344. [Google Scholar]
- Yin, L.; Li, X.; Gao, L.; Lu, C.; Zhang, Z. A novel mathematical model and multi-objective method for the low-carbon flexible job shop scheduling problem. Sustain. Comput. Inform. Syst. 2017, 13, 15–30. [Google Scholar] [CrossRef]
- Jiang, T.; Deng, G. Optimizing the low-carbon flexible job shop scheduling problem considering energy consumption. IEEE Access 2018, 6, 46346–46355. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. Available online: http://d.wanfangdata.com.cn/Periodical_dqkx201507013.aspx (accessed on 10 September 2022). [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Piscataway, NJ, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Houck, C.R.; Joines, J.; Kay, M.G. A genetic algorithm for function optimization: A Matlab implementation. Ncsu-Ie Tr 1995, 95, 1–10. [Google Scholar]
- Mirjalili, S. Genetic Algorithm //Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer International Publishing: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf mongoose optimization algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H. Barnacles mating optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103330. [Google Scholar] [CrossRef]
- Muthiah-Nakarajan, V.; Noel, M.M. Galactic swarm optimization: A new global optimization metaheuristic inspired by galactic motion. Appl. Soft Comput. 2016, 38, 771–787. [Google Scholar] [CrossRef]
- Waharte, S.; Trigoni, N. Supporting search and rescue operations with UAVs. In Proceedings of the International Conference on Emerging Security Technologies, Canterbury, UK, 6–7 September 2010; pp. 142–147. [Google Scholar]
- Suyanto, S.; Ariyanto, A.A.; Ariyanto, A.F. Komodo Mlipir Algorithm. Appl. Soft Comput. 2022, 114, 108043. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, S.; Sun, Y. A support vector regression model hybridized with chaotic krill herd algorithm and empirical mode decomposition for regression task. Neurocomputing 2020, 410, 185–201. [Google Scholar] [CrossRef]
- Sun, W.; Xu, Y. Using a back propagation neural network based on improved particle swarm optimization to study the influential factors of carbon dioxide emissions in Hebei Province, China. J. Clean. Prod. 2016, 112, 1282–1291. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, L.; Zhang, Z.; Fan, Q. Twin support vector machine based on improved artificial fish swarm algorithm with application to flame recognition. Appl. Intell. 2020, 50, 2312–2327. [Google Scholar] [CrossRef]
- Goluguri, N.; Devi, K.S.; Srinivasan, P. Rice-net: An efficient artificial fish swarm optimization applied deep convolutional neural network model for identifying the Oryza sativa diseases. Neural Comput. Appl. 2021, 33, 5869–5884. [Google Scholar] [CrossRef]
- Wang, B.; Xue, B.; Zhang, M. Particle swarm optimisation for evolving deep neural networks for image classification by evolving and stacking transferable blocks. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Shan, L.; Qiang, H.; Li, J.; Wang, Z. Chaotic optimization algorithm based on Tent map. Control Decis. 2005, 20, 179–182. [Google Scholar]
- Jamil, M.; Yang, X.-S. A literature survey of benchmark functions for global optimization problems. arXiv 2013, arXiv:1308.4008 2013. [Google Scholar]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Huang, K.; Xiao, Q.; Meng, X.; Geng, G.; Wang, Y.; Lyapustin, A.; Gu, D.; Liu, Y. Predicting monthly high-resolution PM2.5 concentrations with random forest model in the North China Plain. Environ. Pollut. 2018, 242, 675–683. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhang, F.; Du, Z.; Liu, R. Forecasting PM2.5 using hybrid graph convolution-based model considering dynamic wind-field to offer the benefit of spatial interpretability. Environ. Pollut. 2021, 273, 116473. [Google Scholar] [CrossRef] [PubMed]
- An, Y.; Xia, T.; You, R.; Lai, D.; Liu, J.; Chen, C. A reinforcement learning approach for control of window behavior to reduce indoor PM2.5 concentrations in naturally ventilated buildings. Build. Environ. 2021, 200, 107978. [Google Scholar] [CrossRef]
- Kang, Z.; Qu, Z. Application of BP neural network optimized by genetic simulated annealing algorithm to prediction of air quality index in Lanzhou. In Proceedings of the 2017 2nd IEEE International Conference on Computational Intelligence and Applications (ICCIA), Beijing, China, 8–11 September 2017; pp. 155–160. [Google Scholar]
- Li, M.; Wu, W.; Chen, B.; Guan, L.; Wu, Y. Water quality evaluation using back propagation artificial neural network based on self-adaptive particle swarm optimization algorithm and chaos theory. Comput. Water Energy Environ. Eng. 2017, 6, 229. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 concentrations in the conterminous United States using the random forest approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef]






| Function | Range | Fmin |
|---|---|---|
| [−100, 100] | 0 | |
| [−10, 100] | 0 | |
| [−100, 100] | 0 | |
| [−100, 100] | 0 | |
| [−30, 30] | 0 | |
| [−100, 100] | 0 | |
| [−1.28, 1.28] | 0 |
| Function | Range | Fmin |
|---|---|---|
| [−500, 500] | ||
| [−5.12, 5.12] | 0 | |
| [−32, 32] | 0 | |
| [−600, 600] | 0 | |
| [−50, 50] | 0 | |
| [−50, 50] | 0 |
| Function | Range | Fmin |
|---|---|---|
| [−65, 65] | 1 | |
| [−5, 5] | 0.00030 | |
| [−5, 5] | −1.0316 | |
| [−5, 5] | 0.398 | |
| [−2, 2] | 3 | |
| [1, 3] | −3.86 | |
| [0, 1] | −3.32 |
| PSO | GWO | KMA | VWCKMA | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| 9.98 × 10−1 | 0.00 × 100 | 1.23 × 100 | 6.21 × 10−1 | 6.20 × 100 | 3.59 × 100 | 9.98 × 10−1 | 0.00 × 100 | |
| 1.29 × 10−3 | 3.62 × 10−3 | 1.68 × 10−3 | 5.08 × 10−3 | 5.51 × 10−2 | 5.10 × 10−2 | 3.07 × 10−4 | 3.80 × 10−9 | |
| −1.0 × 100 | 6.52 × 10−16 | −1.0 × 100 | 1.48 × 10−8 | −9.4 × 10−1 | 1.27 × 10−1 | −1.0 × 100 | 0.00 × 100 | |
| 3.98 × 10−1 | 0.0 × 100 | 3.98 × 10−1 | 4.19 × 10−4 | 4.94 × 10−1 | 3.04 × 10−1 | 3.98 × 10−1 | 0.00 × 100 | |
| 3.00 × 100 | 6.99 × 10−16 | 3.00 × 100 | 3.61 × 10−6 | 1.46 × 101 | 1.77 × 101 | 3.00 × 100 | 0.00 × 100 | |
| −3.8 × 100 | 2.71 × 10−15 | −3.8 × 100 | 9.66 × 10−4 | −3.7 × 100 | 3.01 × 10−1 | −3.8 × 100 | 0.00 × 100 | |
| −3.2 × 100 | 7.57 × 10−2 | −3.2 × 100 | 6.64 × 10−2 | −2.3 × 100 | 7.57 × 10−1 | −3.3 × 100 | 2.77 × 10−8 | |
| PSO | GWO | KMA | VWCKMA | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| 6.34 × 10−2 | 8.92 × 10−2 | 4.94 × 10−17 | 5.49 × 10−17 | 6.7 × 10−135 | 2.5 × 10−134 | 0.00 × 100 | 0.00 × 100 | |
| 6.51 × 100 | 7.14 × 100 | 1.45 × 10−10 | 7.22 × 10−11 | 3.95 × 10−72 | 1.01 × 10−71 | 0.00 × 100 | 0.00 × 100 | |
| 4.04 × 103 | 4.54 × 103 | 2.71 × 10−4 | 2.32 × 10−4 | 1.2 × 10−107 | 6.5 × 10−107 | 0.00 × 100 | 0.00 × 100 | |
| 4.22 × 100 | 1.31 × 100 | 1.73 × 10−4 | 8.46 × 10−5 | 1.02 × 10−65 | 3.33 × 10−65 | 0.00 × 100 | 0.00 × 100 | |
| 6.90 × 102 | 1.32 × 103 | 2.66 × 101 | 0.86 × 100 | 2.89 × 101 | 1.13 × 102 | 2.84 × 101 | 0.14 × 100 | |
| 1.88 × 10−1 | 6.68 × 10−1 | 1.13 × 10−1 | 1.68 × 10−1 | 5.66 × 100 | 7.31 × 10−1 | 9.91 × 10−2 | 5.90 × 10−2 | |
| 2.31 × 10−2 | 8.39 × 10−3 | 9.46 × 10−4 | 4.29 × 10−4 | 5.00 × 10−3 | 1.12 × 10−2 | 2.59 × 10−3 | 3.06 × 10−3 | |
| −8.9 × 103 | 7.94 × 102 | −6.6 × 103 | 7.96 × 102 | −2.6 × 103 | 8.71 × 102 | −1.2 × 104 | 6.41 × 102 | |
| 4.91 × 101 | 1.53 × 101 | 5.30 × 100 | 2.531 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| 1.11 × 100 | 6.73 × 10−1 | 1.13 × 10−9 | 5.52 × 10−10 | 2.01 × 100 | 6.12 × 100 | 8.88 × 10−16 | 0.00 × 100 | |
| 7.00 × 10−2 | 6.93 × 10−2 | 2.24 × 10−3 | 5.19 × 10−3 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| 7.76 × 10−1 | 7.03 × 10−1 | 1.07 × 10−2 | 6.49 × 10−3 | 1.22 × 100 | 4.03 × 10−1 | 5.68 × 10−3 | 8.82 × 10−3 | |
| 2.10 × 10−1 | 5.44 × 10−1 | 1.23 × 10−1 | 1.15 × 10−1 | 2.94 × 100 | 1.36 × 10−1 | 4.34 × 10−2 | 3.12 × 10−2 | |
| PSO | GWO | KMA | VWCKMA | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| 6.86 × 103 | 4.31 × 103 | 3.99 × 10−6 | 1.31 × 10−6 | 6.8 × 10−137 | 2.2 × 10−136 | 0.00 × 100 | 0.00 × 100 | |
| 2.50 × 102 | 4.62 × 101 | 3.32 × 10−4 | 5.40 × 10−5 | 1.33 × 10−72 | 1.74 × 10−72 | 0.00 × 100 | 0.00 × 100 | |
| 1.02 × 105 | 2.24 × 105 | 8.12 × 102 | 4.24 × 102 | 2.2 × 10−104 | 7.0 × 10−104 | 0.00 × 100 | 0.00 × 100 | |
| 4.62 × 101 | 3.76 × 100 | 9.43 × 10−1 | 5.68 × 10−1 | 4.36 × 10−68 | 8.38 × 10−68 | 0.00 × 100 | 0.00 × 100 | |
| 8.96 × 105 | 2.36 × 105 | 9.82 × 101 | 3.64 × 10−1 | 9.89 × 101 | 7.30 × 10−2 | 9.80 × 101 | 6.84 × 10−2 | |
| 1.36 × 104 | 7.92 × 103 | 7.24 × 100 | 8.24 × 10−1 | 1.98 × 101 | 1.04 × 100 | 1.84 × 100 | 7.23 × 10−1 | |
| 1.99 × 101 | 1.85 × 101 | 5.40 × 10−3 | 1.88 × 10−3 | 2.13 × 10−3 | 2.62 × 10−3 | 2.14 × 10−3 | 1.27 × 10−3 | |
| −2.2 × 104 | 1.69 × 103 | −1.8 × 104 | 9.86 × 102 | −7.6 × 103 | 2.38 × 103 | −3.6 × 104 | 1.54 × 103 | |
| 5.02 × 102 | 5.04 × 101 | 2.85 × 101 | 1.22 × 101 | 4.58 × 101 | 1.45 × 102 | 0.00 × 100 | 0.00 × 100 | |
| 1.10 × 101 | 2.99 × 100 | 2.12 × 10−4 | 5.23 × 10−5 | 1.99 × 100 | 6.31 × 100 | 8.88 × 10−16 | 0.00 × 100 | |
| 8.46 × 101 | 5.66 × 101 | 2.90 × 10−3 | 9.15 × 10−3 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| 4.44 × 103 | 9.29 × 103 | 1.59 × 10−1 | 3.49 × 10−2 | 1.53 × 100 | 1.57 × 100 | 1.39 × 10−2 | 4.41 × 10−3 | |
| 5.10 × 105 | 7.95 × 105 | 5.58 × 100 | 7.08 × 10−1 | 9.45 × 100 | 1.66 × 100 | 4.63 × 10−1 | 1.38 × 10−1 | |
| PSO | GWO | KMA | VWCKMA | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| 4.57 × 105 | 4.58 × 103 | 1.37 × 101 | 9.45 × 10−1 | 3.5 × 10−135 | 7.6 × 10−135 | 0.00 × 100 | 0.00 × 100 | |
| 1.89 × 103 | 2.99 × 101 | 2.68 × 100 | 1.63 × 10−1 | 8.21 × 10−70 | 1.05 × 10−69 | 0.00 × 100 | 0.00 × 100 | |
| 8.04 × 104 | 1.51 × 106 | 1.24 × 103 | 1.38 × 103 | 2.1 × 10−119 | 4.6 × 10−119 | 0.00 × 100 | 0.00 × 100 | |
| 6.81 × 101 | 2.51 × 100 | 5.83 × 101 | 6.30 × 105 | 1.15 × 10−65 | 2.20 × 10−65 | 0.00 × 100 | 0.00 × 100 | |
| 6.22 × 105 | 3.48 × 105 | 9.80 × 104 | 7.24 × 10−1 | 9.89 × 101 | 6.63 × 10−2 | 9.80 × 101 | 4.60 × 10−2 | |
| 2.51 × 103 | 1.38 × 104 | 7.60 × 100 | 1.17 × 100 | 1.91 × 101 | 1.50 × 100 | 1.28 × 100 | 2.00 × 10−1 | |
| 8.20 × 103 | 1.07 × 103 | 1.33 × 10−1 | 7.97 × 10−3 | 2.54 × 10−3 | 2.39 × 10−3 | 2.54 × 10−3 | 2.21 × 10−3 | |
| −5.9 × 104 | 2.97 × 103 | −6.4 × 104 | 2.71 × 103 | −1.2 × 105 | 6.03 × 103 | −1.3 × 105 | 9.01 × 103 | |
| 4.96 × 103 | 1.03 × 10−2 | 5.35 × 102 | 7.50 × 101 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| 1.94 × 101 | 2.54 × 10−1 | 3.70 × 10−1 | 8.72 × 10−2 | 2.01 × 100 | 6.12 × 100 | 8.88 × 10−16 | 0.00 × 100 | |
| 4.18 × 103 | 1.60 × 102 | 9.55 × 10−1 | 1.18 × 10−1 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| 5.77 × 102 | 1.30 × 103 | 1.33 × 10−1 | 2.87 × 10−2 | 1.22 × 100 | 1.45 × 10−1 | 1.86 × 10−2 | 7.02 × 10−3 | |
| 5.12 × 105 | 1.21 × 106 | 5.54 × 100 | 7.53 × 10−1 | 9.94 × 100 | 1.30 × 10−1 | 4.19 × 10−1 | 5.16 × 10−2 | |
| PSO | GWO | KMA | VWCKMA | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| 1.31 × 106 | 6.15 × 104 | 4.86 × 102 | 6.86 × 101 | 3.5 × 10−133 | 6.5 × 10−133 | 0.00 × 100 | 0.00 × 100 | |
| 2.23 × 103 | 2.33 × 101 | 3.57 × 101 | 3.34 × 100 | 1.27 × 10−48 | 2.20 × 10−48 | 0.00 × 100 | 0.00 × 100 | |
| 1.03 × 107 | 1.14 × 106 | 1.68 × 106 | 3.75 × 105 | 3.7 × 10−102 | 8.2 × 10−102 | 0.00 × 100 | 0.00 × 100 | |
| 9.91 × 101 | 6.41 × 10−1 | 7.45 × 101 | 2.14 × 100 | 4.36 × 10−65 | 5.67 × 10−65 | 0.00 × 100 | 0.00 × 100 | |
| 3.69 × 109 | 1.36 × 108 | 4.13 × 104 | 1.02 × 104 | 9.98 × 102 | 2.89 × 10−1 | 9.91 × 102 | 4.25 × 10−1 | |
| 1.32 × 106 | 3.36 × 104 | 7.35 × 102 | 9.72 × 101 | 2.17 × 102 | 1.02 × 101 | 3.44 × 101 | 6.53 × 100 | |
| 5.46 × 104 | 5.30 × 103 | 1.45 × 100 | 5.25 × 10−1 | 8.23 × 10−4 | 8.94 × 10−4 | 2.68 × 10−3 | 3.37 × 10−3 | |
| −8.9 × 104 | 3.93 × 103 | −1.1 × 105 | 4.72 × 103 | −2.8 × 105 | 1.55 × 104 | −2.4 × 105 | 1.21 × 104 | |
| 1.16 × 104 | 2.42 × 102 | 1.63 × 103 | 1.74 × 102 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| 1.98 × 101 | 8.90 × 10−2 | 2.52 × 100 | 8.36 × 10−2 | 1.22 × 101 | 1.11 × 101 | 8.88 × 10−16 | 0.00 × 100 | |
| 1.15 × 104 | 4.75 × 10−2 | 5.72 × 100 | 5.99 × 10−1 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| 7.29 × 109 | 6.97 × 108 | 7.58 × 100 | 1.40 × 100 | 1.01 × 100 | 2.23 × 10−1 | 3.70 × 10−3 | 1.21 × 10−2 | |
| 1.60 × 1010 | 1.54 × 109 | 5.59 × 102 | 4.10 × 101 | 100 × 100 | 6.53 × 10−3 | 9.07 × 100 | 1.26 × 100 | |
| Date | AQI | Quality | PM2.5 | PM10 | CO | NO2 | SO2 | O3 |
|---|---|---|---|---|---|---|---|---|
| 1 January 2020 | 135 | Light | 103 | 124 | 45 | 0.9 | 6 | 27 |
| 2 January 2020 | 135 | Light | 103 | 132 | 57 | 1 | 10 | 22 |
| 3 January 2020 | 105 | Light | 79 | 102 | 57 | 1 | 6 | 56 |
| 4 January 2020 | 118 | Light | 89 | 119 | 67 | 1.1 | 8 | 16 |
| … | … | … | … | … | … | … | … | … |
| 29 June 2022 | 106 | Light | 20 | 39 | 24 | 5 | 0.5 | 166 |
| 30 June 2022 | 82 | good | 26 | 50 | 35 | 5 | 0.7 | 138 |
| Model | |||||
|---|---|---|---|---|---|
| BPNN | 12.7518 | 280.2218 | 16.7398 | 34.7621 | 65.238 |
| PSO-BP | 9.9420 | 193.3857 | 13.9063 | 26.0763 | 73.923 |
| KMA-BP | 6.4277 | 64.3231 | 8.0202 | 19.7768 | 80.223 |
| RandomForest | 6.0028 | 66.7176 | 8.1681 | 16.2575 | 83.743 |
| VWCKMA-BP | 5.2226 | 56.1275 | 7.4918 | 14.9152 | 85.085 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhao, M. A Novel Komodo Mlipir Algorithm and Its Application in PM2.5 Detection. Atmosphere 2022, 13, 2051. https://doi.org/10.3390/atmos13122051
Li L, Zhao M. A Novel Komodo Mlipir Algorithm and Its Application in PM2.5 Detection. Atmosphere. 2022; 13(12):2051. https://doi.org/10.3390/atmos13122051
Chicago/Turabian StyleLi, Linxuan, and Ming Zhao. 2022. "A Novel Komodo Mlipir Algorithm and Its Application in PM2.5 Detection" Atmosphere 13, no. 12: 2051. https://doi.org/10.3390/atmos13122051
APA StyleLi, L., & Zhao, M. (2022). A Novel Komodo Mlipir Algorithm and Its Application in PM2.5 Detection. Atmosphere, 13(12), 2051. https://doi.org/10.3390/atmos13122051







