Abstract
Warnings of severe weather with a lead time longer that two hours require the use of skillful numerical weather prediction (NWP) models. In this study, we test the performance of the Commonwealth Scientific and Industrial Research Organisation (CSIRO) Conformal Cubic Atmospheric Model (CCAM) in simulating six high-impact weather events, with a focus on rainfall predictions in South Africa. The selected events are tropical cyclone Dineo (16 February 2017), the Cape storm (7 June 2017), the 2017 Kwa-Zulu Natal (KZN) floods (10 October 2017), the 2019 KZN floods (22 April 2019), the 2019 KZN tornadoes (12 November 2019) and the 2020 Johannesburg floods (5 October 2020). Three configurations of CCAM were compared: a 9 km grid length (MN9km) over southern Africa nudged within the Global Forecast System (GFS) simulations, and a 3 km grid length over South Africa (MN3km) nudged within the 9 km CCAM simulations. The last configuration is CCAM running with a grid length of 3 km over South Africa, which is nudged within the GFS (SN3km). The GFS is available with a grid length of °, and therefore, the configurations allow us to test if there is benefit in the intermediate nudging at 9 km as well as the effects of resolution on rainfall simulations. The South African Weather Service (SAWS) station rainfall dataset is used for verification purposes. All three configurations of CCAM are generally able to capture the spatial pattern of rainfall associated with each of the events. However, the maximum rainfall associated with two of the heaviest rainfall events is underestimated by CCAM with more than 100 mm. CCAM simulations also have some shortcomings with capturing the location of heavy rainfall inland and along the northeast coast of the country. Similar shortcomings were found with other NWP models used in southern Africa for operational forecasting purposes by previous studies. CCAM generally simulates a larger rainfall area than observed, resulting in more stations reporting rainfall. Regarding the different configurations, they are more similar to one another than observations, however, with some suggestion that MN3km outperforms other configurations, in particular with capturing the most extreme events. The performance of CCAM in the convective scales is encouraging, and further studies will be conducted to identify areas of possible improvement.
1. Introduction
South Africa is located in the subtropics, and therefore, its weather is influenced by tropical, subtropical and mid-latitude weather systems. Tropical cyclones make landfall along the eastern coast line of southern Africa, and they occassionally impact the northeastern part of South Africa [1,2,3,4,5]. The subtropical belt is characterized by high pressure with the semi-permanent St. Helena and Mascarene highs to the west and east of southern Africa, with frequent impacts on the Cape south coast, east coast and northeastern parts of the country [6,7]. When the Atlantic high-pressure systems located to the west ridge by extending eastward across South Africa (referred to as ridging highs), they transport moisture from the southwestern Indian ocean into the land [8]). When a ridging high is coupled with an upper midlatitude system such as an upper level trough or a cut-off low, heavy rainfall may occur [9,10,11]. These systems can cause high-impact weather (HIW), which when coupled with societal challenges may result in major disasters [12].
The World Meteorological Organization (WMO) publishes the state of the climate in Africa reports on an annual basis [13,14,15]. These publications report on climate indicators, extreme weather and climate events, and their impacts on human health, water and food security, as well as socioeconomic development. The reports all stress a need for multi-hazard early warning systems (MHEWSs) on the African continent to strengthen climate resilience and climate change adaptation efforts. MHEWSs can potentially mitigate the adverse impacts caused by extreme weather events especially regarding the loss of life and damage to movable property. In his speech on 23 March 2022, the secretary general of the United Nations, his excellency António Guterres urged for an increase in coverage of MHEWSs, and the WMO has been tasked to lead efforts to ensure that everyone has access to MHEWSs in the next five years [16]. An MHEWS has many components to it, with observations and numerical weather prediction (NWP) models as the basic requirements for such a system to exist (e.g., [17]).
In South Africa, a number of models are used to forecast weather and to produce climate predictions and projections. In case of the former i.e., NWP, the South African Weather Service (SAWS) employs the UK Met Office (Met Office) Unified Model (UM) as its main operational system [18,19], which replaced the National Centers for Environmental Prediction (NCEP) regional Eta Model [20,21]. Other NWP models used in southern Africa for operational purposes are the Consortium for Small Scale Modeling (COSMO) and the Weather Research and Forecasting (WRF) [22,23]. The three models were compared in a recent study when simulating HIW events in South Africa, and all three captured the selected events [24]. The centers responsible for these models are working on replacing them. The UM is being replaced with LFric [25], which is a cube-based system that offers quasi-uniform resolution and computational advantages. The Deutchscher Wetterdienst (DWD) and its partners are in the process of replacing COSMO with the Icosahedral Nonhydrostatic (ICON) Limited Area Mode (LAM) for NWP purposes [26].
Another model that has been in use in South Africa is the Commonwealth Scientific and Industrial Research Organisation (CSIRO) Conformal Cubic Atmospheric Model (CCAM) [27]. The model was used in the past for NWP purposes with a grid length of 15 km [18]; however, most of the work completed with the model over South Africa has focused on climate change projections [3,28,29]. CCAM solves the primitive equations on a conformal-cubic grid, which is a cube that is conformally projected onto the spherical Earth’s surface. CCAM was the first full atmospheric model to exploit the computational advantages and scalability of solving the primitive equations on the quasi-uniform conformal cubic grid. CCAM can also be applied with variable resolution to provide higher resolution over an area of interest, with decreasing resolution as one moves from an area of interest [30]. CCAM has also been applied successfully as a seamless model, for NWP, seasonal forecasting and climate change projections in South Africa [31]. CCAM is receiving increasing attention in South Africa and for building local model development capacity; due to its seamless nature, it can operate as a global and regional model, and it has been in use in the country for almost two decades.
The spatial resolution used by models including for NWP has been increasing over time due to the increased availability of super-computing resources [32]. Well-resourced NWP centers run downscalings at convection-permitting resolutions. Although CCAM has been tested for NWP purposes in South Africa, these tests were performed at lower resolutions, with grid lengths of more than 10 km [18,31]. In order for CCAM to be considered for operational forecasting, its performance, especially when simulating HIW, needs to be tested. CCAM has been tested with a grid length of 4 km over Australia and found to produce better solar radiation information compared to the global model that provided the forcing data [33]. In this study, the performance of CCAM when simulating rainfall is studied for six HIW events in South Africa. The methodology followed in the study is discussed in Section 2, and the results are in Section 4, with the summary and conclusions in Section 5.
2. Model, Data and Simulations
Simulations of six HIW events discussed in Section 3 were performed using CCAM. CCAM is described in Section 2.1, the simulations setup is described in Section 2.2, observations used for verification are described in Section 2.3 and objective verification measures are described in Section 2.4.
2.1. Model Description
CCAM was developed at CSIRO, Melbourne, Australia in the 1990s [34]. It is a non-hydrostatic model, and its differencing is applied using the semi-implicit and semi-Lagrangian techniques for efficiency. CCAM also uses a reversible staggering of the grid (R-Grid), switching between the A and C grids. CCAM solves momentum, energy and mass conservation equations given by Equations (1), (2) and (3), respectively.
Here, u is the flow velocity, T is the temperature, p is the pressure, is the virtual temperature, is the geopotential including virtual temperature contributions, f is the Coriolis parameter, and is the gas constant for dry air. is the specific heat of water vapor at constant pressure and is the pressure vertical velocity. D is the divergence term, and the various N terms denote contributions from physical parametrizations
The cloud microphysics scheme in CCAM is single moment and based on Rotstayn [35], and it was extended to include graupel [36]. The radiation scheme is based on the Geophysical Fluid Dynamics Laboratory Coupled Model 3 (GFDL-CM3) and is described in Freidenreich and Ramaswamy [37] and Schwarzkopf and Ramaswamy [38]. The turbulent mixing is represented with a turbulent kinetic energy-based scheme described by Hurley [39]. Cumulus schemes are used to represent the deep convection process that the models cannot resolve explicitly. Generally, as resolution increases in models, these schemes are switched off where the understanding is that the convection is resolved. The suggested thresholds where the convection schemes can be switched off range from about 4 km [40] to around 1 km [41] and 100 m [42]. CCAM represents an interesting case with its variable resolution mode that implies that the scheme in the model needs to be scale aware, similar to schemes such as the Multi-Scale Kain–Fritsch [43,44,45] and Grell–Freitas schemes [46]. CCAM employs a mass flux cumulus convection scheme, the CSIRO9, which is based on the Arakawa mass flux scheme [47]. A description of CCAM and its different components can be found on https://confluence.csiro.au/display/CCAM/CCAM (accessed on 1 September 2022).
2.2. Model Set up
CCAM was run on South Africa’s Centre for High Performance Computing (CHPC) Dell cluster with 1536 cores of Haswell Intel processors. CCAM was nudged with the National Centers for Environmental Prediction (NCEP) Global Forecast System (GFS) data [48], which runs with a grid length of 0.25°. The target resolution of the simulations is a grid length of 3 km, which is considered to be convection permitting [49]. Three configurations are tested as follows:
- CCAM running with a grid length of 9 km over most of southern Africa shown in Figure 1a, nudged within the GFS data. This configuration is referred to as MN9km in this study.
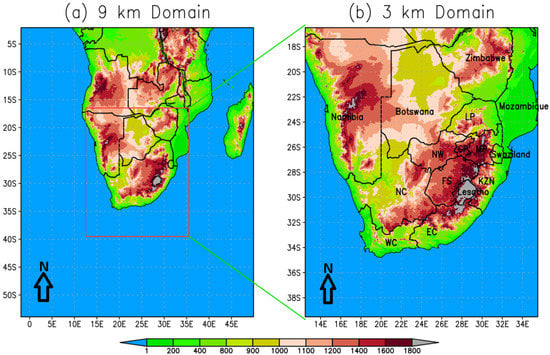 Figure 1. The simulation domain where CCAM runs with the highest resolution, with 9 km resolution across southern African and 3 km across South Africa. The colored contours are altitude above sea level in m.
Figure 1. The simulation domain where CCAM runs with the highest resolution, with 9 km resolution across southern African and 3 km across South Africa. The colored contours are altitude above sea level in m. - CCAM running with a grid length of 3 km over South Africa shown in Figure 1b. The simulations are nudged within the 9 km CCAM simulations above and referred to as MN3km.
- CCAM running with a grid length of 3 km on the same domain as MN3km shown in Figure 1b; however, it is nudged directly within the GFS data. This configuration is referred to as SN3km.
Spectral nudging is applied for surface pressure, air temperature, water vapor and winds every three hours for MN9km and SN3km, which is the time scale at which the GFS data are available. For MN3km, the spectral nudging is applied every one hour. Thirty hour simulations were made for each of the six selected case studies, with the first six hours being considered as the spin-up period [50]. The names of South Africa’s neighboring countries are written out in full, while the provinces that will be mentioned later on in the study are abbreviated in Figure 1b. LP is Limpopo, GP is Gauteng, NW is Northwest, FS is Free State, MP is Mpumalanga, NC is Northern Cape, WC is Western Cape, EC is Eastern Cape, and KZN is Kwa-Zulu Natal, which make up South Africa’s nine provinces. The six case studies will be discussed in Section 3.
2.3. Observation Data
Observed twenty-four hour rainfall data from SAWS were used in this study for verification purposes. For each of the case studies described in Section 3, the number of stations that reported twenty-four rainfall exceeds 1000. Specifically, the number of stations that reported observations successfully is 1454 on 16 February 2017, 1452 on 7 June 2017, 1445 on 9 October 2017, 1357 on 22 April 20219, 1365 on 12 November 2019 and 1271 on 5 October 2020. The ERA5 reanalysis are considered as observations to indicate the prevailing synoptic scale circulation at 12h00Z on all the selected days for the case studies. ERA5 reanalyses are the latest climate reanalysis product from ECMWF [51]. ERA5 combines vast amounts of historical observations into global estimates using the Integrated Forecasting System (IFS) and data assimilation systems.
2.4. Verification
The Mean Error (ME) and Root Mean Square Error (RMSE) [52] were calculated as shown below:
where F represents data from one of the simulations, O represents the observations, i labels stations, and N is the total number of stations for each of the case studies.
In addition to the ME and RMSE, the Probability of Detecting Yes (PODY), the False Alarm Rate (FAR), and the Critical Success Index (CSI) are also calculated for a number of thresholds, starting with mm, and then 5 mm, followed by 10 mm and increments of 10 up to 60 mm. The PODY, FAR and CSI are defined based on the contingency Table 1 [52].

Table 1.
Contingency table for calculating the skill scores.
PODY indicates the proportion of correctly predicted events from total observed events. PODY ranges between 0 and 1, with 1 being the perfect score, and it is given by:
FAR indicates the proportion of false alarms to all forecasts, and it ranges from 0 to 1, with 0 being a perfect score. It is defined as:
CSI indicates the proportion of hits in all predicted and missed events. It ranges between 0 and 1, with 1 being a perfect score and is given by:
3. Case Study Descriptions
The cases of weather system occurrences were selected due to their high impact as well as to ensure there is at least one system to represent the tropics, subtropics and midlatitudes (Table 2). Five of the selected case studies are listed in the Center for Research on the Epidemiology of Disasters (CRED) Emergency Events Database (EM-DAT).The majority of the cases were found to be associated with a cut-off low-pressure system. At the time of writing, there had already been another cut-off low event that resulted in the loss of life of over 500 people on 11 April 2022; however, that event is not included in this study. The twenty-four hour spatial distribution of rainfall associated with each of the six case studies is shown in Figure 2, while the ERA5 sea-level pressure (shaded colors) and 500 hPa level geo-potential heights (white labeled contours) are shown in the top panel of Figure 3 and Figure 4. The corresponding CCAM simulations are from MN9km because it has a domain size large enough to show circulation extending into the adjacent oceans. Each of the case studies are discussed below and divided according to synoptic weather system types.

Table 2.
Selected case studies of high-impact weather in South Africa.
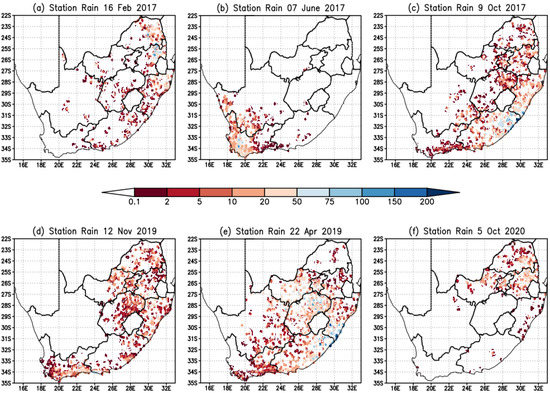
Figure 2.
Observed twenty-four rainfall (mm) on (a) 16 February 2017, (b) 7 June 2017, (c) 9 October 2017, (d) 12 November 2019, (e) 22 April 2019, and (f) 5 October 2020.
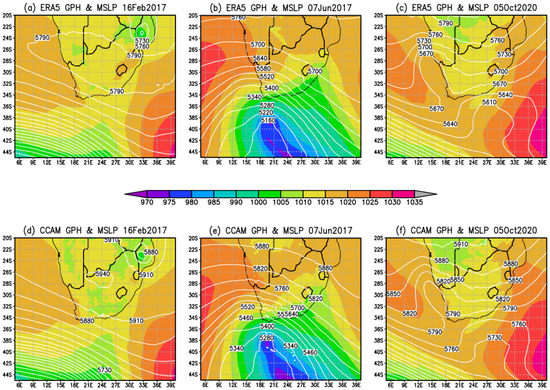
Figure 3.
The ERA5 reanalysis sea level pressure in shaded colors and 500 hPa geopotential heights in white labeled contours for (a) 16 February 2017, (b) 7 June 2017, (c) 5 October 2020, and the same variables for CCAM MN9km (d) 16 February 2017, (e) 7 June 2017 (f) 5 October 2020.
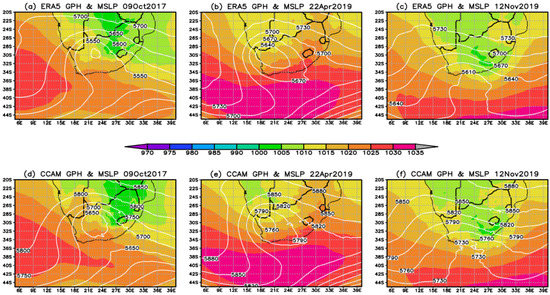
Figure 4.
The ERA5 reanalysis sea level pressure in shaded colors and 500 hPa geopotential heights in white labeled contours for (a) 9 October 2017, (b) 22 April 2019 and (c) 12 November 2019 and the same variables for CCAM MN9km (d) 9 October 2017, (e) 22 April 2019 and (f) 12 November 2019.
3.1. Tropical System
The tropical cyclone case considered in this study is Dineo, which formed on 13 February 2017 in the Mozambique Channel and dissipated on 17 February. The system impacted on a number of southern African countries including Mozambique, Zimbabwe and Botswana, and it has been a subject for a number of studies. For example, Moses and Ramotonto [53] assessed the performance of the ECMWF Integrated Forecast System (IFS) model and GFS on forecasting the system over Botswana and found the GFS to outperform the IFS on maximum rainfall location and amount. In Zimbabwe, the system was used to study the behavior of social workers during disasters, and it was found that the profession was reactive [54]. The current study focuses on 16 February 2017, when rainfall was reported over the northeastern parts of South Africa. On this day, the system had already deteriorated to an ex-tropical cyclone depression as shown in Figure 3 and the SAWS weather map [55]. The event impacted the northern parts of KZN, the MP and LP provinces of South Africa (Figure 2a). Ref. Meyiwa [56] studied the event using WRF and found the model underestimated the rainfall at a number of stations in the northeast of South Africa.
3.2. Coupled Tropical and Midlatitude Systems
On 12 November 2019, a surface trough coupled with a cut-off low resulted in widespread rainfall, which was associated with severe thunderstorms. The circulation plot shown in Figure 4c shows the surface trough over land and an upper-level trough south of the country. The SAWS synoptic chart indicated the presence of a cut-off low system on this day [57]. Rainfall was observed over most of the eastern half of South Africa (Figure 2d). The amount of rainfall reported, is however, generally less than for the other events being studied. The thunderstorms resulted in a series of tornadoes in the midlands of KwaZulu Natal province, in New Hanover. Ref. Mahomed [58] studied the event using SAWS weather radar data and lightning information and found that the storm that produced the tornadoes was a supercell. The supercell that produced the tornado was characterized by a rapid increase in the flash rate followed by a rapid decline, which was an indication of a tornado on the ground.
An upper-level trough and a surface trough (Figure 3c) occurred on 5 October 2020, resulting in some flooding in Johannesburg ([59]). Johannesburg is the financial capital of South Africa and is located in the Gauteng province indicated by GP in Figure 1b. The SAWS synoptic weather map [60] shows that there was a surface trough to the northeast of the country. The existence of an upper trough resulted in the heavy rainfall over the northeastern parts of the country.
3.3. Coupled Subtropical and Mid Latitude Systems
The subtropics are characterized by a high pressure belt which promotes subsidence, and therefore, rainfall occurrence is considered an anomaly [61]. The unique topography of South Africa characterized by a sharp escarpment and narrow coasts allows for ridging anticyclones to be associated with orographic lifting and rainfall. About half of annual rainfall over the south coast is due to ridging anticyclones [11]. Since the focus of the study is heavy rainfall, the subtropics are represented by ridging highs that occur in conjunction with midlatitude systems. Two events are selected, where cut-off low systems occurred in conjunction with a ridging St Helena high, one on 9 October 2017 and another 22 April 2019. The two events caused flooding, damage to property and loss of life in the KZN province (Figure 1b). For the April 2019 event, over 80 lives were lost due to flooding and property damage associated with the severe weather event. The ridging high can be seen clearly on the SAWS synoptic weather maps [62,63] and ERA5 renalysis (Figure 4a,b) which also shows the location of the cut-off low systems. The two cases were part of the intense cut-off low systems analyzed by Muofhe et al. [64] to determine the performance of the UM in forecasting these systems. The heavy rainfall associated with 9 October 2017 was restricted to the southeast coast and adjacent interior (Figure 2c), while the 22 April 2019 event resulted in high amounts of rainfall also in the central interior provinces (Figure 2e).
3.4. Midlatitude Systems
A strong cold front [65] (Figure 3b) made landfall over the Western Cape on 7 June 2017, resulting in high waves and strong to gale force winds that caused damage to property. The event was the focus of a study by Barnes et al. [66] who showed that it was associated with Rossby wave breaking and an intrusion of high potential vorticity (PV) from the lower stratosphere. The event also resulted in scattered showers and thundershowers over the western Cape. Figure 2b shows rainfall associated with this event over the western parts of the Western Cape as well as parts of the Northern Cape. The event is referred to locally as the “Cape storm”.
4. Results
This section discusses twenty-four rainfall simulations for the six case studies discussed in Section 3. Section 4.1 discusses the observed twenty-four hour rainfall across the country and how it compares to the different CCAM simulations. The distribution of rainfall across the different stations is discussed in Section 4.2, the verification is discussed in Section 4.3, and the partitioning of the resolved rainfall versus the convective rainfall from the cumulus scheme is discussed in Section 4.4.
4.1. Total Rainfall
For all the selected events, CCAM is able to capture the relevant weather systems and associated rainfall patterns; however, there are some shortcomings. The MN9km simulated sea level pressure and 500 hPa of the six events are shown in the bottom panel of Figure 3 and Figure 4 alongside the ERA5 reanalysis. CCAM and ERA5 synoptic events were found to be generally similar, and they are aligned with the simulated rainfall that show that the synoptic systems were captured well. We first show the total amount of rainfall summed from across all the stations that reported rainfall in Figure 5a. In order to undertake this comparison, the model rainfall was interpolated to each station locations. Any amount from mm is considered as recorded rainfall. The total observed and simulated rainfall is highest for two cut-off lows with ridging high systems, followed by the 12 November 2019 event, which was also a cut-off low (Figure 5a and Table 3 columns two to five). The total observed rainfall is higher than simulated for 22 April 2019, while the opposite is found for the 9 October 2017 event. For other events with lower rainfall, there is a generally good comparison between the simulations and observations. The MN3km simulated more rainfall in general compared to the SN3km and MN9km configurations for the case studies. This results in this configuration being closer to the observations for the tropical cyclone Dineo event (16 February 2017), the 2019 KZN floods (22 April 2019), and the 2020 KZN tornadoes event (12 November 2019). The configuration overestimates rainfall for the Cape storm (7 June 2017), 2017 KZN floods (9 October 2017) and for the Johannesburg floods (5 October 2020). Regarding total rainfall, it is the best performing configuration of the three for three case studies.
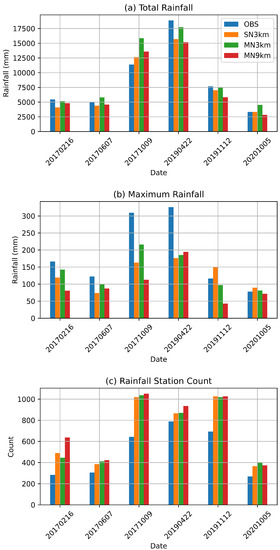
Figure 5.
Observed and simulated (a) total twenty-four hour rainfall summed across all stations, (b) maximum twenty-four hour rainfall, and (c) stations that reported more mm of rain in a twenty-four hour period.

Table 3.
The twenty-four hour rainfall summed across all the stations that reported rainfall in columns 2 to 5 and number of stations that reported more than 0.1 mm of rainfall in columns 6 to 9, for observations, the different CCAM configurations and for the six events.
Figure 5b shows the maximum recorded twenty-four hour rainfall across all the stations. Some stations recorded rainfall amounts of over 300 mm in a space of twenty-four hours for the two KZN flood events associated with the highest rainfall amount. For 22 April 2019, all model configurations do not simulate maximum rainfall of over 200 mm, while for 9 October 2017, the MN3KM simulates rainfall of over 200 mm. The general message from four of the six events is that the model tends to underestimate the extreme rainfall events. However, it should be kept in mind that even for the 3 km resolution simulations, rainfall is averaged over a 3 km × 3 km grid box, whereas rainfall from stations are recorded at a point. The MN3km configuration simulates a higher maximum rainfall for three of the six events than the other two configurations where the simulated rainfall is underestimated. Ref. Meyiwa [56], who used WRF with a 6 km grid length to simulate tropical cyclone Dineo, found WRF underestimated rainfall in some stations. Ref. Mugume et al. [67] compared the performance of WRF and COSMO with 7 km grid length when simulating extreme rainfall events in Uganda and found both models to underestimate the intensity of the events. MN9km simulates a lower maximum in general; however, for the highest rainfall event, it simulated a slightly higher maximum compared to the other two events.
The total number of stations that reported rainfall of over mm is shown in Figure 5c and Table 3 columns six to eight. More stations reported rainfall in the 2019 Kwa-Zulu Natal floods, which is followed by the 2019 KZN tornadoes event and then the 2017 KZN events. The model does not capture this effect; the two latter events are associated with the most stations reporting rainfall, which are followed by the 2019 KZN floods. A general message for all case studies is that CCAM overestimates the number of stations that report rainfall; however, the extent of the overestimation is event specific. For example, there is a big difference between the number of stations that recorded rainfall and those that are simulated to have recorded rainfall for the 2017 KZN floods and 2019 KZN tornado events. The configuration with the lowest resolution, MN9km, reports more stations in general than all the other configurations for four of the case studies; however, the difference between different model configurations is generally smaller than between all the simulations and the observations. This result is explored further in Section 4.2 where the rainfall distribution is discussed.
We show examples of two cut-off lows with ridging high events that resulted in the highest amount of rainfall of the six events that occurred in October 2017 (Figure 6) and April 2019 (Figure 7) to show the spatial distribution of rainfall from observations and the different CCAM configurations. The shaded colors indicate rainfall of mm and above in a twenty-four hour period. The heaviest rainfall on 9 October 2017 (Figure 6) was observed in the southern parts of KZN and northern parts of the EC province (Figure 1). CCAM is able to capture this feature with all the configurations. However, all configurations extend the heavy rainfall across most of the eastern coastline, which is a feature that is not observed. The model is able to distinguish well provinces that received rainfall from those that did not.
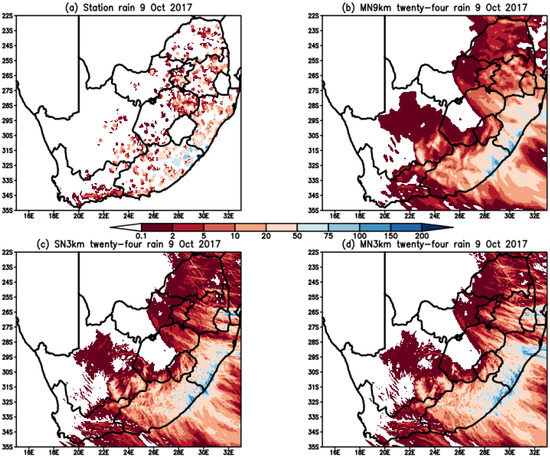
Figure 6.
Observed twenty-four rainfall (mm) on (a) 9 October 2017 and CCAM simulated rainfall for (b) SN3km (c) MN3km and (d) MN9km, for the same day.
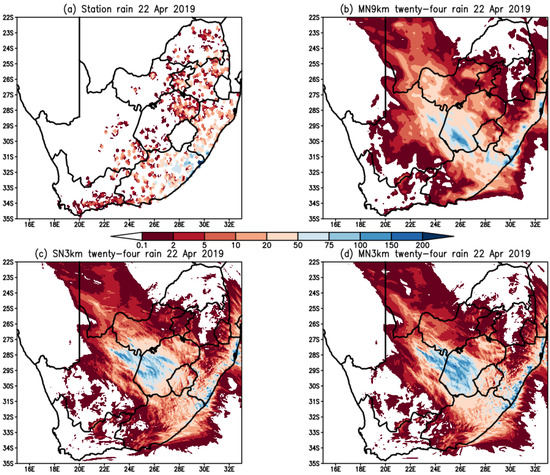
Figure 7.
Observed twenty-four rainfall (mm) on (a) 22 April 2019 and CCAM simulated rainfall for (b) SN3km (c) MN3km and (d) MN9km, for the same day.
The 22 April 2019 event is different from the October 2017 event in that the heaviest rainfall is not only restricted to the coastal provinces in the east, but NW and FS provinces (Figure 1b) also received heavy rainfall (Figure 7). For the coast, CCAM once again extends the heavy rainfall to the north of Kwa-Zulu Natal, which is a feature found for the October 2017 event. A previous study of the same event with a different model, the Met Office UM, showed the same feature [19]. Another aspect is that the model progressed the system inland slower than observed. This is shown by the simulated heaviest rainfall occurring in the western half of the FS province and the northeastern part of the NC province. The observed heaviest rainfall was in the eastern half of the Free State province and southwestern parts of the Northwest province. This is in agreement with a previous study by Muofhe et al. [64] which showed that heaviest rainfall is usually mislocated in another NWP model, especially in the mature stages of the cut-off low systems.
4.2. Rainfall Distribution
We use scatter plots as a start to understand the rainfall distribution in the observations and the three CCAM configurations. Figure 8 shows these for all six case studies. A perfect arrangement would be for all the points to be along a 45 degree line, indicating an agreement in rainfall amount and location between the model forecasts and observations. The x-axis and y-axis range are set to be similar in all the plots, and the range was set up to include all the available points. The plots confirms that the model did not capture the highest observed rainfall amounts with the exception of the 5 October 2020 event where SN3km simulated a rainfall amount exceeding 80 mm, which was not observed. There is an almost continuous surface of points between 0 and about 40 mm, the lower range where observed and simulated frequencies are the highest.
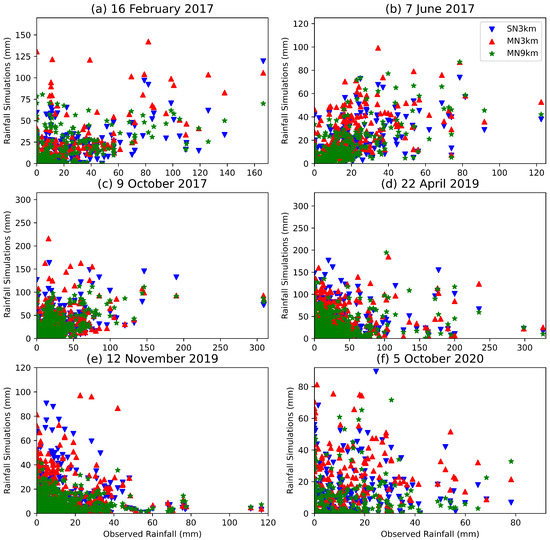
Figure 8.
The observation and CCAM simulations scatter plot for (a) tropical cyclone Dineo, (b) the Cape storm, (c) the KZN 2017 October floods, (d) the KZN 2019 April floods, (e) the KZN 2019 tornadoes and (f) the Johannesburg floods.
The results discussed in Section 4.1 showed that the number of stations reporting simulated rainfall is more than those observed. The observed and simulated rainfall was split into bins to provide an indication of the rainfall distribution across all the stations (Figure 9). This metric evaluates the model simulated rainfall distribution across a range of categories without the location penalty [68] associated with traditional skill score. The first bin is rainfall amounts starting from to 5 mm, followed by 5 mm to 10 mm, and then bins with 10 mm increments up to 60 mm. For all the case studies, the model simulates a higher frequency of small rainfall amounts than observed. This is at least partially due to the fact that the model rainfall is averaged into grid boxes of either 9 km × 9 km or 3 km × 3 km in dimension. The tropical cyclone example of 16 February 2017 (Figure 9a) shows the MN9km configuration as worse performing with four times the number of stations simulating rainfall than observed. The MN3km is the best performing; however, it is closer to SN3km than to the observations.
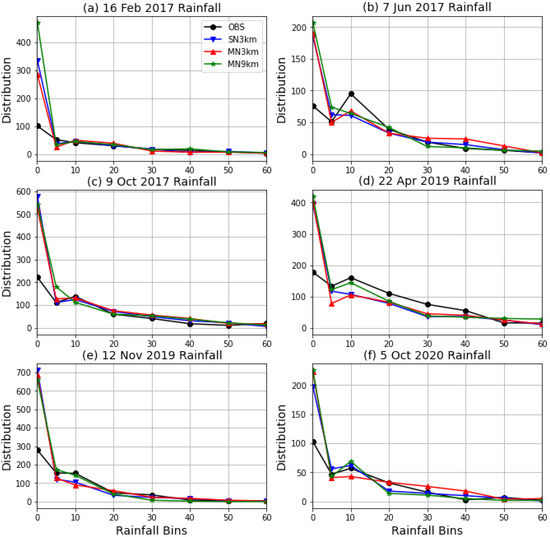
Figure 9.
The number of stations at which rainfall is simulated in the 0.1 to 5 mm, 5 to 10 mm, and 10 to 60 mm ranges with intervals of 10 mm for all six events in the following order: (a) tropical cyclone Dineo, (b) the Cape storm, (c) the KZN 2017 October floods, (d) the KZN 2019 April floods, (e) the KZN 2019 tornadoes and (f) the Johannesburg floods.
For 7 June 2017, the cold front event, 95 stations reported rainfall amounts ranging between 10 and 20 mm, while for simulations, the number of stations ranges from 61 to 68. For the 22 April 2019 event, which is the one associated with the most rainfall of the six cases, the model underestimated the stations with rainfall in the 10–20, 20–30, 30–40, and 40–50 mm bins. For the other events, and bins, the number of stations is generally similar between the model configurations and the observations. The level of correspondence between the observation and simulations is explored further in Section 4.3.
4.3. Verification Results
The ME and RMSE as defined in Section 2.4 are discussed here and presented in Table 4. We use these in conjunction with PODY, FAR and CSI also defined in Section 2.4 to gain further understanding on the performance of CCAM in simulating rainfall associated with HIW. All the measures discussed in this section penalise the model for misrepresenting the rainfall location. The latter scores were calculated for different thresholds, as will be discussed further. The ME results are aligned with Figure 5, which showed that the model underestimated the total rainfall for tropical cyclone Dineo, 2019 KZN floods and 2019 KZN tornadoes. For the 2017 Cape storm, the MN3km overestimated rainfall. The general statistics, as well as the RSME, are similar to each other, showing that there are small differences amongst the different model configurations. These results therefore indicate that the simulations are generally similar with very comparable performance statistics.

Table 4.
The ME in column 2 to 4 and RMSE in columns 5 to 7 for different CCAM configurations and for the six events.
PODY provides a fraction of the stations where rainfall was simulated and observed as a percentage of all hits and misses. A perfect score of 1 occurs when all the grid points are hits and there are no misses. The results for different thresholds as defined in Section 2.4 are shown in Figure 10. The score for a threshold of mm is high across all the six events, and it drops off generally with higher thresholds at different rates. For tropical cyclone Dineo, the MN9km and MN3km outperform SN3km up to a threshold of 40 mm. The MN3km outperforms all the configurations from a threshold of 30 mm and PODY remains above 0.4 even with a threshold of 60 mm. This is an interesting finding that illustrates the benefits of multi-nudging results in strongly forced systems such as tropical cyclones being captured better. Although the different configurations are generally close to one another in performance, the red line which represents MN3km seems be higher generally, especially with higher thresholds.
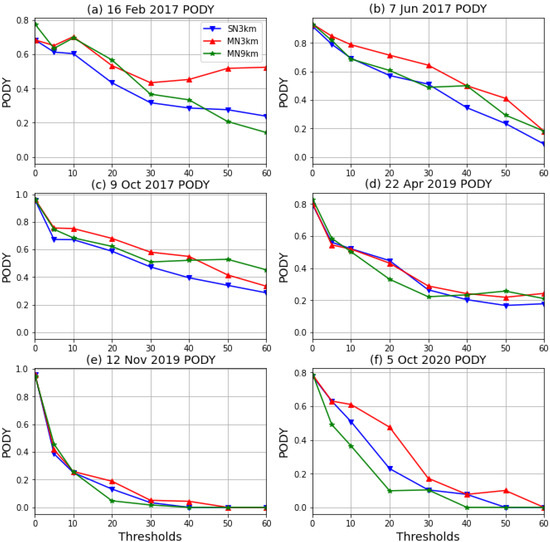
Figure 10.
The probability of detecting yes score for the three configurations and for all six events in the following order: (a) tropical cyclone Dineo, (b) the Cape storm, (c) the KZN 2017 October floods, (d) the KZN 2019 April floods, (e) the KZN 2019 tornadoes and (f) the Johannesburg floods.
Unlike with PODY, a perfect FAR score is 0, which implies that the model should not simulate rainfall over stations that do not report it. FAR for all six case studies and the three configurations are shown in Figure 11. For tropical cyclone Dineo, the false alarms are high for the mm thresholds and drop to 0.3 for the next threshold of 5 mm. After that, these increase gradually, with MN9km as the worst performer from a threshold of 30 mm. MN3km seems to perform generally better than the other two configurations. For the Cape storm, there is a similar feature of a higher FAR at 0.1 mm and a lower value at 5 mm. The false alarms increase as the thresholds increase. MN3km seems to be performing worst in general for this event. The drop to 0 by the MN9km configuration for the 12 November 2019 event is because this configuration did not simulate rainfall above 50 mm; therefore, there are no false alarms. An increase in FAR indicates that although higher values of rainfall are simulated, the simulated location does not match the observed location.
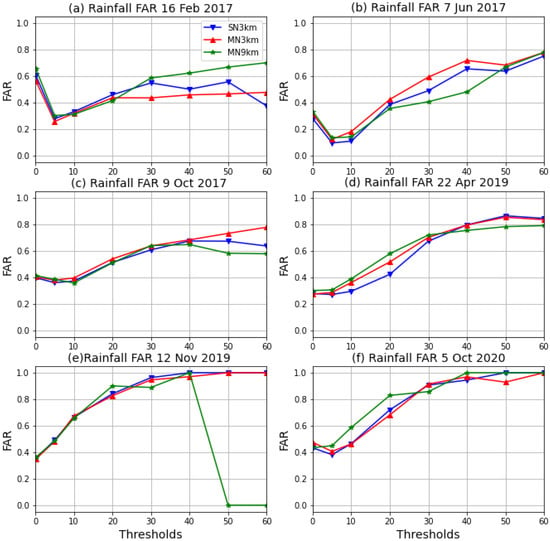
Figure 11.
The False Alarm Rate for the three configurations and for all six events in the following order: (a) tropical cyclone Dineo, (b) the Cape storm, (c) the KZN 2017 October floods, (d) the KZN 2019 April floods, (e) the KZN 2019 tornadoes and (f) the Johannesburg floods.
The CSI (Figure 12) provides overall performance by showing the fraction of hits to all hits, plus false alarms, plus misses. Similar to PODY, the CSI should ideally be 1, with false alarms and misses being 0. MN3km outperforms the other configurations with tropical cyclone Dineo. The CSI exceeds 0.3 with thresholds of 30 mm and higher. For the Cape storm, the model performance is generally similar with MN3km outperforming the other configurations slightly except with the 40 mm threshold where MN9km is better. For the 9 October 2017 event, the different configurations perform similarly generally, with MN9km outperforming the others with the 50 mm and 60 mm thresholds. CCAM performs better and up to higher thresholds for the more organized events, in particular, tropical cyclone Dineo and the Cape storm. For 12 November 2019, smaller amounts of rainfall were distributed across the south and east of the country, and CCAM’s performance drops off very quickly, reaching zero by a 30 mm threshold.
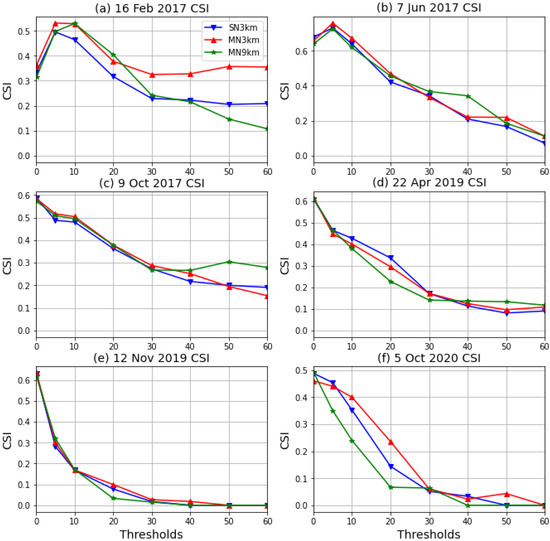
Figure 12.
The Critical Success Index for the three configurations and for all six events in the following order (a) tropical cyclone Dineo, (b) the Cape storm, (c) the KZN 2017 October floods, (d) the KZN 2019 April floods, (e) the KZN 2019 tornadoes and (f) the Johannesburg floods.
4.4. Subgrid vs. Resolved Rainfall
This section of the study looks at the comparison between the convective rainfall produced by the convective scheme and the total rainfall for all three configurations. The interest in this regard is to see if the contribution of the convection scheme to total rainfall decreases with higher resolution. For the configurations being studied here, we are more interested in how the 9 km grid compares to the 3 km grid. This is because for any subgrid model, the expectation is that reliance on parametrization reduces as resolution increases [69]. With CCAM allowing a variable resolution configuration, the schemes need to adjust with different resolution, automatically.
Rainfall maps similar to Figure 13 were produced for all the events to compare the amount of convective rainfall to total rainfall. The upper row shows total rainfall from MN9km and MN3km, while the lower row shows the corresponding convective rainfall. The MN9km convective rainfall (Figure 13c) has higher values of rainfall compared to MN3km (Figure 13d). This means the CSIRO9 cumulus scheme produces less rainfall at 3 km compared to at 9 km which is a desired effect indicating that the scheme is scale aware. MN3km simulated heavier total rainfall in general, which the figure shows is a result of resolved rainfall not the convective scheme. The discussions above showed that MN3km has better skill in capturing extreme rainfall events, and this figure suggests that it is a result of higher resolution and the heavy rainfall being captured.
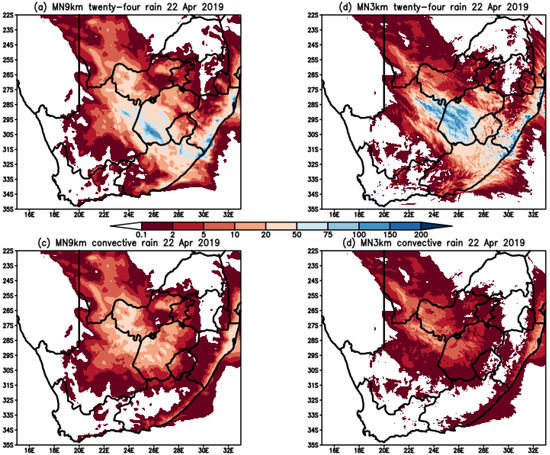
Figure 13.
CCAM simulated twenty-four rainfall (mm) on 22 April 2019 for (a) MN9km and (b) MN3km, and convective rainfall from the cumulus scheme for (c) MN9km and (d) MN3km.
To confirm that the convective rainfall is lower at high spatial resolution for all the selected events, a bar chart that corresponds to Figure 5 was prepared to indicate how convective rainfall compares to total rainfall. The results are shown in Figure 14, where Figure 14a shows that the contribution of convective rainfall to total rainfall is higher when a grid length of 9 km is used compared to the 3km configurations. The contribution is especially higher for the Dineo tropical cyclone and the KZN tornadoes event. The convective rainfall contribution to total rainfall with the 3 km configurations is less than 10% for most of the events. The results indicate that the convection schemes should not be switched off completely when a grid length of amount 3 km is used. The results support Roberts [41], who recommend that the cumulus schemes remain on at these resolutions but be applied in a reduced manner. The results from our study also indicate that the contribution of the convective schemes to total rain differs for different weather systems, suggesting that scale-aware schemes should be applied instead of schemes that need to be switched off manually at a certain resolution.
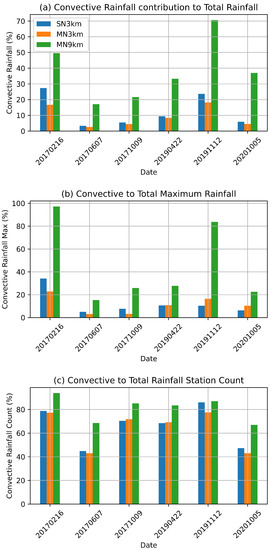
Figure 14.
Percent contribution of convective rainfall to (a) total rainfall, (b) maximum rainfall and (c) number of stations reporting rainfall of more 0.1 mm of rain.
The maximum convective rainfall simulated for the two events is also comparatively high relative to the maximum of the total rainfall at above 80% (Figure 14b). For the other events including the two with highest total rainfall, the maximum convective rainfall is less than 0.3 of the total maximum rainfall. This shows that most of the rainfall from the heavy rainfall events was resolved by the model. Figure 14c shows the percentage of stations where convective rainfall of over mm was simulated. This result shows that a high percentage of stations do simulate convective rainfall—even with a grid length of 3 km, although the contribution to total rainfall is less with higher resolution.
We also prepared the scatter plot of convective to total rainfall shown in Figure 15. The convective rainfall is added to the resolved rainfall to give total rainfall; therefore, the points in these plots are limited to the 45 deg line and lower because the convective rainfall cannot exceed the total rainfall. For the two events with the highest contribution of convective rainfall to total rain, there are points along 45 deg line indicating that, for some stations, the total rainfall was a result of convective rainfall only. For the other events, the convective rainfall is below 20 mm.
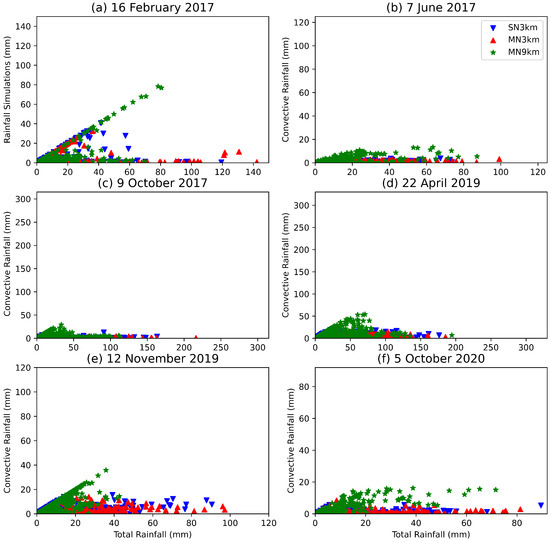
Figure 15.
The total simulated rainfall to convective rainfall scatter plot for (a) tropical cyclone Dineo, (b) the Cape storm, (c) the KZN 2017 October floods, (d) the KZN 2019 April floods, (e) the KZN 2019 tornadoes and (f) the Johannesburg floods.
5. Summary and Conclusions
Warnings of extreme weather with a lead time longer than 2 h require the use of NWP models [32]. In this study, we analyzed simulations of rainfall associated with six HIW events in South Africa. The events were selected to provide a mixture of tropical, subtropical and midlatitude influence.The selected events are tropical cyclone Dineo (16 February 2017), the Cape storm (7 June 2017), the 2017 KZN floods (10 October 2017), the 2019 KZN floods (22 April 2019), the 2019 KZN tornadoes (12 November 2019) and the 2020 Johannesburg floods (5 October 2020). All the selected events resulted in damage to property, displacement of people and loss of life in some circumstances. The model used is the CSIRO developed CCAM, which is the first model to use a cube-based dynamical core. The model has been used successfully in South Africa for NWP, seasonal forecasting and climate change projections [31]. Although CCAM has been used for NWP in South Africa, the grid length used exceeded 10 km [18]; here, we test CCAM with a 9 km and 3 km grid and therefore in the convective scales. Three configurations are compared as follows: (1) CCAM running 9 km across southern Africa nudged within the GFS [48] (MN9km), (2) CCAM running with a grid length of 3 km over South Africa nudged in the 9 km CCAM simulations (MN3km) and (3) CCAM running with a grid length 3 km over South Africa nudged within the GFS directly (SN3km). SAWS rainfall observations are used for verification purposes, and CCAM simulations are matched to the station points using bilinear interpolation.
All CCAM configurations were able to capture the synoptic weather system and rainfall for all six events. The rainfall analysis made includes measures that do not disquality the model for mirepresenting the rainfall location such as total and maximum rainfall across all the stations as well as the rainfall distributions. The traditional measures, in particular, the ME, RMSE, PODY, FAR and CSI that penalise the model for missing the location are also used.The total amount of rainfall summed across all the stations was found to be generally similar between CCAM and the observations. For the events with the most rainfall, the two KZN floods, CCAM was found to underestimate the maximum rainfall by more than 100 mm. For the events with lessor rainfall, the peaks were not missed by much. Other previous studies have also found that WRF and COSMO models struggle with capturing the extreme events using grid lengths of 6 and 7 km over northeast South Africa and Uganda (e.g., [56,67]). In a thunderstorm study conducted by Keat et al. [70], it was found that the UM was not able to simulate the intensity of the extreme thunderstorms in the northeastern parts of South Africa.
CCAM captures the location of rainfall in general; however, there are shortcomings. For example, for the KZN floods, CCAM extends the heavy rainfall across the whole coast of KZN, while the heaviest rainfall was only observed in the south and north of the Eastern Cape. This feature was also found in the UM using grid lengths of and km [19]. CCAM also mislocated the inland heavy rainfall, advancing it slower than observed. This mislocation of rainfall with cut-off low systems was also found by Muofhe et al. [64] using the UM. On rainfall distribution, CCAM was found to generate a larger rainfall area compared to observations resulting in more stations simulating rainfall than observed. The use of intermediate nudging for MN3km seems to produce some differences that are positive. For example, the MN3km improves the maximum rainfall forecast compared to the other configurations. In the case of tropical cyclone Dineo, MN3km was found to perform much better even with higher thresholds going up to about 60 mm. This result suggests that reducing the resolution jump may have some benefit even when the stretched grid downscaling approach is applied.
The study can conclude that CCAM is able, in general, to capture the HIW events in South Africa. Shortcomings in CCAM were also found in other NWP models [64,67], COSMO, WRF and UM used for NWP purposes within SADC [22,23,24] in previous studies. Further studies on CCAM will include sensitivity studies with the cloud microphysics, planetary boundary layer and cumulus schemes with HIW events, and cases with limited synoptic forcing.
Author Contributions
M.-J.M.B., F.A.E. and J.M conceptualized the study, R.M., M.T., G.T.R. and P.T.M. implemented CCAM and associated software, M.-J.M.B. and L.L. made formal analyses, M.M. and J.M. provided observation data, M.-J.M.B., F.A.E. and J.M. acquired funding, M.-J.M.B. wrote the original draft, and M.A.B., H.C., T.N. and F.A.E. reviewed and edited the text. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded through the AIMS NEI Women in Climate Change Science (WiCCS) fellowship and the Water Research Commission contract C2020/2021-00596.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Model simulations can be made available on request from the authors, the SAWS observations can be requested from info2@weathersa.co.za.
Acknowledgments
The authors acknowledge the South African Centre for High-Performance Computing (CHPC) for use of their HPC system and the South African Weather Service for providing observation data for the study.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Reason, C.J.C.; Keibel, A. Tropical Cyclone Eline and Its Unusual Penetration and Impacts over the Southern African Mainland. Weather. Forecast. 2004, 19, 789–805. [Google Scholar] [CrossRef]
- Mavume, A.; Rydberg, L.; Rouault, M.; Lutjeharms, J. Climatology and Landfall of Tropical Cyclones in the South- West Indian Ocean. West. Indian Ocean J. Mar. Sci. 2010, 8, 15–36. [Google Scholar] [CrossRef]
- Malherbe, J.; Engelbrecht, F.; Landman, W. Projected changes in tropical cyclone climatology and landfall in the Southwest Indian Ocean region under enhanced anthropogenic forcing. Clim. Dyn. 2013, 40, 2867–2886. [Google Scholar] [CrossRef]
- Chikoore, H.; Vermeulen, J.; Jury, M. Tropical cyclones in the Mozambique Channel: January–March 2012. Nat. Hazards 2015, 77, 2081–2095. [Google Scholar] [CrossRef]
- Davis-Reddy, C.; Vincent, K. Climate Risk and Vulnerability: A Handbook for Southern Africa, 2nd ed.; CSIR: Pretoria, South Africa, 2017; p. 193. [Google Scholar]
- Sun, X.; Cook, K.H.; Vizy, E.K. The South Atlantic subtropical high: Climatology and interannual variability. J. Clim. 2017, 30, 3279–3296. [Google Scholar] [CrossRef]
- Xulu, N.G.; Chikoore, H.; Bopape, M.J.M.; Nethengwe, N.S. Climatology of the mascarene high and its influence on weather and climate over Southern Africa. Climate 2020, 8, 86. [Google Scholar] [CrossRef]
- Ndarana, T.; Mpati, S.; Bopape, M.J.; Engelbrecht, F.; Chikoore, H. The flow and moisture fluxes associated with ridging South Atlantic Ocean anticyclones during the subtropical southern African summer. Int. J. Climatol. 2021, 41, E1000–E1017. [Google Scholar] [CrossRef]
- Singleton, A.; Reason, C. Variability in the characteristics of cut-off low pressure systems over subtropical southern Africa. Int. J. Climatol. A J. R. Meteorol. Soc. 2007, 27, 295–310. [Google Scholar] [CrossRef]
- Favre, A.; Hewitson, B.; Lennard, C.; Cerezo-Mota, R.; Tadross, M. Cut-off lows in the South Africa region and their contribution to precipitation. Clim. Dyn. 2013, 41, 2331–2351. [Google Scholar] [CrossRef]
- Engelbrecht, C.J.; Landman, W.A.; Engelbrecht, F.A.; Malherbe, J. A synoptic decomposition of rainfall over the Cape south coast of South Africa. Clim. Dyn. 2015, 44, 2589–2607. [Google Scholar] [CrossRef]
- Dube, K.; Nhamo, G.; Chikodzi, D. Flooding trends and their impacts on coastal communities of Western Cape Province, South Africa. GeoJournal 2021, 87, 453–468. [Google Scholar] [CrossRef] [PubMed]
- World Meteorological Organization. State of the Climate in Africa 2019; WMO: Geneva, Switzerland, 2020; p. 33. [Google Scholar]
- World Meteorological Organization. State of the Climate in Africa 2020; WMO: Geneva, Switzerland, 2021; p. 39. [Google Scholar]
- World Meteorological Organization. State of the Climate in Africa 2021; WMO: Geneva, Switzerland, 2022; p. 48. [Google Scholar]
- UN News. UN Weather Agency to Spearhead 5 year Early Warning Plan, Boosting Climate Action; United Nation: San Francisco, CA, USA, 2022. [Google Scholar]
- Shilenje, Z.W.; Ogwang, B.A. The role of Kenya meteorological service in weather early warning in Kenya. Int. J. Atmos. Sci. 2015, 2015, 302076. [Google Scholar] [CrossRef]
- Landman, S.; Engelbrecht, F.A.; Engelbrecht, C.J. A short-range weather prediction system for South Africa based on a multi-model approach. Water SA 2012, 38, 765–774. [Google Scholar] [CrossRef][Green Version]
- Bopape, M.J.M.; Sebego, E.; Ndarana, T.; Maseko, B.; Netshilema, M.; Gijben, M.; Landman, S.; Phaduli, E.; Rambuwani, G.; Van Hemert, L.; et al. Evaluating South African weather service information on idai tropical cyclone and KwaZulu-natal flood events. S. Afr. J. Sci. 2021, 117, 1–13. [Google Scholar] [CrossRef]
- Dyson, L.; Van Heerden, J. The heavy rainfall and floods over the northeastern interior of South Africa during February 2000. S. Afr. J. Sci. 2001, 97, 80–86. [Google Scholar]
- Riphagen, H.; Bruyère, C.; Jordaan, W.; Poolman, E.; Gertenbach, J. Experiments with the NCEP regional Eta Model at the South African Weather Bureau, with emphasis on terrain representation and its effect on precipitation predictions. Mon. Weather Rev. 2002, 130, 1246–1263. [Google Scholar] [CrossRef]
- Bopape, M.J.M.; Sithole, H.M.; Motshegwa, T.; Rakate, E.; Engelbrecht, F.; Archer, E.; Morgan, A.; Ndimeni, L.; Botai, J. A regional project in support of the SADC cyber-infrastructure framework implementation: Weather and climate. Data Sci. J. 2019, 18, 34. [Google Scholar] [CrossRef]
- Meque, A.; Gamedze, S.; Moitlhobogi, T.; Booneeady, P.; Samuel, S.; Mpalang, L. Numerical weather prediction and climate modelling: Challenges and opportunities for improving climate services delivery in Southern Africa. Clim. Serv. 2021, 23, 100243. [Google Scholar] [CrossRef]
- Mulovhedzi, P.T.; Rambuwani, G.T.; Bopape, M.J.; Maisha, R.; Monama, N. Model inter-comparison for short-range forecasts over the southern African domain. S. Afr. J. Sci. 2021, 117, 1–12. [Google Scholar] [CrossRef]
- Melvin, T.; Mullerworth, S.; Ford, R.; Maynard, C.; Hobson, M. LFRic: Building a new Unified Model. Egu Gen. Assem. Conf. Abstr. 2017, 19, 13021. [Google Scholar]
- De Lucia, C.; Bucchignani, E.; Mastellone, A.; Adinolfi, M.; Montesarchio, M.; Cinquegrana, D.; Mercogliano, P.; Schiano, P. A Sensitivity Study on High Resolution NWP ICON—LAM Model over Italy. Atmosphere 2022, 13, 540. [Google Scholar] [CrossRef]
- Mcgregor, J.L.; Dix, M.R. The CSIRO conformal-cubic atmospheric GCM. In IUTAM Symposium on Advances in Mathematical Modelling of Atmosphere and Ocean Dynamics; Springer: Dordrecht, The Netherlands, 2001; pp. 197–202. [Google Scholar]
- Engelbrecht, F.; McGregor, J.; Engelbrecht, C. Dynamics of the Conformal-Cubic Atmospheric Model projected climate-change signal over southern Africa. Int. J. Climatol. A J. R. Meteorol. Soc. 2009, 29, 1013–1033. [Google Scholar] [CrossRef]
- Garland, R.M.; Matooane, M.; Engelbrecht, F.A.; Bopape, M.J.M.; Landman, W.A.; Naidoo, M.; Van der Merwe, J.; Wright, C.Y. Regional projections of extreme apparent temperature days in Africa and the related potential risk to human health. Int. J. Environ. Res. Public Health 2015, 12, 12577–12604. [Google Scholar] [CrossRef] [PubMed]
- Thatcher, M.; McGregor, J.L. Using a scale-selective filter for dynamical downscaling with the conformal cubic atmospheric model. Mon. Weather Rev. 2009, 137, 1742–1752. [Google Scholar] [CrossRef]
- Engelbrecht, F.; Landman, W.A.; Engelbrecht, C.; Landman, S.; Bopape, M.; Roux, B.; McGregor, J.; Thatcher, M. Multi-scale climate modelling over Southern Africa using a variable-resolution global model. Water SA 2011, 37, 647–658. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef]
- Huang, J.; Thatcher, M. Assessing the value of simulated regional weather variability in solar forecasting using numerical weather prediction. Sol. Energy 2017, 144, 529–539. [Google Scholar] [CrossRef]
- McGregor, J.L.; Dix, M.R. An updated description of the conformal-cubic atmospheric model. In High Resolution Numerical Modelling of the Atmosphere and Ocean; Springer Science & Business Media: New York, NY, USA, 2008; pp. 51–75. [Google Scholar]
- Rotstayn, L.D. A physically based scheme for the treatment of stratiform clouds and precipitation in large-scale models. I: Description and evaluation of the microphysical processes. Q. J. R. Meteorol. Soc. 1997, 123, 1227–1282. [Google Scholar]
- Lin, Y.L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Appl. Meteorol. Climatol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Freidenreich, S.; Ramaswamy, V. A new multiple-band solar radiative parameterization for general circulation models. J. Geophys. Res. Atmos. 1999, 104, 31389–31409. [Google Scholar] [CrossRef]
- Schwarzkopf, M.D.; Ramaswamy, V. Radiative effects of CH4, N2O, halocarbons and the foreign-broadened H2O continuum: A GCM experiment. J. Geophys. Res. Atmos. 1999, 104, 9467–9488. [Google Scholar] [CrossRef]
- Hurley, P. Modelling mean and turbulence fields in the dry convective boundary layer with the eddy-diffusivity/mass-flux approach. Bound.-Layer Meteorol. 2007, 125, 525–536. [Google Scholar] [CrossRef]
- Weisman, M.; Skamarock, W.; Klemp, J. The Resolution Dependence of Explicitly Modeled Convective Systems. Mon. Weather Rev. 1997, 125, 527–548. [Google Scholar] [CrossRef]
- Roberts, N. Assessing the spatial and temporal variation in the skill of precipitation forecasts from an NWP model. Meteorol. Appl. 2008, 15, 163–169. [Google Scholar] [CrossRef]
- Bryan, G.; Wyngaard, J.; Fritsch, J. Resolution Requirements for the Simulation of Deep Moist Convection. Mon. Weather Rev. 2003, 131, 2394. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain-Fritsch convective parameterization: An update. J. Clim. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Zheng, Y.; Alpaty, K.; Herwehe, J.A.; Del Genio, A.D.; Niyogi, D. Improving high-resolution weather forecasts using the Weather Research and Forecasting (WRF) model with an updated Kain-Fritsch scheme. Mon. Weather Rev. 2016, 144, 833–860. [Google Scholar] [CrossRef]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- McGregor, J. A new convection scheme using a simple closure. In Current Issues in the Parameterization of Convection: Extended Abstracts of Presentations at the Fifteenth Annual BMRC Modelling Workshop; Meighen, P.J., Hollis, A.J., Eds.; Bureau of Meteorology Research Centre: Melbourne, VIC, Australia, 2003; pp. 33–36. [Google Scholar]
- Sela, J.G. Implementation of the sigma pressure hybrid coordinate into GFS. NCEP Off. Note 2009, 461, 1–25. [Google Scholar]
- Steeneveld, G.J.; Peerlings, E. Mesoscale Model Simulation of a Severe Summer Thunderstorm in The Netherlands: Performance and Uncertainty Assessment for Parameterised and Resolved Convection. Atmosphere 2020, 11, 811. [Google Scholar] [CrossRef]
- Champion, A.; Hodges, K. Importance of resolution and model configuration when downscaling extreme precipitation. Tellus A 2014, 66, 23993. [Google Scholar] [CrossRef][Green Version]
- Hersbach, H.; Dee, D. ERA5 Reanalysis is in Production; ECMWF: Reading, UK, 2016. [Google Scholar]
- Beusch, L.; Foresti, L.; Gabella, M.; Hamann, U. Satellite-Based Rainfall Retrieval: From Generalized Linear Models to Artificial Neural Networks. Remote Sens. 2018, 10, 939. [Google Scholar] [CrossRef]
- Moses, O.; Ramotonto, S. Assessing forecasting models on prediction of the tropical cyclone Dineo and the associated rainfall over Botswana. Weather Clim. Extrem. 2018, 21, 102–109. [Google Scholar] [CrossRef]
- Mhlanga, C.; Muzingili, T.; Mpambela, M. Natural disasters in Zimbabwe: The primer for social work intervention. Afr. J. Soc. Work 2019, 9, 46–54. [Google Scholar]
- South African Weather Service. Synoptic Weather Map for 16 February 2017. Available online: https://www.weathersa.co.za/Documents/Publications/20170216.pdf (accessed on 1 June 2022).
- Meyiwa, S. Numerical Modelling of Tropical Cyclone Dineo and Its Rainfall Impacts over North-Eastern South Africa. Master’s Thesis, Faculty of Science, University of Cape Town, Cape Town, South Africa, 2019. [Google Scholar]
- South African Weather Service. Synoptic Weather Map for 12 November 2019. Available online: https://www.weathersa.co.za/Documents/Publications/20191112.pdf (accessed on 1 June 2022).
- Mahomed, M. Detection and Early Warning of Lightning and Extreme Storm Events in KwaZulu-Natal, South Africa. Ph.D. Thesis, School of Agricultural, Earth and Environmental Sciences, Pietermaritzburg, South Africa, 2020. [Google Scholar]
- Njilo, N. Roads Flooded as Afternoon Storms Hit Joburg. Available online: https://www.timeslive.co.za/news/south-africa/2020-10-05-roads-flooded-as-afternoon-storms-hit-joburg/ (accessed on 1 June 2022).
- South African Weather Service. Synoptic Weather Map for 5 October 2020. Available online: https://www.weathersa.co.za/Documents/Publications/20201005.pdf (accessed on 1 June 2022).
- Peixoto, J.; Oort, A.H. The climatology of relative humidity in the atmosphere. J. Clim. 1996, 9, 3443–3463. [Google Scholar] [CrossRef]
- South African Weather Service. Synoptic Weather Map for 9 October 2017. Available online: https://www.weathersa.co.za/Documents/Publications/20171009.pdf (accessed on 1 June 2022).
- South African Weather Service. Synoptic Weather Map on 22 April 2022. Available online: https://www.weathersa.co.za/Documents/Publications/20220422.pdf (accessed on 1 June 2022).
- Muofhe, T.P.; Chikoore, H.; Bopape, M.J.M.; Nethengwe, N.S.; Ndarana, T.; Rambuwani, G.T. Forecasting intense cut-off lows in South Africa using the 4.4 km Unified Model. Climate 2020, 8, 129. [Google Scholar] [CrossRef]
- South African Weather Service. Synoptic Weather Map for 7 June 2017. Available online: https://www.weathersa.co.za/Documents/Publications/20170607.pdf (accessed on 1 June 2022).
- Barnes, M.A.; Turner, K.; Ndarana, T.; Landman, W.A. Cape storm: A dynamical study of a cut-off low and its impact on South Africa. Atmos. Res. 2021, 249, 105290. [Google Scholar] [CrossRef]
- Mugume, I.; Basalirwa, C.; Waiswa, D.; Nsabagwa, M.; Ngailo, T.J.; Reuder, J.; Ulrich, S.; Semujju, M. A comparative analysis of the performance of COSMO and WRF models in quantitative rainfall prediction. Int. J. Mar. Environ. Sci. 2018, 12, 130–138. [Google Scholar]
- Lean, H.W.; Clark, P.A.; Dixon, M.; Roberts, N.M.; Fitch, A.; Forbes, R.; Halliwell, C. Characteristics of High-Resolution Versions of the Met Office Unified Model for Forecasting Convection over the United Kingdom. Mon. Weather Rev. 2008, 136, 3408–3424. [Google Scholar] [CrossRef]
- Stensrud, D. Parametrization schemes. Keys to understanding numerical weather prediction models, Reprint of the 2007 hardback ed.; In Parameterization Schemes: Keys to Understanding Numerical Weather Prediction Models, Cambridge University Press: Cambridge, UK, 2007; p. 480. [Google Scholar] [CrossRef]
- Keat, W.J.; Stein, T.H.; Phaduli, E.; Landman, S.; Becker, E.; Bopape, M.J.M.; Hanley, K.E.; Lean, H.W.; Webster, S. Convective initiation and storm life cycles in convection-permitting simulations of the Met Office Unified Model over South Africa. Q. J. R. Meteorol. Soc. 2019, 145, 1323–1336. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).