Physical and Chemical Characteristics of Dew and Rain in North-West Africa with Focus on Morocco: Mapping Past and Future Evolution (2005–2100)
Abstract
1. Introduction
2. Meteorological Data and Methods
2.1. Studied Area
2.2. Data Extraction
2.2.1. Measured Data (Years 2005–2020)
2.2.2. Climate Model Data CNRM-CM5/ALADIN63 (Years 2006–2100)
2.3. Dew Yield Estimation
2.4. Kriging Maps
2.5. Monthly Evapotranspiration
3. Results and Discussion
3.1. Past Evolution (2005–2020)
3.1.1. Dew Yield
3.1.2. Comparison with Direct Dew Yield Measurements
3.1.3. Rain
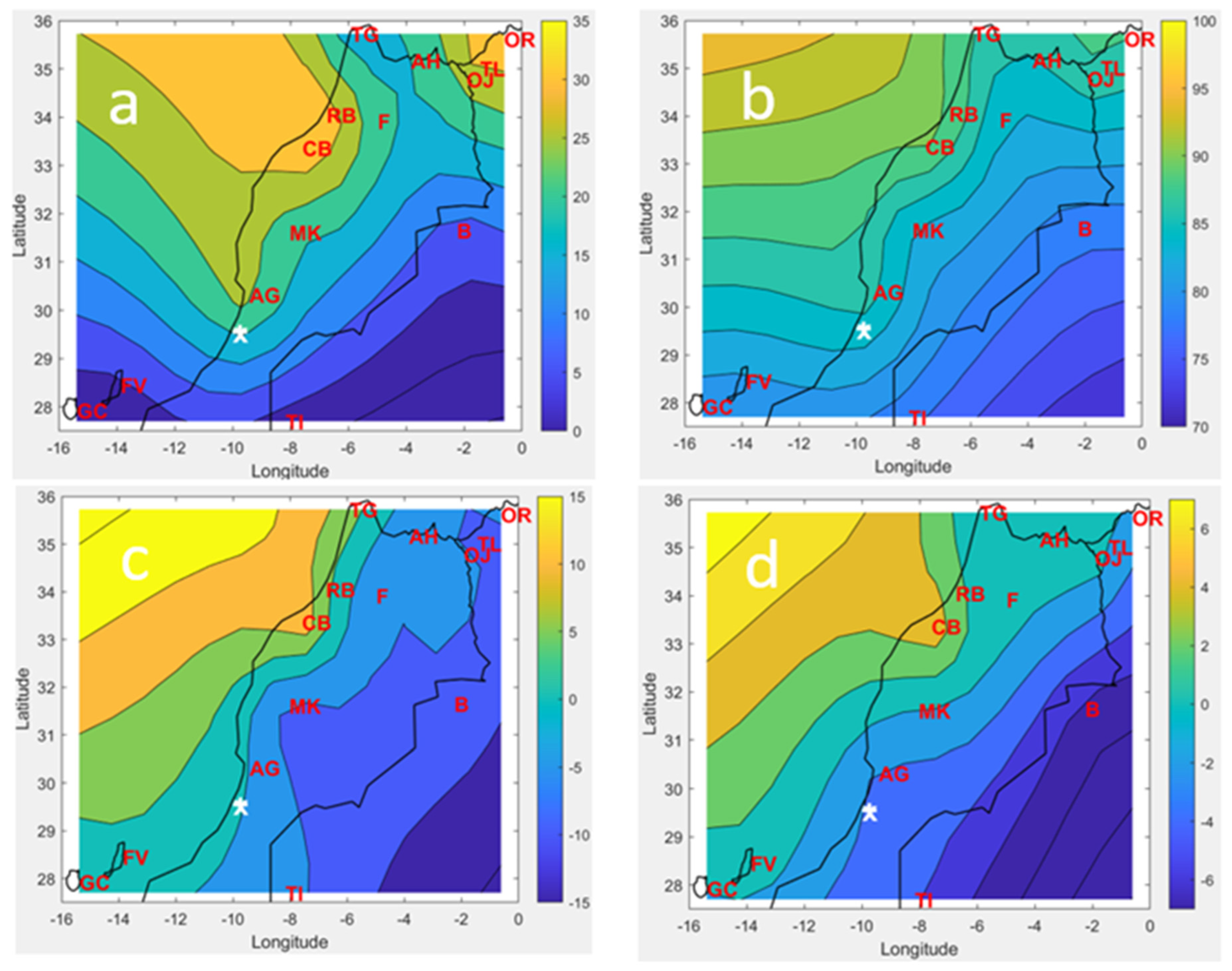
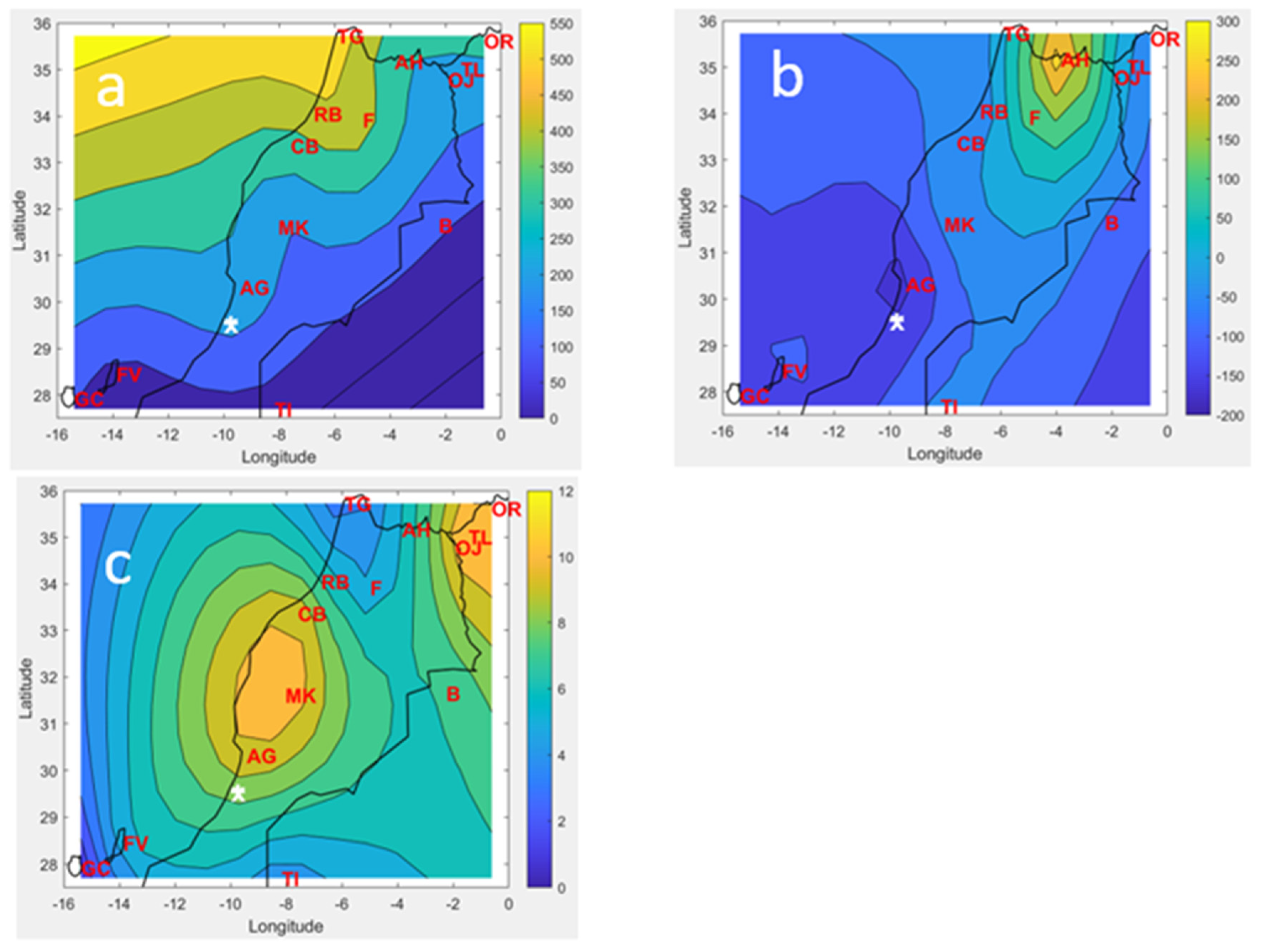
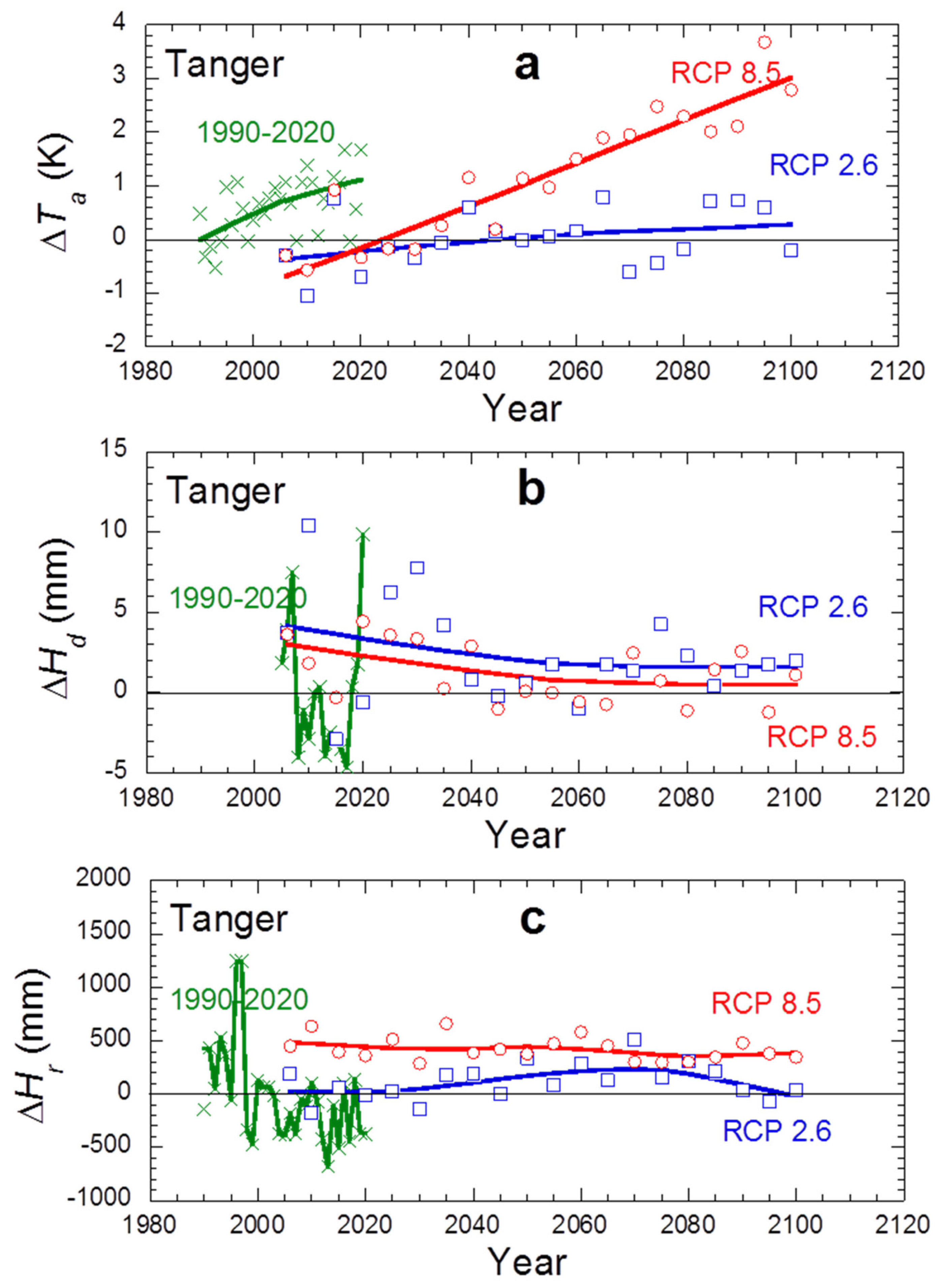
3.2. Projected Climate Evolution 2020–2100
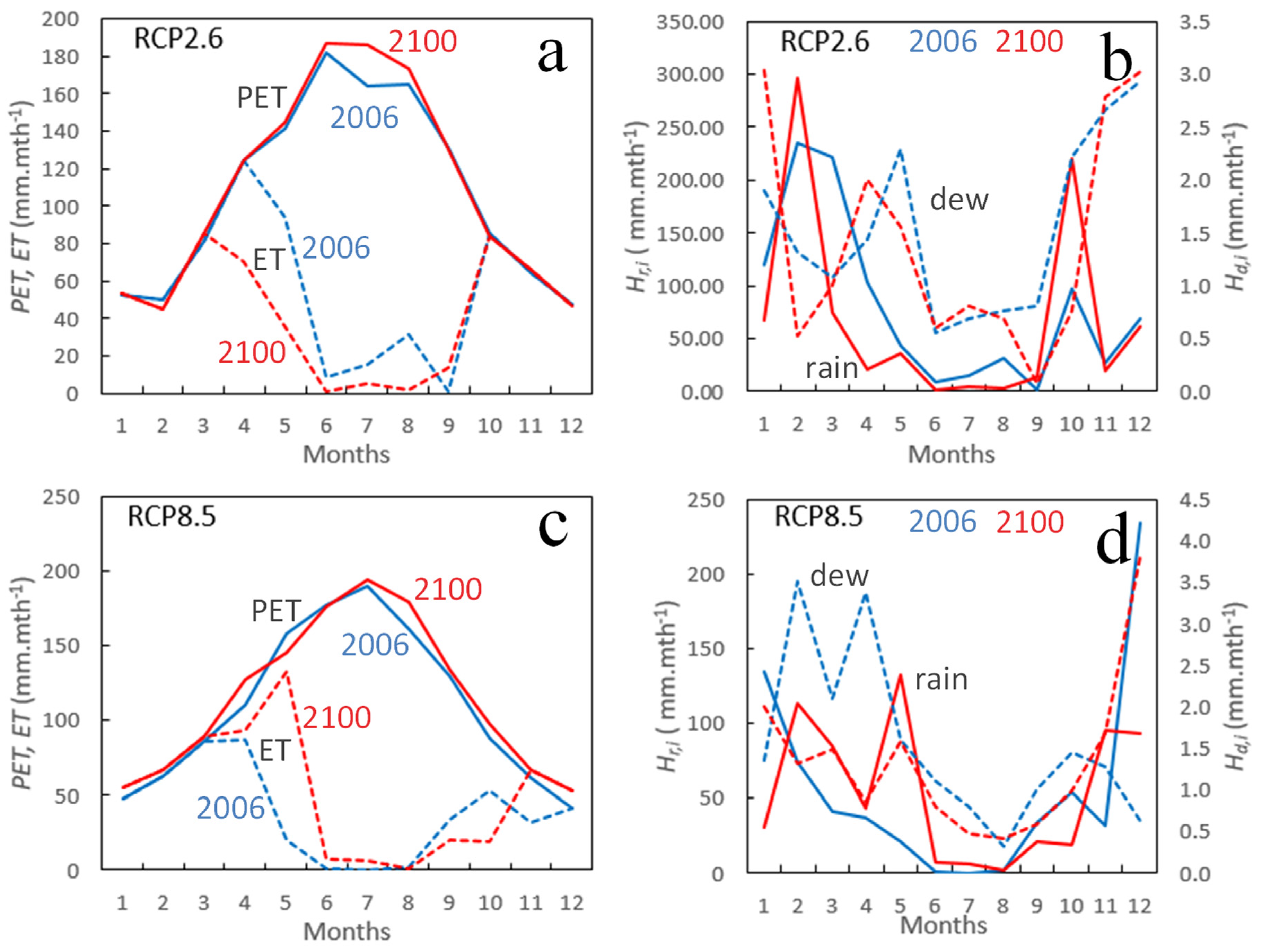
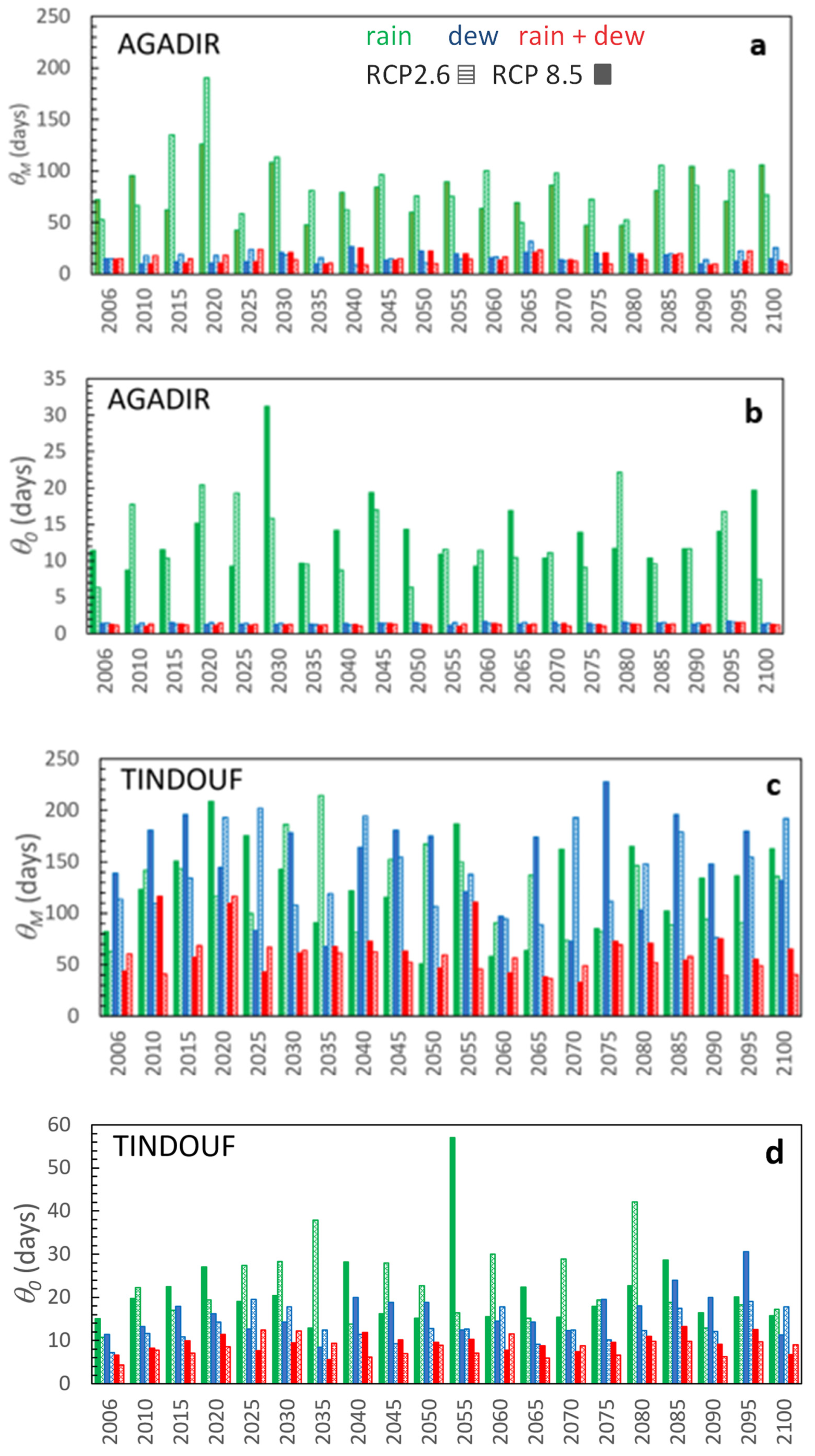
3.2.1. Typical Tendencies
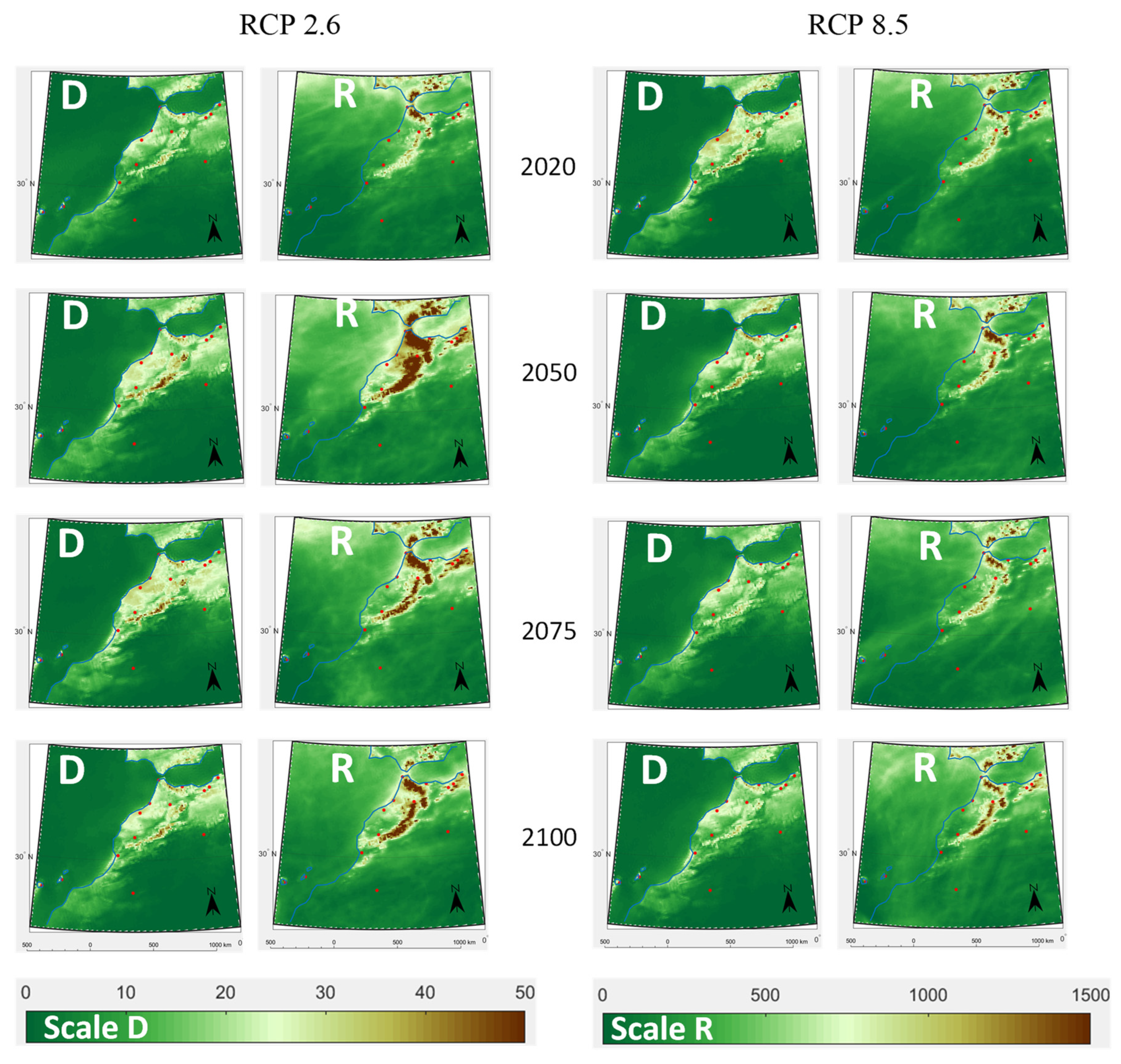
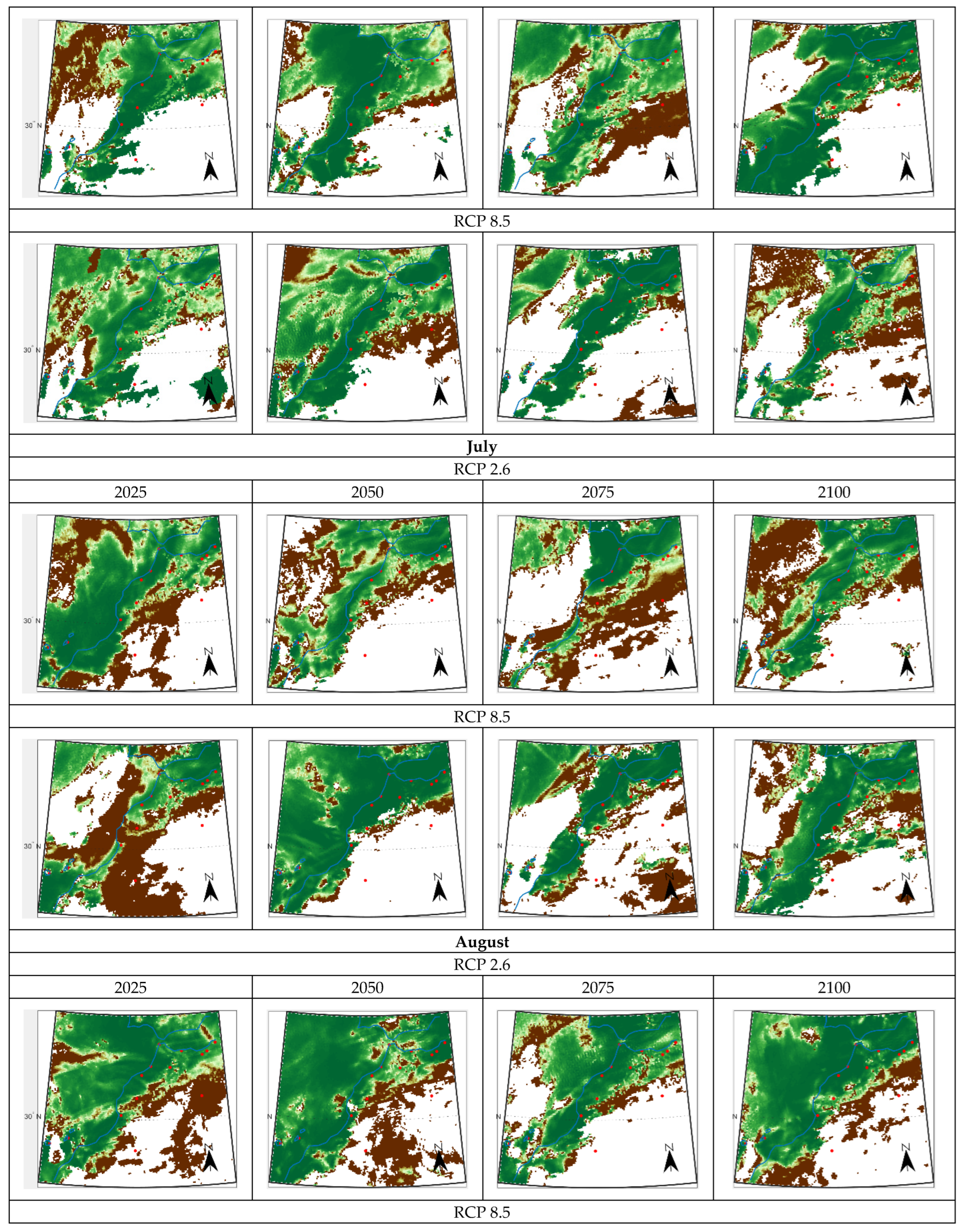
3.2.2. Dew and Rain Maps Evolution
3.3. Correlation between Dew and Rain Amounts
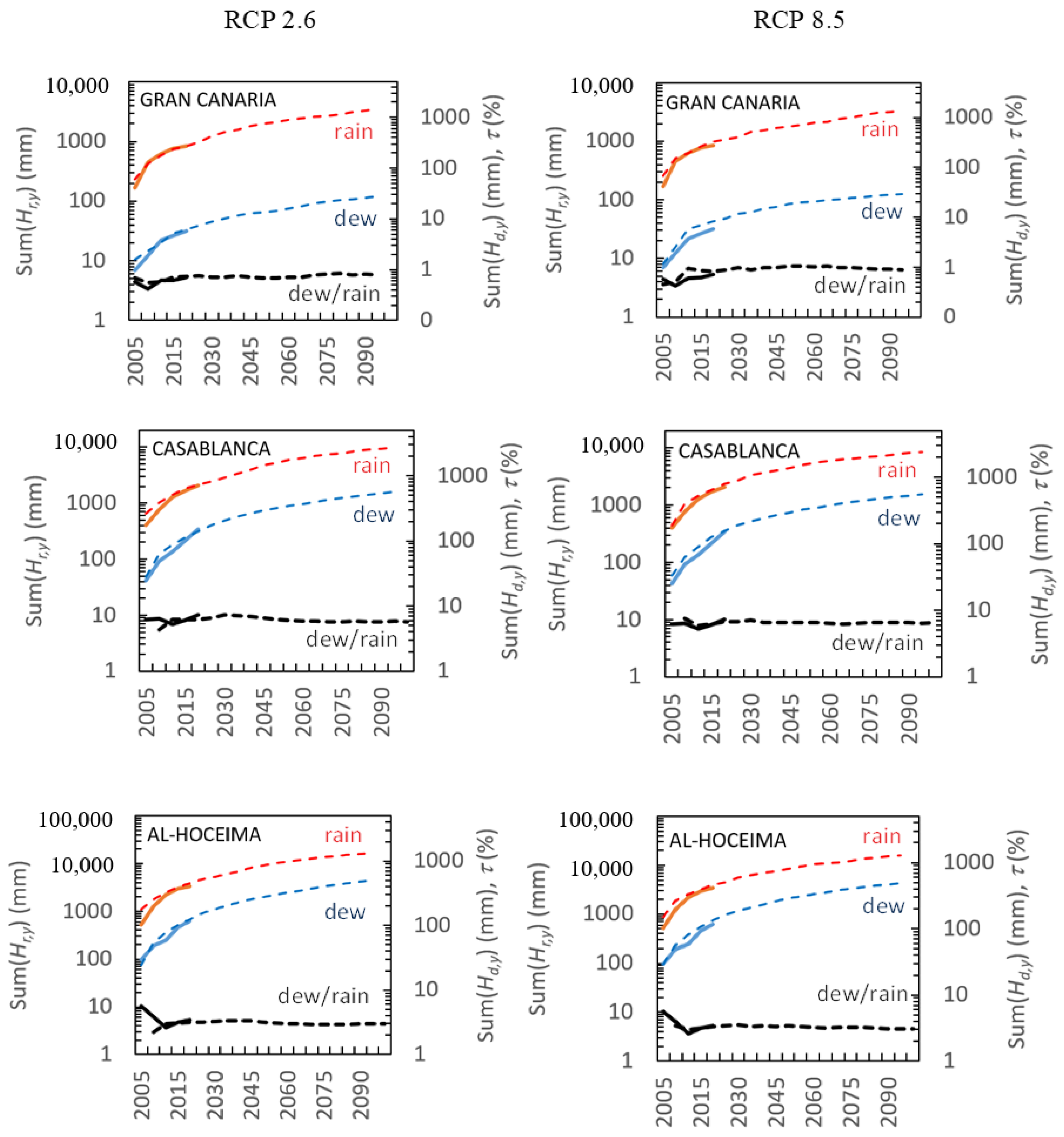
3.3.1. Cumulated Dew and Rain Yields
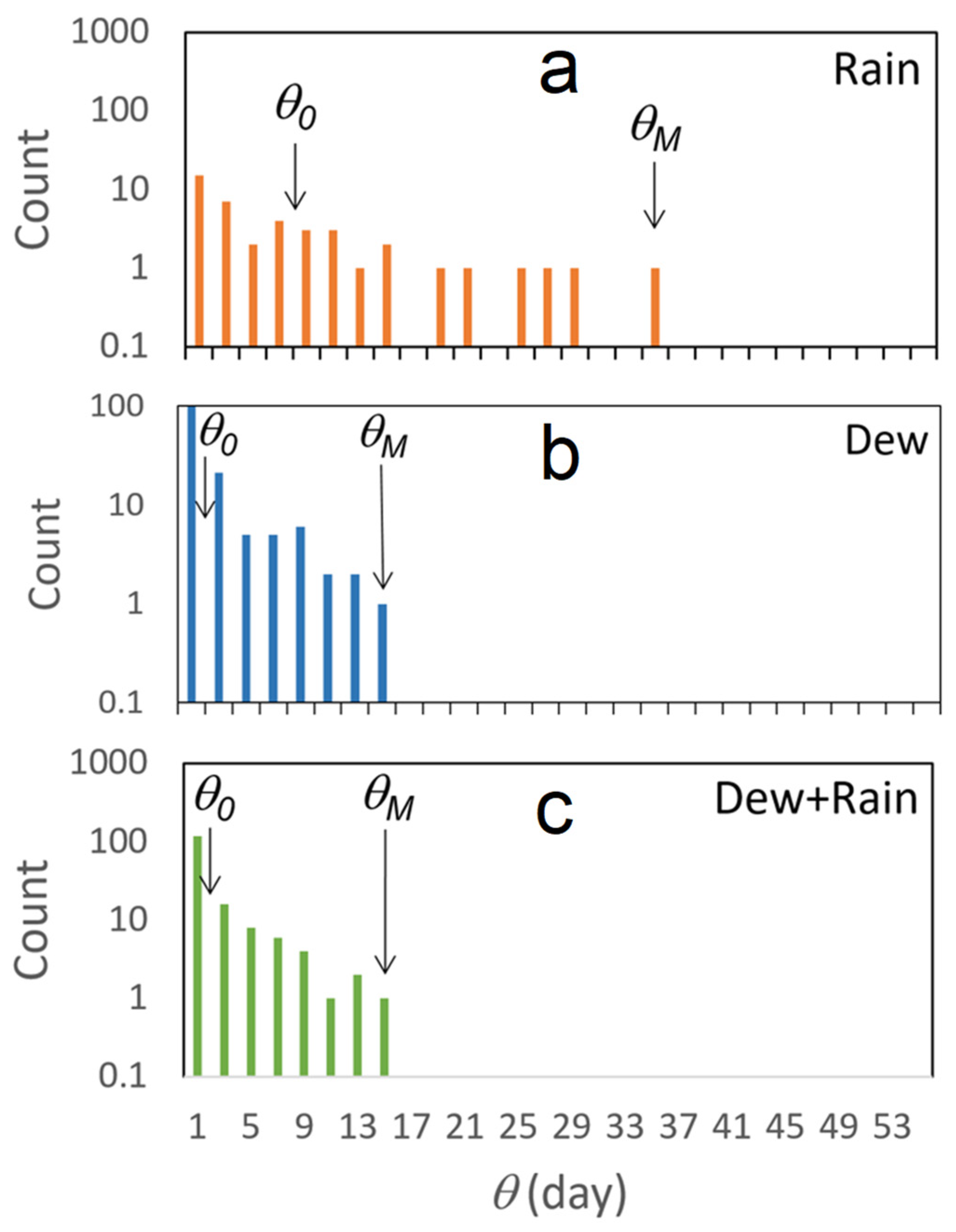
3.3.2. Dew and Rain Events Periods
3.3.3. Potential (PET) and Real (ET) Evapotranspirations
3.4. Chemical Composition
3.4.1. Previous Studies
3.4.2. Chemical Composition: A New Approach
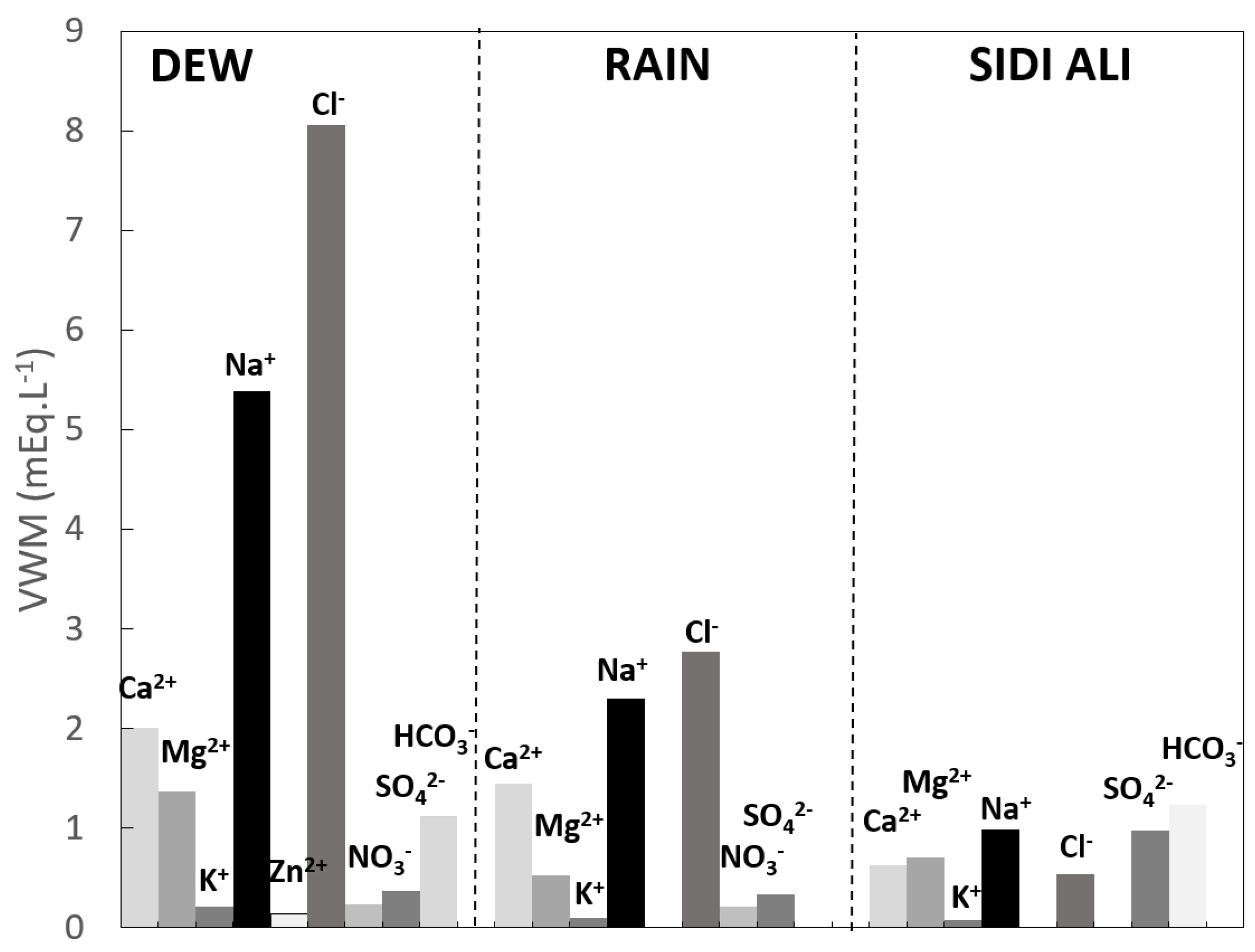
3.4.2.1. Dew, Rain and Spring Water Ionic Concentrations
3.4.2.2. Effect of Water Volume
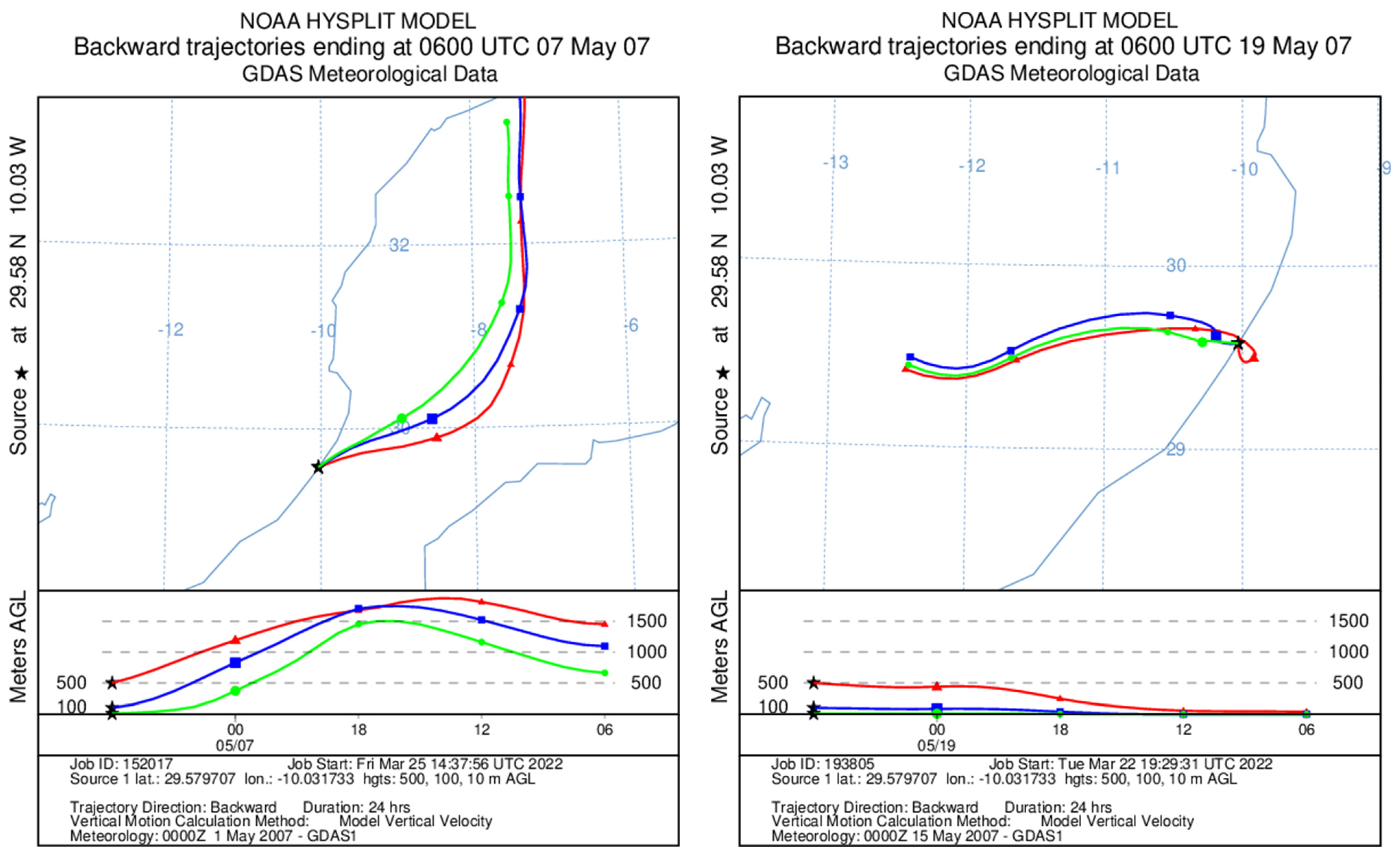
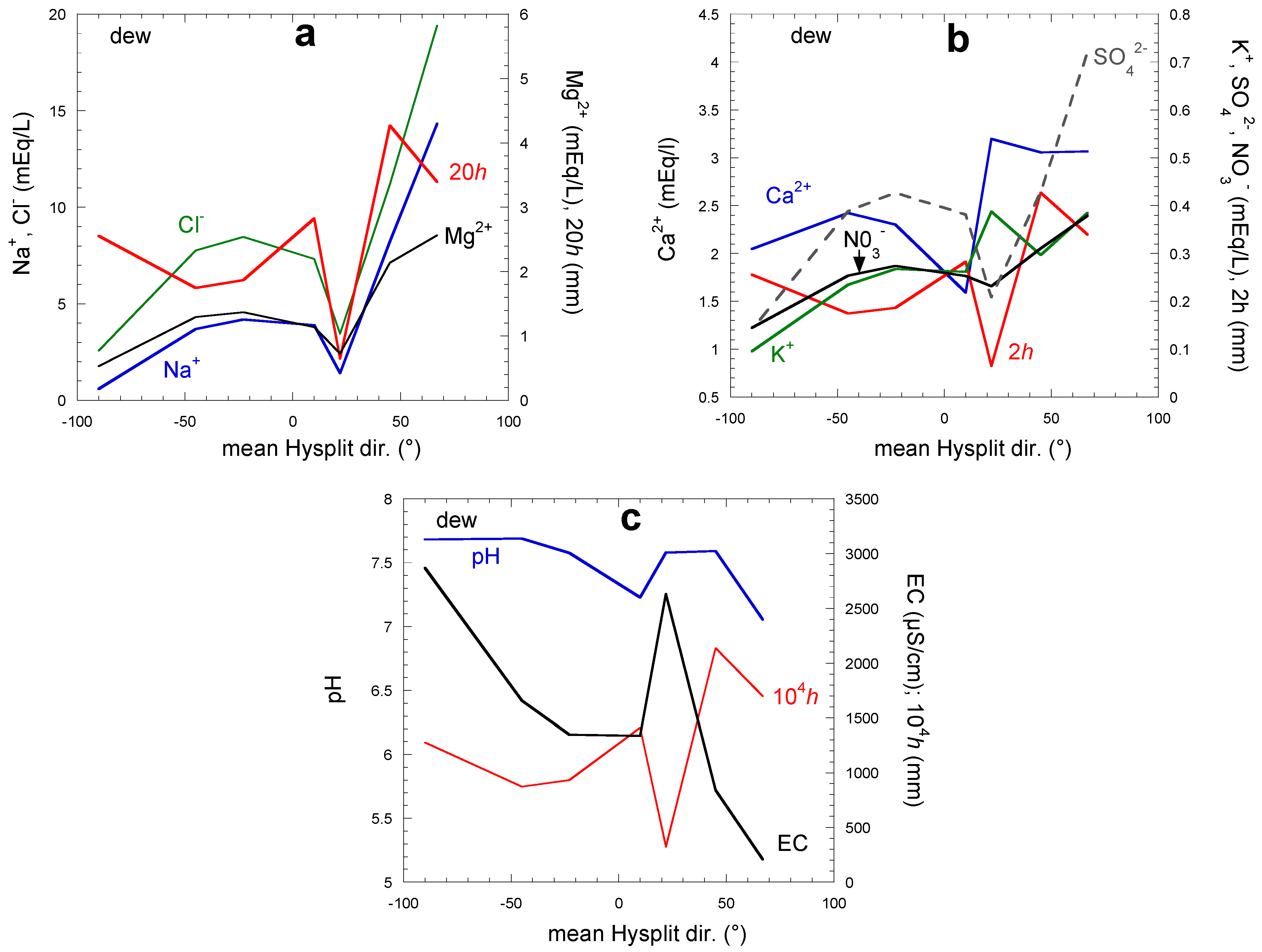
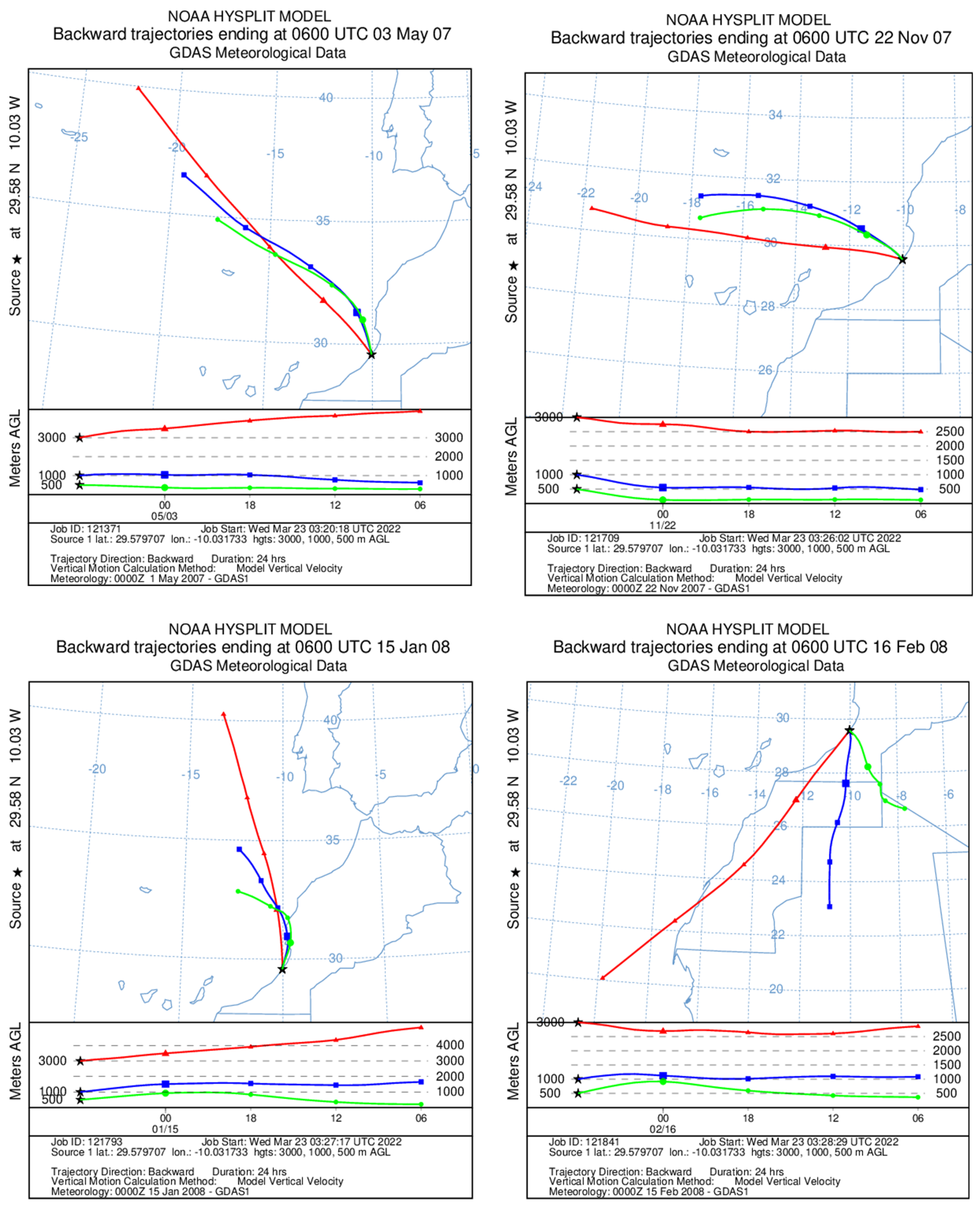
3.4.2.3. Dew Air Flux Backward Trajectories
3.4.2.4. Dew Seasonal Variations
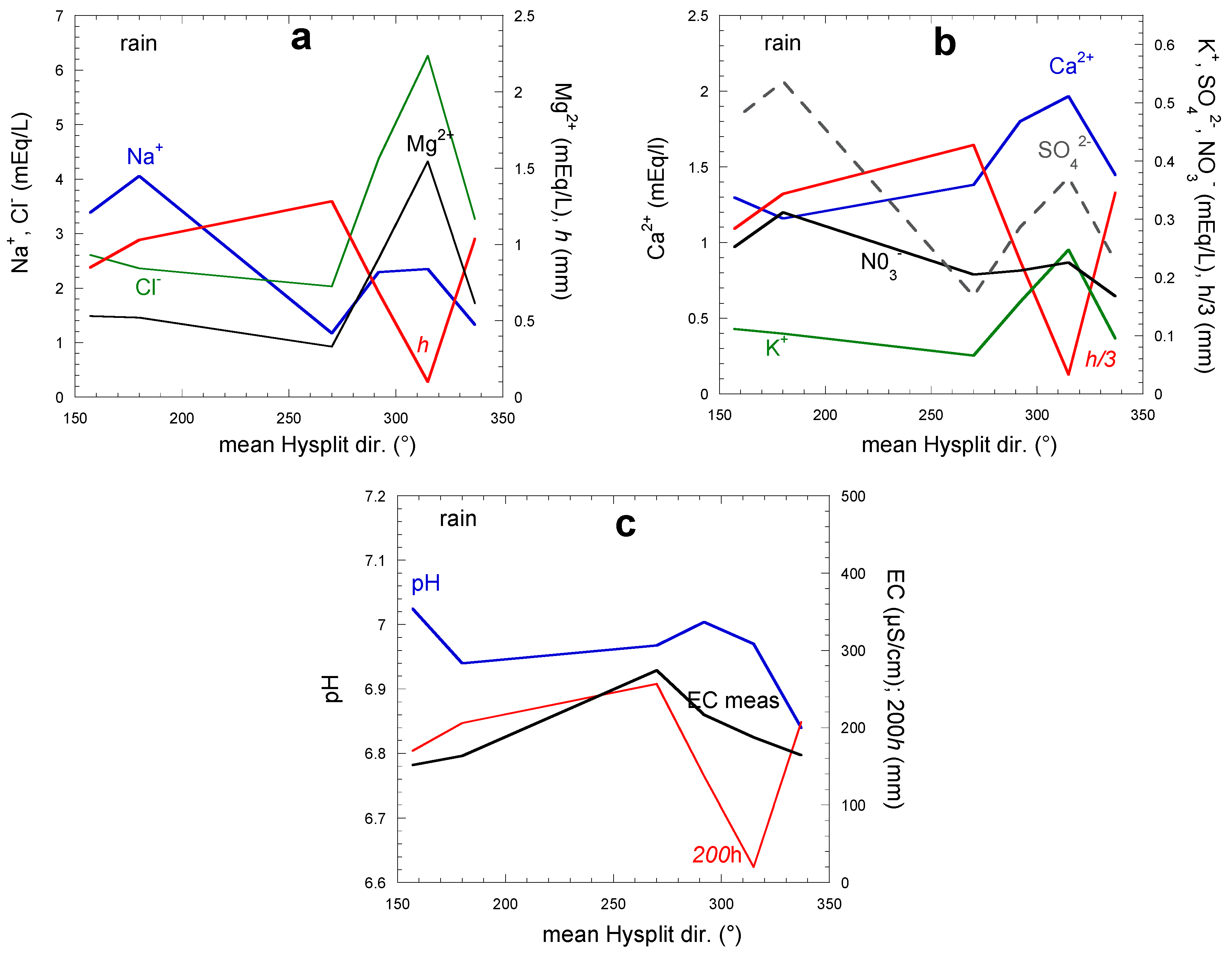
3.4.2.5. Rain Air Flux Backward Trajectories
3.4.2.6. Rain Seasonal Variations and Volume Dependence
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Kriging Method
References
- Tramblay, Y.; Badi, W.; Driouech, F.; El Adouni, S.; Neppel, L.; Servat, E. Climate change impacts on extreme precipitation in Morocco. Glob. Plan. Chang. 2012, 82–83, 104–114. [Google Scholar] [CrossRef]
- Schilling, J.; Hertig, E.; Tramblay, Y.; Scheffran, J. Climate change vulnerability, water resources and social implications in North Africa. Reg. Environ. Chang. 2020, 20, 15. [Google Scholar] [CrossRef]
- Schilling, J.; Freier, K.P.; Hertig, E.; Scheffran, J. Climate change, vulnerability and adaptation in North Africa with focus on Morocco. Agric. Ecosys. Environ. 2012, 156, 12–26. [Google Scholar] [CrossRef]
- Terink, W.; Immerzeel, W.W.; Droogers, P. Climate change projections of precipitation and reference evapotranspiration for the Middle East and Northern Africa until 2050. Int. J. Clim. 2013, 33, 3055–3072. [Google Scholar] [CrossRef]
- Tahiri, A.; Amraoui, F.; Sinan, M.; Bouchaou, L.; Berrada, F.; Benjmel, K. Influence of climate variability on water resource availability in the upper basin of Oum-Er-Rabiaa, Morocco. Groundw. Sustain. Dev. 2022, 19, 100814. [Google Scholar] [CrossRef]
- Chergui, B.; Fahd, S.; Santos, X.; Pausas, J.G. Socioeconomic factors drive fire-regime variability in the Mediterranean basin. Ecosystems 2018, 21, 619–628. [Google Scholar] [CrossRef]
- Choukri, F.; Raclot, D.; Naimi, M.; Chikhaoui, M.; Nunes, J.P.; Huard, F.; Hérivaux, C.; Sabir, M.; Pépin, Y. Distinct and combined impacts of climate and land use scenarios on water availability and sediment loads for a water supply reservoir in northern Morocco. Int. Soil Water Conserv. Res. 2020, 8, 141–153. [Google Scholar] [CrossRef]
- Seif-Ennasr, M.; Zaaboul, R.; Hirich, A.; Caroletti, G.N.; Bouchaou, L.; Beraaouz, E.H.; McDonnell, A.; Choukr-Allah, R. Climate change and adaptive water management measures in Chtouka Aït Baha region (Morocco). Sci. Total Environ. 2016, 573, 862–875. [Google Scholar] [CrossRef]
- Lefebvre, G.; Redmond, L.; Germain, C.; Palazzi, E.; Terzago, S.; Willm, L.; Poulin, B. Predicting the vulnerability of seasonally-flooded wetlands to climate change across the Mediterranean Basin. Sci. Total Environ. 2019, 692, 546–555. [Google Scholar] [CrossRef]
- Tramblay, Y.; Koutroulis, A.; Samaniego, L.; Vicente-Serranod, S.M.; Volaire, F.; Boone, A.; Le Page, M.; Llasat, M.C.; Albergel, C.; Burak, S.; et al. Challenges for drought assessment in the Mediterranean region under future climate scenarios. Earth-Sci. Rev. 2020, 210, 103348. [Google Scholar] [CrossRef]
- Marras, P.A.; Lima, D.C.A.; Soares, P.M.M.; Cardoso, R.M.; Medas, D.; Dore, E.; De Giudici, G. Future precipitation in a Mediterranean island and streamflow changes for a small basin using EURO-CORDEX regional climate simulations and the SWAT model. J. Hydrol. 2021, 603, 127025. [Google Scholar] [CrossRef]
- Grillakis, M.G. Increase in severe and extreme soil moisture droughts for Europe under climate change. Sci. Total Environ. 2019, 660, 1245–1255. [Google Scholar] [CrossRef]
- Carvalho, M.J.; Melo-Gonçalves, P.; Teixeira, J.C.; Rocha, A. Regionalization of Europe based on a K-Means Cluster Analysis of the climate change of temperatures and precipitation. Phys. Chem. Earth 2016, 94, 22–28. [Google Scholar] [CrossRef]
- Harbouze, R.; Pellissier, J.-P.; Rolland, J.-P.; Khechimi, W. Rapport de synthèse sur l’agriculture au Maroc; CIHEAM-IAMM: Montpellier, France, 2019; 104p. [Google Scholar]
- Werz, M.; Conley, L. Climate Change, Migration, and Conflict in Northwest Africa. Rising Dangers and Policy Options ACROSS the Arc of Tension; Report 2012; Heinrich Boll Stiftung, Center for Amirican Progress: Brussels, Belgium, 2012; p. 84. [Google Scholar]
- Desmidt, S. Climate change and security in North Africa. Focus on Algeria, Morocco and Tunisia. Cascades 2021, 1–44. [Google Scholar]
- Beysens, D. Dew Water; River Publishers: Gistrup, Denmark, 2018; p. 200. [Google Scholar]
- Lekouch, I.; Lekouch, K.; Muselli, M.; Mongruel, A.; Kabbachi, B.; Beysens, D. Rooftop dew, fog and rain collection in southwest Morocco and predictive dew modeling using neural networks. J. Hydrol. 2012, 448–449, 60–72. [Google Scholar] [CrossRef]
- Beysens, D. Estimating dew yield worldwide from a few meteo data. Atmos. Res. 2016, 167, 146–155. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; Van Vuuren, D.P.; Kram, T. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, B.C.; Carter, T.R.; Ebi, K.; Harrison, P.A.; Kemp-Benedict, E.; Kok, K.; Kriegler, E.; Preston, B.L.; Riahi, K.; Sillmann, J.; et al. Achievements and needs for the climate change scenario framework. Nat. Clim. Chang. 2020, 10, 1074–1084. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- ECMWF. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/projections-cordex-domains-single-levels?tab=overview (accessed on 1 March 2021).
- Lekouch, I.; Muselli, M.; Kabbachi, B.; Ouazzani, J.; Melnytchouk-milimouk, I.; Beysens, D. Dew, fog, and rain as supplementary sources of water in south-western Morocco. Energy 2011, 36, 2257–2265. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Zeroual, A.; Assani, A.; Meddi, M.; Alkama, R. Assessment of climate change in Algeria from 1951 to 2098 using the Köppen–Geiger climate classification schem. Clim. Dyn. 2019, 52, 227–243. [Google Scholar] [CrossRef]
- Arya, P.S. Introduction to Micrometeorology; Acadamic Press: San Diego, CA, USA, 2001; p. 420. [Google Scholar]
- Weather Underground Database. Available online: https://www.wunderground.com (accessed on 13 February 2021).
- NOAA. Available online: https://www.forecast.weather.gov (accessed on 13 February 2021).
- Muselli, M.; Clus, O.; Ortega, P.; Milimouk, I.; Beysens, D. Physical, chemical and biological characteristics of dew and rain water during the dry oceans on of tropical islands. Atmos 2020, 12, 69. [Google Scholar] [CrossRef]
- Météociel Database. Available online: https://www.meteociel.fr (accessed on 13 February 2021).
- Trosseille, J.; Mongruel, A.; Royon, L.; Beysens, D. Effective surface emissivity during dew water condensation. Int. J. Heat Mass Transf. 2022, 183, 122078. [Google Scholar] [CrossRef]
- Tomaszkiewicz, M.; Najm, A.; Beysens, D.; Alameddine, I.; Zeid, E.B.; El-Fadel, M. Projected climate change impacts upon dew yield in the Mediterranean basin. Sci. Total. Environ. 2016, 566–567, 1339–1348. [Google Scholar] [CrossRef]
- Martinez, W.A.; Melo, C.E.; Melo, O.O. Median Polish Kriging for space–time analysis of precipitation. Spat. Stat. 2017, 19, 1–20. [Google Scholar] [CrossRef]
- Pue, J.D.; Botula, Y.D.; Nguyen, P.M.; Meirvenne, M.V.; Cornelis, W.M. Introducing a Kriging-based Gaussian Process approach in pedotransfer functions: Evaluation for the prediction of soil water retention with temperate and tropical datasets. J. Hydrol. 2021, 597, 125770. [Google Scholar] [CrossRef]
- Muselli, M.; Beysens, D. Mapping past, present and future dew and rain water resources for biocrust evolution in southern Africa. J. Hydrol. Hydromech. 2021, 69, 400–420. [Google Scholar] [CrossRef]
- Amani, A.; Lebel, T. Lagrangian Kriging for the estimation of Sahelian rainfall at small time steps. J. Hydrol. 1997, 192, 125–157. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Kwon, H.H.; Kim, Y.T. A Bayesian Kriging model applied for spatial downscaling of daily rainfall from GCMs. J. Hydrol. 2021, 597, 126095. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Han, C.; Liu, Z. Evaluation of 18 models for calculating potential evapotranspiration in different climatic zones of China. Agric. Water Manag. 2021, 244, 106545. [Google Scholar] [CrossRef]
- Robineau, T.; Rodler, A.; Morille, B.; Ramier, D.; Sage, J.; Musy, M.; Graffin, V.; Berthier, E. Coupling hydrological and microclimate models to simulate evapotranspiration from urban green areas and air temperature at the district scale. Urban Clim. 2022, 44, 101179. [Google Scholar] [CrossRef]
- El Mansouri, B. Calcul de la réserve utile des sols pour une gestion rationnelle des eaux de l’irrigation. In Proceedings of the Recherche et Développement en Gestion Intégrée des Ressources Hydriques au Sud-Est du Maroc, International Conference, Ouarzazate, Morocco, 1–2 April 2004. [Google Scholar]
- Aoubouazza, M. Influence des propriétés hydrodynamiques du sol sur la sensibilité au dépérissement du cèdre dans le causse moyen-atlasique central marocain. Rev. Mar. Sci. Agron. Vét. 2017, 5, 293–303. [Google Scholar]
- Infoclimat. Available online: https://www.infoclimat.fr/ (accessed on 13 February 2021).
- MarocMétéo, Etat du Climat en 2020. Report of the Equipment, transport, logistic and water Minister. 2021. Available online: https://www.marocmeteo.ma/ (accessed on 1 May 2022). (In French).
- Sebbar, A.; Hsaine, M.; Fougrache, H.; Saloui, A.; Badri, W. Impact du changement climatique sur la région montagneuse du moyen Atlas au Maroc. In Proceedings of the XXXIIIème Colloque de l’Association Internationale de Climatologie, Rennes, France, 1–4 July 2020; pp. 619–624. [Google Scholar]
- Driouech, F. Distribution des Précipitations Hivernales sur le Maroc dans le cadre d’un Changement Climatique: Descente D’échelle et Incertitudes. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, 6 October 2010. [Google Scholar]
- Khomsi, K.; Mahe, G.; Tramblay, Y.; Sinan, M.; Snoussi, M. Trends in rainfall and temperature extremes in Morocco. Nat. Hazards Earth Syst. Sci. Discuss. 2015, 3, 1175–1201. [Google Scholar]
- Agoumi, A.; Debbarh, A. Ressources en eau et bassins versants du Maroc: 50 ans de développement (1955–2005). In 50 ans de Développement Humain et Perspectives 2025: Cadre Naturel, Environnement et Territoires; OIEau Association: Paris, France, 2005; pp. 9–58. [Google Scholar]
- Douville, H.; Ribes, A.; Decharme, B.; Alkama, R.; Sheffield, J. Anthropogenic influence on multidecadal changes in reconstructed global evapotranspiration. Nat. Clim. Chang. 2013, 3, 59–62. [Google Scholar] [CrossRef]
- Bartholomeus, R.P.; Stagge, J.H.; Tallaksen, L.M.; Witte, J.P.M. Sensitivity of potential evaporation estimates to 100 years of climate variability. Hydrol. Earth Syst. Sci. 2015, 19, 997–1014. [Google Scholar] [CrossRef]
- Büdel, B.; Darienko, T.; Deutschewitz, K.; Dojani, S.; Friedl, S.; Mohr, K.I.; Salisch, M.; Reisser, W.; Weber, B. Southern African biological soil crusts are ubiquitous and highly diverse in drylands, being restricted by rainfall frequency. Microb. Ecol. 2009, 57, 229–247. [Google Scholar] [CrossRef]
- Raggio, J.; Green, A.; Pintado, A.; Sancho, L.G.; Büdel, B. Functional performance of biocrust across Europe and its implications for drylands. J. Arid Environ. 2021, 186, 104402. [Google Scholar] [CrossRef]
- Pan, Y.; Wan, X.; Zhang, Y. Dew formation characteristics in a revegetation-stabilized desert ecosystem in Shapotou area, northern China. J. Hydrol. 2010, 387, 265–272. [Google Scholar] [CrossRef]
- Li, S.; Bowker, M.A.; Xiao, B. Biocrust enhance non rainfall water deposition and alter its distribution in dryland soils. J. Hydrol. 2021, 595, 126050. [Google Scholar] [CrossRef]
- Li, S.; Xiao, B.; Kidron, G.J. Moss-dominated biocrust enhance water vapor sorption capacity of surface soil and increase non-rainfall water deposition in drylands. Geoderma 2021, 388, 114930. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhao, W. Dew formation and its variation in Haloxylon ammodendron plantations at the edge of a desert oasis, northwestern China. Agric. For. Meteorol. 2017, 247, 541–550. [Google Scholar] [CrossRef]
- Kidron, G.J. The enigmatic absence of cyanobacterial biocrust from the Namib fog belt: Do dew and fog hold the key? Flora 2019, 257, 151416. [Google Scholar] [CrossRef]
- Lekouch, I. (OPUR International, Paris, France); Muselli, M. (OPUR International, Paris, France); Melnytchouk-Milimouk, I. (OPUR International, Paris, France); Beysens, D. (OPUR International, Paris, France) Personal communication, 2021.
- Nilsson, T.; Vargas, W.E.; Niklasson, G.A.; Granqvist, C.G. Condensation of water by radiative cooling. Renew. Energy 1994, 5, 310–317. [Google Scholar] [CrossRef]
- Nilsson, T. Initial experiments on dew collection in Sweden and Tanzania. Sol. Energy Mat. Solar Cells 1996, 40, 23–32. [Google Scholar] [CrossRef]
- OPUR. Organisation pour l’Utilisation de la Rosée. Available online: www.opur.fr (accessed on 15 November 2022).
- Olive, P.; Dassargues, A.; Grière, O.; Ruthy, I.; El Youbi, A. Caractérisation Isotopique des eaux de Granit et de l’auréole METAMORPHIQUE d’Oulmès (Maroc Central). Integrated Water Resources Management and Challenges of the Sustainable Development. In Proceedings of the GIRE3D International Congress on Integrated Water Resources Management and Challenges of the Sustainable Development; 2006. Available online: http://hdl.handle.net/2268/3459 (accessed on 13 February 2021).
- WHO WHO Guidelines for Drinking-Water Quality (GDWQ). 2017. Available online: https://www.who.int/publications/i/item/9789241549950 (accessed on 1 September 2022).
- WHO. WHO Guidelines for Drinking-Water Quality (GDWQ). 2022. Available online: https://www.who.int/publications/i/item/9789240045064 (accessed on 1 September 2022).
- Chang, T.Y.; Kuntasal, G.; Pierson, W.R. Night-time N2O5/NO3 chemistry and nitrate in dew water. Atmos. Environ. 1986, 21, 1345–1351. [Google Scholar] [CrossRef]
- Beysens, D.; Ohayon, C.; Muselli, M.; Clus, O. Chemical and biological characteristics of dew and rain water in an urban coastal area (Bordeaux, France). Atmos. Environ. 2006, 40, 3710–3723. [Google Scholar] [CrossRef]
- Draxler, R.R.; Rolph, G.D. HYSPLIT (HYbrid Single-Particle Lafrangian Integrated Trajectory) Model. 2010. Available online: http://www.arl.noaa.gov/ready/hysplit4.html (accessed on 13 February 2021).
- NOAA. 2022. Available online: http://www.arl.noaa.gov/ (accessed on 1 April 2022).
- Ambade, B.; Sankar, T.K.; Kumar, A.; Sethi, S.S. Characterization of PAHs and n-alkanes in atmospheric aerosol of Jamshedpur City, India. J. Hazard. Toxic Radioact. Waste 2020, 24, 04020003. [Google Scholar] [CrossRef]
- Ambade, B.; Sethi, S.S.; Chintalacheruvu, M.R. Distribution, risk assessment, and source apportionment of polycyclic aromatic hydrocarbons (PAHs) using positive matrix factorization (PMF) in urban soils of East India. Environ. Geochem. Health 2022, 1–15. [Google Scholar] [CrossRef]
- Kumar, P.; Rao, B.; Burman, A.; Kumar, S.; Samui, P. Spatial variation of permeability and consolidation behaviors of soil using ordinary kriging method. Groundw. Sustain. Dev. 2023, 20, 100856. [Google Scholar] [CrossRef]
- Bargaoui, Z.; Chebbi, A. Comparison of two Kriging interpolation methods applied to spatiotemporal rainfall. J. Hydrol. 2009, 365, 56–73. [Google Scholar] [CrossRef]
- Lepioufle, J.M.; Leblois, E.; Creutin, J.D. Variography of rainfall accumulation in presence of advection. J. Hydrol. 2012, 464–465, 494–504. [Google Scholar] [CrossRef]
- Van de Beek, C.Z.; Leijnse, H.; Torfs, P.J.J.F.; Uijlenhoet, R. Seasonal semi-variance of Dutch rainfall at hourly to daily scales. Adv. Water Resour. 2012, 45, 76–85. [Google Scholar] [CrossRef]
- Rahmawati, N. Space-time variogram for daily rainfall estimates using rain gauges and satellite data in mountainous tropical Island of Bali, Indonesia (Preliminary Study). J. Hydrol. 2020, 590, 125177. [Google Scholar] [CrossRef]
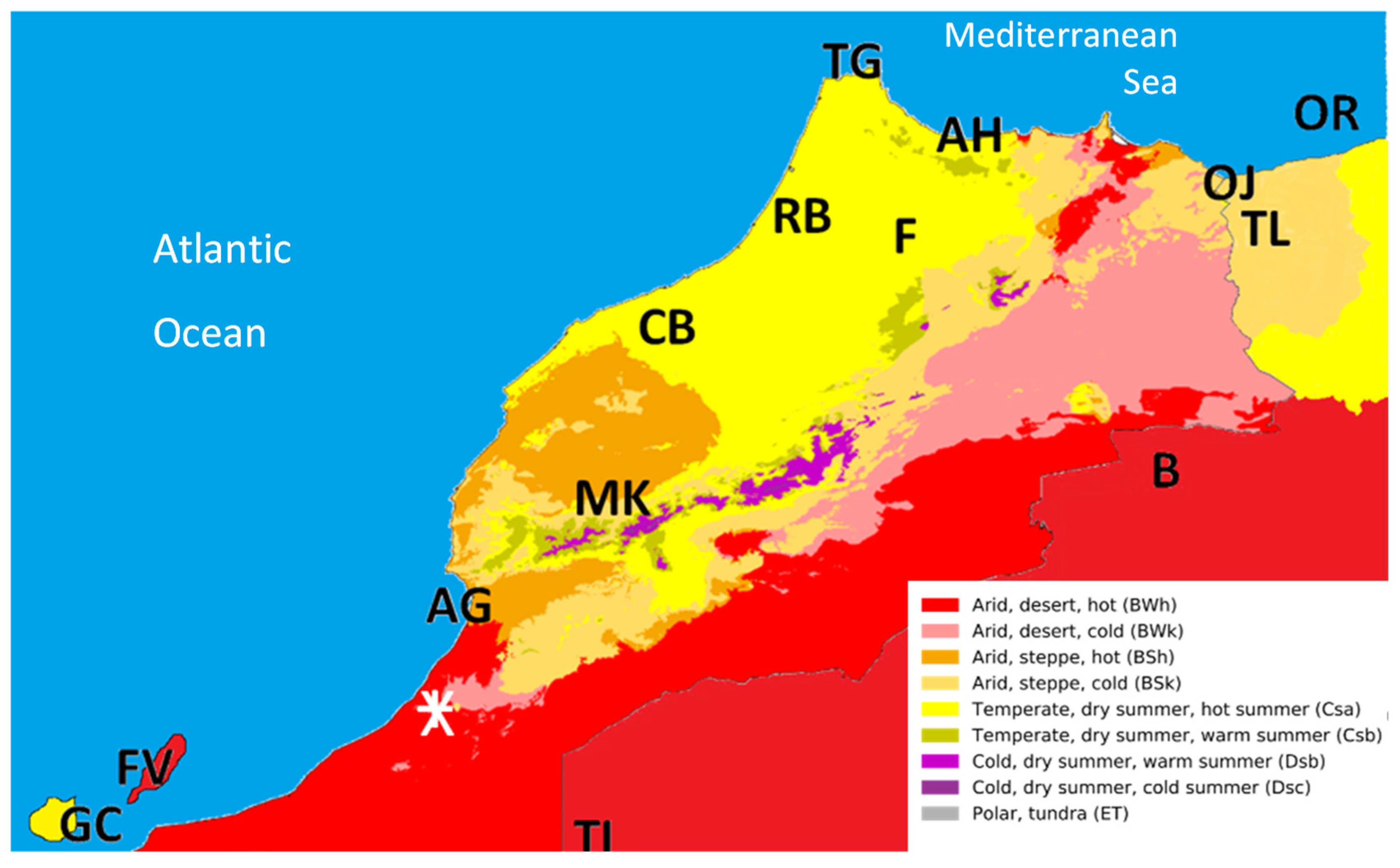







| Country | Airport | Abbreviations | Köppen- Geiger Climate | Lat | Long | Lat Dec. | Long Dec. | Alt (m) | Missing Data (%) | Distance from the Sea (km) |
|---|---|---|---|---|---|---|---|---|---|---|
| Spain | Gran Canaria | GC | Csa | 27° 55′ 55″ N | 15° 23′ 12″ W | 27.932 | −15.387 | 24 | 0.0 | 1 |
| Spain | Fuerteventura | FV | BWh | 28° 27′ 10″ N | 13° 51′ 50″ W | 28.453 | −13.864 | 26 | 0.0 | 1 |
| Morocco | Agadir | AG | BSh | 30° 19′ 30″ N | 9° 24′ 47″ W | 30.325 | −9.413 | 69 | 0.2 | 2 |
| Algeria | Tindouf | TI | Csa | 27° 42′ 00″ N | 8° 10′ 00″ W | 27.700 | −8.167 | 443 | 0.1 | 275 |
| Morocco | Marrakech | MK | BSh | 31° 36′ 54″ N | 8° 02′ 17″ W | 31.615 | −8.038 | 471 | 0.1 | 137 |
| Morocco | Casablanca | CB | Csa | 33° 22′ 05″ N | 7° 35′ 17″ W | 33.368 | −7.588 | 200 | 0.2 | 1 |
| Morocco | Rabat | RB | Csa | 34° 03′ 04″ N | 6° 45′ 05″ W | 34.051 | −6.751 | 84 | 0.1 | 4 |
| Morocco | Tanger | TG | Csa | 35° 43′ 43″ N | 5° 55′ 01″ W | 35.729 | −5.917 | 19 | 0.2 | 4 |
| Morocco | Fès | F | Csa | 33° 55′ 39″ N | 4° 58′ 41″ W | 33.927 | −4.978 | 579 | 0.4 | 134 |
| Morocco | Al-Hoceima | AH | Csa | 35° 10′ 37″ N | 3° 50′ 23″ W | 35.177 | −3.840 | 27 | 0.7 | 1 |
| Algeria | Béchar | B | Csa | 31° 39′ 02″ N | 2° 15′ 11″ W | 31.651 | −2.253 | 811 | 0.1 | 393 |
| Morocco | Oujda | OJ | BSk | 34° 47′ 15″ N | 1° 55′ 26″ W | 34.788 | −1.924 | 468 | 0.2 | 44 |
| Algeria | Tlemcen | TL | Csa | 35° 00′ 55″ N | 1° 27′ 03″ W | 35.015 | −1.451 | 248 | 0.0 | 27 |
| Algeria | Oran | OR | Csa | 35° 37′ 38″ N | 0° 36′ 41″ W | 35.627 | −0.611 | 91 | 0.0 | 11 |
| Observation | N (Oktas) |
|---|---|
| CLR | 0 |
| FEW | 1 |
| SCT | 3 |
| BKN | 5 |
| OVC | 8 |
| Site | Hd,y (mm·year−1) | Hd,I (mm·mth−1) | αd,y (mm·yr−1) | (mm·yr−1) | αd,i (mm·mth−1) | (mm·mth−1) | Yearly Frequency (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Minimum | Maximum | Mean | Minimum | Maximum | ||||||
| Gran Canaria | 1.3 | 0.6 | 1.9 | 0.08 | 0.0 | 0.9 | 0.02 | 1.13 | 0.002 | 0.094 | 18.4 |
| Fuerteventura | 3.7 | 1.1 | 9.9 | 1.57 | 0.0 | 5.7 | 0.18 | 2.24 | 0.001 | 0.186 | 37.9 |
| Agadir | 28.0 | 20.8 | 35.9 | 2.67 | 0.5 | 5.6 | −0.08 | 28.71 | −0.001 | 2.398 | 80.7 |
| Tindouf | 1.0 | 0.1 | 2.7 | 0.09 | 0.0 | 1.4 | −0.09 | 1.83 | −0.001 | 0.147 | 8.3 |
| Marrakech | 18.8 | 4.7 | 32.8 | 1.24 | 0.0 | 11.1 | −0.69 | 24.64 | −0.005 | 2.028 | 60.4 |
| Casablanca | 32.1 | 18.9 | 54.3 | 1.82 | 0.4 | 8.9 | 2.05 | 14.69 | 0.014 | 1.314 | 78.3 |
| Rabat | 34.9 | 25.6 | 47.3 | 1.62 | 1.0 | 6.6 | −0.22 | 36.82 | −0.002 | 3.056 | 75.9 |
| Tanger | 14.9 | 10.3 | 24.8 | 0.53 | 0.2 | 4.2 | −0.03 | 15.13 | −0.003 | 1.281 | 55.8 |
| Fès | 21.9 | 14.2 | 36.5 | 2.13 | 0.0 | 9.0 | −0.06 | 22.45 | −0.001 | 1.898 | 58.7 |
| Al-Hoceima | 19.5 | 5.1 | 39.9 | 2.78 | 0.1 | 6.1 | 1.02 | 10.79 | 0.007 | 0.929 | 70.0 |
| Béchar | 6.4 | 0.8 | 11.6 | 2.64 | 0.0 | 6.5 | −0.43 | 10.06 | −0.003 | 0.801 | 22.1 |
| Oujda | 25.6 | 19.5 | 34.8 | 0.08 | 0.2 | 7.1 | 0.50 | 21.28 | 0.003 | 1.798 | 65.3 |
| Tlemcen | 33.4 | 23.6 | 43.8 | 1.57 | 0.4 | 6.9 | −0.83 | 40.48 | −0.006 | 3.345 | 71.7 |
| Oran | 31.7 | 23.6 | 40.9 | 2.67 | 0.4 | 7.5 | 0.15 | 30.49 | 0.001 | 2.542 | 74.2 |
| Site | Hr,y (mm) | Hr,i (mm) | αr,y (mm·yr−1) | H0r,y (mm·yr−1) | αr,i (mm·mth−1) | h0r,i (mm·mth−1) | Yearly Frequency (%) | r (%) RCP2.6 RCP8.5 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Minimum | Maximum | Mean | Minimum | Maximum | |||||||
| Gran Canaria | 112 | 38 | 281 | 9.3 | 0 | 113 | −6.907 | 170.76 | −0.0488 | 14.042 | 11.2 | 0.7 ± 0.1 0.9 ± 0.2 |
| Fuerteventura | 61 | 10 | 131 | 5.1 | 0 | 69 | −3.059 | 87.33 | −0.0208 | 7.1134 | 7.4 | 7.7 ± 0.9 9.9 ± 1.6 |
| Agadir | 294 | 10 | 1114 | 24.5 | 0 | 662 | −8.209 | 364.13 | −0.0534 | 29.678 | 8.2 | 8.2 ± 0.8 8.0 ± 0.7 |
| Tindouf | 58 | 4 | 144 | 4.8 | 0 | 120 | 0.048 | 57.68 | 0.0021 | 4.6384 | 3.2 | 1.2 ± 0.2 1.1 ± 0.1 |
| Marrakech | 184 | 68 | 324 | 15.3 | 0 | 139 | −1.514 | 197.47 | −0.0113 | 16.472 | 11.9 | 2.8 ± 0.2 3.3 ± 0.2 |
| Casablanca | 346 | 82 | 624 | 28.8 | 0 | 213 | −3.743 | 387.17 | −0.0268 | 31.447 | 16.8 | 6.1 ± 0.6 6.5 ± 0.3 |
| Rabat | 488 | 117 | 1236 | 40.7 | 0 | 326 | 0.645 | 482.88 | 0.003 | 40.413 | 19.9 | 4.4 ± 0.4 5.1 ± 0.4 |
| Tanger | 549 | 99 | 920 | 45.8 | 0 | 355 | −2.8744 | 573.48 | −0.0136 | 47.071 | 21.5 | 2.1 ± 0.2 2.0 ± 0.2 |
| Fès | 472 | 130 | 844 | 39.3 | 0 | 216 | 3.371 | 443.88 | 0.0204 | 37.414 | 19.1 | 2.4 ± 0.2 2.5 ± 0.1 |
| Al-Hoceima | 302 | 78 | 562 | 25.2 | 0 | 255 | −0.734 | 309.06 | −0.0088 | 26.081 | 15.8 | 3.0 ± 0.2 3.3 ± 0.1 |
| Béchar | 116 | 8 | 276 | 9.67 | 0 | 236 | −6.5135 | 171.22 | −0.043 | 13.802 | 7.6 | 2.9 ± 0.3 3.1 ± 0.6 |
| Oujda | 255 | 61 | 760 | 21.2 | 0 | 466 | −7.474 | 318.78 | −0.0596 | 27.025 | 15.6 | 3.6 ± 0.2 4.0 ± 0.2 |
| Tlemcen | 282 | 153 | 427 | 23.5 | 0 | 111 | −3.551 | 311.72 | −0.027 | 26.068 | 17.8 | 4.0 ± 0.2 4.3 ± 0.1 |
| Oran | 331 | 206 | 534 | 27.6 | 0 | 144 | −3.955 | 364.56 | −0.025 | 30.006 | 18.6 | 2.9 ± 0.2 3.5 ± 0.2 |
| θM (Days) | R | D | R + D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RCP2.6 | Airport | Mean | Min | Max | Mean | Min | Max | Mean | Min | Max |
| Gran Canaria | 83.4 ± 33.7 | 45.0 | 167.6 | 115.0 ± 27.0 | 70.3 | 157.5 | 62.5 ± 23.7 | 32.3 | 126.7 | |
| Fuerteventura | 135.1 ± 45.1 | 74.4 | 242.3 | 40.6 ± 12.4 | 26.0 | 79.0 | 36.5 ± 10.7 | 21.9 | 57.8 | |
| Agadir | 87.5 ± 32.3 | 49.9 | 190.6 | 17.2 ± 5.5 | 8.8 | 31.6 | 15.0 ± 4.6 | 8.8 | 24.0 | |
| Tindouf | 122.8 ± 39.8 | 63.0 | 214.6 | 140.5 ± 39.3 | 76.5 | 201.9 | 57.5 ± 16.7 | 36.8 | 116.5 | |
| Marrakech | 40.7 ± 10.6 | 22.6 | 62.6 | 26.6 ± 7.7 | 13.0 | 41.9 | 20.6 ± 4.4 | 12.8 | 26.5 | |
| Casablanca | 47.6 ± 17.4 | 25.9 | 98.5 | 9.6 ± 2.7 | 5.8 | 15.4 | 7.6 ± 2.3 | 4.9 | 12.9 | |
| Rabat | 39.7 ± 13.0 | 23.1 | 78.9 | 9.3 ± 1.7 | 6.8 | 14.0 | 6.7 ± 1.5 | 4.4 | 10.3 | |
| Tanger | 41.5 ± 12.3 | 25.5 | 70.1 | 13.3 ± 3.1 | 9.8 | 23.9 | 10.4 ± 2.6 | 6.1 | 15.8 | |
| Fès | 26.2 ± 6.4 | 15.6 | 38.1 | 18.5 ± 7.4 | 10.9 | 39.9 | 12.2 ± 3.1 | 6.5 | 19.9 | |
| Al-Hoceima | 36.9 ± 9.9 | 20.5 | 60.1 | 14.2 ± 3.7 | 9.6 | 22.6 | 12.9 ± 3.2 | 8.9 | 19.9 | |
| Béchar | 63.3 ± 22.8 | 29.6 | 116.5 | 107.2 ± 29.1 | 66.8 | 173.9 | 44.2 ± 14.1 | 27.6 | 74.1 | |
| Oujda | 36.1 ± 10.5 | 20.0 | 57.3 | 13.6 ± 3.1 | 7.9 | 21.6 | 11.7 ± 3.3 | 7.6 | 17.9 | |
| Tlemcen | 38.9 ± 11.0 | 23.4 | 57.1 | 11.5 ± 3.4 | 5.8 | 18.0 | 10.7 ± 3.4 | 5.8 | 18.0 | |
| Oran | 38.6 ± 11.6 | 24.8 | 70.1 | 10.8 ± 2.4 | 6.8 | 16.8 | 8.8 ± 2.6 | 4.9 | 14.3 | |
| Statistics | 59.9 ± 40.4 | 15.6 | 242.3 | 39.1 ± 46.7 | 5.8 | 201.9 | 22.7 ± 20.8 | 4.4 | 126.7 | |
| RCP8.5 | Gran Canaria | 91.6 ± 30.9 | 41.6 | 176.6 | 98.6 ± 31.6 | 60.3 | 193.6 | 62 ± 20.6 | 37.0 | 105.5 |
| Fuerteventura | 152.4 ± 54.2 | 71.4 | 280.0 | 41.0 ± 14.9 | 23.0 | 84.9 | 37.3 ± 16.0 | 19.5 | 84.9 | |
| Agadir | 77.2 ± 22.7 | 42.6 | 126.3 | 16.0 ± 4.8 | 9.5 | 26.6 | 15.5 ± 4.9 | 8.9 | 25.1 | |
| Tindouf | 125.9 ± 43.5 | 51.1 | 208.6 | 148.0 ± 44.0 | 67.8 | 227.9 | 65.0 ± 23.3 | 33.0 | 116.4 | |
| Marrakech | 50.3 ± 17.9 | 24.8 | 98.3 | 30.7 ± 11.6 | 16.9 | 60.9 | 23.4 ± 6.6 | 15.8 | 42.9 | |
| Casablanca | 56.4 ± 21.6 | 31.1 | 93.5 | 9.4 ± 2.0 | 5.8 | 13.5 | 8.3 ± 2.4 | 4.9 | 12.8 | |
| Rabat | 58.7 ± 26.1 | 24.4 | 127.1 | 8.7 ± 2.0 | 5.9 | 13.5 | 6.7 ± 1.7 | 4.6 | 11.8 | |
| Tanger | 53.8 ± 22.4 | 27.4 | 90.9 | 14.8 ± 3.4 | 8.8 | 22.6 | 12.3 ± 3.9 | 6.8 | 22.6 | |
| Fès | 28.2 ± 7.1 | 16.7 | 48.0 | 23.5 ± 11.8 | 11.0 | 60.5 | 14.4 ± 5.5 | 7.8 | 30.0 | |
| Al-Hoceima | 37.1 ± 11.5 | 20.3 | 68.3 | 17.1 ± 4.9 | 10.8 | 30.0 | 14.4 ± 3.3 | 9.6 | 23.6 | |
| Béchar | 64.4 ± 19.1 | 35.3 | 111.3 | 114.8 ± 38.8 | 65.5 | 182.9 | 45.6 ± 16.6 | 21.9 | 83.8 | |
| Oujda | 40.6 ± 13.8 | 21.9 | 70.3 | 15.1 ± 4.7 | 8.5 | 24.0 | 13.9 ± 4.5 | 7.9 | 23.3 | |
| Tlemcen | 41.3 ± 13.7 | 22.0 | 68.0 | 11.1 ± 3.6 | 6.9 | 22.8 | 9.9 ± 2.4 | 5.9 | 14.8 | |
| Oran | 51.8 ± 20.2 | 25.5 | 96.6 | 11.2 ± 2.6 | 6.8 | 19.8 | 8.5 ± 2.2 | 5.5 | 14.8 | |
| Statistics | 66.4 ± 42.8 | 16.7 | 280.0 | 40.0 ± 47.8 | 5.8 | 227.9 | 24.1 ± 22.2 | 4.6 | 116.4 | |
| θ0 (days) | R | D | R + D | |||||||
| Airport | Mean | Min | Max | Mean | Min | Max | Mean | Min | Max | |
| RCP2.6 | Gran Canaria | 14.7 ± 5.3 | 8.6 | 27.8 | 11.3 ± 3.4 | 7.4 | 22.4 | 6.3 ± 1.4 | 4.4 | 9.9 |
| Fuerteventura | 27.3 ± 9.3 | 12.8 | 44.9 | 3.3 ± 0.6 | 2.6 | 5.0 | 3.0 ± 0.5 | 2.3 | 4.3 | |
| Agadir | 12.6 ± 4.7 | 6.3 | 22.2 | 1.4 ± 0.1 | 1.2 | 1.6 | 1.2 ± 0.1 | 1.0 | 1.5 | |
| Tindouf | 22.3 ± 8.1 | 10.8 | 42.1 | 13.4 ± 3.5 | 7.2 | 19.6 | 8.4 ± 2.1 | 4.4 | 12.5 | |
| Marrakech | 5.4 ± 1.3 | 3.2 | 8.8 | 2.1 ± 0.3 | 1.3 | 2.8 | 1.5 ± 0.2 | 1.0 | 1.9 | |
| Casablanca | 4.5 ± 0.9 | 3.1 | 6.2 | 1.0 ± 0.1 | 0.8 | 1.2 | 0.8 ± 0.1 | 0.7 | 0.9 | |
| Rabat | 3.8 ± 0.7 | 2.3 | 5.3 | 1.0 ± 0.1 | 0.8 | 1.2 | 0.7 ± 0.1 | 0.6 | 0.9 | |
| Tanger | 3.4 ± 0.6 | 2.2 | 4.6 | 1.6 ± 0.2 | 1.2 | 2.0 | 1.0 ± 0.1 | 0.8 | 1.3 | |
| Fès | 2.6 ± 0.4 | 1.6 | 3.3 | 1.1 ± 0.1 | 0.9 | 1.2 | 0.9 ± 0.1 | 0.7 | 1.0 | |
| Al-Hoceima | 3.7 ± 0.6 | 2.6 | 4.7 | 1.0 ± 0.1 | 0.9 | 1.2 | 0.9 ± 0.1 | 0.7 | 1.0 | |
| Béchar | 9.7 ± 1.7 | 6.5 | 13.3 | 5.0 ± 1.2 | 3.4 | 8.0 | 3.4 ± 0.7 | 2.5 | 4.7 | |
| Oujda | 3.7 ± 0.6 | 2.4 | 4.9 | 1.5 ± 0.2 | 1.1 | 1.7 | 1.0 ± 0.1 | 0.8 | 1.2 | |
| Tlemcen | 3.6 ± 0.6 | 2.2 | 4.8 | 1.2 ± 0.1 | 1.0 | 1.3 | 0.9 ± 0.1 | 0.7 | 1.0 | |
| Oran | 3.7 ± 0.6 | 2.8 | 5.1 | 1.4 ± 0.2 | 1.2 | 1.7 | 1.0 ± 0.1 | 0.8 | 1.1 | |
| Statistics | 8.6 ± 8.5 | 1.6 | 44.9 | 3.3 ± 4.1 | 0.8 | 22.4 | 2.2 ± 2.4 | 0.6 | 12.5 | |
| RCP8.5 | Gran Canaria | 17.9 ± 4.0 | 13.0 | 28.8 | 10.0 ± 2.0 | 6.26 | 15.08 | 6.4 ± 1.0 | 4.4 | 8.4 |
| Fuerteventura | 38.3 ± 22.3 | 18.9 | 115.1 | 3.1 ± 0.3 | 2.60 | 3.65 | 2.9 ± 0.3 | 2.5 | 3.3 | |
| Agadir | 13.7 ± 5.1 | 8.7 | 31.2 | 1.4 ± 0.2 | 1.12 | 1.72 | 1.3 ± 0.1 | 1.0 | 1.5 | |
| Tindouf | 21.4 ± 9.3 | 12.9 | 57.1 | 16.4 ± 5.0 | 8.42 | 30.59 | 9.3 ± 2.0 | 5.6 | 13.2 | |
| Marrakech | 6.0 ± 1.0 | 4.2 | 8.0 | 2.4 ± 0.4 | 1.51 | 3.40 | 1.7 ± 0.3 | 1.1 | 2.4 | |
| Casablanca | 4.9 ± 0.7 | 3.6 | 6.1 | 1.0 ± 0.1 | 0.86 | 1.23 | 0.8 ± 0.1 | 0.7 | 1.0 | |
| Rabat | 4.2 ± 0.7 | 2.6 | 5.4 | 1.0 ± 0.1 | 0.86 | 1.13 | 0.7 ± 0.1 | 0.6 | 0.8 | |
| Tanger | 3.5 ± 0.6 | 2.0 | 4.4 | 1.7 ± 0.2 | 1.36 | 2.10 | 1.1 ± 0.1 | 0.8 | 1.3 | |
| Fès | 2.8 ± 0.4 | 2.0 | 3.8 | 1.1 ± 0.2 | 0.82 | 1.53 | 0.9 ± 0.1 | 0.7 | 1.3 | |
| Al-Hoceima | 3.8 ± 0.6 | 2.5 | 4.7 | 1.2 ± 0.1 | 0.98 | 1.40 | 1.0 ± 0.1 | 0.8 | 1.2 | |
| Béchar | 10.9 ± 2.5 | 7.8 | 16.4 | 5.2 ± 1.1 | 3.26 | 7.36 | 3.6 ± 0.7 | 2.6 | 5.1 | |
| Oujda | 3.8 ± 0.7 | 2.7 | 5.1 | 1.5 ± 0.2 | 1.14 | 1.85 | 1.1 ± 0.1 | 0.8 | 1.4 | |
| Tlemcen | 3.8 ± 0.7 | 2.8 | 5.7 | 1.2 ± 0.1 | 0.98 | 1.45 | 0.9 ± 0.1 | 0.7 | 1.1 | |
| Oran | 3.9 ± 0.6 | 2.8 | 5.1 | 1.4 ± 0.1 | 1.13 | 1.55 | 1.0 ± 0.1 | 0.8 | 1.1 | |
| Statistics | 9.9 ± 11.8 | 2 | 115.1 | 3.5 ± 4.5 | 0.8 | 30.6 | 2.3 ± 2.5 | 0.6 | 13.2 | |
| DEW (17 Samples) | RAIN (8 Samples) | Sidi Ali | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | VWM | Min | Max | Mean | SD | VWM | (£) | ||
| V (mL) | 33 | 334 | 156 | 99 | - | 100 | 2230 | 977 | 649 | - | - | |
| TH (°f) | 6.1 | 42.7 | 19.6 | 9.8 | 16.9 | 2.4 | 20.8 | 12.0 | 6.0 | 9.9 | 6.7 | |
| pH (*) | 6.8 | 7.9 | 7.5 | 0.3 | 7.5 | 6.7 | 7.1 | 6.9 | 0.2 | 6.9 | 6.5 ± 0.30 | |
| pH (**) | 6.8 | 7.9 | 7.5 | 0.3 | - | 6.5 | 7.2 | 6.9 | 0.2 | - | - | |
| EC (mS.cm−1) (*) | 59 | 2920 | 1243 | 936 | 1075 | 15 | 406 | 186 | 142 | 73 | 280 ± 20 | |
| EC (mS.cm−1) ($) | 39 | 4230 | 759 | 755 | - | 15 | 2081 | 276 | 269 | - | - | |
| Cations | Ca2+ | 0.831 | 5.398 | 2.442 | 1.162 | 2.005 | 0.368 | 2.526 | 1.540 | 0.655 | 1.447 | 0.624 ± 0.095 |
| mEq·L−1 | Mg2+ | 0.354 | 3.133 | 1.478 | 0.937 | 1.366 | 0.114 | 2.200 | 0.851 | 0.667 | 0.529 | 0.708 ± 0.305 |
| K+ | 0.046 | 0.477 | 0.258 | 0.135 | 0.212 | 0.018 | 0.248 | 0.131 | 0.076 | 0.096 | 0.077 ± 0.018 | |
| Na+ | 0.766 | 14.280 | 5.476 | 4.757 | 5.384 | 0.265 | 8.193 | 2.990 | 3.022 | 2.306 | 0.992 ± 0.222 | |
| Cu2+ | 0.001 | 0.033 | 0.016 | 0.010 | 0.014 | - | - | - | - | - | - | |
| Zn2+ | 0.000 | 1.400 | 0.141 | 0.355 | 0.145 | - | - | - | - | - | - | |
| Pb2+ | 0.00004 | 0.00008 | 0.00005 | 0.00001 | 0.00005 | - | - | - | - | - | - | |
| Anions | Cl− | 1.716 | 19.539 | 8.573 | 5.740 | 8.056 | 0.699 | 10.908 | 4.147 | 3.342 | 2.777 | 0.542 ± 0.141 |
| mEq·L−1 | NO3− | 0.088 | 0.464 | 0.257 | 0.111 | 0.230 | 0.039 | 0.490 | 0.226 | 0.131 | 0.210 | 0.003 ± 0.002 |
| SO42− | 0.115 | 1.127 | 0.419 | 0.275 | 0.366 | 0.026 | 0.995 | 0.351 | 0.276 | 0.338 | 0.979 ± 0.625 | |
| HCO3− | 1.000 | 1.400 | 1.141 | 0.150 | 1.117 | - | - | - | - | - | 1.234 ± 0.251 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muselli, M.; Lekouch, I.; Beysens, D. Physical and Chemical Characteristics of Dew and Rain in North-West Africa with Focus on Morocco: Mapping Past and Future Evolution (2005–2100). Atmosphere 2022, 13, 1974. https://doi.org/10.3390/atmos13121974
Muselli M, Lekouch I, Beysens D. Physical and Chemical Characteristics of Dew and Rain in North-West Africa with Focus on Morocco: Mapping Past and Future Evolution (2005–2100). Atmosphere. 2022; 13(12):1974. https://doi.org/10.3390/atmos13121974
Chicago/Turabian StyleMuselli, Marc, Imad Lekouch, and Daniel Beysens. 2022. "Physical and Chemical Characteristics of Dew and Rain in North-West Africa with Focus on Morocco: Mapping Past and Future Evolution (2005–2100)" Atmosphere 13, no. 12: 1974. https://doi.org/10.3390/atmos13121974
APA StyleMuselli, M., Lekouch, I., & Beysens, D. (2022). Physical and Chemical Characteristics of Dew and Rain in North-West Africa with Focus on Morocco: Mapping Past and Future Evolution (2005–2100). Atmosphere, 13(12), 1974. https://doi.org/10.3390/atmos13121974







