Bias Correction and Evaluation of Precipitation Data from the CORDEX Regional Climate Model for Monitoring Climate Change in the Wadi Chemora Basin (Northeastern Algeria)
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Description
2.3. Bias Correction Method
2.4. Spatial Analysis
2.5. Evaluation of Bias Correction Approach
2.6. Analysis Future Projections
Mann–Kendall Trend Test
3. Results and Discussion
3.1. Historical Simulation before and after Bias Correction
3.1.1. Daily Scale
3.1.2. Monthly Scale
3.1.3. Seasonal Scale
3.1.4. Annual Scale
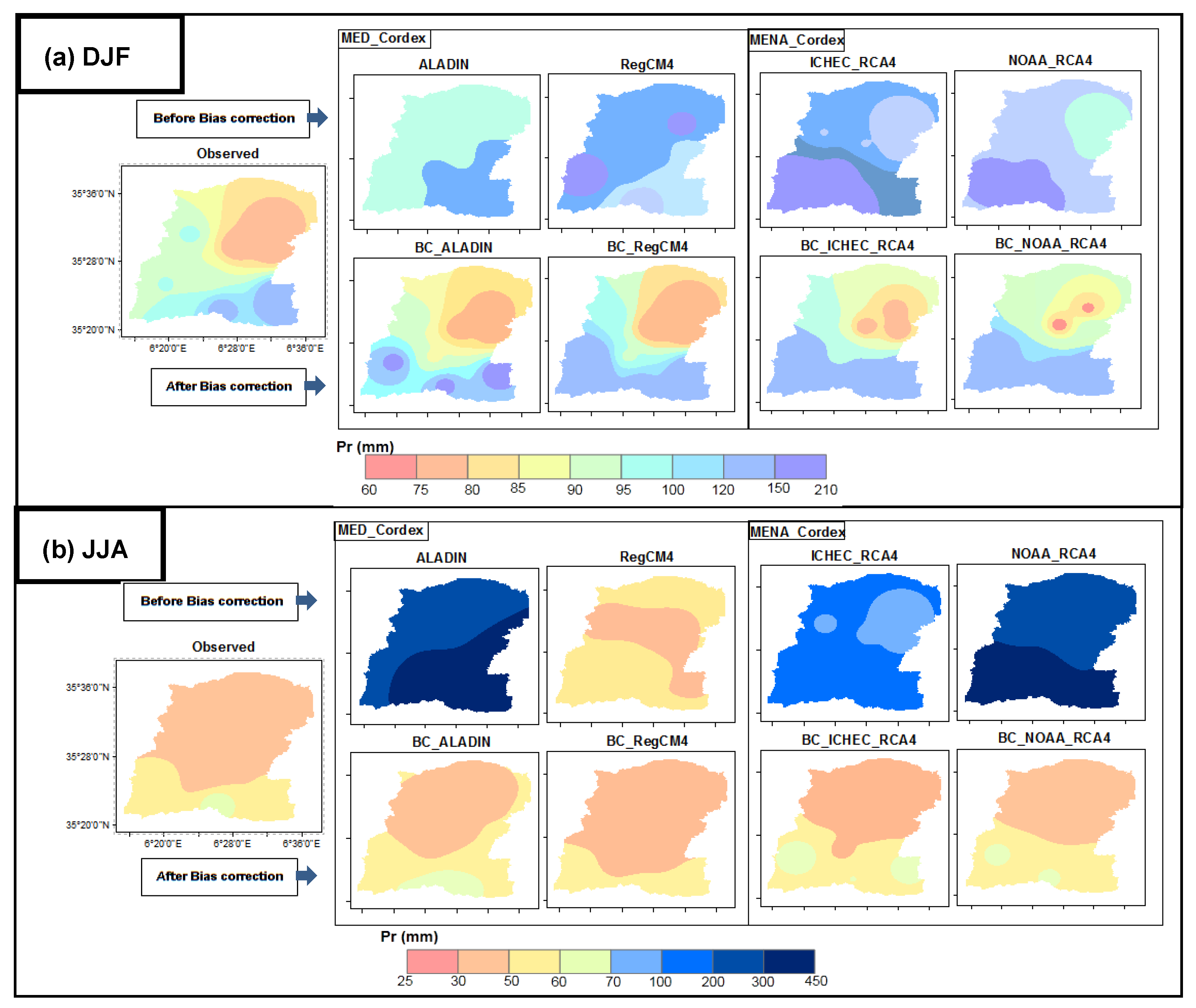
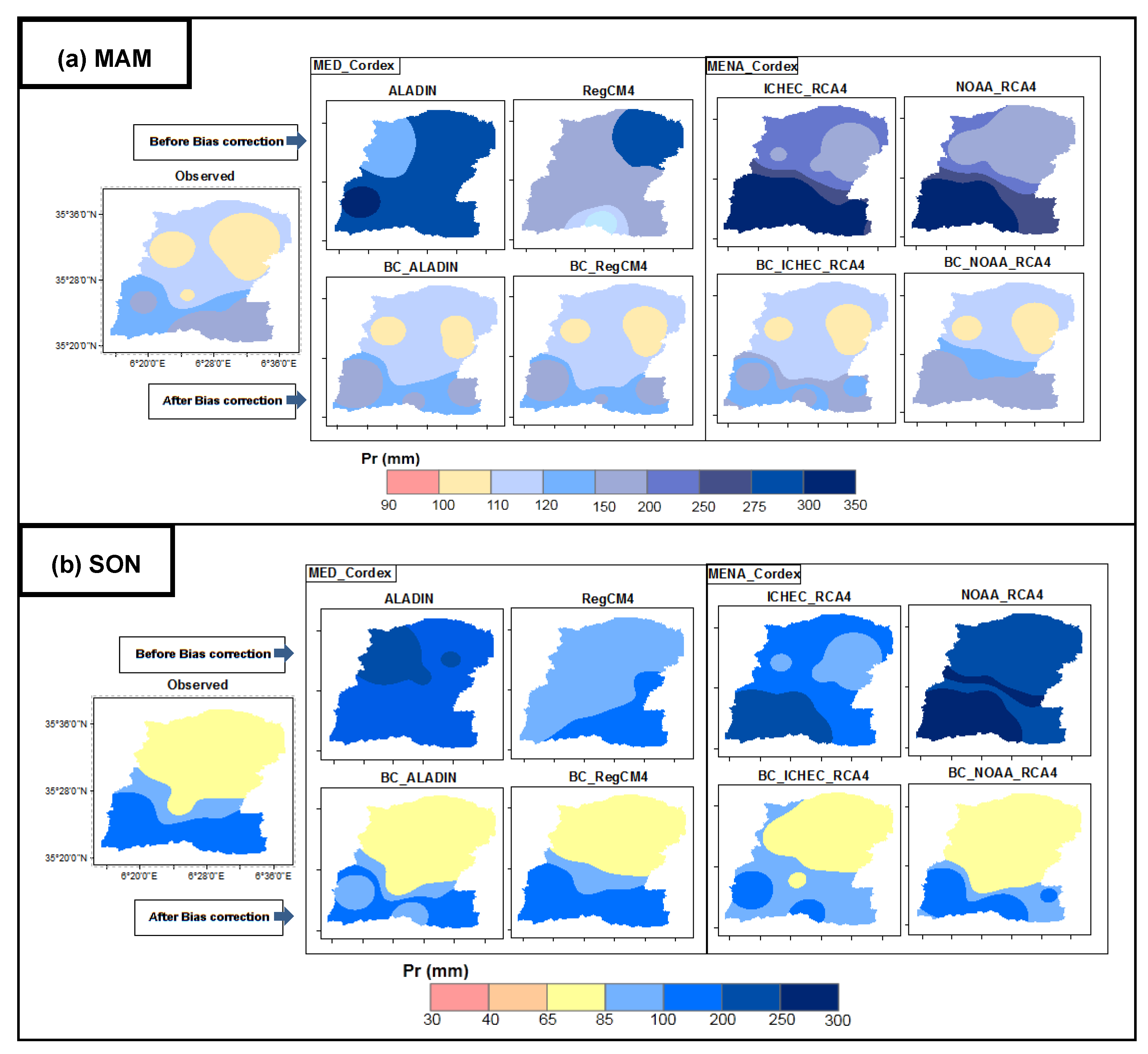
3.2. Spatial Analysis
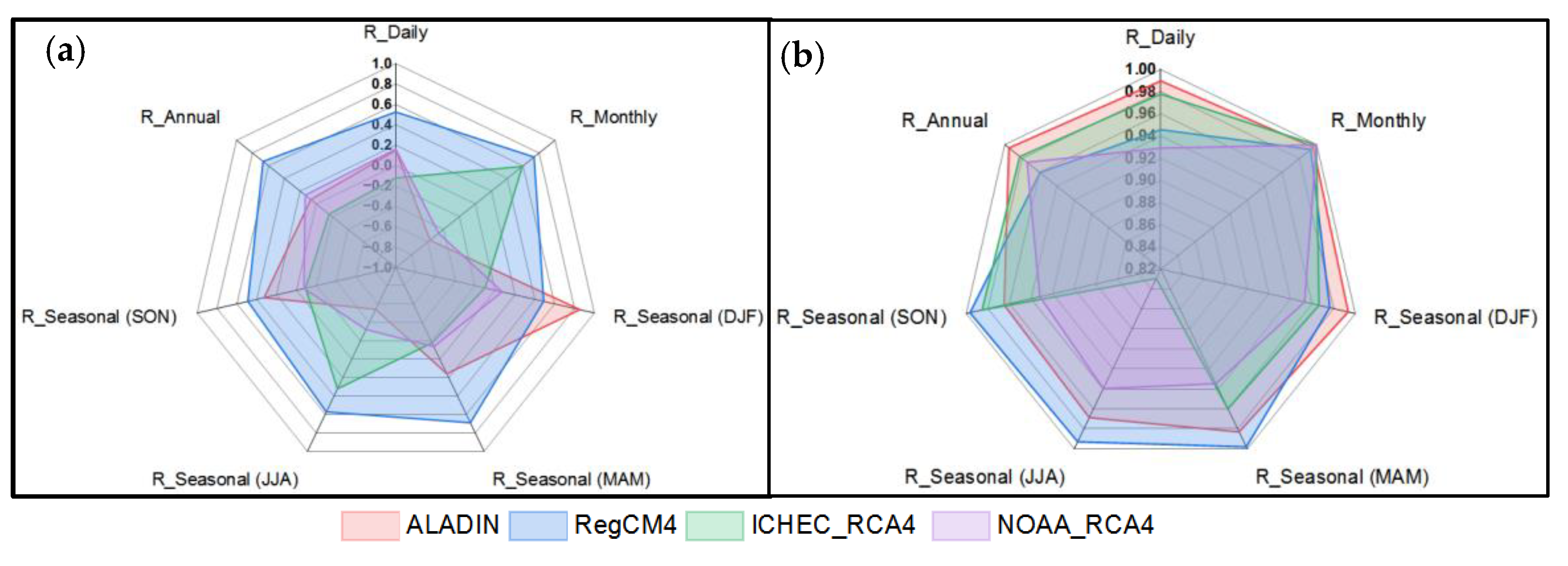
3.3. Evaluation of Bias Correction Method
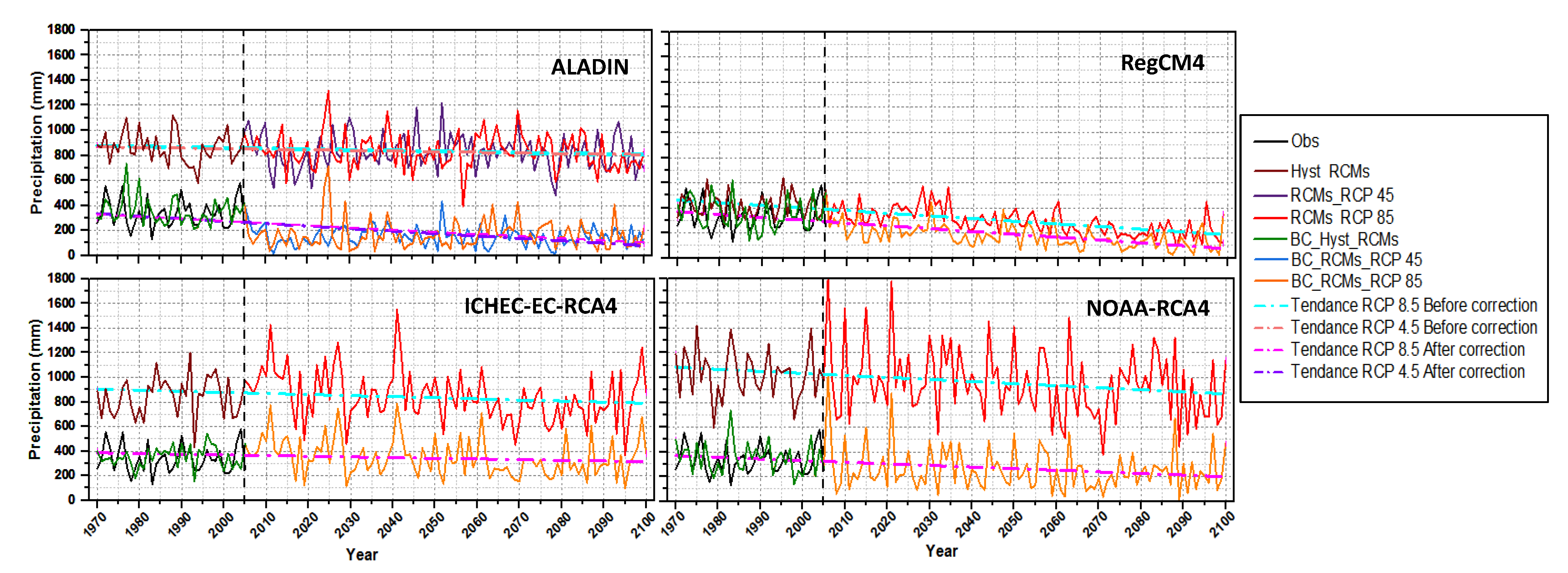
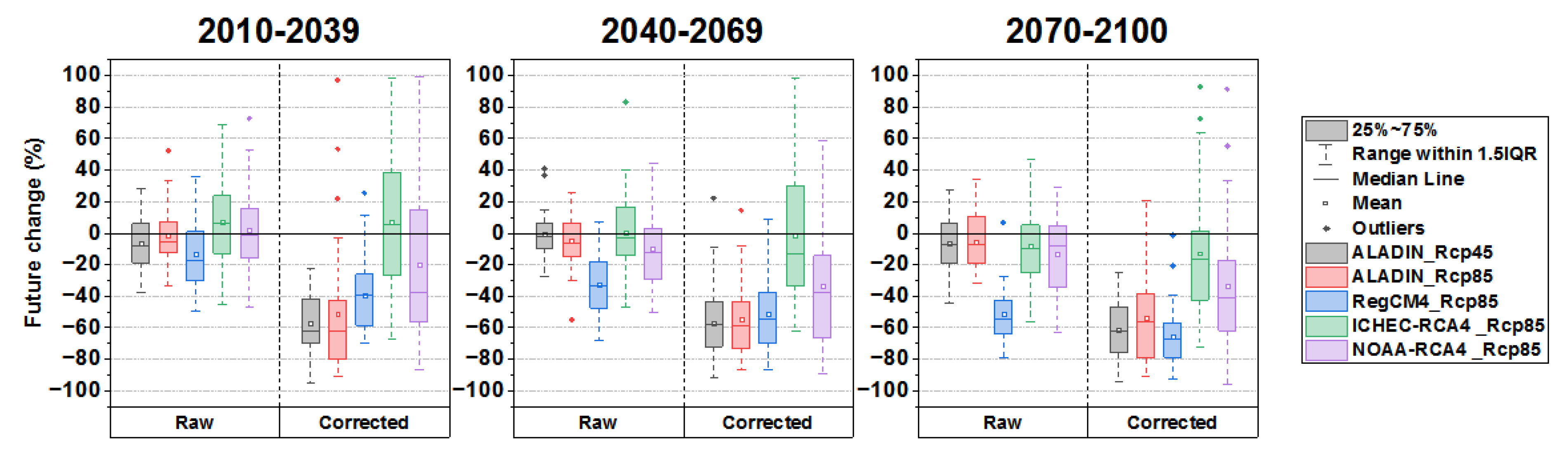
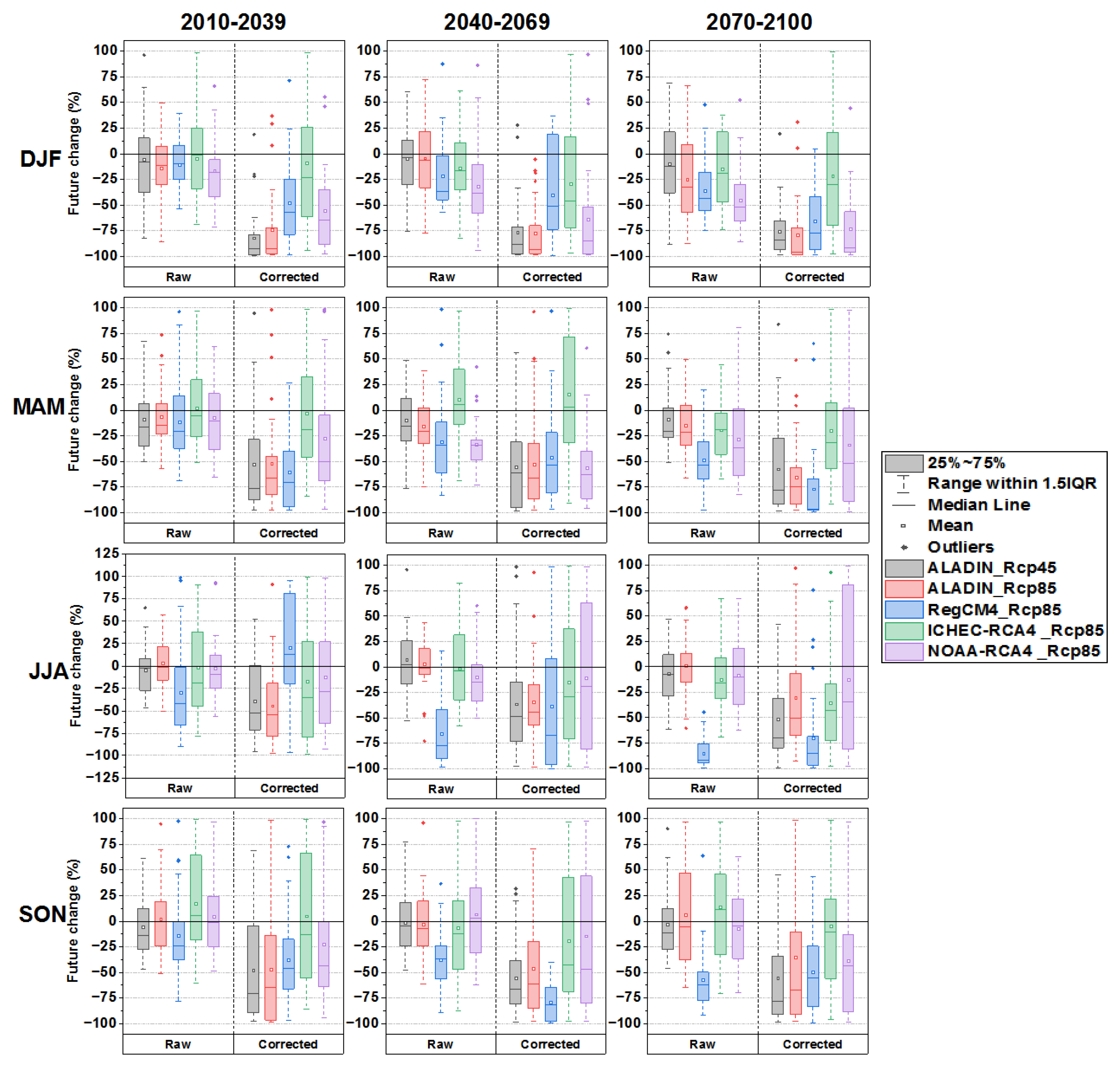
3.4. Future Projections
4. Conclusions and Recommendation
- The model’s resolution is not considered an influential factor in this study area, because it has been found that a model with a medium resolution of 22° (e.g., ICHEC-RCA4 from the MENA CORDEX) can outperform a model with a high resolution of 11° on occasion (e.g., RegCM4 from MED CORDEX in the daily and seasonal time steps);
- There is a relationship between the elevations and the performance of MENA-CORDEX models RCA4v1 driven by two GCMs, ICHEC-EC-EARTH and NOAA-GFDL-GFDL-ESM2M, since they performed better at lower elevations (from 1000 m to 1112 m) and poorly at higher altitudes (from 1160 m to 1650 m);
- For future projection and with respect to the corrected baseline (the historic period of 1970–2005), the adjusted RCPs of the four RCMs revealed a decreasing trend of average precipitation over the period 2006–2100 (2006–2099 for ICTP-RegCM4-3v1);
- Dividing the future time into sub-periods allowed us to see the behavior of each model individually in terms of forecasting the average precipitation in the near (2010–2039), medium (2040–2069), and long-term future (2070–2100). In summary, after adjusting the models, all of them predict a decrease that affects the four seasons of the three sub-periods, which leads to an annual decrease as well, reaching an average of 66%;
- Furthermore, our proposed approach can contribute to a reduction in precipitation prediction uncertainties and in the establishment of sustainable water resources management plans for mitigating natural disasters caused by future climate changes. We plan to extend the applicability and accessibility of the suggested method to a hydrological model, which will contribute considerably to the preparation for and adaptation to uncertain climate changes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maibach, E.; Myers, T.; Leiserowitz, A. Climate Scientists Need to Set the Record Straight: There Is a Scientific Consensus That Human-caused Climate Change Is Happening. Earths Future 2014, 2, 295–298. [Google Scholar] [CrossRef]
- Harvey, B.J. Human-Caused Climate Change Is Now a Key Driver of Forest Fire Activity in the Western United States. Proc. Natl. Acad. Sci. USA 2016, 113, 11649–11650. [Google Scholar] [CrossRef]
- Trenberth, K.E. Climate Change Caused by Human Activities Is Happening and It Already Has Major Consequences. J. Energy Nat. Resour. Law 2018, 36, 463–481. [Google Scholar] [CrossRef]
- Eyring, V.; Gillett, N.P.; Achutarao, K.M.; Barimalala, R.; Barreiro Parrillo, M.; Bellouin, N.; Cassou, C.; Durack, P.J.; Kosaka, Y.; McGregor, S.; et al. Human Influence on the Climate System. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 423–552. [Google Scholar] [CrossRef]
- Shayegh, S.; Moreno-Cruz, J.; Caldeira, K. Adapting to Rates versus Amounts of Climate Change: A Case of Adaptation to Sea-Level Rise. Environ. Res. Lett. 2016, 11, 104007. [Google Scholar] [CrossRef]
- Gasim, M.B.; Juahir, H.; Azid, A.; Kamarudin, M.K.A.; Hassan, A.R.; Hairoma, N.; Sukono, S.; Subartini, B.; Damayanti, P.P.; Supian, S. Potential of Sea Level Rise Impact on South China Sea: A Preliminary Study in Terengganu, Malaysia. J. Fundam. Appl. Sci. 2018, 10, 156–168. [Google Scholar] [CrossRef]
- Swapna, P.; Ravichandran, M.; Nidheesh, G.; Jyoti, J.; Sandeep, N.; Deepa, J.S.; Unnikrishnan, A.S. Sea-Level Rise. In Assessment of Climate Change over the Indian Region: A Report of the Ministry of Earth Sciences (MoES), Government of India; Krishnan, R., Sanjay, J., Gnanaseelan, C., Mujumdar, M., Kulkarni, A., Chakraborty, S., Eds.; Springer: Singapore, 2020; pp. 175–189. [Google Scholar] [CrossRef]
- Hauer, M.E.; Fussell, E.; Mueller, V.; Burkett, M.; Call, M.; Abel, K.; McLeman, R.; Wrathall, D. Sea-Level Rise and Human Migration. Nat. Rev. Earth Environ. 2020, 1, 28–39. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Nicholls, N.; Easterling, D.; Goodess, C.M.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M.; et al. Changes in Climate Extremes and Their Impacts on the Natural Physical Environment. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Field, C.B., Barros, V., Stocker, T.F., Dahe, Q., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 109–230. [Google Scholar] [CrossRef]
- Peterson, T.; Heim, R.; Hirsch, R.; Kaiser, D.; Brooks, H.; Diffenbaugh, N.; Dole, R.; Giovannettone, J.; Guirguis, K.; Karl, T.; et al. Monitoring and Understanding Changes in Heat Waves, Cold Waves, Floods and Droughts in the United States: State of Knowledge. Bull. Am. Meteorol. Soc. 2013, 94, 821–834. [Google Scholar] [CrossRef]
- Thuy Vy, D.N.; Léonard, B. Climate Variability and Extreme Weather Events in the Mediterranean Region; Université Grenoble Alpes: Grenoble, France, 2021. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Ruane, A.C.; Vautard, R.; Arnell, N.; Coppola, E.; Cruz, F.A.; Dessai, S.; Islam, A.S.; Rahimi, M.; Ruiz Carrascal, D.; et al. Climate Change Information for Regional Impact and for Risk Assessment. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1767–1926. [Google Scholar] [CrossRef]
- Trenberth, K. Changes in Precipitation with Climate Change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate Change Projections for the Mediterranean Region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Raible, C.C.; Ziv, B.; Saaroni, H.; Wild, M. Winter Synoptic-Scale Variability over the Mediterranean Basin under Future Climate Conditions as Simulated by the ECHAM5. Clim. Dyn. 2010, 35, 473–488. [Google Scholar] [CrossRef]
- Piras, M.; Mascaro, G.; Deidda, R.; Vivoni, E.R. Impacts of Climate Change on Precipitation and Discharge Extremes through the Use of Statistical Downscaling Approaches in a Mediterranean Basin. Sci. Total Environ. 2016, 543, 952–964. [Google Scholar] [CrossRef]
- Raymond, F.; Ullmann, A.; Tramblay, Y.; Drobinski, P.; Camberlin, P. Evolution of Mediterranean Extreme Dry Spells during the Wet Season under Climate Change. Reg. Environ. Chang. 2019, 19, 2339–2351. [Google Scholar] [CrossRef]
- Tuel, A.; Eltahir, E.A.B. Why Is the Mediterranean a Climate Change Hot Spot? J. Clim. 2020, 33, 15. [Google Scholar] [CrossRef]
- Tramblay, Y.; Koutroulis, A.; Samaniego, L.; Vicente-Serrano, S.M.; Volaire, F.; Boone, A.; Le Page, M.; Llasat, M.C.; Albergel, C.; Burak, S.; et al. Challenges for Drought Assessment in the Mediterranean Region under Future Climate Scenarios. Earth-Sci. Rev. 2020, 210, 103348. [Google Scholar] [CrossRef]
- Bazza, M.; Kay, M.; Knutson, C. Drought Characteristics and Management in North Africa and the Near East; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2018; ISBN 13: 978-92-5-130683-3. [Google Scholar]
- Ouatiki, H.; Boudhar, A.; Ouhinou, A.; Arioua, A.; Hssaisoune, M.; Bouamri, H.; Benabdelouahab, T. Trend Analysis of Rainfall and Drought over the Oum Er-Rbia River Basin in Morocco during 1970–2010. Arab. J. Geosci. 2019, 12, 128. [Google Scholar] [CrossRef]
- Ben Abdelmalek, M.; Nouiri, I. Study of Trends and Mapping of Drought Events in Tunisia and Their Impacts on Agricultural Production. Sci. Total Environ. 2020, 734, 139311. [Google Scholar] [CrossRef]
- Fragaszy, S.R.; Jedd, T.; Wall, N.; Knutson, C.; Fraj, M.B.; Bergaoui, K.; Svoboda, M.; Hayes, M.; McDonnell, R. Drought Monitoring in the Middle East and North Africa (MENA) Region: Participatory Engagement to Inform Early Warning Systems. Bull. Am. Meteorol. Soc. 2020, 101, E1148–E1173. [Google Scholar] [CrossRef]
- Ghenim, A.N.; Megnounif, A. Ampleur de la sécheresse dans le bassin d’alimentation du barrage Meffrouche (Nord-Ouest de l’Algérie). Physio-Géo 2013, 7, 35–49. [Google Scholar] [CrossRef]
- Meddi, H.; Meddi, M.; Assani, A.A. Study of Drought in Seven Algerian Plains. Arab. J. Sci. Eng. 2014, 39, 339–359. [Google Scholar] [CrossRef]
- Djellouli, F.; Bouanani, A.; Baba-Hamed, K. Caractérisation de La Sécheresse et Du Comportement Hydrologique Au Niveau Du Bassin Versant de l’oued Louza (Algérie Occidentale). Tech. Sci. Méthodes 2019, 6, 23–34. [Google Scholar] [CrossRef]
- Bendjema, L.; Baba-Hamed, K.; Bouanani, A. Characterization of the Climatic Drought Indices Application to the Mellah Catchment, North-East of Algeria. J. Water Land Dev. 2019, 43, 28–40. [Google Scholar] [CrossRef]
- Bougara, H.; Hamed, K.B.; Borgemeister, C.; Tischbein, B.; Kumar, N. A Comparative Assessment of Meteorological Drought in the Tafna Basin, Northwestern Algeria. J. Water Land Dev. 2021, 78–93. [Google Scholar] [CrossRef]
- Weart, S. The Development of General Circulation Models of Climate. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2010, 41, 208–217. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Gulizia, C.; Camilloni, I. Comparative Analysis of the Ability of a Set of CMIP3 and CMIP5 Global Climate Models to Represent Precipitation in South America. Int. J. Climatol. 2015, 35, 583–595. [Google Scholar] [CrossRef]
- PCMDI—CMIP5 Overview. Available online: https://pcmdi.llnl.gov/mips/cmip5/ (accessed on 9 March 2022).
- Buser, C.M.; Künsch, H.R.; Weber, A. Biases and Uncertainty in Climate Projections: Uncertainty in Climate Projections. Scand. J. Stat. 2010, 37, 179–199. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, L.; Lee, S.-K.; Wu, L.; Mechoso, C.R. A Global Perspective on CMIP5 Climate Model Biases. Nat. Clim. Chang. 2014, 4, 201–205. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.-S.; Shiru, M.S. Uncertainty Analysis of Monthly Precipitation in GCMs Using Multiple Bias Correction Methods under Different RCPs. Sustainability 2020, 12, 7508. [Google Scholar] [CrossRef]
- Vrac, M.; Stein, M.L.; Hayhoe, K.; Liang, X.-Z. A General Method for Validating Statistical Downscaling Methods under Future Climate Change. Geophys. Res. Lett. 2007, 34, L18701. [Google Scholar] [CrossRef]
- Benestad, R.E.; Chen, D.; Hanssen-bauer, I. Empirical-Statistical Downscaling; World Scientific Publishing Company Toh Tuck Link: Singapore, 2008; ISBN 13: 978-981-310-729-8. [Google Scholar]
- Xue, Y.; Janjic, Z.; Dudhia, J.; Vasic, R.; De Sales, F. A Review on Regional Dynamical Downscaling in Intraseasonal to Seasonal Simulation/Prediction and Major Factors That Affect Downscaling Ability. Atmos. Res. 2014, 147–148, 68–85. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Y.; Yang, Z. Dynamical Downscaling of Regional Climate: A Review of Methods and Limitations. Sci. China Earth Sci. 2019, 62, 365–375. [Google Scholar] [CrossRef]
- Adachi, S.A.; Tomita, H. Methodology of the Constraint Condition in Dynamical Downscaling for Regional Climate Evaluation: A Review. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Jang, S.; Kavvas, M.L. Downscaling Global Climate Simulations to Regional Scales: Statistical Downscaling versus Dynamical Downscaling. J. Hydrol. Eng. 2015, 20, A4014006. [Google Scholar] [CrossRef]
- Walton, D.; Berg, N.; Pierce, D.; Maurer, E.; Hall, A.; Lin, Y.-H.; Rahimi, S.; Cayan, D. Understanding Differences in California Climate Projections Produced by Dynamical and Statistical Downscaling. J. Geophys. Res. Atmos. 2020, 125, e2020JD032812. [Google Scholar] [CrossRef]
- CORDEX | Regional Climate Model Evaluation System. Available online: https://rcmes.jpl.nasa.gov/content/cordex (accessed on 12 March 2022).
- Noguer, M.; Jones, R.; Murphy, J. Sources of Systematic Errors in the Climatology of a Regional Climate Model over Europe. Clim. Dyn. 1998, 14, 691–712. [Google Scholar] [CrossRef]
- Misra, V. Addressing the Issue of Systematic Errors in a Regional Climate Model. J. Clim. 2007, 20, 801–818. [Google Scholar] [CrossRef][Green Version]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. HESS Opinions “Should We Apply Bias Correction to Global and Regional Climate Model Data?”. Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef]
- Sørland, S.L.; Schär, C.; Lüthi, D.; Kjellström, E. Bias Patterns and Climate Change Signals in GCM-RCM Model Chains. Environ. Res. Lett. 2018, 13, 074017. [Google Scholar] [CrossRef]
- Dosio, A.; Paruolo, P. Bias Correction of the ENSEMBLES High-Resolution Climate Change Projections for Use by Impact Models: Evaluation on the Present Climate. J. Geophys. Res. 2011, 116, D16106. [Google Scholar] [CrossRef]
- Muerth, M.J.; Gauvin St-Denis, B.; Ricard, S.; Velázquez, J.A.; Schmid, J.; Minville, M.; Caya, D.; Chaumont, D.; Ludwig, R.; Turcotte, R. On the Need for Bias Correction in Regional Climate Scenarios to Assess Climate Change Impacts on River Runoff. Hydrol. Earth Syst. Sci. 2013, 17, 1189–1204. [Google Scholar] [CrossRef]
- Ruffault, J.; Martin-StPaul, N.K.; Duffet, C.; Goge, F.; Mouillot, F. Projecting Future Drought in Mediterranean Forests: Bias Correction of Climate Models Matters! Theor. Appl. Climatol. 2014, 117, 113–122. [Google Scholar] [CrossRef]
- Johnson, F.; Sharma, A. What Are the Impacts of Bias Correction on Future Drought Projections? J. Hydrol. 2015, 525, 472–485. [Google Scholar] [CrossRef]
- Sangelantoni, L.; Tomassetti, B.; Colaiuda, V.; Lombardi, A.; Verdecchia, M.; Ferretti, R.; Redaelli, G. On the Use of Original and Bias-Corrected Climate Simulations in Regional-Scale Hydrological Scenarios in the Mediterranean Basin. Atmosphere 2019, 10, 799. [Google Scholar] [CrossRef]
- Ghimire, U.; Srinivasan, G.; Agarwal, A. Assessment of Rainfall Bias Correction Techniques for Improved Hydrological Simulation. Int. J. Climatol. 2019, 39, 2386–2399. [Google Scholar] [CrossRef]
- Worku, G.; Teferi, E.; Bantider, A.; Dile, Y.T. Statistical Bias Correction of Regional Climate Model Simulations for Climate Change Projection in the Jemma Sub-Basin, Upper Blue Nile Basin of Ethiopia. Theor. Appl. Climatol. 2020, 139, 1569–1588. [Google Scholar] [CrossRef]
- Zeroual, A.; Assani, A.A.; Meddi, H.; Bouabdelli, S.; Zeroual, S.; Alkama, R. Assessment of Projected Precipitations and Temperatures Change Signals over Algeria Based on Regional Climate Model: RCA4 Simulations. In Water Resources in Algeria—Part I; Negm, A.M., Bouderbala, A., Chenchouni, H., Barceló, D., Eds.; The Handbook of Environmental Chemistry; Springer International Publishing: Cham, Switzerland, 2020; Volume 97, pp. 135–159. [Google Scholar] [CrossRef]
- Mami, A.; Raimonet, M.; Yebdri, D.; Sauvage, S.; Zettam, A.; Perez, J.M.S. Future Climatic and Hydrologic Changes Estimated by Bias-Adjusted Regional Climate Model Outputs of the Cordex-Africa Project: Case of the Tafna Basin (North-Western Africa). Int. J. Glob. Warm. 2021, 23, 58. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical Bias Correction for Daily Precipitation in Regional Climate Models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of Downscaling Method in Quantifying the Impact of Climate Change on Hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-Statistical Downscaling and Error Correction of Regional Climate Models and Its Impact on the Climate Change Signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias Correction of Regional Climate Model Simulations for Hydrological Climate-Change Impact Studies: Review and Evaluation of Different Methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias Correction of Daily Precipitation Simulated by a Regional Climate Model: A Comparison of Methods: Bias Correction of Daily Precipitation Simulated by a Regional Climate Model. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Chen, H.; Guo, J.; Zhang, Z.; Xu, C.-Y. Prediction of Temperature and Precipitation in Sudan and South Sudan by Using LARS-WG in Future. Theor. Appl. Climatol. 2013, 113, 363–375. [Google Scholar] [CrossRef]
- Switanek, M.B.; Troch, P.A.; Castro, C.L.; Leuprecht, A.; Chang, H.-I.; Mukherjee, R.; Demaria, E.M.C. Scaled Distribution Mapping: A Bias Correction Method That Preserves Raw Climate Model Projected Changes. Hydrol. Earth Syst. Sci. 2017, 21, 2649–2666. [Google Scholar] [CrossRef]
- Reiter, P.; Gutjahr, O.; Schefczyk, L.; Heinemann, G.; Casper, M. Does Applying Quantile Mapping to Subsamples Improve the Bias Correction of Daily Precipitation?: Does Quantile Mapping Benefit from Subsampling? Int. J. Climatol. 2018, 38, 1623–1633. [Google Scholar] [CrossRef]
- Heo, J.-H.; Ahn, H.; Shin, J.-Y.; Kjeldsen, T.R.; Jeong, C. Probability Distributions for a Quantile Mapping Technique for a Bias Correction of Precipitation Data: A Case Study to Precipitation Data Under Climate Change. Water 2019, 11, 1475. [Google Scholar] [CrossRef]
- Ayugi, B.; Tan, G.; Ruoyun, N.; Babaousmail, H.; Ojara, M.; Wido, H.; Mumo, L.; Ngoma, N.H.; Nooni, I.K.; Ongoma, V. Quantile Mapping Bias Correction on Rossby Centre Regional Climate Models for Precipitation Analysis over Kenya, East Africa. Water 2020, 12, 801. [Google Scholar] [CrossRef]
- Ngai, S.T.; Tangang, F.; Juneng, L. Bias Correction of Global and Regional Simulated Daily Precipitation and Surface Mean Temperature over Southeast Asia Using Quantile Mapping Method. Glob. Planet. Chang. 2017, 149, 79–90. [Google Scholar] [CrossRef]
- Zeroual, A.; Assani, A.A.; Meddi, M.; Alkama, R. Assessment of Climate Change in Algeria from 1951 to 2098 Using the Köppen–Geiger Climate Classification Scheme. Clim. Dyn. 2019, 52, 227–243. [Google Scholar] [CrossRef]
- Taïbi, S.; Meddi, M.; Mahé, G. Seasonal Rainfall Variability in the Southern Mediterranean Border: Observations, Regional Model Simulations and Future Climate Projections. Atmósfera 2019, 32, 39–54. [Google Scholar] [CrossRef]
- Hadour, A.; Mahé, G.; Meddi, M. Watershed Based Hydrological Evolution under Climate Change Effect: An Example from North Western Algeria. J. Hydrol. Reg. Stud. 2020, 28, 100671. [Google Scholar] [CrossRef]
- Bouabdelli, S.; Meddi, M.; Zeroual, A.; Alkama, R. Hydrological Drought Risk Recurrence under Climate Change in the Karst Area of Northwestern Algeria. J. Water Clim. Chang. 2020, 11, 164–188. [Google Scholar] [CrossRef]
- Lafitte, R. Structure et relief de l’Aurès (Algérie). Bull. Assoc. Géogr. Fr. 1939, 16, 34–40. [Google Scholar] [CrossRef]
- Hassen, M.B. Etude De La Vulnerabilite A La Desertification Par Des Methodes Quantitatives Numeriques Dans Le Massif Des Aures (algerie). Ph.D. Thesis, Université de Batna 2, Fesdis, Batna, Algeria, 2009. [Google Scholar]
- Osborn, T.J.; Hulme, M. Development of a Relationship between Station and Grid-Box Rainday Frequencies for Climate Model Evaluation. J. Clim. 1997, 10, 1885–1908. [Google Scholar] [CrossRef]
- Bhowmik, A.K.; Costa, A.C. Representativeness Impacts on Accuracy and Precision of Climate Spatial Interpolation in Data-Scarce Regions: Data Representativeness Impacts on Climate Spatial Interpolation. Meteorol. Appl. 2015, 22, 368–377. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Evaluation of Multiple Climate Data Sources for Managing Environmental Resources in East Africa. Hydrol. Earth Syst. Sci. 2018, 22, 4547–4564. [Google Scholar] [CrossRef]
- Caroletti, G.N.; Coscarelli, R.; Caloiero, T. Validation of Satellite, Reanalysis and RCM Data of Monthly Rainfall in Calabria (Southern Italy). Remote Sens. 2019, 11, 1625. [Google Scholar] [CrossRef]
- Bhattacharya, T.; Khare, D.; Arora, M. Evaluation of Reanalysis and Global Meteorological Products in Beas River Basin of North-Western Himalaya. Environ. Syst. Res. 2020, 9, 24. [Google Scholar] [CrossRef]
- Ayoub, A.B.; Tangang, F.; Juneng, L.; Tan, M.L.; Chung, J.X. Evaluation of Gridded Precipitation Datasets in Malaysia. Remote Sens. 2020, 12, 613. [Google Scholar] [CrossRef]
- Mengistu, A.G.; Woldesenbet, T.A.; Dile, Y.T. Evaluation of the Performance of Bias-Corrected CORDEX Regional Climate Models in Reproducing Baro–Akobo Basin Climate. Theor. Appl. Climatol. 2021, 144, 751–767. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Regional Climate Models for Hydrological Impact Studies at the Catchment Scale: A Review of Recent Modeling Strategies: Regional Climate Models for Hydrological Impact Studies. Geogr. Compass 2010, 4, 834–860. [Google Scholar] [CrossRef]
- Teng, J.; Potter, N.J.; Chiew, F.H.S.; Zhang, L.; Wang, B.; Vaze, J.; Evans, J.P. How Does Bias Correction of Regional Climate Model Precipitation Affect Modelled Runoff? Hydrol. Earth Syst. Sci. 2015, 19, 711–728. [Google Scholar] [CrossRef]
- Sennikovs, J.; Bethers, U. Statistical Downscaling Method of Regional Climate Model Results for Hydrological Modelling. In Proceedings of the 18th World IMACS/MODSIM CONGRESS, Cairns, Australia, 13–17 July 2009; pp. 3962–3968. [Google Scholar]
- Mendez, M.; Maathuis, B.; Hein-Griggs, D.; Alvarado-Gamboa, L.-F. Performance Evaluation of Bias Correction Methods for Climate Change Monthly Precipitation Projections over Costa Rica. Water 2020, 12, 482. [Google Scholar] [CrossRef]
- Taye, M.T.; Alamirew, T.; Berhanu, D. Performance of Bias Correction Methods for Hydrological Impact Study in Lake Tana Sub-Basin. 2018. Available online: https://www.researchgate.net/publication/331891618 (accessed on 15 February 2021).
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing Bias Correction Methods in Downscaling Meteorological Variables for a Hydrologic Impact Study in an Arid Area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Chen, F.-W.; Liu, C.-W. Estimation of the Spatial Rainfall Distribution Using Inverse Distance Weighting (IDW) in the Middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Keblouti, M.; Ouerdachi, L.; Boutaghane, H. Spatial Interpolation of Annual Precipitation in Annaba-Algeria—Comparison and Evaluation of Methods. Energy Procedia 2012, 18, 468–475. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, H.; Yang, D.; Qin, Y.; Gao, B.; Cong, Z. Spatial Interpolation of Daily Precipitation in a High Mountainous Watershed Based on Gauge Observations and a Regional Climate Model Simulation. J. Hydrometeorol. 2017, 18, 845–862. [Google Scholar] [CrossRef]
- Demissie, T.A.; Sime, C.H. Assessment of the Performance of CORDEX Regional Climate Models in Simulating Rainfall and Air Temperature over Southwest Ethiopia. Heliyon 2021, 7, e07791. [Google Scholar] [CrossRef]
- Chang, C.L.; Lo, S.L.; Yu, S.L. Applying Fuzzy Theory and Genetic Algorithm to Interpolate Precipitation. J. Hydrol. 2005, 314, 92–104. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend Detection in Hydrologic Data: The Mann–Kendall Trend Test under the Scaling Hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Worku, G.; Teferi, E.; Bantider, A.; Dile, Y.T.; Taye, M.T. Evaluation of Regional Climate Models Performance in Simulating Rainfall Climatology of Jemma Sub-Basin, Upper Blue Nile Basin, Ethiopia. Dyn. Atmos. Oceans 2018, 83, 53–63. [Google Scholar] [CrossRef]
- Van Vooren, S.; Van Schaeybroeck, B.; Nyssen, J.; Van Ginderachter, M.; Termonia, P. Evaluation of CORDEX Rainfall in Northwest Ethiopia: Sensitivity to the Model Representation of the Orography. Int. J. Climatol. 2019, 39, 2569–2586. [Google Scholar] [CrossRef]
- Ngai, S.T.; Juneng, L.; Tangang, F.; Chung, J.X.; Supari, S.; Salimun, E.; Cruz, F.; Ngo-Duc, T.; Phan-Van, T.; Santisirisomboon, J.; et al. Projected Mean and Extreme Precipitation Based on Bias-Corrected Simulation Outputs of CORDEX Southeast Asia. Weather Clim. Extrem. 2022, 37, 100484. [Google Scholar] [CrossRef]
- Torma, C.Z.; Kis, A.; Pongrácz, R. Evaluation of EURO-CORDEX and Med-CORDEX Precipitation Simulations for the Carpathian Region: Bias Corrected Data and Projected Changes. Időjárás 2020, 124, 25–46. [Google Scholar] [CrossRef]
- Park, J.-H.; Oh, S.-G.; Suh, M.-S. Impacts of Boundary Conditions on the Precipitation Simulation of RegCM4 in the CORDEX East Asia Domain: Precipitation Simulation of RegCM4. J. Geophys. Res. Atmos. 2013, 118, 1652–1667. [Google Scholar] [CrossRef]
- Luhunga, P.; Botai, J.; Kahimba, F. Evaluation of the Performance of CORDEX Regional Climate Models in Simulating Present Climate Conditions of Tanzania. J. South. Hemisph. Earth Syst. Sci. 2016, 66, 32–54. [Google Scholar] [CrossRef]
- Koné, B.; Diedhiou, A.; Touré, N.E.; Sylla, M.B.; Giorgi, F.; Anquetin, S.; Bamba, A.; Diawara, A.; Kobea, A.T. Sensitivity Study of the Regional Climate Model RegCM4 to Different Convective Schemes over West Africa. Earth Syst. Dyn. 2018, 9, 1261–1278. [Google Scholar] [CrossRef]
- Assamnew, A.D.; Tsidu, G.M. The Performance of Regional Climate Models Driven by Various General Circulation Models in Reproducing Observed Rainfall over East Africa. Theor. Appl. Climatol. 2020, 142, 1169–1189. [Google Scholar] [CrossRef]
- Ghenim, A.N.; Megnounif, A. Analysis of rainfall in Northwestern Algeria. Sécheresse 2013, 24, 107–114. [Google Scholar] [CrossRef]
- Hamlaoui-Moulai, L.; Mesbah, M.; Souag-Gamane, D.; Medjerab, A. Detecting Hydro-Climatic Change Using Spatiotemporal Analysis of Rainfall Time Series in Western Algeria. Nat. Hazards 2013, 65, 1293–1311. [Google Scholar] [CrossRef]
- Bougara, H.; Hamed, K.B.; Borgemeister, C.; Tischbein, B.; Kumar, N. Analyzing Trend and Variability of Rainfall in The Tafna Basin (Northwestern Algeria). Atmosphere 2020, 11, 347. [Google Scholar] [CrossRef]
- Tramblay, Y.; Ruelland, D.; Somot, S.; Bouaicha, R.; Servat, E. High-Resolution Med-CORDEX Regional Climate Model Simulations for Hydrological Impact Studies: A First Evaluation of the ALADIN-Climate Model in Morocco. Hydrol. Earth Syst. Sci. 2013, 17, 3721–3739. [Google Scholar] [CrossRef]
- Philandras, C.M.; Nastos, P.T.; Kapsomenakis, J.; Douvis, K.C.; Tselioudis, G.; Zerefos, C.S. Long Term Precipitation Trends and Variability within the Mediterranean Region. Nat. Hazards Earth Syst. Sci. 2011, 11, 3235–3250. [Google Scholar] [CrossRef]
- Brouziyne, Y.; Abouabdillah, A.; Hirich, A.; Bouabid, R.; Zaaboul, R.; Benaabidate, L. Modeling Sustainable Adaptation Strategies toward a Climate-Smart Agriculture in a Mediterranean Watershed under Projected Climate Change Scenarios. Agric. Syst. 2018, 162, 154–163. [Google Scholar] [CrossRef]
- Meddi, M.; Eslamian, S. Uncertainties in Rainfall and Water Resources in Maghreb Countries Under Climate Change. In African Handbook of Climate Change Adaptation; Oguge, N., Ayal, D., Adeleke, L., da Silva, I., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 1967–2003. [Google Scholar] [CrossRef]
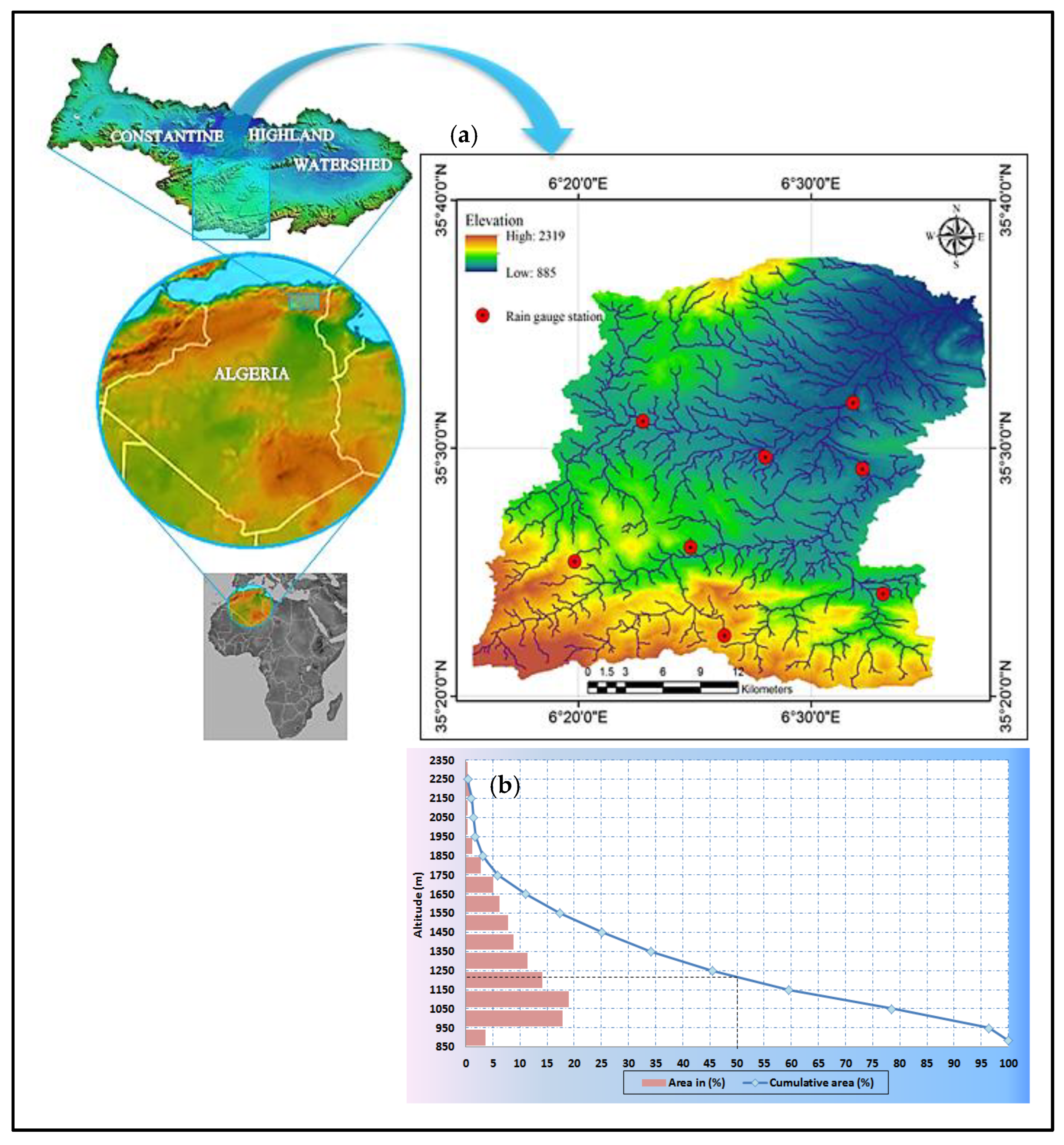

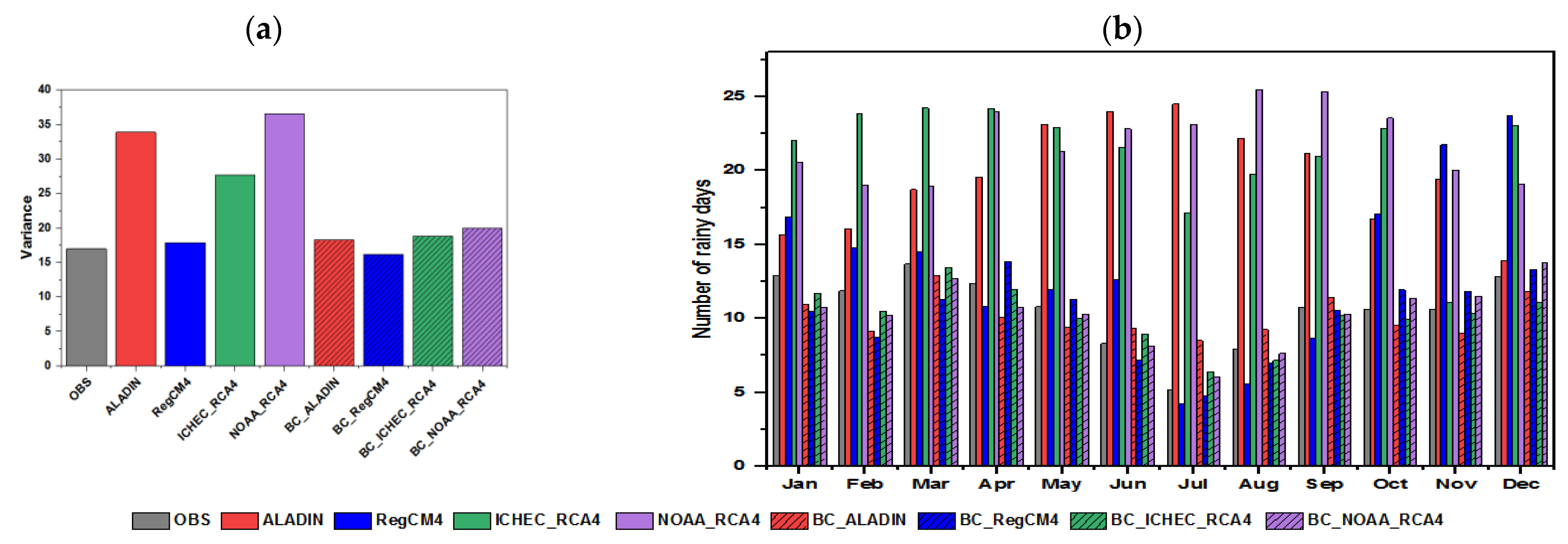

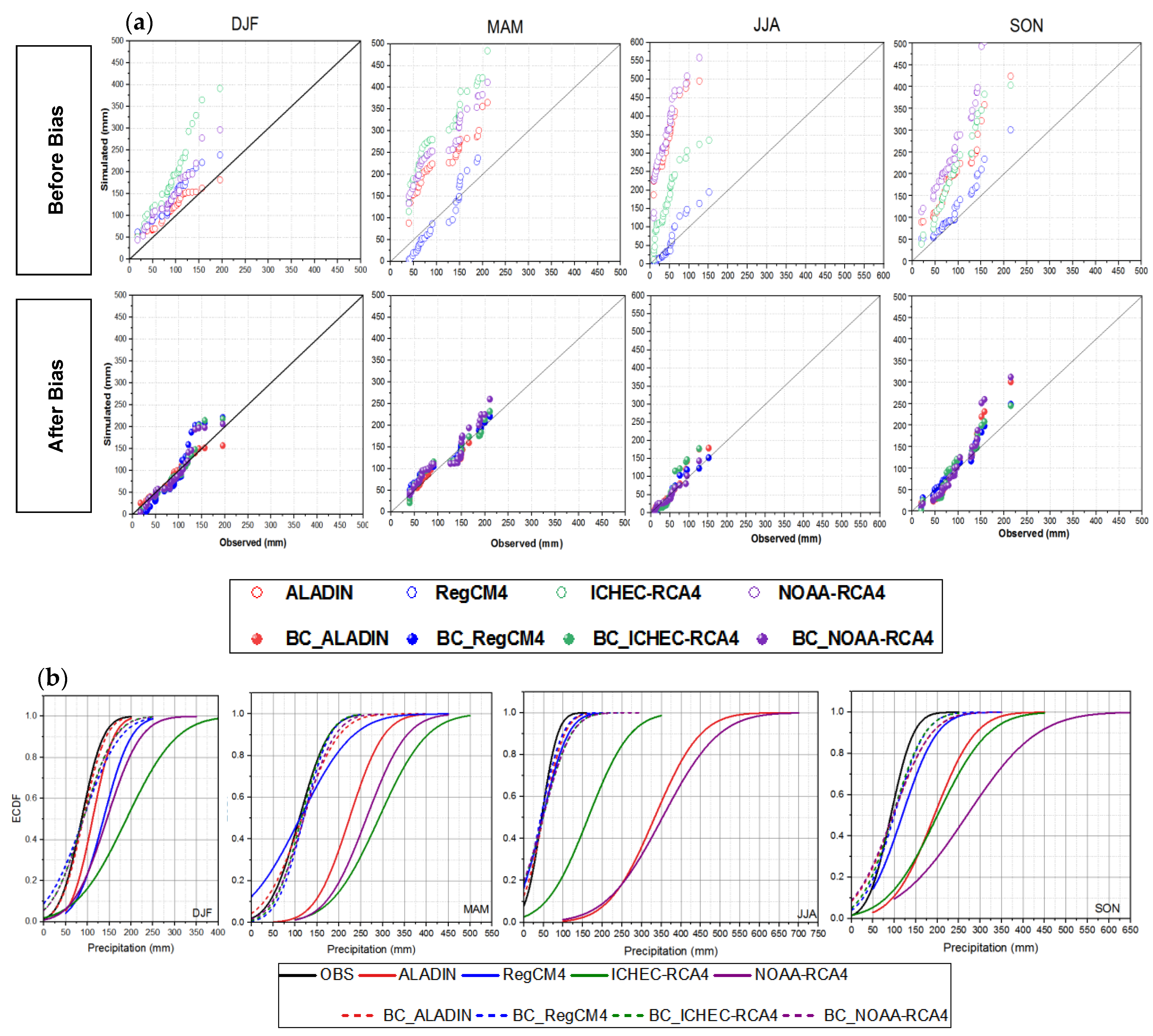

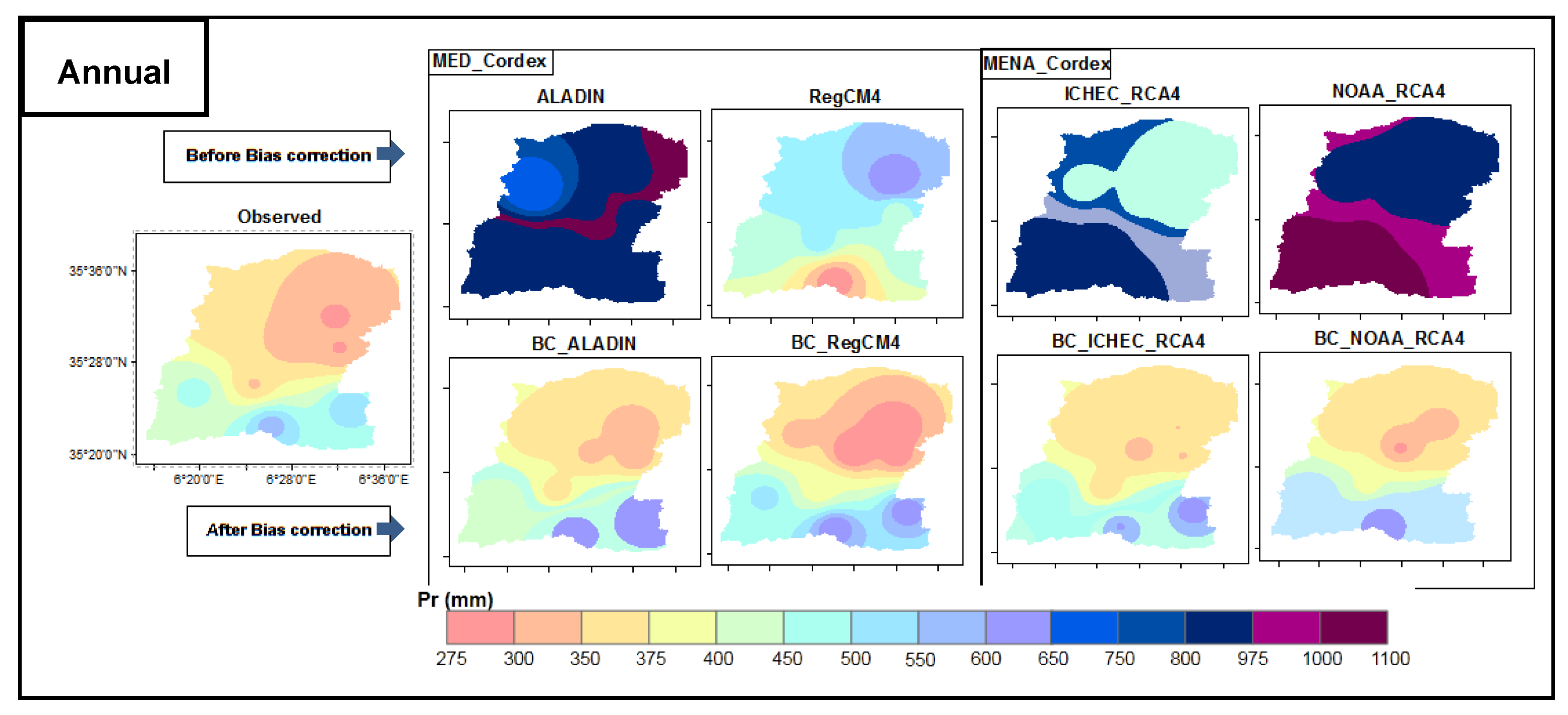

| Code | Station Name | Lat ° | Lon ° | Alt (m) | Period |
|---|---|---|---|---|---|
| 070403 | Reboa | 35.29 | 6.32 | 1002 | Sep 1969–Dec 2005 |
| 070405 | Ain Tinn | 35.22 | 6.26 | 1650 | Sep 1969–Feb 2014 |
| 070406 | Foum Toub | 35.24 | 6.33 | 1160 | Sep 1969–Aug 2013 |
| 070407 | Baiou | 35.25 | 6.19 | 1510 | Sep 1969–Feb 2014 |
| 070408 | Bouhmar | 35.26 | 6.24 | 1275 | Sep 1969–Sep 2012 |
| 070409 | Timgad | 35.29 | 6.28 | 1000 | Sep 1969–Feb 2014 |
| 070410 | Sidi Macer | 35.31 | 6.22 | 1112 | Sep 1969–Feb 2014 |
| CORDEX Domain | Resolution | Institution | Driving Model | CMIP5 Experiment | RCM Model |
|---|---|---|---|---|---|
| MENA-22 | Intermediate resolution (25 km, 0.22°) | SMHI | ICHEC-EC-EARTH | Historical rcp85 | NOAA-RCA4 |
| NOAA-GFDL-GFDL-ESM2M | Historical rcp85 | ICHEC-RCA4 | |||
| MED-11 | high resolution (12 km, 0.11°) | CNRM | CNRM-CM5 | Historical rcp45 rcp85 | ALADIN |
| ICTP | ICTP-RegCM4 | Historical rcp85 | RegCM4 |
| Kendall’s Tau | p-Value | Alpha | Sen’s Slope | Trend | |
|---|---|---|---|---|---|
| ALADIN_Rcp 45 | −0.0863 | 0.144 | 0.05 | −0.4729 | Not significant |
| ALADIN_Rcp 85 | −0.1011 | 0.0871 | 0.05 | −0.5705 | Not significant |
| RegCM4_Rcp 85 | −0.5024 | <0.0001 | 0.05 | −2.1233 | Significantly decreasing |
| ICHEC-RCA4_Rcp 85 | −0.1160 | 0.0495 | 0.05 | −0.9348 | Significantly decreasing |
| NOAA-RCA4_Rcp 85 | −0.1635 | 0.0056 | 0.05 | −1.6848 | Significantly decreasing |
| BC_ALADIN_Rcp 45 | −0.3924 | <0.0001 | 0.05 | −1.7151 | Significantly decreasing |
| BC_ALADIN_Rcp 85 | −0.3031 | <0.0001 | 0.05 | −1.5788 | Significantly decreasing |
| BC_RegCM4_Rcp 85 | −0.4953 | <0.0001 | 0.05 | −2.1075 | Significantly decreasing |
| BC_ICHEC-RCA4_Rcp 85 | −0.1406 | 0.0173 | 0.05 | −0.7195 | Significantly decreasing |
| BC_NOAA-RCA4_Rcp 85 | −0.2207 | 0.0002 | 0.05 | −1.3015 | Significantly decreasing |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derdour, S.; Ghenim, A.N.; Megnounif, A.; Tangang, F.; Chung, J.X.; Ayoub, A.B. Bias Correction and Evaluation of Precipitation Data from the CORDEX Regional Climate Model for Monitoring Climate Change in the Wadi Chemora Basin (Northeastern Algeria). Atmosphere 2022, 13, 1876. https://doi.org/10.3390/atmos13111876
Derdour S, Ghenim AN, Megnounif A, Tangang F, Chung JX, Ayoub AB. Bias Correction and Evaluation of Precipitation Data from the CORDEX Regional Climate Model for Monitoring Climate Change in the Wadi Chemora Basin (Northeastern Algeria). Atmosphere. 2022; 13(11):1876. https://doi.org/10.3390/atmos13111876
Chicago/Turabian StyleDerdour, Samiya, Abderrahmane Nekkache Ghenim, Abdesselam Megnounif, Fredolin Tangang, Jing Xiang Chung, and Afiqah Bahirah Ayoub. 2022. "Bias Correction and Evaluation of Precipitation Data from the CORDEX Regional Climate Model for Monitoring Climate Change in the Wadi Chemora Basin (Northeastern Algeria)" Atmosphere 13, no. 11: 1876. https://doi.org/10.3390/atmos13111876
APA StyleDerdour, S., Ghenim, A. N., Megnounif, A., Tangang, F., Chung, J. X., & Ayoub, A. B. (2022). Bias Correction and Evaluation of Precipitation Data from the CORDEX Regional Climate Model for Monitoring Climate Change in the Wadi Chemora Basin (Northeastern Algeria). Atmosphere, 13(11), 1876. https://doi.org/10.3390/atmos13111876





