Abstract
One of the most important challenges in atmospheric science and, in particular, in numerical weather predictions (NWP), is to forecast extreme weather events. These events affect very localized areas in space, recording high pluviometric accumulations in short time intervals. In this context, with the present study, we aim to analyze the extreme meteorological event that occurred in the northwestern and eastern parts of Sicily on 15 July 2020, by using the weather research and forecasting (WRF) model. In particular, during the afternoon, several storms affected those areas, causing intense precipitation, with maximum rainfall concentrated on the city of Palermo and in the Etna area. The rainfall at the end of the event reached 134 mm in Palermo and 49 mm in Catania, recorded by the Sicilian network meteorological stations. Because the event at Palermo was strongly localized, the analyses have been carried out by employing different sets of numerical simulations, by means of the WRF model, with horizontal spatial grid resolutions of 9, 3, and 1 km. Furthermore, the output of the performed simulation has been used to assess the thermodynamic profile and atmospheric instability indices. It allowed us to check the adopted parameters against those usually implemented in the flash flood scenario. By using the finest grid resolutions (3 and 1 km), the WRF model was able to provide more accurate predictions of the rainfall accumulation, even if they were strongly localized. Conversely, the implementation of less-refined spatial domain (9 km) did not allow us to obtain predictive estimates of precipitation.
1. Introduction
One of the most important challenges of meteorological modeling is the development of models that can predict, with high success rates, both spatial and temporal localization where a meteorological impulsive (i.e., developing in short time and space intervals) event develops, as well as its evolution [1,2,3,4].
Furthermore, in the prediction of the genesis of extreme weather events, the optimization of limited area models (LAMs) [5,6] plays a fundamental role. In fact, these phenomena occur on a local scale [7] and their intensity depends on orographic factors [8,9,10,11], such as the presence of reliefs near the coast. Sicily, an island located in the southern Mediterranean (southern Italy, see Figure 1), is often affected by extreme weather events [12,13] due to its geographical position and its complex orographic morphology.
Figure 1.
Map showing the position of Sicily in the south of Italy (edited from Google Earth).
In this context, modeling chains with high spatial resolutions can play a fundamental role for a good simulation of the dynamics of the atmosphere [14,15].
The weather research and forecasting (WRF) model [16] is a numerical weather prediction (NWP) system developed as a result of a collaboration between the National Center for Atmospheric Research (NCAR), National Centers for Environmental Prediction (NCEP), and the Earth System Research Laboratory (ESRL) of the National Oceanic and Atmospheric Administration (NOAA), designed for both research needs and operational forecasting of meteorological phenomena. The WRF model is used both for scientific and application purposes, such as numerical simulations of atmospheric dynamics and numerical weather forecasts.
In this context, the study was aimed at finding the best configurations of the WRF model, version 4.1.2 [17], specifically optimized for Sicily, which is a territory with a complex orography [18,19].
In fact, the meteorological condition of Sicily is often affected by the orographic forcing of air caused by the presence of mountain ranges and volcanic areas (e.g., Etna). These thermodynamic processes (adiabatic expansions and compressions) are theoretically studied through the Ruchardt experiment [20] and the frequency analysis procedure [21]. Furthermore, in order to study the effects of the immissions in the atmosphere of volcanic tephra, it is possible to carry out simulations of the WRF model coupled with a chemistry module, named WRF-Chem [22,23,24].
With the aim of studying one of these weather events, along with its impact on the Sicilian territory, in the present work we analyze a meteorological event registered on 15 July 2020, which affected the northwestern and the eastern parts of Sicily. In particular, during the afternoon, several thunderstorms affected the northern and eastern areas of Sicily, causing intense rainfall. The maximum rainfall accumulations were concentrated on the city of Palermo and on the Etna area. The accumulated rainfall at the end of the event, recorded by the meteorological stations of the Decentralized-Hydrogeological Functional Center (CFD-Idro) of the DRPC of Sicily, reached 134 mm in Palermo and 49 mm in Catania.
In Figure 2, we show the cumulative rainfall precipitations in the course of 15 July 2020 registered by the weather stations of the CFD-Idro Sicily. Note that the whole territory has been divided into the so-called homogeneous alert zones, rather than into provinces. As shown in Figure 2, a prominent amount of rainfall has been strongly localized in Palermo; other non-neglibile precipitations have been recorded in the eastern part of Sicily, close to the Etna volcano.
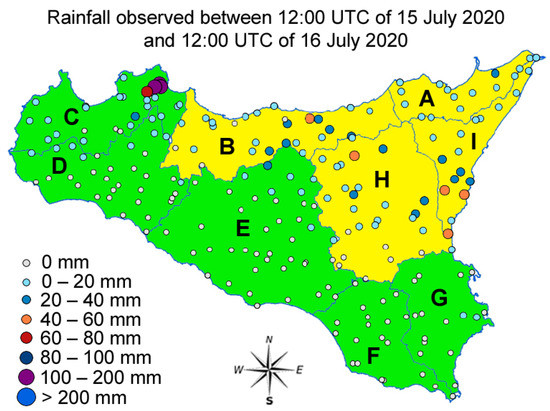
Figure 2.
Rainfall accumulations recorded by the meteorological stations of the CFD-Idro Sicily (points). The alert levels of the CFD-Idro for the meteo-hydrogeological risk issued on 15 July 2020, for the different homogeneous alert zones (A, B, C, D, E, F, G, H, I), are indicated in green (criticality: absent, operational phase: generic vigilance) and yellow (criticality: ordinary, operational phase: attention).
Such localized events, both in time and space, can be hardly predicted by the main national and international meteorological models. Indeed, based on such predictions, the Sicilian CFD-Idro did not issue any meteorological alert for the city of Palermo, as can be observed in Figure 2 (see the green zone on the western part of Sicily).
Because the studied event has been strongly localized, in particular on the Palermo area, we have investigated the effect of the WRF model grid resolution on the accuracy of rainfall predictions. This choice has been due also to the fact that extreme weather events develop within spatial dimensions often smaller than those of the horizontal spatial resolution grid typical of LAMs [25,26,27]. Specifically, three different sets of simulations, corresponding to spatial domains with grid resolutions equal to 9, 3, and 1 km, have been performed. In addition, the model has been specifically parameterized in order to implement high-resolution digital land and land use data, as done in a previous work concerning the WRF application to the Sicilian territory [28]. In this regard, the impact of the complex orography played an important role in feeding the convection system recorded on this city due to mountainous reliefs close to the sea surface, located in the southern part of Palermo, played a decisive role in feeding the convection system recorded on this city. A further input of the model is constituted by the surface sea temperature (SST).
2. Description of the Case Study
2.1. The Weather Research and Forecasting Model
In the present work, the 4.1.2 version of the WRF model (available at the following link: https://www2.mmm.ucar.edu/wrf/users/wrf_files/ (accessed on 20 September 2021)) with the ARW core, has been optimized.
The ARW dynamics solver integrates the compressible, nonhydrostatic Euler equations. The equations are cast in flux form by using variables that have conservation properties [29]. Furthemore, the ARW equations are formulated by using a terrain-following hydrostatic-pressure vertical coordinate [30,31]. The horizontal grid used by ARW core is Arakawa C-grid staggering [17]. Along the vertical, a domain consisting of 65 levels, up to 50 hPa, was used.
The initial and boundary conditions were acquired by the global model (GM) global forecast system (GFS) at 0.25 degrees (available at the following link: https://nomads.ncep.noaa.gov/cgi-bin/filter_gfs_0p25.pl (accessed on 16 May 2022)) with a time interval resolution of 1 h processed starting from the 00Z run relative to 15 July 2020. The real-time global sea surface temperature analysis (RTG-SST) with a resolution of 0.083 degrees was used (available at the following link: ftp://ftp.ncep.noaa.gov/pub/data/nccf/com/gfs/prod (accessed on 16 May 2022)). Values of RTG-SST for 15 July 2020 are reported in Figure 3; as is visible, the SST are generally between 20 and 30 degrees. Note that the Tyrrhenian sea, which laps the northeastern coasts of Sicily, is quite warm. An accurate dealing of SST is crucial, in order to characterize the appearance of extreme events.

Figure 3.
Values of RTGSST with a resolution of 0.083 degrees, referred to 15 July 2020.
Given the strongly local nature of the investigated phenomenon, the nesting protocol has been necessary [32,33]. According to this technique, it is possible to implement a large parent domain to obtain a second nested domain with higher spatial resolution and therefore a finer spacing grid. The nesting procedure allows us to focus on the areas of the domain of interest, solving the primitive equations in their finer grid.
In the present study, the one-way nesting configuration has been adopted [34,35]. In its framework, information travels unidirectionally from the parent domain to the nested domain, without coming back. First, the simulation of the parent domain is performed, and the obtained outputs provide the boundary conditions for the nested domain, processed in the subsequent step.
In the present work, we have made use of three different domains, reported in Figure 4; specifically, starting from a parent domain with resolution of 9 km, we have obtained a first nested domain with resolution of 3 km and then a second nested domain with resolution of 1 km (ratio 1/3).
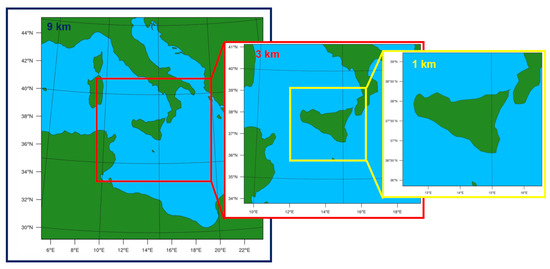
Figure 4.
Representation of the nested domains performed in this work. Starting from a parent domain with a resolution of 9 km (left), a nested domain of 3 km has been built (center) which, in turn, has been used to obtain the final domain of 1 km (right).
The corresponding improvement of the represented orography, upon going from the first to the second nested domain, is reproduced in Figure 5.
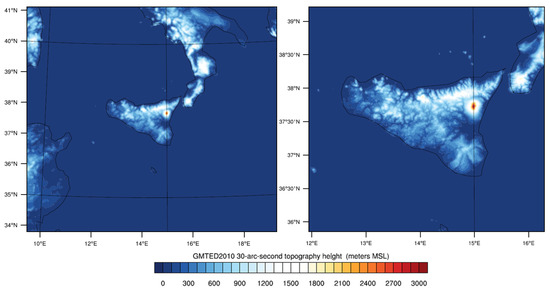
Figure 5.
Orography resulting from the domains of 3 km (left) and 1 km (right).
More detail on the model capability to reproduce the complex orography of Sicily can be gained by comparing the height of its northern mountain ranges as obtained from the spatial domain of 3 km and 1 km. Such a comparison is shown in Figure 6; specifically, we have extrapolated the values of the altitudes by carrying out a horizontal cross-section in the proximity of the northern mountainous reliefs of Sicily. It is possible to note how the model with spatial resolution at 1 km is able to better approximate the complexity of the geographical orography, in comparison to the model with spatial resolution at 3 km. The great accuracy of the domain of 1 km can be appreciated by considering the higher number of points used to sample the considered cross-section. As a consequence, the estimate of the maximum heights of the aforementioned mountain ranges is more accurate and closer to reality.
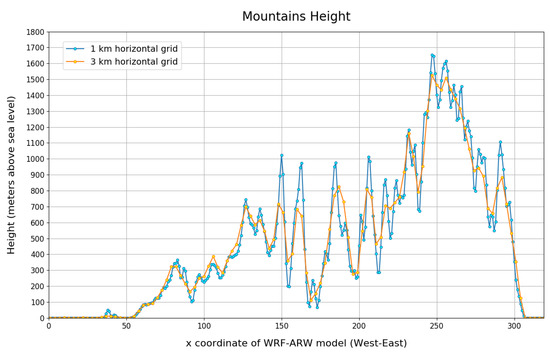
Figure 6.
Height of the northern mountains of Sicily above the sea level obtained by performing an horizontal cross correlation. The comparison between the domains of 3 km and 1 km is explicitly reported.
In the three domains examined, for long-wave and short-wave radiations, the rapid radiative transfer model for GCM (RRTMG) scheme [36] was used. In addition, the above models were also used for the schemes of Mellor–Yamada–Janjic [37,38] for the boundary layer and the Noah land surface model [39]. We have used the Thompson microphysical scheme [40], a well-known double-moment scheme widely tested especially for high-resolution simulations. For the cumulus parameterizations, the Kain–Fritsch scheme [41] was used in the 9-km domain; in domains at 3 and 1 km, the explicit convection was used [42,43]. The choice of parameterizations was based on the results obtained in the numerous case studies previously treated for the same geographic area (the following published articles are shown as examples in [44,45,46]).
2.2. Synoptic Analysis
The 500 hPa geopotential height and the winds at 300 hPa that characterize the day of 15 July 2020 are shown in Figure 7 and Figure 8; data have been downloaded from the ERA5 reanalysis [47], which has 137 vertical levels and about 30 km of horizontal resolution. Geopotential fields were obtained by downloading ERA5 hourly data on pressure levels (available from 1979 to present) in NetCDF format (https://www.unidata.ucar.edu/software/netcdf/) from the Copernicus Climate datastore (https://cds.climate.copernicus.eu/ (accessed on 16 May 2022)).
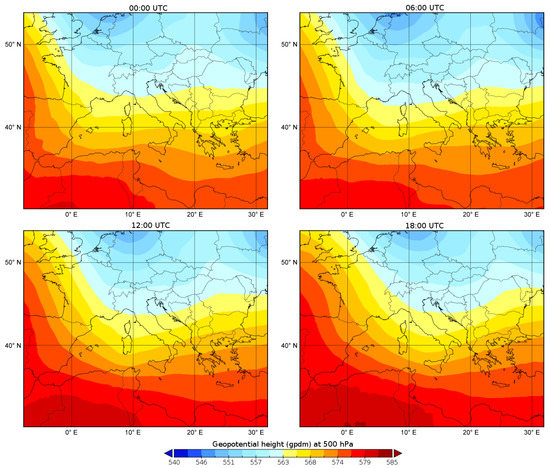
Figure 7.
The 500 hPa geopotential height (gpdm) at 00:00 UTC, 06:00 UTC, 12:00 UTC and 18:00 UTC.
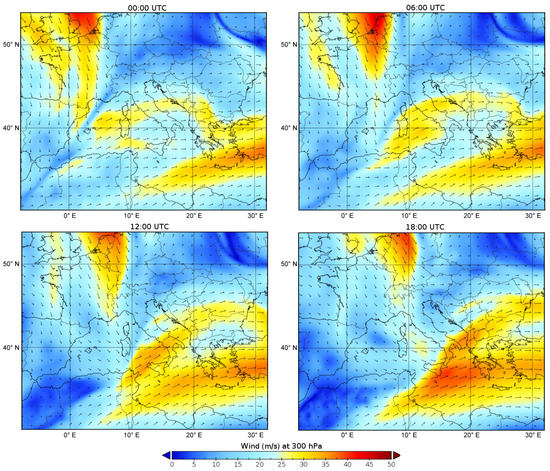
Figure 8.
Wind speed [m/s] at 300 hPa at 00:00 UTC, 06:00 UTC, 12:00 UTC and 18:00 UTC.
The sequence of 500 hPa geopotential heights (Figure 7), shows that a trough of Atlantic origin reached the central Mediterranean, first affecting the southern Tyrrhenian, and then the northwestern part of the Sicily in the central hours of the day (i.e., between 12:00 and 15:00, local time). In these hours, the genesis of heat storms was more favorable. In addition, Sicily was the demarcation area of a North African anticyclone high-pressure field on whose northern edge flows an intense branch of the subtropical jet stream (Figure 8).
At 500 hPa to 300 hPa, the geopotential height counters (not shown) tend to fan out over and near Sicily, generating an area of effective divergence at upper levels (see the 500-hPa wind vectors in Figure 9), which favors the suction of the pre-existing hot, humid air mass into the region (see Figure 10 where surface dewpoint temperatures reached 23 °C).
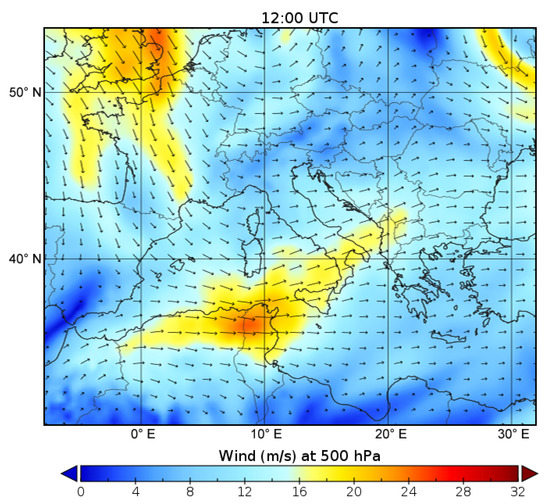
Figure 9.
Divergence in altitude near Sicily. Flow from west to northwest to the south of the island, and from the southwest just to the north.
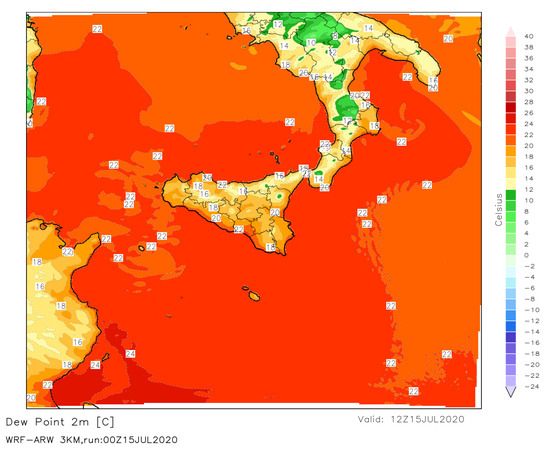
Figure 10.
Dewpoint calculated at an altitude of 2 m above the ground, obtained by the WRF model with a 3-km domain and referred to 12:00 UTC of 15 July 2020.
The convective available potential energy (CAVE) is another important indicator of the atmospheric instability. It is defined as
where and indicates the height of the free convection level and equilibrium layer, is the virtual temperature of a given air parcel, is the virtual temperature of the environment, g is the gravity acceleration, and z is the altitude. High values of CAPE generally signal high atmospheric instability, because in this case there is a lot of potential energy available to give rise to cumulus and cumulonimbus clouds, with possible severe weather hazards. Typical ranges of the CAPE values associated with the generation of thunderstorms [48] are reported in Table 1.

Table 1.
Numerical values of CAPE associated to the formation of thunderstorms.
In this context, it is worth noting that the surface CAPE (Figure 11) near the mountains surrounding Palermo assumes values close to 1500 J/kg, with peaks over 2000 J/kg in correspondence of the Gulf of Palermo.
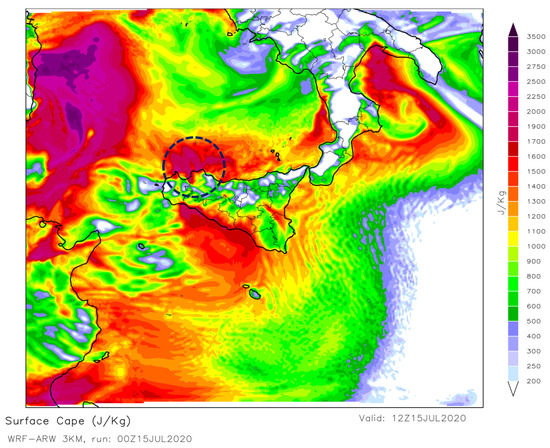
Figure 11.
The area of enhanced CAPE near Palermo for 12:00 UTC of 15 July 2020, as simulated by the 3-km grid-spaced WRF configuration, is shown.
The meteorological picture is completed by analyzing the Skew-T diagrams. The model forecast Skew-T for a grid point proximal to the Gulf of Palermo verifying at 12:00 UTC of 15 July 2020, is shown in Figure 12. In particular, we note that the CAPE value for the proximal grid point was 2252 J/kg, indicating high convective instability there.
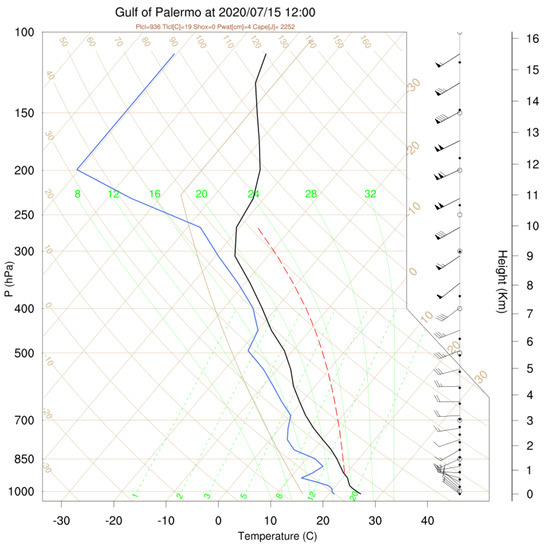
Figure 12.
WRF Skew-T profile for a model grid point (Longitude 12.796 E Latitude 38.176 N) located in the Gulf of Palermo at 12:00 UTC of 15 July 2020.
To test the prediction of the vertical state of the atmosphere obtained through the simulation carried out with the WRF model, it was considered appropriate to make a comparison with observed data. The most proximal point where a radio sounding is carried out is Trapani Birgi (about 70 km as the crow flies from Palermo). The figures below show the Skew-T predicted by the WRF model in the grid point proximal to Trapani Birgi (Figure 13) and the observed one, available online in the website of the University of Wyoming (Figure 14). The agreement between the expected and observed values of the CAPE and the precipitable water (PW) is shown in Figure 13 and Figure 14.
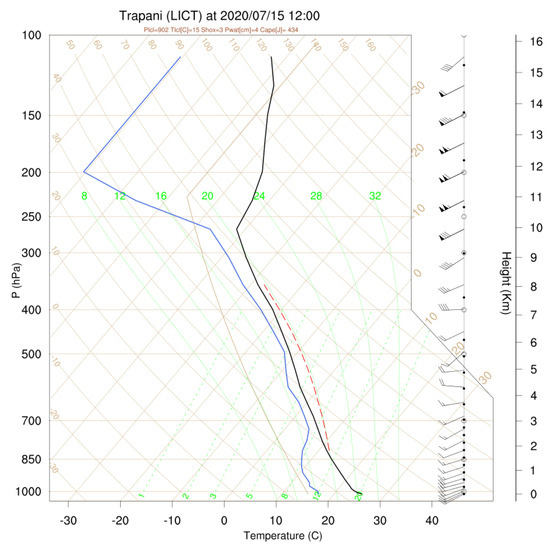
Figure 13.
Skew-T profile as simulated by the WRF 1 km model for the grid location corresponding to Trapani Birgi at 12:00 UTC of 15 July 2020.
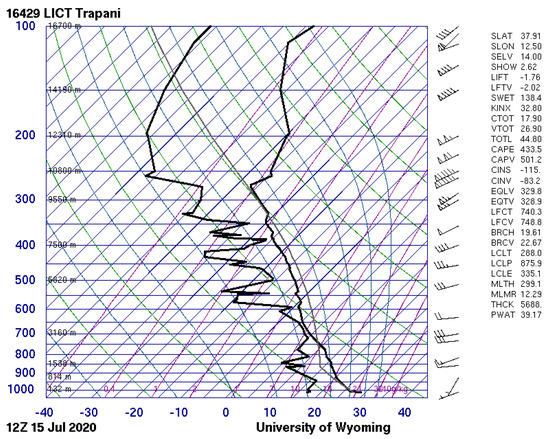
Figure 14.
Skew-T diagram obtained from a radio sounding carried out in Trapani Birgi at 12:00 UTC of 15 July 2020 (image used by permission from the University of Wyoming, see http://weather.uwyo.edu/upperair/sounding.html (accessed on 16 May 2022)).
It is also noteworthy that the advective contribution in terms of sensible heat and humidity transport provided by the “warm conveyor belt”. This conveyor belt, which preceded the transit of the trough axis, was characterized by a southerly flow of PW from North Africa. It was also characterized by high PW quantities, flowing below the evident injection of dry air at high altitude, in a thin layer of approximately 600 hPa.
The circulation on a synoptic scale was initially arranged from NW and from W/SW at the passage of the trough axis on the western sectors of Palermo; then, it began to be arranged mainly from N/NE on the eastern area. Precisely in conjunction with this confluence area in the lower layers (see Figure 15), we witnessed the passage of the core of minimum geopotential height and the advection of positive vorticity at an altitude of 500 hPa.
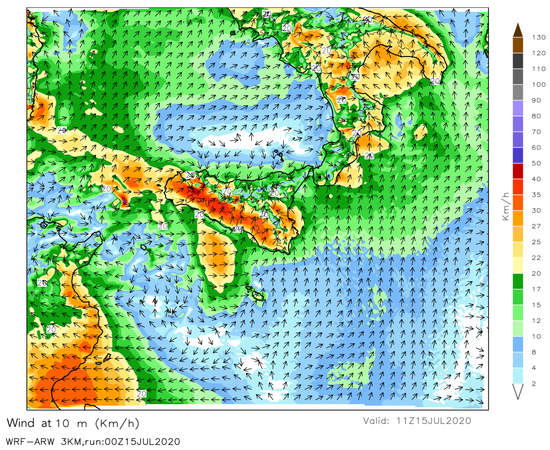
Figure 15.
Wind map at 10 m obtained by using the WRF model at 3 km. The black arrows indicate the direction of the wind; the color bar indicates the speed. Furthermore, from this figure it is possible to see the confluence area close to Palermo.
The orographic forcing also played a decisive role, favoring the overcoming of the stable air layer close to the ground, with inhibition values in the low layers quantified in over 100 J/kg from the radio sounding of Trapani Birgi at 12 UTC. This is due to the presence of exposed slopes of the mountain ranges in the southern part of Palermo. This synoptic framework has meant that the heat storms generated in the hinterland of Palermo have bolstered the storm cell through the “cold pool” self-regeneration mechanism.
For a better description of the location of the event under consideration, we show in Figure 16 the map of the rains accumulated during the 24 h of 15 July, obtained from the interpolation of the data recorded by the regional meteorological monitoring network of Sicily.
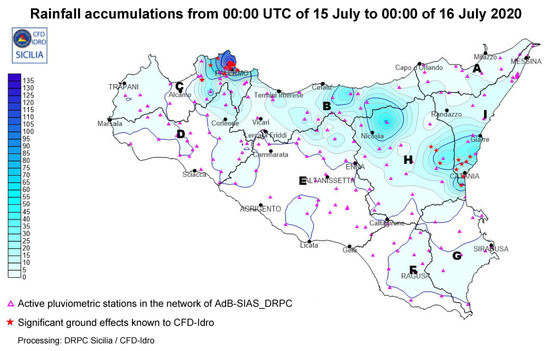
Figure 16.
Rainfall accumulations (in mm) in the 24 h from 00:00 UTC of 15 July to 00:00 UTC of 16 July 2020.
It is evident that the most significant events occurred in the Ionian sector of Sicily and, in particular, in the Palermo area. On the basis of the available data of the CFD-Idro Sicilia, it is possible to observe that the pluviometric event recorded in Palermo has exceeded return periods of 100 years (see Figure 17).
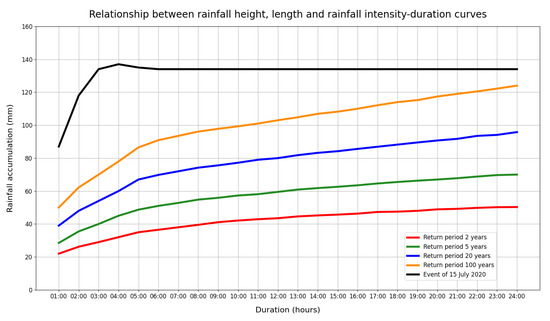
Figure 17.
The figure shows the return periods, calculated on the basis of the available data of the CFD-Idro Sicilia. In particular, the curves represent, respectively, events with a return period of two years (red), five years (green), twenty years (blue), and one hundred years (orange). The black curve represents the event recorded on 15 July 2020.
It may be also worth noting that the meteorological event recorded in Palermo was strongly localized both in space and time, because it occurred in a short time span (2 h). For this reason, it is appropriate to show the precipitation recorded at time intervals of 10 min (Figure 18) by the meteorological station that recorded the maximum rainfall accumulation.

Figure 18.
Rainfall accumulations, reported along intervals of 10 min, detected by the Palermo weather station belonging to the Servizio Informativo Agrometeorologico Siciliano (SIAS).
After a short break (visible in Figure 18, between 14:40 and 15:00 UTC), the city of Palermo witnessed a sudden resumption of precipitation, which assumed a semi-stationary character for about 2 h, given the windward regeneration. It is possible to assume that the passage of the jet stream helped to tilt the axis of the updraft, inhibiting its dissipation. At the end of the event, 134 mm of total rainfall was recorded in the city of Palermo, with a maximum hourly intensity of about 90 mm/h.
This event caused serious effects on the ground. Indeed, widespread flooding occurred in various urban areas, generating the paralysis of main roads with the flooding of underpasses and widespread damage to movable and immovable property. Furthermore, the initial information also suggested the presence of victims, but, luckily, with the development of the rescue actions, this concern disappeared [49].
3. Results and Discussion
The aim of this paper is to assess the ability of the WRF model to improve the meteorological forecasts provided by the national models, as well as to verify its dependence on the considered spatial domain. In particular, the precipitation forecasts obtained from the simulations will be evaluated. It is important to highlight that, considering the indications provided by the national numerical models, the DRPC reported the following significant phenomena, predicted for 15 July 2020—from isolated to scattered rainfall, predominantly backhand or thunderstorm, over Sicily, with low cumulative quantities, up to punctually moderate in inland areas of central–eastern Sicily. The quantitative precipitation forecast for these areas reported isolated rains in the non-impulsive precipitation section and isolated storms (with probability > 30%) in the impulsive precipitation section. Predicted rainfall from 12:00 UTC to 18:00 UTC were between 15 and 30 mm. For the remaining sectors, including Palermo, isolated rains were reported in the non-impulsive rainfall section and isolated thunderstorms (with probability between 10% and 30%) in the impulsive rainfall section. Predicted precipitations ranged from 5 to 20 mm from 12:00 UTC to 18:00 UTC.
In this context, the first simulation has been performed by adopting a spatial grid resolution of 9 km, and initialized with the data provided by the GFS model. The obtained rainfall predictions are reported in Figure 19. They provide scattered rainfall over most of the Italy, with more intense accumulations in the eastern areas of Sicily (with peaks close to 50 mm). In the western sector, precipitation between 5 and 30 mm was expected between 12:00 and 18:00 UTC. No evidence of significant rainfall on the western part of Sicily emerged.
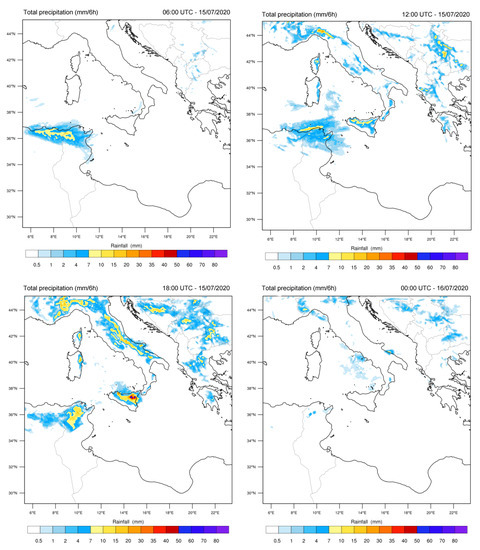
Figure 19.
Cumulative rainfall every six hours predicted by the WRF model with a domain of 9 km and calculated at 06:00 UTC (top left), 12:00 UTC (top right) and 18:00 UTC (bottom left) of 15 July 2020, and 00:00 UTC (bottom right) of 16 July 2020.
Then, a further simulation has been performed, with a spatial grid resolution of 3 km, obtained by the nesting technique using the simulation output with a spatial grid resolution of 9 km as parent domain. On the basis of this simulation (see Figure 20), we may predict that during the central hours of the day (12:00–15:00, local time), locally intense thunderstorms first affected the northwestern area of Sicily, and then involved central–eastern Sicily in the early afternoon; in the evening, these phenomena were rapidly depleting.
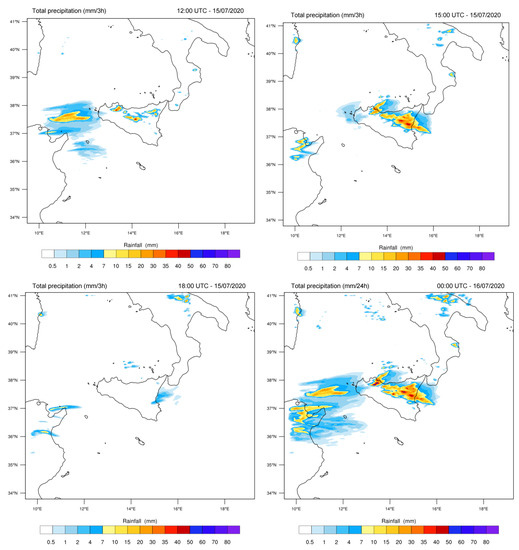
Figure 20.
Cumulative rainfall every three hours predicted by the WRF model with a domain of 3 km and calculated at 12:00 UTC (top left), 15:00 UTC (top right) and 18:00 UTC (bottom left) of 15 July 2020. The cumulative rainfall calculated along the whole day are reported in the bottom right panel.
In order to evaluate the forecast performance of the WRF model, we extracted and compared the rainfall accumulations predicted in the simulations with the domain of 3 km in the grid points close to the geographical coordinates of 10 weather stations of the network of meteorological stations of the Regional Department of Civil Protection (DRPC) of Sicily, chosen on the basis of the time evolution of the meteorological event. In particular, six meteorological stations located in the northwestern sector of Sicily (Misilmeri, Monreale, Palermo, Piana degli Albanesi, San Cipirello, San Giuseppe Jato; see Figure 21) and four located in the eastern sector of Sicily (Catania, Linguaglossa–North Etna, Paternò, and Randazzo; see Figure 22) were examined.
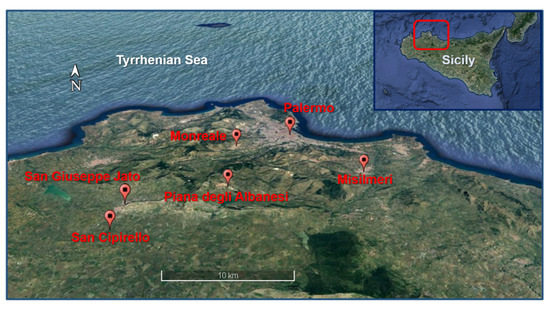
Figure 21.
Map showing six weather stations on the northwestern part of Sicily (edited from Google Earth).

Figure 22.
Map showing four weather stations on the eastern part of Sicily (edited from Google Earth).
Figure 23 shows the accumulated precipitation values recorded by the selected meteorological stations. In particular, for the northwestern sector of Sicily, the greatest rainfall was recorded in Palermo (134 mm) and in Monreale (69 mm); the greatest rainfall accumulations in the eastern sector were recorded in Catania (49 mm) and in Paternò (37 mm).
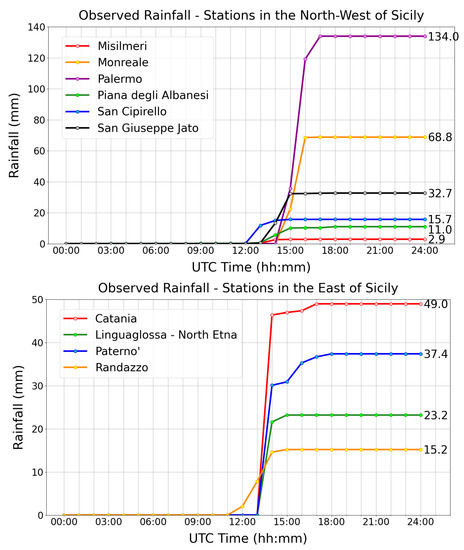
Figure 23.
Cumulative rainfall observed during the whole day of 15 July 2020, in correspondence of six stations placed in the northwestern part of Sicily (top) and of four weather stations placed in the eastern part of Sicily (bottom).
The WRF model with a 3-km domain did not reproduce the rainfall accumulation recorded during the highly localized event that occurred in the city of Palermo. However, unlike other models which did not predict the event in the northwestern Sicily, the 3-km simulation carried out with the WRF model was able to provide a maximum rainfall close to, and locally even higher than, 60 mm in 3 h.
The forecast underestimates the rainfall accumulations on the city of Palermo (13.5 mm at the end of the event). On the other hand, the model shows that in the same area, between 11:00 and 13:00 UTC, there was a rain rate of a downpour, with maximum rainfall accumulations of 63.2 mm on Monreale, 60.7 mm on the Piana degli Albanesi, and 55.1 in Misilmeri, all places close to the mountains located in the southern part of Palermo. With regard to the eastern sector of Sicily, the model predicts widespread rainfall with a maximum peak of 44.1 mm on Linguaglossa–Etna Nord, and values of 30.5 mm on Catania, 28.7 mm on Randazzo, and 26.8 mm on Paternò. Results are reported in Figure 24.
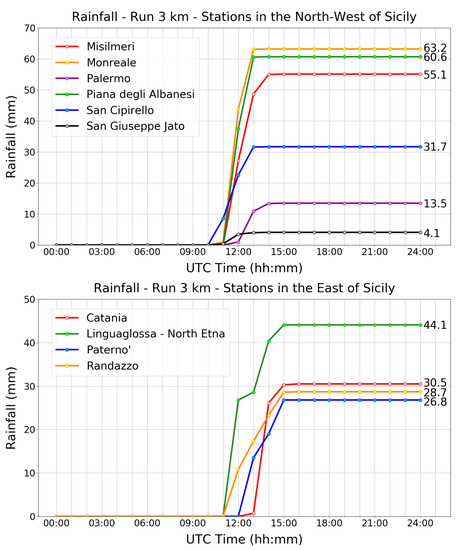
Figure 24.
Cumulative rainfall predicted by the WRF model for the whole day of 15 July 2020, with a domain of 3 km and in correspondence of six stations placed in the western part of Sicily (top) and of four weather stations placed in the eastern part of Sicily (bottom).
With the aim of better reproducing this strongly localized event, we have then performed a WRF simulation by adopting a spatial domain with a grid spacing of 1 km.
As shown in Figure 25, in the obtained three-hour maps of precipitations, in this case the highly localized event in the city of Palermo is well reproduced by the model. The precipitation map obtained at 15:00 UTC (top right panel) clearly shows high rainfall accumulations in very good correspondence with the Palermo weather stations. Precipitation observed in the proximity of the Etna volcano are also well predicted.
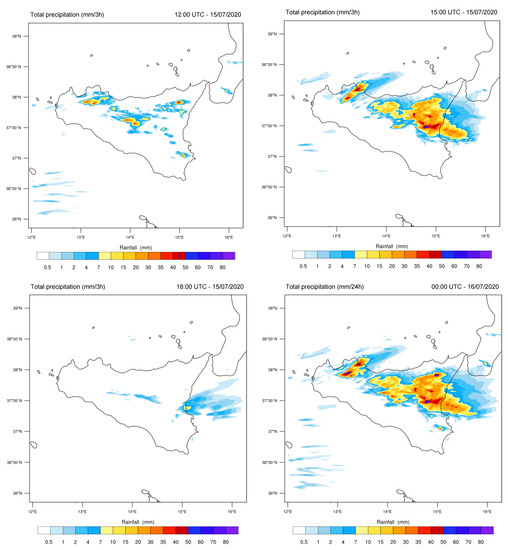
Figure 25.
Cumulative rainfall every three hours predicted by the WRF model with a domain of 1 km and calculated at 12:00 UTC (top left), 15:00 UTC (top right), and 18:00 UTC (bottom left) of 15 July 2020. The cumulative rainfall calculated along the whole day are reported in the bottom right panel.
Cumulative rainfall predicted by the WRF model with 1 km of spatial grid resolution were extracted and compared in the grid points close to the same weather stations analyzed in Figure 24. Figure 26 shows that the model predicts a flood precipitation rate between 12:00 and 14:00 UTC, in correspondence with Palermo, where the total accumulation at the end of the event was equal to 51.4 mm. A similar value (57 mm) is predicted for the weather station of San Giuseppe Jato, in the inner part of the province of Palermo (see Figure 21).
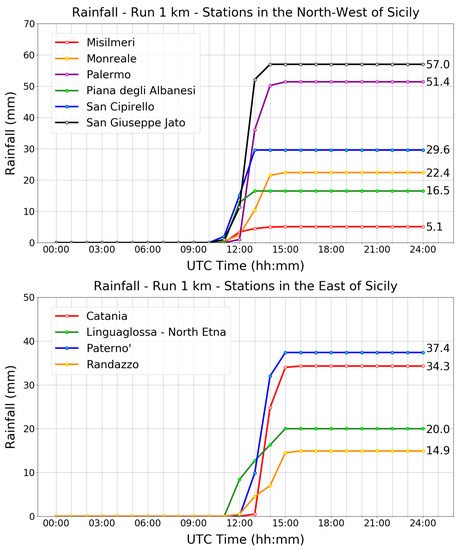
Figure 26.
Cumulative rainfall predicted by the WRF model for the whole day of 15 July 2020, with a domain of 1 km and in correspondence of six stations placed in the western part of Sicily (top) and of four weather stations placed in the eastern part of Sicily (bottom).
As far as the eastern sector is concerned, the 1-km simulation predicted widespread precipitation in the eastern sector of Sicily, with a peak of 37.4 mm on Paternò, 34.3 mm on Catania, 20 mm on Linguaglossa–Etna Nord and 14.9 mm on Randazzo (see Figure 22).
In order to verify the improved precision of the WRF model with a 1-km domain in comparison with the 3-km domain, we have performed a comparison among both of them and the rainfall values registered by the network of meteorological stations of the DRPC. Such a comparison is shown in Table 2. In particular, it is important to note that, although the WRF model with a 3-km domain predicts significant rainfall accumulation in the northwestern sector, it does not catch the exact position where the weather event takes place. Conversely, even if the final rainfall values registered on Palermo (134 mm) are not reproduced, the WRF model with a 1-km domain is considerably more precise in locating the various rainfall accumulations. Moreover, the latter improves the estimate of the precipitations on Palermo, predicting 51 mm in comparison with the 13 mm of the 3-km domain. Values predicted in the east part of Sicily are also more precise.

Table 2.
Comparison among cumulative rainfall values (in mm) at the end of the event observed by the DRPC weather stations and those predicted by the WRF model with spatial domains of 3 km and 1 km.
Additionally, in order to verify the accuracy of the model for the prediction of rainfall accumulations, we have computed the root mean square error (RMSE), taking into account observed values and the results of WRF simulations, both 3 km and 1 km of resolution. Results highlight that for the event of 15 July 2020, the performances of WRF 1-km simulation are better than those of WRF 3 km. In particular, the implementation of the finer resolution allowed us to decrease the RMSE value from 46. 98% (3-km model) to 31.83% (1-km model).
Analysis of Flash Flood Scenario
Finally, to evaluate the vertical atmosphere and compare it to flash flood scenario profile, a customized script has been developed with the aim of reproducing the radiosounding and theta-E diagram starting from the output of the WRF 1-km model.
The script is composed of two parts: the first is a client interface written in Javascript that loads the parameters from the output of the WRF. The second, written in Python, uses the library sharppy [50], which takes as initial parameters the main variables (temperature, RH, pressure, wind components for different vertical levels) from the output of the WRF. This script calculates the thermodynamic indices and performs an hodograph analysis.
The same output has been produced feeding the RAOB software (universal rawinsonde observation program) with the same starting parameters obtained from Wrfout.
In reference to the flash flood scenario, the following key indicators have been considered:
- tall skinny CAPE profile;
- uniformly deep moisture profile;
- high value of precipitable water;
- thick warm cloud depth.
- available moisture / K index / TT Index;
- slow storm movement;
- upper-level divergence;
- nearby surface boundary;
- poor lapse rate.
The first step was the automatic selection of the rows of interest (12:00 UTC–15:00 UTC) and the conversion/operations between the units. Furthermore, from the mixing ratio (U), we have obtained the RH value using the table of saturation mixing ratio to get Us (maximum possible water vapor amount) and the equation RH = U/Us.
In this way, all the data for the main five parameters have been stored in a specific numpy array.
In order to create the sounding, another function was used to have the dewpoint value instead of relative humidity.
For the standard thermodynamic indices, we have used standard function of the library and stored them in a specific array with the “key” value of the indices.
It has been used an interpolation function for the shear (0–3 km, 0–6 km) to find the pressure values which correspond to the specific level.
For the composite indices, we have used specific functions based on the common literature [51,52].
The script created also the plot (Figure 27) of the radiosounding and the theta-e profile. In particular, the radiosounding shows the temperature and dewpoint profile and also the theoretical air parcel line; in this case is at the right side respect to the temperature profile shows instability.
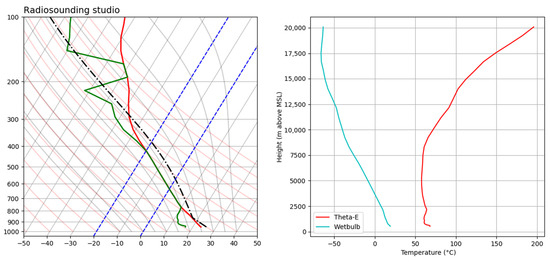
Figure 27.
Radiosounding profile (left), theta-E and wetbulb profile (right), obtained with data from WRF 1 km.
The final output of the script is a JSON file with all the calculated parameters. In Table 3, the most significant parameters are reported.

Table 3.
Numerical values of calculated parameters obtained through the customized script.
Additionally, we have developed a custom output in order to have the output data in the Raob format to be imported in the Raob software and re-create the same scenario for double checking. The Javascript client side allows us also to compare the parameters between:
- our custom script;
- real radiosounding for LICT from Wyoming University; and
- reanalysis sounding from GFS/ERA5.
Looking at the output of the script (first column of the Table 4), it is possible to check the presence of elements related to available moisture: high value of Td surface and Td (850 hPa), very high value of precipitable water (40 mm), high K index (38), very high value of theta-E (850 hPa). On the other hand, the prediction of the instability has been forecasted very well: the CAPE value greater than 1200, the TT index is 49, and the Litfed Index is −5 [53,54].

Table 4.
Table of comparison between parameters using WRF 1 km and GFS, ERA5 reanalysis.
Table 4 shows the comparison between some significant parameters for flash flood scenario in reference mainly to moisture, instability, and upper forcing. A comparison has been done between WRF 1 km and the global model. We choose the global model (GFS and ERA5 reanalysis) as a reference for comparison as this permits us to understand the different behavior in terms of a forecast of local high-resolution phenomena.
4. Conclusions
In the present work, we have investigated a meteorological event which took place in Sicily (Italy) on 15 July 2020 by means of the WRF model. The interest in such a phenomenon is due to its highly localized behavior, both in time and space. Typical meteorological models generally are not able to reproduce strongly localized pluviometric rainfall, especially if they are not properly configured for complex landscapes like Sicily, and if they do not implement highly resolved spatial grids. As proof of this, we have first performed WRF simulations of the model with a spatial resolution of 9 km, obtaining, for the day at issue, low-intensity rainfall scattered over most of the regional territory; slightly more intense accumulations were expected on the eastern areas. Conversely, the WRF model with a spatial resolution of 3 km, specially configured for Sicily, predicted the genesis of storms in the areas concerned.
However, to gain a satisfactory agreement with data observed by weather stations of the network of meteorological stations of the Regional Department of Civil Protection (DRPC) of Sicily, it has been necessary to implement a domain with a spatial resolution of 1 km.
Furthermore, the WRF model with spatial grid resolution of 1 km showed a high ability to produce accurate parameters for forecasting the flash flood scenario, compared to the global models GFS and the ERA5 reanalyses.
Upon summarizing the model predictions, it is shown that that the WRF model, if implemented in a high-resolution geographical domain and properly optimized for the territory under study, can be a valid tool for precise forecasts, including of localized and extreme weather events. It is also worth noting that an important role is played by the meteorologist who, on the basis of simulation output and of a careful analysis of the weather conditions (e.g., analysis of the thermodynamic vertical profile and atmospheric instability indices), can be able to predict the genesis of dangerous meteorological events.
Author Contributions
All authors contributed to conceptualization, methodology, investigation, writing, reviewing, and editing of the present work. All authors have read and agreed to the published version of the manuscript.
Funding
This work is to be framed within the Progetto di Ricerca e Sviluppo “SECESTA ViaSafe: applicazione della rete di monitoraggio della ricaduta di cenere vulcanica dell’Etna alla gestione della mobilità nel territorio etneo”, CUP code G69J18001010007, project identification code 08CT6202000208 in the context of the Programma Operativo Nazionale “Ricerca e Innovazione” 2014–2020 (PON R&I 2014–2020).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the Regional Department of Civil Protection (DRPC) of Sicily for data concerning the rainfall accumulations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cassola, F.; Ferrari, F.; Mazzino, A.; Lacorata, G.; Rotunno, R. Numerical simulations of Mediterranean heavy precipitation events with the WRF model: A verification exercise using different approaches. Atmos. Res. 2015, 164, 210–225. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lee, J.W. Assessment of the WRF model in reproducing a flash-flood heavy rainfall event over Korea. Atmos. Res. 2009, 93, 818–831. [Google Scholar] [CrossRef]
- Liu, J.; Bray, M.; Han, D. Sensitivity of the Weather Research and Forecasting (WRF) model to downscaling ratios and storm types in rainfall simulation. Hydrol. Process. 2012, 26, 3012–3031. [Google Scholar] [CrossRef]
- Chawla, I.; Osuri, K.K.; Mujumdar, P.P.; Niyogi, D. Assessment of the Weather Research and Forecasting (WRF) model for simulation of extreme rainfall events in the upper Ganga Basin. Hydrol. Earth Syst. Sci. 2018, 22, 1095–1117. [Google Scholar] [CrossRef]
- Avolio, E.; Federico, S. WRF simulations for a heavy rainfall event in southern Italy: Verification and sensitivity tests. Atmos. Res. 2018, 209, 14–35. [Google Scholar] [CrossRef]
- Mesinger, F. Limited Area Modeling: Beginnings, state of the art, outlook. In 50th Anniversary of Numerical Weather Prediction Commemorative Symposium, Book of Lectures; European Meteorological Society: Bonn, Germany, 2021; pp. 91–118. [Google Scholar]
- Coleman, J.; Law, K. Meteorology. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Rontu, L. Studies on Orographic Effects in a Numerical Weather Prediction Model; Finnish Meteorological Institute: Helsinki, Finland, 2007.
- Ntwali, D.; Ogwang, B.A.; Ongoma, V. The impacts of topography on spatial and temporal rainfall distribution over Rwanda based on WRF model. Atmos. Clim. Sci. 2016, 6, 145–157. [Google Scholar] [CrossRef]
- Lee, J.W.; Hong, S.Y. A numerical simulation study of orographic effects for a heavy rainfall event over Korea using the WRF model. Atmosphere 2006, 16, 319–332. [Google Scholar]
- Moya-Álvarez, A.S.; Martínez-Castro, D.; Kumar, S.; Estevan, R.; Silva, Y. Response of the WRF model to different resolutions in the rainfall forecast over the complex Peruvian orography. Theor. Appl. Climatol. 2019, 137, 2993–3007. [Google Scholar] [CrossRef]
- Mastrantonas, N.; Herrera-Lormendez, P.; Magnusson, L.; Pappenberger, F.; Matschullat, J. Extreme precipitation events in the Mediterranean: Spatiotemporal characteristics and connection to large-scale atmospheric flow patterns. Int. J. Climatol. 2021, 41, 2710–2728. [Google Scholar] [CrossRef]
- Dayan, U.; Nissen, K.; Ulbrich, U. Review Article: Atmospheric conditions inducing extreme precipitation over the eastern and western Mediterranean. Nat. Hazards Earth Syst. Sci. 2015, 15, 2525–2544. [Google Scholar] [CrossRef]
- Iriza, A.; Dumitrache, R.C.; Lupascu, A.; Stefan, S. Studies regarding the quality of numerical weather forecasts of the WRF model integrated at high-resolutions for the Romanian territory. Atmósfera 2016, 29, 11–21. [Google Scholar] [CrossRef]
- Uddin, M.J.; Samad, M.; Mallik, M. Impact of Horizontal Grid Resolutions for Thunderstorms Simulation over Bangladesh Using WRF-ARW Model. Dhaka Univ. J. Sci. 2021, 69, 43–51. [Google Scholar] [CrossRef]
- Powers, J.G. The Weather Research and Forecasting Model Overview, System Efforts, and Future Directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; Mesoscale and Microscale Meteorology Laboratory NCAR: Boulder, CO, USA, 2019. [Google Scholar]
- Castorina, G.; Colombo, F.; Caccamo, M.T.; Cannuli, A.; Insinga, V.; Maiorana, E.; Magazù, S. Cultural Heritage and Natural Hazard: How WRF Model Can Help to Protect and Safe Archaeological Sites. Int. J. Res. Environ. Sci. 2017, 3, 37–42. [Google Scholar]
- Colombo, F.; Castorina, G.; Caccamo, M.T.; Insinga, V.; Maiorana, E.; Magazù, S. IT Technologies for Science Application: Using Meteorological Local Area Model to Contrast the Hydrogeological Risks. Hydrol. Curr. Res. 2017, 8, 4. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Castorina, G.; Catalano, F.; Magazù, S. Rüchardt’s experiment treated by Fourier transform. Eur. J. Phys. 2019, 40, 025703. [Google Scholar] [CrossRef]
- Castorina, G.; Caccamo, M.T.; Magazù, S. A new approach to the adiabatic piston problem through the arduino board and innovative frequency analysis procedures. In New Trends in Physics Education Research; Magazù, S., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2018; pp. 133–156. [Google Scholar]
- Grell, G.A.; Peckham, S.E.; Schmitz, R.; McKeen, S.A.; Frost, G.; Skamarock, W.C.; Eder, B. Fully coupled “online” chemistry within the WRF model. Atmos. Environ. Atmos. Environ. 2005, 39, 6957–6975. [Google Scholar] [CrossRef]
- Rizza, U.; Brega, E.; Caccamo, M.T.; Castorina, G.; Morichetti, M.; Munaò, G.; Passerini, G.; Magazù, S. Analysis of the ETNA 2015 Eruption Using WRF-Chem Model and Satellite Observations. Atmosphere 2020, 11, 1168. [Google Scholar] [CrossRef]
- Rizza, U.; Donnadieu, F.; Magazu, S.; Passerini, G.; Castorina, G.; Semprebello, A.; Morichetti, M.; Virgili, S.; Mancinelli, E. Effects of Variable Eruption Source Parameters on Volcanic Plume Transport: Example of the 23 November 2013 Paroxysm of Etna. Remote Sens. 2021, 13, 4037. [Google Scholar] [CrossRef]
- Roger, S.R.; Pielke, A. Mesoscale Meteorological Modeling; Academic Press Inc: Cambridge, MA, USA, 2013; Volume 98. [Google Scholar]
- Holton, J.R. An Introduction to Dynamic Meteorology, 4th ed.; Elsevier Academic Press: Burlington, NJ, USA, 2004; Volume 88. [Google Scholar]
- Sarah, N.; Robert, S.; Ray, P.; Chen, K.; Lassman, A.; Brownlee, J. Grids in Numerical Weather and Climate Models. In Climate Change and Regional/Local Responses; InTech: London, UK, 2013. [Google Scholar]
- Caccamo, M.T.; Castorina, G.; Colombo, F.; Insinga, V.; Maiorana, E.; Magazù, S. Weather forecast performances for complex orographic areas: Impact of different grid resolutions and of geographic data on heavy rainfall event simulations in Sicily. Atmos. Res. 2017, 198, 22–33. [Google Scholar] [CrossRef]
- Ooyama, K.V. A thermodynamic foundation for modeling the moist atmosphere. J. Atmos. Sci. 1990, 47, 2580–2593. [Google Scholar] [CrossRef]
- Laprise, R. The Euler equations of motion with hydrostatic pressure as an independent variable. Mon. Weather Rev. 1992, 120, 197–207. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J. Prototypes for the WRF (Weather Research and Forecasting) model. Am. Meteorol. Soc. 2001. J11–J15, preprints. [Google Scholar]
- Wang, S.; Huang, S.; Li, Y. Sensitive numerical simulation and analysis of rainstorm using nested WRF model. J. Hydrodyn. 2006, 18, 578–586. [Google Scholar] [CrossRef]
- Jee, J.B.; Kim, S. Sensitivity Study on High-Resolution WRF Precipitation Forecast for a Heavy Rainfall Event. Atmosphere 2017, 8, 96. [Google Scholar] [CrossRef]
- Wang, W.; Gill, D. WRF nesting. In WRF Tutorial; NCAR: Boulder, CO, USA, 2012. [Google Scholar]
- Emmanouil, G.; Vlachogiannis, D.; Sfetsos, A. Exploring the ability of the WRF-ARW atmospheric model to simulate different meteorological conditions in Greece. Atmos. Res. 2021, 247, 105226. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Mesinger, F. Forecasting upper tropospheric turbulence within the framework of the Mellor-Yamada 2.5 closure. In Research Activities in Atmospheric and Oceanic Modelling; CAS/JSC WGNE Rep. No. 18; WMO: Geneva, Switzerland, 1993; pp. 4.28–4.29. [Google Scholar]
- Mukul Tewari, N.; Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; et al. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 10 January 2004; pp. 11–15. [Google Scholar]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain-Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Villalba-Pradas, A.; Tapiador, F.J. Empirical values and assumptions in the convection schemes of numerical models. Geosci. Model Dev. 2022, 15, 3447–3518. [Google Scholar] [CrossRef]
- Somses, S.; Bopape, M.J.M.; Ndarana, T.; Fridlind, A.; Matsui, T.; Phaduli, E.; Limbo, A.; Maikhudumu, S.; Maisha, R.; Rakate, E. Convection Parametrization and Multi-Nesting Dependence of a Heavy Rainfall Event over Namibia with Weather Research and Forecasting (WRF) Model. Climate 2020, 8, 112. [Google Scholar] [CrossRef]
- Castorina, G.; Caccamo, M.T.; Magazù, S. Study of convective motions and analysis of the impact of physical parametrization on the WRF-ARW forecast model. Atti della Accademia Peloritana 2019, 97, A19. [Google Scholar]
- Castorina, G.; Caccamo, M.T.; Colombo, F.; Magazù, S. The Role of Physical Parameterizations on the Numerical Weather Prediction: Impact of Different Cumulus Schemes on Weather Forecasting on Complex Orographic Areas. Atmosphere 2021, 12, 616. [Google Scholar] [CrossRef]
- Castorina, G.; Caccamo, M.T.; Magazù, S.; Restuccia, L. Multiscale mathematical and physical model for the study of nucleation processes in meteorology. Atti della Accademia Peloritana 2018, 96, A6. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Radu, R.; Schepers, D.; Simmons, A.; Soci, C.; et al. Global reanalysis: Goodbye ERA-Interim, hello ERA5. ECMWF Newsl. 2019, 159, 17–24. [Google Scholar]
- Giuliacci, M.; Corazzon, P.; Giuliacci, A. Prevedere il Tempo con Internet; Alpha Test: Milano, Italy, 2007. [Google Scholar]
- Francipane, A.; Pumo, D.; Sinagra, M.; La Loggia, G.; Noto, L.V. A paradigm of extreme rainfall pluvial floods in complex urban areas: The flood event of 15 July 2020 in Palermo (Italy). Nat. Hazards Earth Syst. Sci. 2021, 21, 2563–2580. [Google Scholar] [CrossRef]
- Blumberg, W.G.; Halbert, K.T.; Supinie, T.A.; Marsh, P.T.; Thompson, R.L.; Hart, J.A. SHARPpy: An open-source sounding analysis toolkit for the atmospheric sciences. Bull. Am. Meteorol. Soc. 2017, 98, 1625–1636. [Google Scholar] [CrossRef]
- Thompson, R.L.; Smith, B.T.; Grams, J.S.; Dean, A.R.; Broyles, C. Convective Modes for Significant Severe Thunderstorms in the Contiguous United States. Part II: Supercell and QLCS Tornado Environments. Weather Forecast. 2012, 27, 1136–1154. [Google Scholar] [CrossRef]
- Bunkers, M.J.; Barber, D.A.; Thompson, R.L.; Edwards, R.; Garner, J. Choosing a Universal Mean Wind for Supercell Motion Prediction. J. Oper. Meteorol. 2014, 2, 115–129. [Google Scholar] [CrossRef]
- Daley, W.M.; Baker, D.J.; Kelly, J.J., Jr. Service Assessment-Central Florida Tornado Outbreak February 22–23; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1998.
- Miller, R.C. Notes on Analysis and Severe-Storm Forecasting Procedures of the Air Force Global Weather Central; AWS: Ashburn, VA, USA, 1975; Volume 200. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).