Regional Predictions of Air Pollution in Guangzhou: Preliminary Results and Multi-Model Cross-Validations
Abstract
1. Introduction
2. Methods, Data, and Model Simulation Evaluation
2.1. Model Descriptions
2.1.1. WRF-Chem Model Configuration
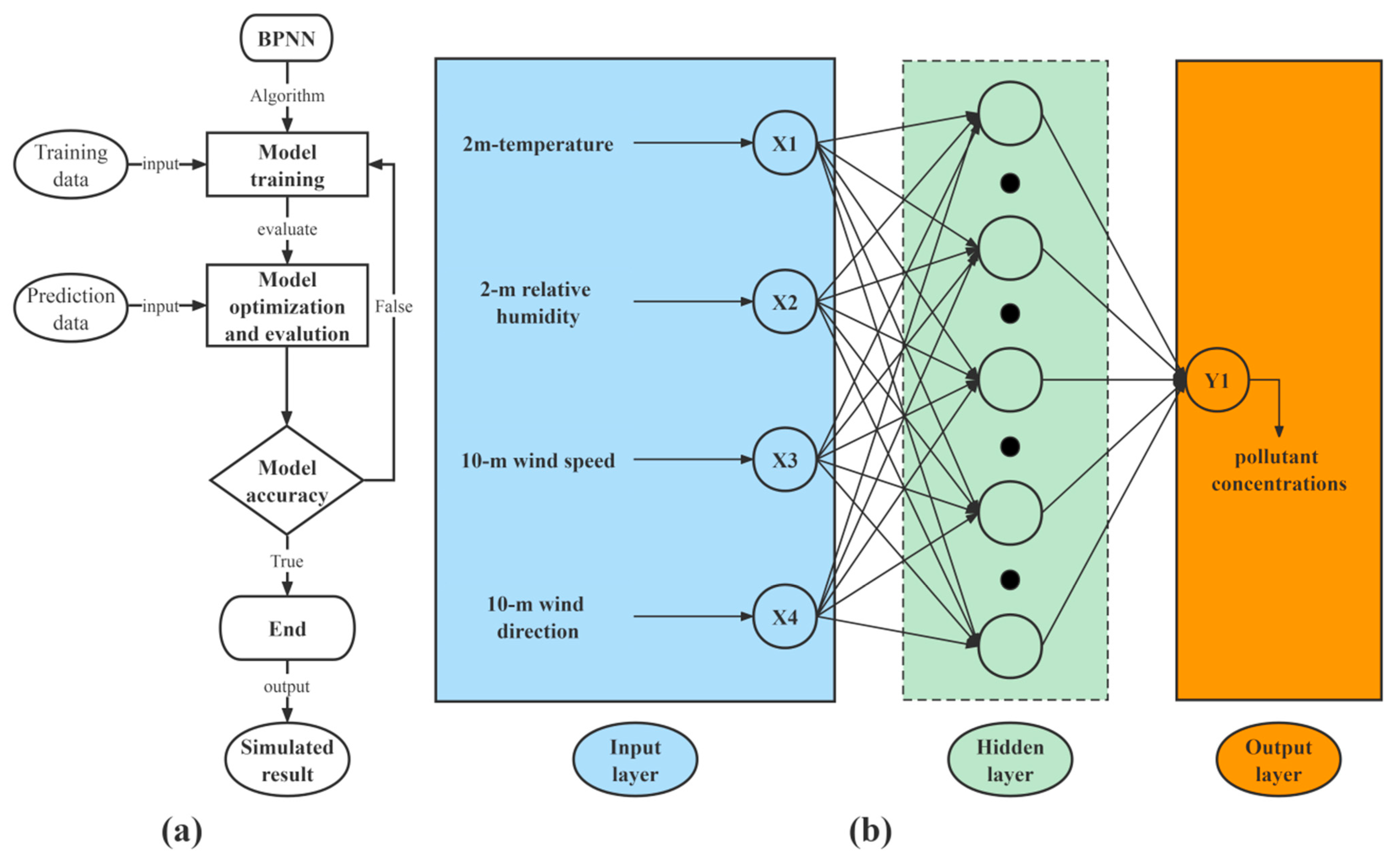
2.1.2. Back Propagation Neural Network
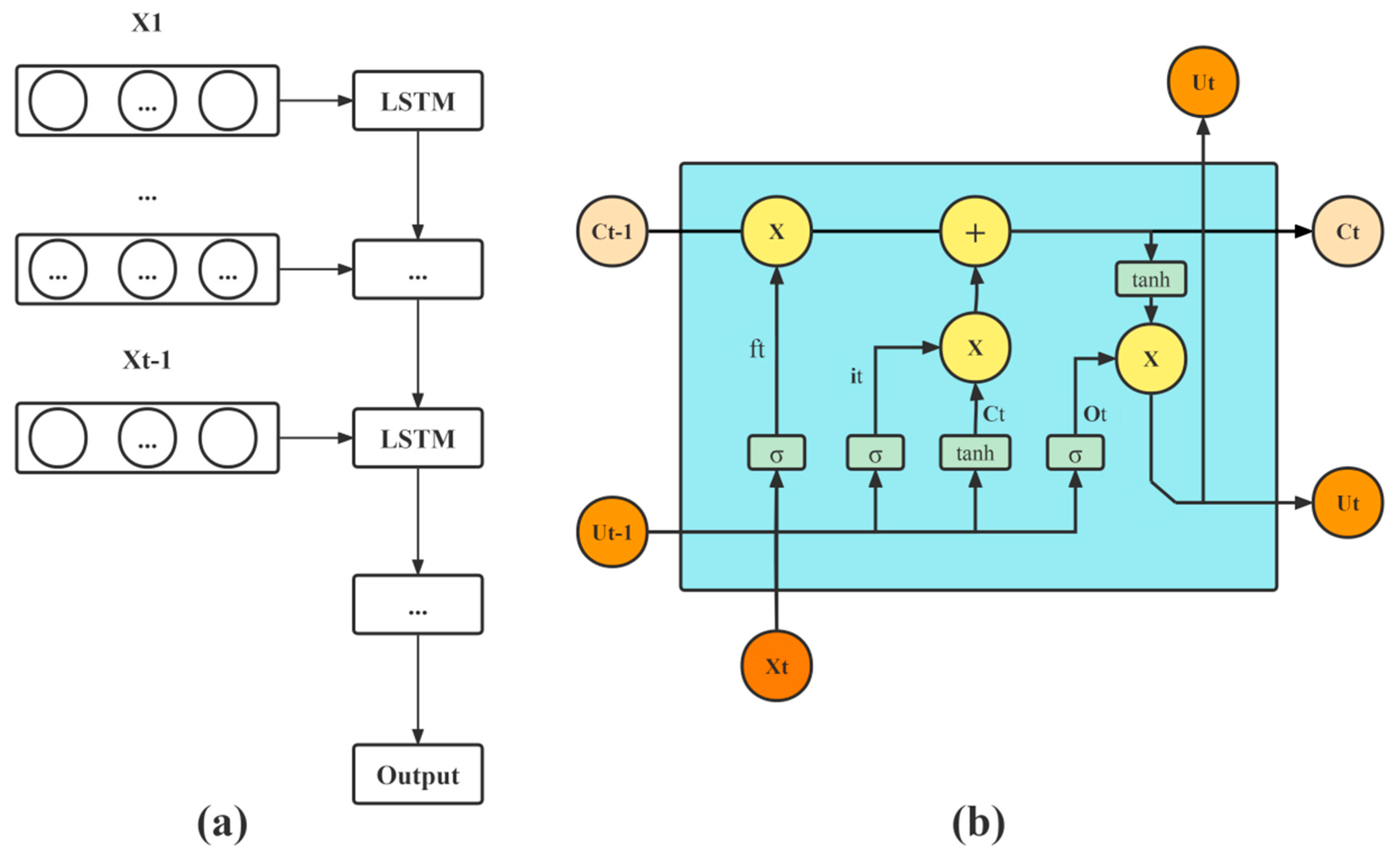
2.1.3. Long Short-Term Memory
2.2. Observed Data
2.3. Model Simulation Evaluation
- (1)
- MB and ME are, respectively, the average and absolute error between the simulated results (Cm) and the observed results (Co). They can show actual situations of the simulated value errors. RMSE is the arithmetic square root of the mean square error (MSE), while the MSE is the average value of the square of the error between the simulated results (Cm) and the observed results (Co). The smaller the values of MB, ME, and RMSE, the better the accuracy of the model simulated result.
- (2)
- To evaluate the simulation ability of the models, we choose the Pearson CC to measure how well the simulated results fit the observed results. The larger the CC value, the better the regression effect and the more accurate the model. If the value of R is more than 0.6, we think the model has good accuracy.
- (3)
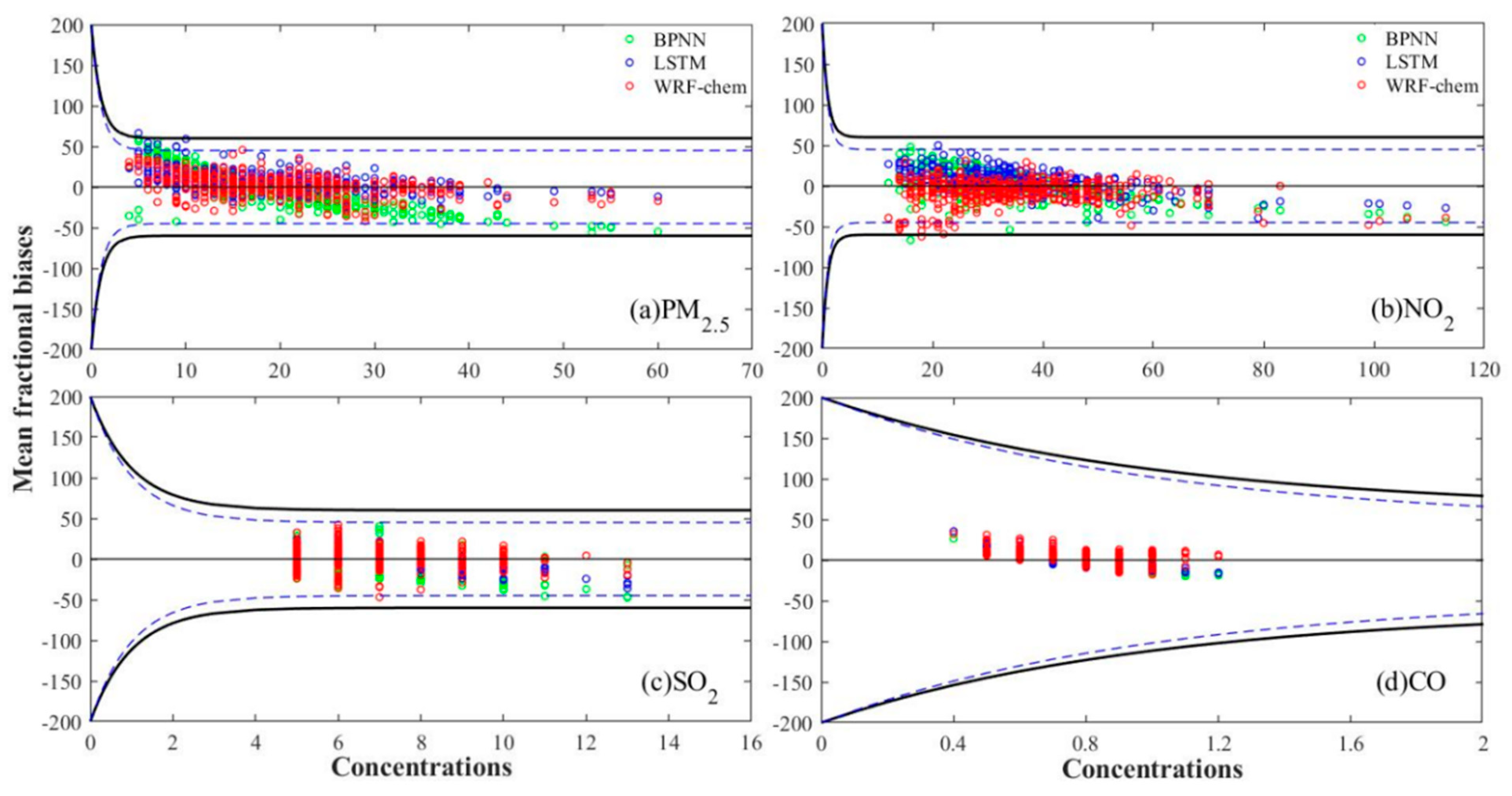
- NMB or (and) MFB can provide a good sense of the model performance, in that it does not need an observation-based minimum threshold. The NMB ranges from −100% to +∞ while MFB from −200% to +200%. These indices have the advantage of limiting the maximum deviation; meanwhile, they are widely used for evaluating the model performance in the accuracy of the pollutant concentration simulations. The model performance has met the criteria when the MFB is less than or equal to ± 60% [59]. In this study, the model is regarded as having superior model performance when the MFB is <± 45%.
3. Results
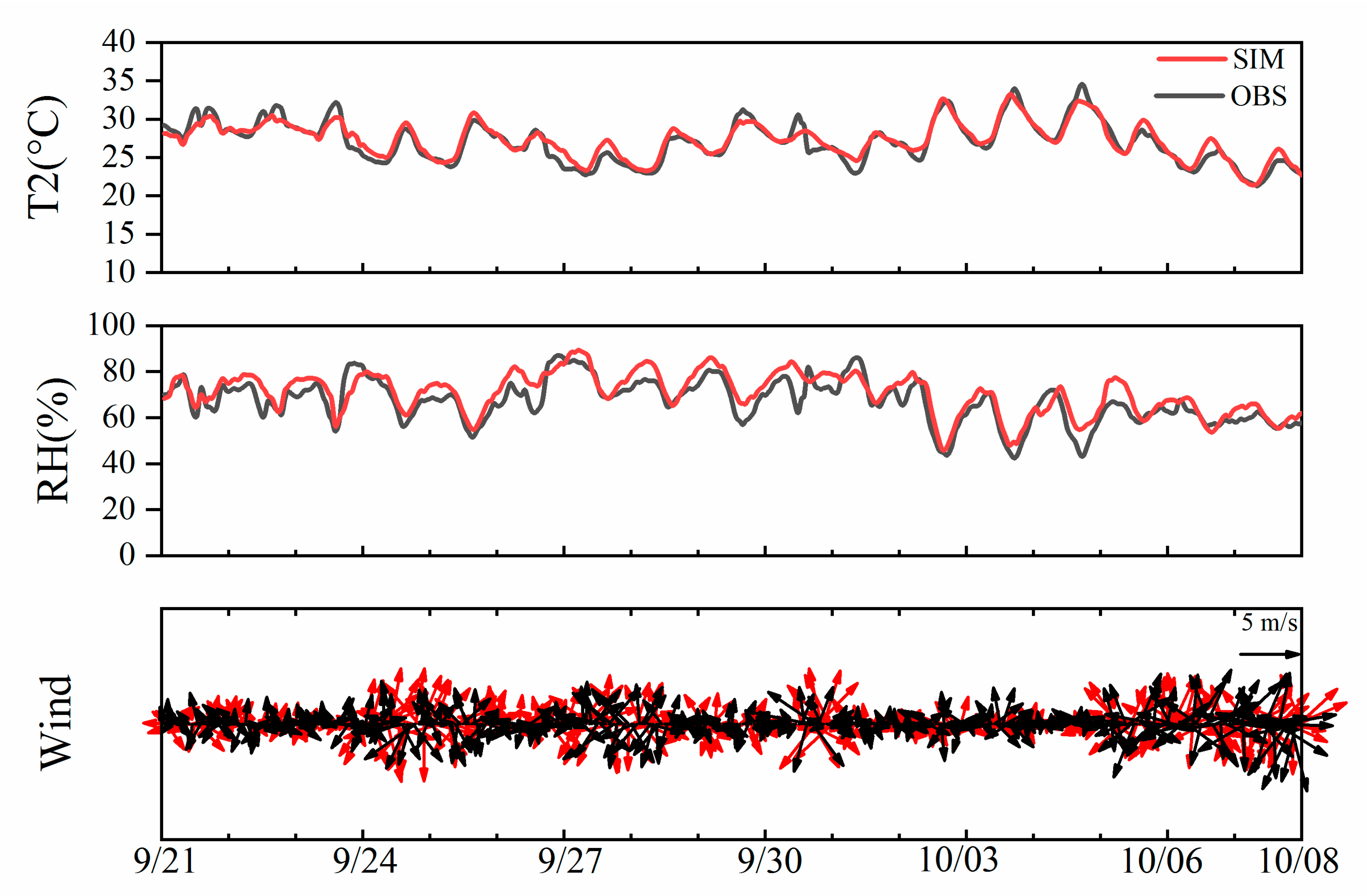
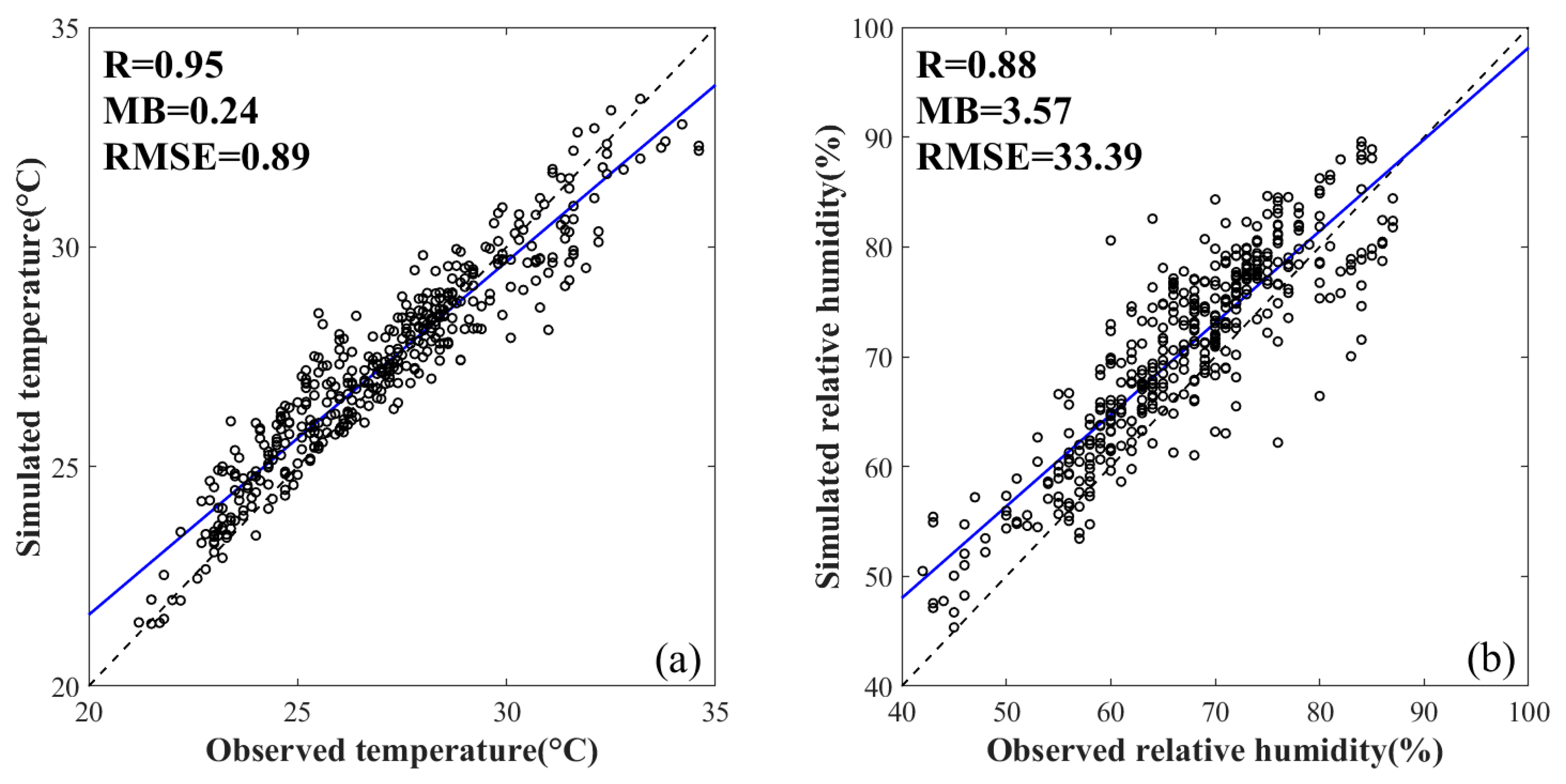
3.1. Meteorological Element Evaluation
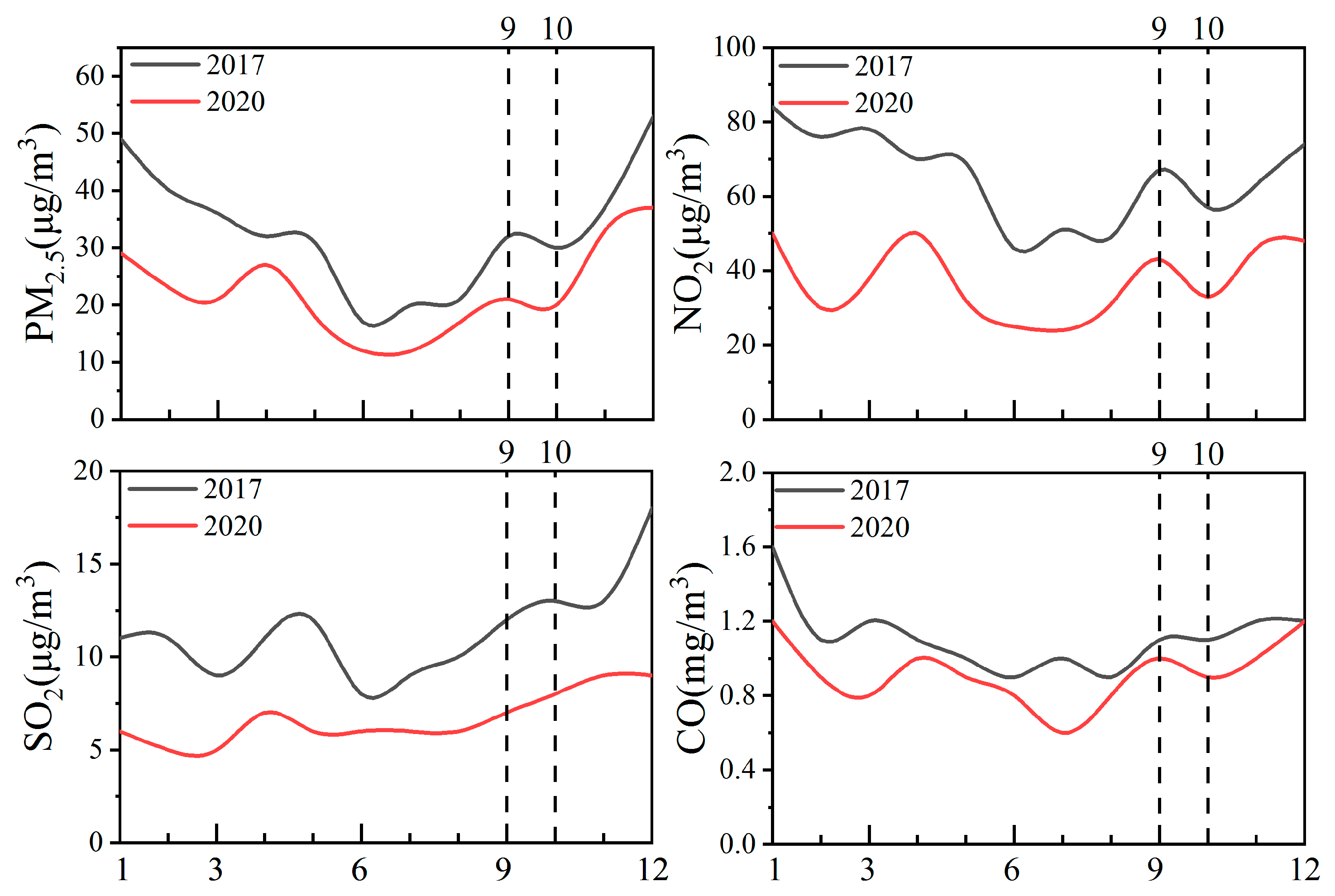
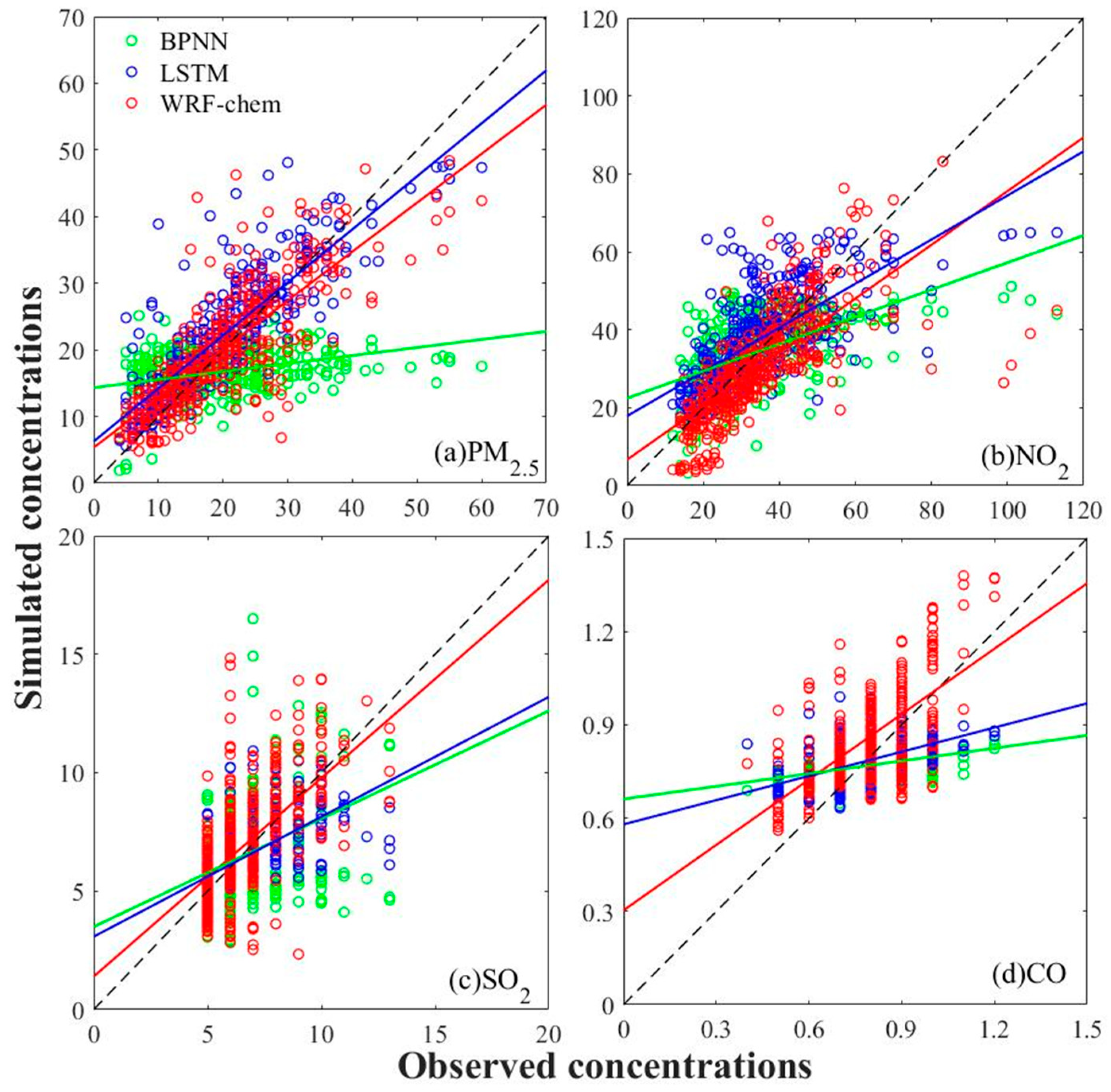
3.2. Pollutant Concentration Evaluation
4. Discussion
5. Conclusions
- (1)
- Compared with the monitoring station observations, WRF-Chem can reasonably simulate the magnitude and temporal variations in the air pollutant concentrations, capture the peaks of the observed concentrations, and conform to the evaluation criterion for model performance.
- (2)
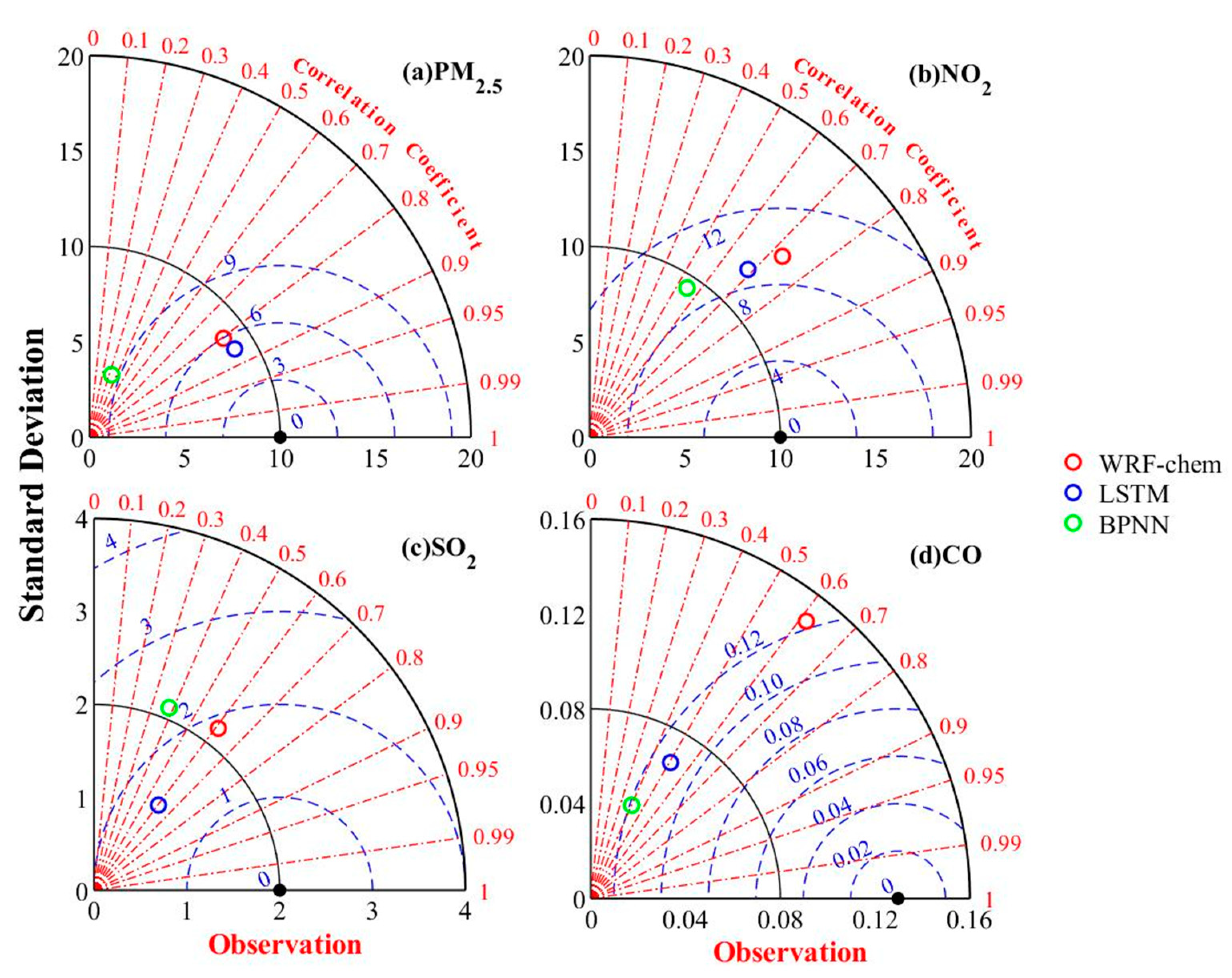
- For the PM2.5 concentration simulations, WRF-Chem was superior to the BPNN model in all respects such as simulation bias, correlation coefficient, and model performance. Although the WRF-Chem correlation coefficient and model performance were slightly worse than those of the LSTM, WRF-Chem more effectively simulated the extremum than the LSTM. For the other pollutant concentrations, the WRF-Chem model correlation coefficients and model performances were better than those of the LSTM and BPNN. According to the negligible simulation error, excellent simulation performance, and high correlation, the WRF-Chem simulation was superior and the most reasonable for all pollutants.
- (3)
- As model input data, the observed pollutant concentrations were directly related to the NN model simulated results. In other words, the types and amounts of input data had a crucial influence on the simulation accuracies and performances of the NN models, especially for the BPNN model. If there are enough types and amounts of input data, the BPNN model can use the gradient search technique to minimize the MSE between the output data and testing data. In this case, the BPNN model can accurately simulate the pollutant concentrations. The LSTM model simulated the pollutant concentrations by effectively and automatically extracting the temporal correlations within the previous concentrations (the input data), so they also influenced the LSTM model performance. The LSTM model can capture the pollutant concentrations and have considerable model performance, on condition that the pollutant concentration time series had obvious regularities. However, insufficient types and amounts of input data, and the limited accuracies of the SO2 and CO measuring apparatuses, ultimately resulted in relatively poor NN models’ performance.
- (4)
- The meteorological input data, which served as the initial and boundary meteorological conditions for the WRF-Chem model, were indispensable. Meanwhile, the meteorological input data helped us obtain precise meteorological element simulations, and ultimately enhance the simulation accuracy of the pollutant concentration. As emission input data, the emissions inventories directly provide the emissions data (i.e., the emission rate and the emission allocation) to the WRF-Chem model, so the modified emissions inventories can contribute largely and positively to accurate pollutant concentration simulations in the study.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Hyslop, N.P. Impaired visibility: The air pollution people see. Atmos. Environ. 2009, 43, 182–195. [Google Scholar] [CrossRef]
- Akimoto, H. Global air quality and pollution. Science 2003, 302, 1716–1719. [Google Scholar] [CrossRef] [PubMed]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef]
- Manzoor, S.; Kulshrestha, U. Atmospheric aerosols: Air quality and climate change perspectives. Curr. World Environ. 2015, 10, 738–746. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Smith, S.J.; Easter, R.; Ma, P.L.; Qian, Y.; Yu, H.B.; Rasch, P.J. Global source attribution of sulfate concentration and direct and indirect radiative forcing. Atmos. Chem. Phys. 2017, 17, 8903–8922. [Google Scholar] [CrossRef]
- Chen, Z.; Cui, L.; Cui, X.; Li, X.; Yu, K.; Yue, K.; Dai, Z.; Zhou, J.; Jia, G.; Zhang, J. The association between high ambient air pollution exposure and respiratory health of young children: A cross sectional study in Jinan, China. Sci. Total Environ. 2019, 656, 740–749. [Google Scholar] [CrossRef]
- El Morabet, R. Effects of Outdoor Air Pollution on Human Health. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Gautam, S.; Patra, A.K.; Kumar, P. Status and chemical characteristics of ambient PM2.5 pollutions in China: A review. Environ. Dev. Sustain. 2019, 21, 1649–1674. [Google Scholar] [CrossRef]
- Gautam, S.; Yadav, A.; Tsai, C.J.; Kumar, P. A review on recent progress in observations, sources, classification and regulations of PM2.5 in Asian environments. Environ. Sci. Pollut. Res. 2016, 23, 21165–21175. [Google Scholar] [CrossRef]
- Tuccella, P.; Curci, G.; Visconti, G.; Bessagnet, B.; Menut, L.; Park, R.J. Modeling of gas and aerosol with WRF/Chem over Europe: Evaluation and sensitivity study. J. Geophys. Res. Atmos. 2012, 117, D03303. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Y.; Hao, J. Simulating aerosol–radiation–cloud feedbacks on meteorology and air quality over eastern China under severe haze conditions in winter. Atmos. Chem. Phys. 2015, 15, 2387–2404. [Google Scholar] [CrossRef]
- Yu, Y.U.; Liao, L.; Cui, X.D.; Chen, F. Effects of different anthropogenic emission inventories on simulated air pollutants concentrations: A case study in Zhejiang Province. Clim. Environ. Res. 2017, 22, 519–537. [Google Scholar]
- Cheng, C.T.; Wang, W.C.; Chen, J.P. Simulation of the effects of increasing cloud condensation nuclei on mixed-phase clouds and precipitation of a front system. Atmos. Res. 2010, 96, 461–476. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn Sate–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Jat, R.; Gurjar, B.R.; Lowe, D. Regional pollution loading in winter months over India using high resolution WRF-Chem simulation. Atmos. Res. 2021, 249, 105326. [Google Scholar] [CrossRef]
- Grell, G.A.; Peckham, S.E.; Schmitz, R.; McKeen, S.A.; Wilczak, J.; Eder, B. Fully coupled ‘‘online’’ chemistry within the WRF model. Atmos. Environ. 2005, 39, 6957–6975. [Google Scholar] [CrossRef]
- Baro, R.; Jimenez-Guerrero, P.; Balzarini, A.; Curci, G.; Forkel, R.; Grell, G.; Hirtl, M.; Honzak, L.; Langer, M.; Perez, J.L. Sensitivity analysis of the microphysics scheme in WRF-Chem contributions to AQMEII phase 2. Atmos. Environ. 2015, 115, 620–629. [Google Scholar] [CrossRef]
- Mohan, M.; Gupta, M. Sensitivity of PBL parameterizations on PM10 and ozone simulation using chemical transport model WRF-Chem over a sub-tropical urban airshed in India. Atmos. Environ. 2018, 185, 53–63. [Google Scholar] [CrossRef]
- Zhou, G.; Xu, J.; Xie, Y.; Chang, L.; Gao, W.; Gu, Y.; Zhou, J. Numerical air quality forecasting over eastern China: An operational application of WRF-Chem. Atmos. Environ. 2017, 153, 94–108. [Google Scholar] [CrossRef]
- Sha, T.; Ma, X.; Jia, H.; Tian, R.; Chang, Y.; Cao, F.; Zhang, Y. Aerosol chemical component: Simulations with WRF-Chem and comparison with observations in Nanjing. Atmos. Environ. 2019, 218, 116982. [Google Scholar] [CrossRef]
- Wang, X.; Xiang, Y.; Liu, W.; Lv, L.; Dong, Y.; Fan, G.; Ou, J.P.; Zhang, T.S. Vertical profiles and regional transport of ozone and aerosols in the Yangtze River Delta during the 2016 G20 summit based on multiple lidars. Atmos. Environ. 2021, 259, 118506. [Google Scholar] [CrossRef]
- Matsui, H.; Koike, M.; Kondo, Y.; Takegawa, N.; Kita, K.; Miyazaki, Y.; Hu, M.; Chang, S.Y.; Blake, J.D.; Fast, R.A.; et al. Spatial and temporal variations of aerosols around Beijing in summer 2006: Model evaluation and source apportionment. J. Geophys. Res. 2009, 114, D22207. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Djalalova, I.; McKeen, S.; Bianco, L.; Bao, J.W.; Grell, G.; Peckham, S.; Mathur, R.; McQueen, J.; Lee, P. Analysis of regional meteorology and surface ozone during the TexAQS II field program and an evaluation of the NMM-CMAQ and WRF-Chem air quality models. J. Geophys. Res. 2009, 114, D00F14. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Wang, L.; Zhang, Q.; Duan, F.; He, K. Application of WRF/Chem over East Asia: Part II. Model improvement and sensitivity simulations. Atmos. Environ. 2016, 124, 301–320. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Wang, L.; Zhang, Q.; Duan, F.; He, K. Application of WRF/Chem over East Asia: Part I. Model evaluation and intercomparison with MM5/CMAQ. Atmos. Environ. 2016, 124, 285–300. [Google Scholar] [CrossRef]
- Pérez, P.; Trier, A.; Reyes, J. Prediction of PM2.5 concentrations several hours in advance using neural networks in Santiago, Chile. Atmos. Environ. 2000, 34, 1189–1196. [Google Scholar] [CrossRef]
- Zheng, H.; Shang, X. Study on prediction of atmospheric PM2.5 based on RBF neural network. In Proceedings of the 2013 Fourth International Conference on Digital Manufacturing & Automation, Shinan, China, 29–30 June 2013; pp. 1287–1289. [Google Scholar]
- Zhao, J.; Deng, F.; Cai, Y.; Chen, J. Long short-term memory-Fully connected (LSTM-FC) neural network for PM 2.5 concentration prediction. Chemosphere 2019, 220, 486–492. [Google Scholar] [CrossRef]
- Gu, J.; Yang, B.; Brauer, M.; Zhang, K.M. Enhancing the evaluation and interpretability of data-driven air quality models. Atmos. Environ. 2021, 246, 118–125. [Google Scholar] [CrossRef]
- Patra, A.K.; Gautam, S.; Majumdar, S.; Prashant, K. Prediction of particulate matter concentration profile in an opencast copper mine in India using an artificial neural network model. Air Qual. Atmos. Health 2016, 9, 697–711. [Google Scholar] [CrossRef]
- Ni, X.L.; Cao, C.X.; Zhou, Y.K.; Cui, X.H.; Singh, R.P. Spatio-Temporal Pattern Estimation of PM2.5 in Beijing-Tianjin-Hebei Region Based on MODIS AOD and Meteorological Data Using the Back Propagation Neural Network. Atmosphere 2018, 9, 105. [Google Scholar] [CrossRef]
- Li, X.; Peng, L.; Yao, X.J.; Cui, S.L.; Hu, Y.; You, C.Z.; Chi, T.H. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back propagating errors. Nature 1986, 5, 533–536. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar]
- Zaveri, R.A.; Peters, L.K. A new lumped structure photochemical mechanism for large-scale applications. J. Geophys. Res. Atmos. 1999, 104, 30387–30415. [Google Scholar] [CrossRef]
- Zaveri, R.A.; Easter, R.C.; Fast, J.D.; Peters, L.K. Model for simulating aerosol interactions and chemistry (MOSAIC). J. Geophys. Res. Atmos. 2008, 113, D13204. [Google Scholar] [CrossRef]
- Chen, S.H.; Sun, W.Y. A one-dimensional time dependent cloud model. J. Meteorol. Soc. Jpn. 2002, 80, 99–118. [Google Scholar] [CrossRef]
- Grell, G.A.; Dezső, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29, 1693. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and Verification of the Unified NOAH Land Surface Model in the WRF Model. 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction. pp. 11–15. Available online: https://www2.mmm.ucar.edu/wrf/users/physics/phys_refs/LAND_SURFACE/noah.pdf (accessed on 22 May 2022).
- Madronich, S. Photodissociation in the Atmosphere: 1. Actinic flux and the effects of ground reflections and clouds. J. Geophys. Res. 1987, 92, 9740–9752. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Geng, G.N.; Hong, C.P.; Liu, F.; Song, Y.; Tong, D.; Zheng, B.; Cui, H.Y.; Man, H.Y.; et al. Anthropogenic emission inventories in China: A review. Natl. Sci. Rev. 2017, 4, 834–866. [Google Scholar] [CrossRef]
- Zheng, B.; Tong, D.; Li, M.; Liu, F.; Hong, C.P.; Geng, G.N.; Li, H.Y.; Li, X.; Peng, L.Q.; Qi, J.; et al. Trends in China’s anthropogenic emissions since 2010 as the consequence of clean air actions. Atmos. Chem. Phys. 2018, 18, 14095–14111. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, J.; Zhang, X.; Tian, X.; Zhang, J.; Wang, Y.; Duan, J.; Li, X. Synergy of satellite and ground based observations in estimation of particulate matter in eastern China. Sci. Total Environ. 2012, 433, 20–30. [Google Scholar] [CrossRef]
- Yao, L.; Lu, N. Spatiotemporal distribution and short-term trends of particulate matter concentration over china, 2006-2010. Environ. Sci. Pollut. Res. 2014, 21, 9665–9675. [Google Scholar] [CrossRef]
- Mao, X.; Shen, T.; Feng, X. Prediction of hourly ground-level PM2.5 concentrations 3 days in advance using neural networks with satellite data in eastern China. Atmos. Pollut. Res. 2017, 8, 1005–1015. [Google Scholar] [CrossRef]
- Reich, S.L.; Gomez, D.R.; Dawidowski, L.E. Artificial neural network for the identification of unknown air pollution sources. Atmos. Environ. 1999, 33, 3045–3052. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Kalchbrenner, N.; Danihelka, I.; Graves, A. Grid Long Short-Term Memory. arXiv 2015, arXiv:1507.01526. [Google Scholar]
- Lu, R.; Turco, R.P.; Jacobson, M.Z. An integrated air pollution modeling system for urban and regional scales: 2. simulations for SCAQS 1987. J. Geophys. Res. Atmos. 1997, 102, 6081–6098. [Google Scholar] [CrossRef]
- Boylan, J.W.; Russell, A.G. PM and light extinction model performance metrics, goals, and criteria for three-dimensional air quality models. Atmos. Environ. 2006, 40, 4946–4959. [Google Scholar] [CrossRef]
- Hussein, T.; Karppinen, A.; Kukkonen, J.; Härkönen, J.; Aalto, P.; Hämeri, K.; Kerminen, V.M.; Kulmala, M. Meteorological dependence of size-fractionated number concentrations of urban aerosol particles. Atmos. Environ. 2006, 40, 1427–1440. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Q.; Kurokawa, J.I.; Woo, J.H.; He, K.B.; Lu, Z.F.; Ohara, T.; Song, Y.; Streets, D.G.; Carmichael, G.R.; et al. MIX: A mosaic Asian anthropogenic emission inventory under the international collaboration framework of the MICS-Asia and HTAP. Atmos. Chem. Phys. 2017, 17, 935–963. [Google Scholar] [CrossRef]
- Teixeira, J.C.; Carvalho, A.C.; Tuccella, P.; Curci, G.; Rocha, A. WRF-Chem sensitivity to vertical resolution during a saharan dust event. Phys. Chem. Earth-Parts A/B/C 2016, 94, 188–195. [Google Scholar] [CrossRef]
- Kolehmainen, M.; Martikainen, H.; Ruuskanen, J. Neural networks and periodic components used in air quality forecasting. Atmos. Environ. 2001, 35, 815–825. [Google Scholar] [CrossRef]
- Li, G.H.; Bei, N.F.; Cao, J.J.; Hu, R.J.; Wang, J.R.; Feng, T.; Wang, Y.C.; Liu, S.X.; Zhang, Q.; Tie, X.X.; et al. A possible pathway for rapid growth of sulfate during haze days in China. Atmos. Chem. Phys. 2017, 17, 3301–3316. [Google Scholar] [CrossRef]
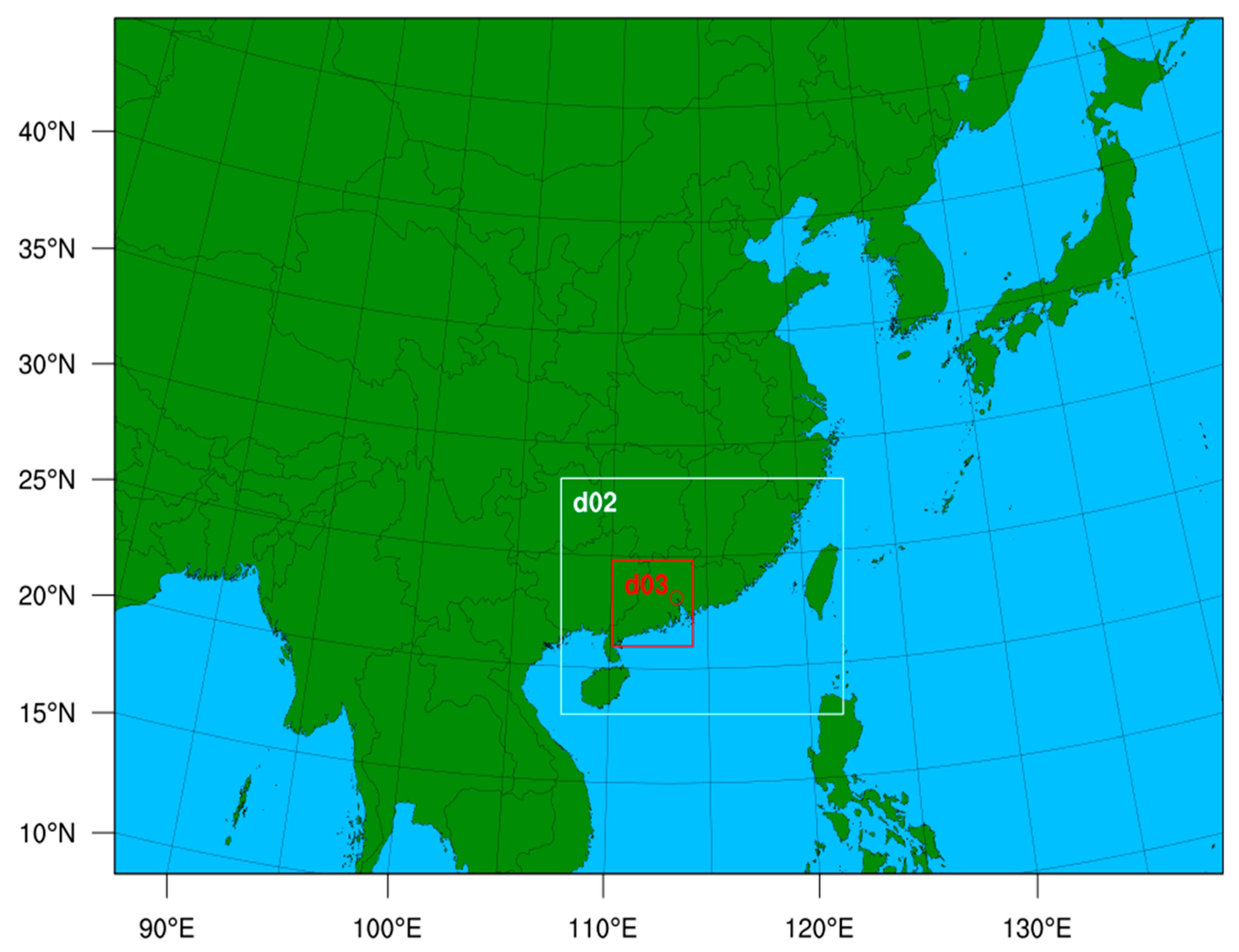
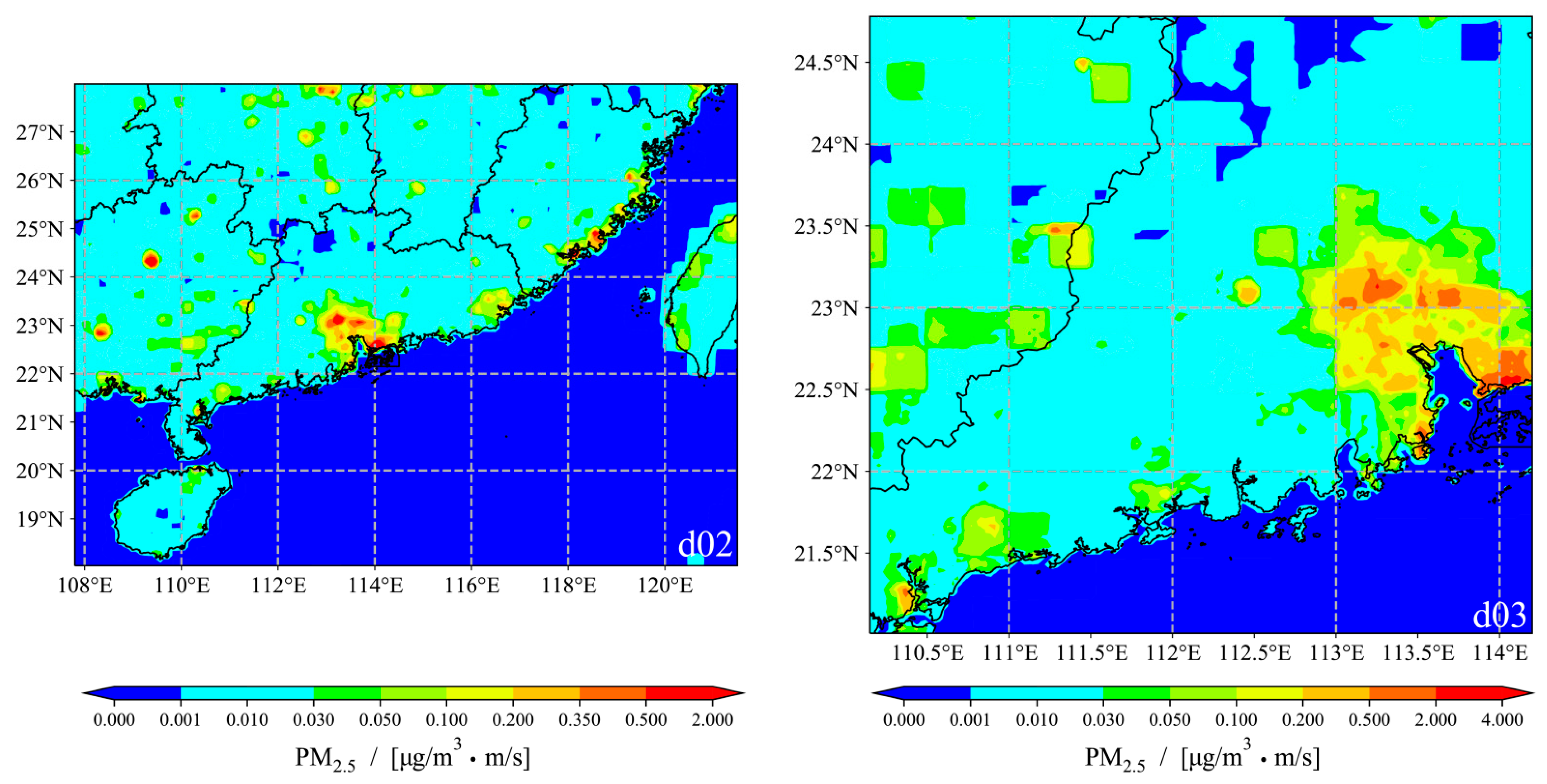

| Study Area (Place) | Pollutant Types | Key Contributions | Author (Year) |
|---|---|---|---|
| Thomson Farm, Harvard Forest | PM2.5, O3, SO2, NOX | They first published the comparison of the WRF-Chem model simulations and other CTMs’ simulations. | Grell et al. (2005) [16] |
| Europe | PM2.5, PM10, O3, SO2, | They used different microphysical schemes in the WRF-Chem model and compared the different simulation results with the observed results. | Rocio et al. (2015) [17] |
| Delhi | PM10, O3 | They evaluated the WRF-Chem model’s performance in Delhi by using the different PBL schemes. | Mohan et al. (2018) [18] |
| Eastern China | PM2.5, SO2, NO2, CO | They evaluated the WRF-Chem model’s performance in eastern China, and the simulation error reasons were analyzed. | Zhou et al. (2017) [19] |
| Nanjing | PM2.5, SO2, NO2, NH3 | They used the WRF-Chem model to simulate the pollutant concentrations, with the model successfully reproducing four localized haze episodes in Nanjing. | Sha et al. (2019) [20] |
| East Asia | PM2.5, CO, NO2, SO2, O3 | They found that the WRF-Chem model was better than the CMAQ model for pollutant simulation performance over East Asia. | Zhang et al. (2016) [25] |
| Beijing–Tianjin–Hebei (BTH) region | PM2.5 | They used the BPNN model approach to successfully predict the pollutant concentrations in the study area for the period 2014–2016. | Ni et al. (2018) [31] |
| Beijing city | PM2.5 | They proposed the LSTME model to predict the pollutant concentrations, with the model superior to several other NN models. | Li et al. (2017) [32] |
| Description | WRF Options |
|---|---|
| Microphysics | Purdue Lin Scheme (Chen and Sun, 2002) [40] |
| Cumulus parameterization | Grell 3D (Grell and Dévényi, 2002) [41] |
| Longwave radiation model | RRTMG scheme (Mlawer et al., 1997) [42] |
| Shortwave radiation model | RRTMG scheme (Iacono et al., 2008) [43] |
| Planetary boundary layer (PBL) scheme | Yonsei University, YSU (Hong et al., 2006) [44] |
| Surface layer physics | Revised MM5 Monin–Obukhov scheme (Jiménez et al., 2012) [45] |
| Land surface model | Unified Noah land surface model (Tewari et al., 2004) [46] |
| Photolysis scheme | Madronich (TUV) (Madronich, 1987) [47] |
| Type | Description | Measuring Apparatus |
|---|---|---|
| T2 | Observed actual value of temperature | Vaisala WXT520 |
| RH | Observed actual value of relative humidity | Vaisala WXT520 |
| WS | Observed actual value of wind speed | Vaisala WXT520 |
| WD | Observed actual value of wind direction | Vaisala WXT520 |
| PM2.5 | Observed actual value of PM2.5 concentration | Thermo Scientific 5030i |
| NO2 | Observed actual value of NO2 concentration | Thermo Scientific 42i |
| CO | Observed actual value of CO concentration | Thermo Scientific 48i |
| SO2 | Observed actual value of SO2 concentration | Thermo Scientific 43i |
| Abbr. | Equation | Criteria | Proposal |
|---|---|---|---|
| MB | - | - | |
| ME | - | - | |
| SD | - | - | |
| RMSE | - | - | |
| NMB | −60%~ +60% | −45%~ +45% | |
| MFB | −60%~ +60% | −45%~ +45% |
| Variables | MB | ME | SD | RMSE | R |
|---|---|---|---|---|---|
| T2 | 0.24 | 0.72 | 0.91 | 0.89 | 0.95 |
| RH | 3.57 | 4.82 | 4.55 | 33.39 | 0.88 |
| WS | 0.37 | 0.81 | 1.00 | 1.13 | 0.64 |
| Variables | Models | NMB (%) | MFB (%) | R |
|---|---|---|---|---|
| PM2.5 | WRF-Chem | 6.49 | 0.020 | 0.80 |
| LSTM | 11.32 | 0.026 | 0.85 | |
| BPNN | −15.29 | −0.041 | 0.33 | |
| NO2 | WRF-Chem | −11.96 | −0.031 | 0.73 |
| LSTM | 7.95 | 0.019 | 0.68 | |
| BPNN | −7.16 | 0.018 | 0.55 | |
| SO2 | WRF-Chem | 5.04 | 0.012 | 0.61 |
| LSTM | −10.49 | −0.026 | 0.60 | |
| BPNN | −23.92 | −0.059 | 0.38 | |
| CO | WRF-Chem | 7.93 | 0.019 | 0.61 |
| LSTM | −1.79 | −0.004 | 0.50 | |
| BPNN | −3.95 | −0.010 | 0.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, Z.; Cui, S.; Pei, C.; Ye, Z.; Wu, X.; Lei, L.; Luo, T.; Zhang, Z.; Li, X.; Zhu, W. Regional Predictions of Air Pollution in Guangzhou: Preliminary Results and Multi-Model Cross-Validations. Atmosphere 2022, 13, 1527. https://doi.org/10.3390/atmos13101527
Qiao Z, Cui S, Pei C, Ye Z, Wu X, Lei L, Luo T, Zhang Z, Li X, Zhu W. Regional Predictions of Air Pollution in Guangzhou: Preliminary Results and Multi-Model Cross-Validations. Atmosphere. 2022; 13(10):1527. https://doi.org/10.3390/atmos13101527
Chicago/Turabian StyleQiao, Zhi, Shengcheng Cui, Chenglei Pei, Zhou Ye, Xiaoqing Wu, Lei Lei, Tao Luo, Zihan Zhang, Xuebin Li, and Wenyue Zhu. 2022. "Regional Predictions of Air Pollution in Guangzhou: Preliminary Results and Multi-Model Cross-Validations" Atmosphere 13, no. 10: 1527. https://doi.org/10.3390/atmos13101527
APA StyleQiao, Z., Cui, S., Pei, C., Ye, Z., Wu, X., Lei, L., Luo, T., Zhang, Z., Li, X., & Zhu, W. (2022). Regional Predictions of Air Pollution in Guangzhou: Preliminary Results and Multi-Model Cross-Validations. Atmosphere, 13(10), 1527. https://doi.org/10.3390/atmos13101527









