Improving Ensemble Volcanic Ash Forecasts by Direct Insertion of Satellite Data and Ensemble Filtering
Abstract
1. Introduction
2. Methodology
2.1. Introduction
2.2. Observations
2.3. Dispersion Model Details
2.3.1. Volcanic Source
2.3.2. Distal Source
2.4. Ensemble Filtering
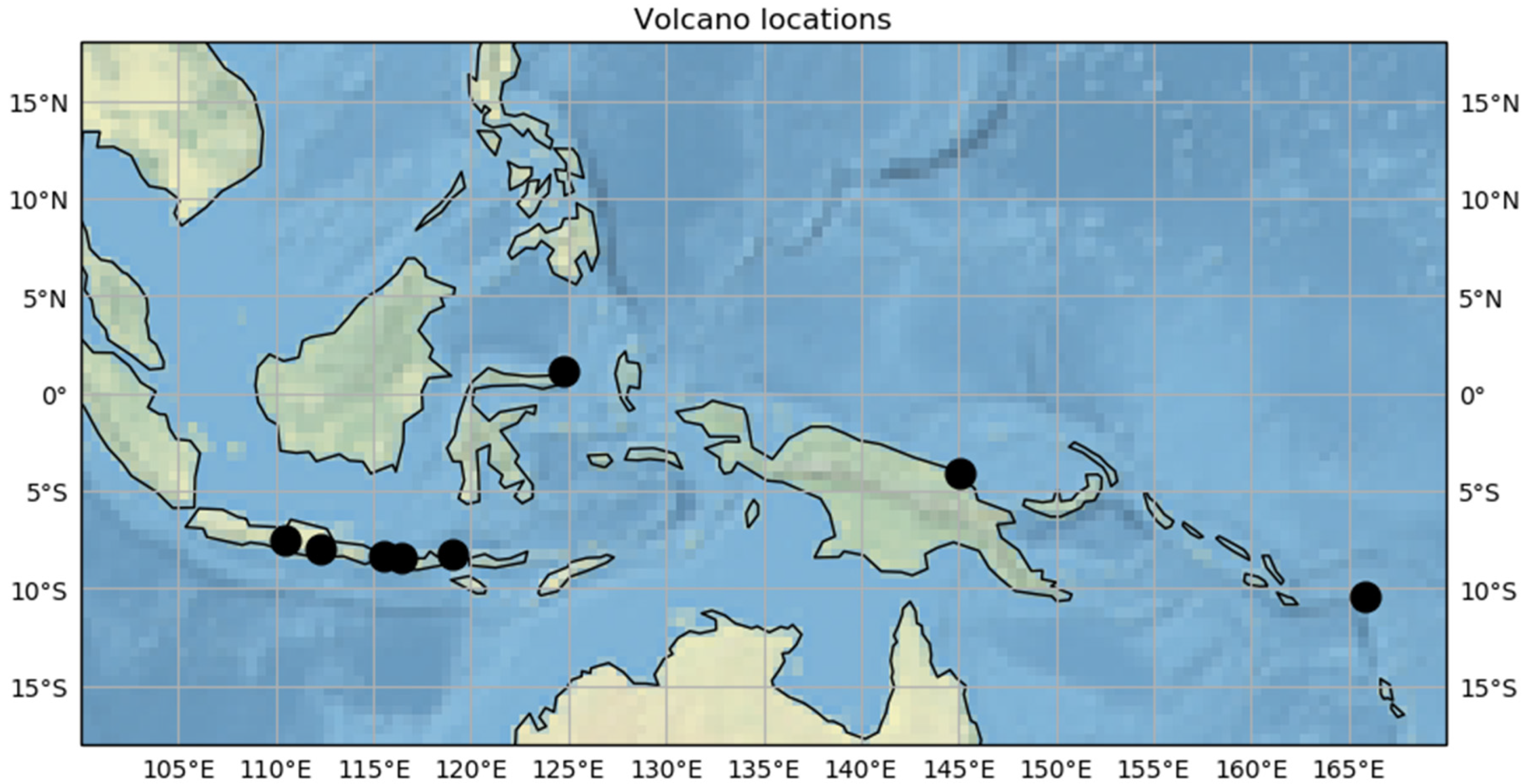
3. Eruption Case Studies and Experimental Setup
4. Results
4.1. General Verification Results
4.2. Comparison of Spatial Patterns for Selected Case Studies
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casadevall, T.J. Volcanic Ash and Aviation Safety: Proceedings of the First International Symposium on Volcanic Ash and Aviation Safety; US Government Printing Office: Washington, DC, USA, 1994.
- Mastin, L.; Guffanti, M.; Servranckx, R.; Webley, P.; Barsotti, S.; Dean, K.; Durant, A.; Ewert, J.; Neri, A.; Rose, W.; et al. A multidisciplinary effort to assign realistic source parameters to models of volcanic ash-cloud transport and dispersion during eruptions. J. Volcanol. Geotherm. Res. 2009, 186, 10–21. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C. Using Satellite Data to Determine Empirical Relationships between Volcanic Ash Source Parameters. Atmosphere 2020, 11, 342. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Japan. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Corradini, S.; Merucci, L.; Prata, F.; Piscini, A. Volcanic ash and SO2in the 2008 Kasatochi eruption: Retrievals comparison from different IR satellite sensors. J. Geophys. Res. Space Phys. 2010, 115, D2. [Google Scholar] [CrossRef]
- Francis, P.N.; Cooke, M.C.; Saunders, R.W. Retrieval of physical properties of volcanic ash using Meteosat: A case study from the 2010 Eyjafjallajökull eruption. J. Geophys. Res. Space Phys. 2012, 117, D20. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Heidinger, A.; Sieglaff, J.M. Automated retrievals of volcanic ash and dust cloud properties from upwelling infrared measurements. J. Geophys. Res. Atmos. 2013, 118, 1436–1458. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Sieglaff, J.M.; Cintineo, J. Spectrally Enhanced Cloud Objects—A generalized framework for automated detection of volcanic ash and dust clouds using passive satellite measurements: 1. Multispectral analysis. J. Geophys. Res. Atmos. 2015, 120, 7813–7841. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Sieglaff, J.M.; Cintineo, J. Spectrally Enhanced Cloud Objects—A generalized framework for automated detection of volcanic ash and dust clouds using passive satellite measurements: 2. Cloud object analysis and global application. J. Geophys. Res. Atmos. 2015, 120, 7842–7870. [Google Scholar] [CrossRef]
- Eckhardt, S.; Prata, A.J.; Seibert, P.; Stebel, K.; Stohl, A. Estimation of the vertical profile of sulfur dioxide injection into the atmosphere by a volcanic eruption using satellite column measurements and inverse transport modeling. Atmos. Chem. Phys. Discuss. 2008, 8, 3881–3897. [Google Scholar] [CrossRef]
- Kristiansen, N.I.; Stohl, A.; Prata, F.; Richter, A.; Eckhardt, S.; Seibert, P.; Hoffmann, A.; Ritter, C.; Bitar, L.; Duck, T.J.; et al. Remote sensing and inverse transport modeling of the Kasatochi eruption sulfur dioxide cloud. J. Geophys. Res. Space Phys. 2010, 115, D2. [Google Scholar] [CrossRef]
- Stohl, A.; Prata, A.J.; Eckhardt, S.; Clarisse, L.; Durant, A.; Henne, S.; Kristiansen, N.I.; Minikin, A.; Schumann, U.; Seibert, P.; et al. Determination of time- and height-resolved volcanic ash emissions and their use for quantitative ash dispersion modeling: The 2010 Eyjafjallajökull eruption. Atmos. Chem. Phys. Discuss. 2011, 11, 4333–4351. [Google Scholar] [CrossRef]
- Seibert, P.; Kristiansen, N.I.; Richter, A.; Eckhardt, S.; Prata, A.J.; Stohl, A. Uncertainties in the inverse modelling of sulphur dioxide eruption profiles. Geomat. Nat. Hazards Risk 2011, 2, 201–216. [Google Scholar] [CrossRef]
- Boichu, M.; Menut, L.; Khvorostyanov, D.; Clarisse, L.; Clerbaux, C.; Turquety, S.; Coheur, P.-F. Inverting for volcanic SO2 flux at high temporal resolution using spaceborne plume imagery and chemistry-transport modelling: The 2010 Eyjafjallajökull eruption case study. Atmos. Chem. Phys. Discuss. 2013, 13, 8569–8584. [Google Scholar] [CrossRef]
- Boichu, M.; Clarisse, L.; Khvorostyanov, D.; Clerbaux, C. Improving volcanic sulfur dioxide cloud dispersal forecasts by progressive assimilation of satellite observations. Geophys. Res. Lett. 2014, 41, 2637–2643. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Potts, R.; Lucas, C. A probabilistic inverse method for volcanic ash dispersion modelling. ANZIAM J. 2016, 55, 194–209. [Google Scholar] [CrossRef][Green Version]
- Moxnes, E.D.; Kristiansen, N.I.; Stohl, A.; Clarisse, L.; Durant, A.; Weber, K.; Vogel, A. Separation of ash and sulfur dioxide during the 2011 Grímsvötn eruption. J. Geophys. Res. Atmos. 2014, 119, 7477–7501. [Google Scholar] [CrossRef]
- Kristiansen, N.I.; Prata, A.J.; Stohl, A.; Carn, S.A. Stratospheric volcanic ash emissions from the 13 February 2014 Kelut eruption. Geophys. Res. Lett. 2015, 42, 588–596. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Potts, R.J. A simple inversion method for determining optimal dispersion model parameters from satellite detections of volcanic sulfur dioxide. J. Geophys. Res. Atmos. 2015, 120, 9702–9717. [Google Scholar] [CrossRef]
- Chai, T.; Crawford, A.; Stunder, B.; Pavolonis, M.J.; Draxler, R.; Stein, A. Improving volcanic ash predictions with the HYSPLIT dispersion model by assimilating MODIS satellite retrievals. Atmos. Chem. Phys. Discuss. 2017, 17, 2865–2879. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C.; Potts, R.J. Estimation of optimal dispersion model source parameters using satellite detections of volcanic ash. J. Geophys. Res. Atmos. 2017, 122, 8207–8232. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C.; Potts, R.J. Toward quantitative forecasts of volcanic ash dispersal: Using satellite retrievals for optimal estimation of source terms. J. Geophys. Res. Atmos. 2017, 122, 8187–8206. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C.; Potts, R.J. Quantitative Verification and Calibration of Volcanic Ash Ensemble Forecasts Using Satellite Data. J. Geophys. Res. Atmos. 2018, 123, 4135–4156. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C. A Computationally Efficient Ensemble Filtering Scheme for Quantitative Volcanic Ash Forecasts. J. Geophys. Res. Atmos. 2021, 126, e2020JD033094. [Google Scholar] [CrossRef]
- Harvey, N.; Dacre, H.; Webster, H.; Taylor, I.; Khanal, S.; Grainger, R.; Cooke, M. The Impact of Ensemble Meteorology on Inverse Modeling Estimates of Volcano Emissions and Ash Dispersion Forecasts: Grímsvötn 2011. Atmosphere 2020, 11, 1022. [Google Scholar] [CrossRef]
- Lucas, C.; Majewski, L. Evaluation of GEOCAT Volcanic Ash Algorithm for Use in BoM—A Report of the Improved Volcanic Ash Detection and Prediction Project; Bureau Research Report 004; Bureau of Meteorology: Melbourne, Australia, 2015. [Google Scholar]
- Lucas, C.; Zidikheri, M.J. Volcat Satellite Retrievals for Selected Case Studies. 2019. Available online: http://doi.org/10.5281/zenodo.3579613 (accessed on 15 September 2021).
- Wilkins, K.L.; Mackie, S.; Watson, M.; Webster, H.N.; Thomson, D.J.; Dacre, H.F. Data insertion in volcanic ash cloud forecasting. Ann. Geophys. 2015, 57, 24. [Google Scholar] [CrossRef]
- Wilkins, K.L.; Watson, I.M.; Kristiansen, N.I.; Webster, H.N.; Thomson, D.J.; Dacre, H.F.; Prata, A.J. Using data insertion with the NAME model to simulate the 8 May 2010 Eyjafjallajökull volcanic ash cloud. J. Geophys. Res. Atmos. 2015, 121, 306–323. [Google Scholar] [CrossRef]
- Wilkins, K.; Western, L.; Watson, I. Simulating atmospheric transport of the 2011 Grímsvötn ash cloud using a data insertion update scheme. Atmos. Environ. 2016, 141, 48–59. [Google Scholar] [CrossRef]
- Draxler, R.R.; Hess, G.D. An overview of the HYSPLIT_4 modelling system for trajectories. Aust. Meteorol. Mag. 1998, 47, 295–308. [Google Scholar]
- O’Kane, T.J.; Naughton, M.J.; Xiao, Y. The Australian community climate and earth system simulator global and regional ensemble prediction scheme. ANZIAM J. 2008, 50, 385–398. [Google Scholar] [CrossRef]
- Dare, R.A.; Smith, D.H.; Naughton, M.J. Ensemble Prediction of the Dispersion of Volcanic Ash from the 13 February 2014 Eruption of Kelut, Indonesia. J. Appl. Meteorol. Clim. 2016, 55, 61–78. [Google Scholar] [CrossRef]
- Dare, R.A. Sedimentation of Volcanic Ash in the HYSPLIT Dispersion Model; Centre for Australian Weather and Climate Research: Melbourne, Australia, 2015. [Google Scholar]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Prata, A.J.; Prata, A.T. Eyjafjallajökull volcanic ash concentrations determined using Spin Enhanced Visible and Infrared Imager measurements. J. Geophys. Res. Space Phys. 2012, 117, 23. [Google Scholar] [CrossRef]
- Hobbs, P.V.; Radke, L.F.; Lyons, J.H.; Ferek, R.J.; Coffman, D.J.; Casadevall, T.J. Airborne measurements of particle and gas emissions from the 1990 volcanic eruptions of Mount Redoubt. J. Geophys. Res. Space Phys. 1991, 96, 18735–18752. [Google Scholar] [CrossRef]
- Webster, H.N.; Thomson, D.J.; Johnson, B.T.; Heard, I.P.C.; Turnbull, K.; Marenco, F.; Kristiansen, N.I.; Dorsey, J.; Minikin, A.; Weinzierl, B.; et al. Operational prediction of ash concentrations in the distal volcanic cloud from the 2010 Eyjafjallajökull eruption. J. Geophys. Res. Space Phys. 2012, 117, D20. [Google Scholar] [CrossRef]
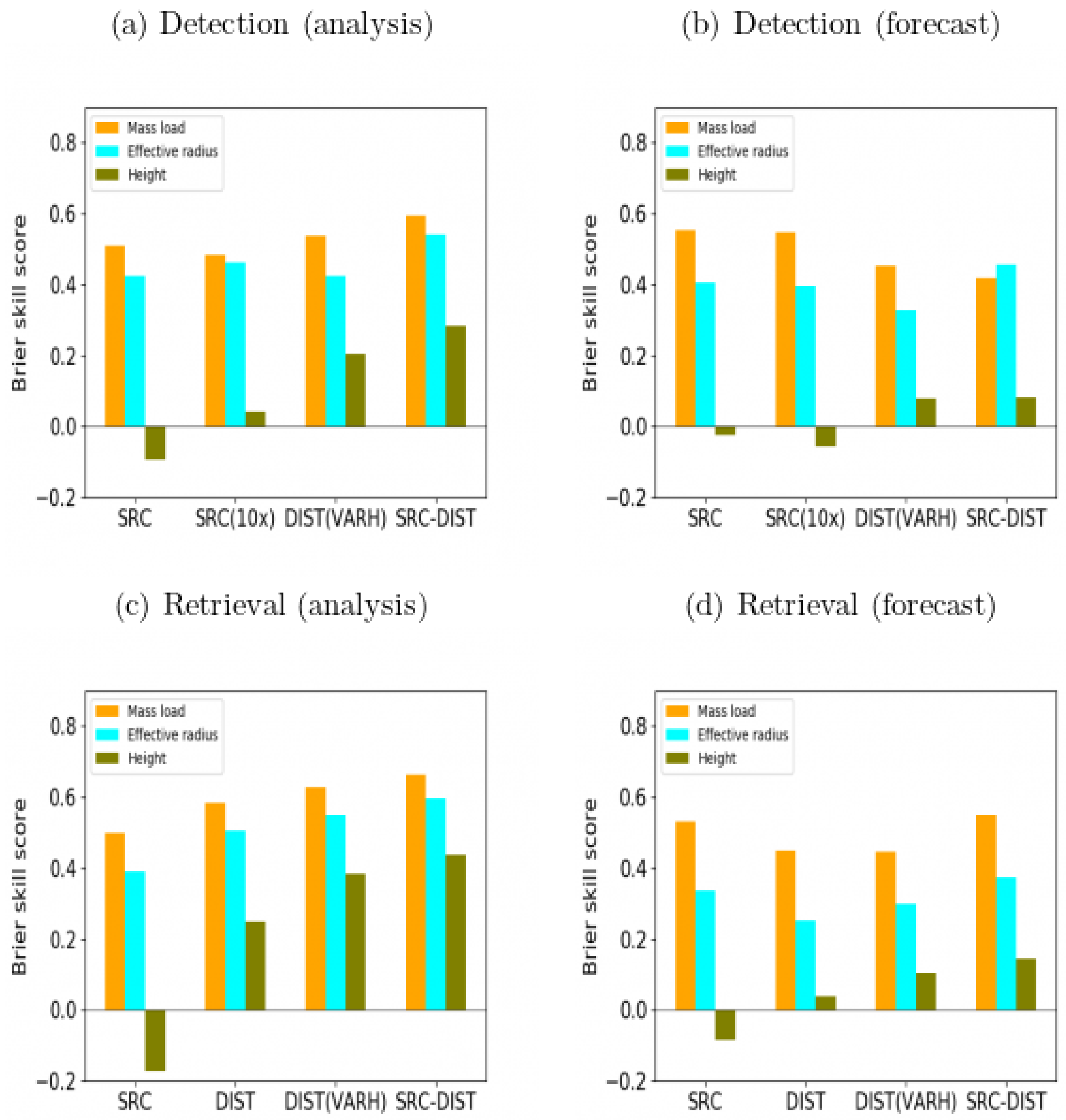
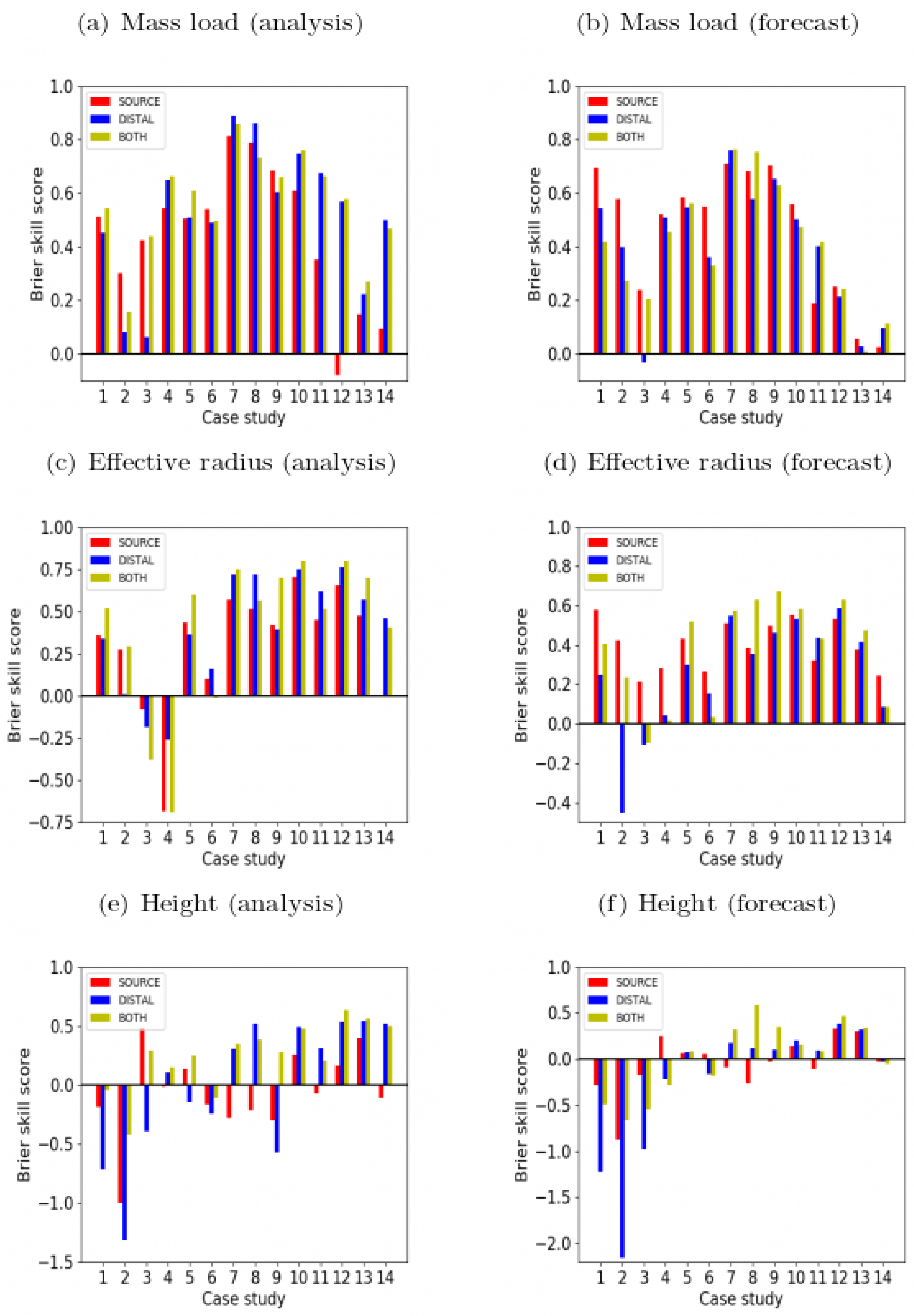
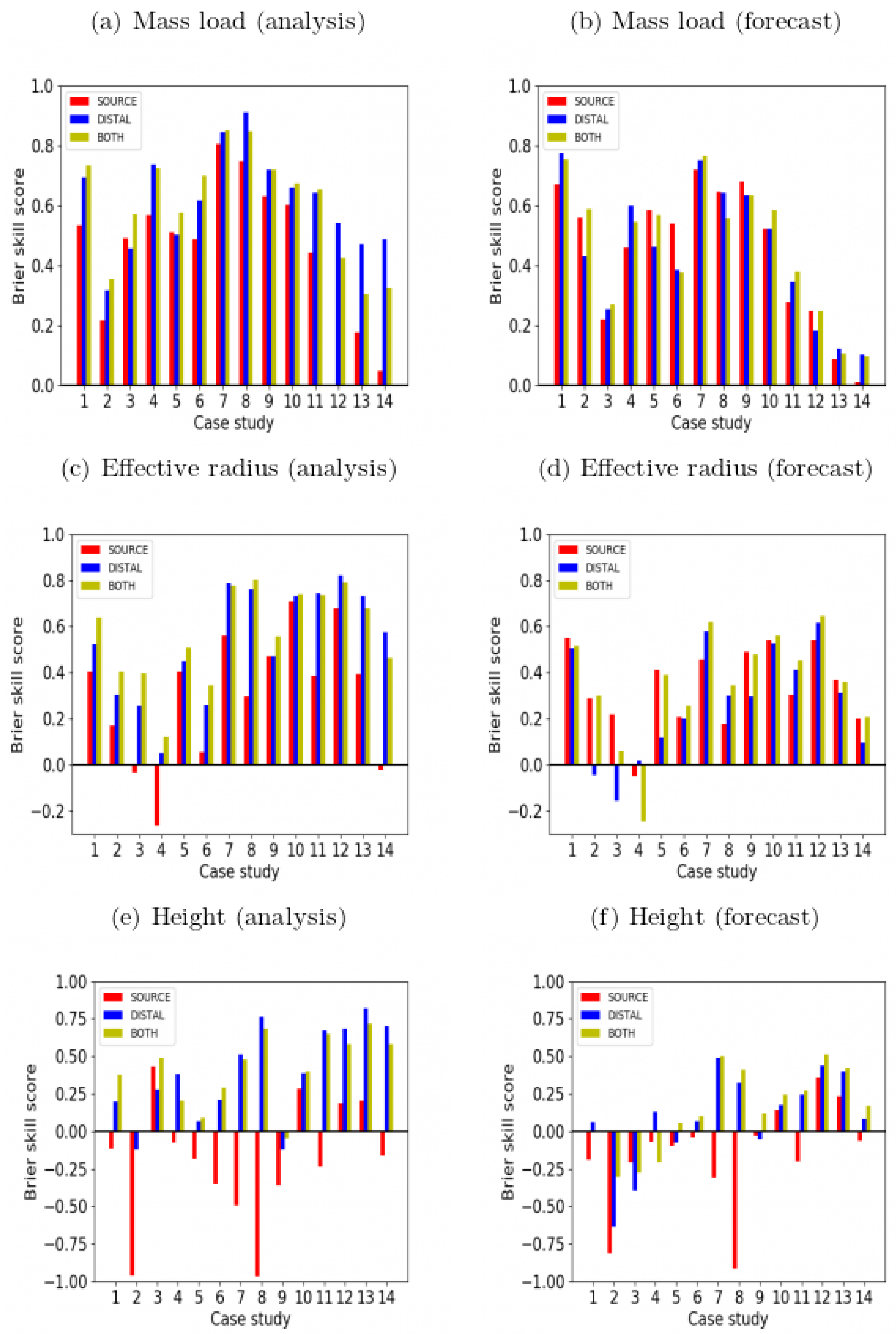
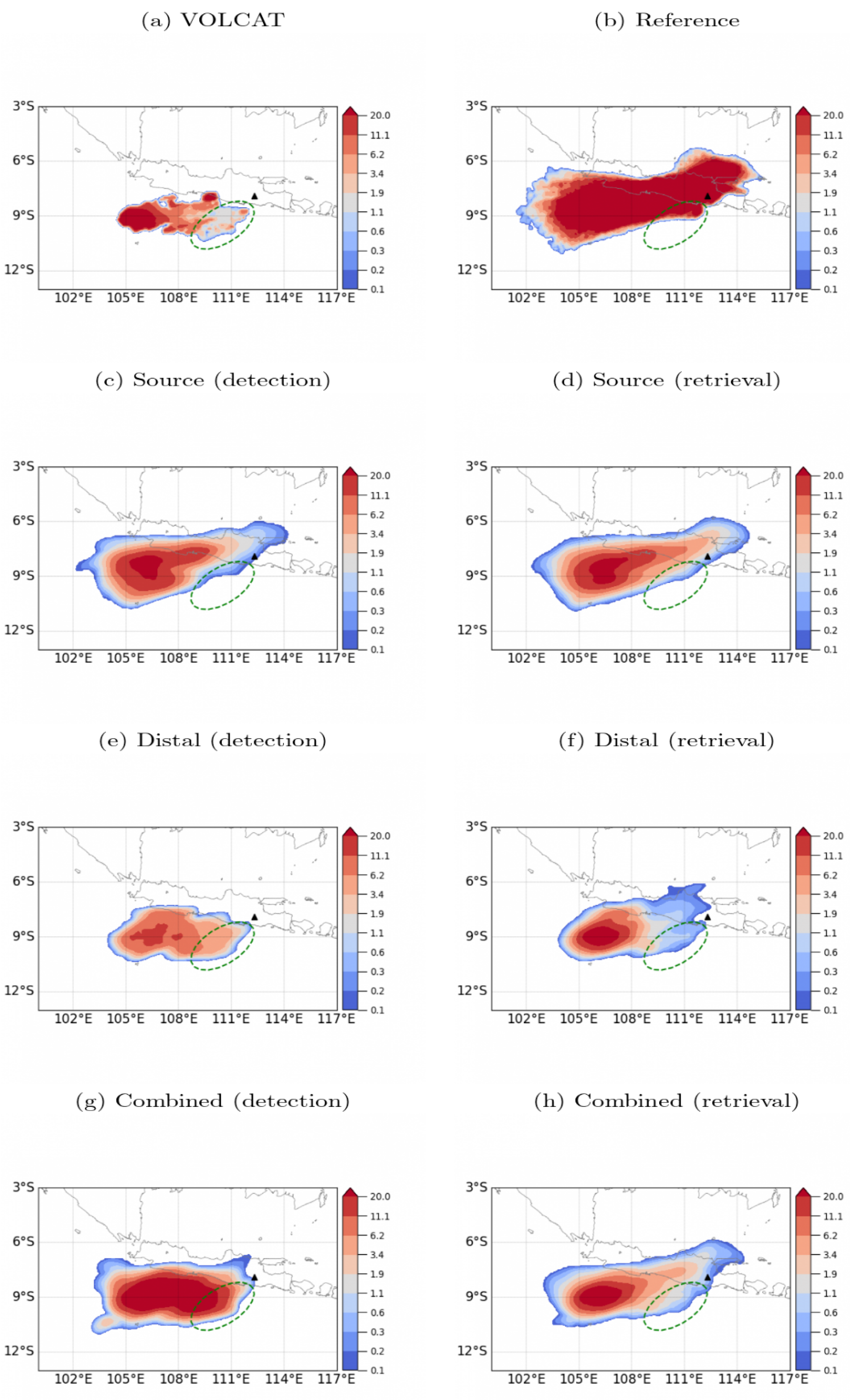
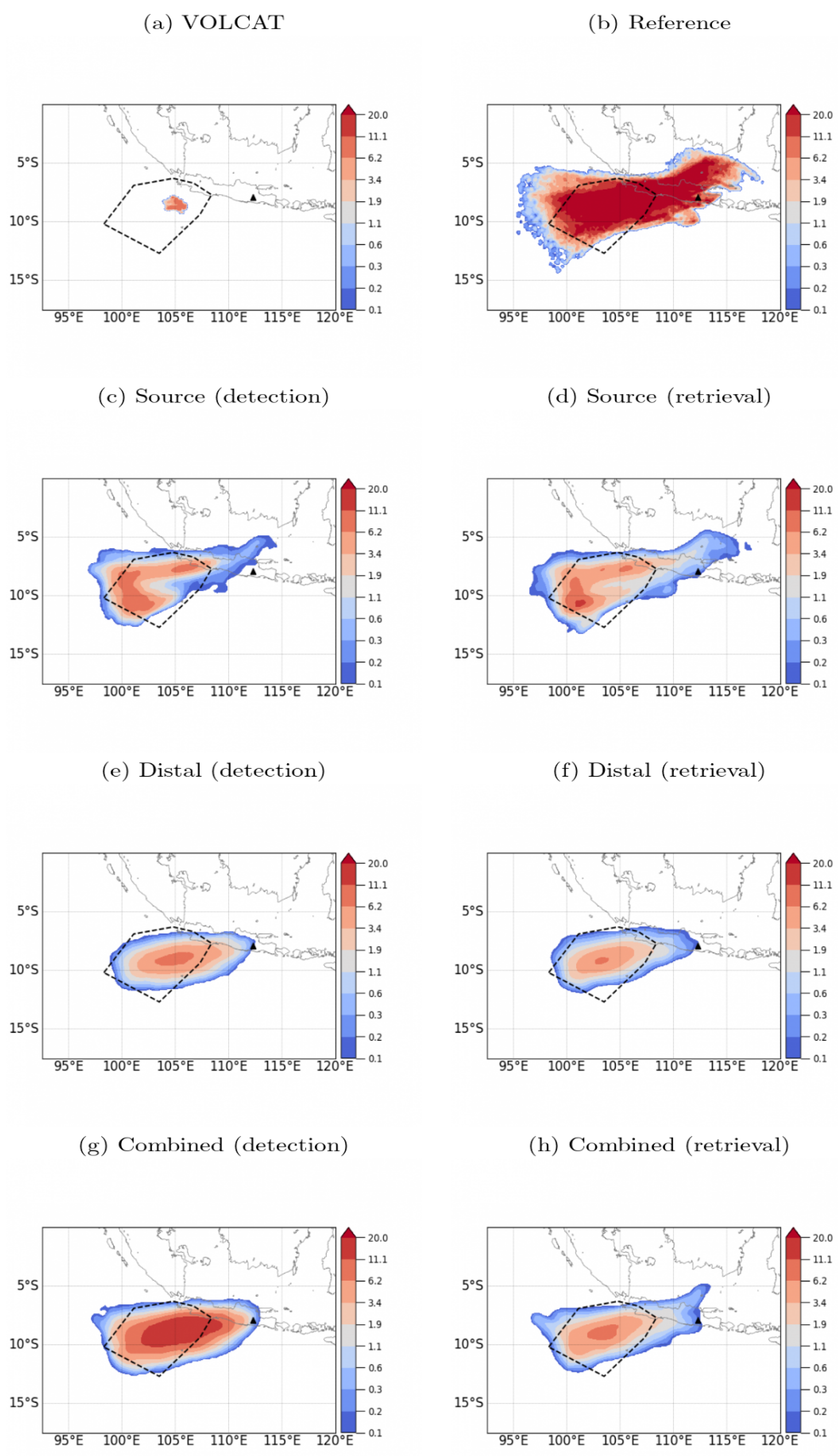
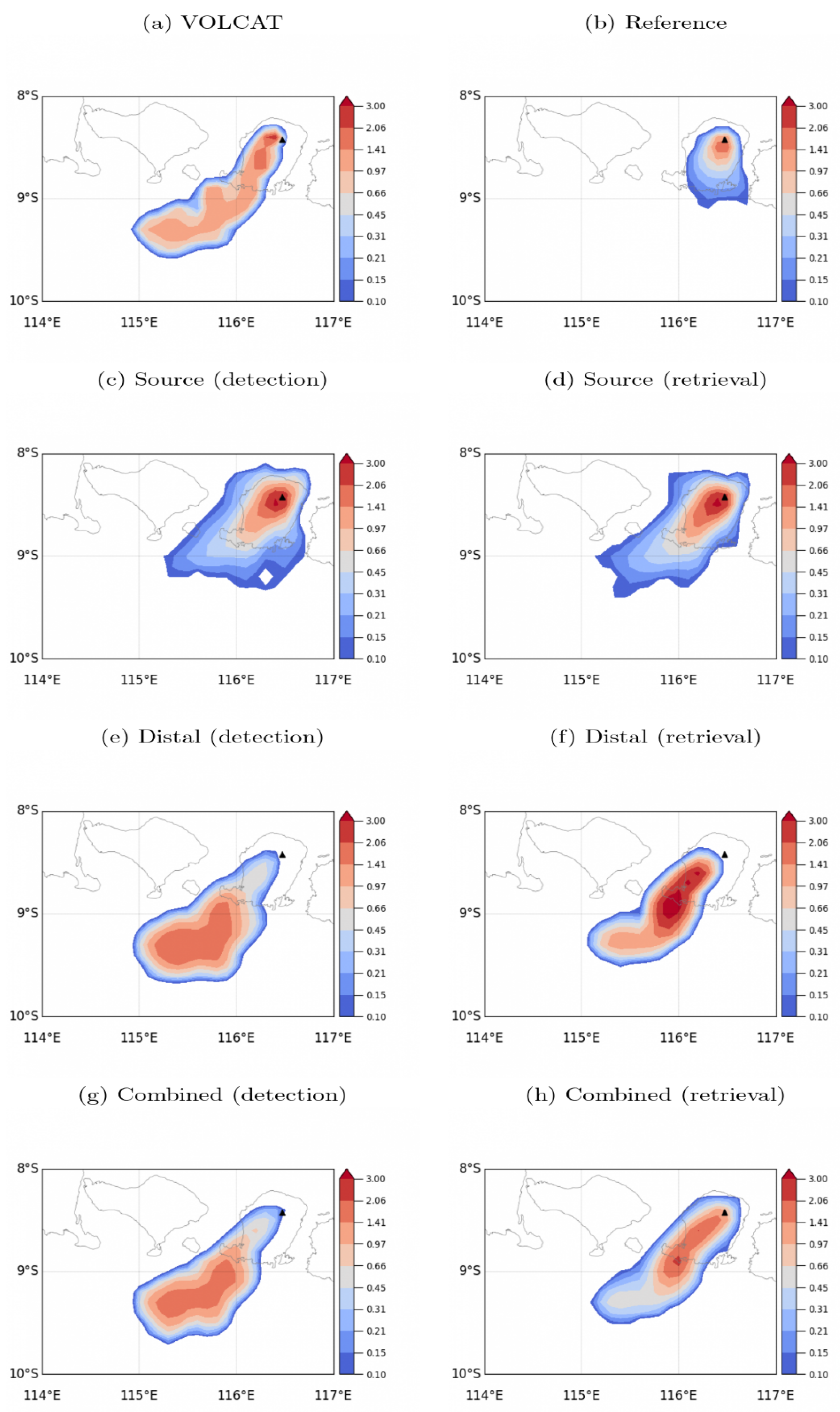

| Variant Name | Initialization Type | Filtering Observations | Sampled (Variable) Parameters | Number of Analysis Ensemble Members | |
|---|---|---|---|---|---|
| 1 | SRC (retrieval) | Cylinder source | Retrievals and detections | Cloud top height ( | 240 (720) |
| 2 | SRC (detection) | Cylinder source | Detections | Same as 1 | Same as 1 |
| 3 | DIST (retrieval) | Distal (retrieval; top height fixed) | Retrievals and detections | Initial time ( Cloud thickness () | 480–1200 |
| 4 | DIST(VARH) (retrieval) | Distal (retrieval; top height varied) | Retrievals and detections | Initial time ( Cloud top height ( Cloud thickness () | Same as 3 |
| 5 | DIST(VARH) (detection) | Distal (top height varied) | Detections | Same as 4 | Same as 3 |
| 6 | SRC-DIST (retrieval) | Cylinder source and distal (retrieval; top height varied) | Retrievals and detections | Same as 4 | 1200–2640 |
| 7 | SRC-DIST (detection) | Cylinder source and distal (detection; top height varied) | Detections | Same as 4 | 1200–2640 |
| 8 | SRC(10×) | Cylinder source | Detections | Same as 1, 2 | 2400 (7200) |
| 9 | Reference | Simple line source | - | - | 24 |
| Index | Volcano | Location | Eruption Time and Date | Approx. Duration (h) | Estimated Height (km a.s.l.) |
|---|---|---|---|---|---|
| 1 | Kelut | 112.31° E, 7.93° S | 1600Z/13/02/2014 | 3.0 | 26 |
| 2 | Sangeang Api I | 119.07° E, 8.20° S | 0800Z/30/05/2014 | 1.0 | 15–20 |
| 3 | Manam | 145.04° E, 4.08° S | 0130Z/31/07/2015 | 1.0 | 20 |
| 4 | Tinakula | 165.80° E, 10.38° S | 2330Z/20/10/2017 | 1.0 | 17 |
| 5 | Sangeang Api II | Same as 2 | 1700Z/30/05/2014 | 1.0 | 15–16 |
| 6 | Manam | Same as 3 | 0300Z/08/12/2018 | 3.0 | 13–14 |
| 7 | Soputan I | 124.73° E, 1.11° N | 2240Z/04/01/2016 | 1.0 | 12–13 |
| 8 | Soputan II | Same as 7 | 0600Z/05/01/2016 | 1.0 | 12–13 |
| 9 | Sangeang Api III | Same as 2, 5 | 2000Z/30/05/2014 | 1.0 | 14–15 |
| 10 | Merapi | 110.44° E, 7.54° S | 0030Z/11/05/2018 | 2.5 | 8 |
| 11 | Rinjani III | 116.47° E, 8.42° S | 0300Z/01/08/2016 | 1.0 | 6–10 |
| 12 | Agung | 115.51° E, 8.34° S | 1130Z/24/05/2019 | 0.5 | 6–7 |
| 13 | Rinjani I | Same as 11 | 1200Z/04/11/2015 | 48.0 | 6 |
| 14 | Rinjani II | Same as 11, 13 | 0000Z/05/11/2015 | 48.0 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zidikheri, M.J.; Lucas, C. Improving Ensemble Volcanic Ash Forecasts by Direct Insertion of Satellite Data and Ensemble Filtering. Atmosphere 2021, 12, 1215. https://doi.org/10.3390/atmos12091215
Zidikheri MJ, Lucas C. Improving Ensemble Volcanic Ash Forecasts by Direct Insertion of Satellite Data and Ensemble Filtering. Atmosphere. 2021; 12(9):1215. https://doi.org/10.3390/atmos12091215
Chicago/Turabian StyleZidikheri, Meelis J., and Chris Lucas. 2021. "Improving Ensemble Volcanic Ash Forecasts by Direct Insertion of Satellite Data and Ensemble Filtering" Atmosphere 12, no. 9: 1215. https://doi.org/10.3390/atmos12091215
APA StyleZidikheri, M. J., & Lucas, C. (2021). Improving Ensemble Volcanic Ash Forecasts by Direct Insertion of Satellite Data and Ensemble Filtering. Atmosphere, 12(9), 1215. https://doi.org/10.3390/atmos12091215







