Copula-Based Drought Monitoring and Assessment According to Zonal and Meridional Temperature Gradients
Abstract
:1. Introduction
2. Materials and Methods
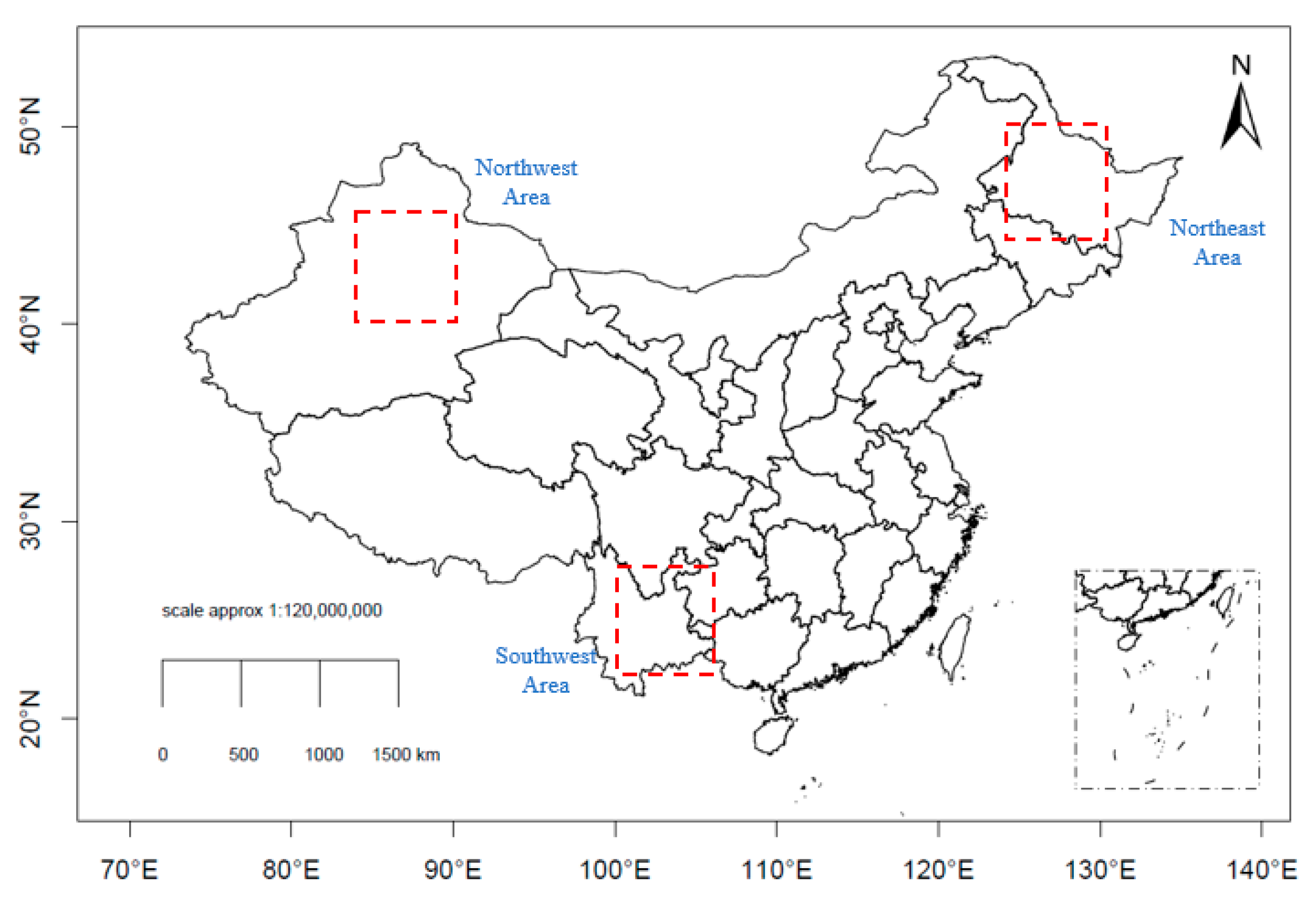
2.1. Study Area and Data
2.2. Standardized Precipitation Evapotranspiration Index
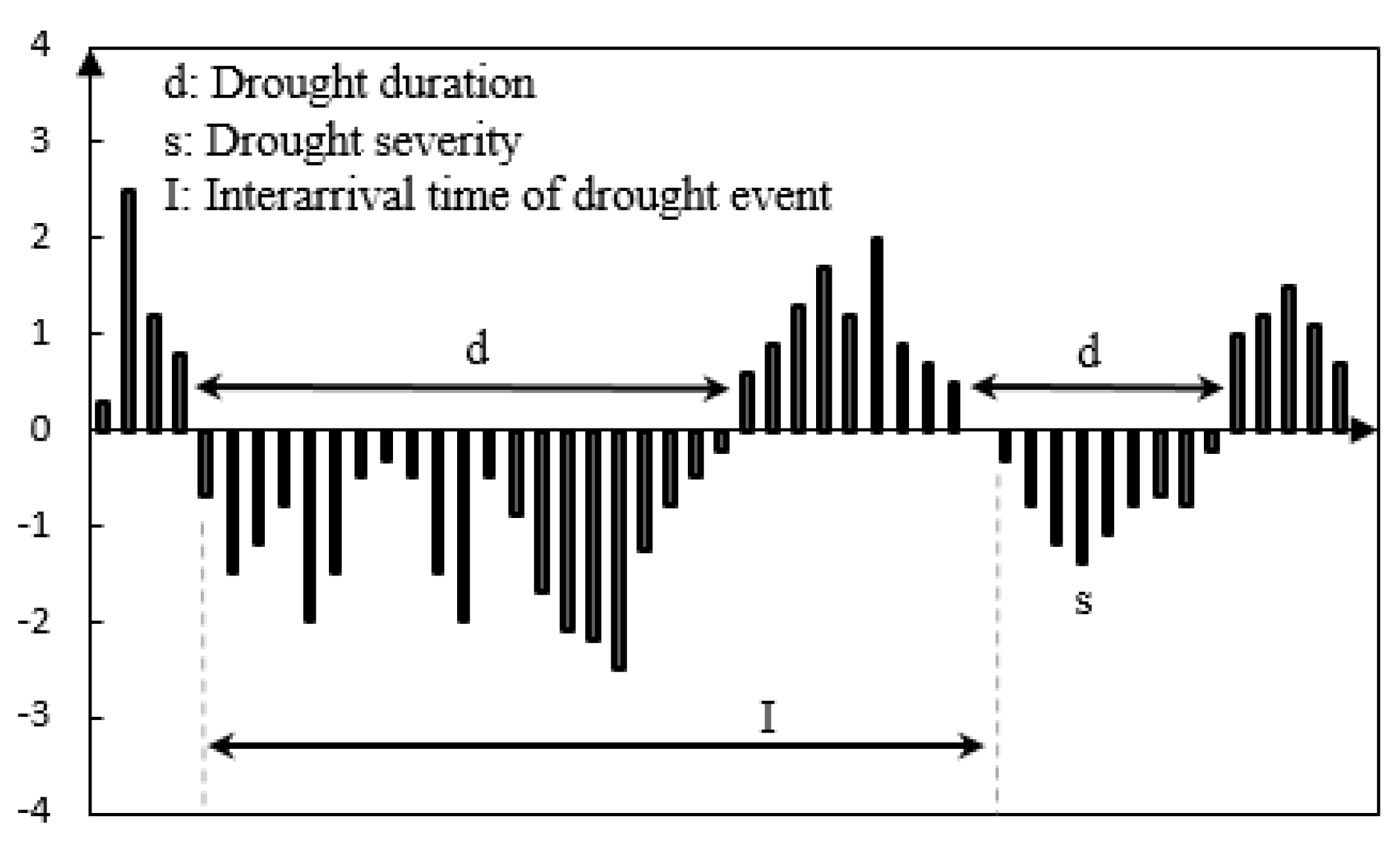
2.3. Definition of Drought Characteristics
2.4. Trend Analysis
2.5. Meridional and Zonal Temperature Gradients
2.6. Copula Functions
3. Results
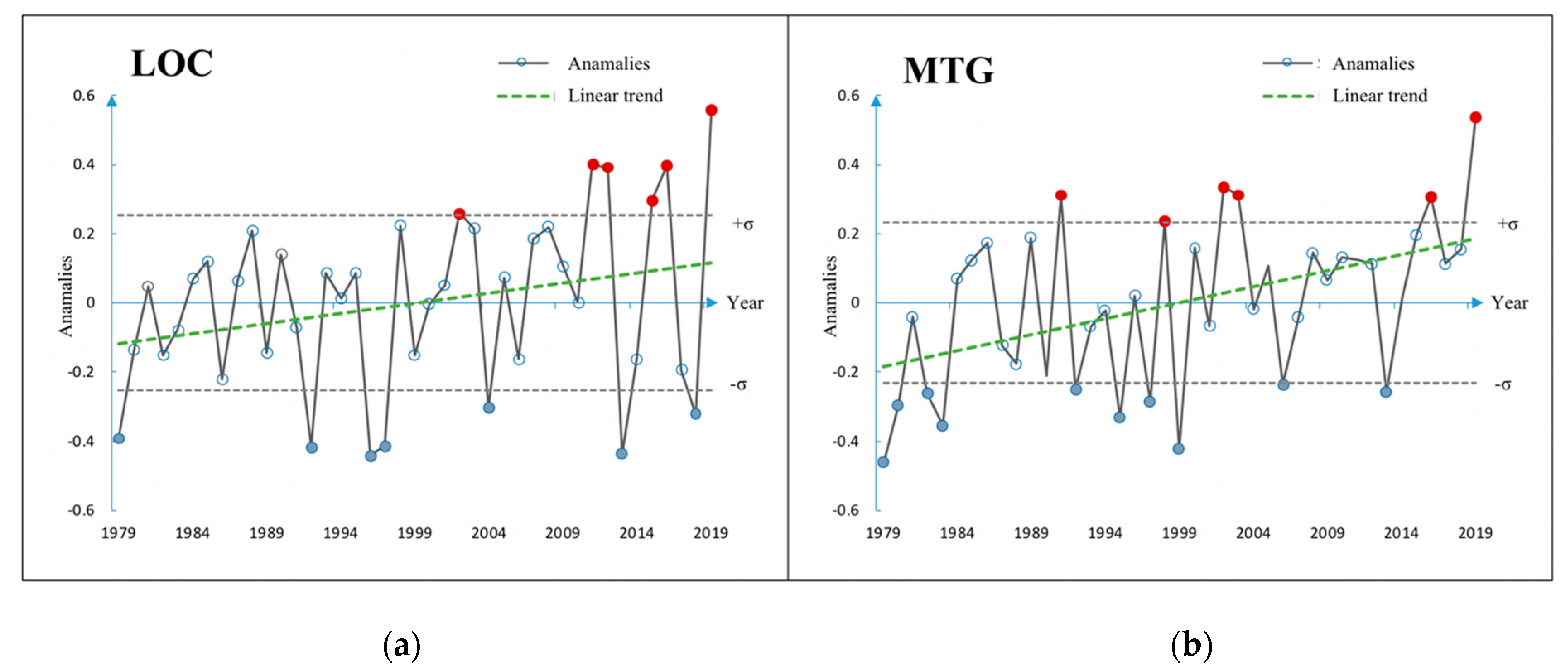
3.1. Changes in Large-Scale Temperature
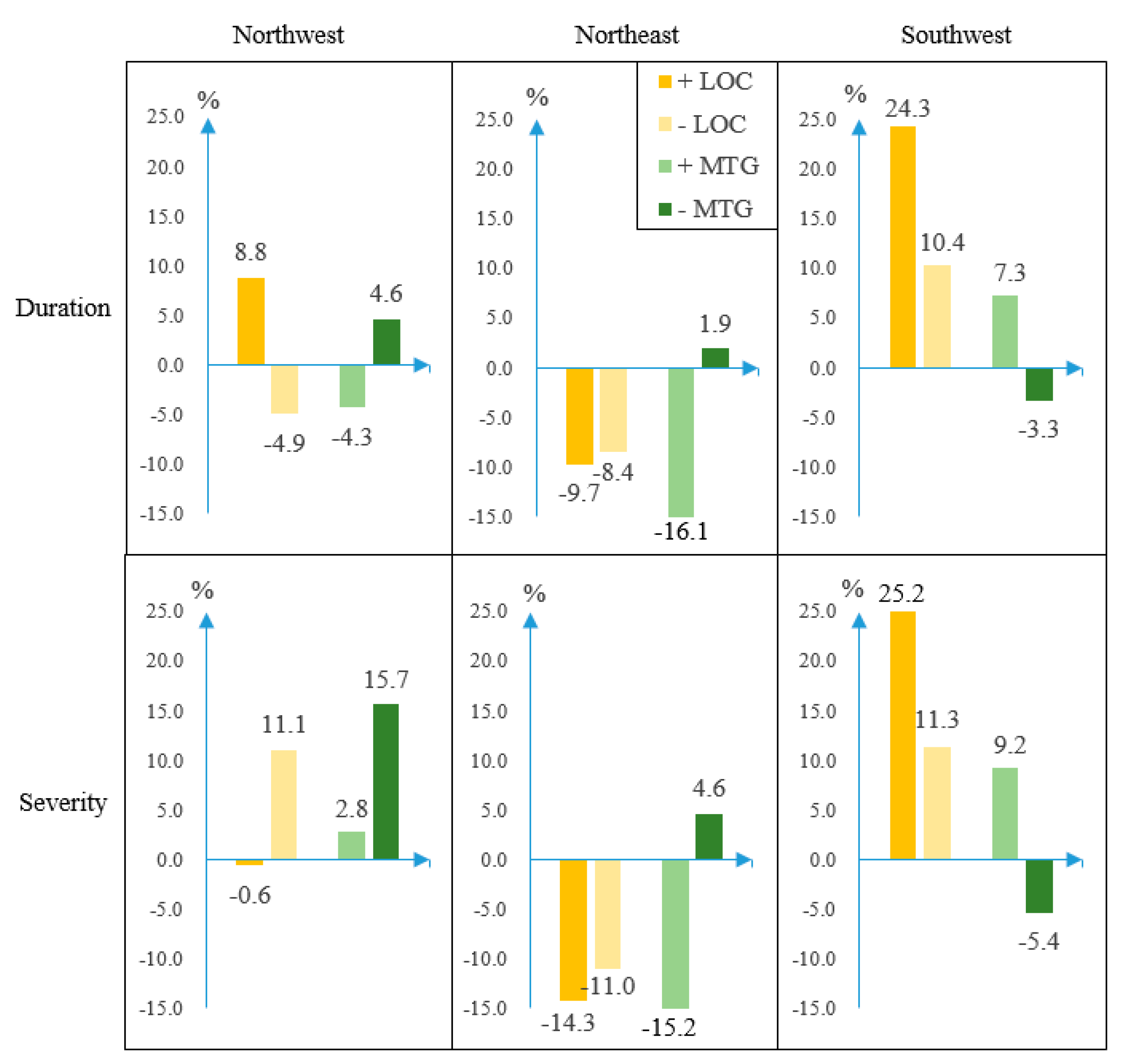
3.2. Composite Anomalies of Drought Characteristics Associated with LOC/MTG
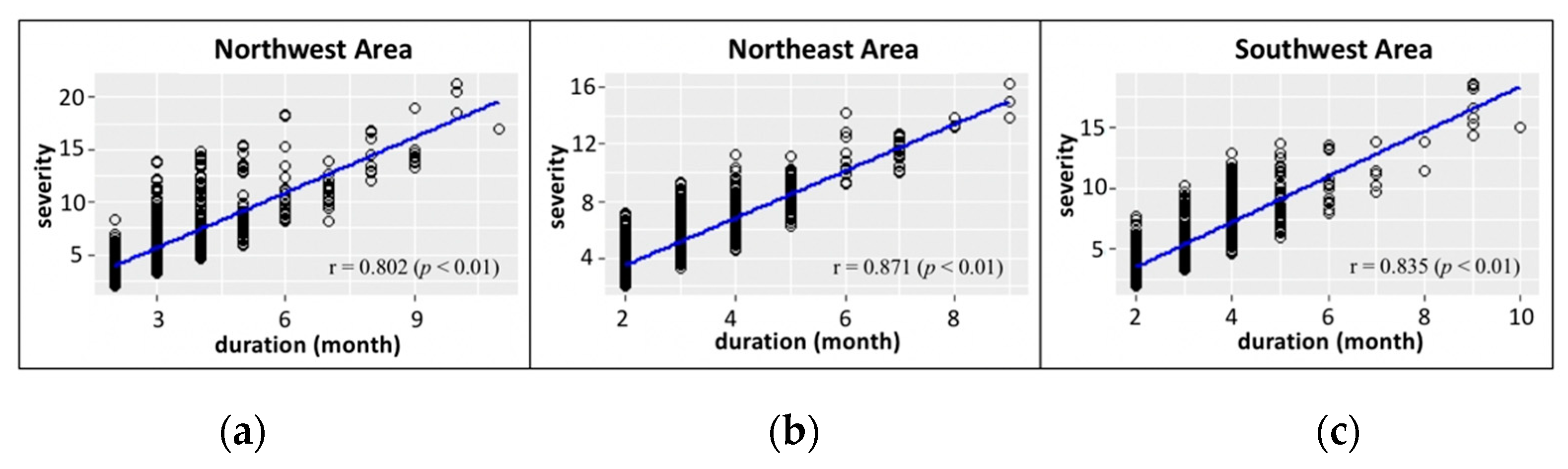
3.3. Changes in Drought Duration and Severity in China
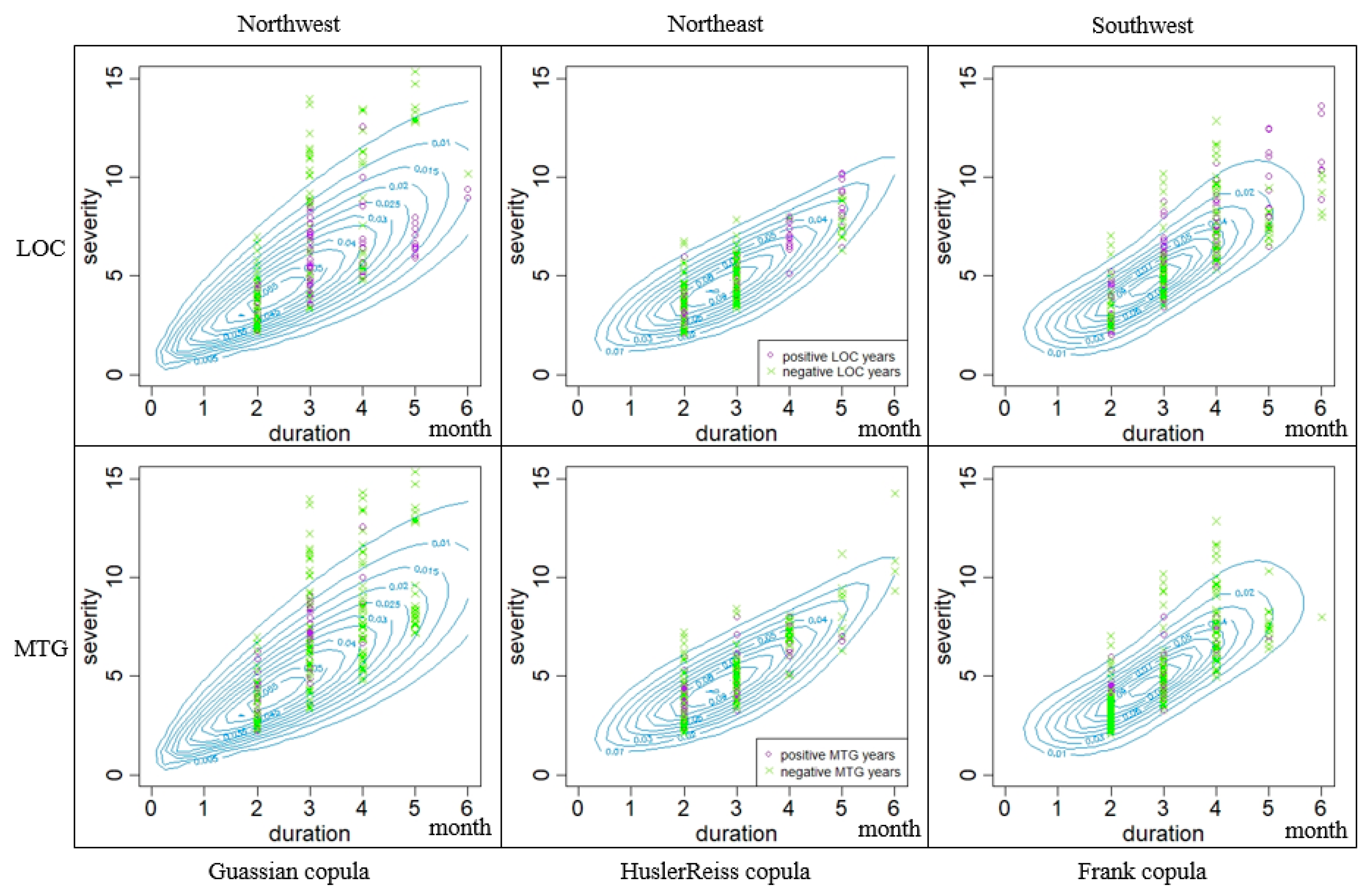
3.4. Joint Distribution of Drought Duration and Severity
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van Lanen, H.A.J. Hydrological Drought-Processes and Estimation Methods for Streamflow and Groundwater; Developments in Water Science; Elsevier Science BV: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Arash, M.R.; Bijan, G.; Davar, K.; Zahra, G.; Samira, A.A. Integrated meteorological and hydrological drought model: A management tool for proactive water resources planning of semi-arid regions. Adv. Water Resour. 2017, 107, 336–353. [Google Scholar]
- Luo, D.; Ye, L.L.; Sun, D.C. Risk evaluation of agricultural drought disaster using a grey cloud clustering model in Henan province, China. Int. J. Disaster Risk Reduct. 2020, 49, 101759. [Google Scholar] [CrossRef]
- Muneta, Y.; Hiroaki, I.; Sawada, Y.; Suzuki, Y.S.; Toshio, K.; Asif, N.; Cheema, M.J.M. A multi-sector multi-region economic growth model of drought and the value of water: A case study in Pakistan. Int. J. Disaster Risk Reduct. 2020, 43, 101368. [Google Scholar]
- Crausbay, S.; Ramirez, A.R.; Carter, S.L.; Cross, M.S.; Hall, K.R.; Bathke, D.J.; Betancourt, J.L.; Colt, S.; Cravens, A.E.; Dalton, M.S.; et al. Defining Ecological Drought for the Twenty-First Century. Bull. Am. Meteorol. Soc. 2017, 98, 2543–2550. [Google Scholar] [CrossRef]
- Bradford, J.B.; Schlaepfer, D.R.; Lauenroth, W.K.; Palmquist, K.A. Robust ecological drought projections for drylands in the 21st century. Glob. Chang. Biol. 2020, 26, 3906–3919. [Google Scholar] [CrossRef] [PubMed]
- Le Comte, D. Weather highlights around the world. Weatherwise 1995, 48, 20–22. [Google Scholar] [CrossRef]
- Le Comte, D. Weather highlights around the world. Weatherwise 1994, 47, 23–26. [Google Scholar] [CrossRef]
- Phillips, D. The Climates of Canada; Environment Canada: Ottawa, ON, 1990; p. 176. [Google Scholar]
- Feyen, L.; Dankers, R. Impact of global warming on streamflow drought in Europe. J. Geophys. Res. Atmos. 2009, 114, D17. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Li, Y.; Song, S.; Yao, N. Spatial comparability of drought characteristics and related return periods in mainland China over 1961–2013. J. Hydrol. 2017, 550, 549–567. [Google Scholar] [CrossRef]
- Ding, Y.; Hayes, M.J.; Widhalm, M. Measuring economic impacts of drought: A review and discussion. Disaster Prev. Manag. 2011, 20, 434–446. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Y.; Waddington, S.R.; Dixon, J.; Joshi, A.K.; De Vicente, M.C. The relative importance of drought and other water-related constraints for major food crops in South Asian farming systems. Food Secur. 2011, 3, 19–33. [Google Scholar] [CrossRef]
- Seneviratne, S. Changes in climate extremes and their impacts on the natural physical environment: An overview of the IPCC SREX report. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012. [Google Scholar]
- Jefferson, M. IPCC fifth assessment synthesis report: “Climate change 2014: Longer report”. Crit. Anal. Technol. Forecast. Soc. Change 2014, 92, 362–363. [Google Scholar] [CrossRef]
- Stewart, I.T.; Rogers, J.; Graham, A. Water security under severe drought and climate change: Disparate impacts of the recent severe drought on environmental flows and water supplies in Central California. J. Hydrol. X 2020, 7, 100054. [Google Scholar] [CrossRef]
- Martínez-Valderrama, J.; Ibanez, J.; Ibanez, M.A.; Alcala, F.J.; Sanjuan, M.E.; Ruiz, A.; Del Barrio, G. Assessing the sensitivity of a Mediterranean commercial rangeland to droughts under climate change scenarios by means of a multidisciplinary integrated model. Agric. Syst. 2021, 187, 103021. [Google Scholar] [CrossRef]
- Noorisameleh, Z.; Khaledi, S.; Khaledi, A.; Firouzabadi, P.Z.; Gough, W.A.; Mirza, M.M.Q. Comparative evaluation of impacts of climate change and droughts on river flow vulnerability in Iran. Water Sci. Eng. 2021, 13, 265–274. [Google Scholar] [CrossRef]
- Rehana, J.; Naidu, G.S. Development of hydro-meteorological drought index under climate change—Semi-arid river basin of Peninsular India. J. Hydrol. 2021, 594, 125973. [Google Scholar] [CrossRef]
- Dai, A.G. Increasing drought under global warming in observations and models. Nat. Clim. Change 2012, 3, 52–58. [Google Scholar] [CrossRef]
- Dai, A.G. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Change 2011, 2, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Byun, H.R.; Wilhite, D.A. Objective quantification of drought severity and duration. Am. Meteorol. Soc. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheimm, CA, USA, 17–23 January 1993. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Dore, M.H.I. Climate change and changes in global precipitation patterns: What do we know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; Zhai, P.; Zhang, Q. Variations in droughts over China: 1951–2003. Geophys. Res. Lett. 2005, 32, 353–368. [Google Scholar] [CrossRef]
- Jeong, M.S.; Kim, J.-S.; Oh, S.M.; Moon, Y.-I. Sensitivity of summer precipitation over the Korean Peninsula to temperature gradients. Int. J. Clim. 2015, 35, 836–845. [Google Scholar] [CrossRef]
- Jain, S.; Lall, U.; Mann, M.E. Seasonality and Interannual Variations of Northern Hemisphere Temperature: Equator-to-Pole Gradient and Ocean–Land Contrast. J. Clim. 1999, 12, 1086–1100. [Google Scholar] [CrossRef]
- Xu, H. Arctic climate is more sensitive to global warming than expected. In Resources, Environment and Engineering; Xie, L.Q., Ed.; London, UK, 2014; Volume 28, pp. 232–233. [Google Scholar]
- Quiring, S.M.; Papakryiakou, T.N. An evaluation of agricultural drought indices for the Canadian prairies. Agric. For. Meteorol. 2003, 118, 49–62. [Google Scholar] [CrossRef]
- Funk, C.; Shukla, S. Drought early warning—definitions, challenges, and opportunities. In Drought Early Warning and Forecasting; Elsevier: Amsterdam, The Netherlands, 2020; pp. 23–42. [Google Scholar]
- Kim, T.-W.; Valdes, J.B.; Yoo, C. Nonparametric approach for bivariate drought characterization using Palmer drought index. J. Hydrol. Eng. 2006, 11, 134–143. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Entropy based method for bivariate drought analysis. J. Hydrol. Eng. 2013, 18, 780–786. [Google Scholar] [CrossRef]
- Shiau, J.T.; Shen, H.W. Recurrence analysis of hydrologic droughts of differing severity. J. Water Resour. Plan. Manag. 2001, 127, 30–40. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Cancelliere, A.; Rossi, G. An analytical formulation of return period of drought severity. Stoch. Environ. Res. Risk Assess. 2003, 17, 157–174. [Google Scholar] [CrossRef]
- González, J.; Valdés, J.B. Bivariate Drought Recurrence Analysis Using Tree Ring Reconstructions. J. Hydrol. Eng. 2015, 8, 247–258. [Google Scholar] [CrossRef]
- Salas, J.D.; Fu, C.J.; Cancelliere, A.; Dustin, D.; Bode, D.; Pineda, A.; Vincent, E. Characterizing the Severity and Risk of Drought in the Poudre River, Colorado. J. Water Resour. Plan. Manag. 2005, 131, 383–393. [Google Scholar] [CrossRef]
- Cancelliere, A.; Salas, J.D. Drought Probabilities and Return Period for Annual Streamflows Series. J. Hydrol. 2010, 391, 77–89. [Google Scholar] [CrossRef]
- Yang, X.Q.; Xiao, J. Analysis of precipitation change trend and mutation in Hainan Island based on Mann Kendall. Flood Control. Drought Relief 2020, 30, 27–30. (In Chinese) [Google Scholar]
- Xu, H.; Song, Y.P.; Goldsmith, Y.; Lang, Y.C. Meridional ITCZ shifts modulate tropical/subtropical Asian monsoon rainfall. Sci. Bull. 2019, 64, 1737–1739. [Google Scholar] [CrossRef] [Green Version]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J. Changes in drought characteristics over China using the standardized precipitation evapotranspiration index. J. Clim. 2015, 28, 5430–5447. [Google Scholar] [CrossRef]
- Hamed, K.H. Exact distribution of the Mann-Kendall trend test statistic for persistent data. J. Hydrol. 2009, 365, 86–94. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Dong, L.Y. Application of Drought Index Based on Copula Function Model and FDA Method. Master’s Thesis, Chongqing University, Chongqing, China, 2019. [Google Scholar]
- Genest, C.; MacKay, J. The Joy of Copulas: Bivariate Distributions with Uniform Marginals. Am. Stat. 1986, 40, 280–283. [Google Scholar]
- Cherubini, U.; Luciano, E. Bivariate option pricing with copulas. Appl. Math. Finance 2002, 9, 69–85. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Zhang, G.; Gao, G.; Lu, E. Characteristic analysis of agricultural drought disaster in China during1951–2007. J. Nat. Disasters 2010, 19, 201–206. [Google Scholar]
- Chen, F.; Li, L.M. Researches on spatial and temporal succession law of agricultural drought in the past 60 years in China. J. South China Normal Univ. Nat. Sci. Ed. 2011, 36, 111–114. [Google Scholar]
- Yao, Y.; Zheng, Y.G. The temporal and spatial characteristics of flood and drought during the recent 60 years in China. Agric. Res. Arid Areas 2017, 35, 228–232. [Google Scholar]
- Zeng, Z.Q.; Wu, W.X.; Li, Y.M.; Zhou, Y.; Zhang, Z.; Zhang, S.; Guo, Y.; Huang, H.; Li, Z. Spatiotemporal Variations in Drought and Wetness from 1965 to 2017 in China. Water 2020, 12, 2097. [Google Scholar] [CrossRef]


| Category | SPEI Index |
|---|---|
| Normal | (−0.5, +∞) |
| Slight drought | (−1.0, −0.5) |
| Moderate drought | (−1.5, −1.0) |
| Severe drought | (−2.0, −1.5) |
| Extreme drought | (−∞, −2.0] |
| Area | Category of Copula Function | Parameter Estimates | Goodness of Fit Evaluation Standard | |
|---|---|---|---|---|
| AIC | BIC | |||
| Northwest | Gaussian copula | 0.8271 | −601.2871 | −596.9415 |
| Student’s copula | 0.8271 | −599.1858 | −590.4946 | |
| GH copula | 2.345 | −546.6435 | −542.2979 | |
| Frank copula | 8.183 | −573.2539 | −568.9083 | |
| Galambos copula | 1.645 | −554.9031 | −550.5575 | |
| HuslerReiss copula | 2.252 | −565.7303 | −561.3846 | |
| Northeast | Gaussian copula | 0.8319 | −820.555 | −815.905 |
| Student’s copula | 0.8337 | −822.6324 | −813.3318 | |
| GH copula | 2.701 | −907.3378 | −902.6875 | |
| Frank copula | 8.604 | −791.2964 | −786.6461 | |
| Galambos copula | 2.003 | −909.7965 | −905.1462 | |
| HuslerReiss copula | 2.635 | −910.1736 | −905.5233 | |
| Southwest | Gaussian copula | 0.8291 | −775.5213 | −773.5139 |
| Student’s copula | 0.8291 | −773.5139 | −764.3061 | |
| GH copula | 2.436 | −737.7691 | −733.1652 | |
| Frank copula | 8.816 | −784.6019 | −779.998 | |
| Galambos copula | 1.727 | −744.8849 | −740.2809 | |
| HuslerReiss copula | 2.335 | −757.1334 | −752.5294 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otkur, A.; Wu, D.; Zheng, Y.; Kim, J.-S.; Lee, J.-H. Copula-Based Drought Monitoring and Assessment According to Zonal and Meridional Temperature Gradients. Atmosphere 2021, 12, 1066. https://doi.org/10.3390/atmos12081066
Otkur A, Wu D, Zheng Y, Kim J-S, Lee J-H. Copula-Based Drought Monitoring and Assessment According to Zonal and Meridional Temperature Gradients. Atmosphere. 2021; 12(8):1066. https://doi.org/10.3390/atmos12081066
Chicago/Turabian StyleOtkur, Abudureymjang, Dian Wu, Yin Zheng, Jong-Suk Kim, and Joo-Heon Lee. 2021. "Copula-Based Drought Monitoring and Assessment According to Zonal and Meridional Temperature Gradients" Atmosphere 12, no. 8: 1066. https://doi.org/10.3390/atmos12081066
APA StyleOtkur, A., Wu, D., Zheng, Y., Kim, J.-S., & Lee, J.-H. (2021). Copula-Based Drought Monitoring and Assessment According to Zonal and Meridional Temperature Gradients. Atmosphere, 12(8), 1066. https://doi.org/10.3390/atmos12081066








