Operational Forecasting of Tropical Cyclone Rapid Intensification at the National Hurricane Center
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. RI Forecast Tools
3.1.1. Deterministic Guidance
3.1.2. Probabilistic Guidance
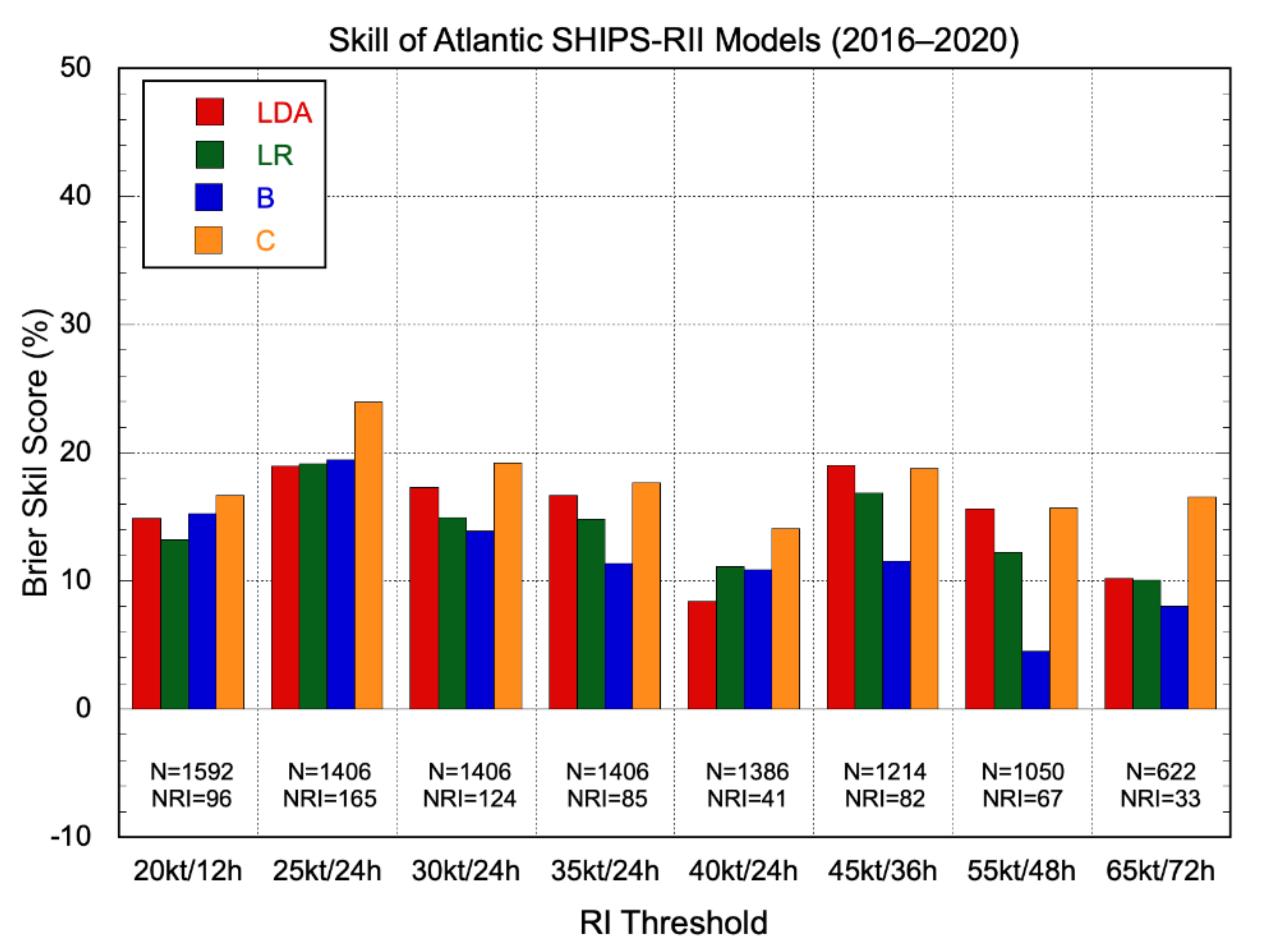
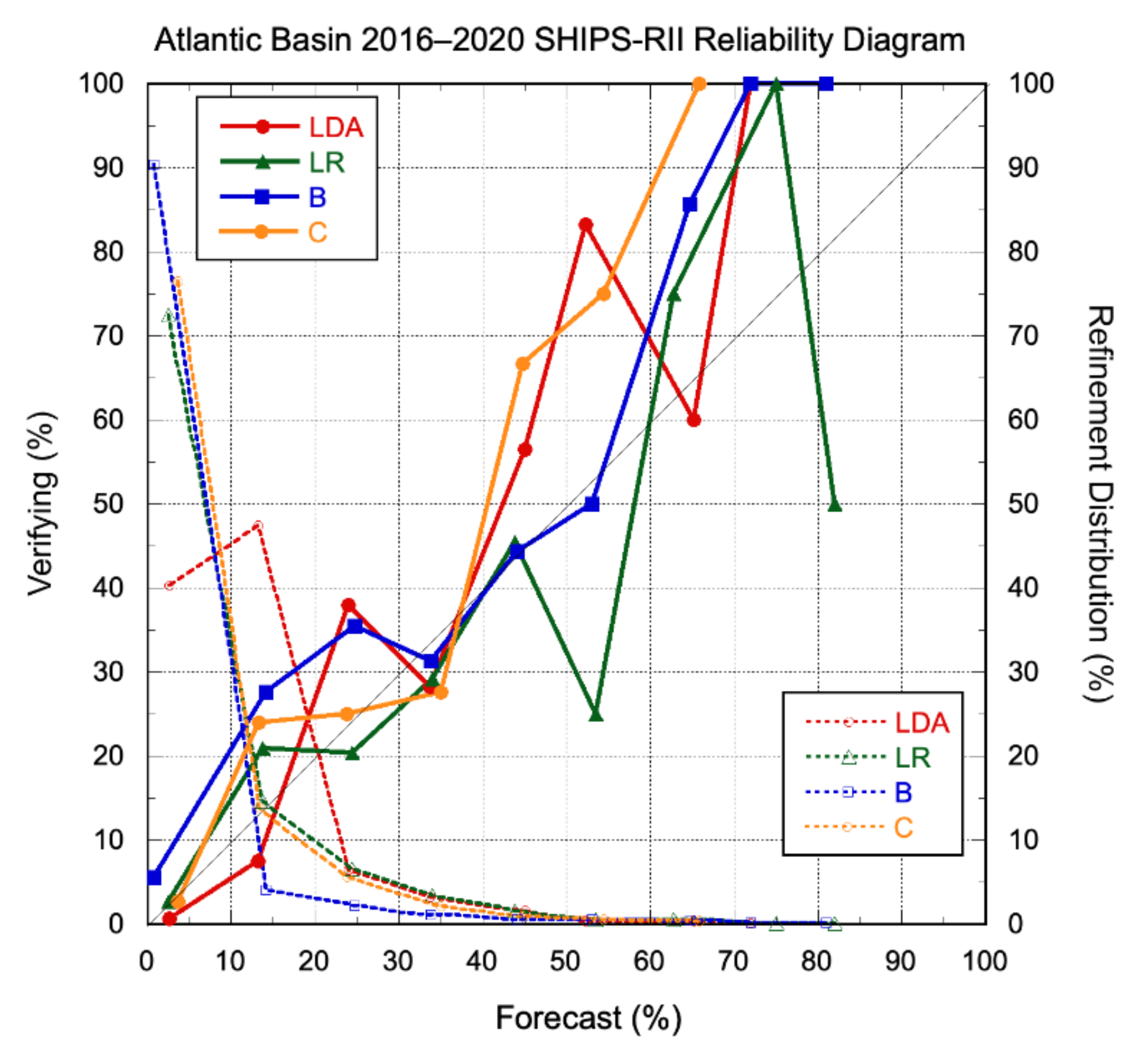
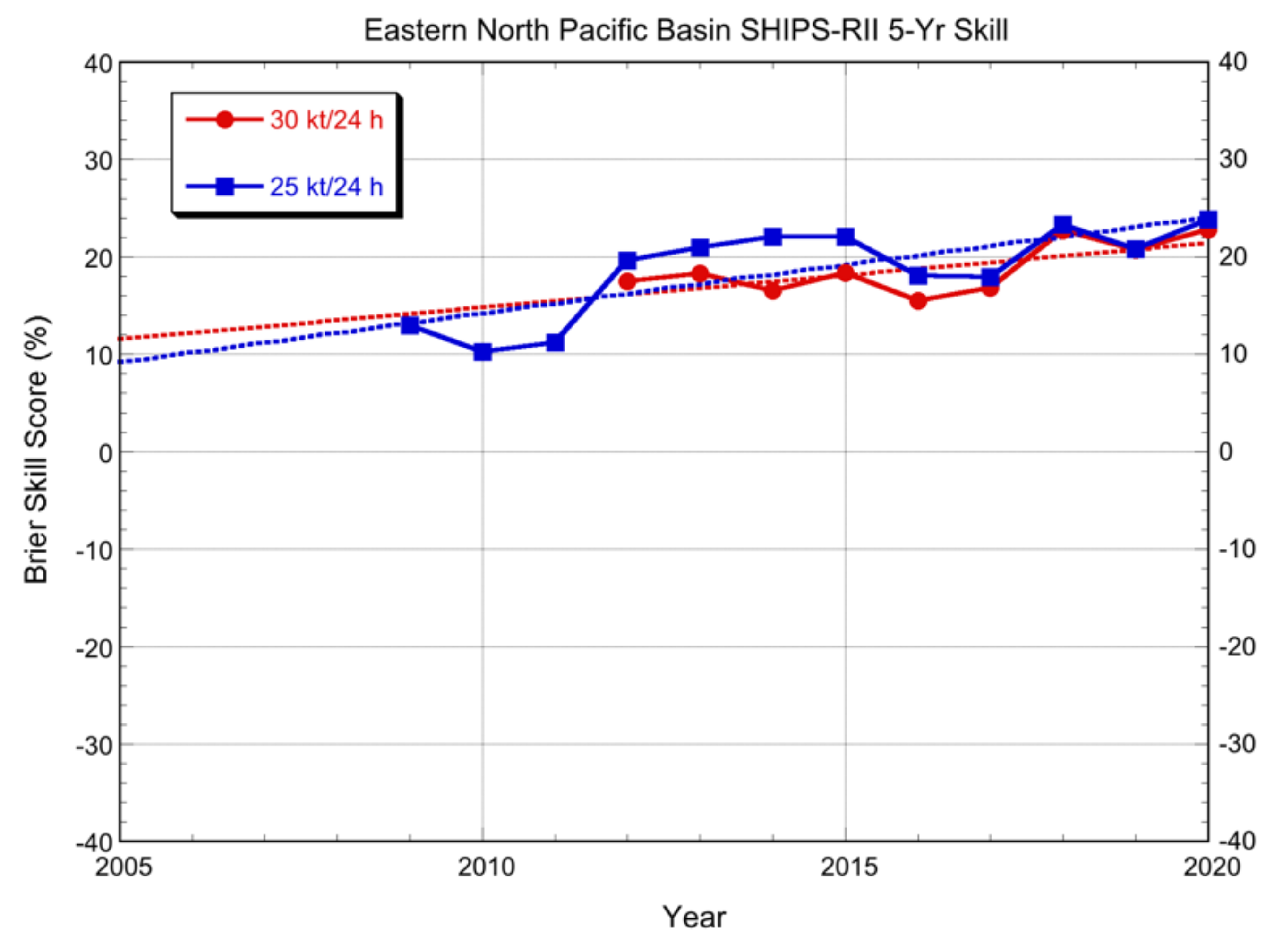
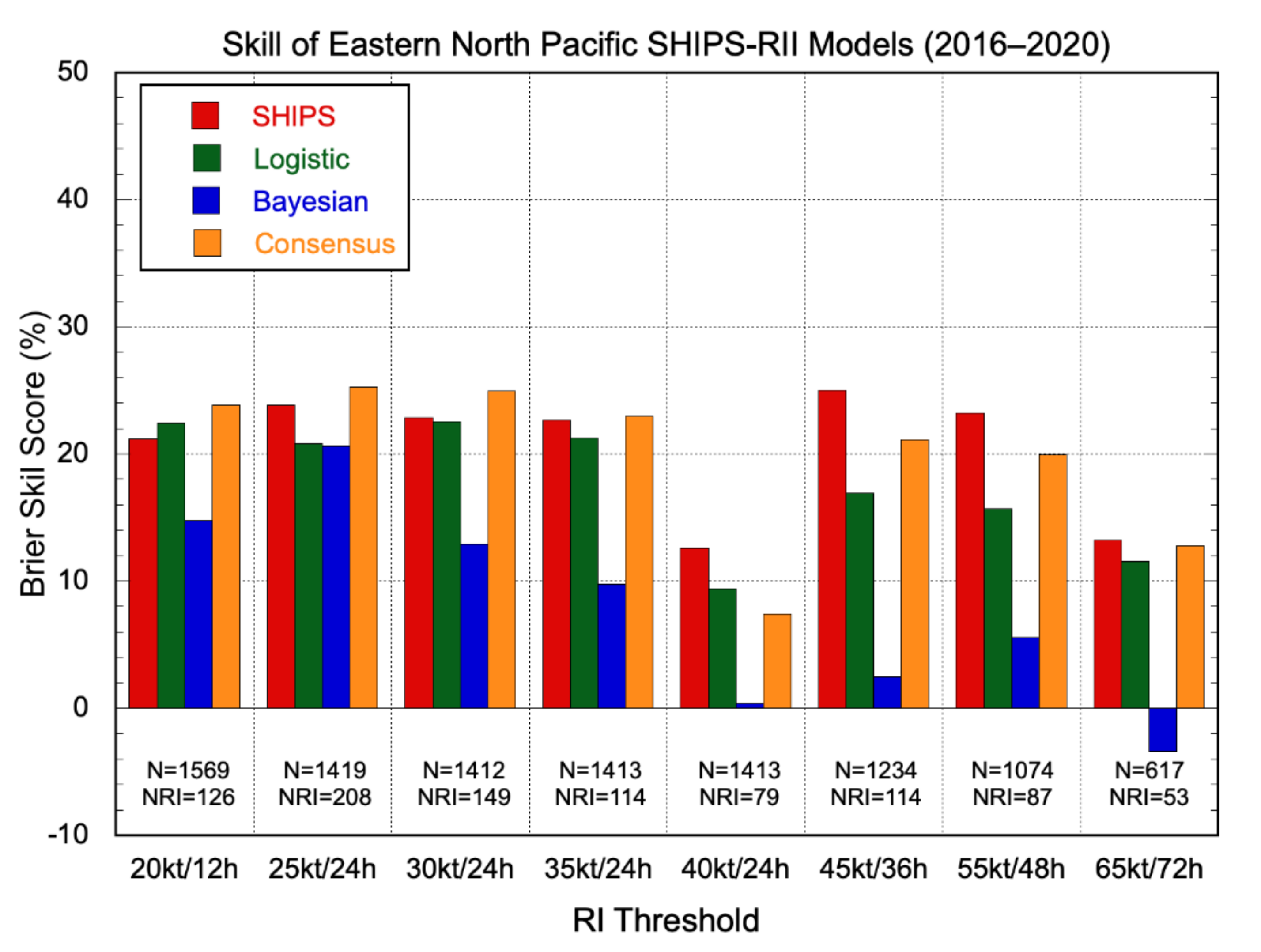
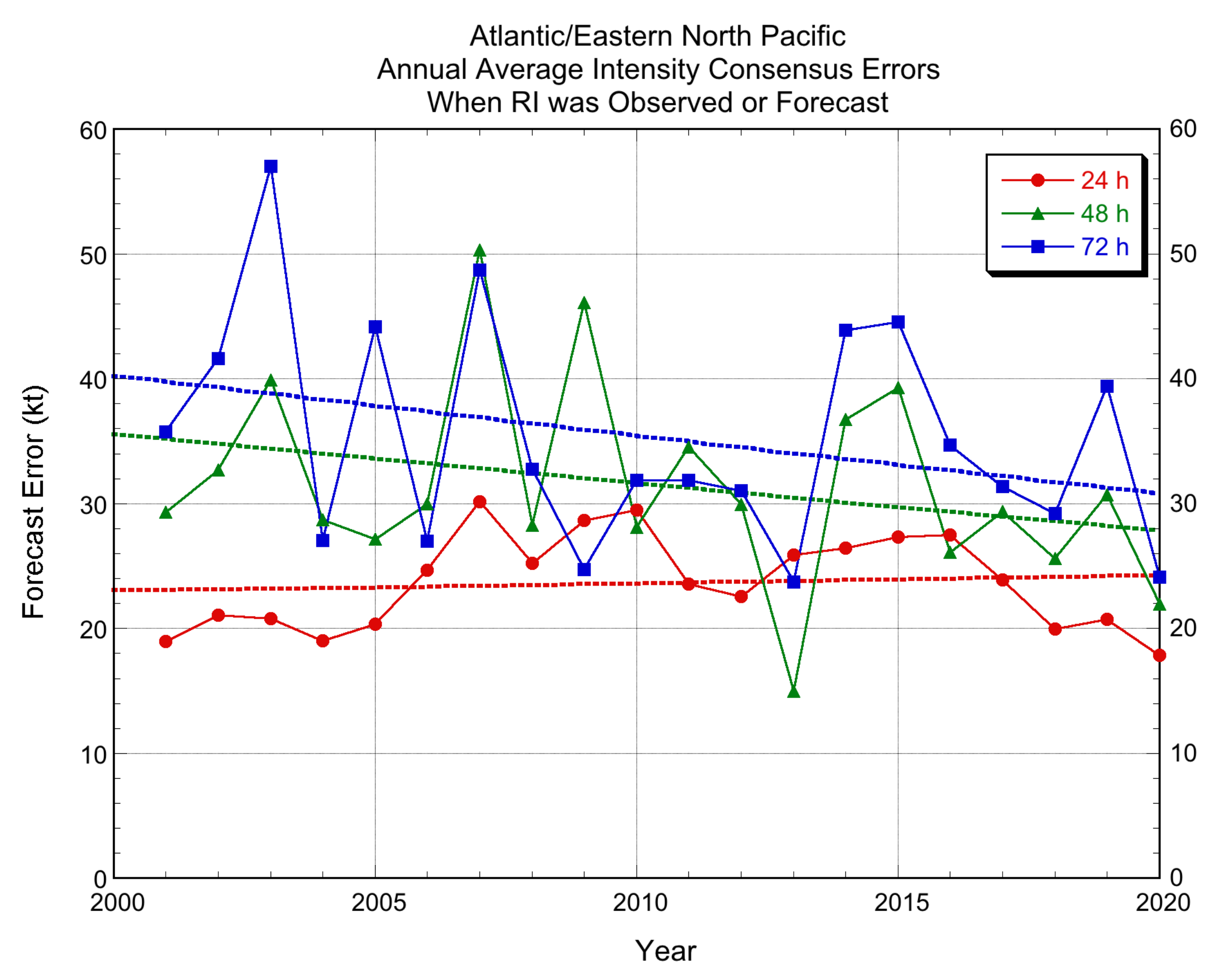
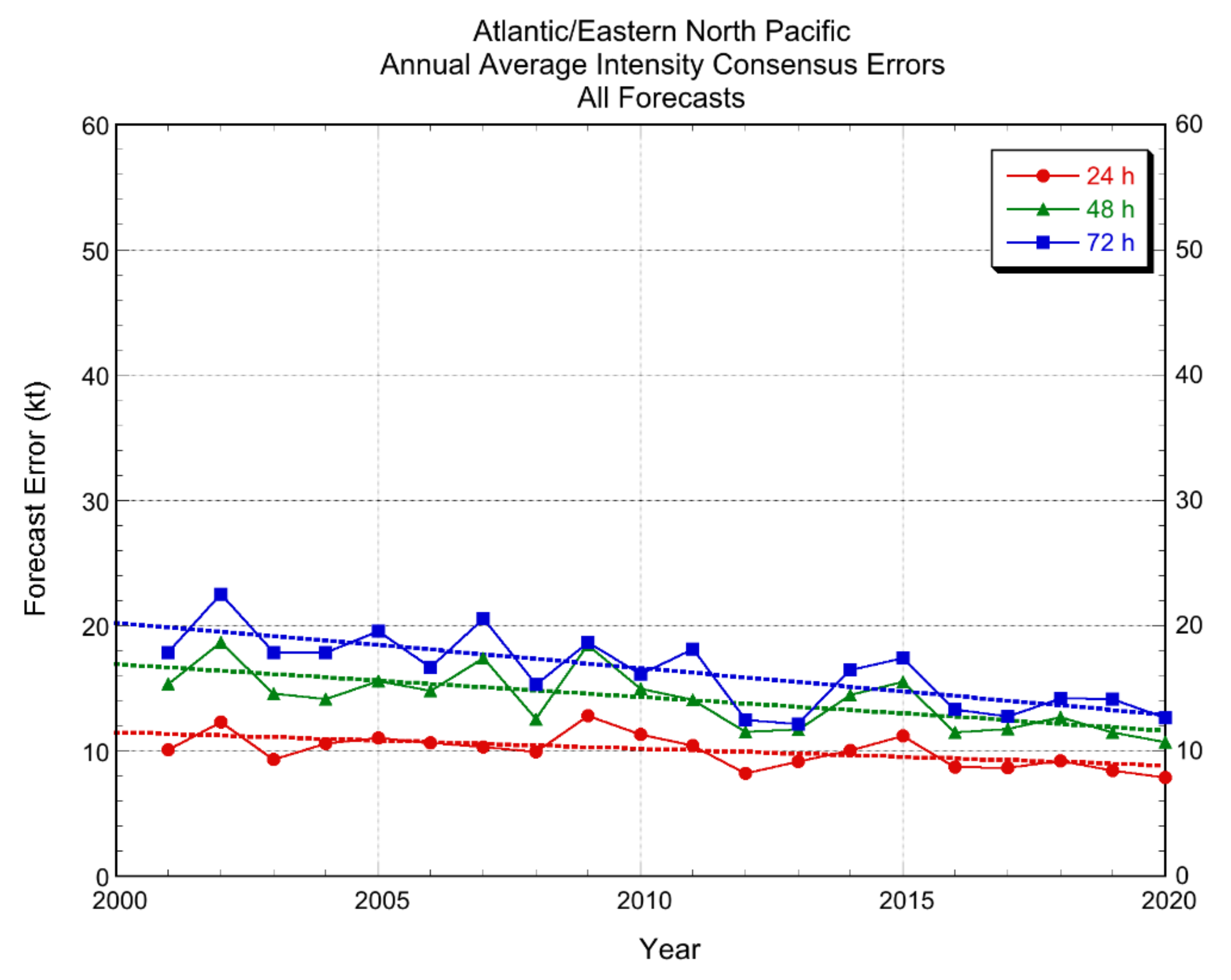
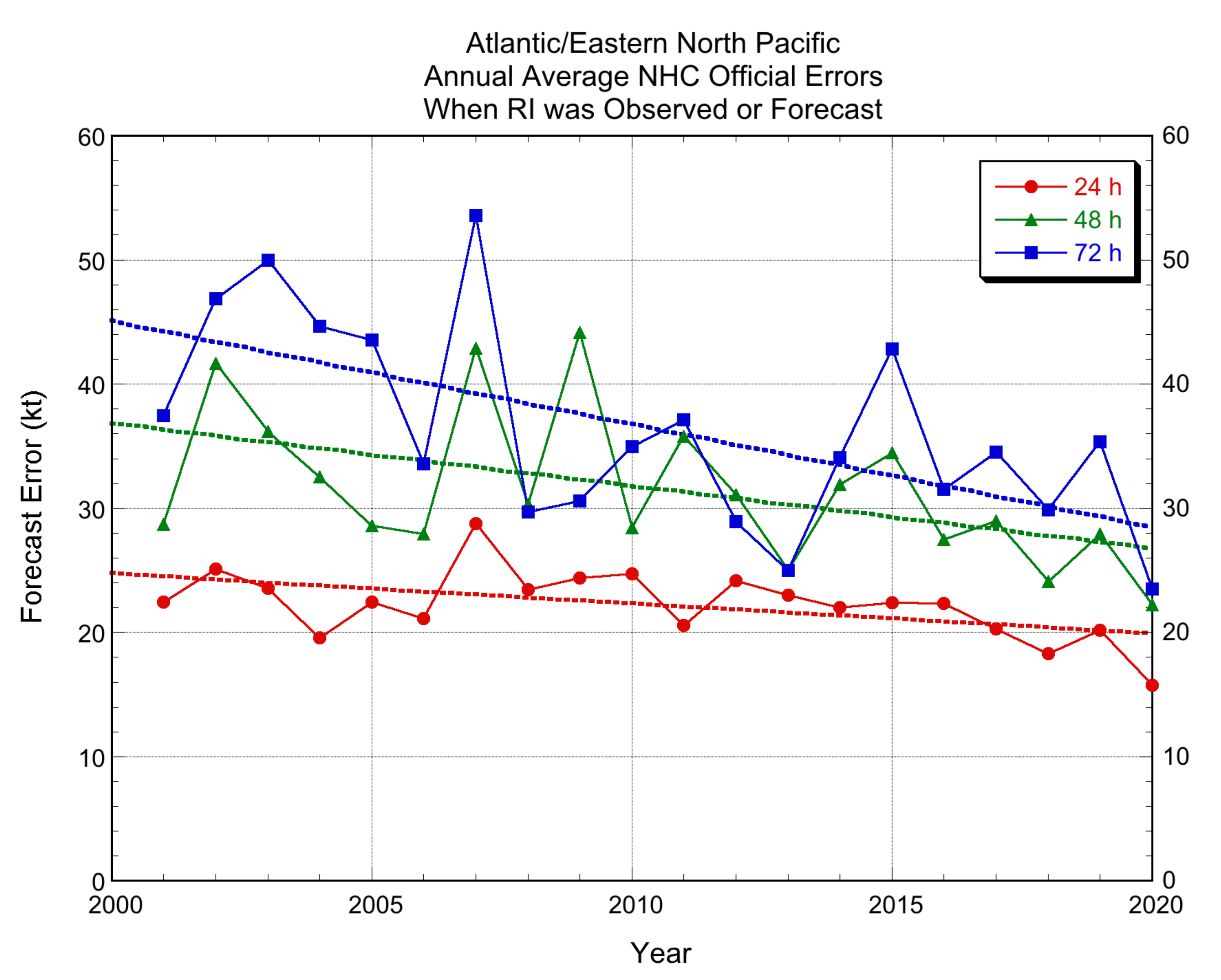
3.2. Verification Results
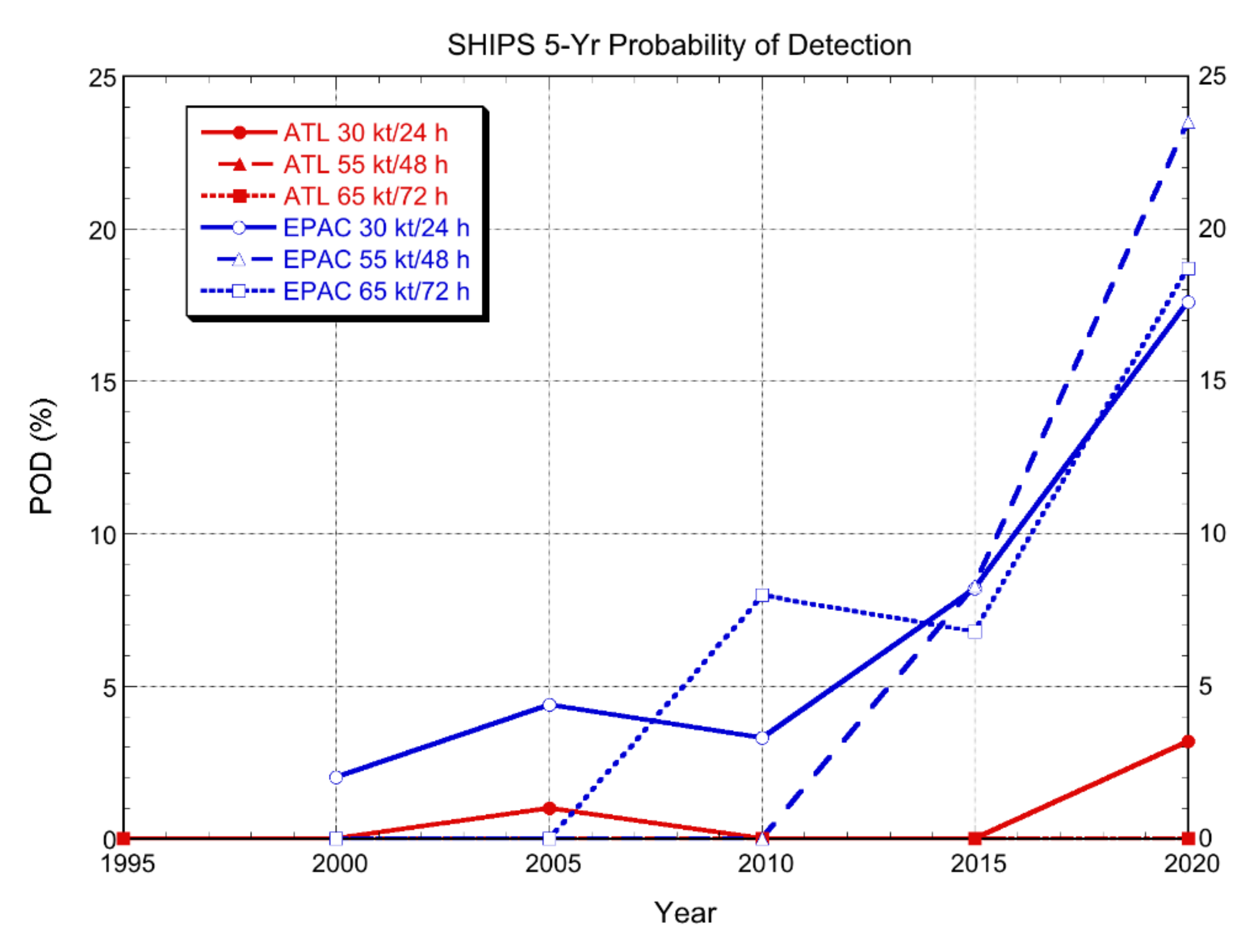
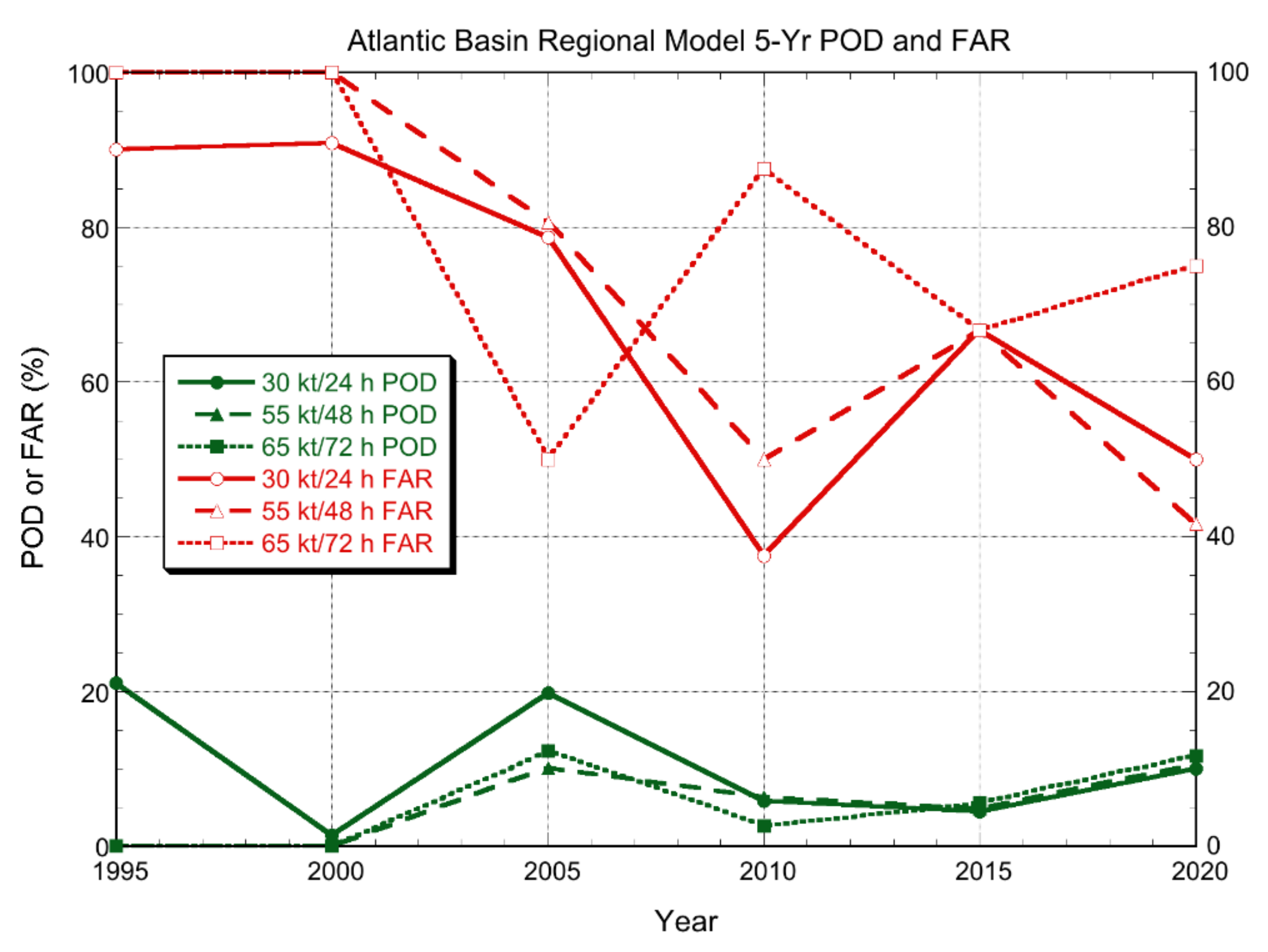
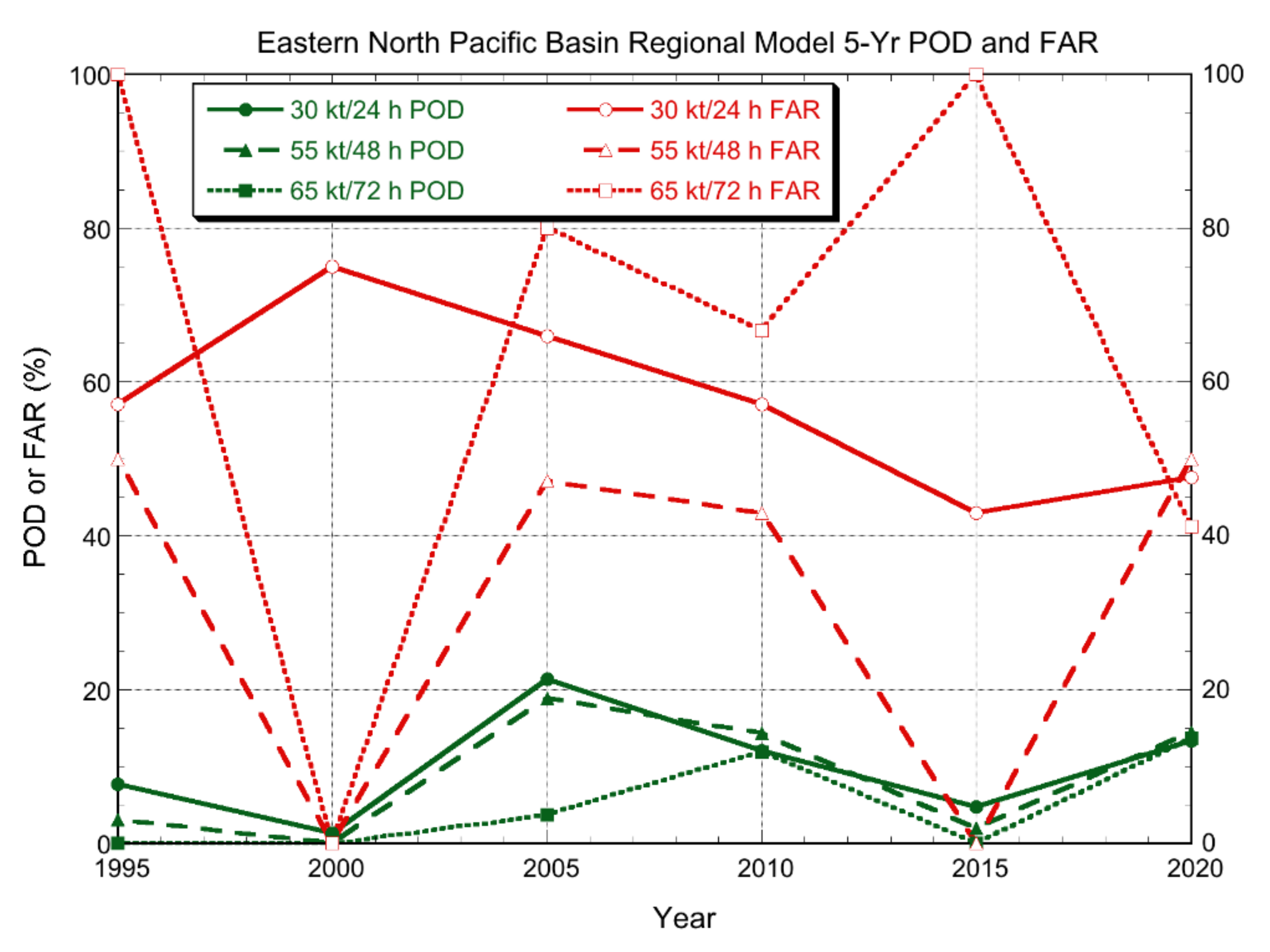
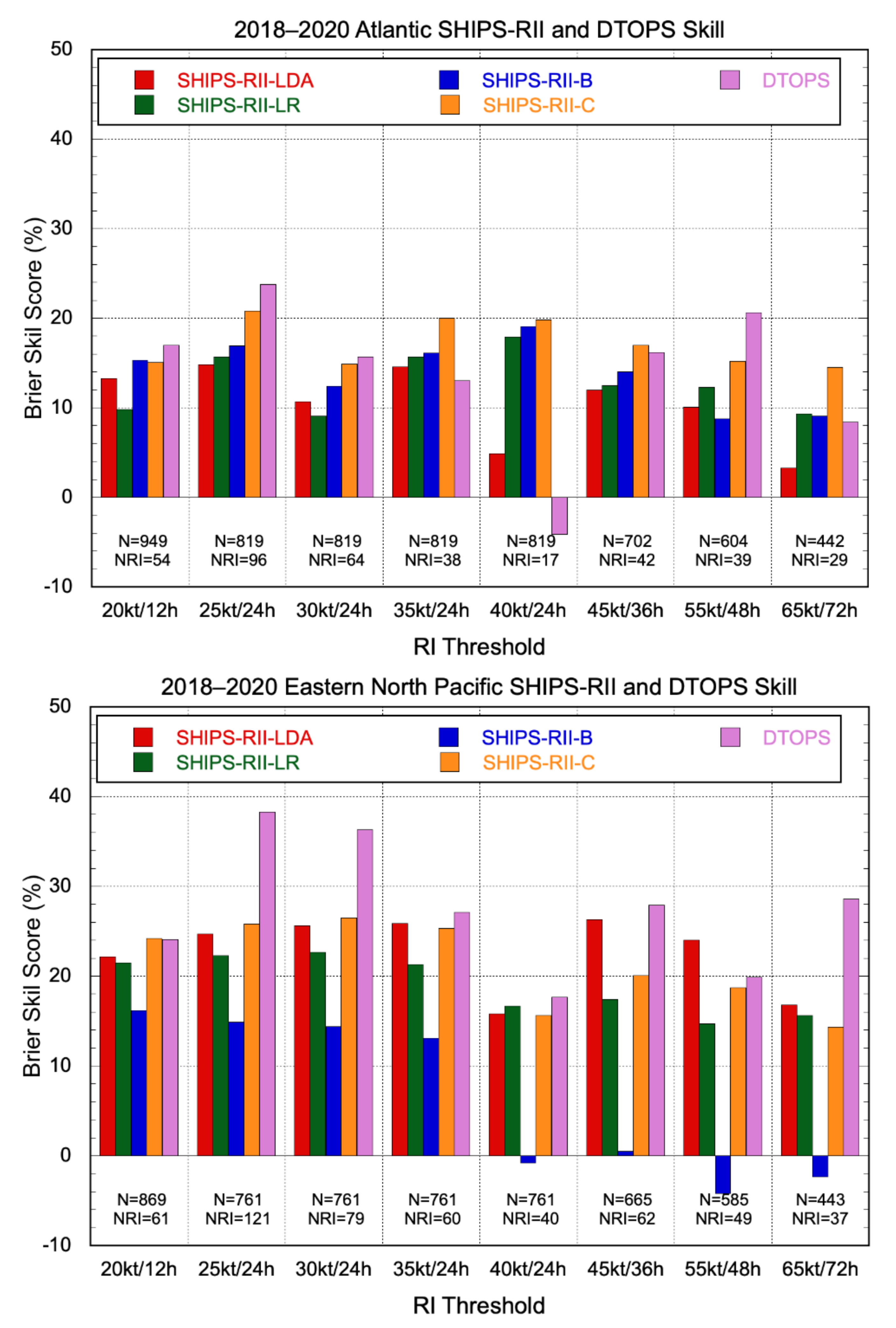
3.2.1. Deterministic Models
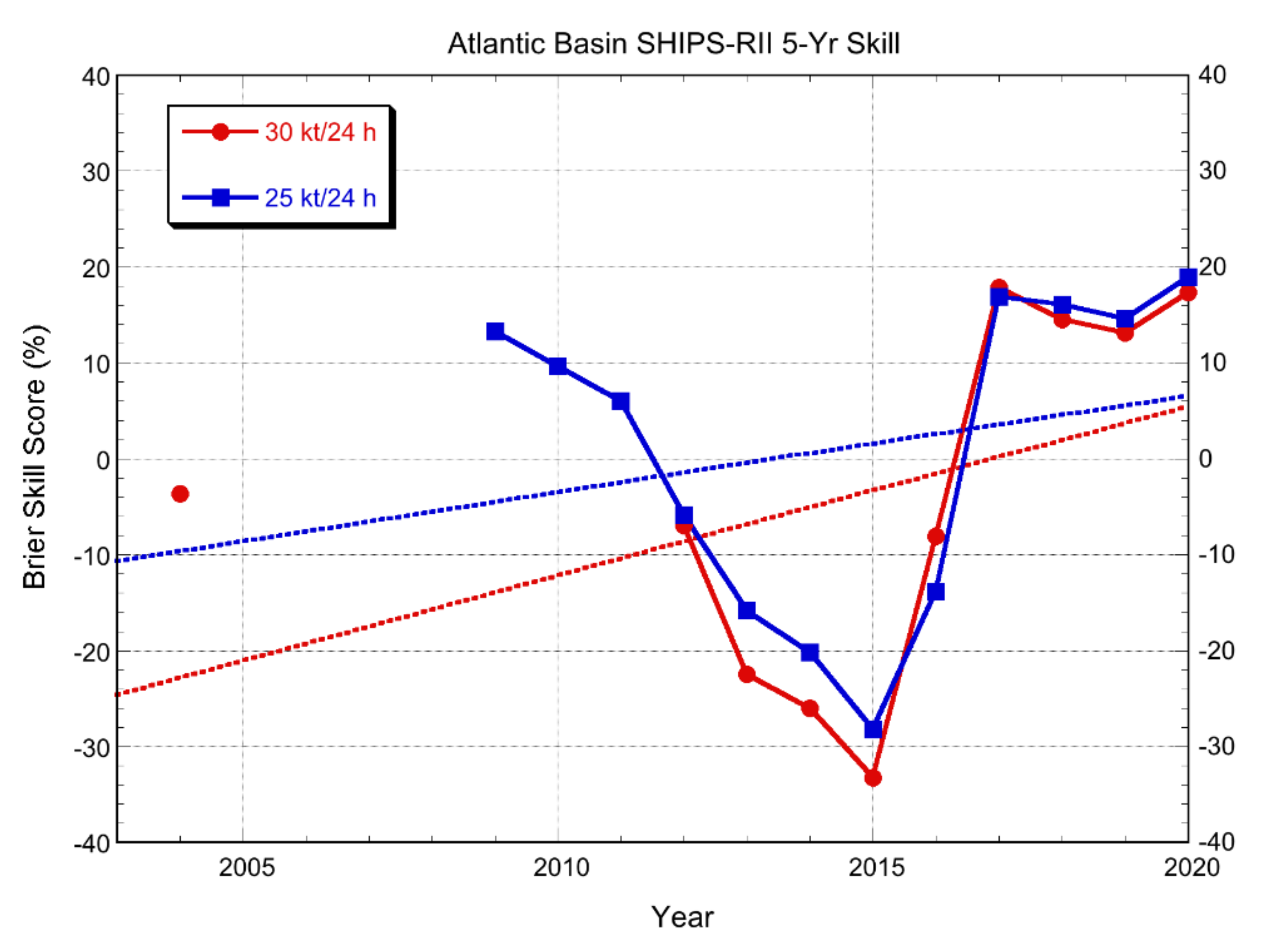
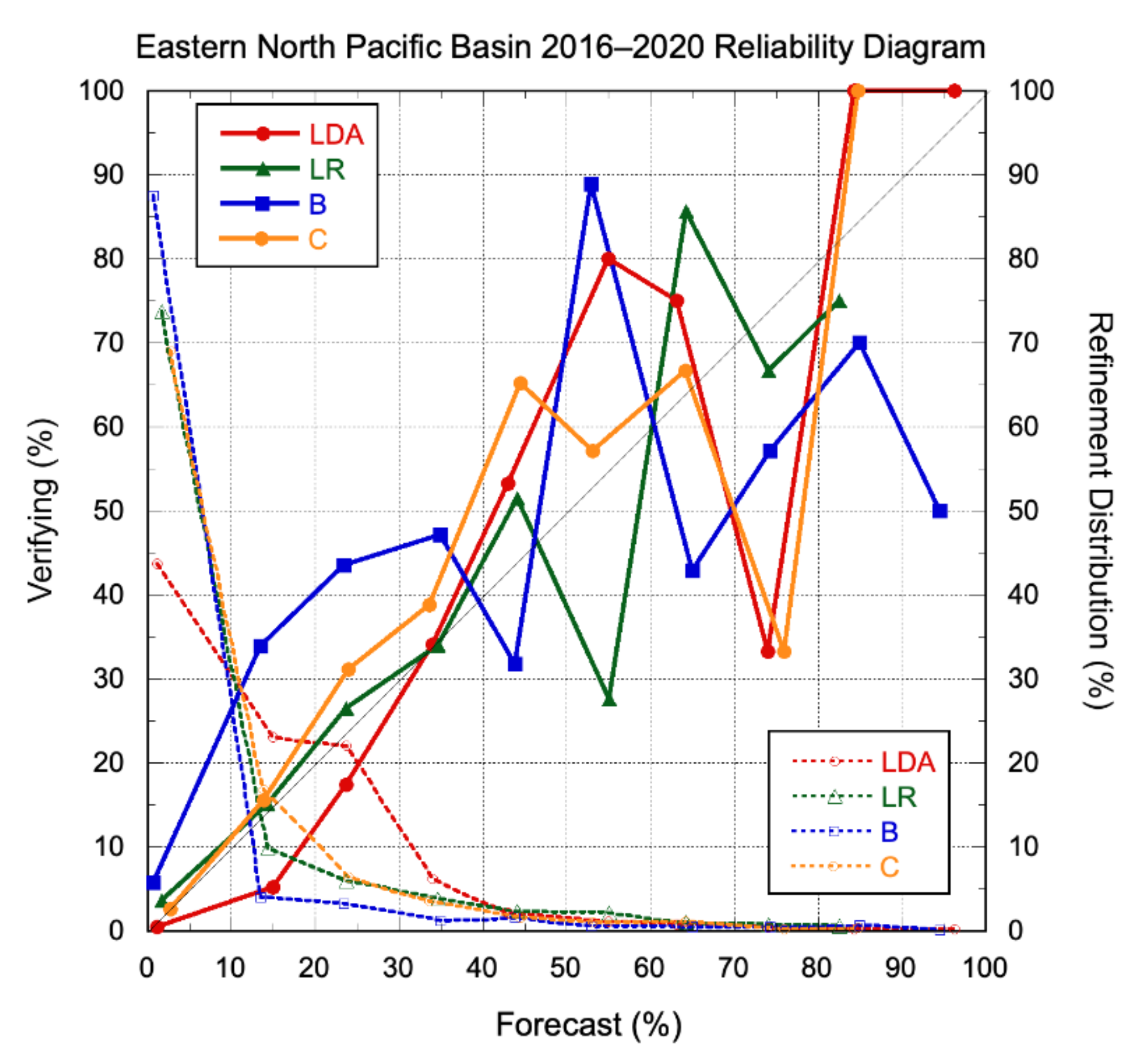
3.2.2. Probabilistic Models
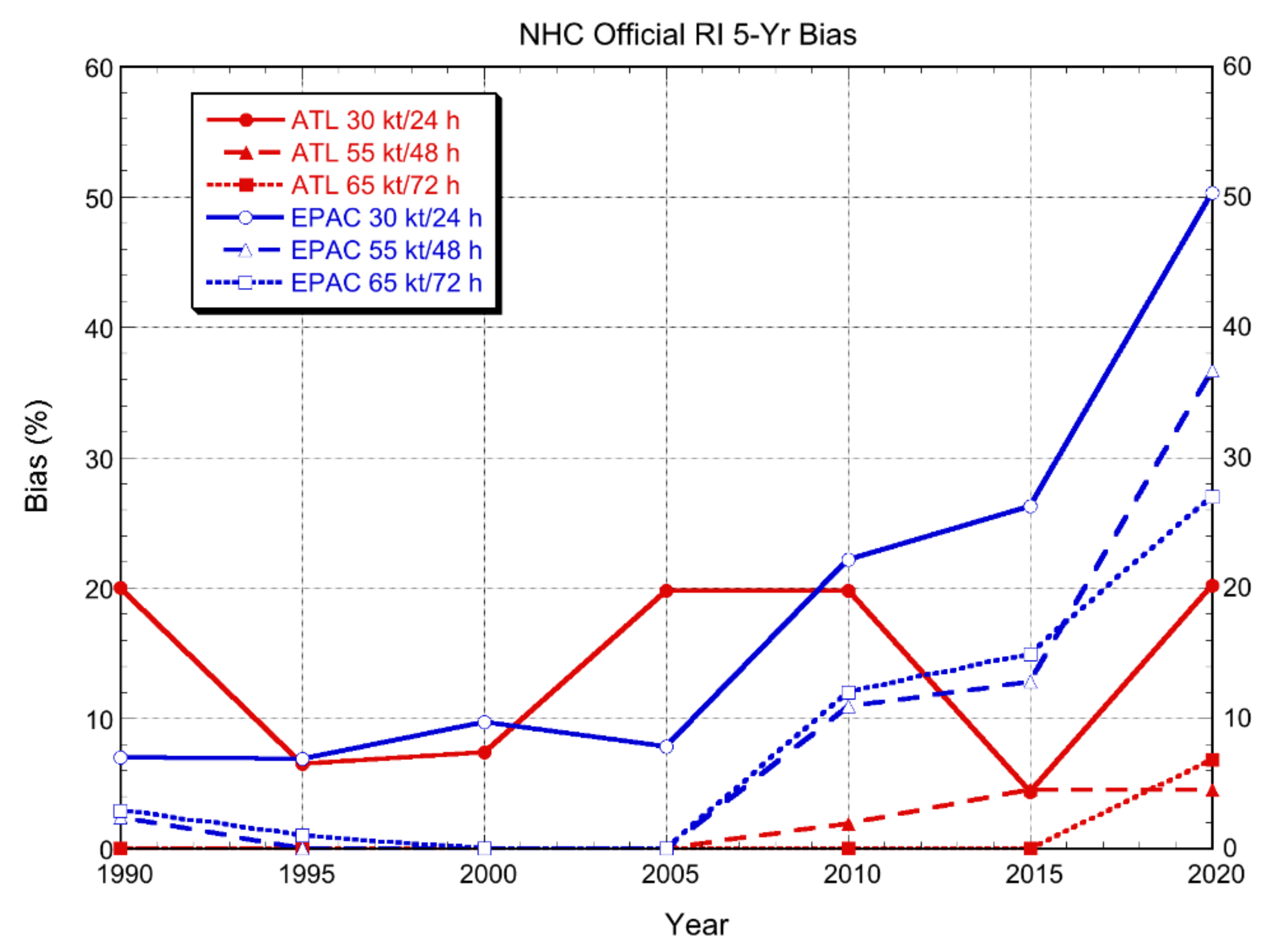
3.2.3. NHC Official Forecasts
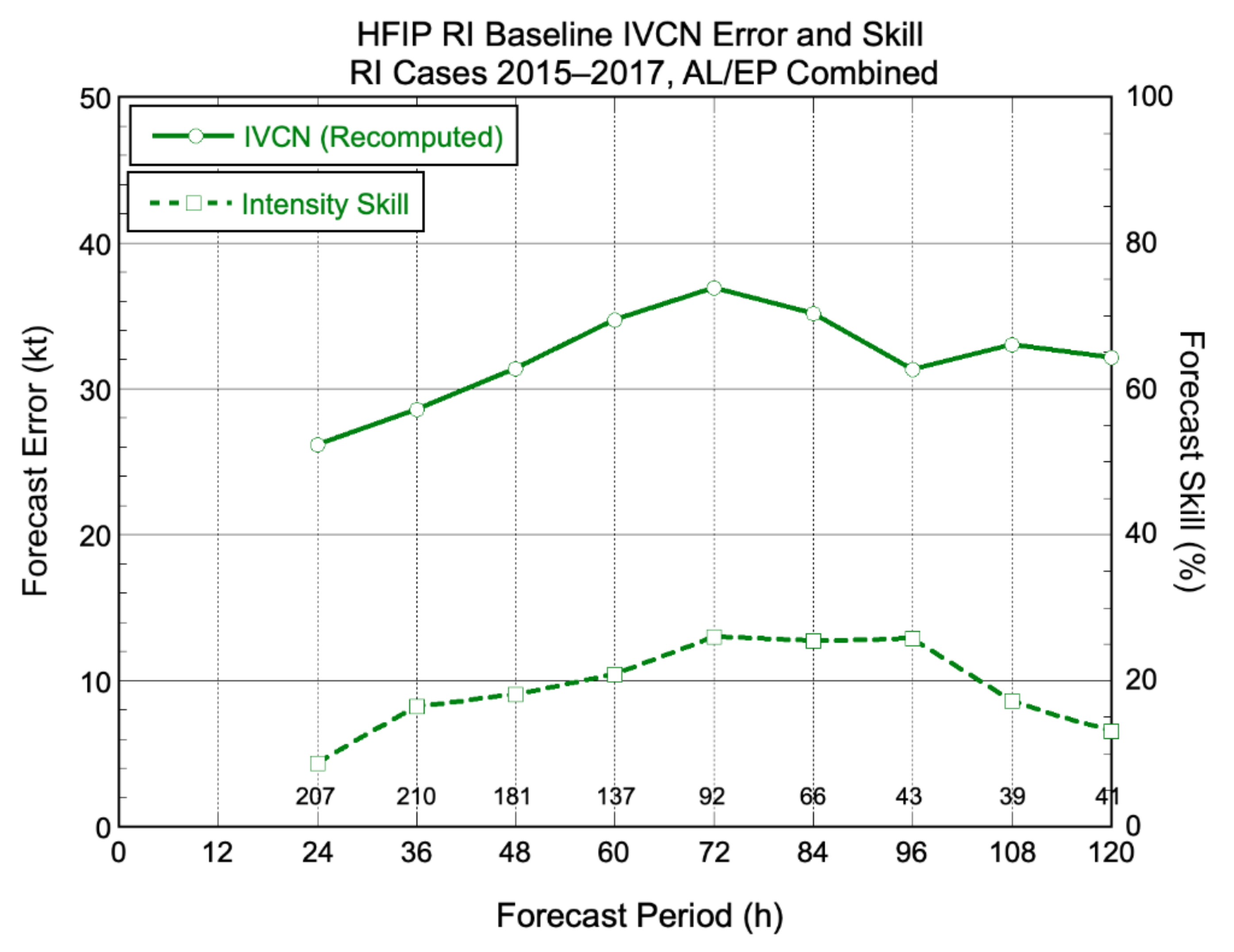
3.3. A new HFIP Performance Measure for RI
- A 30-kt or larger increase in the best-track intensity, relative to the best-track intensity 24 h prior to the verification time;
- A 30-kt or larger forecast increase in intensity in IVCN or in any of the IVCN member models, relative to the forecast intensity 24 h prior to the verification time.
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cangialosi, J.P.; Blake, E.; DeMaria, M.; Penny, A.; Latto, A.; Rappaport, E.; Tallapragada, V. Recent Progress in Tropical Cyclone Intensity Forecasting at the National Hurricane Center. Weather Forecast. 2020, 35, 1913–1922. [Google Scholar] [CrossRef]
- DeMaria, M.; Mainelli, M.; Shay, L.K.; Knaff, J.A.; Kaplan, J. Further Improvements in the Statistical Hurricane In-tensity Prediction Scheme (SHIPS). Weather Forecast. 2005, 20, 531–543. [Google Scholar] [CrossRef]
- DeMaria, M. A Simplified Dynamical System for Tropical Cyclone Intensity Prediction. Mon. Weather Rev. 2009, 137, 68–82. [Google Scholar] [CrossRef]
- Tallapragada, V. Overview of the NOAA/NCEP operational hurricane weather research and forecast (HWRF) modelling system. In Advanced Numerical Modeling and Data Assimilation Techniques for Tropical Cyclones; Springer: Dordrecht, The Netherlands, 2016; pp. 51–106. [Google Scholar] [CrossRef]
- Kieu, C.; Evans, C.; Jin, Y.; Doyle, J.D.; Jin, H.; Moskaitis, J. Track Dependence of Tropical Cyclone Intensity Forecast Errors in the COAMPS-TC Model. Weather Forecast. 2021, 36, 469–485. [Google Scholar] [CrossRef]
- DeMaria, M.; Sampson, C.R.; Knaff, J.A.; Musgrave, K.D. Is tropical cyclone intensity guidance improving? Bull. Am. Meteorol. Soc. 2014, 95, 387–398. [Google Scholar] [CrossRef]
- Simon, A.; Penny, A.B.; DeMaria, M.; Franklin, J.L.; Pasch, R.J.; Rappaport, E.N.; Zelinsky, D.A. A description of the re-al-time HFIP Corrected Consensus Approach (HCCA) for Tropical Cyclone Track and Intensity Guidance. Weather Forecast. 2018, 33, 37. [Google Scholar] [CrossRef]
- Trabing, B.C.; Bell, M.M. Understanding error distributions of hurricane intensity forecasts during rapid intensity changes. Weather Forecast. 2020, 35, 2219–2234. [Google Scholar] [CrossRef]
- Na, W.; McBride, J.L.; Zhang, X.-H.; Duan, Y.-H. Understanding biases in tropical cyclone intensity forecasting. Weather Forecast. 2018, 33, 129–138. [Google Scholar] [CrossRef]
- Kaplan, J.; DeMaria, M. Large-Scale Characteristics of Rapidly Intensifying Tropical Cyclones in the North Atlantic Basin. Weather Forecast. 2003, 18, 1093–1108. [Google Scholar] [CrossRef]
- Rogers, R.F.; Reasor, P.D.; Zhang, J.A. Multiscale Structure and Evolution of Hurricane Earl (2010) during Rapid Intensification. Mon. Weather Rev. 2015, 143, 536–562. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Peng, M.S.; Fu, B.; Li, T. Quantifying Environmental Control on Tropical Cyclone Intensity Change. Mon. Weather Rev. 2010, 138, 3243–3271. [Google Scholar] [CrossRef]
- Sampson, C.R.; Schrader, A.J. The Automated Tropical Cyclone Forecasting System (Version 3.2). Bull. Am. Meteorol. Soc. 2000, 81, 1231–1240. [Google Scholar] [CrossRef]
- Cangialosi, J. National Hurricane Center Forecast Verification Report: 2019 Hurricane Season. 2019. Available online: https://www.nhc.noaa.gov/verification/pdfs/Verification_2019.pdf (accessed on 1 March 2021).
- Bender, M.A.; Marchok, T.; Tuleya, R.E.; Ginis, I.; Tallapragada, V.; Lord, S.J. Hurricane Model Development at GFDL: A Collaborative Success Story from a Historical Perspective. Bull. Am. Meteorol. Soc. 2019, 100, 1725–1736. [Google Scholar] [CrossRef]
- Levine, R.A.; Wilks, D.S. Statistical Methods in the Atmospheric Sciences. J. Am. Stat. Assoc. 2000, 95, 344. [Google Scholar] [CrossRef]
- Kaplan, J.; DeMaria, M.; Knaff, J.A. A revised tropical cyclone rapid intensification index for the Atlantic and east Pacific basins. Weather Forecast. 2010, 25, 220–241. [Google Scholar] [CrossRef]
- Kaplan, J.; Rozoff, C.M.; DeMaria, M.; Sampson, C.R.; Kossin, J.P.; Velden, C.S.; Cione, J.J.; Dunion, J.P.; Knaff, J.A.; Zhang, J.A.; et al. Evaluating Environmental Impacts on Tropical Cyclone Rapid Intensification Predictability Utilizing Statistical Models. Weather Forecast. 2015, 30, 1374–1396. [Google Scholar] [CrossRef]
- Knaff, J.A.; Sampson, C.R.; Musgrave, K.D. An Operational Rapid Intensification Prediction Aid for the Western North Pacific. Weather Forecast. 2018, 33, 799–811. [Google Scholar] [CrossRef]
- Rozoff, C.M.; Kossin, J.P. New Probabilistic Forecast Models for the Prediction of Tropical Cyclone Rapid Intensification. Weather Forecast. 2011, 26, 677–689. [Google Scholar] [CrossRef]
- HFIP. 2018. Available online: http://hfip.org/sites/default/files/documents/hfip-strategic-plan-20190625.pdf (accessed on 1 March 2021).
- Landsea, C.W.; Franklin, J.L. Atlantic Hurricane Database Uncertainty and Presentation of a New Database Format. Mon. Weather Rev. 2013, 141, 3576–3592. [Google Scholar] [CrossRef]
- Hazelton, A.; Zhang, Z.; Liu, B.; Dong, J.; Alaka, G.; Wang, W. 2019 Atlantic hurricane forecasts from the Glob-al-Nested Hurricane Analysis and Forecast System: Composite statistics and key events. Weather Forecast. 2020. [Google Scholar] [CrossRef]
- Torn, R.; DeMaria, M. Validation of Ensemble-Based Probabilistic Tropical Cyclone Intensity Change. Atmosphere 2021, 12, 373. [Google Scholar] [CrossRef]
- Cloud, K.A.; Reich, B.J.; Rozoff, C.M.; Alessandrini, S.; Lewis, W.E.; Monache, L.D. A Feed Forward Neural Network Based on Model Output Statistics for Short-Term Hurricane Intensity Prediction. Weather Forecast. 2019, 34, 985–997. [Google Scholar] [CrossRef]
- Su, H.; Wu, L.; Jiang, J.H.; Pai, R.; Liu, A.; Zhai, A.J.; Tavallali, P.; DeMaria, M. Applying Satellite Observations of Tropical Cyclone Internal Structures to Rapid Intensification Forecast with Machine Learning. Geophys. Res. Lett. 2020, 47, 10. [Google Scholar] [CrossRef]
| Parameter | Definition |
|---|---|
| a | Event forecasted and observed |
| b | Event forecasted but not observed |
| c | Event not forecasted but observed |
| d | Event not forecasted and not observed |
| a/(a + c) | Probability of detection (POD) |
| b/(a + b) | False alarm ratio (FAR) |
| (a + b)/(a + c) | Bias (Bd) |
| ATCF Model Name | Type | Years in Operations |
|---|---|---|
| SHIPS | Statistical–dynamical | 1991–2020 |
| LGEM | Statistical–dynamical | 2006–2020 |
| GFDI | Regional dynamical | 1996–2016 |
| HWFI | Regional dynamical | 2007–2020 |
| HMNI | Regional dynamical | 2017–2020 |
| GFSI | Global dynamical | 1994–2020 |
| ICON | Consensus | 2006–2020 |
| IVCN | Consensus | 2008–2020 |
| HCCA | Consensus | 2015–2020 |
| Model Name | Type | Years in Operations |
| SHIPS-RII-T | Threshold method | 2001–2005 |
| SHIPS-RII-LDA | Linear discriminant analysis | 2006–2020 |
| SHIPS-RII-LR | Logistic regression | 2016–2020 |
| SHIPS-RII-B | Bayesian method | 2016–2020 |
| SHIPS-RII-C | Consensus | 2016–2020 |
| DTOPS | Consensus logistic regression | 2018–2020 |
| Predictor | Definition | Normalized Coefficient (AL) | Normalized Coefficient (EP) |
|---|---|---|---|
| Intercept term | b0 in Equation (4) | −3.94 | −4.27 |
| GFSI ΔV | GFS intensity change forecast (kt) | 1.34 | 1.13 |
| EMXI ΔP | ECMWF pressure change forecast (mb) | 0.49 | 0.67 |
| HWFI ΔV | HWFI intensity change forecast (kt) | −0.26 | 0.37 |
| LGEM ΔV | LGEM intensity change forecast (kt) | 0.42 | 0.02 |
| SHIPS ΔV | SHIPS intensity change forecast (kt) | 0.70 | 2.37 |
| (TC Intensity)2 | TC initial intensity (kt) squared | −2.52 | −3.93 |
| (TC Intensity) * cos(latitude) | TC initial intensity (kt) multiplied by the cosine of TC initial latitude | 3.33 | 4.13 |
| (HWFI ΔV)*(SHIPS ΔV) | HWFI intensity change forecast multiplied by SHIPS intensity change forecast (kt) | 0.30 | −0.53 |
| Standardized STD(GFS ΔV) | (see table caption) | 0.10 | −0.75 |
| Standardized STD(ECMWF ΔP) | 0.21 | 0.36 | |
| Standardized STD(HWFI ΔV) | 0.01 | 0.02 | |
| Standardized STD(LGEM ΔV) | −0.31 | −0.14 | |
| Standardized STD(SHIPS ΔV) | 0.17 | −0.14 |
| Atlantic | 30 kt/24 h | 55 kt/48 h | 65 kt/72 h | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Years | N | N-RI | %RI | N | N-RI | %RI | N | N-RI | %RI |
| 1986–1990 | 176.8 | 9.0 | 5.1 | 141.0 | 3.4 | 2.4 | 108.6 | 3.4 | 3.1 |
| 1991–1995 | 215.4 | 12.4 | 5.8 | 168.2 | 6.0 | 3.6 | 136.0 | 5.4 | 4.0 |
| 1996–2000 | 278.8 | 19.0 | 6.8 | 230.6 | 8.8 | 3.8 | 190.4 | 11.0 | 5.8 |
| 2001–2005 | 348.6 | 20.2 | 5.8 | 282.0 | 14.8 | 5.2 | 227.6 | 17.8 | 7.8 |
| 2006–2010 | 217.8 | 19.2 | 8.8 | 167.8 | 10.4 | 6.2 | 132.4 | 8.6 | 6.5 |
| 2011–2015 | 218.8 | 9.2 | 4.2 | 164.6 | 4.4 | 2.7 | 122.0 | 4.2 | 3.4 |
| 2016–2020 | 351.4 | 24.8 | 7.1 | 279.4 | 13.2 | 4.7 | 219.6 | 8.8 | 4.0 |
| 1986–2020 | 258.2 | 16.3 | 6.3 | 204.8 | 8.7 | 4.3 | 162.4 | 8.5 | 5.2 |
| Eastern Pacific | 30 kt/24 h | 55 kt/48 h | 65 kt/72 h | ||||||
| Years | N | N-RI | %RI | N | N-RI | %RI | N | N-RI | %RI |
| 1988–1990 | 312.7 | 23.7 | 7.6 | 269.7 | 14.0 | 5.2 | 221.7 | 11.7 | 5.3 |
| 1991–1995 | 383.0 | 35.0 | 9.1 | 320.2 | 24.6 | 7.7 | 268.4 | 19.2 | 7.2 |
| 1996–2000 | 253.6 | 20.6 | 8.1 | 195.8 | 11.8 | 6.0 | 150.8 | 9.2 | 6.1 |
| 2001–2005 | 248.4 | 18.0 | 7.2 | 188.6 | 11.4 | 6.0 | 140.0 | 7.8 | 5.6 |
| 2006–2010 | 244.0 | 18.0 | 7.4 | 189.4 | 9.2 | 4.9 | 139.8 | 5.0 | 3.6 |
| 2011–2015 | 314.6 | 34.2 | 10.9 | 245.2 | 21.8 | 8.9 | 187.2 | 14.8 | 7.9 |
| 2016–2020 | 318.8 | 33.0 | 10.4 | 249.8 | 19.6 | 7.8 | 193.6 | 14.8 | 7.6 |
| 1988–2020 | 295.5 | 26.2 | 8.9 | 235.0 | 16.2 | 6.9 | 183.8 | 11.8 | 6.4 |
| POD | Atlantic | Eastern Pacific | ||||
|---|---|---|---|---|---|---|
| 30 kt/24 h | 55 kt/48 h | 65 kt/72 h | 30 kt/24 h | 55 kt/48 h | 65 kt/72 h | |
| SHIPS | 3 | 0 | 0 | 18 | 24 | 19 |
| LGEM | 4 | 0 | 0 | 14 | 13 | 15 |
| HWFI | 10 | 11 | 12 | 13 | 14 | 14 |
| HMNI | 21 | 4 | 6 | 16 | 15 | 7 |
| GFSI | 1 | 0 | 0 | 7 | 3 | 1 |
| IVCN | 3 | 0 | 0 | 7 | 14 | 8 |
| HCCA | 9 | 5 | 0 | 31 | 29 | 23 |
| OFCL | 14 | 3 | 2 | 35 | 22 | 18 |
| FAR | Atlantic | Eastern Pacific | ||||
| 30 kt/24 h | 55 kt/48 h | 65 kt/72 h | 30 kt/24 h | 55 kt/48 h | 65 kt/72 h | |
| SHIPS | 33 | 0 | 0 | 34 | 43 | 42 |
| LGEM | 17 | 100 | 0 | 23 | 48 | 35 |
| HWFI | 50 | 42 | 75 | 48 | 50 | 41 |
| HMNI | 50 | 85 | 78 | 51 | 21 | 56 |
| GFSI | 0 | 0 | 0 | 45 | 40 | 0 |
| IVCN | 0 | 0 | 0 | 30 | 13 | 25 |
| HCCA | 21 | 0 | 100 | 43 | 40 | 39 |
| OFCL | 32 | 33 | 67 | 31 | 39 | 35 |
| Atlantic Basin | ||||
|---|---|---|---|---|
| Intensity Change (kt) | Interval (h) | N | NRI | Frequency of RI (%) |
| 20 | 12 | 7792 | 385 | 4.9 |
| 25 | 24 | 6775 | 738 | 10.9 |
| 30 | 24 | 6775 | 464 | 6.8 |
| 35 | 24 | 6775 | 262 | 3.9 |
| 40 | 24 | 6775 | 162 | 2.4 |
| 45 | 36 | 5883 | 271 | 4.6 |
| 55 | 48 | 5126 | 239 | 4.7 |
| 65 | 72 | 3917 | 208 | 5.3 |
| EasternPacific Basin | ||||
| Intensity Change (kt) | Interval (h) | N | NRI | Frequency of RI (%) |
| 20 | 12 | 9481 | 602 | 6.3 |
| 25 | 24 | 8414 | 1055 | 12.5 |
| 30 | 24 | 8414 | 723 | 8.6 |
| 35 | 24 | 8414 | 523 | 6.2 |
| 40 | 24 | 8414 | 354 | 4.2 |
| 45 | 36 | 7439 | 495 | 6.7 |
| 55 | 48 | 6542 | 384 | 5.9 |
| 65 | 72 | 4975 | 235 | 4.7 |
| Verification Time (h) | Baseline (kt) | Target (kt) |
|---|---|---|
| 24 | 26.1 | 13.1 |
| 36 | 28.6 | 14.3 |
| 48 | 31.4 | 15.7 |
| 60 | 34.7 | 17.3 |
| 72 | 36.9 | 18.5 |
| 84 | 35.1 | 17.6 |
| 96 | 31.3 | 15.6 |
| 108 | 33.0 | 16.5 |
| 120 | 32.1 | 16.1 |
| Year | Models Used in Consensus |
|---|---|
| 2001 | DSHP, GFDI |
| 2002 | DSHP, GFDI |
| 2003 | DSHP, GFDI |
| 2004 | DSHP, GFDI |
| 2005 | DSHP, GFDI |
| 2006 | DSHP, GHMI |
| 2007 | DSHP, GHMI |
| 2008 | DSHP, LGEM, GHMI, HWFI, GFNI |
| 2009 | DSHP, LGEM, GHMI, HWFI, GFNI |
| 2010 | DSHP, LGEM, GHMI, HWFI, GFNI |
| 2011 | DSHP, LGEM, GHMI, HWFI, GFNI |
| 2012 | DSHP, LGEM, GHMI, HWFI, GFNI |
| 2013 | DSHP, LGEM, GHMI, HWFI |
| 2014 | DSHP, LGEM, GHMI, HWFI |
| 2015 | DSHP, LGEM, GHMI, HWFI |
| 2016 | DSHP, LGEM, GHMI, HWFI, CTCI |
| 2017 | DSHP, LGEM, HWFI, CTCI |
| 2018 | DSHP, LGEM, HWFI, CTCI, HMNI |
| 2019 | DSHP, LGEM, HWFI, CTCI, HMNI |
| 2020 | DSHP, LGEM, HWFI, CTCI, HMNI |
| Verification Time (h) | 2015 Cases (AL/EP/Total) | 2016 Cases (AL/EP/Total) | 2017 Cases (AL/EP/Total) | 2015–2017 Cases (AL/EP/Total) | 2018–2020 Cases (AL/EP/Total) |
|---|---|---|---|---|---|
| 24 | 12/61/73 | 20/38/58 | 45/31/76 | 77/130/207 | 92/125/217 |
| 36 | 11/55/66 | 24/36/60 | 48/35/83 | 83/127/210 | 80/109/189 |
| 48 | 9/46/55 | 24/30/54 | 40/31/71 | 73/108/181 | 78/99/177 |
| 60 | 8/37/45 | 19/23/42 | 28/21/49 | 55/82/137 | 65/67/132 |
| 72 | 8/23/31 | 13/18/31 | 15/15/30 | 36/56/92 | 62/36/98 |
| 84 | 3/16/19 | 16/13/29 | 9/9/18 | 28/38/66 | 59/23/82 |
| 96 | 0/14/14 | 12/6/18 | 7/4/11 | 19/24/43 | 48/9/57 |
| 108 | 0/8/8 | 14/3/17 | 10/4/14 | 24/15/39 | 31/7/38 |
| 120 | 0/5/5 | 16/4/20 | 11/5/16 | 27/14/41 | 29/8/37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
DeMaria, M.; Franklin, J.L.; Onderlinde, M.J.; Kaplan, J. Operational Forecasting of Tropical Cyclone Rapid Intensification at the National Hurricane Center. Atmosphere 2021, 12, 683. https://doi.org/10.3390/atmos12060683
DeMaria M, Franklin JL, Onderlinde MJ, Kaplan J. Operational Forecasting of Tropical Cyclone Rapid Intensification at the National Hurricane Center. Atmosphere. 2021; 12(6):683. https://doi.org/10.3390/atmos12060683
Chicago/Turabian StyleDeMaria, Mark, James L. Franklin, Matthew J. Onderlinde, and John Kaplan. 2021. "Operational Forecasting of Tropical Cyclone Rapid Intensification at the National Hurricane Center" Atmosphere 12, no. 6: 683. https://doi.org/10.3390/atmos12060683
APA StyleDeMaria, M., Franklin, J. L., Onderlinde, M. J., & Kaplan, J. (2021). Operational Forecasting of Tropical Cyclone Rapid Intensification at the National Hurricane Center. Atmosphere, 12(6), 683. https://doi.org/10.3390/atmos12060683






