Abstract
Maintaining a pleasant indoor environment with low energy consumption is important for healthy and comfortable living in buildings. In previous studies, we proposed the integrated comfort control (ICC) algorithm, which integrates several indoor environmental control devices, including an air conditioner, a ventilation system, and a humidifier. The ICC algorithm is operated by simple on/off control to maintain indoor temperature and relative humidity within a defined comfort range. This simple control method can cause inefficient building operation because it does not reflect the changes in indoor–outdoor environmental conditions and the status of the control devices. To overcome this limitation, we suggest the artificial intelligence integrated comfort control (AI2CC) algorithm using a double deep Q-network(DDQN), which uses a data-driven approach to find the optimal control of several environmental control devices to maintain thermal comfort with low energy consumption. The suggested AI2CC showed a good ability to learn how to operate devices optimally to improve indoor thermal comfort while reducing energy consumption. Compared to the previous approach (ICC), the AI2CC reduced energy consumption by 14.8%, increased the comfort ratio by 6.4%, and decreased the time to reach the comfort zone by 54.1 min.
1. Introduction
The energy consumption of buildings has increased steadily over the years. This increase was caused by a growing demand for higher comfort levels with heating, ventilation, and air-conditioning (HVAC) systems, domestic hot water, lighting, refrigeration, food preparation, etc. Various services in buildings, such as those related to health, education, culture, and leisure, also contribute to increased building energy consumption [1].
As most people in developed nations spend more than 90% of their time indoors, indoor comfort has an important role in and a huge impact on protecting occupants’ health, morale, working efficiency, productivity, and satisfaction [2]. This exemplifies the trend of considerably increased interest in thermal comfort over the last 10 years with a global improvement in quality of life. According to American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE), thermal comfort is affected by temperature, humidity, air velocity, and personal factors [3]; thus, it is necessary to maintain appropriate ranges for these factors.
Various environmental devices have been used to improve indoor thermal comfort, including air conditioners, floor heating systems, ventilation systems, and humidifiers. Although an air conditioner can provide indoor temperature control, it cannot guarantee adequate thermal comfort for humans. Operating an air conditioner can lead to low relative humidity conditions due to the dehumidification process [4]. Dry indoor conditions have negative effects on occupants’ health. Yang et al. [5] showed that influenza viruses could be accelerated when the relative humidity is under 50%. Yoshikuni et al. [6] noted that dry indoor conditions can decrease the hydration level and can increase the need for skin moisturizers. Even though relative humidity is an important factor for thermal comfort, it is not easy to maintain adequate levels of temperature and relative humidity at the same time without considering the interrelationships among environmental control devices.
To maintain satisfactory thermal comfort, Kim et al. [7] suggested the integrated comfort control (ICC) algorithm to combine the control of multiple systems, including an air conditioner, a ventilation system, a humidifier, a dehumidifier, and other auxiliary systems. In addition, Kim and Moon [8] developed an advanced integrated comfort control (AICC) to operate the ICC algorithm based on the behavior of occupants (away, active, and inactive) by coupling an occupancy status prediction model. The ICC and AICC algorithms maintain thermal comfort by using a simple on–off control of multiple environmental devices based on upper and lower limit thresholds. This is a rule-based control (RBC) method that has been widely used to operate building environmental systems due to its relatively simple and easy application. The rules in RBC are usually defined with setpoints of upper and/or lower limit thresholds and simple control loops based on the experience of engineers and facility managers in a building. However, this simple control method can cause inefficient building operation due to substantial instability because of the interactions among various environmental control devices being operated simultaneously. It is also very hard to consider changing environmental conditions (e.g., indoor–outdoor temperature, indoor–outdoor relative humidity, and occupant behavior and patterns) [9].
To overcome this limitation, many studies have been conducted on model-based control methods to reflect the thermal dynamics of buildings and to execute a control algorithm based on the simulation model. In recent years, model predictive control (MPC) has become an outstanding alternative to RBC in the academic literature [10].
For example, Aftab et al. [11] developed an automatic HVAC control system utilizing MPC with a real-time occupancy recognition and prediction model implemented in a low-embedded system that could reduce energy consumption while maintaining indoor thermal comfort. The occupancy model was developed to predict the arrival and departure of occupants and utilized precooling and early shut-off of the HVAC system to improve thermal comfort and save energy. As a result, this method could achieve more than 30% in energy savings while maintaining the comfort level. Hu et al. [12] developed an MPC model for floor heating, which considered influential variables, such as weather conditions, occupancy, and dynamic prices at the same time. Compared with simple on–off control, MPC can help reduce peak demand with energy flexibility and cost-cutting. MPC can be applied in ventilation systems. Berouine et al. [13] indicated that the performance of MPC is much better against proportional integral and state feedback controllers in improving both energy conservation and indoor air quality (IAQ). However, the performance of MPC depends highly on the quality of the building simulation model due to the complexity of the thermal dynamics and various influencing factors of buildings [14].
Some model-free approaches have been suggested based on reinforcement learning to overcome the limitations of model-based methods [15]. A general reinforcement learning approach consists of the following factors: state variable s corresponds to the current situation of the environment, action a corresponds to what an agent can do in each state, reward function r(s,a) corresponds to the expected reward if a certain action is chosen, value function V(s) corresponds to the sum of the reward that an agent should expect to receive in the long-term by choosing an action, while in a specific state, and policy represents the way the reinforcement learning agent behaves. Thus, the reinforcement learning approach can offer mapping that represents a situation in which an agent provides states and the actions that can be taken. Judging from the above, the reinforcement learning approach becomes a problem of determining the optimal policy that can provide maximum rewards in the long term.
Q-learning [16] is one of the most popular reinforcement learning techniques. It can be utilized to achieve the expected reward of possible actions without transition probability. Q-learning explains how an agent finds an optimal action to maximize the cumulative reward. Chen et al. [17] showed that Q-learning could provide optimal control decisions for HVAC and window systems to minimize energy consumption while increasing thermal comfort. Baghaee and Ulusoy [18] reported that applying Q-learning for HVAC control was an appropriate method to maintain good IAQ and energy efficiency, i.e., low indoor CO2 concentrations and energy consumption. Fazenda et al. [19] applied a Q-learning model to turn HVAC on and off for heating, illustrating how the heating system can be controlled automatically based on the tenants’ preferences and occupancy patterns. Yang et al. [20] applied Q-learning to increase the efficiency of photovoltaic thermal modules and geothermal heat pumps by tuning the control parameters. The result showed that the Q-learning model outperformed RBC by over 10%.
However, many state and control actions need to be considered for optimal control of individual indoor environmental devices in a building. Additionally, external environmental conditions and numerous internal heat load factors increase the complexity of the building control system, requiring high computing power for updating [21,22].
Thus, the deep Q-network (DQN) was developed to combine reinforcement learning with a class of artificial neural networks known as deep neural networks [23]. By using artificial neural networks, the parametrizing Q-value reduces the required memory storage and computation time. Yu et al. [24] proposed a control algorithm to decrease HVAC energy cost in a commercial building based on a multi-agent deep reinforcement learning (MADRL) algorithm considering occupancy, thermal comfort, and IAQ. Yoon and Moon [21] developed a performance-based thermal comfort control (PTCC) that combines a thermal comfort performance (PMV) prediction model using Gaussian process regression and a DQN to optimize the control systems, i.e., a variable refrigerant flow system (VRF) and a humidifier, instead of using a conventional set temperature method. As a result, PTCC obtained the optimal action-value that minimized energy consumption while satisfying thermal comfort in a cooling season. Nagy et al. [25] applied DQN to an air-source heat pump for space heating. The proposed DQN algorithm showed a 5.5–10% better cost reduction and a 5–6% reduction of energy consumption over a conventional RBC.
In some cases, DQN approaches have overestimated the action value, leading to poorer policies [26,27]. To overcome the optimism in Q-value estimations, van Hasselt et al. [28] suggested the DDQN algorithm, which uses the current Q-network to select the next greedy action, but evaluates the selected action using the target network. The standard DQN utilizes the same values to both select and evaluate actions. This process makes DQN select overestimated values, resulting in over-optimistic estimates. On the contrary, in DDQN, the target network is separated from the current Q-network, and the current Q-network is utilized to select an action; meanwhile, instead of directly selecting the action based on the maximum Q-value, a target network is used to evaluate the target value.
Valladares et al. [29] applied DDQN to air-conditioning units and ventilation fans to improve thermal comfort and air quality while reducing energy consumption. As a result, the proposed DDQN model could maintain a Predictive Mean Vote(PMV) value ranging from about −0.1 to +0.07 and an average CO2 level under 800 ppm within the comfort range. In addition, the DDQN model reduced energy by 4–5% compared to a traditional control system. Zhang et al. [30] proposed an occupant-central control method to improve the thermal comfort of individual occupants and energy efficiency using bio-sensing and the DDQN model. A bio-sensing device was used to measure the occupant’s skin temperature and to integrate their biological response into the building control loop. As a result, the proposed algorithm improved the group thermal satisfaction by 59%. Liu et al. [31] employed DDQN in a home energy management system to minimize energy costs by optimizing the scheduling of home energy appliances. The result showed that the DDQN algorithm reduced the energy cost more effectively than the particle swarm optimization method. Nagarathinam et al. [32] suggested a multi-agent deep reinforcement learning algorithm to optimize HVAC without sacrificing thermal comfort based on DDQN. In this study, the speed of the training process was improved since a multi-agent was trained on a subset of the HVAC system.
In addition to reinforcement learning, various studies have been conducted to improve thermal comfort and build energy performance. Chegari et al. [33] developed a multi-objective optimization method to optimize building design variables based on an artificial neural network coupled with a metaheuristic algorithm. The results showed that annual thermal energy demand was reduced by 74.52% and that thermal comfort was improved by 4.32% compared to the base design. Zhao and Du [34] proposed a multi-objective optimization method using NSGA-II to find the optimal design for window and shading configurations. The building orientation, configuration of windows and shades, window materials, installation angle, and depth of the shading system were considered parameters. Additionally, many studies investigated the control of indoor environmental devices based on occupancy. Yang and Becerik-Gerber [35] demonstrated how occupancy influences the energy efficiency of HVAC systems according to three perspectives: occupancy transitions, variations, and heterogeneity. The result showed that occupancy affected the energy efficiency of the HVAC operation by 3 to 24%. Anand et al. [36] proposed three occupancy-based operational methods for a variable air volume (VAV) system. First, the supply air was optimized to satisfy the minimum ventilation requirement and maintain the indoor temperature under 24 °C for both occupied and unoccupied zones. Second, if unoccupied for more than 60 min but less than a day, the supply air of the unoccupied zone was minimized to maintain the indoor temperature under 28 °C. Third, no ventilation air was supplied to the unoccupied zone. As a result, the three strategies showed energy-saving potential in the ranges of 23–34%, 19–38%, 21–31%, and 24–34% for the classroom, computer room, open office, and closed office, respectively. Anand et al. [37] utilized actual occupancy data consisting of area-based and row-based occupancy counting to investigate the appropriate ventilation rate of a VAV system. The result showed that the actual ventilation rate was higher than the required rate. This demonstrated the energy-saving potential of VAV systems.
In this study, we aimed to improve the existing ICC in artificial intelligence integrated comfort control (AI2CC) by employing the DDQN to reflect real-time changes in indoor–outdoor environmental conditions (i.e., dry-bulb temperature, relative humidity, and enthalpy) and control factors (on/off status, cooling setpoint (°C), and airflow rate (m3/s)) of multiple systems (air conditioner, ventilation system, and humidifier) that affect thermal comfort and energy consumption.
2. Integrated Comfort Control Algorithm
2.1. Thermal Comfort Range
Thermal comfort is affected by various individual factors, such as age, gender, race, fitness, etc. [38,39]. Thus, we limited the thermal comfort range to apply to Koreans 19 to 24 years old. In this study, the thermal comfort range was calculated based on the comfort index, standard effective temperature (SET*). SET* is an advanced, rational model adopted by ASHRAE 55 [40] to represent thermal comfort. The comfort range in summer was determined using experiments on human subjects and measured data. The result showed that Koreans 19 to 24 years old felt comfortable when the SET* was in the range of 25.4 to 27.5 °C and relative humidity was 40 to 55% with light activity [41]. SET* can be converted to dry-bulb temperature based on the experimental relationship between the two [42]. As shown in Figure 1, the thermal comfort range can be defined as 24.4 to 26.5 °C in dry-bulb temperature, along with relative humidity ranging from 40 to 55% [4].
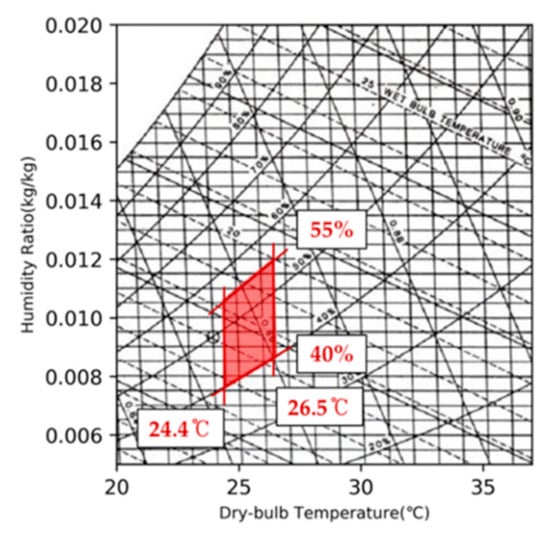
Figure 1.
Comfort range in a cooling season on a psychrometric chart.
2.2. Concept of Integrated Comfort Control
The proposed ICC algorithm integrates multiple environmental control systems, including an air conditioner, a ventilation system, a humidifier, a dehumidifier, and auxiliary systems, to maintain indoor thermal comfort. Figure 2 illustrates the control modes based on the indoor air state, which can be separated into (1) cooling, (2) cooling and humidifying, and (3) humidifying:
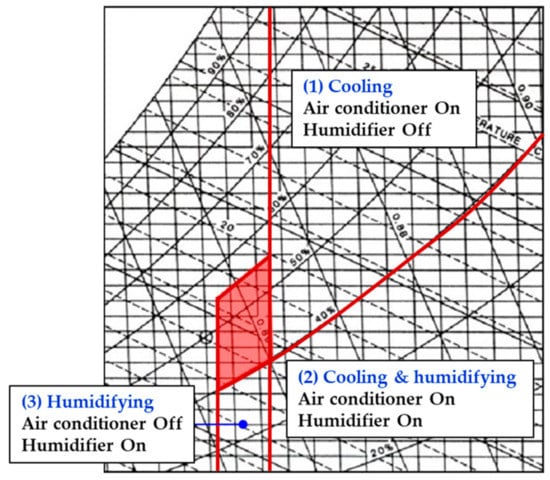
Figure 2.
Control modes based on indoor air initial state.
- (1)
- The cooling zone is where the indoor air temperature is higher than 26.5 °C, and relative humidity is higher than 40%. In this zone, only the air conditioner operates without the humidifier because the state of the indoor air is hot and mild;
- (2)
- The cooling and humidifying zone is where the indoor air temperature is higher than 26.5 °C, and relative humidity is lower than 40%. In this zone, indoor air is hot and dry; hence, both the air conditioner and humidifier can be operated to reach the comfort zone;
- (3)
- The humidifying zone is where the indoor air temperature is between 24 and 26.5 °C, and relative humidity is lower than 40%. Only the humidifier is operated to reach the comfort zone because the indoor air is neutral and dry.
As shown in Figure 3, the first step of the ICC algorithm is to compare indoor and outdoor enthalpy to determine whether the ventilation system is required to operate. It is important because the enthalpy of air contains the sensible and latent heat that determines the cooling load. If indoor enthalpy is higher than outdoor enthalpy, the ventilation system is operated to intake outdoor air. This operation can be helpful to decrease the indoor enthalpy and to reduce the cooling load. In the second step, the operation time of the ventilation system is determined. In the previous study, the operating time was fixed at 10 min because there was no research to determine the optimal operating time of the ventilation system. After the ventilation system operates, the air conditioner and humidifier run based on the indoor air state, as shown in Figure 2 [4].
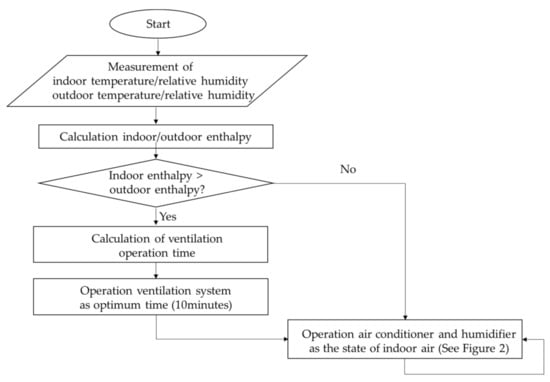
Figure 3.
Flowchart of ICC in the cooling season.
2.3. Limitation of Integrated Comfort Control
The ICC algorithm operates indoor environmental devices based on RBC, including upper and lower limit thresholds (thermal comfort range) and a fixed operating time (10 min for ventilation). This prescriptive control strategy is simple but is not optimal control for two reasons [43]. First, predictive information is not considered to operate indoor environmental devices. For example, if indoor enthalpy is expected to be higher than outdoor enthalpy after 10 min, it is possible to utilize precooling by operating a ventilation system and/or opening windows. However, it is difficult for RBC to employ these predictive controls. The ICC algorithm operates indoor environmental devices without predictive information, such as indoor and outdoor conditions, thermal comfort, and energy consumption. Second, the control sequence is predetermined; thus, it is difficult to customize the control sequence to a specific building and outdoor conditions. The ICC operates the ventilation system for only a specified time (e.g., 10 min) by comparing the initial indoor and outdoor enthalpy. After this, the ventilation system is not operated regardless of the change in indoor and outdoor conditions. To overcome this limitation and to improve the ICC, a DDQN could be employed to develop the AI2CC. The AI2CC reflects factors that affect thermal comfort and energy consumption, such as the environmental conditions (i.e., dry-bulb temperature, relative humidity, and enthalpy) and control factors (on/off status, cooling setpoint (°C), and airflow rate (m3/s)) of multiple devices (air conditioner, ventilation system, and humidifier).
3. Artificial Intelligence Integrated Comfort Control (AI2CC) Using DDQN
3.1. Double Deep Q-Network (DDQN)
Q-learning is a model-free reinforcement learning technique that provides agents with the ability to learn to act optimally in a Markovian domain by experiencing the consequences of actions and rewards [44]. To solve sequential decision problems, reinforcement learning takes on a Markov decision process (MDP), which contains state, action, reward, and discount factors [45]. The state (st) describes the current situation of the environment. In a building environment, states can be defined as indoor–outdoor environmental conditions, such as temperature, humidity, CO2 concentration, illuminance, solar radiance and irradiance, and wind speed, or the status of indoor environmental control devices, such as setpoint, state, and physical time. The action (at) is what an agent can do in each state to try to maximize the future reward. Depending on the action performed by the agent, the next state (st+1) and reward (rt+1) are acquired from the environment. In a building environment, the state (st) can be defined as the status of indoor environmental devices, such as on–off, set point, flow rate, state (e.g., angle and dimming level), and input–output power. The reward is part of the feedback from the environment due to performing a certain action [25,46]. In a building, indoor comfort and the energy consumption of indoor environmental devices are often employed as reward factors, which involves making the indoor condition comfortable with low-energy consumption. The reward function can be described by Equation (1). The agent proceeds with learning to maximize the expected cumulative reward, Gt. The cumulative reward at each time point can be written as Equation (2). In Equation (2), γ ∈ [0, 1] is the discount factor, which is used to penalize the future reward. Figure 4 shows a framework of reinforcement learning:
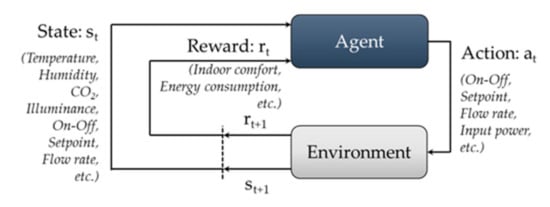
Figure 4.
Reinforcement learning model.
Reinforcement learning utilizes a value function for the agent’s learning to estimate the optimal value. The value function can be divided into two types: state value and action value. The state–value function represents the expected reward the agent will receive from being in a certain state. The action-value function (Q-function) denotes the overall expected rewards for using each action in a certain state. The equations of the state–value and action-value functions can be expressed as (3) and (4) using a form of the Bellman equation:
In Q-learning, the Q-function (4) is used to find the optimal action by updating the Q-function with the maximum reward among the actions in a certain state. The samples for updating Q-learning are state, action, reward, and next state. The updated equation of Q-learning can be written as in (5). In Equation (5), α ∈ [0, 1] is the learning rate to determine the step size at each iteration; this value affects to what extent newly acquired information overrides old information.
Q-learning has limitations in many state–action pairs, such as time-varying continuous states, because it requires high computing power to update [22]. To overcome this limitation, Mnih et al. [23] developed a DQN that combines reinforcement learning with a class of artificial neural networks known as deep neural networks. By using artificial neural networks, the parametrizing Q-value does not require a high-performance computer.
However, reinforcement learning has been shown to be unstable and even diverge when neural networks are used to present Q-values due to correlations between training samples. Small updates to the Q-value cause significant changes to the policy and data distribution. Additionally, the correlation between Q-value and target values causes instability. Thus, two notable components were used in DQN to address these instabilities: target network and experience memory.
- Target Q-network
The DQN utilizes the target Q-network separately from the Q-network. In other words, the DQN employs two networks. The difference between the Q-network and the target Q-network is that they have different parameters: Q-network has θt, and target Q-network has θt−. The Q-network is used to determine the optimal action by adopting the maximum value among parameterized Q-values. The target Q-network with parameter θt− copies the parameter of the Q-network at every C step and is fixed at all other steps.
- Experience memory
The DQN uses experience memory to stack the observed data for a set period. Observed data consist of the agent’s experience (st, at, rt, and st+1) at each time step t. During learning, the experience data are extracted randomly from the memory to update the Q-network. The Q-network is updated to minimize the mean square error with maximum value from the target Q-network by using Equation (6).
However, Q-learning and DQN were found to overestimate the action value, leading to poorer policies [26,27]. This is because the max operator in standard Q-learning and DQN utilizes the same values to select and evaluate actions. To address the optimism in Q-value estimations, van Hasselt et al. [28] proposed the DDQN algorithm. In DDQN, the current Q-network is used to select the next greedy action, and the target network evaluates the selected action. The loss function of DDQN can be described by Equation (7).
3.2. Double Deep Q-Network Training for AI2CC
The existing ICC algorithm has a limitation in satisfying thermal comfort and low-energy consumption effectively due to multiple environmental systems being operated by simple on/off control. The indoor environment is affected by various influencing factors, such as outdoor conditions, the status of indoor environmental systems, occupants’ activities, and many others [47]. However, simple on/off control cannot reflect the complexity of influencing factors [9]. To overcome this limitation, we tried to improve the ICC in AI2CC by employing DDQN.
- State variables
The states are what the agent receives from the environment. These values are used as input for each control step. In this study, 11 states were selected to describe the indoor environment, outdoor environment, and the states of indoor environmental devices. Table 1 presents the information of each state. All environmental state values were simulated in EnergyPlus, and the states of indoor environmental devices are represented by values determined by DDQN as optimal actions in the previous time step. To normalize the state data, min–max normalization is used to convert state values into decimals between 0 and 1.

Table 1.
States for DDQN.
- Control actions
The action is how the DDQN agent controls the environment. In DDQN, the agent is optimized to find the most appropriate action among all possible action combinations. As shown in Table 2, we can select the control action for an air conditioner, a ventilation system, and a humidifier. There are 10 possible actions for the air conditioner, two for the ventilation system, and two for the humidifier. In other words, there were 40 possible actions based on multiplying the number of actions of each device. As with the state variables, min–max normalization is utilized to normalize the control actions to normalize the action data.

Table 2.
Actions for DDQN.
- Reward function
The reward shows evaluating the effect for a certain action in a state. As shown in Equation (8), two reward factors, rtc and rec, are used to consider thermal comfort and energy consumption at the same time:
Equations (9) and (10) represent the rewards for thermal comfort and energy consumption. The reward for thermal comfort (rtc) is provided differently depending on whether indoor temperature and relative humidity are in the comfort zone. If the indoor condition is in the comfort zone, a positive reward of 10 is provided because thermal comfort was achieved. On the contrary, if the indoor environment is not in the comfort zone, a reward of −10 is provided to impose a penalty:
The reward for energy consumption (rec) includes the electrical energy used by the air conditioner, ventilation system, and humidifier. This reward is provided as a penalty in to minimize energy consumption:
4. Implementation of AI2CC
4.1. Simulation Model
In this study, a simulation model was created for the building-integrated control testbed (BICT) at Dankook University in Yongin, Korea. The BICT is an experimental chamber that consists of an air conditioner, a ventilation system, a humidifier, a dehumidifier, automatic blinds, and various sensors to monitor the indoor environment. The exterior of the BICT and environmental control devices are shown in Figure 5. The sizes and building materials of the BICT were modeled in EnergyPlus, along with the system specifications for the air conditioner, ventilation system, and humidifier.
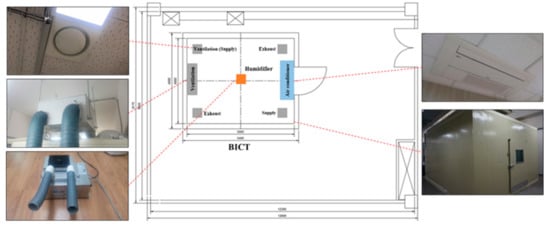
Figure 5.
Floor plan of the BICT and indoor environmental control devices.
Table 3 shows the construction and configuration of the BICT, along with detailed information on the environmental control systems. As explained in [7], we calibrated the EnergyPlus model for the BICT with measured indoor dry-bulb temperature and relative humidity. The simulation results were confirmed to be sufficiently accurate for the system performance and heating/cooling loads in the BICT.

Table 3.
Construction and configuration of BICT.
4.2. Co-Simulation Platform for AI2CC
In this study, the Python module eppy was utilized to connect the control actions for the DDQN algorithm and the EnergyPlus building simulation program [48]. Figure 6 shows a schematic diagram of the co-simulation approach employed in this study. The DDQN was implemented on the Keras library, which is open-source software that provides a Python interface for the TensorFlow library. When the current state values simulated in the EnergyPlus are transferred to Python, the DDQN factors derive the optimal control action that satisfies thermal comfort with low-energy consumption based on the input state. The optimum control action is input to the control variables in association with EnergyPlus, and a simulation is performed to generate the state value of the next state. This process is repeated automatically, enabling optimal control based on environmental data.
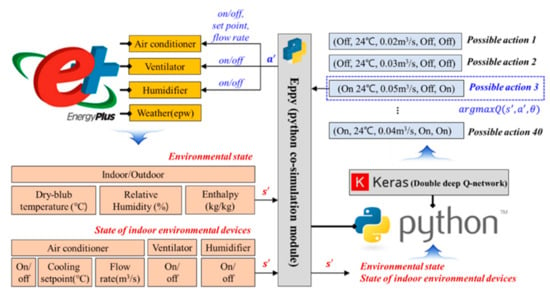
Figure 6.
Co-simulation for AI2CC.
4.3. Training of the AI2CC
The timestep for the EnergyPlus simulation was set to 60 per hour or one minute steps. This means 1440 simulations were performed on EnergyPlus per one day. In this study, EnergyPlus running for one day was regarded as one episode, and 2000 episodes were iterated to explore the optimal DDQN policy. As shown in Table 4, the summer climate in Korea is hot and humid [49]. We selected 8 June in Seoul, Korea, to train the DDQN algorithm on the weather profile. This is because the climate on 8 June showed low enthalpy at dawn and in the evening and high enthalpy in the afternoon; thus, it could effectively show the optimal operation of the AI2CC according to changes in the outdoor environment. Additionally, it was suitable to show the need for a humidifier due to the dehumidification process when operating the air conditioner.

Table 4.
Various climate elements for Korea in the summer season (1981–2010).
In our implementation of the AI2CC, we used the Adam optimizer [50] for gradient-based optimization with a learning rate of 0.25 × 10−3. The minibatch size to train the agents was 32, and the discount factor was γ = 0.99. The target network was updated every 1.44 × 104 at the end of 10 episodes. The activation function for the neural network was rectified linear unit (ReLU) and linear activation on the output layer. There were two hidden layers with 30 neurons determined by the model selection equation [51]. The replay memory size was set to 105 to store the experience of the EnergyPlus simulation. At each timestep of the simulation, the agents’ experience (st, at, rt, and st+1) was stored in replay memory, as shown in Table 5. These experience samples were extracted randomly from the replay memory to update the Q-network.

Table 5.
Components of replay memory.
Figure 7 shows the average Q-value of the AI2CC in each episode during the training process. The Q-value represents the sum of the rewards obtained during one episode. As the episodes progress, the Q-value increases, and the AI2CC learns how to operate the indoor environmental devices optimally. Additionally, the fluctuations in Q-values become stabilized, indicating that the trained AI2CC has learned enough.
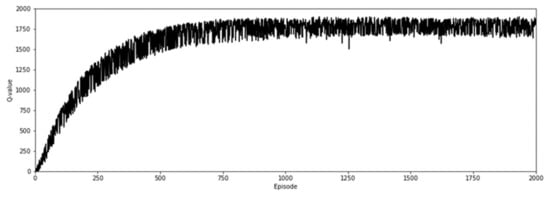
Figure 7.
Convergence of AI2CC.
5. Evaluation of AI2CC
5.1. Case Studies
The proposed AI2CC was evaluated for typical days during the cooling season based on the developed co-simulation platform. The AI2CC algorithm results obtained using the DDQN algorithm were compared to the existing ICC algorithm in terms of energy consumption (kWh), comfort ratio (%), and time to reach the comfort zone (minutes). Total energy consumption is the sum of energy consumption of the air conditioner, ventilation system, and humidifier. The comfort ratio is defined as the ratio of the duration within the comfort zone to the reference time [4]. In this study, the reference time was set to 24 h, which is the setting period of the EnergyPlus simulation. The comfort ratio is described by equation [11]. The time to reach the comfort zone is based on the time from the initial indoor conditions:
As shown in Table 6, case studies were conducted in Seoul, Korea, on 8 June, a day with hot and dry conditions when cooling and humidifying were required. Figure 8 shows the temperature and relative humidity when no devices were operating on 8 June. We selected that day as the simulation case for two reasons: (1) As shown in Figure 8, the outdoor temperature was lower than 26.5 °C, the upper limit of the thermal comfort range from 0 to 764 min and 1090 to 1440 min. In this period, we assumed that the AI2CC would fully utilize the ventilation system to decrease the cooling load by bringing in outdoor air. (2) When no devices operate, indoor relative humidity was around 40%, the lower limit of the thermal comfort range. It can be assumed that indoor relative humidity is kept under 40% when the air conditioner operates. We believed that this outdoor condition shows the efficiency of humidifier operation between the previous ICC and the AI2CC algorithm. To set the internal heat gain, we supposed that one person worked with light activity (a laptop) in the BICT (Table 6).

Table 6.
Simulation conditions.
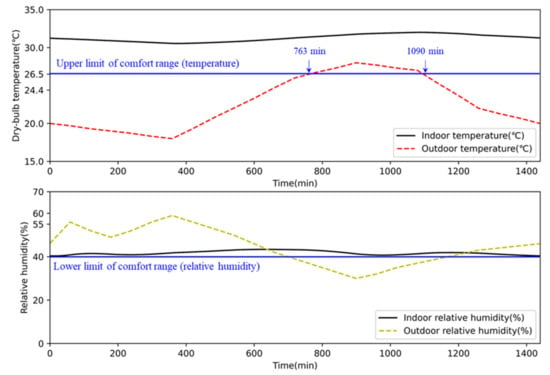
Figure 8.
Temperature and relative humidity during the uncontrolled period (8 June).
5.2. Performance of AI2CC
As shown in Figure 9, Figure 10 and Figure 11, energy consumption with the AI2CC decreased, while the comfort ratio increased as the DDQN learning process went on. In the early stage (1–30 episodes) of DDQN learning, the agent started off acting randomly to generate simulation data to learn the optimal action. Because of the agent’s randomization, in this stage, there were cases where the comfort ratio was too low (episode 7: energy consumption 2.48 kWh, comfort ratio 0.1%) and energy consumption was too high (episode 30: energy consumption 6.01 kWh, comfort ratio: 99.1%).
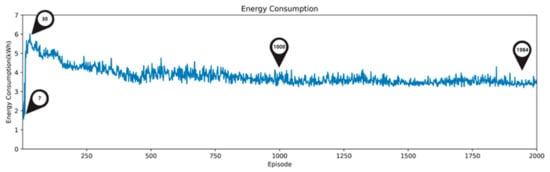
Figure 9.
Energy consumption of AI2CC per episode.
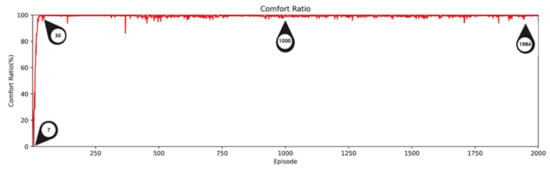
Figure 10.
Comfort ratio of AI2CC per episode.
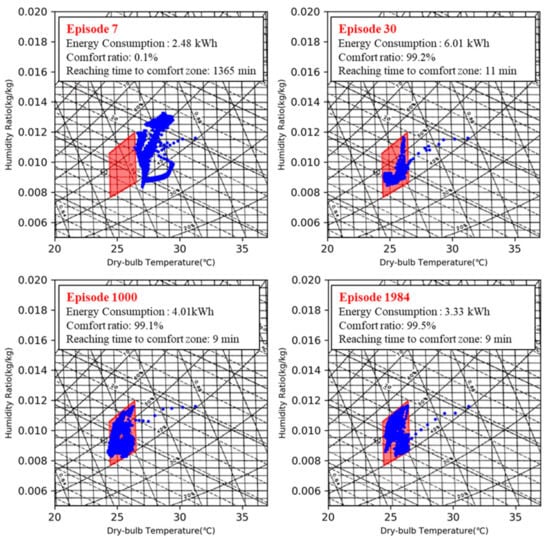
Figure 11.
Indoor status profile of AI2CC per episode.
After 30 episodes, the comfort ratio was mostly 99.0% or more, indicating that DDQN learning for thermal comfort was almost completed. On the contrary, energy consumption decreased slowly and consistently as DDQN learning progressed, as shown in episode 30 (6.01 kWh), episode 1000 (4.01 kWh), and episode 1984 (3.33 kWh) in Figure 9 and Figure 11. This shows that the AI2CC learned how to operate indoor devices optimally to maintain thermal comfort with low energy consumption as learning progressed.
In this study, we evaluated ICC and AI2CC by comparing the algorithms based on energy consumption, comfort ratio, and time to reach the comfort zone (Table 7), and indoor air profile and device states using ICC (Figure 12 and Figure 13) and AI2CC (Figure 14 and Figure 15). Table 7 expresses the performance of the AI2CC as the average value of the last 50 episodes in DDQN learning. Figure 14 and Figure 15 show the indoor air profile according to the operation of each device of the AI2CC in episode 1984 in the DDQN learning process.

Table 7.
Comparison of ICC and AI2CC.
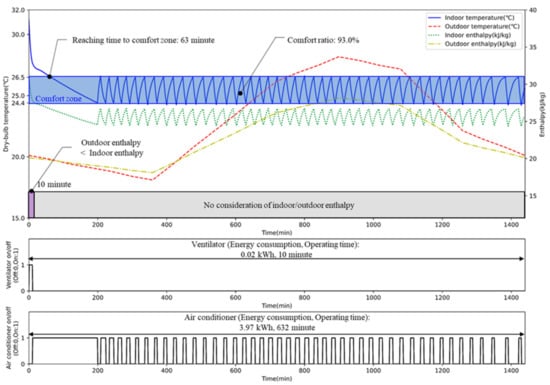
Figure 12.
Indoor temperature and device states using ICC.
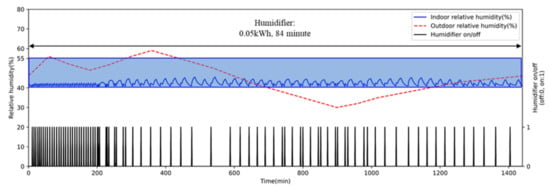
Figure 13.
Indoor relative humidity and humidifier state using ICC.
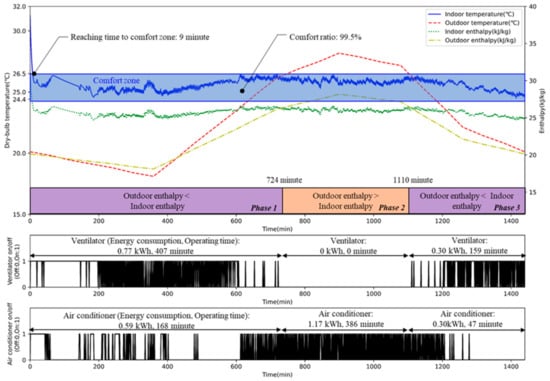
Figure 14.
Indoor temperature and device states using AI2CC (episode 1984).
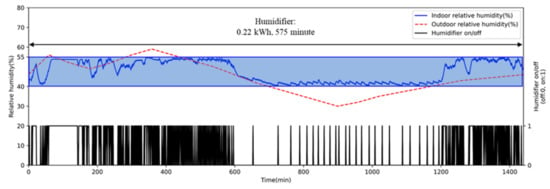
Figure 15.
Indoor relative humidity and humidifier state using AI2CC (episode 1984).
- Energy Consumption
As shown in Table 7, the total energy consumption of the AI2CC was 3.44 kWh, which is 14.8% lower than the energy required by the ICC algorithm (4.04 kWh). Although there was additional energy consumption owing to the operation of the ventilation system and the humidifier in AI2CC compared to ICC, this increase was offset by the decrease in energy consumption by the air conditioner.
To be specific, in terms of the ventilation system, ICC operated the ventilation system for only 10 min, consuming 0.02 kWh before the air conditioner began running (see Figure 12). This operation aimed at reducing the cooling load by exchanging high-enthalpy indoor air and low-enthalpy outdoor air, as mentioned in Section 3.2. With AI2CC, the ventilation system used 1.15 kWh for one day (1440 min), showing different on–off statuses depending on the indoor and outdoor enthalpy variations. As shown in Figure 14, we divided one day into three phases according to the indoor and outdoor enthalpy to explain the operation of AI2CC. For phases 1 and 3 with higher indoor than outdoor enthalpy, AI2CC mainly operated the ventilation system for 407 min out of 724 min (phase 1) and 159 min out of 330 min (phase 3). When outdoor enthalpy was lower than indoor enthalpy, AI2CC utilized the ventilation system to bring cool air from the outside to reduce the cooling load. On the contrary, there was no ventilation system operation in phase 2, when outdoor enthalpy was higher than indoor (see Figure 14). This shows that AI2CC learned the availability of operating the ventilation system according to indoor and outdoor enthalpy to reduce total energy consumption.
Concerning the operation of the humidifier, ICC turned it on and off repeatedly at a relative humidity of around 40%. Thus, indoor relative humidity was maintained at around 40%, consuming 0.05 kWh of electricity (see Figure 13). On the contrary, the indoor relative humidity of AI2CC was well maintained between 40 and 60%, indicating a relatively wider distribution than ICC (see Figure 15). This caused AI2CC to use more energy consumption for the humidifier than ICC.
Concerning the air conditioner, the AI2CC algorithm consumed 2.08 kWh of electric energy, which is 47.6% lower than the energy required by the ICC algorithm (3.97 kWh; see Table 7). There was no significant difference in operating time between ICC (632 min) and AICC (601 min). However, there was a significant difference in energy consumption of the air conditioner due to the different cooling loads. Figure 16 shows the average cooling load of AI2CC (187.9 W), a decrease of 53.0% compared to ICC (399.6 W). AI2CC reduced the cooling load by using the ventilation system to bring in low-enthalpy outside air when possible.
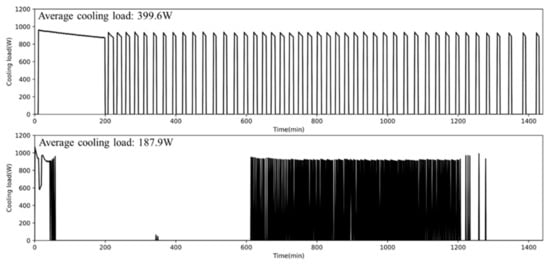
Figure 16.
Cooling load of an air conditioner (upper: ICC, lower: AI2CC).
- Thermal comfort
Table 7 shows that the room with AI2CC reached the comfort zone 54.1 min faster than the one with ICC. Additionally, the comfort ratio of AICC was 99.4%, which was 6.4% higher compared to ICC. As shown in Figure 12, ICC operated the ventilation system and air conditioner separately based on the specified sequence. This rule-based control of ICC caused inefficient control by operating the ventilation system for only 10 min even though the room could reach the comfort zone faster by using the ventilation system and air conditioner at the same time. According to Figure 14, AI2CC showed a different method from ICC by operating the air conditioner and ventilation system simultaneously to take in low-enthalpy outdoor air. This operation decreased the time to reach the comfort zone and helped increase the comfort ratio.
6. Discussion
The results show that AI2CC performed better than ICC in terms of energy consumption and thermal comfort. Compared with the previous ICC, AI2CC reflected the indoor– outdoor conditions and indoor environmental device control factors by employing DDQN.
Other studies have demonstrated that reinforcement learning could be applied to HVAC systems [24], heat pumps [25], windows [52], water heaters [53], and lighting systems [54]. These studies showed good energy savings and improved indoor comfort. However, they dealt with only individual systems, representing a limited situation in built environments [55]. In this paper, the suggested AI2CC showed improved optimal control for maintaining good thermal comfort by operating various indoor environmental control devices simultaneously, whenever possible.
However, this study had the following limitations:
- Our previous study proposed AICC algorithm, which combines ICC with an occupancy detection model to change the thermal comfort range according to occupancy status [8]. However, in this paper, for AI2CC, the occupancy activity was fixed as light work at a desk. Thus, we could not reflect the dynamic thermal comfort range, which changes continuously according to occupancy status.
- In this study, we adopted thermal comfort to evaluate indoor comfort conditions. However, comfort conditions are affected by thermal comfort and indoor air quality and visual comfort [56]. A more sophisticated and integrated indoor comfort index could be studied and machine learning techniques in built environments.
In future research, we will further our study as follows:
- Vary the thermal comfort range according to occupancy status [39]. To satisfy the thermal comfort needs for various activities, we will combine the occupancy status detection algorithm with the AI2CC to apply an appropriate comfort range based on occupancy status (e.g., working, sleeping, resting, or exercising).
- In a building, reinforcement learning could improve indoor comfort, such as thermal comfort, air quality, light requirement, and noise [57]. In addition to thermal comfort, IAQ (e.g., CO2 and particulate matter) and visual comfort (e.g., illuminance and glare) will be added to the evaluation factors of indoor comfort conditions. Other devices may be included in the control to satisfy these factors, such as air purifiers, kitchen hood, and blinds.
In conclusion, applying AI2CC could lead to a more effective and improved control approach in buildings.
7. Conclusions
In this study, we suggest AI2CC by employing DDQN to reflect real-time changes in indoor–outdoor conditions and indoor environmental device control factors that affect thermal comfort and energy consumption. AI2CC integrates various environmental control devices, such as an air conditioner, a ventilation system, and a humidifier. At the early stage of DDQN learning, AI2CC showed high energy consumption and a low comfort ratio because agents acted randomly to learn optimal actions. However, as DDQN learning progressed, AI2CC learned how to operate indoor devices optimally to improve indoor thermal comfort while reducing total energy consumption. The suggested AI2CC was compared with the previous ICC algorithm in terms of energy performance, thermal comfort, and time to reach the comfort zone.
AI2CC reduced total energy consumption by 14.8% compared to ICC. More specifically, AI2CC consumed more energy by operating the ventilation system compared to the ICC algorithm. However, the operation of the ventilation system could bring in more low-enthalpy outdoor air, which led to reduced energy consumption by the air conditioner. In the air conditioner operation, the AI2CC algorithm consumed 47.6% less energy than the ICC algorithm. AI2CC consumed slightly more energy for the humidifier, but this increase was offset by the decreased energy consumption of the air conditioner. Concerning thermal comfort, the comfort ratio of AI2CC was 6.4% higher than that of ICC. This is because AI2CC operated the air conditioner and ventilation system together to take in low-enthalpy outdoor air. This operation decreased the time to reach the comfort zone by 54.1 min compared to ICC. Compared to the ICC algorithm, the superiority of the AI2CC algorithm was validated. Using AI2CC, indoor environmental control devices were operated based on the changing indoor–outdoor environmental conditions. ICC operated the ventilation system for only 10 min when the outdoor enthalpy was lower than the indoor enthalpy at the early stage of the algorithm. ICC operated indoor environmental devices by simple on/off without considering the indoor–outdoor environmental conditions. On the other hand, AI2CC operated the indoor environmental devices differently depending on indoor–outdoor environmental conditions. To be specific, AI2CC utilized the ventilation system actively when it was judged to be advantageous for energy consumption and thermal comfort. Due to the operation of the ventilation system, the energy consumption of the air conditioner decreased, which led to a reduction in overall energy consumption. Additionally, the comfort ratio and time to reach the comfort zone were improved.
Author Contributions
Data curation, S.-H.K.; Formal analysis, S.-H.K.; Investigation, S.-H.K.; Methodology, Y.-R.Y. and J.-W.K.; Visualization, S.-H.K.; Writing—original draft, S.-H.K. and H.-J.M.; Writing—review & editing, H.-J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (no. 2021R1A2B5B02002699).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008. [Google Scholar] [CrossRef]
- Shaikh, P.H.; Nor, N.B.M.; Nallagownden, P.; Elamvazuthi, I. Building energy management through a distributed fuzzy inference system. Int. J. Eng. Technol. 2013, 5, 3236–3242. [Google Scholar]
- ASHRAE. Thermal Environmental Conditions for Human Occupancy; ANSI/ASHRAE Standard 55-2004; American Society of Heating, Refrigerating and Air Conditioning Engineers, Inc.: Atlanta, GA, USA, 2004. [Google Scholar]
- Moon, H.J.; Yang, S.H. Evaluation of the energy performance and thermal comfort of an air conditioner with temperature and humidity controls in a cooling season. HVAC R Res. 2014. [Google Scholar] [CrossRef]
- Yang, W.; Elankumaran, S.; Marr, L.C. Relationship between Humidity and Influenza A Viability in Droplets and Implications for Influenza’s Seasonality. PLoS ONE 2012, 7, e46789. [Google Scholar] [CrossRef]
- Yoshikuni, K.; Tagami, H.; Inoue, K.; Yamada, M. Evaluation of the influence of ambient temperature and humidity on the hydration level of the stratum corneum. Nippon Hifuka Gakkai Zasshi. Jpn. J. Dermatol. 1985. [Google Scholar] [CrossRef]
- Kim, J.W.; Yang, W.; Moon, H.J. An integrated comfort control with cooling, ventilation, and humidification systems for thermal comfort and low energy consumption. Sci. Technol. Built Environ. 2017, 23, 264–276. [Google Scholar] [CrossRef]
- Kim, S.H.; Moon, H.J. Case study of an advanced integrated comfort control algorithm with cooling, ventilation, and humidification systems based on occupancy status. Build. Environ. 2018, 133, 246–264. [Google Scholar] [CrossRef]
- Shaikh, P.H.; Nor, N.B.M.; Nallagownden, P.; Elamvazuthi, I.; Ibrahim, T. A review on optimized control systems for building energy and comfort management of smart sustainable buildings. Renew. Sustain. Energy Rev. 2014, 34, 409–429. [Google Scholar] [CrossRef]
- Serale, G.; Fiorentini, M.; Capozzoli, A.; Bernardini, D.; Bemporad, A. Model Predictive Control (MPC) for enhancing building and HVAC system energy efficiency: Problem formulation, applications and opportunities. Energies 2018, 11, 631. [Google Scholar] [CrossRef]
- Aftab, M.; Chen, C.; Chau, C.K.; Rahwan, T. Automatic HVAC control with real-time occupancy recognition and simulation-guided model predictive control in low-cost embedded system. Energy Build. 2017, 154, 141–156. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F.; Jørgensen, J.B.; Li, R. Price-responsive model predictive control of floor heating systems for demand response using building thermal mass. Appl. Therm. Eng. 2019, 153, 316–329. [Google Scholar] [CrossRef]
- Berouinev, A.; Ouladsine, R.; Bakhouya, M.; Lachhab, F.; Essaaidi, M. A Model Predictive Approach for Ventilation System Control in Energy Efficient Buildings. In Proceedings of the 2019 4th World Conference on Complex Systems (WCCS), Ouarzazate, Morocco, 22–25 April 2019; pp. 9–14. [Google Scholar] [CrossRef]
- Wei, T.; Wang, Y.; Zhu, Q. Deep Reinforcement Learning for Building HVAC Control. Proc. Des. Autom. Conf. 2017, 2017. [Google Scholar] [CrossRef]
- Li, B.; Xia, L. A multi-grid reinforcement learning method for energy conservation and comfort of HVAC in buildings. IEEE Int. Conf. Autom. Sci. Eng. 2015, 2015, 444–449. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H. Learning from Delayed Rewards; University of Cambridge: Cambridge, UK, 1989. [Google Scholar]
- Chen, Y.; Norford, L.K.; Samuelson, H.W.; Malkawi, A. Optimal control of HVAC and window systems for natural ventilation through reinforcement learning. Energy Build. 2018, 169, 195–205. [Google Scholar] [CrossRef]
- Baghaee, S.; Ulusoy, I. User comfort and energy efficiency in HVAC systems by Q-learning. In Proceedings of the 26th IEEE Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Fazenda, P.; Veeramachaneni, K.; Lima, P.; O’Reilly, U.M. Using reinforcement learning to optimize occupant comfort and energy usage in HVAC systems. J. Ambient Intell. Smart Environ. 2014, 6, 675–690. [Google Scholar] [CrossRef]
- Yang, L.; Nagy, Z.; Goffin, P.; Schlueter, A. Reinforcement learning for optimal control of low exergy buildings. Appl. Energy 2015. [Google Scholar] [CrossRef]
- Yoon, Y.R.; Moon, H.J. Performance based thermal comfort control (PTCC) using deep reinforcement learning for space cooling. Energy Build. 2019, 203. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Kling, W.L.; Gibescu, M. Unsupervised energy prediction in a Smart Grid context using reinforcement cross-building transfer learning. Energy Build. 2016, 116, 646–655. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Yu, L.; Sun, Y.; Xu, Z.; Shen, C.; Yue, D.; Jiang, T.; Guan, X. Multi-Agent Deep Reinforcement Learning for HVAC Control in Commercial Buildings. IEEE Trans. Smart Grid 2021, 12, 407–419. [Google Scholar] [CrossRef]
- Nagy, A.; Kazmi, H.; Cheaib, F.; Driesen, J. Deep reinforcement learning for optimal control of space heating. arXiv 2018, arXiv:1805.03777. [Google Scholar]
- Thrun, S.; Schwartz, A. Issues in Using Function Approximation for Reinforcement Learning. In Proceedings of the Connectionist Models Summer School, Hillsdale, NJ, USA, 21 June–3 July 1993; pp. 1–9. [Google Scholar]
- van Hasselt, H. Insights in Reinforcement Learning: Formal Analysis and Empirical Evaluation of Temporal-Difference Learning Algorithms. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2011. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-Learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI-16), Phoenix, AZ, USA, 12–17 February 2016; pp. 2094–2100. [Google Scholar]
- Valladares, W.; Galindo, M.; Gutiérrez, J.; Wu, W.C.; Liao, K.K.; Liao, J.C.; Lu, K.C.; Wang, C.C. Energy optimization associated with thermal comfort and indoor air control via a deep reinforcement learning algorithm. Build. Environ. 2019, 155, 105–117. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Z.; Loftness, V. Bio-sensing and reinforcement learning approaches for occupant-centric control. ASHRAE Trans. 2019, 125, 364–371. [Google Scholar]
- Liu, Y.; Zhang, D.; Gooi, H.B. Optimization strategy based on deep reinforcement learning for home energy management. CSEE J. Power Energy Syst. 2020, 6, 572–582. [Google Scholar] [CrossRef]
- Nagarathinam, S.; Menon, V.; Vasan, A.; Sivasubramaniam, A. MARCO—Multi-Agent Reinforcement learning based COntrol of building HVAC systems. In Proceedings of the Eleventh ACM International Conference on Future Energy Systems, Melbourne, Australia, 22–26 June 2020; ACM: New York, NY, USA, 2020; pp. 57–67. [Google Scholar]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. Multi-objective optimization of building energy performance and indoor thermal comfort by combining artificial neural networks and metaheuristic algorithms. Energy Build. 2021, 239. [Google Scholar] [CrossRef]
- Zhao, J.; Du, Y. Multi-objective optimization design for windows and shading configuration considering energy consumption and thermal comfort: A case study for office building in different climatic regions of China. Sol. Energy 2020, 206, 997–1017. [Google Scholar] [CrossRef]
- Yang, Z.; Becerik-Gerber, B. How does building occupancy influence energy efficiency of HVAC systems? Energy Procedia 2016, 88, 775–780. [Google Scholar] [CrossRef]
- Anand, P.; Sekhar, C.; Cheong, D.; Santamouris, M.; Kondepudi, S. Occupancy-based zone-level VAV system control implications on thermal comfort, ventilation, indoor air quality and building energy efficiency. Energy Build. 2019, 204. [Google Scholar] [CrossRef]
- Anand, P.; Cheong, D.; Sekhar, C. Computation of zone-level ventilation requirement based on actual occupancy, plug and lighting load information. Indoor Built Environ. 2020, 29, 558–574. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; de Dear, R.; Luo, M.; Lin, B.; He, Y.; Ghahramani, A. Individual difference in thermal comfort: A literature review Individual di ff erence in thermal comfort : A literature review. Build. Environ. 2018, 138, 181–193. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Z.; Ke, K.; Cao, B.; Zhai, Y.; Zhou, X. Human metabolic rate and thermal comfort in buildings: The problem and challenge. Build. Environ. 2018, 131, 44–52. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, Z. Standard effective temperature based adaptive-rational thermal comfort model. Appl. Energy 2020, 264, 114723. [Google Scholar] [CrossRef]
- Kum, J.S.; Kim, D.K.; Choi, K.H.; Kim, J.R.; Lee, K.H.; Choi, H.S. Experimental study on thermal comfort sensation of Korean (Part II: Analysis of subjective judgement in summer experiment). Korean J. Sci. Emot. Sensib. 1998, 1, 65–73. [Google Scholar]
- Bae, G.N.; Lee, C. Evaluation of Korean Thermal Sensation in Office Buildings During the Summer Season. Korean J. Air Cond. Refrig. Eng. 1995, 7, 341–352. [Google Scholar]
- Wang, Z.; Hong, T. Reinforcement learning for building controls: The opportunities and challenges. Appl. Energy 2020, 269. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.P. Dayan Q-Learning. Mach. Learn. 1992, 292, 279–292. [Google Scholar] [CrossRef]
- Givan, B.; Parr, R. An Introduction to Markov Decision Processes. Available online: http://faculty.kfupm.edu.sa/coe/ashraf/RichFilesTeaching/COE101_540/Projects/givan1.pdf (accessed on 9 April 2021).
- Claessens, B.J.; Vanhoudt, D.; Desmedt, J.; Ruelens, F. Model-free control of thermostatically controlled loads connected to a district heating network. Energy Build. 2017, 159, 1–10. [Google Scholar] [CrossRef]
- Frontczak, M.; Wargocki, P. Literature survey on how different factors influence human comfort in indoor environments. Build. Environ. 2011, 46, 922–937. [Google Scholar] [CrossRef]
- Philip, S. Eppy Documentation; Github Repository. 2019. Available online: https://pypi.org/project/eppy/ (accessed on 9 April 2021).
- Korea Metorrological Administration. Korea Cimate Change Report; Korea Metorrological Administration: Seoul, Korea, 2013.
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Paola, J. Neural Network Classification of Multispectral Imagery. Master’s Thesis, The University of Arizona, Tucson, AZ, USA, 1994. [Google Scholar]
- May, R. The Reinforcement Learning Method: A Feasible and Sustainable Control Strategy for Efficient Occupant-Centred Building Operation in Smart Cities. Ph.D. Thesis, Dalarna University, Falun, Sweden, 2019. [Google Scholar]
- Ruelens, F.; Claessens, B.J.; Quaiyum, S.; De Schutter, B.; Babuška, R.; Belmans, R. Reinforcement Learning Applied to an Electric Water Heater: From Theory to Practice. IEEE Trans. Smart Grid 2018, 9, 3792–3800. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhao, Q.; Wang, F.; Jiang, Y.; Xia, L.; Ding, J. Satisfaction based Q-learning for integrated lighting and blind control. Energy Build. 2016, 127, 43–55. [Google Scholar] [CrossRef]
- Pargfrieder, J.; Jörgl, H.P. An integrated control system for optimizing the energy consumption and user comfort in buildings. In Proceedings of the 2002 IEEE Symposium on Computer-Aided Control System Design, Glasgow, UK, 20–20 September 2002; pp. 127–132. [Google Scholar] [CrossRef]
- Profile, S.E.E. Thermal comfort and indoor air quality. Green Energy Technol. 2012, 84, 1–13. [Google Scholar] [CrossRef]
- Dalamagkidis, K.; Kolokots, D. Reinforcement Learning for Building Environmental Control. Reinf. Learn. 2008. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).